2-Rainbow domination number of Cartesian products: $C_{n}\square C_{3}$ and $C_{n}\square C_{5}$

Abstract

A function $f:V(G)\rightarrow \mathcal P (\{1,\ldots ,k\})$ is called a $k$-rainbow dominating function of $G$ (for short $kRDF$ of $G)$ if $\bigcup \nolimits _{u\in N(v)}f(u)=\{1,\ldots ,k\},$ for each vertex $v\in V(G)$ with $f(v)=\varnothing .$ By $w(f)$ we mean $\sum _{v\in V(G)}\left|f(v)\right|$ and we call it the weight of $f$ in $G.$ The minimum weight of a $kRDF$ of $G$ is called the $k$-rainbow domination number of $G$ and it is denoted by $\gamma _{rk}(G).$ We investigate the $2$-rainbow domination number of Cartesian products of cycles. We give the exact value of the $2$-rainbow domination number of $C_{n}\square C_{3}$ and we give the estimation of this number with respect to $C_{n}\square C_{5},$ $(n\ge 3).$ Additionally, for $n=3,4,5,6,$ we show that $\gamma _{r2}(C_{n}\square C_{5})=2n.$

1 Introduction

For notation and graph theory terminology not given here, we follow Diestel (1997) and also Haynes et al. (1998). Let $G=(V(G),E(G))$ be a finite, simple and undirected graph with vertex set $V(G)$ and edge set $E(G).$ The open neighborhood of a vertex $v$ is $N(v)=\{u\in V(G):uv\in E(G)\}$ and the closed neighborhood of $v$ is $N[v]=\{v\}\cup N(v).$ For two subsets $A,B$ of $V(G),$ $E(A,B)=\{ab\in E(G):a\in A,b\in B\}.$

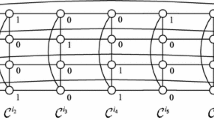
The Cartesian product $G\square H$ of graphs $G$ and $H$ is the graph with vertex set $V(G)\times V(H),$ where two vertices are adjacent if and only if they are equal in one coordinate and adjacent in the other. We restrict our attention to the Cartesian product of $C_{n}$ and $C_{m},$ $n,m\ge 3.$ Let $V(C_{n})=\{1,2,\ldots ,n\},$ $E(C_{n})= \{i(i+1),1n:i=1,2,\ldots ,n-1\}$ and $V(C_{m})=\{1,2,\ldots ,m\},$ $E(C_{m})=\{j(j+1),1m:j=1,2,\ldots ,m-1\}.$ Let $(i,j)$ be a vertex of $C_{n}\square C_{m}$—instead of $(i,j)$ we write $v_{ij}.$ By $\mathcal C ^{i}=\{v_{i1},v_{i2},\ldots ,v_{im}\}$ we mean the $i$th column of $C_{n}\square C_{m}.$

A function $f:V(G)\rightarrow \mathcal P(\{ 1,\ldots ,k\})$ is called a $k$-rainbow dominating function of $G$ (for short $kRDF$ of $G),$ if $\bigcup \nolimits _{u\in N(v)}f(u)=\{1,\ldots ,k\}$ for each vertex $v\in V(G)$ with $f(v)=\varnothing .$ By $w(f)$ we mean $\sum _{v\in V(G)}\left|f(v)\right|$ and we call it the weight of a function $f$ in $G.$ The minimum weight of a $kRDF$ of $G$ is called the $k$-rainbow domination number of $G$ and it is denoted by $\gamma _{rk}(G).$ If $f$ is a $2RDF$ function of $G$ and $w(f)=\gamma _{r2}(G),$ then $f$ is called a $\gamma _{r2}$-function. Let $X\subset V(G).$ By $w(f(X))$ we mean $\sum _{v\in X}\left|f(v)\right|.$ Thus $w(f)=w(f(V(G)).$ For more information about rainbow domination we refer the reader to Brešar and Šumenjak (2007), Chunling et al. (2009), Wu and Rad (2010), Xu (2009).

The concept of rainbow domination seems to be of independent interest and it attracted several authors. In particular, Hartnell and Rall (2004) obtained a couple of observations about rainbow domination, for instance, $\gamma _{rk}(G)\le k\gamma (G),$ where $\gamma (G)$ is the domination number of $G.$ Moreover, the concept of 2-rainbow domination of a graph $G$ coincides with the ordinary domination of the prism $G\square K_{2}$ (Brešar et al. 2008). Since for any graph $H,$ $\gamma (H)\ge \left|V(H)\right|/(\Delta (H)+1)$ we have $\gamma _{r2}(G)=\gamma (G\square K_{2})\ge 2|V(G)|/\left( \Delta (G)+2\right).$ As a consequence, we have

$$\begin{aligned} \frac{nm}{3}\le \gamma _{r2}(C_{n}\square C_{m})\le 2\gamma (C_{n}\square C_{m}). \end{aligned}$$

(1)

In this paper, we show that these bounds are attained for some classes of cycles.

For a $2RDF$ of $C_{n}\square C_{m},$ instead of $f(v_{ij})=\varnothing , f(v_{ij})=\{1\}, f(v_{ij})=\{2\},$ we simply write $f(v_{ij})=0, f(v_{ij})=1$ or $f(v_{ij})=2,$ respectively.

Further, instead of, for example,

$$\begin{aligned} f\left(\begin{array}{l@{\quad }l@{\quad }l@{\quad }l} v_{13}&v_{23}&\ldots&v_{n3} \\ v_{12}&v_{22}&\ldots&v_{n2} \\ v_{11}&v_{21}&\ldots&v_{n1} \end{array}\right)=\left( \begin{array}{l@{\quad }l@{\quad }l@{\quad }l} 0&0&\ldots&2 \\ 0&2&\ldots&0 \\ 1&0&\ldots&0 \end{array}\right), \end{aligned}$$

we simply write

$$\begin{aligned} f(V(C_{n}\square C_{3}))=\left(\begin{array}{l@{\quad }l@{\quad }l@{\quad }l} 0&0&\ldots&2 \\ 0&2&\ldots&0 \\ 1&0&\ldots&0 \end{array}\right). \end{aligned}$$

It is clear from the context that (in our example) $f(v_{11})=1, f(v_{12})=0, f(v_{13})=0\$ and so on.

2 2-Rainbow domination number of $C_{n}\square C_{3}$

Lemma 1

For $n\ge 3,$

$$\begin{aligned} n\le \gamma _{r2}(C_{n}\square C_{3})\le \left\{ \begin{array}{ll} n,&if n\equiv 0 \mod 6, \\ n+1,&if n\equiv 1,2,3,5 \mod 6, \\ n+2,&if n\equiv 4 \mod 6. \end{array}\right. \end{aligned}$$

Proof

The lower bound follows from (1) for $m=3.$ To show the upper bound we define the functions $f$ as follows:

For $l\ge 1,$

$$\begin{aligned} f(V(C_{6l}\square C_{3}))&= \left( \begin{array}{l@{\quad }l@{\quad }l@{\quad }l@{\quad }l@{\quad }l|l} 0&0&1&0&0&2&\\ 0&2&0&0&1&0&- \\ 1&0&0&2&0&0&\end{array}\right);\\ f(V(C_{6l+1}\square C_{3}))&= \left( \begin{array}{l@{\quad }l@{\quad }l@{\quad }l@{\quad }l@{\quad }l@{\quad }l|l@{\quad }l@{\quad }l@{\quad }l@{\quad }l@{\quad }l|l} 0&0&1&1&0&0&2&0&0&1&0&0&2&\\ 0&2&2&0&0&1&0&0&2&0&0&1&0&- \\ 1&0&0&0&2&0&0&1&0&0&2&0&0&\end{array}\right);\\ f(V\left( C_{6l+2}\square C_{3}\right) )&= \left( \begin{array}{l@{\quad }l|l@{\quad }l@{\quad }l@{\quad }l@{\quad }l@{\quad }l|l} 0&2&0&0&1&0&0&2&\\ 1&0&0&2&0&0&1&0&- \\ 1&0&1&0&0&2&0&0&\end{array}\right). \end{aligned}$$

For $l\ge 0,$

$$\begin{aligned} f(V\left( C_{6l+3}\square C_{3}\right) )&= \left( \begin{array}{l@{\quad }l@{\quad }l|l@{\quad }l@{\quad }l@{\quad }l@{\quad }l@{\quad }l|l} 0&0&2&0&0&1&0&0&2&\\ 0&\{1,2\}&0&0&2&0&0&1&0&- \\ 1&0&0&1&0&0&2&0&0&\end{array}\right) ;\\ f(V(C_{6l+4}\square C_{3}))&= \left( \begin{array}{l@{\quad }l@{\quad }l@{\quad }l|l@{\quad }l@{\quad }l@{\quad }l@{\quad }l@{\quad }l|l} 0&2&0&2&0&0&1&0&0&2&\\ 0&2&1&0&0&2&0&0&1&0&- \\ 1&0&0&2&1&0&0&2&0&0&\end{array}\right) ;\\ f(V\left( C_{6l+5}\square C_{3}\right) )&= \left( \begin{array}{l@{\quad }l@{\quad }l@{\quad }l@{\quad }l|l@{\quad }l@{\quad }l@{\quad }l@{\quad }l@{\quad }l|l} 0&0&1&0&2&0&0&1&0&0&2&\\ 0&2&0&0&1&0&2&0&0&1&0&- \\ 1&0&0&2&0&1&0&0&2&0&0&\end{array}\right) ; \end{aligned}$$

where “$-$” means that we repeat the block

$$\begin{aligned} \begin{array}{|l@{\quad }l@{\quad }l@{\quad }l@{\quad }l@{\quad }l} 0&0&1&0&0&2 \\ 0&2&0&0&1&0 \\ 1&0&0&2&0&0 \end{array} \end{aligned}$$

at most $l-1$ times. It is not difficult to observe that $f$ is a 2RDF of $C_{n}\square C_{3}$ and

$$\begin{aligned} w(f)=\left\{ \begin{array}{l@{\quad }l} n,&if n\equiv 0 \mod 6, \\ n+1,&if n\equiv 1,2,3,5 \mod 6, \\ n+2,&if n\equiv 4 \mod 6, \end{array}\right. \end{aligned}$$

proving the result.$\square$

To show that $w(f)$ in Lemma 1 equals the 2-rainbow domination number of $C_{n}\square C_{3}$ we use the concept introduced in Chunling et al. (2009).

Let $f$ be any $2RDF$ of $C_{n}\square C_{m}$ and let

$$\begin{aligned} V_{0}&= \{v\in C_{n}\square C_{m}:f(v)=\varnothing \}, \\ V_{1}&= \{v\in C_{n}\square C_{m}:f(v)=\{1\} \text{ or} f(v)=\{2\}\}, \\ V_{2}&= \{v\in C_{n}\square C_{m}:f(v)=\{1,2\}\}, \\ V_{i_{1}i_{2}}&= \{v\in V_{0}:\left|N(v)\cap V_{t}\right|=i_{t},t=1,2\},\\ E_{1}&= \{uv\in E(C_{n}\square C_{m}):u,v\in V_{1}\}, \\ E_{2}&= \{uv\in E(C_{n}\square C_{m}):u,v\in V_{2}\}, \\ E_{12}&= \{uv\in E(C_{n}\square C_{m}):u\in V_{1},v\in V_{2}\}. \end{aligned}$$

Obviously $V=V(C_{n}\square C_{m})=V_{0}\cup V_{1}\cup V_{2},$ $V_{i}\cap V_{j}=\varnothing ,i,j=0,1,2, i\ne j.$

Let

$$\begin{aligned} \mathcal W =\left\{ V_{01},V_{02},V_{03},V_{04},V_{11},V_{12},V_{13},V_{20},V_{21}, V_{22},V_{30},V_{31},V_{40}\right\} . \end{aligned}$$

Observe that the collection $\mathcal W$ is pairwise disjoint and $V_{0}=\bigcup \nolimits _{S\in \mathcal W }S.$

Now, we establish $\left|E(V_{0},V_{1})\right|.$ On the one hand,

$$\begin{aligned} \left|E(V_{0},V_{1})\right|=4\left|V_{1}\right|-\left|E_{12}\right|-2\left|E_{1}\right|\end{aligned}$$

and on the other hand,

$\left|E(V_{0},V_{1})\right|=\left|V_{11}\right|+\left|V_{12}\right|+\left|V_{13}\right|+2\left|V_{20}\right|+2\left|V_{21}\right|+2\left|V_{22}\right|+3\left|V_{30}\right|+3\left|V_{31}\right|+4\left|V_{40}\right|.$

Similarly, $\left|E(V_{0},V_{2})\right|=4\left|V_{2}\right|-\left|E_{12}\right|-2\left|E_{2}\right|$ and $\left|E(V_{0},V_{2})\right|=\left|V_{01}\right|+\left|V_{11}\right|+\left|V_{21}\right|+\left|V_{31}\right|+2\left|V_{02}\right|+2\left|V_{12}\right|+2\left|V_{22}\right|+3\left|V_{03}\right|+3\left|V_{13}\right|+4\left|V_{04}\right|.$ Therefore, $\left|E(V_{0},V_{1})\right|+2\left|E(V_{0},V_{2})\right|=4\left|V_{1}\right|+8\left|V_{2}\right|-2\left|E_{1}\right|-3\left|E_{12}\right|-4\left|E_{2}\right|$ and $\left|E(V_{0},V_{1})\right|+2\left|E(V_{0},V_{2})\right|=2(\left|V\right|-\left|V_{1}\right|-\left|V_{2}\right|)+\left|V_{11}\right|+3\left|V_{12}\right|+5\left|V_{13}\right|+2\left|V_{21}\right|+4\left|V_{22}\right|+\left|V_{30}\right|+3\left|V_{31}\right|+2\left|V_{40}\right|+2\left|V_{02}\right|+4\left|V_{03}\right|+6\left|V_{04}\right|.$ Hence (because of $\left|V\right|=mn$) $6\left|V_{1}\right|+12\left|V_{2}\right|-3\left|E_{12}\right|-2\left|E_{1}\right|-4\left|E_{2}\right|=2mn+2\left|V_{2}\right|+\left|V_{11}\right|+3\left|V_{12}\right|+5\left|V_{13}\right|+2\left|V_{21}\right|+4\left|V_{22}\right|+\left|V_{30}\right|+3\left|V_{31}\right|+2\left|V_{40}\right|+2\left|V_{02}\right|+4\left|V_{03}\right|+6\left|V_{04}\right|.$

Since $w(f)=\left|V_{1}\right|+2\left|V_{2}\right|,$ thus

$6w(f)=2mn+2\left|V_{2}\right|+\left|V_{11}\right|+3\left|V_{12}\right|+5\left|V_{13}\right|+2\left|V_{21}\right|+4\left|V_{22}\right|+\left|V_{30}\right|+3\left|V_{31}\right|+2\left|V_{40}\right|+2\left|V_{02}\right|+4\left|V_{03}\right|+6\left|V_{04}\right|+3\left|E_{12}\right|+2\left|E_{1}\right|+4\left|E_{2}\right|.$

Let

$$\begin{aligned} \beta&= 2\left|{V}_{2}\right|+\left|{V}_{11}\right|+3\left|{V}_{12}\right|+5\left|V_{13}\right|+2\left|V_{21}\right|+4\left|V_{22}\right|+\left|V_{30}\right|\nonumber \\&+3\left|{V}_{31}\right|+2\left|V_{40}\right|+2\left|{V}_{02}\right|+4\left|V_{03}\right|+6\left|{V}_{04}\right|\nonumber \\&+3\left|{E}_{12}\right|+2\left|{E}_{1}\right|+4\left|{E}_{2}\right|, \end{aligned}$$

(2)

so

$$\begin{aligned} 6w(f)=2nm+\beta . \end{aligned}$$

(3)

Lemma 2

Let $f$ be a $2RDF$ of $C_{n}\square C_{3}.$ If $w(f(\mathcal C ^{i}))=0$ for some $i\in \{1,2,\ldots ,n\},$ then $w(f)\ge n+2.$

Proof

We may assume without loss of generality that $w(f(\mathcal C ^{2}))=0.$ Consider the following cases:

• (1) If $|\left( \mathcal C ^{1}\cup \mathcal C ^{3}\right) \cap V_{2}|\ge 3,$ then $\left|V_{2}\right|\ge 3,$ $\left|E_{2}\right|\ge 1$ and by (2), $\beta \ge 2\left|V_{2}\right|+4\left|E_{2}\right|\ge 10.$

• (2) If $|\left( \mathcal C ^{1}\cup \mathcal C ^{3}\right) \cap V_{2}|=2,$ then $|E_{12}|\ge 2$ and $\beta \ge 2\left|V_{2}\right|+3\left|E_{12}\right|\ge 10.$

• (3) If $|\left( \mathcal C ^{1}\cup \mathcal C ^{3}\right) \cap V_{2}|=1,$ then $|E_{12}|\ge 2,$ $|E_{1}|\ge 2$ and $\beta \ge 2\left|V_{2}\right|+2\left|E_{1}\right|+3\left|E_{12}\right|\ge 12.$

• (4) If $|\left( \mathcal C ^{1}\cup \mathcal C ^{3}\right) \cap V_{1}|=6,$ then $|E_{1}|\ge 6$ and $\beta \ge 2\left|E_{1}\right|\ge 12.$

Further from (3), $w(f)=\left\lceil n+\frac{\beta }{6} \right\rceil \ge \left\lceil n+\frac{10}{6}\right\rceil =n+2,$ as desired.$\square$

Theorem 3

$$\begin{aligned} \gamma _{r2}(C_{n}\square C_{3})=\left\{ \begin{array}{l@{\quad }l} n,&if n\equiv 0 \mod 6, \\ n+1,&if n\equiv 1,2,3,5 \mod 6, \\ n+2,&if n\equiv 4 \mod 6. \end{array}\right. \end{aligned}$$

Proof

From Lemma 1 we have that $\gamma _{r2}(C_{n}\square C_{3})=n$ for $n\equiv 0\,\text{ mod}\, 6.$

For the proof it suffices to show that one cannot construct a $2RDF$ $f$ of $C_{n}\square C_{3}$ with $w(f)=n$ for $n\equiv 1,2,3,5 \,\text{ mod}\, 6$ and with $w(f)\le n+1$ for $n\equiv 4 \,\text{ mod}\, 6.$

Suppose that $n\equiv 1,2,3,5 \,\text{ mod}\, 6,$ and suppose $f$ is $2RDF$ of $C_{n}\square C_{3}$ such that $w(f)=n.$ Lemma 2 implies that $w(f(\mathcal C ^{i}))=1$ for $i=1,2,\ldots ,n.$ Without loss of generality assume that $f(v_{11})=1.$

First note that $f(v_{21})=0.$ Indeed, if $f(v_{21})\in V_{1},$ then $w(f(\mathcal C ^{3}))\ge 2$ (otherwise $v_{22}$ and $v_{23}$ would not be dominated).

So either $v_{22}\in V_{1}$ or $v_{23}\in V_{1}.$ Suppose that $v_{22}\in V_{1},$ then $f(v_{22})=2\, ({\text{ otherwise}}\, w(f(C^{3}))\ge 2).$ Observe that it must be that $f(v_{33})=1,$ since $v_{23}$ must be dominated. Continuing in this way, we obtain that

 

This shows that $f$ is not a $2RDF$ of $C_{n}\square C_{3}$ for $n\equiv 1,2,3,4,5 \,\text{ mod}\, 6,$ because of $v_{13}\in V_{0}$ but $2\notin \bigcup \nolimits _{x\in N(v_{13})}f(x).$

The similar fact holds for $f(v_{23})=2.$ Namely, we have the following situation:  

Therefore, $\gamma _{r2}(C_{n}\square C_{3})>n$ for $n\equiv 1,2,3,4,5 \,\text{ mod}\, 6.$ By Lemma 1 we have that $\gamma _{r2}(C_{n}\square C_{3})=n+1$ for $n\equiv 1,2,3,5 \,\text{ mod}\,6.$

Finally, suppose that $\gamma _{r2}(C_{n}\square C_{3})=n+1$ for $n\equiv 4 \,\text{ mod}\, 6.$ By Lemma 2, we may assume that $w(f(\mathcal C ^{i}))=1$ for $i=1,2,\ldots ,n-1.$ Suppose that $f(v_{11})=1.$ By above we have

 

or

 

and it is easy to check that one cannot dominate all vertices of $\mathcal C ^{1}\cup \mathcal C ^{6l+3}\cup \mathcal C ^{6l+4}$ to obtain a $2RDF$ with $w(f)=n+1.$ So, by Lemma 1 we have that $\gamma _{r2}(C_{n}\square C_{3})=n+2$ for $n\equiv 4 \,\text{ mod}\, 6.$ $\square$

Roughly speaking, $\gamma _{r2}(C_{n}\square C_{3})$ is very close to the general lower bound in (1). Note that for $C_{6l}\square C_{3}$ the lower bound in (1) is attained.

3 2-Rainbow domination number of $C_{n}\square C_{5}$

Now, we give an upper bound of the 2-rainbow domination number of $C_{n}\square C_{5}.$ Moreover, we show that this bound is attained for small $n.$ We do believe that it is also attained for any $n\ge 3.$ First we give the useful result.

Lemma 4

For any $n\ge 8$ there exist nonnegative integers $a,b$ such that $n=5a+3b.$

In general, the above fact is known as Frobenius problem.

Theorem 5

For $n\ge 3, \gamma _{r2}(C_{n}\square C_{5})\le 2n.$

Proof

For $n\le 7,$ let us define the functions $f$ as follows

$$\begin{aligned} f_{3}&= f(V(C_{3}\square C_{5}))=\left( \begin{array}{l@{\quad }l@{\quad }l} 2&0&0 \\ 0&0&1 \\ 0&2&0 \\ 1&0&2 \\ 0&1&0\end{array} \right), \quad f(V(C_{4}\square C_{5}))=\left( \begin{array}{l@{\quad }l@{\quad }l@{\quad }l} 2&2&0&0 \\ 0&0&1&1 \\ 0&2&0&0 \\ 1&0&0&2 \\ 0&0&1&0 \end{array} \right),\\ f_{5}&= f(V(C_{5}\square C_{5}))=\left( \begin{array}{l@{\quad }l@{\quad }l@{\quad }l@{\quad }l} 2&1&0&0&0 \\ 0&0&0&2&1 \\ 0&2&1&0&0 \\ 1&0&0&0&2 \\ 0&0&2&1&0 \end{array}\right). \end{aligned}$$

Observe that

$$\begin{aligned} f_{3}|f_{3}\overset{df}{=}\left( \left. \begin{array}{l@{\quad }l@{\quad }l} 2&0&0 \\ 0&0&1 \\ 0&2&0 \\ 1&0&2 \\ 0&1&0 \end{array} \right|\begin{array}{l@{\quad }l@{\quad }l} 2&0&0 \\ 0&0&1 \\ 0&2&0 \\ 1&0&2 \\ 0&1&0\end{array}\right) \end{aligned}$$

is a 2RDF of $C_{6}\square C_{5}.$ Further,

$$\begin{aligned} f(V(C_{7}\square C_{5}))=\left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} 2&1&0&0&2&0&0 \\ 0&0&0&1&0&0&1 \\ 0&2&2&0&2&2&0 \\ 1&0&0&1&0&0&2 \\ 0&0&2&0&0&1&0 \end{array} \right). \end{aligned}$$

By above, it is an easy exercise to check that $w(f)=2n,$ for $n\le 7.$

Additionally, note that the functions $f_{5}|f_{5}, f_{5}|f_{3}$ and $f_{3}|f_{5}$ are also 2RDFs of $C_{10}\square C_{5},$ $C_{8}\square C_{5}, C_{8}\square C_{5},$ respectively.

Let $n\ge 8,$ then by Lemma 4 we have $n=5a+3b, a,b\ge 0.$ Let $f:V(C_{n})\rightarrow \mathcal P(\{ 1,2\})$ be defined as follows:

$$\begin{aligned} f(V(C_{n}\square C_{5}))=\overset{a~\text{ times}}{\overbrace{f_{5}\left|\cdots \right|{f}_{5}|}}\overset{b~\text{ times}}{\overbrace{f_{3}\left|\cdots \right|{f}_{3}}}. \end{aligned}$$

it is easy to verify that $f$ is a $2RDF$ of $C_{n}\square C_{5} (n\ge 8)$ and $w(f)=2n.$ Therefore, $\gamma _{r2}(C_{n}\square C_{5})\le 2n (n\ge 3),$ as desired.$\square$

Our aim is to show that for $n=3,4,5,6,$ $\gamma _{r2}(C_{n}\square C_{5})=2n.$ For this purpose, we prove the following Lemma.

Lemma 6

Let $f$ be a $2RDF$ of $C_{n}\square C_{5}$ and $\mathcal C ^{r},\mathcal C ^{s},\mathcal C ^{t}$ be three consecutive columns of $C_{n}\square C_{5}.$

• (i) If $w(f(\mathcal C ^{s}))=0,$ then $w(f\left( \mathcal C ^{r}\cup \mathcal C ^{t}\right) )\ge 10.$

• (ii) If $w(f(\mathcal C ^{s}))=1,$ then $w(f\left( \mathcal C ^{r}\cup \mathcal C ^{t}\right) )\ge 6.$

Proof

The proof follows immediately from the definition of a $2RDF.$ $\square$

Theorem 7

For $n=3,4,5,6, \gamma _{r2}(C_{n}\square C_{5})=2n.$

Proof

By Theorem 3 $\gamma _{r2}(C_{5}\square C_{3})=\gamma _{r2}(C_{3}\square C_{5})=6,$ as required. Further, by Theorem 5, it suffices to show that $\gamma _{r2}(C_{n}\square C_{5})\ge 2n$ for $n=4,5,6.$ Let $f$ be a $\gamma _{r2}$-function of $C_{n}\square C_{5}$ for $n=4,5,6.$ If $w(f(\mathcal C ^{i}))\ge 2$ for any $i\in \{1,2,\ldots ,n\},$ then $\gamma _{r2}(C_{n}\square C_{5})\ge 2n.$ Otherwise, there exists $k\in \{1,2,\ldots ,n\}$ such that $w(f(\mathcal C ^{k}))\le 1.$ Without loss of generality suppose that $k=2.$

First assume that $w(f(\mathcal C ^{2}))=0.$ By Lemma 6 (i) for $s=2, w\left(f\left(\mathcal C ^{1}\cup \mathcal C ^{3}\right)\right)\ge 10.$ Thus for $n=4,5$ we have $\gamma _{r2}\left(C_{n}\square C_{5}\right)\ge 2n.$ Further, suppose that $\gamma _{r2}\left(C_{5}\square C_{6}\right)=w\left(f\left( \mathcal C ^{1}\cup \mathcal C ^{2}\cup \mathcal C ^{3}\right) \right)+w\left(f\left( \mathcal C ^{4}\cup \mathcal C ^{5}\cup \mathcal C ^{6}\right) \right)\le 11.$ This implies that $w\left(f\left( \mathcal C ^{4}\cup \mathcal C ^{5}\cup \mathcal C ^{6}\right) \right)=1$ but then $f$ is not a $2RDF.$

It remains to consider the case where $w(f(\mathcal C ^{2}))=1$ and $w(f(\mathcal C ^{i}))\ne 0$ for other $i.$ From Lemma (ii) for $s=2,$ we have $w\left(f\left( \mathcal C ^{1}\cup \mathcal C ^{3}\right)\right)\ge 6.$ Further $w\left(f\left( \mathcal C ^{1}\cup \mathcal C ^{2}\cup \mathcal C ^{3}\right)\right) \ge 7.$ Therefore, $\gamma _{r2}(C_{5}\square C_{4})\ge 2n=8.$

Let $n=5.$ Suppose that $w(f)=w(f\left( \mathcal C ^{1}\cup \mathcal C ^{2}\cup \mathcal C ^{3}\right) )+w(f\left( \mathcal C ^{4}\cup \mathcal C ^{5}\right) )\le 9,$ so $w(f(\mathcal C ^{4}))=1=w(f(\mathcal C ^{5})).$ Applying Lemma 6 (ii) to $\mathcal C ^{4}$ and $\mathcal C ^{5}$ we get $w(f(\mathcal C ^{3}))\ge 5$ and $w(f(C^{1}))\ge 5.$ Thus we obtain $\gamma _{r2}(C_{5}\Box C_{5})\ge 5+1+5+1+1=13.$ However, this contradicts our assumption.

Let $n=6.$ Suppose that $\gamma _{r2}(C_{5}\Box C_{6})=w(f(\mathcal C ^{1}\cup \mathcal C ^{2}\cup \mathcal C ^{3}\cup \mathcal C ^{4}\cup \mathcal C ^{5}\cup \mathcal C ^{6}))=w(f(\mathcal C ^{1}\cup \mathcal C ^{2}\cup \mathcal C ^{3}))+w(f(\mathcal C ^{4}\cup \mathcal C ^{5}\cup \mathcal C ^{6}))\le 11.$ Thus we have $w(f(\mathcal C ^{4}\cup \mathcal C ^{5}\cup \mathcal C ^{6}))=3$ or $4.$ The condition $w(f(\mathcal C ^{4}\cup \mathcal C ^{5}\cup \mathcal C ^{6}))=3$ implies that $w(f(\mathcal C ^{4}))=w(f(\mathcal C ^{5}))=w(f(\mathcal C ^{6}))=1$ but it is impossible by Lemma 6 (ii). For $w(f(\mathcal C ^{4}\cup \mathcal C ^{5}\cup \mathcal C ^{6}))=4$ the possibilities for $w(f(\mathcal C ^{4})),$ $w(f(\mathcal C ^{5})),$ $w(f(\mathcal C ^{6})),$ are (i) $1,1,2,$ (ii) $2,1,1,$ (iii) $1,2,1.$ Cases (i) and (ii) can be eliminated because of Lemma 6 (ii). In case (iii), applying Lemma 6 (ii) to $\mathcal C ^{4}$ and $\mathcal C ^{5}$ we get $w(f(\mathcal C ^{3}))\ge 4$ and $w(f(\mathcal C ^{1}))\ge 4.$ Thus we obtain $\gamma _{r2}(C_{5}\square C_{6})\ge 4+1+4+1+2+1=13.$ However, this contradicts our assumption.$\square$

Since $\gamma (C_{5}\square C_{5})=5,$ we have that $\gamma _{r2}(C_{5}\square C_{5})=10=2\gamma (C_{5}\square C_{5}),$ see Klavžar and Seifter (1995). Thus for this graph the upper bound in (1) is attained.