Abstract
Locally adaptive differential frames (gauge frames) are a well-known effective tool in image analysis, used in differential invariants and PDE-flows. However, at complex structures such as crossings or junctions, these frames are not well defined. Therefore, we generalize the notion of gauge frames on images to gauge frames on data representations \(U:\mathbb {R}^{d} \rtimes S^{d-1} \rightarrow \mathbb {R}\) defined on the extended space of positions and orientations, which we relate to data on the roto-translation group SE(d), \(d=2,3\). This allows to define multiple frames per position, one per orientation. We compute these frames via exponential curve fits in the extended data representations in SE(d). These curve fits minimize first- or second-order variational problems which are solved by spectral decomposition of, respectively, a structure tensor or Hessian of data on SE(d). We include these gauge frames in differential invariants and crossing-preserving PDE-flows acting on extended data representation U and we show their advantage compared to the standard left-invariant frame on SE(d). Applications include crossing-preserving filtering and improved segmentations of the vascular tree in retinal images, and new 3D extensions of coherence-enhancing diffusion via invertible orientation scores.
Similar content being viewed by others
1 Introduction
Many existing image analysis techniques rely on differential frames that are locally adapted to image data. This includes methods based on differential invariants [33, 39, 50, 60], partial differential equations [38, 60, 71], and non-linear and morphological scale spaces [12, 13, 72], used in various image processing tasks such as tracking and line detection [6], corner detection and edge focussing [8, 39], segmentation [66], active contours [15, 16], DTI data processing [45, 46], feature-based clustering, etc. These local coordinate frames (also known as ‘gauge frames’ according to [10, 33, 39]) provide differential frames directly adapted to the local image structure via a structure tensor or a Hessian of the image. Typically the structure tensor (based on first-order Gaussian derivatives) is used for adapting to edge-like structures, while the Hessian (based on second-order Gaussian derivatives) is used for adapting to line-like structures. The primary benefit of the gauge frames is that they allow to include adaptation for anisotropy and curvature in a rotation and translation invariant way. See Fig. 1, where we have depicted local adaptive frames based on eigenvector decomposition of the image Hessian at some given scale, of the MR image in the background.
Left locally adaptive frames (gauge frames) in the image domain computed as the eigenvectors of the Hessian of the image at each location. Right such gauge frames can be used for adaptive anisotropic diffusion and geometric reasoning. However, at complex structures such as blob-structures/crossings, the gauge frames are ill defined causing fluctuations
It is sometimes problematic that such locally adapted differential frames are directly placed in the image domain \(\mathbb {R}^{d}\) \((d=2,3)\), as at the vicinity of complex structures, e.g., crossings, textures, bifurcations, one typically requires multiple local spatial coordinate frames. To this end, one effective alternative is to extend the image domain to the joint space of positions and orientations \(\mathbb {R}^{d} \rtimes S^{d-1}\). The advantage is that it allows to disentangle oriented structures involved in crossings, and to include curvature, cf. Fig. 2. Such extended domain techniques rely on various kinds of lifting, such as coherent state transforms (also known as invertible orientation scores) [2, 6, 27, 34], continuous wavelet transforms [6, 23, 27, 63], orientation lifts [11, 73], or orientation channel representations [32]. In case one has to deal with more complex diffusion-weighted MRI techniques, the data in extended position orientation domain can be obtained after a modeling procedure as in [1, 65, 67, 68]. In this article we will not discuss in detail on how such a new image representation or lift \(U:\mathbb {R}^{d} \rtimes S^{d-1} \rightarrow \mathbb {R}\) is to be constructed from gray-scale image \(f:\mathbb {R}^{d} \rightarrow \mathbb {R}\), and we assume it to be a sufficiently smooth given input. Here \(U({\mathbf{x }},{\mathbf{n }})\) is to be considered as a probability density of finding a local oriented structure (i.e., an elongated structure) at position \({\mathbf{x }} \in \mathbb {R}^{d}\) with orientation \({\mathbf{n }} \in S^{d-1}\).
We aim for adaptive anisotropic diffusion of images which takes into account curvature. At areas with low orientation confidence (in blue) isotropic diffusion is required, whereas at areas with high orientation confidence (in red) anisotropic diffusion with curvature adaptation is required. Application of locally adaptive frames in the image domain suffers from interference (3rd column), whereas application of locally adaptive frames in the domain \(\mathbb {R}^{d} \rtimes S^{d-1}\) allows for adaptation along all the elongated structures (4th column) (Color figure online)
When processing data in the extended position orientation domain, it is often necessary to equip the domain with a structure that links the data across different orientation channels, in such a way that a notion of alignment between local orientations is taken into account. This is achieved by relating data on positions and orientations to data on the roto-translation group \(SE(d)=\mathbb {R}^{d} \rtimes SO(d)\). This idea resulted in contextual image analysis methods [4, 17, 20, 26, 27, 30, 53, 63, 64, 70, 73] and appears in models of low-level visual perception and their relation with the functional architecture of the visual cortex [5, 11, 19, 49, 57–59]. Following the conventions in [30], we denote functions on the coupled space of positions and orientations by \(U:\mathbb {R}^d\rtimes S^{d-1}\rightarrow \mathbb {R}\). Then, its extension \(\tilde{U}:SE(d)\rightarrow \mathbb {R}\) is given by
for all \({\mathbf{x }}\in \mathbb {R}^d\) and all rotations \({\mathbf{R }}\in SO(d)\), and given reference axis \({\mathbf{a }} \in S^{d-1}\). Throughout this article \({\mathbf{a }}\) is chosen as follows:
Then, we can identify the joint space of positions and orientations \(\mathbb {R}^d\rtimes S^{d-1}\) by
where this quotient structure is due to (1), and where \(SO(d-1)\) is identified with all rotations on \(\mathbb {R}^d\) that map reference axis \({\mathbf{a }}\) onto itself. Note that in Eq. (1) the tilde indicates we consider data on the group instead of data on the quotient. If \(d=2\), the tildes can be ignored as \(\mathbb {R}^2\rtimes S^1 =SE(2)\). However, for \(d\ge 3\) this distinction is crucial and necessary details on (3) will follow in the beginning of Sect. 6.
In this article, our quest is to find locally optimal differential frames in SE(d) relying on similar Hessian- and/or structure-tensor type of techniques for gauge frames on images, recall Fig. 1. Then, the frames can be used to construct crossing-preserving differential invariants and adaptive diffusions of data in SE(d). In order to find these optimal frames, our main tool is the theory of curve fits. Early works on curve fits have been presented [37, 54] where the notion of curvature consistency is applied to inferring local curve orientations, based on neighborhood co-circularity continuation criteria. This approach was extended to 2D texture flow inference in [7], by lifting images in position and orientation domain and inferring multiple Cartan frames at each point. Our work is embedded in a Lie group framework where we consider the notion of exponential curve fits via formal variational methods. Exponential curves in the SE(d)-curved geometry are the equivalents of straight Footnote 1 lines in the Euclidean geometry. If \(d=2\), the spatial projection of these exponential curves are osculating circles, which are used for constructing the curvature consistency in [54], for defining the tensor voting fields in [52], and for local modeling association fields in [19]. If \(d=3\), the spatial projection of exponential curves are spirals with constant curvature and torsion. Based on co-helicity principles, similar spirals have been used in neuroimaging applications [61] or for modeling heart fibers [62]. In these works curve fits are obtained via efficient discrete optimization techniques, which are beyond the scope of this article.
In Fig. 3, we present an example for \(d=2\) of the overall pipeline of including locally adaptive frames in a suitable diffusion operators \(\varPhi \) acting in the lifted domain \(\mathbb {R}^{2}\rtimes S^1\). For \(d>2\) the same pipeline applies. Here, an exponential curve fit \(\gamma ^{{\mathbf{c }}^*}_{g}(t)\) (in blue, with spatial projection in red) at a group element \(g\in SE(d)\) is characterized by \((g, {\mathbf{c }}^{*}(g))\), i.e., a starting point g and an tangent vector \({\mathbf{c }}^{*}(g)\) that should be aligned with the structures of interest. In essence, this paper explains in detail how to compute \({\mathbf{c }}^{*}(g)\) as this will be the principal direction the differential frame will be aligned with, and then gives appropriate conditions for fixing the remaining directions in the frame.
The overall pipeline of image processing \(f \mapsto \varUpsilon f\) via left-invariant operators \(\varPhi \). In this pipeline we construct an invertible orientation score \(W_\psi f\) (Sect. 7.1), we fit an exponential curve (Sect. 5,6), we obtain the gauge frame (Sect. 3 and Appendix 1), we construct a non-linear diffusion, and finally we apply reconstruction (Sect. 7.1). The main focus of this paper is curve fitting, where we compute per element \(g=(x,y,\theta )\) an exponential curve fit \(\gamma ^{{\mathbf{c }}^*}_{g}(t)\) (in blue, with spatial projection in red) with tangent \(\dot{\gamma }_g^{{\mathbf{c }}^{*}}(0)={\mathbf{c }}^{*}(g)=(c^1,c^2,c^3)^T\) at g. Based on this fit we construct for each g, a local frame \(\{\left. \mathcal {B}_{1}\right| _{g}, \left. \mathcal {B}_{2}\right| _{g},\left. \mathcal {B}_{3}\right| _{g}\}\) which are used in our operators \(\varPhi \) on the lift (here \(\varPhi \) is a non-linear diffusion operator) (Color figure online)
The main contribution of this article is to provide a general theory for finding locally adaptive frames in the roto-translation group SE(d), for \(d=2,3\). Some preliminary work on exponential curve fits of the second order on SE(2) has been presented in [34, 35, 63]. In this paper we formalize these previous methods (Theorems 2 and 3) and we extend them to first-order exponential curve fits (Theorem 1). Furthermore, we generalize both approaches to the case \(d=3\) (Theorems 4, 5, 6, 7, and 8). All theorems contain new results except for Theorems 2 and 3. The key ingredient is to consider the fits as formal variational curve optimization problems with exact solutions derived by spectral decomposition of structure tensors and Hessians of the data \(\tilde{U}\) on SE(d). In the SE(3)-case we show that in order to obtain torsion-free exponential curve fits with well-posed projection on \(\mathbb {R}^{3}\rtimes S^{2}\), one must resign to a twofold optimization algorithm. To show the potential of considering these locally adaptive frames, we employ them in medical image analysis applications, in improved differential invariants and improved crossing-preserving diffusions. Here, we provide for the first time coherence-enhancing diffusions via 3D invertible orientation scores [42, 43], extending previous methods [34, 35, 63] to the 3D Euclidean motion group.
1.1 Structure of the Article
We start the body of this article reviewing preliminary differential geometry tools in Sect. 2. Then, in Sect. 3 we describe how a given exponential curve fit induces the locally adaptive frame. In Sect. 4 we provide an introduction by reformulating the standard gauge frames construction in images in a group-theoretical setting. This gives a roadmap towards SE(2)-extensions explained in Sect. 5, where we deal with exponential curve fits of the first order in Sect. 5.2 computed via a structure tensor, and exponential curves fits of second order in Sect. 5.3 computed via the Hessian of the data \(\tilde{U}\). In the latter case we have two options for the curve optimization problem: one solved by the symmetric sum, and one by the symmetric product of the non-symmetric Hessian. The curve fits in SE(2) in Sect. 5 are extended to curve fits in SE(3) in Sect. 6. It starts with preliminaries on the quotient (3) and then it follows the same structure as the previous section. Here we present the twofold algorithm for computing the torsion-free exponential curve fits.
In Sect. 7 we consider experiments regarding medical imaging applications and feasibility studies. We first recall the theory of invertible orientation scores needed for the applications. In the SE(2)-case we present crossing-preserving multi-scale vessel enhancing filters in retinal imaging, and in the SE(3)-case we include a proof of concept of crossing-preserving (coherence-enhancing diffusion) steered by gauge frames via invertible 3D orientation scores.
Finally, there are 5 appendices. Appendix 1 supplements Sect. 3 by explaining the construction of the frame for \(d=2,3\). Appendix 2 describes the geometry of neighboring exponential curves needed for formulating the variational problems. Appendix 3 complements the twofold approach in Sect. 6. Appendix 4 provides the definition of the Hessian used in the paper. Finally, Table 1 in Appendix 5 contains a list of symbols, their explanations and references to the equation in which they are defined. We advise the reader to keep track of this table. Especially, in the more technical sections: Sects. 5 and 6.
2 Differential Geometrical Tools
Relating our data to data on the Euclidean motion group, via Eq. (1), allows us to use tools from Lie group theory and differential geometry. In this section we explain these tools that are important for our notion of an exponential curve fit to smooth data \(\tilde{U}:SE(d) \rightarrow \mathbb {R}\). Often, we consider the case \(d=2\) for basic illustration. Later on, in Sect. 6, we consider the case \(d=3\) and extra technicalities on the quotient structure will enter.
2.1 The Roto-Translation Group
The data \(\tilde{U}:SE(d) \rightarrow \mathbb {R}\) is defined on the group SE(d) of rotations and translations acting on \(\mathbb {R}^{d}\). As the concatenation of two rigid body motions is again a rigid body motion, the group SE(d) is equipped with the following group product:
where we recognize the semi-direct product structure \(SE(d)=\mathbb {R}^{d} \rtimes SO(d)\), of the translation group \(\mathbb {R}^{d}\) with rotation group \(SO(d)=\{\mathbf{R } \in \mathbb {R}^{d\times d}\,|\, \mathbf{R }^{T}=\mathbf{R }^{-1},\det {\mathbf {R}}=1\}\). The groups SE(d) and SO(d) have dimension
Note that \(n_2=3\), \(n_3=6\). One may represent elements g from SE(d) by the following matrix representation
We will often avoid this embedding into the set of invertible \((d+1) \times (d+1)\) matrices, in order to focus on the geometry rather than the algebra.
2.2 Left-Invariant Operators
In image analysis applications operators \(\tilde{U} \mapsto \tilde{\varPhi }(\tilde{U})\) need to be left-invariant and not right-invariant [24, 34]. Left-invariant operators \(\tilde{\varPhi }\) in the extended domain correspond to rotation and translation invariant operators \(\varUpsilon \) in the image domain, which is a desirable property. On the other hand, right-invariance boils down to isotropic operators in the image domain which is an undesirable restriction. By definition \(\tilde{\varPhi }\) is left-invariant and not right-invariant if it commutes with the left-regular representation \(\mathcal {L}\) (and not with the right-regular representation \(\mathcal {R}\)). Representations \(\mathcal {L},\mathcal {R}\) are given by
for all \(h,g \in SE(d)\). So operator \(\tilde{\varPhi }\) must satisfy \(\tilde{\varPhi } \circ \mathcal {L}_{g}= \mathcal {L}_{g} \circ \tilde{\varPhi }\) and \(\tilde{\varPhi } \circ \mathcal {R}_{g}\ne \mathcal {R}_{g} \circ \tilde{\varPhi }\) for all \(g \in SE(d)\).
2.3 Left-Invariant Vector Fields and Dual Frame
A special case of left-invariant operators are left-invariant derivatives. More precisely (see Remark 1 below), we need to consider left-invariant vector fields \(g \mapsto \mathcal {A}_{g}\), as the left-invariant derivative \(\mathcal {A}_{g}\) depends on the location g where it is attached. Intuitively, the left-invariant vector fields \(\{\mathcal {A}_{i}\}_{i=1}^{n_i}\) provide a local moving frame of reference in the tangent bundle T(SE(d)), which comes in naturally when including alignment of local orientations in the image processing of \(\tilde{U}\).
Formally, the left-invariant vector fields are obtained by taking a basis  in the tangent space at the unity element
in the tangent space at the unity element  , and then one uses the push-forward \((L_{g})_*\) of the left multiplication
, and then one uses the push-forward \((L_{g})_*\) of the left multiplication
to obtain the corresponding tangent vectors in the tangent space \(T_{g}(SE(d))\). Thus, one associates to each \(A_{i}\) a left-invariant field \(\mathcal {A}_{i}\) given by
where we consider each \(\mathcal {A}_{i}\) as a differential operator on smooth locally defined functions \(\tilde{\phi }\) given by
An explicit way to construct and compute the differential operators \(\left. \mathcal {A}_{i}\right| _{g}\) from  is via
is via
where \(A \mapsto e^A=\sum \nolimits _{k=0}^{\infty } \frac{A^k}{k!}\) denotes the matrix exponential from Lie algebra  to Lie group SE(d). The differential operators \(\{\mathcal {A}_{i}\}_{i=1}^{n_d}\) induce a corresponding dual frame \(\{\omega ^{i}\}_{i=1}^{n_d}\), which is a basis for the co-tangent bundle \(T^{*}(SE(d))\). This dual frame is given by
to Lie group SE(d). The differential operators \(\{\mathcal {A}_{i}\}_{i=1}^{n_d}\) induce a corresponding dual frame \(\{\omega ^{i}\}_{i=1}^{n_d}\), which is a basis for the co-tangent bundle \(T^{*}(SE(d))\). This dual frame is given by
where \(\delta ^{i}_{j}\) denotes the Kronecker delta. Then the derivative of a differentiable function \(\tilde{\phi }: SE(d) \rightarrow \mathbb {R}\) is expressed as follows:
Remark 1
In differential geometry, there exist two equivalent viewpoints [3, Ch. 2] on tangent vectors \(\mathcal {A}_{g} \in T_{g}(SE(d))\): either one considers them as tangents to locally defined curves; or one considers them as differential operators on locally defined functions. The connection between these viewpoints is as follows. We identify a tangent vector \(\dot{\tilde{\gamma }}(t) \in T_{\tilde{\gamma }(t)}(SE(d))\) with the differential operator \((\dot{\tilde{\gamma }}(t))(\tilde{\phi }) := \frac{d}{dt} \tilde{\phi }(\tilde{\gamma }(t))\) for all locally defined, differentiable, real-valued functions \(\tilde{\phi }\).
Next we express tangent vectors explicitly in the left-invariant moving frame of reference, by taking a directional derivative:
with \(\dot{\tilde{\gamma }}(t)= \sum \limits _{i=1}^{n_d} \dot{\tilde{\gamma }}^{i}(t)\left. \mathcal {A}_{i}\right| _{\tilde{\gamma }(t)}\), and with \(\tilde{\phi }\) smooth and defined on an open set around \(\tilde{\gamma }(t)\). Eq. (13) will play a crucial role in Sect. 5 (exponential curve fits for \(d=2\)) and Sect. 6 (exponential curve fits for \(d=3\)).
Example 1
For \(d=2\) we take  ,
,  ,
,  . Then we have the left-invariant vector fields
. Then we have the left-invariant vector fields
The dual frame is given by
For explicit formulas for left-invariant vector fields in SE(3) see [18, 30].
2.4 Exponential Curves in SE(d)
Let \((\mathbf{c }^{(1)},\mathbf{c }^{(2)})^T \in \mathbb {R}^{d+r_d}=\mathbb {R}^{n_d}\) be a given column vector, where \(\mathbf{c }^{(1)}=(c^1,\ldots ,c^{d}) \in \mathbb {R}^d\) denotes the spatial part and \(\mathbf{c }^{(2)}=(c^{d+1},\ldots , c^{n_d}) \in \mathbb {R}^{r_d}\) denotes the rotational part. The unique exponential curve passing through \(g \in SE(d)\) with initial velocity \(\mathbf{c }(g)=\sum \nolimits _{i=1}^{n_d} c^{i}\left. \mathcal {A}_{i}\right| _{g}\) equals
with  denoting a basis of
denoting a basis of  . In fact such exponential curves satisfy
. In fact such exponential curves satisfy
and thereby have constant velocity in the moving frame of reference, i.e., \(\dot{\tilde{\gamma }}^{i}=c^{i}\) in Eq. (13). A way to compute the exponentials is via matrix exponentials and (6).
Example 2
If \(d=2\) we have exponential curves:
which are circular spirals with
for the case \(c^{3}\ne 0\), and all \(t\ge 0\) and straight lines with
for the case \(c^{3}=0\), where \(g_0=(x_0,y_0,\theta _{0}) \in SE(2)\). See the left panel in Fig. 4.
Left horizontal exponential curve \(\tilde{\gamma }^{\mathbf{c }}_g\) in SE(2) with \(\mathbf{c }=(1,0,1)\). Its projection on the ground plane reflects co-circularity, and the curve can be obtained by a lift (30) from its spatial projection. Right the distribution \(\Delta \) of horizontal tangent vector fields as a sub-bundle in the tangent bundle T(SE(2))
Example 3
For \(d=3\), the formulae for exponential curves in SE(3) are given in for example [18, 30]. Their spatial part are circular spirals with torsion \(\varvec{\tau }(t)=\frac{|\mathbf{c }^{(1)} \cdot \mathbf{c }^{(2)}|}{\Vert \mathbf{c }^{(1)}\Vert }\, \varvec{\kappa }(t)\) and curvature
Note that their magnitudes are constant:
2.5 Left-Invariant Metric Tensor on SE(d)
We use the following (left-invariant) metric tensor:

where \(\dot{\tilde{\gamma }}=\sum _{i=1}^{n_d}\dot{\tilde{\gamma }}^{i} \left. \mathcal {A}_{i}\right| _{\tilde{\gamma }}\), and with stiffness parameter \(\mu \) along any smooth curve \(\tilde{\gamma }\) in SE(d). Now, for the special case of exponential curves, one has \(\dot{\tilde{\gamma }}^{i}= c^{i}\) is constant. The metric allows us to normalize the speed along the curves by imposing a normalization constraint
We will use this constraint in the fitting procedure in order to ensure that our exponential curves (17) are parameterized by Riemannian arclength t.
2.6 Convolution and Haar Measure on SE(d)
In general a convolution of data \(\tilde{U}:SE(d)\rightarrow \mathbb {R}\) with kernel \(\tilde{K}:SE(d)\rightarrow \mathbb {R}\) is given by

for all \(h=(\mathbf{x }',\mathbf{R }') \in SE(d)\), where Haar measure \(\overline{\mu }\) is the direct product of the usual Lebesgue measure on \(\mathbb {R}^d\) with the Haar measure on SO(d).
2.7 Gaussian Smoothing and Gradient on SE(d)
We define the regularized data
where \(\mathbf{s }=(s_p,s_o)\) are the spatial and angular scales, respectively, of the separable Gaussian smoothing kernel defined by
This smoothing kernel is a product of the heat kernel \(G_{s_p}^{\mathbb {R}^d}(\mathbf{x })=\frac{e^{-\frac{\Vert \mathbf{x }\Vert ^2}{4s_p}}}{(4\pi s_p)^{d/2}}\) on \(\mathbb {R}^{d}\) centered at \(\mathbf{0 }\) with spatial scale \(s_p>0\), and a heat kernel \(G_{s_o}^{S^{d-1}}(\mathbf{R }\mathbf{a })\) on \(S^{d-1}\) centered around \(\mathbf{a } \in S^{d-1}\) with angular scale \(s_o>0\).
By definition the gradient \(\nabla \tilde{U}\) of image data \(\tilde{U}:SE(d) \rightarrow \mathbb {R}\) is the Riesz representation vector of the derivative \(\mathrm{d}\tilde{U}\):

relying on \(\mathbf{M }_{\mu }\) as defined in (24). Here, following standard conventions in differential geometry,  denotes the inverse of the linear map associated to the metric tensor (23). Then, the Gaussian gradient is defined by
denotes the inverse of the linear map associated to the metric tensor (23). Then, the Gaussian gradient is defined by
2.8 Horizontal Exponential Curves in SE(d)
Typically, in the distribution \(\tilde{U}\) (e.g., if \(\tilde{U}\) is an orientation score of a gray-scale image) the mass is concentrated around so-called horizontal exponential curves in SE(d) (see Fig. 3). Next we explain this notion of horizontal exponential curves.
A curve \(t \mapsto (x(t),y(t)) \in \mathbb {R}^2\) can be lifted to a curve \(t \mapsto \tilde{\gamma }(t)=(x(t),y(t),\theta (t))\) in SE(2) via
Generalizing to \(d\ge 2\), one can lift a curve \(t \mapsto \mathbf{x }(t) \in \mathbb {R}^d\) towards a curve \(t \mapsto \gamma (t)=(\mathbf{x }(t),\mathbf{n }(t))\) in \(\mathbb {R}^{d}\rtimes S^{d-1}\) by setting
A curve \(t \mapsto \mathbf{x }(t)\) can be lifted towards a family of lifted curves \(t \mapsto \tilde{\gamma }(t)=(\mathbf{x }(t),\mathbf{R }_{\mathbf{n }(t)})\) into the roto-translation group SE(d) by setting \(\mathbf{R }_{\mathbf{n }(t)} \in SO(d)\) such that it maps reference axis \(\mathbf{a }\) onto \(\mathbf{n }(t)\):
Here we use \(\mathbf{R }_{\mathbf{n }}\) to denote any rotation that maps reference axis \(\mathbf{a }\) onto \(\mathbf{n }\). Clearly, the choice of rotation is not unique for \(d>2\), e.g., if \(d=3\) then \(\mathbf{R }_{\mathbf{n }} \mathbf{R }_{\mathbf{a },\alpha }\mathbf{a }=\mathbf{a }\) regardless the value of \(\alpha \), where \(\mathbf{R }_{\mathbf{a },\alpha }\) denotes the counterclockwise 3D rotation about axis \(\mathbf {a}\) by angle \(\alpha \).
Next we study the implication of restriction (31) on the tangent bundle of SE(d).
-
For \(d=2\), we have restriction \(\dot{\mathbf{x }}(t)=(\dot{x}(t), \dot{y}(t))=\Vert \dot{\mathbf{x }}(t)\Vert (\cos \theta (t),\sin \theta (t))\), i.e.,
$$\begin{aligned} \dot{\tilde{\gamma }} \in \left. \Delta \right| _{\tilde{\gamma }}, \ \text {with }\Delta= & {} \text {span}\{\cos \theta \partial _x+\sin \theta \partial _y, \partial _{\theta }\}\nonumber \\= & {} \text {span}\{\mathcal {A}_1,\mathcal {A}_3\}, \end{aligned}$$(32)where \(\Delta \) denotes the so-called horizontal part of tangent bundle T(SE(2)). See Fig. 4.
-
For \(d=3\), we impose the constraint:
$$\begin{aligned} \dot{\tilde{\gamma }}(t) \in \varDelta _{\tilde{\gamma }(t)}, \ \text {with }\varDelta := \text {span}\{\mathcal {A}_{3},\mathcal {A}_{4}, \mathcal {A}_{5}\}, \end{aligned}$$(33)where \(\mathcal {A}_3= \mathbf{n } \cdot \nabla _{\mathbb {R}^3}\), since then spatial transport is always along \(\mathbf{n }\) which is required for for (31).
Curves \(\tilde{\gamma }(t)\) satisfying the constraint (32) for \(d=2\), and (33) for \(d=3\) are called horizontal curves. Note that \(\text {dim}(\varDelta )=d\).
Next we study how the restriction applies to the particular case of exponential curves on SE(d).
-
For \(d=2\) horizontal exponential curves are obtained from (18), (19), (20) by setting \(c^{2}=0\).
-
For \(d=3\), we use a different reference axis \(\mathbf{a }\), and horizontal exponential curves are obtained from (16) by setting \(c^1=c^2=c^6=0\).
If exponential curves are not horizontal, then we indicate how much the local tangent of the exponential curve points outside the spatial part of \(\Delta \), by a ‘deviation from horizontality angle’ \(\chi \), which is given by
Example 4
In case \(d=2\) we have \(n_2=3\), \(\mathbf{a }=(1,0)^T\). The horizontal part of the tangent bundle \(\Delta \) is given by (32), and horizontal exponential curves are obtained from (18) by setting \(c^2=0\). For exponential curves in general, we have deviation from horizontality angle
An exponential curve in SE(2) is horizontal if and only if \(\chi =0\). See Fig. 4, where in the left we have depicted a horizontal exponential curve and where in the right we have visualized distribution \(\Delta \).
Example 5
In case \(d=3\), we have \(n_3=6\), \(\mathbf{a }=(0,0,1)^T\). The horizontal part of the tangent bundle is given by (33), and horizontal exponential curves are characterized by \(c^{3}, c^{4}, c^{5}\) whereas \(c^{1}=c^{2}=c^6=0\). By Eq. (22) these curves have zero torsion \(|\tau |=0\) and constant curvature \(\frac{\sqrt{(c^4)^2+(c^{5})^2}}{c^3}\) and thus they are planar circles. For exponential curves in general, we have deviation from horizontality angle
An exponential curve in SE(3) is horizontal if and only if \(\chi =0\) and \(c^6=0\).
Locally adaptive frame \(\{\left. \mathcal {B}_{1}\right| _{g}, \left. \mathcal {B}_{2}\right| _{g}, \left. \mathcal {B}_{3}\right| _{g}\}\) (in blue) in \(T_{g}(SE(2))\) (with g placed at the origin) is obtained from frame \(\{\left. \mathcal {A}_{1}\right| _{g}, \left. \mathcal {A}_{2}\right| _{g}, \left. \mathcal {A}_{3}\right| _{g}\}\) (in red) and \(\mathbf{c }(g)\), via normalization and two subsequent rotations \(\mathbf{R }^{\mathbf{c }}=\mathbf{R }_{2}\mathbf{R }_{1}\), see Eq. (36), revealing deviation from horizontality \(\chi \), and spherical angle \(\nu \) in Eq. (37). Vector field \(\mathcal {A}_{1}\) takes a spatial derivative in direction \(\mathbf{n }\), whereas \(\mathcal {B}_{1}\) takes a derivative along the tangent \(\mathbf{c }\) of the local exponential curve fit (Color figure online)
3 From Exponential Curve Fits to Gauge Frames on SE(d)
In Sects. 5 and 6 we will discuss techniques to find an exponential curve \(\tilde{\gamma }^{\mathbf{c }}_g(t)\) that fits the data \(\tilde{U}:SE(d)\rightarrow \mathbb {R}\) locally. Let \(\mathbf{c }(g)=(\tilde{\gamma }^{\mathbf{c }}_g)'(0)\) be its tangent vector at g.
In this section we assume that the tangent vector \(\mathbf{c }(g)=(\mathbf{c }^{(1)}(g),\mathbf{c }^{(2)}(g))^T \in R^{d+r_d}=\mathbb {R}^{n_d}\) is given. From this vector we will construct a locally adaptive frame \( \{\left. \mathcal {B}_{1}\right| _g,\ldots ,\left. \mathcal {B}_{n_d}\right| _{g}\}\), orthonormal w.r.t.  -metric in such a way that
-metric in such a way that
-
1.
the main spatial generator (\(\mathcal {A}_{1}\) for \(d=2\) and \(\mathcal {A}_{d}\) for \(d>2\)) is mapped onto \(\left. \mathcal {B}_{1}\right| _{g}= \sum \nolimits _{i=1}^{n_d}c^{i}(g) \left. \mathcal {A}_{i}\right| _{g}\),
-
2.
the spatial generators \(\{\left. \mathcal {B}_{i}\right| _{g}\}^d_{i=2}\) are obtained from the other left-invariant spatial generators \(\{\left. \mathcal {A}_{i}\right| _g\}^d_{i=1}\) by a planar rotation of \(\mathbf{a }\) onto \(\frac{{\mathbf{c }}^{(1)}}{\Vert {\mathbf{c }}^{(1)}\Vert }\) by angle \(\chi \). In particular, if \(\chi =0\), the other spatial generators do not change their direction. This allows us to still distinguish spatial generators and angular generators in our adapted frame.
Next we provide for each \(g \in SE(d)\) the explicit construction of a rotation matrix \(\mathbf{R }^{\mathbf{c }(g)}\) and a scaling by \(\mathbf{M }_{\mu ^{-1}}\) on \(T_g(SE(d))\), which maps frame \(\{\left. \mathcal {A}_{1}\right| _g,\ldots ,\left. \mathcal {A}_{n_d}\right| _{g}\}\) onto \(\{\left. \mathcal {B}_{1}\right| _g,\ldots ,\left. \mathcal {B}_{n_d}\right| _{g}\}\).
The construction for \(d>2\) is technical and provided in Theorem A in Appendix 1. However, the whole construction of the rotation matrix \(\mathbf{R }^{\mathbf{c }}\) via a concatenation of two subsequent rotations is similar to the case \(d=2\) that we will explain next.
Consider \(d=2\) where the frames \(\{\mathcal {A}_{1},\mathcal {A}_{2},\mathcal {A}_{3}\}\) and \(\{\mathcal {B}_{1},\mathcal {B}_{2},\mathcal {B}_{3}\}\) are depicted in Fig. 5 The explicit relation between the normalized gauge frame and the left-invariant vector field frame is given by
with \(\underline{\mathcal {A}}:=(\mathcal {A}_1,\mathcal {A}_{2},\mathcal {A}_{3})^T\), \(\underline{\mathcal {B}}:=(\mathcal {B}_1,\mathcal {B}_{2},\mathcal {B}_{3})^T\), and with rotation matrix
where the rotation angles are the deviation from horizontality angle \(\chi \) and the spherical angle
Recall that \(\chi \) is given by (35). The multiplication \(\mathbf{M }_{\mu }^{-1}\underline{\mathcal {A}}\) ensures that each of the vector fields in the locally adaptive frame is normalized w.r.t. the  -metric, recall (23).
-metric, recall (23).
Remark 2
When imposing isotropy (w.r.t. the metric  ) in the plane orthogonal to \(\mathcal {B}_{1}\), there is a unique choice \(\mathbf{R }^{\mathbf{c }}\) mapping \((1,0,0)^T\) onto \((\mu c^{1},\mu c^{2},c^{3})^T\) such that it keeps the other spatial generator in the spatial subspace of \(T_g(SE(2))\) (and with \(\chi =0 \Leftrightarrow \mathcal {B}_{2}=\mu ^{-1}\mathcal {A}_{2}\)). This choice is given by (37).
) in the plane orthogonal to \(\mathcal {B}_{1}\), there is a unique choice \(\mathbf{R }^{\mathbf{c }}\) mapping \((1,0,0)^T\) onto \((\mu c^{1},\mu c^{2},c^{3})^T\) such that it keeps the other spatial generator in the spatial subspace of \(T_g(SE(2))\) (and with \(\chi =0 \Leftrightarrow \mathcal {B}_{2}=\mu ^{-1}\mathcal {A}_{2}\)). This choice is given by (37).
The generalization to the d-dimensional case of the construction of a locally adaptive frame \(\{\mathcal {B}_{i}\}_{i=1}^{n_d}\) from \(\{\mathcal {A}_{i}\}_{i=1}^{n_d}\) and the tangent vector \(\mathbf{c }\) of a given exponential curve fit \(\tilde{\gamma }^{\mathbf{c }}_g(\cdot )\) to data \(\tilde{U}:SE(d)\rightarrow \mathbb {R}\) is explained in Theorem 7 in Appendix 1.
4 Exponential Curve Fits in \(\mathbb {R}^{d}\)
In this section we reformulate the classical construction of a locally adaptive frame to image f at location \(\mathbf{x } \in \mathbb {R}^d\), in a group-theoretical way. This reformulation seems technical at first sight, but helps in understanding the formulation of projected exponential curve fits in the higher dimensional Lie group SE(d).
4.1 Exponential Curve Fits in \(\mathbb {R}^{d}\) of the First Order
We will take the structure tensor approach [9, 48], which will be shown to yield first-order exponential curve fits.
The Gaussian gradient
with Gaussian kernel
is used in the definition of the structure matrix:
with \(s=\frac{1}{2}\sigma ^2_{s}\), and \(\rho =\frac{1}{2}\sigma ^2_{\rho }\) the scale of regularization typically yielding a non-degenerate and positive definite matrix. In the remainder we use short notation \(\mathbf {S}^{s,\rho }:=\mathbf {S}^{s,\rho }(f)\). The structure matrix appears in solving the following optimization problem where for all \(\mathbf{x } \in \mathbb {R}^{d}\) we aim to find optimal tangent vector
In this optimization problem we find the tangent \(\mathbf{c }^{*}(\mathbf{x })\) which minimizes a (Gaussian) weighted average of the squared directional derivative \(|\nabla ^{s}f(\mathbf{x }') \cdot \mathbf{c }|^2\) in the neighborhood of \(\mathbf{x }\). The second identity in (41), which directly follows from the definition of the structure matrix, allows us to solve optimization problem (41) via the Euler–Lagrange equation
since the minimizer is found as the eigenvector \(\mathbf{c }^{*}(\mathbf{x })\) with the smallest eigenvalue \(\lambda _1\).
Now let us put Eq. (41) in group-theoretical form by reformulating it as an exponential curve fitting problem. This is helpful in our subsequent generalizations to SE(d). On \(\mathbb {R}^{d}\) exponential curves are straight lines:
and on \(T(\mathbb {R}^{d})\) we impose the standard flat metric tensor  . In (41) we replace the directional derivative by a time derivative (at \(t=0\)) when moving over an exponential curve:
. In (41) we replace the directional derivative by a time derivative (at \(t=0\)) when moving over an exponential curve:
where
Because in (41) we average over directional derivatives in the neighborhood of \(\mathbf{x }\) we now average the time derivatives over a family of neighboring exponential curves \(\gamma _{\mathbf{x }',\mathbf{x }}^{\mathbf{c }}(t)\), which are defined to start at neighboring positions \(\mathbf{x }'\) but having the same spatial velocity as \(\gamma _{\mathbf{x }}^{\mathbf{c }}(t)\). In \(\mathbb {R}^{d}\) the distinction between \(\gamma _{\mathbf{x }',\mathbf{x }}^{\mathbf{c }}(t)\) and \(\gamma _{\mathbf{x }'}^{\mathbf{c }}(t)\) is not important but it will be in the SE(d)-case.
Definition 1
Let \(\mathbf{c }^{*}(\mathbf{x }) \in T_{\mathbf{x }}(\mathbb {R}^{d})\) be the minimizer in (44). We say \(\gamma _{\mathbf{x }}(t)= \mathbf{x }+\exp _{\mathbb {R}^{d}}({t \mathbf{c }^{*}(\mathbf{x }))}\) is the first-order exponential curve fit to image data \(f: \mathbb {R}^{d} \rightarrow \mathbb {R}\) at location \(\mathbf{x }\).
4.2 Exponential Curve Fits in \(\mathbb {R}^{d}\) of the Second Order
For second-order exponential curve fits we need the Hessian matrix defined by
with \(G_s\) the Gaussian kernel given in Eq. (39). From now on we use short notation \(\mathbf{H }^{s}:=\mathbf{H }^{s}(f)\). When using the Hessian matrix for curve fitting we aim to solve
In this optimization problem we find the tangent \(\mathbf{c }^{*}(\mathbf{x })\) which minimizes the second-order directional derivative of (Gaussian) regularized data \(G_{s} * f\). When all Hessian eigenvalues have the same sign we can solve the optimization problem (47) via the Euler–Lagrange equation
and the minimizer is found as the eigenvector \(\mathbf{c }^{*}(\mathbf{x })\) with the smallest eigenvalue \(\lambda _1\).
Family of neighboring exponential curves, given a fixed point \(g \in SE(2)\) and a fixed tangent vector \(\mathbf{c }=\mathbf{c }(g) \in T_{g}(SE(2))\). Left our choice of family of exponential curves \(\gamma _{h,g}^{\mathbf{c }}\) for neighboring \(h \in SE(2)\). Right exponential curves \(\gamma ^{\mathbf{c }}_h\) with \(\mathbf{c }=\mathbf{c }(g)\) are not suited for local averaging in our curve fits. The red curves start from g (indicated with a dot), the blue curves from \(h\ne g\) (Color figure online)
Now, we can again put Eq. (47) in group-theoretical form by reformulating it as an exponential curve fitting problem. This is helpful in our subsequent generalizations to SE(d). We again rely on exponential curves as defined in (43). In (47) we replace the second-order directional derivative by a second-order time derivative (at \(t=0\)) when moving over an exponential curve:
Remark 3
In general the eigenvalues of Hessian matrix \(\mathbf{H }^s\) do not have the same sign. In this case we still take \(\mathbf {c}^*(\mathbf {x})\) as the eigenvector with smallest absolute eigenvalue (representing minimal absolute principal curvature), though this no longer solves (47).
Definition 2
Let \(\mathbf{c }^{*}(\mathbf{x }) \in T_{\mathbf{x }}(\mathbb {R}^{d})\) be the minimizer in (49). We say \(\gamma _{\mathbf{x }}(t)= \mathbf{x }+\exp _{\mathbb {R}^{d}}({t \mathbf{c }^{*}(\mathbf{x }))}\) is the second-order exponential curve fit to image data \(f: \mathbb {R}^{d} \rightarrow \mathbb {R}\) at location \(\mathbf{x }\).
Remark 4
In order to connect optimization problem (49) with the first-order optimization (44), we note that (49) can also be written as an optimization over a family of curves \(\gamma _{\mathbf{x }',\mathbf{x }}^{\mathbf{c }}\) defined in (45):
because of linearity of the second-order time derivative.
5 Exponential Curve Fits in SE(2)
As mentioned in the introduction, we distinguish between two approaches: a first-order optimization approach based on a structure tensor on SE(2), and a second-order optimization approach based on the Hessian on SE(2). The first-order approach is new, while the second-order approach formalizes the results in [28, 34]. They also serve as an introduction to the new, more technical, SE(3)-extensions in Sect. 6.
All curve optimization problems are based on the idea that a curve (or a family of curves) fits the data well if a certain quantity is preserved along the curve. This preserved quantity is the data \(\tilde{U}(\tilde{\gamma }(t))\) for the first-order optimization, and the time derivative \(\frac{d}{dt}\tilde{U}(\tilde{\gamma }(t))\) or the gradient \(\nabla \tilde{U}(\tilde{\gamma }(t))\) for the second-order optimization. After introducing a family of curves similar to the ones used in Sect. 4 we will, for all three cases, first pose an optimization problem, and then give its solution in a subsequent theorem.
In this section we rely on group-theoretical tools explained in Sect. 2 (only the case \(d = 2\)), listed in panels (a) and (b) in our table of notations presented in Appendix 5. Furthermore, we introduce notations listed in the first part of panel (c) in our table of notations in Appendix 5.
5.1 Neighboring Exponential Curves in SE(2)
Akin to (45) we fix reference point \(g \in SE(2)\) and velocity components \(\mathbf{c }=\mathbf{c }(g) \in \mathbb {R}^3\), and we shall rely on a family \(\{\tilde{\gamma }_{h,g}^{\mathbf{c }}\}\) of neighboring exponential curves around \(\tilde{\gamma }^{\mathbf{c }}_g\). As we will show in subsequent Lemma 1 neighboring curve \(\tilde{\gamma }^{\mathbf{c }}_{h,g}\) departs from h and has the same spatial and rotational velocity as the curve \(\tilde{\gamma }^{\mathbf{c }}_g\) departing from g. This geometric idea is visualized in Fig. 6, where it is intuitively explained why one needs the initial velocity vector \(\tilde{\mathbf{R }}_{h^{-1}g}\mathbf{c }\), instead of \(\mathbf{c }\) in the following definition for the exponential curve departing from a neighboring point h close to g.
Definition 3
Let \(g \in SE(2)\) and \(\mathbf{c }=\mathbf{c }(g) \in \mathbb {R}^{3}\) be given. Then we define the family \(\{\tilde{\gamma }_{h,g}^{\mathbf{c }}\}\) of neighboring exponential curves
with rotation matrix \(\tilde{\mathbf{R }}_{h^{-1}g} \in SO(3)\) defined by
for all \(g=(\mathbf{x },\mathbf{R }) \in SE(2)\) and all \(h=(\mathbf{x }',\mathbf{R }') \in SE(2)\), with \(\mathbf{R },\mathbf{R }' \in SO(2)\) a counterclockwise rotation by, respectively, angle \(\theta \) and \(\theta '\).
Lemma 1
Exponential curve \(\tilde{\gamma }_{h,g}^{\mathbf{c }}\) departing from \(h\in SE(2)\) given by (51) has the same spatial and angular velocity as exponential curve \(\tilde{\gamma }^{\mathbf{c }}_g\) departing from \(g \in SE(2)\).
On the Lie algebra level, we have that the initial velocity component vectors of the curves \(\tilde{\gamma }^{\mathbf{c }}_g\) and \(\tilde{\gamma }_{h,g}^{\mathbf{c }}\) relate via \(\mathbf{c } \mapsto \tilde{\mathbf{R }}_{h^{-1}g} \mathbf{c }\).
On the Lie group level, we have that the curves themselves \(\tilde{\gamma }^{\mathbf{c }}_g(\cdot )=(\mathbf{x }_{g}(\cdot ),\mathbf{R }_{g}(\cdot ))\), \(\tilde{\gamma }_{h,g}^{\mathbf{c }}(\cdot )= (\mathbf{x }_{h}(\cdot ),\mathbf{R }_{h}(\cdot ))\) relate via
Proof
The proof follows from the proof of a more general theorem on the SE(3) case which follows later (in Lemma 3).
\(\square \)
Remark 5
Eq. (53) is the extension of Eq. (45) on \(\mathbb {R}^{2}\) to the SE(2) group.
Additional geometric background is given in Appendix 2.
5.2 Exponential Curve Fits in SE(2) of the First Order
For first-order exponential curve fits we solve an optimization problem similar to (44) given by
with \(\tilde{V}=\tilde{G}_{\mathbf{s }}*\tilde{U}\), \(g=(\mathbf{x },\mathbf{R })\), \(h=(\mathbf{x }',\mathbf{R }')\) and \(\mathrm{d}\overline{\mu }(h)=\mathrm{d}\mathbf{x }' \mathrm{d}\mu _{SO(2)}(\mathbf{R }')=\mathrm{d}\mathbf{x }' \mathrm{d}\theta '\). Here we first regularize the data with spatial and angular scale \(\mathbf{s }=(s_{p},s_o)\) and then average over a family of curves where we use spatial and angular scale \(\varvec{\rho }=(\rho _{p},\rho _o)\). Here \(s_{p},\rho _p>0\) are isotropic scales on \(\mathbb {R}^{2}\) and \(s_{o}, \rho _o>0\) are scales on \(S^{1}\) of separable Gaussian kernels, recall (27). Recall also (24) for the definition of the norm \(\Vert \cdot \Vert _{\mu }\). When solving this optimization problem the following structure matrix appears
In the remainder we use short notation \(\mathbf{S }^{\mathbf{s },\varvec{\rho }}:=\mathbf{S }^{\mathbf{s },\varvec{\rho }}(\tilde{U})\). We assume that \(\tilde{U}\), \(\varvec{\rho }, \mathbf{s }\), and g are chosen such that \(\mathbf{S }^{\mathbf{s },\varvec{\rho }}(g)\) is a non-degenerate matrix. The optimization problem is solved in the next theorem.
Theorem 1
(First-Order Fit via Structure Tensor) The normalized eigenvector \(\mathbf{M }_{\mu }\mathbf{c }^{*}(g)\) with smallest eigenvalue of the rescaled structure matrix \(\mathbf{M }_{\mu }\mathbf{S }^{\mathbf{s },\varvec{\rho }}(g)\mathbf{M }_{\mu }\) provides the solution \(\mathbf{c }^{*}(g)\) to optimization problem (54).
Proof
We will apply four steps. In the first step we write the time derivative as a directional derivative, in the second step we express the directional derivative in the gradient. In the third step we put the integrand in matrix-vector form. In the final step we express our optimization functional in the structure tensor and solve the Euler–Lagrange equations.
For the first step we use (51) and the fundamental property (17) of exponential curves such that via application of (13):
where we use short notation \(\tilde{\mathbf {R}}_{h^{-1}g} \mathbf{c } = \sum _{i=1}^{3} (\tilde{\mathbf {R}}_{h^{-1}g} \mathbf{c })^i \mathcal {A}_i |_h\).
In the second step we use the definition of the gradient (28) and the metric tensor (23) to rewrite this expression to

Then, in the third step we write this in vector-matrix form and we obtain via (28)

where we used the fact that \(\mathbf{M }_{\mu ^{2}}\) and \(\tilde{\mathbf {R}}_{h^{-1}g}^{T}\) commute.
Finally, we use the structure tensor definition (55) to rewrite the convex optimization functional in (54) as
while the boundary condition \(\Vert \mathbf{c }\Vert _{\mu }=1\) can be written as
The Euler–Lagrange equation reads \(\nabla \mathcal {E}(\mathbf{c }^{*})=\lambda _{1}\nabla \varphi (\mathbf{c }^{*})\), with \(\lambda _{1}\) the smallest eigenvalue of \(\mathbf{M }_{\mu }\mathbf{S }^{\mathbf{s },\varvec{\rho }}(g)\mathbf{M }_{\mu }\) and we have
from which the result follows. \(\square \)
The next remark explains the frequent presence of the \(\mathbf{M }_{\mu }\) matrices in (69).
Remark 6
The diagonal \(\mathbf{M }_{\mu }\) matrices enter the functional due to the gradient definition (28), and they enter the boundary condition via \(\Vert \mathbf{c }\Vert _{\mu }^2=\mathbf{c }^T \mathbf{M }_{\mu ^2} \mathbf{c }=1\). In both cases they come from the metric tensor (23). Parameter \(\mu \) which controls the stiffness of the exponential curves has physical dimension \([\text {Length}]^{-1}\). As a result, the normalized eigenvector \(\mathbf {M}_{\mu } \mathbf{c }^{*}(g)\) is, in contrast to \(\mathbf{c }^{*}(g)\), dimensionless.
5.3 Exponential Curve Fits in SE(2) of the Second Order
We now discuss the second-order optimization approach based on the Hessian matrix. At each \(g\in SE(2)\) we define a \(3\times 3\) non-symmetric Hessian matrix
and where i denotes the row index and j denotes the column index, and with \(\tilde{G}_{\mathbf{s }}\) a Gaussian kernel with isotropic spatial part as described in Eq. (27). In the remainder we write \(\mathbf{H }^{\mathbf{s }} :=\mathbf{H }^{\mathbf{s }}(\tilde{U})\).
Remark 7
As the left-invariant vector fields are non-commutative, there are many ways to define the Hessian matrix on SE(2), since the ordering of the left-invariant derivatives matters. From a differential geometrical point of view our choice (62) is correct, as we motivate in Appendix 4.
For second-order exponential curve fits we consider 2 different optimization problems. In the first case we minimize the second-order derivative along the exponential curve:

In the second case we minimize the norm of the first-order derivative of the gradient of the neighboring family of exponential curves:

with again \(\tilde{V}=\tilde{G}_{\mathbf{s }}*\tilde{U}\).
Remark 8
Optimization problem (63) can also be written as an optimization problem over the neighboring family of curves, as it is equivalent to problem:
In the next two theorems we solve these optimization problems.
Theorem 2
(Second-Order Fit via Symmetric Sum Hessian) Let \(g \in SE(2)\) be such that the eigenvalues of the rescaled symmetrized Hessian
have the same sign. Then the normalized eigenvector \(\mathbf{M }_{\mu }\mathbf{c }^{*}(g)\) with smallest eigenvalue of the rescaled symmetrized Hessian matrix provides the solution \(\mathbf{c }^{*}(g)\) of optimization problem (63).
Proof
Similar to the proof of Theorem 1 we first write the time derivative as a directional derivative using Eq. (13). Since now we have a second-order derivative this step is applied twice:
Then we write the result in matrix-vector form and split the matrix in a symmetric and anti-symmetric part
where only the symmetric part remains. Finally, the optimization functional in (63) (which is convex if the eigenvalues have the same sign) can be written as
Again we have the boundary condition \(\varphi (\mathbf{c })=\mathbf{c }^T \mathbf{M }_{\mu ^2} \mathbf{c }-1=0\). The result follows using the Euler–Lagrange formalism \(\nabla \mathcal {E}(\mathbf{c }^{*})=\lambda _{1}\nabla \varphi (\mathbf{c }^{*})\):
which boils down to finding the eigenvector with minimal absolute eigenvalue \(|\lambda _{1}|\) which gives our result. \(\square \)
Theorem 3
(Second-Order Fit via Symmetric Product Hessian) Let \(\rho _p,\rho _o, s_p,s_o>0\). The normalized eigenvector \(\mathbf{M }_{\mu }\mathbf{c }^{*}(g)\) with smallest eigenvalue of matrix
provides the solution \(\mathbf{c }^{*}(g)\) of optimization problem (64).
Proof
First we use the definition of the gradient (28) and then we again rewrite the time derivative as a directional derivative:
for \(\tilde{\mathbf{c }} = \tilde{\mathbf{R }}_{h^{-1} g} \mathbf{c }\), recall (52), and where \(\mu _i=\mu \) for \(i=1,2\) and \(\mu _i=1\) for \(i=3\). Here we use \(\tilde{\gamma }_{h,g}^{\mathbf{c }}(0)=h\), and the formula for left-invariant vector fields (10). Now insertion of (71) into the metric tensor  (23) yields
(23) yields

Finally, the convex optimization functional in (64) can be written as
Again we have the boundary condition \(\varphi (\mathbf{c })=\mathbf{c }^T \mathbf{M }_{\mu ^2} \mathbf{c }-1=0\) and the result follows by application of the Euler–Lagrange formalism: \(\nabla \mathcal {E}(\mathbf{c }^{*})=\lambda _{1}\nabla \varphi (\mathbf{c }^{*})\). \(\square \)
6 Exponential Curve Fits in SE(3)
In this section we generalize the exponential curve fit theory from the preceding chapter on SE(2) to SE(3). Because our data on the group SE(3) was obtained from data on the quotient \(\mathbb {R}^{3}\rtimes S^{2}\), we will also discuss projections of exponential curve fits on the quotient.
We start in Sect. 6.1 with some preliminaries on the quotient structure (3). Here we will also introduce the concept of projected exponential curve fits. Subsequently, in Sect. 6.2, we provide basic theory on how to obtain the appropriate family of neighboring exponential curves. More details can be found in Appendix 2. In Sect. 6.3 we formulate exponential curve fits of the first order as a variational problem. For that we define the structure tensor on SE(3), which we use to solve the variational problem in Theorems 4 and 5. Then we present the twofold algorithm for achieving torsion-free exponential curve fits. In Sect. 6.4 we formulate exponential curve fits of the second order as a variational problem. Then we define the Hessian tensor on SE(3), which we use to solve the variational problem in Theorem 6. Again torsion-free exponential curve fits are accomplished via a twofold algorithm.
Throughout this section we will rely on the differential geometrical tools of Sect. 2, listed in panels (a) and (b) in in Table 1 in Appendix 5. We also generalize concepts on exponential curve fits introduced in the previous section to the case \(d=3\) (requiring additional notation). They are listed in panel (c) in the table in Appendix 5.
6.1 Preliminaries on the Quotient \(\mathbb {R}^{3} \rtimes S^2\)
Now let us set \(d=3\), and let us assume input U is given and let us first concentrate on its domain. This domain equals the joint space \(\mathbb {R}^{3} \rtimes S^{2}\) of positions and orientations of dimension 5, which we identified with a 5-dimensional group quotient of SE(3), where SE(3) is of dimension 6 (recall (3)). For including a notion of alignment it is crucial to include the non-commutative relation in (4) between rotations and translation, and not to consider the space of positions and orientations as a flat Cartesian product. Therefore, we model the joint space of positions and orientations as the Lie group quotient (3), where
for reference axis \(\mathbf{a }=\mathbf e _{z}=(0,0,1)^T\). Within this quotient structure two rigid body motions \(g=(\mathbf{x },\mathbf{R }), g'=(\mathbf{x }',\mathbf{R }') \in SE(3)\) are equivalent if
Furthermore, one has the action \(\odot \) of \(g=(\mathbf{x },\mathbf{R }) \in SE(3)\) onto \((\mathbf y ,\mathbf{n }) \in \mathbb {R}^{3} \times S^{2}\), which is defined by
As a result we have
Thereby, a single element in \(\mathbb {R}^{3} \rtimes S^{2}\) can be considered as the equivalence class of all rigid body motions that map reference position and orientation \((\mathbf{0 },\mathbf{a })\) onto \((\mathbf{x },\mathbf{n })\). Similar to the common identification of \(S^{2}\equiv SO(3)/SO(2)\), we denote elements of the Lie group quotient \(\mathbb {R}^{3}\rtimes S^{2}\) by \((\mathbf{x },\mathbf{n })\).
6.1.1 Legal Operators
Let us recall from Sect. 3 that exponential curve fits induce gauge frames. Note that both the induced gauge frame \(\{\mathcal {B}_1,\ldots , \mathcal {B}_{6}\}\) and the non-adaptive frame \(\{\mathcal {A}_{1},\ldots ,\mathcal {A}_{6}\}\) are defined on the Lie group SE(3), and cannot be defined on the quotient. Nevertheless, combinations of them can be well defined on \(\mathbb {R}^{3}\rtimes S^2\) (e.g., \(\Delta _{\mathbb {R}^{3}}=\mathcal {A}_{1}^{2}+\mathcal {A}_{2}^{2}+\mathcal {A}_{3}^{2}\) is well defined on the quotient). This brings us to the definition of so-called legal operators, as shown in [29, Thm. 1]. In short, the operator \(\tilde{U} \mapsto \tilde{\varPhi }(\tilde{U})\) is legal (left-invariant and well defined on the quotient) if and only if
recall (7), where
with the \(\mathbf{R }_\mathbf{e _{z},\alpha }\) the counterclockwise rotation about \(\mathbf e _{z}\). Such legal operators relate one-to-one to operators \(\varPhi : \mathbb {L}_{2}(\mathbb {R}^{3} \rtimes S^{2}) \rightarrow \mathbb {L}_{2}(\mathbb {R}^{3} \rtimes S^{2})\) via
relying consequently on (1).
6.1.2 Projected Exponential Curve Fits
Action (74) allows us to map a curve \(\tilde{\gamma }(\cdot )=(\mathbf{x }(\cdot ),\mathbf{R }(\cdot ))\) in SE(3) onto a curve \((\mathbf{x }(\cdot ),\mathbf{n }(\cdot ))\) on \(\mathbb {R}^{3} \rtimes S^2\) via
This can be done with exponential curve fits \(\tilde{\gamma }^{\mathbf{c }=\mathbf{c }^{*}(g)}_{g}(t)\) to define projected exponential curve fits.
Definition 4
We define for \(g=(\mathbf{x },\mathbf{R }_{\mathbf{n }})\) the projected exponential curve fit
Lemma 2
The projected exponential curve fit is well defined on the quotient, i.e., the right-hand side of (78) is independent of the choice of \(\mathbf{R }_{\mathbf{n }}\) s.t. \(\mathbf{R }_{\mathbf{n }} \mathbf e _z = \mathbf{n }\), if the optimal tangent found in our fitting procedure satisfies:
and for all \(g\in SE(3)\), with
Illustration of the family of curves \(\tilde{\gamma }_{h,g}^{\mathbf{c }}\) in SE(3). Left The (spatially projected) exp-curve \(t \mapsto P_{\mathbb {R}^{3}}\tilde{\gamma }^{\mathbf{c }}_{g}(t)\), with \(g=(\mathbf{x },\mathbf{R }_{\mathbf{n }})\) in red. The frames indicate the rotation part \(P_{SO(3)}\tilde{\gamma }^{\mathbf{c }}_{g}(t)\), which for clarity we depicted only at two time instances t. Middle neighboring exp-curve \(t \mapsto \tilde{\gamma }^{\mathbf{c }}_{g,h}(t)\) with \(h=(\mathbf{x }',\mathbf{R }_{\mathbf{n }})\), \(\mathbf{x }\ne \mathbf{x }'\) in blue, i.e., neighboring exp-curve departing with same orientation and different position. Right exp-curve \(t \mapsto \tilde{\gamma }^{\mathbf{c }}_{g,h}(t)\) with \(h=(\mathbf{x },\mathbf{R }_{\mathbf{n }'})\), \(\mathbf{n }'\ne \mathbf{n }\), i.e., the neighboring exp-curve departing with same position and different orientation (Color figure online)
Proof
For well-posed projected exponential curve fits we need the right-hand side of (78) to be independent of \(\mathbf{R }_{\mathbf{n }}\) s.t. \(\mathbf{R }_{\mathbf{n }} \mathbf e _z = \mathbf{n }\), i.e., it should be invariant under \(g \rightarrow g h_{\alpha }\). Therefore, we have the following constraint on the fitted curves:
Then the constraint on the optimal tangent (79) follows from fundamental identity
which holdsFootnote 2 for all \(h_{\alpha }\). We apply this identity (82) to the right-hand side of (81) and use the definition of \(\odot \) defined in (74) yielding:
Finally our constraint (79) follows from \(\mathbf Z _{\alpha }^T=\mathbf Z _{\alpha }^{-1}\). \(\square \)
6.2 Neighboring Exponential Curves in SE(3)
Here we generalize the concept of family of neighboring exponential curves (45) in the \(\mathbb {R}^d\)-case, and Definition 3 in the SE(2)-case, to the SE(3)-case.
Definition 5
Given a fixed reference point \(g \in SE(3)\) and velocity component \(\mathbf{c }=\mathbf{c }(g)=(\mathbf{c }^{(1)}(g),\mathbf{c }^{(2)}(g)) \in \mathbb {R}^6\), we define the family \(\{\tilde{\gamma }_{h,g}^{\mathbf{c }}(\cdot )\}\) of neighboring exponential curves by
with rotation matrix \(\tilde{\mathbf{R }}_{h^{-1}g} \in SO(6)\) defined by
for all \(g=(\mathbf{x },\mathbf{R }), h=(\mathbf{x }',\mathbf{R }') \in SE(3)\).
The next lemma motivates our specific choice of neighboring exponential curves. The geometric idea is visualized in Fig. 7 and is in accordance with Fig. 6 on the SE(2)-case.
Lemma 3
Exponential curve \(\tilde{\gamma }_{h,g}^{\mathbf{c }}\) departing from \(h=(\mathbf{x }',\mathbf{R }')\in SE(3)\) given by (84) has the same spatial and rotational velocity as exponential curve \(\tilde{\gamma }^{\mathbf{c }}_g\) departing from \(g=(\mathbf{x },\mathbf{R }) \in SE(3)\).
On the Lie algebra level, we have that the initial velocity component vectors of the curves \(\tilde{\gamma }^{\mathbf{c }}_g\) and \(\tilde{\gamma }_{h,g}^{\mathbf{c }}\) relate via \(\mathbf{c } \mapsto \tilde{\mathbf{R }}_{h^{-1}g} \mathbf{c }\).
On the Lie group level, we have that the curves themselves \(\tilde{\gamma }^{\mathbf{c }}_g(\cdot )=(\mathbf{x }_{g}(\cdot ),\mathbf{R }_{g}(\cdot ))\), \(\tilde{\gamma }_{h,g}^{\mathbf{c }}(\cdot )= (\mathbf{x }_{h}(\cdot ),\mathbf{R }_{h}(\cdot ))\) relate via
Proof
See Appendix 2. \(\square \)
Remark 9
Lemma 3 extends Lemma 1 to the SE(3) case. When projecting the curves \(\tilde{\gamma }_{g}^{\mathbf{c }}\) and \(\tilde{\gamma }_{h,g}^{\mathbf{c }}\) into the quotient, one has that curves \(\tilde{\gamma }_{g}^{\mathbf{c }} \odot (\mathbf{0 },\mathbf{a })\) and \(\tilde{\gamma }_{h,g}^{\mathbf{c }} \odot (\mathbf{0 },\mathbf{a })\) in \(\mathbb {R}^{3}\rtimes S^2\) carry the same spatial and angular velocity.
Remark 10
In order to construct the family of neighboring exponential curves in SE(3), one applies the transformation \(\mathbf{c } \mapsto \tilde{\mathbf{R }}_{h^{-1}g} \mathbf{c }\) in the Lie algebra. Such a transformation preserves the left-invariant metric:

for all \(h \in SE(3)\) and all \(t \in \mathbb {R}\). For further differential geometrical details see Appendix 2.
6.3 Exponential Curve Fits in SE(3) of the First Order
Now let us generalize the first-order exponential curve fits of Theorem 1 to the setting of \(\mathbb {R}^{3}\rtimes S^{2}\). Here we first consider the following optimization problem on SE(3) (generalizing (44)):
Recall that \(\Vert \cdot \Vert _{\mu }\) was defined in (24), \(\tilde{V}\) in (26), and \(\mu \) in (25). The reason for including the condition \(c^6=0\) will become clear after defining the structure matrix.
6.3.1 The Structure Tensor on SE(3)
We define structure matrices \(\mathbf {S}^{\mathbf{s },\varvec{\rho }}\) of \(\tilde{U}\) by
where we use matrix \(\tilde{\mathbf{R }}_{h^{-1}g}\) defined in Eq. (85). Again we use short notation \(\mathbf {S}^{\mathbf{s },\varvec{\rho }} :=\mathbf {S}^{\mathbf{s },\varvec{\rho }} (\tilde{U})\).
Remark 11
By construction (1) and (10) we have
so the null space of our structure matrix includes
Remark 12
We assume that \(\mathbf{s }=(s_{p}, s_{o})\) and function \(\tilde{U}\) are chosen in such a way that the null space of the structure matrix is precisely equal to \(\mathcal {N}\) (and not larger).
Due to the assumption in Remark 12, we need to impose the condition
in our exponential curve optimization to avoid non-uniqueness of solutions. To clarify this, we note that the optimization functional in (88) can be rewritten as
as we will show in the next theorem where we solve the optimization problem for first-order exponential curve fits. Indeed, for uniqueness we need (91) as otherwise we would have \(\mathcal {E}(\mathbf{c }+\mathbf{M }_{\mu ^{-2}}\mathbf{c }_0)=\mathcal {E}(\mathbf{c })\) for all \(\mathbf{c }_0 \in \mathcal {N}\).
Theorem 4
(First-Order Fit via Structure Tensor) The normalized eigenvector \(\mathbf{M }_{\mu }\mathbf{c }^{*}(g)\) with smallest non-zero eigenvalue of the rescaled structure matrix \(\mathbf{M }_{\mu }\mathbf{S }^{\mathbf{s },\varvec{\rho }}(g)\mathbf{M }_{\mu }\) provides the solution \(\mathbf{c }^{*}(g)\) to optimization problem (88).
Proof
All steps (except for the final step of this proof, where the additional constraint \(c^6=0\) enters the problem) are analogous to the proof of the first-order method in the SE(2) case: the proof of Theorem 1. We will now shortly repeat these first steps. First we rewrite the time derivative as a directional derivative which is then rewritten to the gradient

We then put this result in matrix-vector form:

This again yields the following optimization functional
So, just as in the SE(2)-case we have the following Euler–Lagrange equations:
Again the second equality in (95) follows from the first by multiplication by \(\mathbf{M }_{\mu }^{-1}\).
Finally, the constraint \(c^{6}=0\) is included in our optimization problem (88) to excluded the null space (90) from the optimization; therefore, we take the eigenvector with the smallest non-zero eigenvalue providing us the final result. \(\square \)
6.3.2 Projected Exponential Curve Fits in \(\mathbb {R}^{3}\rtimes S^{2}\)
In reducing the problem to \(\mathbb {R}^{3} \rtimes S^{2}\) we first note that
with \(\mathbf Z _{\alpha }\) defined in Eq. (80), and where we recall \(h_{\alpha }=(\mathbf{0 },\mathbf{R }_\mathbf{e _{z},\alpha })\).
In the following theorem we summarize the well-posedness of our projected curve fits on data \(U:\mathbb {R}^{3}\rtimes S^2 \rightarrow \mathbb {R}\) and use the quotient structure to simplify the structure tensor.
Theorem 5
(First-Order Fit and Quotient Structure) Let \(g=(\mathbf{x },\mathbf{R }_{\mathbf{n }})\) and \(h=(\mathbf{x }',\mathbf{R }_{\mathbf{n }'})\) where \(\mathbf{R }_{\mathbf{n }}\) and \(\mathbf{R }_{\mathbf{n }'}\) denote any rotation which maps \(\mathbf e _z\) onto \(\mathbf{n }\) and \(\mathbf{n }'\), respectively. Then, the structure tensor defined by (89) can be expressed as
The normalized eigenvector \(\mathbf{M }_{\mu }\mathbf{c }^{*}(\mathbf{x },\mathbf{R }_{\mathbf{n }})\) with smallest non-zero eigenvalue of the rescaled structure matrix \(\mathbf{M }_{\mu }\mathbf{S }^{\mathbf{s },\varvec{\rho }}(g)\mathbf{M }_{\mu }\) provides the solution of (88) and defines a projected curve fit in \(\mathbb {R}^{3}\rtimes S^{2}\):
which is independent of the choice of \(\mathbf{R }_{\mathbf{n }'}\) and \(\mathbf{R }_{\mathbf{n }}\).
Volume rendering of a 3D test-image. The real part of the orientation score (cf. Sect. 7.1) provides us a density U on \(\mathbb {R}^{3}\rtimes S^2\). Left spatial parts of exponential curves (in black) aligned with spatial generator \(\left. \mathcal {A}_{3}\right| _{({\mathbf{x }},\mathbf{R }_{{\mathbf{n }}_{max}({\mathbf{x }})})}\), where \({\mathbf{n }}_\mathrm{max}({\mathbf{x }})= \underset{{\mathbf{n }}\in S^{2}}{\text {argmax}} |U({\mathbf{x }},{\mathbf{n }})|\). Right spatial parts of our exponential curve fits Eq. (104) computed via the algorithm in Sect. 6.3.3, which better follow the curvilinear structures
Proof
The proof consists of two parts. First we prove that (97) follows from the structure tensor defined in (89). Then we use Lemma 2 to prove that our projected exponential curve fit (98) is well defined. For both we use Theorem 4 as our venture point.
For the first part of the proof we note that the integrand in the structure tensor definition Eq. (89) is invariant under \(h \mapsto h h_{\alpha }=h (\mathbf{0 },\mathbf{R }_\mathbf{e _{z},\alpha })\) on the integration variable. To show this we first note that, \(\mathbf Z _{\alpha }\) defined in (80), satisfies \(\mathbf Z _{\alpha }(\mathbf Z _{\alpha })^T=I\). Furthermore, we have
and \(\tilde{G}_{\varvec{\rho }}(h h_{\alpha })=\tilde{G}_{\varvec{\rho }}(h)\). Therefore, integration over third Euler-angle \(\alpha \) is no longer needed in the definition of the structure tensor (89) as it just produces a constant \(2\pi \) factor.
For the second part we apply Lemma 2 and thereby it remains to be shown that condition \(\mathbf{c }^{*}(g h_{\alpha })= \mathbf Z _{\alpha }^T \mathbf{c }^{*}(g)\) is satisfied. This directly follows from (96):
which shows our condition. \(\square \)
6.3.3 Torsion-Free Exponential Curve Fits of the First Order via a Twofold Approach
Theorem 4 provides us exponential curve fits that possibly carry torsion. From Eq. (22) we deduce that the torsion norm of such an exponential curve fit is given by \(|\tau |=\frac{1}{\Vert \mathbf{c }^{(1)}\Vert } (c^{1}c^{4}+c^{2}c^5 +c^{3}c^6)|\kappa |\). Together with the fact that we exclude the null space \(\mathcal {N}\) from our optimization domain by including constraint \(c^6=0\), this results in insisting on zero torsion along horizontal exponential curves where \(c^{1}=c^{2}=0\). Along other exponential curves torsion appears if \(c^{1}c^{4}+c^{2}c^5\ne 0\).
Now the problem is that insisting, a priori, on zero torsion for horizontal curves while allowing non-zero torsion for other curves is undesirable. On top of this, torsion is a higher order less-stable feature than curvature. Therefore, we would like to exclude it altogether from our exponential curve fits presented in Theorems 4 and 5, by a different theory and algorithm. The results of the algorithm show that even if structures do have torsion, the local exponential curve fits do not need to carry torsion in order to achieve good results in the local frame adaptation, see, e.g., Fig. 8.
The constraint of zero torsion forces us to split our exponential curve fit into a twofold algorithm:
- Step 1 :
-
Estimate at \(g \in SE(3)\) the spatial velocity part \(\mathbf{c }^{(1)}(g)\) from the spatial structure tensor.
- Step 2 :
-
Move to a different location \(g_{new} \in SE(3)\) where a horizontal exponential curve fit makes sense and then estimate the angular velocity \(\mathbf{c }^{(2)}\) from the rotation part of the structure tensor over there.
This forced splitting is a consequence of the next lemma.
Lemma 4
Consider the class of exponential curves with non-zero spatial velocity \(\mathbf{c }^{(1)}\ne \mathbf{0 }\) such that their spatial projections do not have torsion. Within this class the constraint \(c^{6}=0\) does not impose constraints on curvature if and only if the exponential curve is horizontal.
Proof
For a horizontal curve \(\tilde{\gamma }^{\mathbf{c }}_{g}(t)\) we have \(\chi =0 \Leftrightarrow c^{1}=c^{2}=0\) and indeed \(|\tau | = \frac{{\mathbf{c }}^{(1)} \cdot {\mathbf{c }}^{(2)} |\kappa |}{\Vert {\mathbf{c }}^{(1)}\Vert }=c^{6}|\kappa |=0\) and we see that constraints \(c^{6}=0\) and \(|\tau |=0\) reduce to only one constraint. The curvature magnitude stays constant along the exponential curve and the curvature vector at \(t=0\), recall Eq. (21), is in this case given by
which can be any vector orthogonal to spatial velocity \(\mathbf{c }^{(1)}=(0,0,c^{3})^T\). Now let us check whether the condition is necessary. Suppose \(t \mapsto \tilde{\gamma }_{g}^{\mathbf{c }}(t)\) is not horizontal, and suppose it is torsion free with \(c^6=0\). Then we have \(c^{1}c^{4}+c^{2}c^{5}=0\), as a result the initial curvature
is both orthogonal to vector \(\mathbf{c }^{(1)}=(c^1,c^2,c^3)^T\) and orthogonal to \((-c^2,c^1,0)^T\), and thereby constrained to a one dimensional subspace. \(\square \)
From these observations we draw the following conclusion for our exponential curve fit algorithms.
Conclusion In order to allow for all possible curvatures in our torsion-free exponential curve fits, we must relocate the exponential curve optimization at \(g \in SE(3)\) in \(\tilde{U}:SE(3) \rightarrow \mathbb {R}\) to a position \(g_{new} \in SE(3)\) where a horizontal exponential curve can be expected. Subsequently, we can use Lemma 3 to transport the horizontal and torsion-free curve through \(g_{new}\), back to a torsion-free exponential curve through g.
This conclusion is the central idea behind our following twofold algorithm for exponential curve fits.
6.3.4 Algorithm Twofold Approach
The algorithm follows the subsequent steps:
Step 1a Initialization. Compute structure tensor \(\mathbf {S}^{\mathbf{s },\varvec{\rho }}(g)\) from input image \(U:\mathbb {R}^{3} \times S^{2} \rightarrow \mathbb {R}^{+}\) via Eq. (97).
Step 1b Find the optimal spatial velocity:
for \(g=(\mathbf{x },\mathbf{R }_{\mathbf{n }}\)), which boils down to finding the eigenvector with minimal eigenvalue of the \(3\times 3\) spatial sub-matrix of the structure tensor (89).
Step 2a Given \(\mathbf{c }^{(1)}(g)\) we aim for an auxiliary set of coefficients, where we also take into account rotational velocity. To achieve this in a stable way we move to a different location in the group:
and apply the transport of Lemma 3 afterwards. At \(g_{new}\), we enforce horizontality, see Remark 13 below, and we consider the auxiliary optimization problem
Here zero deviation from horizontality (34) and zero torsion (22) is equivalent to the imposed constraint:
Step 2b The auxiliary coefficients \(\mathbf{c }_{new}(g_{new})=(0,0\), \(c^{3}(g_{new}), c^{4}(g_{new}),c^{5}(g_{new}),0)^{T}\) of a torsion-free, horizontal exponential curve fit \(\tilde{\gamma }_{g_{new}}^{\mathbf{c }_{new}}\) through \(g_{new}\). Now we apply transport (via Lemma 3) of this horizontal exponential curve fit towards the corresponding exponential curve through g:
This gives the final, torsion-free, exponential curve fit \(t \mapsto \tilde{\gamma }_{g}^{\mathbf{c }^{*}(g)}(t)\) in SE(3), yielding the final output projected curve fit
with \(g=(\mathbf{x },\mathbf{R }_{\mathbf{n }})\), recall Eq. (74).
Remark 13
In step 2a of our algorithm we jump to a new location \(g_{new}=(\mathbf{x },\mathbf{R }_{\mathbf{n }_{new}})\) with possibly different orientation \(\mathbf{n }_{new}\) such that spatial tangent vector
points in the same direction as \(\mathbf{n }_{new} \in S^2\), recall Eq. (31), from which it follows that \(\mathbf{n }_{new}\) is indeed given by (101). If \(\mathbf{c }^{(1)}=(c^{1},c^{2},c^{3})^T=\mathbf{a }=(0,0,1)^T\) then \(\mathbf{n }_{new}=\mathbf{n }\).
Lemma 5
The preceding algorithm is well defined on the quotient \(\mathbb {R}^{3}\rtimes S^{2}=SE(3)/(\{{\mathbf {0}}\}\times SO(2))\).
Proof
To show that the preceeding algorithm is well defined on the quotient, we need to show that the final result (104) is independent on both the choice of of \(\mathbf{R }_{\mathbf{n }} \in SO(3)\) s.t. \(\mathbf{R }_{\mathbf{n }}\mathbf e _{z}=\mathbf{n }\) and the choice of \(\mathbf{R }_{\mathbf{n }_\mathrm{new}} \in SO(3)\) s.t. \(\mathbf{R }_{\mathbf{n }_\mathrm{new}}\mathbf e _{z}=\mathbf{n }_{new}\).
First, we show independence on the choice of \(\mathbf{R }_{\mathbf{n }}\). We apply Lemma 2 and thereby it remains to be shown that condition \(\mathbf{c }^{*}_\mathrm{final}(g h_{\alpha })= \mathbf Z _{\alpha }^T \mathbf{c }^{*}_\mathrm{final}(g)\) is satisfied. This follows directly from Eq. (103) if as long as \(\mathbf{n }_{new}\) found in Step 2a is independent of the choice of \(\mathbf{R }_{\mathbf{n }}\). This property indeed follows from \(\mathbf{c }^{(1)}(g h_{\alpha }) = \mathbf{R }_\mathbf{e _{z},\alpha }^T \mathbf{c }^{(1)}(g)\) which can be proven analogously to (99). Then we have
So we conclude that (104) is indeed independent on the choice of \(\mathbf{R }_{\mathbf{n }}\).
Finally, Eq. (104) is independent of the choice of \(\mathbf{R }_{\mathbf{n }_\mathrm{new}}\). This follows from \(\mathbf{c }_\mathrm{new}(g h_{\alpha }) = \mathbf Z _{\alpha }^T \mathbf{c }_\mathrm{new}(g)\) in Step 2a. Then \(\mathbf{c }^{*}_\mathrm{final}\) in Eq. (103) is independent of the choice of \(\mathbf{R }_{\mathbf{n }_\mathrm{new}}\) because \(\mathbf Z _{\alpha }^{T}\) in \(\mathbf{c }_\mathrm{new} \mapsto \mathbf Z _{\alpha }^{T} \mathbf{c }_\mathrm{new}\) is canceled by \(\mathbf{R }_\mathrm{new} \mapsto \mathbf{R }_\mathrm{new} \mathbf{R }_\mathbf{e _{z},\alpha }\) in Eq. (103). \(\square \)
In Fig. 8 we provide an example of spatially projected exponential curve fits in SE(3) via the twofold approach. Here we see that the resulting gauge frames better follow the curvilinear structures of the data (in comparison to the normal left-invariant frame).
6.4 Exponential Curve Fits in SE(3) of the Second Order
In this section we will generalize Theorem 2 to the case \(d=3\), where again we include the restriction to torsion-free exponential curves.
6.4.1 The Hessian on SE(3)
For second-order curve fits we consider the following optimization problem:
with \(\tilde{V}=\tilde{G}_{\mathbf{s }}*\tilde{U}\). Before solving this optimization problem in Theorem 6, we first define the \(6\times 6\) non-symmetric Hessian matrix by
and where \(i=1,\ldots ,6\) denotes the row index, and \(j=1,\ldots , 6\) denotes the column index. Again we write \(\mathbf{H }^{\mathbf{s }}:=\mathbf{H }^{\mathbf{s }} (\tilde{U})\).
Theorem 6
(Second-Order Fit via Symmetric Sum Hessian) Let \(g \in SE(3)\) be such that the symmetrized Hessian matrix \(\frac{1}{2} \mathbf{M }_{\mu }^{-1}( \mathbf{H }^{\mathbf{s }}(g)+ (\mathbf{H }^{\mathbf{s }}(g))^T) \mathbf{M }_{\mu }^{-1}\) has eigenvalues with the same sign. Then the normalized eigenvector \(\mathbf{M }_{\mu }\mathbf{c }^{*}(g)\) with smallest absolute non-zero eigenvalue of the symmetrized Hessian matrix provides the solution \(\mathbf{c }^{*}(g)\) of optimization problem (106).
Proof
Similar to the proof of Theorem 2 (only now with summations from 1 to 5). Again we include our additional constraint \(c^6=0\) by taking the smallest non-zero eigenvalue. \(\square \)
Remark 14
The restriction to \(g \in SE(3)\) such that the eigenvalues of the symmetrized Hessian carry the same sign is necessary for a unique solution of the optimization. Note that in case of our first-order approach via the positive definite structure tensor, no such cumbersome constraints arise. In case \(g \in SE(3)\) is such that the eigenvalues of the symmetrized Hessian have different sign there are 2 options:
-
1.
Move towards a neighboring point where the Hessian eigenvalues have the same sign and apply transport (Lemma 3, Fig. 7) of the exponential curve fit at the neighboring point.
-
2.
Take \(\mathbf{c }^{*}(g)\) still as the eigenvector with smallest absolute eigenvalue (representing minimal absolute principal curvature), though this no longer solves (106).
In black the spatially projected part of exponential curve fits \(t \mapsto \gamma ^{\mathbf{c }}_{g}(t)\) of the second kind (fitted to the real part of the 3D invertible orientation score, for details see Fig. 10) of the 3D image visualized via volume rendering. Left output of the twofold approach outlined in Sect. 6.4.2. Right output of the twofold approach outlined in Appendix 3 with \(s_p=\frac{1}{2}\), \(s_o=\frac{1}{2} (0.4)^2\), \(\mu =10\)
6.4.2 Torsion-Free Exponential Curve Fits of the Second Order via a Twofold Algorithm
In order to obtain torsion-free exponential curve fits of the second order via our twofold algorithm, we follow the same algorithm as in Subsection 6.3.3, but now with the Hessian field \(\mathbf{H }^{\mathbf{s }}\) (107) instead of the structure tensor field.
Step 1a Initialization. Compute Hessian \(\mathbf {H}^{\mathbf{s }}(g)\) from input image \(U:\mathbb {R}^{3} \times S^{2} \rightarrow \mathbb {R}^{+}\) via Eq. (107).
Step 1b Find the optimal spatial velocity by (100) where we replace \(\mathbf{M }_{\mu ^2} \mathbf {S}^{\mathbf{s },\varvec{\rho }}(g) \mathbf{M }_{\mu ^2} \) by \(\mathbf {H}^{\mathbf{s }}(g)\).
Step 2a We again fit a horizontal curve at \(g_{new}\) given by (101). The procedure is done via (102) where we again replace \(\mathbf{M }_{\mu ^2} \mathbf {S}^{\mathbf{s },\varvec{\rho }}(g) \mathbf{M }_{\mu ^2} \) by \(\mathbf {H}^{\mathbf{s }}(g)\).
Step 2b Remains unchanged. We again apply Eq. (103) and Eq. (104).
There are some serious computational technicalities in the efficient computation of the entries of the Hessian for discrete input data, but this is outside the scope of this article and will be pursued in future work.
Remark 15
In Appendix 3 we propose another twofold second-order exponential curve fit method. Here one solves a variational problem for exponential curve fits where exponentials are factorized over, respectively, spatial and angular part. Empirically, this approach performs good (see, e.g., Fig. 9).
7 Image Analysis Applications
In this section we present examples of applications where the use of gauge frame in SE(d) obtained via exponential curve fits is used for defining data-adaptive left-invariant operators. Before presenting the applications, we start by briefly summarizing the invertible orientation score theory in Sect. 7.1.
In case \(d=2\) the application presented is the enhancing of the vascular tree structure in 2D retinal images via differential invariants based on gauge frames. This is achieved by extending the classical Frangi vesselness filter [36] to distributions \(\tilde{U}\) on SE(2). Gauge frames in SE(2) can also be used in non-linear multiple-scale crossing-preserving diffusions as demonstrated in [63], but we will not discuss this application in this paper.
In case \(d=3\) the envisioned applications include blood vessel detection in 3D MR angiography, e.g., the detection of the Adamkiewicz vessel, relevant for surgery planning. Also in extensions towards fiber-enhancement of diffusion-weighted MRI [29, 30] the non-linear diffusions are of interest. Some preliminary practical results have been conducted on such 3D datasets [21, 23, 42], but here we shall restrict ourselves to very basic artificial 3D datasets to show a proof of concept, and leave these three applications for future work.
7.1 Invertible Orientation Scores
In the image analysis applications discussed in this section our function \(U:\mathbb {R}^{d} \rtimes S^{d-1} \rightarrow \mathbb {R}\) is given by the real part of an invertible orientation score:
where \(\mathbf{R }_{\mathbf{n }}\) is any rotation mapping reference axis \(\mathbf{a }\) onto \(\mathbf{n } \in S^{d-1}\), where \(f\in \mathbb {L}_2(\mathbb {R}^d)\) denotes a input image, and where \(\psi \) is a so-called ’cake-wavelet’ and with
For \(d >2\) we restrict ourselves to wavelets \(\psi \) satisfying
and for all rotations \({\mathbf{R }}_{\mathbf{a },\alpha } \in \text {Stab}(\mathbf{a })\) (for \(d=3\) this means for all rotations about axis \(\mathbf{a }\), Eq. (2)). As a result U is well defined on the left cosets \(\mathbb {R}^{d}\rtimes S^{d-1}=SE(d)/(\{{\mathbf {0}}\} \times SO(d-1))\) as the choice of \(\mathbf{R }_{\mathbf{n }} \in SO(d)\) mapping \({\mathbf{a }}\) onto \({\mathbf{n }}\) is irrelevant. See Fig. 10 for an example of a 3D orientation score.
Visualization of one iso-level of the real part of an invertible orientation score of a 3D image created via the cake-wavelet in Fig. 11
Visualization of cake-wavelets in 2D (top) and 3D (bottom). In 2D we fill up the ‘pie’ of frequencies with overlapping “cake pieces,” and application of an inverse DFT (see [6]) provides wavelets whose real and imaginary parts are, respectively, line and edge detectors. In 3D we include anti-symmetrization and the Funk transform [22] on \(\mathbb {L}_{2}(S^2)\) to obtain the same, see [42]. The idea is to redistribute spherical data from orientations towards circles laying in planes orthogonal to those orientations. Here, we want the real part of our wavelets to be line detectors (and not plate detectors) in the spatial domain. In the figure one positive iso-level is depicted in orange and one negative iso-level is depicted in blue (Color figure online)
If we restrict to disk-limited images, exact reconstruction is performed via the adjoint:
if \(\psi \) is an admissible wavelet. The condition for admissibility of wavelets \(\psi \) are given in [24]. In this article, the wavelets \(\psi \) are given either by the 2D ‘cake-wavelets’ used in [6, 23] or by their recent 3D equivalents given in [42]. Detailed formulas and recipes to construct such wavelets efficiently can be found in [42] and in order to provide the global intuitive picture they are depicted in Fig. 11.
In the subsequent sections we consider two types of operators acting on the invertible orientation scores (recall \(\varPhi \) in the commuting diagram of Fig. 3):
-
1.
for \(d=2\), differential invariants on orientation scores based on gauge frames \(\{\mathcal {B}_{1},\mathcal {B}_{2},\mathcal {B}_{3}\}\).
-
2.
for \(d=2,3\), non-linear adaptive diffusions steered along the gauge frames, i.e.,
$$\begin{aligned} W(\mathbf{x },\mathbf{n },t)=\widetilde{W}(\mathbf{x },\mathbf{R }_{\mathbf{n }},t)=\varPhi _{t}(\tilde{U})(\mathbf{x },\mathbf{R }_{\mathbf{n }}), \end{aligned}$$(111)where \(\widetilde{W}(g,t)\), with \(t\ge 0\), is the solution of
$$\begin{aligned} \left\{ \begin{array}{ll} \frac{\partial \tilde{W}}{\partial t}(g,t)= \sum \limits _{i=1}^{n_d} D_{ii}\left. (\mathcal {B}_{i})^2\right| _{g} \tilde{W}(g,t), \\ \tilde{W}(g,0)=\tilde{U}(g), \end{array} \right. \end{aligned}$$(112)where the gauge frame is induced by an exponential curve fit to data \(\tilde{U}\) at location \(g \in SE(d)\).
7.2 Experiments in SE(2)
We consider the application of enhancing and detecting the vascular tree structure in retinal images. Such image processing task is highly relevant as the retinal vasculature provides non-invasive observation of the vascular system. A variety of diseases such as glaucoma, age-related macular degeneration, diabetes, hypertension, arteriosclerosis, or Alzheimer’s affect the vasculature and may cause functional or geometric changes [41]. Automated quantification of these defects promises massive screenings for vascular-related diseases on the basis of fast and inexpensive retinal photography. To automatically assess the state of the retinal vascular tree, vessel segmentation is needed. Because retinal images usually suffer from low contrast on small scales, the vasculature in the images needs to be enhanced prior to the segmentation. One well-established approach is the Frangi vesselness filter [36] which is used in robust retinal vessel segmentation methods [14, 51]. However, a drawback of the Frangi filter is that it cannot handle crossings or bifurcations that make up an important part of the vascular network. This is precisely where the orientation score framework and the presented locally adaptive frame theory comes into play.
From left to right: retinal image f (from HRF database), multi-scale vesselness filtering results for the multi-scale Frangi vesselness filter on \(\mathbb {R}^{2}\), our SIM(2)-vesselness via invertible multi-scale orientation score based on left-invariant frame \(\{\mathcal {A}_{1},\mathcal {A}_{2},\mathcal {A}_{3}\}\), and based on adaptive frame \(\{\mathcal {B}_{1},\mathcal {B}_{2},\mathcal {B}_{3}\}\)
The SE(2)-vesselness filter, extending Frangi vesselness [36] to SE(2) (cf. [40]) and based on the locally adapted frame \(\{\mathcal {B}_{1},\mathcal {B}_{2},\mathcal {B}_{3}\}\) is given by the following left-invariant operator:

with \(\sigma _{1}=\frac{1}{2}\) and \(\sigma _{2}=0.2 \Vert \mathcal {B}_{2}^{\,2}\tilde{U}+\mathcal {B}_{3}^{\, 2}\tilde{U}\Vert _{\infty }\). Here the decomposition of the vesselness in structureness, anisotropy, and convexity follows the same general principles of the vesselness. As in vessels are line-like structures, we use the exponential curve fits of second order obtained via the symmetric product of the Hessian (i.e., solving the optimization problem in Theorem 3).
Similarly to the vesselness filter [36], we need a mechanism to robustly deal with vessels of different width. This is why for this application we extend the (all-scale) orientation scores to multiple-scale invertible orientation scores. Such multiple-scale orientation scores [63] coincide with wavelet transforms on the similitude group \(SIM(2)=\mathbb {R}^{2} \rtimes SO(2) \times \mathbb {R}^{+}\), where one uses a B-spline [32, 69] basis decomposition along the log-radial axis in the Fourier domain. In our experiments we used \(N=4, 12\), or 20 orientation layers and a decomposition centered around \(M=4\) discrete scales \(a_l\) given by
\(l=0,\ldots ,M-1\) where \(a_{\max }\) is inverse proportional to the Nyquist-frequency \(\rho _n\) and \(a_{\min }\) close to the inner scale [33] induced by sampling (see [63] for details). Then, the multiple-scale orientation score is given by the following wavelet transform \(\mathcal {W}_{\psi }f:SIM(2) \rightarrow \mathbb {C}\):
and we again set \(U:=\text {Re}\{\mathcal {W}_{\psi }f\}\). Finally we define the total integrated multiple-scale SIM(2)-vesselness by
where SE(2)-vesselness operator \(\varPhi \) is given by Eq. (113), and where \(\mu _{\infty }\) and \(\mu _{i,\infty }\) denote maxima w.r.t. sup-norm \(\Vert \cdot \Vert _{\infty }\) taken over the subsequent terms.
Note that another option for constructing a SIM(2)-vesselness is to use the non-adaptive left-invariant frame \(\{\mathcal {A}_{1},\mathcal {A}_{2},\mathcal {A}_{3}\}\) instead of the gauge frame. This non-adaptive SE(2)-vesselness operator is obtained by simply replacing the \(\mathcal {B}_{i}\) operators by the \(\mathcal {A}_{i}\) operators in Eq. (113) accordingly.
The aim of the experiments presented in this section is to show the following advantages:
- Advantage 1 :
-
The improvement of considering the multiple-scale vesselness filter via gauge frames in SE(2), compared to multiple-scale vesselness [36] acting directly on images.
- Advantage 2 :
-
Further improvement when using the gauge frames instead of using the left-invariant vector fields in SE(2)-vesselness (113).
In the following experiment, we test these 3 techniques (Frangi vesselness [36], SIM(2)-vesselness via the non-adaptive left-invariant frame, and the newly proposed SIM(2)-vesselness via gauge frames) on the publically availableFootnote 3 High-Resolution Fundus (HRF) dataset [47], containing manually segmented vascular trees by medical experts. The HRF dataset consists of wide-field fundus photographs for a healthy, diabetic retinopathy and a glaucoma group (15 images each). A comparison of the 3 vesselness filters on a small patch is depicted in Fig. 12. Here, we see that our method performs better both at crossing and non-crossing structures.
To perform a quantitative comparison, we devised a simple segmentation algorithm to turn a vesselness filtered image \(\mathcal {V}(f)\) into a segmentation. First an adaptive thresholding is applied, yielding a binary image
where \(\varTheta \) is the unit step function, \(G_\gamma \) is a Gaussian of scale \(\gamma =\frac{1}{2}\sigma ^2 \gg 1\) and h is a threshold parameter. In a second step, the connected morphological components in \(f_B\) are subject to size and elongation constraints. Components counting less than \(\tau \) pixels or showing elongations below a threshold \(\nu \) are removed. Parameters \(\gamma , \tau \), and \(\nu \) are fixed at 100 px, 500 px, and 0.85, respectively. The vesselness map \(\mathcal {V}(f):\mathbb {R}^{2} \rightarrow \mathbb {R}\) is one of the three methods considered.
Left comparison of multiple-scale Frangi vesselness and SIM(2)-vesselness via gauge frames. Average accuracy and sensitivity on the HRF dataset over threshold values h. Shaded regions correspond to \(\pm 1 \,\sigma \). Right comparing of SIM(2)-vesselness with and without including the gauge frame (i.e. using \(\{\mathcal {A}_{1},\mathcal {A}_{2},\mathcal {A}_{3}\}\) in Eq. (113))
The segmentation algorithm described above is evaluated on the HRF dataset. Average sensitivity and accuracy over the whole dataset are shown in Fig. 13 as a function of the threshold value h. It can be observed that our method performs considerably better than the one based on the multi-scale Frangi filter. The segmentation results obtained with SIM(2)-vesselness (116) based on gauge frames are more stable w.r.t variations in the threshold h and the performance on the small vasculature has improved as measured via the sensitivity. Average sensitivity and accuracy at a threshold of \(h=0.05\) compare well with other segmentation methods evaluated on the HRF dataset for the healthy cases (see [14, Tab. 5], [40]). On the diabetic retinopathy and glaucoma group, our method even outperforms existing segmentation methods.
Center original image from HRF dataset (healthy subject nr. 5). Rows the soft-segmentation (left) and the corresponding performance maps (right) based on the hard segmentation (117). In green true positives, in blue true negatives, in red false positives, compared to manual segmentation by expert. First row SIM(2)-vesselness (116) based on non-adaptive frame \(\{\mathcal {A}_{1},\mathcal {A}_{2},\mathcal {A}_{3}\}\). Second row SIM(2)-vesselness (116) based on the gauge frame (Color figure online)
Finally, regarding the second advantage we refer to Fig. 14, where the SIM(2)-vesselness filtering via the locally adaptive frame produces a visually much more appealing soft-segmentation of the blood vessels than SIM(2)-vesselness filtering via the non-adaptive frame. It therefore also produces a more accurate segmentation as can be deducted from the comparison in Fig. 13. For comparison, the multiscale Frangi vesselness filter is also computed via summation over single-scale results and max-normalized. Generally, we conclude from the experiments that the locally adaptive frame approach better reduces background noise, showing much less false positives in the final segmentation results. This can be seen from the typical segmentation results on relatively challenging patches in Fig. 15.
Two challenging patches (one close to the optic disk and one far away from the optic disk processed with the same parameters). The gauge frame approach typically reduces false positives (red) on the small vessels, and increases false negatives (blue) at the larger vessels. The top patch shows a missing hole at the top in the otherwise reasonable segmentation by the expert (Color figure online)
7.3 Experiments in SE(3)
We now show first results of the extension of coherence-enhancing diffusion via invertible orientation scores (CEDOS [35]) of 2D images to the 3D setting. Again, data are processed according to Fig. 3. First, we construct an orientation score according to (108), using the 3D cake-wavelets (Fig. 11). For determining the gauge frame we use the first-order structure tensor method in combination with Eq. (118) in Appendix 1. In CEDOS we have \(\varPhi =\varPhi _t\), as defined in (111) and (112), which is a diffusion along the gauge frame.
The diffusion in CEDOS can enhance elongated structures in 3D data while preserving the crossings as can be seen in the two examples in Fig. 16. In these experiments as well as in the example used in Figs. 8, 9, and 10, we used the following 3D cake-wavelet parameters for constructing the 3D invertible orientation scores: \(N_0=42,s_\phi =0.7,k=2,N=20,\gamma =0.85,L=16\) evaluated on a grid of \(21 \times 21 \times 21\) pixels, for details see [42]. The settings for tangent vector estimation using the structure tensor are \(s_p=\frac{1}{2}(1.5)^2,s_0=0,\rho _o=\frac{1}{2}(0.8)^2\), and \(\mu =0.5\). We used \(\rho _p=\frac{1}{2}(2)^2\) for the first dataset (Fig. 16 top), and \(\rho _p=\frac{1}{2}(3.5)^2\) for the second dataset (Fig. 16 bottom). For the diffusion we used \(t=2.5,D_{11}=D_{22}=0.01,D_{33}=1,D_{44}=D_{55}=D_{66}=0.04\), where the diffusion matrix is given w.r.t. gauge frame \(\{\mathcal {B}_{1},\mathcal {B}_{2},\mathcal {B}_{3},\mathcal {B}_{4}, \mathcal {B}_{5},\mathcal {B}_{6}\}\), and normalized frame \(\{\mu ^{-1} \mathcal {A}_{1},\mu ^{-1} \mathcal {A}_{2},\mu ^{-1} \mathcal {A}_{3},\mathcal {A}_{4},\mathcal {A}_{5},\mathcal {A}_{6}\}\).
Results of CEDOS with and without the use of gauge frames, on 3D artificial datasets containing highly curved structures. Gauge frames are obtained, see Appendix 1, via 1st order exponential curve fits using the twofold algorithm of Sect. 6.3.3. a 3D data. b Slice of data. c Curve fits. d Slice+Noise. e Gauge. f No gauge. g 3D data. h Data slice. i Curve fits. j Slice+Noise. k Gauge. l No gauge
The advantages of including the gauge frames w.r.t. the non-adaptive frame can be better appreciated in Fig. 17. Here, we borrow from the neuroimaging community the glyph visualization, a standard technique for displaying distributions \(U:\mathbb {R}^3\times S^2\rightarrow \mathbb {R}^+\). In such visualizations every voxel contains a spherical surface plot (a glyph) in which the radial component is proportional to the output value of the distribution at that orientation, and the colors indicate the orientations. One can observe that diffusion along the gauge frames include better adaptation for curvature. This is mainly due to the angular part in the \(\mathcal {B}_{3}\)-direction, cf. Fig. 18, which includes curvature, in contrast to \(\mathcal {A}_{3}\)-direction. The angular part in \(\mathcal {B}_{3}\) causes some additional angular blurring leading to more isotropic glyphs.
Glyph visualization (see text) of the absolute value of the diffused orientation scores with and without the use of gauge frames in the the artificial dataset depicted in Fig. 16 top. a Data. b Data & Noise. c Enhanced using frame \(\{\mathcal {B}_{1},\ldots ,\mathcal {B}_{6}\}\). d Enhanced using frame \(\{\mathcal {A}_{1},\ldots ,\mathcal {A}_{6}\}\)
8 Conclusion
Locally adaptive frames (‘gauge frames’) on images based on the structure tensor or Hessian of the images are ill-posed at the vicinity of complex structures. Therefore, we create locally adaptive frames on distributions on SE(d), \(d=2,3\) that extend the image domain (with positions and orientations). This gives rise to a whole family of local frames per position, enabling us to deal with crossings and bifurcations. In order to generalize gauge frames in the image domain to gauge frames in SE(d), we have shown that exponential curve fits gives rise to suitable gauge frames. We distinguished between exponential curve fits of the first order and of the second order:
-
1.
Along the first-order exponential curve fits, the first-order variation of the data (on SE(d)) along the exponential curve is locally minimal. The Euler–Lagrange equations are solved by finding the eigenvector of the structure tensor of the data, with smallest eigenvalue.
-
2.
Along the second-order exponential curve fits, a second-order variation of the data (on SE(d)) along the exponential curve is locally minimal. The Euler–Lagrange equations are solved by finding the eigenvector of the Hessian of the data, with smallest eigenvalue.
In SE(2), the first-order approach is new, while the second-order approach formalizes previous results. In SE(3), these two approaches are presented for the first time. Here, it is necessary to include a restriction to torsion-free exponential curve fits in order to be both compatible with the null space of the structure/Hessian tensors and the quotient structure of \(\mathbb {R}^{3} \rtimes S^{2}\). We have presented an effective twofold algorithm to compute such torsion-free exponential curve fits. Experiments on artificial datasets show that even if the elongated structures have torsion, the gauge frame is well adapted to the local structure of the data.
Finally, we considered the application of a differential invariant for enhancing retinal images. Experiments show clear advantages over the classical vesselness filter [36]. Furthermore, we also show clear advantages of including the gauge frame over the standard left-invariant frame in SE(2). Regarding 3D image applications, we managed to construct and implement crossing-preserving coherence-enhancing diffusion via invertible orientation scores (CEDOS), for the first time. However, it has only been tested on artificial datasets. Therefore, in future work we will study the use of locally adaptive frames in real 3D medical imaging applications, e.g., in 3D MR angiography [43]. Furthermore, in future work we will apply the theory of this work and focus on the explicit algorithms, where we plan to release Mathematica implementations of locally adaptive frames in \({ SE}(3)\).
Notes
Exponential curves are auto-parallels w.r.t. ‘-’Cartan connection, see Appendix 1, Eq. (132).
Also known as minus Cartan connection.
References
Aganj, I., Lenglet, C., Sapiro, G., Yacoub, E., Ugurbil, K., Harel, N.: Reconstruction of the orientation distribution function in single and multiple shell q-ball imaging within constant solid angle. MRM. 64(2), 554566 (2010)
Ali, S.T., Antoine, J.-P., Gazeau, J.-P.: Coherent States, Wavelets and Their Generalizations. Springer, New York (2000)
Aubin, T.: A Course in Differential Geometry. Graduate Studies in Mathematics, vol. 27. American Mathematical Society, Providence (2001)
August, J., Zucker, S.W.: The curve indicator random field: curve organization and correlation. Perceptual Organization for Artificial Vision Systems, pp. 265–288. Kluwer Academic, Boston (2000)
Barbieri, D., Citti, G., Sanguinetti, G., Sarti, A.: An uncertainty principle underlying the functional architecture of V1. J. Physiol. Paris 106(5–6), 183–193 (2012)
Bekkers, E., Duits, R., Berendschot, T., ter Haar, B.M.: A multi-orientation analysis approach to retinal vessel tracking. J. Math. Imaging Vis. 49, 583–610 (2014)
Ben-Shahar, O., Zucker, S.W.: The perceptual organization of texture flow: a contextual inference approach. IEEE Trans. PAMI 25(4), 401–417 (2003)
Bergholm, F.: Edge focussing. IEEE Trans. PAMI 9(6), 726–741 (1987)
Bigun, J., Granlund, G.: Optimal orientation detection of linear symmetry. In: ICCV, pp. 433-438 (1987)
Blom, J.: Topological and geometrical aspects of image structure. PhD thesis, University of Utrecht (1992)
Boscain, U., Chertovskih, R.A., Gauthier, J.P., Remizov, A.O.: Hypoelliptic diffusion and human vision: a semi-discrete new twist. SIAM J. Imaging Sci. 7(2), 669–695 (2014)
Breuss, M., Burgeth, B., Weickert, J.: Anisotropic continuous-scale morphology. IbPRIA. LNCS, vol. 4478, pp. 515–522. Springer, Heidelberg (2007)
Burgeth, M., Breuss, M., Didas, S., Weickert, J.: PDE-based morphology for matrix fields: numerical solution schemes. In: Aja-Fernandez, S., de Luis-Garcia, R., Tao, D., Li, X. (eds.) Tensors in Image Processing and Computer Vision, pp. 125–150. Springer, London (2009)
Budai, A., Bock, R., Maier, A., Hornegger, J., Michelson, G.: Robust vessel segmentation in fundus images. Int. J. Biomed. Imaging (2013)
Cao, F.: Geometric Curve Evolution and Image Processing. Springer, Heidelberg (2003)
Caselles, V., Kimmel, R., Sapiro, G.: Geodesic active contours. Int. J. Comput. Vis. 22(1), 61–79 (1997)
Chirikjian, G.S.: Stochastic Models, Information Theory, and Lie Groups. Analytic Methods and Modern Applications, vol. 2. Birkhäuser, Boston (2011)
Chirikjian, G.S., Kyatkin, A.B.: Engineering Applications of Noncommutative Harmonic Analysis: With Emphasis on Rotation and Motion Groups. CRC, Boca Raton (2000)
Citti, G., Sarti, A.: A cortical based model of perceptual completion in the roto-translation space. J. Math. Imaging Vis. 24(3), 307–326 (2006)
Citti, G., Franceschiello, B., Sanguinetti, G., Sarti, A.: Sub-Riemannian mean curvature flow for image processing. Preprint on arXiv:1504.03710 (2015)
Creusen, E.J., Duits, R., Vilanova, A., Florack, L.M.J.: Numerical schemes for linear and non-linear enhancement of DW-MRI. NM-TMA 6(1), 138–168 (2013)
Descoteaux, M., Angelino, E., Fitzgibbons, S., Deriche, R.: Regularized, fast, and robust analytical Q-ball imaging. Magn. Reson. Med. 58(3), 497–510 (2007)
Duits, R., Felsberg, M., Granlund, G., ter Haar Romeny, B.M.: Image analysis and reconstruction using a wavelet transform constructed from a reducible representation of the Euclidean motion group. Int. J. Comput. Vis. 79(1), 79–102 (2007)
Duits, R.: Perceptual organization in image analysis, a mathematical approach based on scale, orientation and curvature. PhD-thesis, TU/e, Eindhoven (2005)
Duits, R., Boscain, U., Rossi, F., Sachkov, Y.: Association Fields via Cuspless Sub-Riemannian Geodesics in SE(2). J. Math. I Vis. 49(2), 384–417 (2014)
Duits, R., van Almsick, M.A.: The explicit solutions of linear left-invariant second order stochastic evolution equations on the 2D-Euclidean motion group. Q. Appl. Math. AMS 66(1), 27–67 (2008)
Duits, R., Franken, E.M.: Left invariant parabolic evolution equations on \({SE}(2)\) and contour enhancement via invertible orientation scores, part I: linear left-invariant diffusion equations on \({SE}(2)\). Q. Appl. Math. AMS 68, 255–292 (2010)
Duits, R., Franken, E.M.: Left invariant parabolic evolution equations on \({SE}(2)\) and contour enhancement via invertible orientation scores, part II: nonlinear left-invariant diffusions on invertible orientation scores. Q. Appl. Math. AMS 68, 293–331 (2010)
Duits, R., Dela Haije, T.C.J., Creusen, E.J., Ghosh, A.: Morphological and linear scale spaces for fiber enhancement in DW-MRI. J. Math. Imaging Vis. 46(3), 326368 (2013)
Duits, R., Franken, E.M.: Left-invariant diffusions on the space of positions and orientations and their application to crossing preserving smoothing of HARDI images. Int. J. Comput. Vis. 92, 231–264 (2011)
Duits, R., Ghosh, A., Dela Haije, T.C.J., Sachkov, Y.L.: Cuspless sub-Riemannian geodesics within the Euclidean motion group SE(d). Neuromathematics of Vision. Springer Series Lecture Notes in Morphogenesis, pp. 173–240. Springer, Berlin (2014)
Felsberg, M.: Adaptive filtering using channel representations. In: Florack, L., et al. (eds.) Mathematical Methods for Signal and Image Analysis and Representation. Computational Imaging and Vision, vol. 41, pp. 35–54. Springer, London (2012)
Florack, L.M.J.: Image Structure. KAP, Dordrecht (1997)
Franken, E.M.: Enhancement of crossing elongated structures in images. PhD-thesis, Department of Biomedical Engineering, Eindhoven University of Technology (2008)
Franken, E.M., Duits, R.: Crossing preserving coherence-enhancing diffusion on invertible orientation scores. Int. J. Comput. Vis. 85(3), 253278 (2009)
Frangi, A.F., Niessen, W.J., Vincken, K.L., Viergever, M.A.: Multiscale Vessel Enhancement Filtering. LNCS, vol. 1496, pp. 130–137. Springer, Berlin (1998)
van Ginkel, M., van de Weijer, J., van Vliet, L.J., Verbeek, P.W.: Curvature estimation from orientation fields. Proc. 11th Scand. Conf. Image Anal. 2, 545–552 (1999)
Guichard, F., Morel, J.-M.: Geometric partial differential equations and iterative filtering. In: Heymans, H.J.A.M., Roerdink, J.B.T.M. (eds.) Mathematical Morphology and Its Applications to Image and Signal Processing, pp. 127–138. KAP, Dordrecht (1998)
ter Haar Romeny, B.M.: Front-End Vision and Multi-Scale Image Analysis, Computational Imaging and Vision, vol. 27. Springer, Berlin (2003)
Hannink, J., Duits, R., Bekkers, E.J.: Multiple scale crossing preserving vesselness. In: MICCAI Proc., LNCS 8674, pp. 603–610 (2014)
Ikram, M.K., Ong, Y.T., Cheung, C.Y., Wong, T.Y.: Retinal vascular caliber measurements: clinical significance, current knowledge and future perspectives. Ophthalmologica 229(3), 125–136 (2013)
Janssen, M.H.J., Duits, R., Breeuwer, M.: Invertible orientation scores of 3D images. In: SSVM 2015. LNCS 9087, pp. 563–575 (2015)
Janssen, M.H.J.: 3D orientation scores applied to MRA vessel analysis. Master Thesis, Department of Biomedical Image Analysis, Eindhoven University of Technology, The Netherlands (2014)
Jost, J.: Riemannian Geometry and Geometric Analysis, 4th edn. Springer, Berlin (2005)
Kindlmann, G., Ennis, D.E., Witaker, R.T., Westin, C.F.: Diffusion tensor analysis with invariant gradients and rotation tangents. IEEE Trans. Med. Imaging 23(11), 1483–1499 (2007)
Kindlmann, G., Estepar, R.S.J., Smith, S.M., Westin, C.F.: Sampling and visualization creases with scale-space particles. IEEE Trans. VCG 15(6), 1415–1424 (2010)
Kohler, T., Budai, A., Kraus, M.F., Odstrcilik, J., Michelson, G., Hornegger, J.: Automatic no-reference quality assessment for retinal fundus images using vessel segmentation. In: IEEE 26th Symposium on CBMS, pp. 95–100 (2013)
Knutsson, H.: Representing local structure using tensors. In: Scandinavian Conference on Image Analysis, pp. 244–251 (1989)
Lawlor, M., Zucker, S.W.: Third order edge statistics: contour continuation, curvature, and cortical connections. In: NIPS, pp. 1763–1771 (2013)
Lindeberg, T.: Scale-Space Theory in Computer Vision. The Springer International Series in Engineering and Computer Science. Kluwer Academic Publishers, Dordrecht (1994)
Lupascu, C.A., Tegolo, D., Trucco, E.: FABC: retinal vessel segmentation using AdaBoost. IEEE Trans. Inf. Technol. 14(5), 1267–1274 (2010)
Medioni, G., Lee, M.S., Tang, C.K.: A Computational Framework for Feature Extraction and Segmentation. Elsevier, Amsterdam (2000)
Mumford, D.: Elastica and computer vision. In: Bajaj, C.L. (ed.) Algebraic Geometry and Its Applications. Springer, New York (1994)
Parent, P., Zucker, S.W.: Trace inference, curvature consistency, and curve detection. IEEE Trans. PAMI 11(8), 823–839 (1989)
Pennec, X., Fillard, P., Ayache, N.: Invariant metric on SPD matrices and use of Frechet mean to define manifold-valued image processing algorithms. A Riemannian framework for tensor computing. Int. J. Comput. Vis. 66(1), 41–66 (2006)
Pennec, X., Arsigny, V.: Exponential Barycenters of the Canonical Cartan connection and invariant means on Lie groups. Matrix Information Geometry, pp. 123–166. Springer, Heidelberg (2012)
Petitot, J.: The neurogeometry of pinwheels as a sub-Riemannian contact structure. J. Phys. Paris 97(2–3), 265–309 (2003)
Sanguinetti, G.: Invariant models of vision between phenomenology, image statistics and neurosciences. PhD thesis, Universidad de la Republica, Uruguay (2011)
Sanguinetti, G., Citti, G., Sarti, A.: A model of natural image edge co-occurrence in the rototranslation group. J Vis 10(14), 37 (2010)
Sapiro, G.: Geometric Partial Differential Equations and Image Analysis. Cambridge University Press, Cambridge (2001)
Savadjiev, P., Campbell, J.S.W., Pike, G.B., Siddiqi, K.: 3D curve inference for diffusion MRI regularization and fibre tractography. Med. Image Anal. 10(5), 799–813 (2006)
Savadjiev, P., Strijkers, G.J., Bakermans, A.J., Piuze, E., Zucker, S.W., Siddiqi, K.: Heart wall myofibers are arranged in minimal surfaces to optimize organ function. PNAS 109(24), 9248–9253 (2012)
Sharma, U., Duits, R.: Left-invariant evolutions of wavelet transforms on the similitude group. Appl. Comput. Harm. Anal. 39, 110–137 (2015)
MomayyezSiahkal, P., Siddiqi, K.: 3D Stochastic completion fields: a probabilistic view of brain connectivity. IEEE Trans. PAMI 35(4), 983–995 (2013)
Sinnaeve, D.: The Stejskal-Tanner Equation generalized for any gradient shape—an overview of most pulse sequences measuring free diffusion. Concepts Magn. Reson. Part A 40A(2), 39–65 (2012)
Staal, J., Abramoff, M.D., Viergever, M.A., van Ginneken, B.: Ridge-based vessel segmentation in color images of the retina. IEEE Trans. Med. Imaging 23, 501–509 (2004)
Tournier, J.D., Yeh, C.H., Calamante, F., Cho, K.H., Connolly, A., Lin, C.P.: Resolving crossing fibres using constrained spherical deconvolution: validation using diffusion-weighted imaging phantom data. NeuroImage 42, 617–625 (2008)
Tuch, D.S., Reese, T.G., Wiegell, M.R., Makris, N., Belliveau, J.W., Wedeen, V.J.: High angular resolution diffusion imaging reveals intravoxel white matter fiber heterogeneity. MRM 48, 577–582 (2002)
Unser, M., Aldroubi, A., Eden, M.: B-Spline signal processing: part I—theory. IEEE Trans. Signal Proc. 41, 831–833 (1993)
van Almsick, M.: Context models of lines and contours. PhD thesis, Department of Biomedical Engineering, Eindhoven University of Technology, the Netherlands (2007)
Weickert, J.: Anisotropic diffusion in image processing. ECMI Series, Teubner-Verlag, Stuttgart (1998)
Welk, M.: Families of generalised morphological scale spaces. Scale Space Methods in Computer Vision. LNCS, vol. 2695, pp. 770–784. Springer, Berlin (2003)
Zweck, J., Williams, L.R.: Euclidean group invariant computation of stochastic completion fields using shiftable-twistable functions. J. Math. Imaging Vis. 21(2), 135–154 (2004)
Acknowledgments
The authors wish to thank J.M. Portegies for fruitful discussions on the construction of gauge frames in SE(3) and T.C.J. Dela Haije for help in optimizing code for the SE(3)-case. Finally, we would like to thank the reviewers and Dr. A.J.E.M. Janssen for careful reading and valuable suggestions on the structure of the paper. The research leading to these results has received funding from the European Research Council under the European Community’s Seventh Framework Programme (FP7/2007-2013) / ERC Grant Lie Analysis, agr. nr. 335555.
Author information
Authors and Affiliations
Corresponding author
Additional information
R. Duits and M. H. J. Janssen are joint main authors.
Appendices
Appendix 1: Construction of the Locally Adaptive Frame from an Exponential Curve Fit
Let \(\tilde{\gamma }_{g}^{\mathbf{c }}(t)= g \, e^{t\sum \limits _{i=1}^{n_d}c^{i}A_{i}}\) be an exponential curve through g that fits data \(\tilde{U}:SE(d) \rightarrow \mathbb {R}\) at \(g \in SE(d)\) in Lie group SE(d) of dimension \(n_d=d(d+1)/2\). In Sect. 5 (\(d=2\)), and in Sect. 6 (\(d=3\)), we provide theory and algorithms to derive such curves. In this section we assume \(\gamma _{g}^{\mathbf{c }}(\cdot )\) is given.
Recall from (17) that the (physical) velocity at time t of the exponential curve \(\tilde{\gamma }_{g}^{\mathbf{c }}\) equals \((\tilde{\gamma }_{g}^{\mathbf{c }})'(t)=\sum \nolimits _{i=1}^{n_d} c^{i} \left. \mathcal {A}_{i}\right| _{g=\tilde{\gamma }_{g}^{\mathbf{c }}(t)}\). Recall that the spatial and, respectively, rotational components of the velocity are stored in the vectors
Let us write \(\mathbf{c }=\left( \begin{array}{c}\mathbf{c }^{(1)}\\ \mathbf{c }^{(2)}\end{array}\right) \in \mathbb {R}^{n_d}\), with \(n_d=d+r_d\).
Akin to the case \(d=2\) discussed in the introduction, we define the Gauge frame via \(\underline{\mathcal {B}}:= (\mathbf{R }^{\mathbf{c }})^T \mathbf{M }_{\mu }^{-1}\underline{\mathcal {A}}\), but now with
For explicit formulae of the left-invariant vector fields in the d-dimensional case we refer to [31].
Now \(\mathbf{R }_{1}\) is the counterclockwise rotation that rotates the spatial reference axis \(\left( \begin{array}{c}\mathbf{a } \\ \mathbf{0 } \end{array}\right) \), recall our convention (2), onto \(\left( \begin{array}{c} \mu \Vert \mathbf{c }^{(1)}\Vert \mathbf{a } \\ \mathbf{c }^{(2)} \end{array} \right) \) strictly within the 2D plane spanned by these two vectors. Rotation \(\mathbf{R }_{2}\) is the counterclockwise rotation that rotates \(\left( \begin{array}{c} \mu \Vert \mathbf{c }^{(1)}\Vert \mathbf{a } \\ \mathbf{c }^{(2)} \end{array}\right) \) onto \(\left( \begin{array}{c}\mu \mathbf{c }^{(1)}\\ \mathbf{c }^{(2)} \end{array}\right) \) strictly within the 2D plane spanned by these two vectors. As a result one has
In particular we have that the preferred spatial direction \(\left( \begin{array}{c} \mathbf{a } \\ \mathbf{0 } \end{array}\right) \cdot \underline{\mathcal {A}}\) is mapped onto \(\left( \begin{array}{c} \mathbf{a } \\ \mathbf{0 } \end{array}\right) \cdot \underline{\mathcal {B}}= \mathbf{c } \cdot \underline{\mathcal {A}}\).
The next theorem shows us that our choice of assigning an entire gauge frame to a single exponential curve fit is the right one for our applications.
Theorem 7
(Construction of the gauge frame) Let \(\mathbf{c }(g)\) denote the local tangent components of exponential curve fit \(t \mapsto \tilde{\gamma }^{\mathbf{c }(g)}_g(t)\) at \(g=(\mathbf{x },\mathbf{R }) \in SE(d)\) in the data given by \( \tilde{U}(\mathbf{x },\mathbf{R })=U(\mathbf{x },\mathbf{R }\mathbf{a })\). Consider the mapping of the frame of left-invariant vector fields \(\left. \underline{\mathcal {A}}\right| _{g}\) to the locally adaptive frame:
with \(\mathbf{R }^{\mathbf{c }}=\mathbf{R }_{2} \mathbf{R }_{1} \in SO(n_d)\), with subsequent counterclockwise planar rotations \(\mathbf{R }_{1}, \mathbf{R }_{2}\) given by (119). Then the mapping \(\underline{\mathcal {A}}_{g} \mapsto \underline{\mathcal {B}}_{g}\) has the following properties:
-
The main spatial tangent direction \((L_{g})_* { \left( \begin{array}{c}\mathbf{a }\\ \mathbf{0 }\end{array}\right) } \cdot \left. \underline{\mathcal {A}}\right| _{e}\) is mapped to exponential curve fit direction \(\mathbf{c }^{T}(g) \cdot \left. \underline{\mathcal {A}}\right| _{g}\).
-
Spatial left-invariant vector fields that are
 -orthogonal to this main spatial direction stay in the spatial part of the tangent space \(T_{g}(SE(d))\) under rotation \(\mathbf{R }^{\mathbf{c }}\) and they are invariant up to normalization under the action (120) if and only if the exponential curve fit is horizontal.
-orthogonal to this main spatial direction stay in the spatial part of the tangent space \(T_{g}(SE(d))\) under rotation \(\mathbf{R }^{\mathbf{c }}\) and they are invariant up to normalization under the action (120) if and only if the exponential curve fit is horizontal.
Proof
Regarding the first property we note that
as left-invariant vector fields are obtained by push-forward of the left multiplication. Furthermore, by Eqs. (120) and (119) we have
Regarding the second property, we note that if \(\mathbf{b } \cdot {\mathbf{a }}=0 \Rightarrow \)
and \(\tilde{\gamma }_{g}^{{\mathbf{c }}}\) is horizontal iff \(\frac{{\mathbf{c }}^{(1)}}{\Vert {\mathbf{c }}^{(1)}\Vert }=\mathbf{a }\) in which case the planar rotation \({\mathbf{R }}_{2}\) reduces to the identity and \({\mathbf{R }}_{2}{\mathbf{R }}_{1}\left( \begin{array}{c}\mathbf b \\ {\mathbf{0 }} \end{array} \right) =\left( \begin{array}{c} \mathbf{b } \\ {\mathbf{0 }} \end{array} \right) ^T\) and only spatial normalization by \(\mu ^{-1}\) is applied. \(\square \)
Remark 16
For \(d=2\) and \(\mathbf{a }=(1,0)^T\) the above theorem can be observed in Fig. 5, where main spatial direction \(\mathcal {A}_{1}=\cos \theta \,\partial _{x} +\sin \theta \,\partial _{y}\) is mapped onto \(\mathcal {B}_{1}= \mathbf{c } \cdot \underline{\mathcal {A}}\) and where \(\mathcal {A}_{2}\) is mapped onto \(\mathcal {B}_{2}=\mu ^{-1}(-\sin \chi \mathcal {A}_{1} + \cos \chi \mathcal {A}_{2})\).
Remark 17
For \(d=3\) and \(\mathbf{a }=(0,0,1)^T\) the above theorem can be observed in Fig. 18, where main spatial direction \(\mathcal {A}_{3}=\mathbf{n } \cdot \nabla _{\mathbb {R}^{3}}\) is mapped onto \(\mathcal {B}_{3}=\mathbf{c } \cdot \underline{\mathcal {A}}\), and where \(\mathcal {A}_{1}\) and \(\mathcal {A}_{2}\) are mapped to the strictly spatial generators \(\mathcal {B}_{1}\) and \(\mathcal {B}_{2}\). For further details see [43].
Visualization of the mapping of left-invariant frame \(\left. \{\mathcal {A}_{1},\ldots ,\mathcal {A}_{6}\}\right| _{g}\) onto locally adaptive spatial frame \(\left. \{\mathcal {B}_{1},\ldots , \mathcal {B}_6\}\right| _{g}\) and \(\tilde{\gamma }_{g}^{\mathbf{c }}(\cdot )\) a non-horizontal and torsion-free exponential curve passing trough  . The top row indicates the spatial part in \(\mathbb {R}^3\), whereas the bottom row indicates the angular part in \(S^2\). The top black curve is the spatial projection of \(\tilde{\gamma }_{g}^{\mathbf{c }}(\cdot )\), and the bottom black curve is the angular projection of the exponential curve. After application of \(\mathbf{R }_{2}^T\) the exponential curve is horizontal w.r.t. the frame \(\{\hat{A}_{i}\}\), subsequently \(\mathbf{R }_{1}^{T}\) leaves spatial generators orthogonal to a horizontal curve invariant, so that \(\hat{A}_{1}=\mathcal {B}_{1}\) and \(\hat{A}_{2}=\mathcal {B}_{2}\) are strictly spatial, as is in accordance with Theorem 7. The angular part of \(\mathcal {B}_{3}\) is shown via the curvature at the blue arrow. The spatial part of \(\mathcal {B}_{4}\) and \(\mathcal {B}_{5}\) is depicted in the center of the ball (Color figure online)
. The top row indicates the spatial part in \(\mathbb {R}^3\), whereas the bottom row indicates the angular part in \(S^2\). The top black curve is the spatial projection of \(\tilde{\gamma }_{g}^{\mathbf{c }}(\cdot )\), and the bottom black curve is the angular projection of the exponential curve. After application of \(\mathbf{R }_{2}^T\) the exponential curve is horizontal w.r.t. the frame \(\{\hat{A}_{i}\}\), subsequently \(\mathbf{R }_{1}^{T}\) leaves spatial generators orthogonal to a horizontal curve invariant, so that \(\hat{A}_{1}=\mathcal {B}_{1}\) and \(\hat{A}_{2}=\mathcal {B}_{2}\) are strictly spatial, as is in accordance with Theorem 7. The angular part of \(\mathcal {B}_{3}\) is shown via the curvature at the blue arrow. The spatial part of \(\mathcal {B}_{4}\) and \(\mathcal {B}_{5}\) is depicted in the center of the ball (Color figure online)
Appendix 2: The Geometry of Neighboring Exponential Curves
In this appendix we provide some differential geometry underlying the family of neighboring exponential curves.
First we prove Lemma 3 on the construction of the family \(\{\tilde{\gamma }^{\mathbf{c }}_{h,g}\}\) of neighboring exponential curves in SE(3), recall Fig. 7, and then we provide an alternative coordinate-free definition of \(\tilde{\gamma }^{\mathbf{c }}_{h,g}\) in addition to our Definition 5 .
For the proof of Lemma 3 we will just show equalities (86) as from this equality it directly follows by differentiation w.r.t. t that the exponential curves \(\tilde{\gamma }^{\mathbf{c }}_{h,g}(\cdot )=(\mathbf{x }_{h}(\cdot ),\mathbf{R }_{h}(\cdot ))\) and \(\tilde{\gamma }^{\mathbf{c }}_{g}(\cdot )=(\mathbf{x }_{g}(\cdot ),\mathbf{R }_{g}(\cdot ))\) have the same spatial and angular velocity. For the spatial velocities it is obvious, for the angular velocities, we note that rotational velocity matrices \(\varvec{\varOmega }_{h}\) and \(\varvec{\varOmega }_{g}\) are indeed equal:
where we note that \(\mathbf{R }_g(t)=e^{t \varvec{\varOmega }_g} \mathbf{R }_g(0) = e^{t \varvec{\varOmega }_g} \mathbf{R }\), and \(\mathbf{R }_h(t)=e^{t \varvec{\varOmega }_h} \mathbf{R }_h(0) = e^{t \varvec{\varOmega }_h} \mathbf{R }'\).
Regarding the remaining derivation of (86), we note that it is equivalent to
by group product (4). So we focus on the derivation of this identity. Let us set \(\mathbf Q :=(\mathbf{R }')^T\mathbf{R }\). Now relying on the matrix representation (6) and matrix exponential, we deduce the following identity for  :
:

which holds for all \(\mathbf Q \in SO(3)\), in particular for \(\mathbf Q =(\mathbf{R }')^T\mathbf{R }\). Consequently, we have

from which the result follows. \(\square \)
We conclude From Lemma 3 that our Definition 5 is indeed the right definition for our purposes, but as it is a definition expressed in left-invariant coordinates it also leaves the question what the underlying coordinate-free unitary map from \(T_{g}(SE(3))\) to \(T_{h}(SE(3))\) actually is. Next we answer this question where we keep Eq. (121) in mind.
Definition 6
Let us define the unitary operator  by
by

for each pair \(g=(\mathbf{x },\mathbf{R }), h=(\mathbf{x }',\mathbf{R }') \in SE(3)\).
Remark 18
From (87) it follows that the unitary correspondence between \(T_{\tilde{\gamma }^{\mathbf{c }}_{g}(t)}\) and \(T_{\tilde{\gamma }^{\mathbf{c }}_{h,g}(t)}\) is preserved for all \(t \in \mathbb {R}\).
Definition 7
The coordinate-free definition of \(\tilde{\gamma }^{\mathbf{c }}_{h,g}\) is that it is the unique exponential curve passing through h at \(t=0\) with

Remark 19
The previous definition (Definition 5) follows from the coordinate-free definition (Definition 7). This can be shown via identity (121) which can be rewritten as
which indeed yields

again with \(\mathbf {Q}=(\mathbf{R }')^{T}\mathbf{R }\), \(\text {conj}(g)h=g h g^{-1}\), and \(\text {Ad}(g)=(\text {conj}(g))_*\) is the adjoint representation [44].
Appendix 3: Exponential Curve Fits on SE(3) of the Second Order via Factorization
Instead of applying a second-order exponential curve fit (106) containing a single exponential, one can factorize exponentials, and consider the following optimization:
As shown in Theorem 8 the Euler–Lagrange equations are solved by spectral decomposition of the symmetric Hessian given by
with \(\tilde{V}=\tilde{G}_{\mathbf{s }}*\tilde{U}\). This Hessian differs from the consistent Hessian in Appendix 2.
Theorem 8
(Second-Order Fit via Factorization) Let \(g \in SE(3)\) be such that Hessian matrix \(\mathbf{M }_{\mu }^{-1}(\overline{\mathbf{H }}^{\mathbf{s }}(g)) \mathbf{M }_{\mu }^{-1}\) has two eigenvalues with the same sign. Then the normalized eigenvector \(\mathbf{M }_{\mu }\mathbf{c }^{*}(g)\) with smallest eigenvalue provides the solution \(\mathbf{c }^{*}(g)\) of the following optimization problem (124).
Proof
Define \(F_{1}:=\mathbf{c }^{(1)} \cdot \mathbf A ^{(1)} \in T_{e}(SE(3))\) with \(\mathbf A ^{(1)}:=(A_{1},A_{2},A_{3})^T\). Define \(F_{2}:=\mathbf{c }^{(2)} \cdot \mathbf A ^{(2)} \in T_{e}(SE(3))\) with \(\mathbf A ^{(2)}:=(A_{4},A_{5},A_{6})^T\). Define vector fields \(\mathcal {F}_{1}|_g:= (L_{g})_* F_{1}\), \(\mathcal {F}_{2}|_g:= (L_{g})_* F_{2}\). Then Then
This follows by direct computation and the formula
applied for \((q=g e^{h F_{1}}, k=2)\) and \((q=g, k=1)\).
Therefore, we can express the optimization functional as
with again boundary condition \(\varphi (\mathbf{c })=\mathbf{c }^T \mathbf{M }_{\mu }^2 \mathbf{c }=1\), from which the result follows via Euler–Lagrange \(\nabla \mathcal {E}=\lambda \nabla \varphi \) and left multiplication with \(\mathbf{M }_{\mu }^{-1}\). \(\square \)
This approach can again be decomposed in the twofold approach. Effectively, this means that in Sect. 6.4.2 the upper triangle of the Hessian \(\mathbf{H }^{\mathbf{s }}\) is replaced by the lower triangle, whereas the lower triangle is maintained. This approach performs well in practice; see, e.g., Fig. 9 where the results of the exponential curve fits of second order are similar to exponential curve fits of first order.
Appendix 4: The Hessian Induced by the Left Cartan Connection
In this section we will provide a formal differential geometrical underpinning for our choice of Hessian matrix
where i denotes the row index and j the column index on SE(d), recall the case \(d=2\) in (62) and recall the case \(d=3\) in (107). Recall from Theorems 2, 3 and 6 that this Hessian naturally appears via direct sums or products in our exponential curve fits of second order on SE(d).
Furthermore, we relate our exponential curve fit theory to the theory in [44], where the same idea of second-order fits of auto-parallel curves to a given smooth function \(\tilde{U}:M \rightarrow \mathbb {R}\) in a Riemannian manifold is visible in [44, Eq. 3.3.50]. Here we stress that in the book of Jost [44, Eq. 3.3.50] this is done in the very different context of the torsion-free Levi-Civita connections, instead of the left Cartan connection which does have non-vanishing torsion.
Let us start with the coordinate-free definition of the Hessian induced by a given a connection \(\nabla ^*\) on the co-tangent bundle.
Definition 8
(Coordinate-free definition Hessian) On a Riemannian manifold (M, G) with connection \(\nabla ^*\) on \(T^{*}(M)\), the Hessian of smooth function \(\tilde{U}:M \rightarrow \mathbb {R}\) is defined coordinate independently [44, Def. 3.3.5] by \(\nabla ^{*} d \tilde{U}\).
In coordinate-free form one has (cf. [44, Eq. 3.3.50])
for the auto-parallel (i.e., \(\nabla _{\dot{\gamma }}\dot{\gamma }=0\)) curve \(\gamma (t)\) with tangent \(\gamma '(0)=X_p\) passing through \(c(0)=p\) at time zero.
Remark 20
In many books on differential geometry \(\nabla ^{*}\) is again denoted by \(\nabla \) (we also did this in our previous works [25, 28]). In this appendix, however, we distinguish between the connection \(\nabla \) on the tangent bundle and its adjoint connection \(\nabla ^*\) on the co-tangent bundle \(T^*(SE(d))\).
Let us recall that the structure constants of the Lie algebra are given by
As shown in previous work [28] the left Cartan connectionFootnote 4
\(\nabla \) on  is the (metric compatible) connection whose Christoffel symbols, expressed in the left-invariant moving (co)frame of reference, are equal to the structure constants of the Lie algebra:
is the (metric compatible) connection whose Christoffel symbols, expressed in the left-invariant moving (co)frame of reference, are equal to the structure constants of the Lie algebra:
More precisely, this means that if we compute the covariant derivative of a vector field \(Y=\sum \nolimits _{k=1}^{n_d}y^{k}\mathcal {A}_{k}\) (i.e., a section in T(SE(d)) along the tangent \(\dot{\tilde{\gamma }}(t)=\sum \nolimits _{i=1}^{n_d} \dot{\tilde{\gamma }}^i(t)\, \left. \mathcal {A}_{i}\right| _{\tilde{\gamma }(t)}\) of some smooth curve \(t \mapsto \tilde{\gamma }(t)\) in SE(d). This is done as follows
where we follow the notation in Jost’s book [44, p. 108] and define \(\dot{y}^{k}(t):=\frac{\mathrm{d}}{\mathrm{d}t} y^{k}(\tilde{\gamma }(t))\). By duality this induces the following (adjoint) covariant derivative of a covector field \(\lambda \) (i.e., a section in \(T^{*}(SE(d))\)):
with \(\dot{\lambda }_{i}(t) =\frac{d}{dt} \lambda _{i}(\tilde{\gamma }(t))\). Then by antisymmetry of the structure constants it directly follows (see, e.g., [25]) that the auto-parallel curves are the exponential curves:
Remark 21
Due to torsion of the left Cartan connection, the auto-parallel curves do not coincide with the geodesics w.r.t. metric tensor  . This is in contrast to the Levi–Cevita connection (see, for example, Jost’s book [44, ch:3.3, ch:4]) where auto-parallels are precisely the geodesics (see [44, ch:4.1]).
. This is in contrast to the Levi–Cevita connection (see, for example, Jost’s book [44, ch:3.3, ch:4]) where auto-parallels are precisely the geodesics (see [44, ch:4.1]).
Intuitively speaking this means that in the curved geometry of the left Cartan connection on SE(d) (that is present in the domain of an orientation score, see Fig. 3) the ‘straight curves’ (i.e., the auto-parallel curves) do not coincide with the ‘shortest curves’ (i.e., the Riemannian distance minimizers).
The left Cartan connection is the consistent connection on SE(d) in the sense that auto-parallel curves are the exponential curves studied in this article. Therefore, the consistent Hessian form on SE(d) is induced by the left Cartan connection. Expressing it in the left-invariant frame yields
where i denotes the row index and j the column index. So we conclude from this computation that (127) is the correct consistent Hessian on SE(d) for our purposes.
Remark 22
The left Cartan connection has torsion and is not the same as the standard torsion-free Cartan–Schouten connection on Lie groups, which have also many applications in image analysis an statistics on Lie groups, cf. [55, 56]. Recall that within the orientation score framework, right invariance is undesirable.
Appendix 5: Table of Notations
See Table 1.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Duits, R., Janssen, M.H.J., Hannink, J. et al. Locally Adaptive Frames in the Roto-Translation Group and Their Applications in Medical Imaging. J Math Imaging Vis 56, 367–402 (2016). https://doi.org/10.1007/s10851-016-0641-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10851-016-0641-0


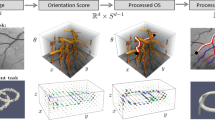



















 -orthogonal to this main spatial direction stay in the spatial part of the tangent space
-orthogonal to this main spatial direction stay in the spatial part of the tangent space 