Rules of Origin and Strategic Choice of Compliance

Abstract

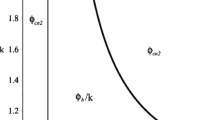
This paper examines how an input supplier’s monopoly power affects exporters’ choice between compliance and noncompliance with rules of origin (ROO) in a free trade area (FTA). When the regional input supplier has monopoly power, the number of compliers largely affects the input price. This is because to meet ROO, exporters must use a certain ratio of the input originated within the area. In such a case, each exporter has an incentive to choose noncompliance with ROO if the rival exporter complies. Because this incentive yields strategic substitution between symmetric exporters, the coexistence of the complier and the non-complier appears in equilibrium. Our model consists of three final-good producers (one in an importing country and two in an exporting country) and one input supplier, which is in the importing country and has monopoly power. We show that within the range of parameter values for which some exporters comply with ROO, the content rate affects the output of the final-good producer in the importing country and the country’s welfare in a U-shaped fashion. The content rate levels that allow the coexistence of the complier and the non-complier minimize welfare.

Appendix: proofs

Proof of proposition 1

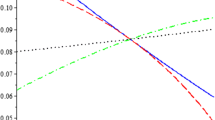
Let us consider exporter 1. Comparing (NC, NC) and (C, NC), the following indifference condition holds: $\pi_1^E\left( {NC,NC} \right)=\pi_1^E\left( {C,NC} \right)$ is equivalent to $\gamma ={{{4\theta \left( {1+3\theta } \right)}} \left/ {{\left( {51-38\theta +39{\theta^2}} \right)}} \right.}\equiv {f_1}\left( \theta \right)$, where γ ≡ τ/a. Similarly, comparing (NC, C) and (C, C), the following indifference condition holds: $\pi_1^E\left( {NC,C} \right)=\pi_1^E\left( {C,C} \right)$ is equivalent to $\gamma ={{{4\theta \left( {1+2\theta -{\theta^2}+4{\theta^3}} \right)}} \left/ {{\left( {3-4\theta +4{\theta^2}} \right)\left( {17-14\theta +17{\theta^2}} \right)}} \right.}\equiv {f_2}\left( \theta \right)$. Note that the exporters are symmetric; subsequently, f ₁(θ) and f ₂(θ) are valid for exporter 2. That is, f ₁(θ) corresponds to exporter 2’s (NC, NC) and (NC, C) cases, and f ₂(θ) corresponds to exporter 2’s (C, NC) and (C, C) cases. Thus, $\gamma \geq {f_1}\left( \theta \right)\Leftrightarrow \pi_1^E\left( {C,NC} \right)\geq \pi_1^E\left( {NC,NC} \right)$, $\gamma \leq {f_1}\left( \theta \right)\Leftrightarrow \pi_1^E\left( {NC,NC} \right)\geq \pi_1^E\left( {C,NC} \right)$, $\gamma \geq {f_2}\left( \theta \right)\Leftrightarrow \pi_1^E\left( {C,C} \right)\geq \pi_1^E\left( {NC,C} \right)$, and $\gamma \leq {f_2}\left( \theta \right)\Leftrightarrow \pi_1^E\left( {NC,C} \right)\geq \pi_1^E\left( {C,C} \right)$. Further, $\gamma \geq {f_1}\left( \theta \right)\Leftrightarrow \pi_2^E\left( {NC,C} \right)\geq \pi_2^E\left( {NC,NC} \right)$, $\gamma \leq {f_1}\left( \theta \right)\Leftrightarrow \pi_2^E\left( {NC,NC} \right)\geq \pi_2^E\left( {NC,C} \right)$, $\gamma \geq {f_2}\left( \theta \right)\Leftrightarrow \pi_2^E\left( {C,C} \right)\geq \pi_2^E\left( {C,NC} \right)$, and $\gamma \leq {f_2}\left( \theta \right)\Leftrightarrow \pi_2^E\left( {C,NC} \right)\geq \pi_2^E\left( {C,C} \right)$. For all θ in (0, 1], C becomes a dominant strategy for all exporters if γ ≥ f ₂(θ). Next, for all θ in (0, 1], NC becomes a dominant strategy for all exporters if γ ≤ f ₁(θ). Finally, for all θ in (0, 1], (C, NC) and (NC, C) are the equilibrium if f ₂(θ) ≥ γ ≥ f ₁(θ). Q.E.D.

Proof of proposition 2

First, ${\pi^L}\left( {NC,NC} \right)={\pi^L}\left( {C,C} \right)$ is equivalent to ${\tau \left/ {a} \right.}={{{-4\theta \left( {1-\theta } \right)}} \left/ {{\left( {3-4\theta +4{\theta^2}} \right)}} \right.}\equiv {q_1}\left( \theta \right)$. q ₁(θ) is nonpositive for all θ in [0, 1], and ${\pi^L}\left( {NC,NC} \right) > {\pi^L}\left( {C,C} \right)$ if γ > q ₁(θ). ${\pi^L}\left( {NC,NC} \right)\geq {\pi^L}\left( {C,C} \right)$ for all $\left( {\theta, \gamma } \right)\in \left[ {0,1} \right]\times \left[ {0,{\tau^{\max }}} \right]$. Next, ${\pi^L}\left( {NC,NC} \right)={\pi^L}\left( {C,NC} \right)$ is equivalent to ${\tau \left/ {a} \right.}={{{-4\theta \left( {-1+\theta } \right)}} \left/ {{\left( {-3+\theta } \right)\left( {1+\theta } \right)}} \right.}\equiv {q_2}\left( \theta \right)$. q ₂(θ) is non-positive for all θ in [0, 1], and ${\pi^L}\left( {NC,NC} \right) > {\pi^L}\left( {C,NC} \right)$ if γ > q ₂(θ). ${\pi^L}\left( {NC,NC} \right)\geq {\pi^L}\left( {C,NC} \right)$ for all $\left( {\theta, \gamma } \right)\in \left[ {0,1} \right]\times \left[ {0,{\tau^{\max }}} \right]$. Finally, ${\pi^L}\left( {C,NC} \right)={\pi^L}\left( {C,C} \right)$ is equivalent to ${\tau \left/ {a} \right.}={{{-4\theta \left( {-3+3\theta -2{\theta^2}+2{\theta^3}} \right)}} \left/ {{\left( {3-4\theta +4{\theta^2}} \right)\left( {3-6\theta +7{\theta^2}} \right)}} \right.}\equiv {q_3}\left( \theta \right)$. q ₃(θ) is nonpositive for all θ in [0, 1], and ${\pi^L}\left( {C,NC} \right) > {\pi^L}\left( {C,C} \right)$ if γ > q ₃(θ). ${\pi^L}\left( {C,NC} \right)\geq {\pi^L}\left( {C,C} \right)$ for all $\left( {\theta, \gamma } \right)\in \left[ {0,1} \right]\times \left[ {0,{\tau^{\max }}} \right]$. Therefore, ${\pi^L}\left( {NC,NC} \right)\geq {\pi^L}\left( {C,NC} \right)={\pi^L}\left( {NC,C} \right)\geq {\pi^L}\left( {C,C} \right)$ for all $\left( {\theta, \gamma } \right)\in \left[ {0,1} \right]\times \left[ {0,{\tau^{\max }}} \right]$. Q.E.D.

Proof of proposition 3

(1) Differentiating y(C, C) and z _j (C, C) with respect to θ, we have $\left( {{{{\partial y}} \left/ {{\partial \theta }} \right.}} \right)\left( {C,C} \right)={{{3a\left( {2\theta -1} \right)}} \left/ {{b{{{\left( {3-4\theta +4{\theta^2}} \right)}}^2}}} \right.}$ and $\left( {\partial {{z}_{j}}/\partial \theta } \right)\left( {C,C} \right) = {{{a\left( {1 - 8\theta + 4{{\theta }^{2}}} \right)}} \left/ {{2b{{{\left( {3 - 4\theta + 4{{\theta }^{2}}} \right)}}^{2}}}} \right.}$. Thus, $\left( {{{{\partial y}} \left/ {{\partial \theta }} \right.}} \right)\left( {C,C} \right)\geq \left( < \right)\;0$ if θ ≥ (<)1/2, and $y\left( {C,C} \right)\left| {_{{\theta ={1 \left/ {2} \right.}}}} \right.=0$. From the numerator of (∂z _j /∂θ), $1-8\theta +4{\theta^2}\geq 0$ if $\theta \leq \left( {{1 \left/ {2} \right.}} \right)\left( {2-\sqrt{3}} \right)$. Thus, $\left( {{{{\partial {z_j}}} \left/ {{\partial \theta }} \right.}} \right)\left( {C,C} \right)\geq \left( < \right)\;0$ if $\theta \leq \left( > \right)\;\left( {{1 \left/ {2} \right.}} \right)\left( {2-\sqrt{3}} \right)\simeq 0.133975$. (2) Differentiating y(C, NC), z ₁(C, NC), and z ₂(C, NC) with respect to θ, we have $\left( {\partial y/\partial \theta } \right)\left( {C,NC} \right) = {{{\left( {a + \tau } \right)\left( {{{\theta }^{2}} + 6\theta - 3} \right)}} \left/ {{2b{{{\left( {3 - 2\theta + 3{{\theta }^{2}}} \right)}}^{2}}}} \right.}$, $\left( {{{{\partial {z_1}}} \left/ {{\partial \theta }} \right.}} \right)\left( {C,NC} \right)={{{\left( {a+\tau } \right)\left( {3{\theta^2}-6\theta -1} \right)}} \left/ {{2b{{{\left( {3-2\theta +3{\theta^2}} \right)}}^2}}} \right.} < 0$, and $\left( {{{{\partial {z_2}}} \left/ {{\partial \theta }} \right.}} \right)\left( {C,NC} \right)={{{\left( {a+\tau } \right)\left( {1-{\theta^2}} \right)}} \left/ {{b{{{\left( {3-2\theta +3{\theta^2}} \right)}}^2}}} \right.}\geq 0$. Here, $\left( {{{{\partial y}} \left/ {{\partial \theta }} \right.}} \right)\left( {C,NC} \right)=\left( {{{{\partial y}} \left/ {{\partial \theta }} \right.}} \right)\left( {NC,C} \right)$, $\left( {{{{\partial {z_1}}} \left/ {{\partial \theta }} \right.}} \right)\left( {C,NC} \right)=\left( {{{{\partial {z_2}}} \left/ {{\partial \theta }} \right.}} \right)\left( {NC,C} \right)$, and $\left( {{{{\partial {z_2}}} \left/ {{\partial \theta }} \right.}} \right)\left( {C,NC} \right)=\left( {{{{\partial {z_1}}} \left/ {{\partial \theta }} \right.}} \right)\left( {NC,C} \right)$. From the numerator of ∂y/∂θ, ${\theta^2}+6\theta -3\geq 0$ if $\theta \geq 2\sqrt{3}-3$. Thus, $\left( {{{{\partial y}} \left/ {{\partial \theta }} \right.}} \right)\left( {C,NC} \right)\geq \left( < \right)\;0$ if $\theta \geq \left( < \right)\;2\sqrt{3}-3\simeq 0.464102$. Further, $y\left( {C,NC} \right)\left| {_{{\theta =2\sqrt{3}-3}}} \right.={{{3\left( {a+\tau } \right)\left( {7-4\sqrt{3}} \right)}} \left/ {{8b\left( {9-5\sqrt{3}} \right)}} \right.} > 0$. Since $\left( {{{{\partial {\pi^L}}} \left/ {{\partial \theta }} \right.}} \right)\left( { \cdot } \right)=2by\left( { \cdot } \right)\left( {{{{\partial y}} \left/ {{\partial \theta }} \right.}} \right)\left( { \cdot } \right)$ and $\left( {{{{\partial \pi_j^E}} \left/ {{\partial \theta }} \right.}} \right)\left( { \cdot } \right)=2b{z_j}\left( { \cdot } \right)\left( {{{{\partial {z_j}}} \left/ {{\partial \theta }} \right.}} \right)\left( { \cdot } \right)$, $\mathrm{sign}\left\{ {\left( {{{{\partial {\pi^L}}} \left/ {{\partial \theta }} \right.}} \right)\left( { \cdot } \right)} \right\}=\mathrm{sign}\left\{ {\left( {{{{\partial y}} \left/ {{\partial \theta }} \right.}} \right)\left( { \cdot } \right)} \right\}$ and $\mathrm{sign}\left\{ {\left( {{{{\partial \pi_j^E}} \left/ {{\partial \theta }} \right.}} \right)\left( { \cdot } \right)} \right\}=\mathrm{sign}\left\{ {\left( {{{{\partial {z_j}}} \left/ {{\partial \theta }} \right.}} \right)\left( { \cdot } \right)} \right\}$. Q.E.D.

Proof of proposition 4

First, comparing (15) with (16), we obtain

$$ W\left( {NC,NC} \right)=W\left( {C,C} \right)\;\Leftrightarrow \frac{{\left( {91a\tau -149{\tau^2}} \right){{{\left( {3-4\theta +4{\theta^2}} \right)}}^2}-4{a^2}\theta \left( {-84+239\theta -292{\theta^2}+128{\theta^3}} \right)}}{{288b{{{\left( {3-4\theta +4{\theta^2}} \right)}}^2}}}=0. $$

This yields the following equations:

$$ \begin{array}{*{20}c} {{\gamma_1}=\frac{{91{{{\left( {3-4\theta +4{\theta^2}} \right)}}^2}+3\sqrt{{-{{{\left( {3-4\theta +4{\theta^2}} \right)}}^2}B}}}}{{298{{{\left( {3-4\theta +4{\theta^2}} \right)}}^2}}},} \\ {{\gamma_2}=\frac{{91{{{\left( {3-4\theta +4{\theta^2}} \right)}}^2}-3\sqrt{{-{{{\left( {3-4\theta +4{\theta^2}} \right)}}^2}B}}}}{{298{{{\left( {3-4\theta +4{\theta^2}} \right)}}^2}}},} \\ \end{array} $$

where $B\equiv -8281-168\theta +26504{\theta^2}-47904{\theta^3}+19184{\theta^4} < 0$. Since γ ₂ < 0 for all θ in [0, 1], we can omit γ ₂. W(NC, NC) > W(C, C) if γ < γ ₁ and W(NC, NC) < W(C, C) if γ > γ ₁. Since γ ₁ > τ ^max for all θ in [0, 1], W(NC, NC) > W(C, C). Second, comparing (16) with (17), we obtain

$$ W\left( {C,C} \right)=W\left( {C,NC} \right)\;\Leftrightarrow \frac{{\left[ {\begin{array}{*{20}c} { - 2a\tau {{{\left( {3-4\theta +4{\theta^2}} \right)}}^2}\left( {819-1572\theta +1538{\theta^2}-708{\theta^3}+99{\theta^4}} \right)} \\ { - {\tau^2}{{{\left( {3-4\theta +4{\theta^2}} \right)}}^2}\left( {1161-3180\theta +3142{\theta^2}-2316{\theta^3}+441{\theta^4}} \right)\ } \\ { + {a^2}\left( {\begin{array}{*{20}c} {\ 26811-125388\theta +357786{\theta^2}-652500{\theta^3}+877067{\theta^4}} \\ {-841192{\theta^5}+595976{\theta^6}-273120{\theta^7}+77616{\theta^8}} \\ \end{array}} \right)} \\ \end{array}} \right]}}{{1152b{{{\left( {3-2\theta +3{\theta^2}} \right)}}^2}{{{\left( {3-4\theta +4{\theta^2}} \right)}}^2}}}=0. $$

Solving W(C, C) = W(C, NC) with respect to τ, we obtain

$$ \begin{array}{*{20}c} {{\gamma_3}=-\frac{{{{{\left( {3-4\theta +4{\theta^2}} \right)}}^2}D-6\left( {9-18\theta +29{\theta^2}-20{\theta^3}+12{\theta^4}} \right)\sqrt{F}}}{{{{{\left( {3-4\theta +4{\theta^2}} \right)}}^2}\left( {1161-3180\theta +3142{\theta^2}-2316{\theta^3}+441{\theta^4}} \right)}},} \\ {{\gamma_4}=-\frac{{{{{\left( {3-4\theta +4{\theta^2}} \right)}}^2}D+6\left( {9-18\theta +29{\theta^2}-20{\theta^3}+12{\theta^4}} \right)\sqrt{F}}}{{{{{\left( {3-4\theta +4{\theta^2}} \right)}}^2}\left( {1161-3180\theta +3142{\theta^2}-2316{\theta^3}+441{\theta^4}} \right)}},} \\ \end{array} $$

where $D\equiv 819-1572\theta +1538{\theta^2}-708{\theta^3}+99{\theta^4} > 0\;and\;\mathrm{F}\equiv 114705-680724\theta +1996874{\theta^2}-3698236{\theta^3}+4594521{\theta^4}-3950392{\theta^5}+2254340{\theta^6}-792944{\theta^7}+106128{\theta^8}$. Since γ ₄ < 0 for all θ in [0, 1], we can omit γ ₄. On the other hand, γ ₃ > 0.7 > τ ^max and γ ₃ is strictly increasing with respect to θ. This implies that W(C, C) > W(C, NC) if γ < γ ₃. Thus, $W\left( {C,C} \right)>W\left( {C,NC} \right)\left( {=W\left( {NC,C} \right)} \right)$. Q.E.D.

Proof of proposition 5

Differentiating (16) and (17) with respect to θ, we obtain

$$ \frac{{\partial W}}{{\partial \theta\ }}\left( {C,C} \right)=\frac{{{a^2}\left( {-14+61\theta -90{\theta^2}+44{\theta^3}+8{\theta^4}} \right)}}{{4b{{{\left( {3-4\theta +4{\theta^2}} \right)}}^3}}}, $$

(A.1)

$$ \frac{{\partial W}}{{\partial \theta\ }}\left( {C,NC} \right)=\frac{{\left[ {\begin{array}{*{20}c} {\left( {17+5\theta -27{\theta^2}+31{\theta^3}-18{\theta^4}} \right){\tau^2}} \\ { + \left( {-7+21\theta -27{\theta^2}+15{\theta^3}+6{\theta^4}} \right){a^2}} \\ { + 2\left( {5+13\theta -27{\theta^2}+23{\theta^3}-6{\theta^4}} \right)a\tau } \\ \end{array}} \right]}}{{4b{{{\left( {3-2\theta +3{\theta^2}} \right)}}^3}}}. $$

(A.2)

From (A.1), the meaning root of $-14+61\theta -90{\theta^2}+44{\theta^3}+8{\theta^4}=0$ is θ = 1/2. Thus, $\left( {{{{\partial W}} \left/ {{\partial \theta }} \right.}} \right)\left( {C,C} \right)\leq \left( > \right)\ 0$ if θ ≤ (>)1/2. From the denominator of (A.2), we solve the inequality $\left( {17+5\theta -27{\theta^2}+31{\theta^3}-18{\theta^4}} \right)\;{\tau^2}+2\left( {5+13\theta -27{\theta^2}+23{\theta^3}-6{\theta^4}} \right)\;a\tau +\left( {-7+21\theta -27{\theta^2}+15{\theta^3}+6{\theta^4}} \right)\ {a^2}\geq 0$ with respect to τ and obtain τ ≤ − a or a × g ⁻¹(θ) ≤ τ. Thus, we obtain $\left( {{{{\partial W}} \left/ {{\partial \theta }} \right.}} \right)\left( {C,NC} \right)=\left( {{{{\partial W}} \left/ {{\partial \theta }} \right.}} \right)\left( {NC,C} \right)\leq \left( > \right)\ 0$ if θ ≤ (>) g (γ), where ${g^{-1 }}\left( \theta \right)\equiv {{{\left( {-7+21\theta -27{\theta^2}+15{\theta^3}+6{\theta^4}} \right)}} \left/ {{\left( {-17-5\theta +27{\theta^2}-31{\theta^3}+18{\theta^4}} \right)}} \right.}$. Q.E.D.