Dynamics of the exponential integrate-and-fire model with slow currents and adaptation

Abstract

In order to properly capture spike-frequency adaptation with a simplified point-neuron model, we study approximations of Hodgkin-Huxley (HH) models including slow currents by exponential integrate-and-fire (EIF) models that incorporate the same types of currents. We optimize the parameters of the EIF models under the external drive consisting of AMPA-type conductance pulses using the current-voltage curves and the van Rossum metric to best capture the subthreshold membrane potential, firing rate, and jump size of the slow current at the neuron’s spike times. Our numerical simulations demonstrate that, in addition to these quantities, the approximate EIF-type models faithfully reproduce bifurcation properties of the HH neurons with slow currents, which include spike-frequency adaptation, phase-response curves, critical exponents at the transition between a finite and infinite number of spikes with increasing constant external drive, and bifurcation diagrams of interspike intervals in time-periodically forced models. Dynamics of networks of HH neurons with slow currents can also be approximated by corresponding EIF-type networks, with the approximation being at least statistically accurate over a broad range of Poisson rates of the external drive. For the form of external drive resembling realistic, AMPA-like synaptic conductance response to incoming action potentials, the EIF model affords great savings of computation time as compared with the corresponding HH-type model. Our work shows that the EIF model with additional slow currents is well suited for use in large-scale, point-neuron models in which spike-frequency adaptation is important.

1 Introduction

Mathematical models describing the dynamics of individual neurons are the basic building blocks used both in the simulation of large-scale neuronal networks and in the resultant derivation of mechanisms explaining neuronal processing in a number of brain areas (Lapicque 1907; Hodgkin and Huxley 1952; Somers et al. 1995; Troyer et al. 1998; Koch 1999; McLaughlin et al. 2000; Wielaard et al. 2001; Gerstner and Kistler 2002; Burkitt 2006a, b). The increasing size and architectural complexity of the neuronal network models employed in a number of current studies has brought about an ever increasing need for simplified yet accurate point-neuron models (Cai et al. 2005; Rangan et al. 2005; Tao et al. 2006). Efficient point-like models of single neurons, such as the Leaky Integrate and Fire (LIF) (Lapicque 1907; Tuckwell 1988a, b; Burkitt 2006a, b) and Exponential Integrate and Fire (EIF) (Fourcaud-Trocme et al. 2003) models, have made possible detailed simulations of brain activity on unprecedented scales, involving millions of neurons on cortical areas several millimeters across (Cai et al. 2005; Rangan et al. 2005). Typically rendering a robust statistical description of the underlying neuronal network mechanisms (Rangan and Cai 2007; Avermann et al. 2012; Nicola and Campbell 2013) while incurring only minor loss of pointwise accuracy relative to the more detailed Hodgkin Huxley (HH) model, these models have succeeded in substantially reducing computational costs.

The need for replacing the HH model by a simpler model is two-fold. First, it is advantageous to consider a smaller number of modeled variables, since each additional variable increases computational cost of model simulations, especially when they are governed by nonlinear differential equations with disparate time scales. Second, more importantly, to resolve the steep action potentials and counter the resulting stiffness of the HH model, its simulations must employ a large number of very small time steps, considerably slowing down the simulations. The simpler Integrate-and-Fire (IF) models sidestep this stiffness by treating action potentials as singularities, be it jump discontinuities or divergences of the membrane potential, and thus replace the laborious and often unnecessary computation of the action-potential details with a relatively simple determination of a neuron’s firing time.

Among the IF models that only take into account the neuronal voltage and external and synaptic current or conductance, the recently proposed EIF model (Fourcaud-Trocme et al. 2003) is believed to be the most accurate in approximating both the time-course of the subthreshold membrane potentials and the neuronal firing times as described by the corresponding HH model. Just as does the HH model, however, the EIF model needs to be augmented in order to describe some important features of neuronal dynamics, such as the decrease in a neuron’s firing rate over time known as spike-frequency adaptation. In particular, while the EIF model without adaptation can capture the effects of a number of fast ionic currents in a single equation describing the neuronal membrane-potential, it cannot alone replicate the spike-frequency attenuation caused by slow currents (Mensi et al. 2012; Pozzorini et al. 2013; Gerstner and Naud 2009). An augmented model with a phenomenological representation of a slow adaptation current was proposed in Brette and Gerstner (2005), which is quite accurate in representing the slowdown of the neuronal spiking under continuous stimulation. However, since slow currents typically do not cause action potentials and therefore their physiologically-based models do not cause the stiffness of the HH model, it may be conceptually advantageous to retain them in the EIF model in their original form, provided the degree of approximation afforded by the resulting augmented EIF model is comparable to that of the model in Brette and Gerstner (2005).

In this work, we adapt the modeling approach of Richardson (2009) to approximate the HH-based description of mammalian pyramidal neuron dynamics with one or two slow currents. In particular, we add to the EIF model the equations for two types of slow currents that induce spike-frequency adaptation. The first is the noninactivating muscarinic potassium current, I _M . This current is known to help regulate the spike threshold (Ermentrout et al. 2001); its impact is profound on long timescales and often goes unnoticed by simplified models that fail to properly address long-term behavior. Together with the muscarinic current, the after-hyperpolarization (AHP) current, I _{A H P} , accounts for spike-frequency adaptation in most biophysically realistic neuron models (Ermentrout et al. 2001). In particular, in neuronal models with several other known currents included, spike-frequency adaptation is only eliminated when both the flow of I _M and I _{A H P} are removed (Yamada et al. 1989). While I _M is primarily responsible for increasing the current threshold, I _{A H P} decreases the slope of the neuron’s voltage trace (Ermentrout et al. 2001; Koch 1999). Both combined produce a very pronounced form of spike-frequency adaptation. As in Brette and Gerstner (2005), we find that a neuronal membrane-potential spike induces a jump in each of these currents, which is necessary to include as part of our model. Under this additional assumption, we show numerically that this modified EIF model renders a highly accurate approximation of the corresponding adaptive HH model both statistically and even pointwise for trajectories, comparable in accuracy to that of the model in Brette and Gerstner (2005). At the same time, this model dramatically reduces the computational cost needed for the adaptive Hodgkin Huxley model. Thus, the modified EIF model may give us a new computationally efficient neuronal model that retains sufficient accuracy for use in large-scale simulations of networks composed of neurons whose firing rates slow down due to slow adaptation currents.

To approximate the HH model with slow currents by a corresponding EIF model, we use an appropriate parameter optimization procedure for the EIF-type model. In particular, as in Badel et al. (2008a, b) , using as the input current a Poisson train of AMPA-type excitatory post synaptic currents for both models, we first fit the current-voltage dependence of the HH model by the exponential-plus-linear form of the EIF model. We then minimize the van Rossum metric (Van Rossum 2001) difference between the spike trains of the HH and EIF models with the same slow current, fitting the jump in this current that occurs at every spike time for the EIF model.

After fitting the parameters of the EIF-type model, we test its accuracy using different types of currents: constant, time-periodic, and Poisson-train coupled through an AMPA-type synapse. Our tests range from comparisons of voltage traces, slow-current traces, and spike times, through voltage and firing-rate statistics, phase response curves, and spike-frequency adaptation, to critical exponents in the transition to persistent firing at sufficiently high external driving by a constant current, and the frequency dependence of the bifurcation diagrams of interspike intervals under time-periodic driving. All of these tests show excellent agreement of the EIF approximations with the corresponding HH models.

The remainder of the paper is organized as follows. In Section 2, we describe the HH model with an additional muscarinic current, the EIF model, and briefly discuss the adaptive EIF model of Brette and Gerstner (2005). We also describe the EIF model with the additional muscarinic current, and the parameter optimization procedure that ensures the closeness of the solutions of this model to those of the corresponding augmented HH model. In Section 3, we describe comparisons between different types of dynamics of the HH and EIF models with the additional muscarinic current, AHP current, and both types of currents. In Section 4, we present a discussion of the results. Finally, in the Appendix, we list the classic HH equations.

2 Methods

We begin this section by discussing the HH model with an additional slow current, which we here take, for definiteness, to be the muscarinic current. We then briefly discuss the EIF model (Fourcaud-Trocme et al. 2003) and the addition of a phenomenological adaptation current to it (Brette and Gerstner 2005), before introducing the EIF model with the added muscarinic current. Finally, we discuss the optimization procedure that we use to find the best fit of the EIF model with the added muscarinic current to the corresponding HH model.

2.1 Hodgkin-Huxley model with a slow adaptation current

For the first fundamental model whose dynamics we will be approximating with a simpler model, we here consider a conductance-based HH mammalian pyramidal cell model with an added slow adaptation current (Destexhe et al.1998). The dynamics of the neuronal membrane potential in this model is governed by the differential equation

$$ C\frac{dV}{dt} = -I_{L}-I_{Na}-I_{K}+I_{syn}+I_{ext}-I_{M}, $$

(1a)

$$ I_{i} = g_{i}(V,t)(V-V_i), $$

(1b)

where V is the membrane potential, C is the membrane capacitance, I _i is a specific current, g _i is the corresponding conductance, and V _i the corresponding reversal potential. The model (1) includes two major ionic currents, namely sodium (I _{N a} ) and potassium ( I _K ), as well as the synaptic current from other neurons ( I _{s y n} ), the leakage current ( I _L ), and possibly an external injected current ( I _{e x t} ). (The external current is given as a function of time and is not in the form (1b).) The difference between the original HH model (17) (discussed in the Appendix, taken from Destexhe and Pare 1999) and the model in Eq. (1) is the addition of the slow, muscarinic current, I _M (Yamada et al. 1989; McCormick et al. 1993; Koch 1999). The model (1) has been used to describe pyramidal neurons; the modeling parameters are chosen according to experimental results (Pare et al. 1998; Destexhe et al. 1998). We refer to it as the muscarinic Hodgkin-Huxley (mHH) model.The dynamics of the sodium and potassium currents in the mHH model (1) are taken to be identical to those found in the HH model, and are described in the Appendix. The muscarinic current is modeled using the equation

$$ I_{M} = \bar{g}_{M} n(V-V_K), $$

(2)

where $\bar {g}_{M}$ is the maximal muscarinic conductance, V _K is the potassium reversal potential, and n is the muscarinic activation variable (Yamada et al. 1989; McCormick et al. 1993; Koch 1999). The dynamics of the activation variable are given by the equation

$$ \frac{dn}{dt} =\frac{1}{3} \left[\alpha_{n}(V) (1-n) - \beta_{n}(V) n\right] =\frac{n_{\infty} - n}{\tau_{n}}, $$

(3a)

with

$$ \alpha_{n}(V)=\frac{0.0001(V+30)}{1-\exp[-(V+30)/9]}, $$

(3b)

$$ \beta_{n}(V)=\frac{-0.0001(V+30)}{1-\exp[(V+30)/9]}, $$

(3c)

$$ n_{\infty}= \frac{\alpha_{n}(V)}{\alpha_{n}(V)+\beta_{n}(V)}, $$

(3d)

$$ \tau_{n} = \frac{1/3}{\alpha_{n}(V)+\beta_{n}(V)}, $$

(3e)

where α _n is the opening rate of the muscarinic ionic channel, β _n is the closing rate, n _∞ is the steady-state value of the activation variable, and τ _n is the relaxation rate. The relaxation rate is reduced by a temperature factor of 3 as described in Pare et al. (1998). A similar formulation of these dynamics is also given in Yamada et al. (1989) for bullfrog sympathetic ganglion cells. Note that the potassium reversal potential is used in defining the muscarinic current (2) because it is an outward potassium current (Yamada et al. 1989; Koch 1999). Also, given that the muscarinic current is noninactivating, only an activation variable is necessary in its modeling. This activation variable is of power one in Eq. (2), reflecting the slowness of the muscarinic current.

For the synaptic current I _{s y n} , we consider pulse trains of the form

$$ I_{syn}=- \bar g_{syn} \sum_{k} G(t-t_k) (V-V_E), $$

(4)

where {t _k } are the incoming spike times,

$$ G(t)= \frac{t}{\tau_{syn}^{2}} e^{-t/\tau_{syn}}H(t), $$

(5)

is the AMPA-type excitatory postsynaptic conductance time course (Brown and Johnston 1983; Koch 1999), H( · ) is the Heaviside function, and V _E is the excitatory reversal potential, which is taken to be 0m V (Koch 1999). We model the incoming spike times {t _k } as a Poisson train to mimic the natural operating regime of a neuron as bombarded by large numbers of spikes arriving independently from other neurons at random times.

As mentioned above, the muscarinic current in the mHH model (1) is one of the two main currents responsible for neuronal spike-frequency adaptation (the other being the AHP current addressed below Yamada et al. 1989). Given a constant input current I _{e x t} , Fig. 1 demonstrates the increasingly slow firing of a model mHH neuron over 300m s. One notices that the interspike intervals between consecutive neuronal action potentials become longer for the mHH model (1) while remaining the same for the HH model (17). While the mHH system (1) models neuronal dynamics with great accuracy, the high computational cost associated with its simulation has motivated a number of simplified models intended to increase computational efficiency for the use in large-scale network models.

Fig. 1

Comparison of HH and mHH voltage traces. The two neurons are under drive by the same constant external current I _ext = 0.77nA over 300ms. Parameter values for the HH model are given in the Appendix, and parameter values for the muscarinic current are given by Eq. (3)

2.2 Exponential integrate and fire model

The most commonly used simplified point-neuron model is the Leaky Integrate-And-Fire (LIF) model (Burkitt 2006a; Lapicque 1907). A LIF neuron is governed by a linear differential equation that disregards the ionic current equations in favor of computational efficiency. The neuronal membrane potential, V , follows simple dynamics of an RC-circuit until it reaches a fixed threshold, V _T . The crossing of this threshold is taken to signify that the neuron has fired, and its membrane potential is instantaneously reset to a lower value, V _R , typically in the range of − 70m V to − 60m V. The RC-circuit-like evolution of the membrane potential resumes immediately or after a fixed refractory period. The details of the membrane-potential spike during the firing of the neuronal action potential are entirely ignored by this model. Nevertheless, the LIF model is quite accurate in reproducing realistic neuronal firing rates and reasonably accurate in describing subthreshold membrane potential dynamics (Carandini et al. 1996; Rauch et al. 2003; Burkitt 2006a, b). It has thus, despite and because of its simplicity, proven to be an indispensable tool in the modeling of large-scale neuronal network dynamics (Troyer et al. 1998; McLaughlin et al. 2000; Wielaard et al. 2001; Cai et al. 2005; Rangan et al. 2005; Tao et al. 2006).

The LIF model does not capture the membrane potential dynamics near or during the action potential, reflecting the fact that the neuronal membrane cannot be described as a linear RC-circuit. Experimental investigations on pyramidal neurons and current-voltage curve analysis of the HH model instead reveal a linear-plus-exponential dependence of the membrane potential on the ionic currents (Badel et al. 2008a, b). Thus, a particularly accurate approximate description of the neuronal membrane potential dynamics was found to be given by the exponential integrate-and-fire (EIF) model (Fourcaud-Trocme et al. 2003)

$$ C\frac{dV}{dt} = -I_L+g_{L} \Delta_{T} \exp\left(\frac{V-V_{T}}{\Delta_{T}}\right)+I_{syn}+I_{ext}, $$

(6)

where V _T is a (soft) firing threshold and Δ _T is the spiking slope factor. A spike in this model occurs when the membrane potential V reaches infinity; V is then reset to the value V _R < V _T . After possibly remaining at V _R for a refractory period, the membrane potential begins evolving according to Eq. (6) again. The accuracy of approximation afforded by the EIF model (6) versus the corresponding HH dynamics was studied in Geisler et al. (2005), in which excellent agreement was reported.

A means of including an adaptation current in an approximation of the mHH model is given by the adaptive Exponential Integrate and Fire (aEIF) model (Brette and Gerstner 2005). This model adds the adaptation current − w to the right-hand side of Eq. (6), where w satisfies the equation τ _w (d w / d t) = a(V − V _L ) − w. In this equation, V _L is the leakage potential, a is the coupling strength, and τ _w is the time-decay rate for the adaptation current. At each action potential, the reset conditions are V → V _R and w → w + b, where V _R is the reset voltage and b accounts for the jump in the adaptation current. The form of the adaptation current dynamics was taken from the analogous adaptive quadratic IF model, which is known to capture a number of neuronal dynamical regimes and their bifurcations (Izhikevich 2003). Comparisons between the voltage traces and spike-times of the mHH and aEIF models show closeness in voltage evolution (Brette and Gerstner 2005); dynamical regimes and bifurcations of the aEIF model are described in Naud et al. (2008) and Touboul and Brette (2008). Further successful fittings of the aEIF model to mHH-type models and recordings of pyramidal cells can be found in Naud et al. (2008), Jolivet et al. (2008), and Clopath et al. (2007).

Nevertheless, because slow currents contribute little to the detailed superthreshold dynamics of the action potentials and affect the dynamics by slowing down their onset through inhibitory-like effects on the subthreshold neuronal voltage, it may be sensible to include these currents in the adaptive model in their original, physiological form. We will carry this out for the muscarinic current in the next section, and the AHP current addressed later on.

2.3 Muscarinic exponential integrate-and-fire model

The drawback of using HH and mHH point-neuron models in network simulations is the need to resolve the steep and narrow action potentials, during which these models become very stiff and demand rather small time-step sizes. In the case of the standard HH model (17), which neglects the muscarinic current in the mHH model (1), replacement by the EIF model (6) successfully reduces this stiffness. Its success can primarily be attributed to the fact that the singularity signifying an EIF-type spike can be either approximated analytically or computed by interchanging the roles of the membrane potential and time as the independent and dependent variables and thus evolving the latter in terms of the former, respectively, and neither of these procedures requires a significant decrease in the time-step size. In both models given by Eqs. (6) and (17), the action potentials are initiated by the fast ionic currents; the slow adaptation currents appear to play a negligible role in this initiation. Because the slow currents do not cause any additional stiffness in the model, there is no need to incorporate the slow currents into the exponential term in the membrane-potential equation. Due to this scale separation, expressions and equations describing their dynamics can be left unaltered. In this vein, the EIF model with a slow current was proposed in (Richardson 2009). Here, we study the accuracy of the approximation with two concrete types of slow currents, the first of which is the slow muscarinic current, I _M , in Eq. (2). Our aim in this section is to investigate strategies for how to best approximate the dynamics of the mHH model with the EIF dynamics accompanied by this slow adaptation current.

In the proposed model, as in the reduction of the HH to EIF model, we replace the fast ionic currents in Eq. (1) by the exponential term as in Eq. (6). However, we also keep the slow muscarinic current (2) to capture the impact of spike-frequency adaptation. The resulting Muscarinic Exponential Integrate and Fire (mEIF) model becomes

$$\begin{array}{@{}rcl@{}} C\frac{dV}{dt} = -I_L&+&g_{L} \Delta_{T} \exp\left(\frac{V-V_{T}}{\Delta_{T}}\right)\\ &+&I_{syn}+I_{ext}-g_Mn(V-V_M), \end{array} $$

(7a)

$$ \frac{dn}{dt} = \frac{n_{\infty} - n}{\tau_{n}}. $$

(7b)

The dynamics of the muscarinic current’s activation variable n are equivalently described in Eq. (3) as in the mHH model (1). The dynamics of the synaptic current I _{s y n} , when used, are described by the pulse train in Eq. (4).The membrane potential spiking and resetting mechanism in Eq. (7a) is the same as for the standard EIF model (6), as described above. During a spike of the mHH model (1), the muscarinic current is seen to undergo a sharp surge, which cannot be calculated analytically from Eqs. (1) and (3), but is necessary for our mEIF model (7) to take into account. Just as in the aEIF model of Brette and Gerstner (2005), we approximate this surge by a jump, whose size j is part of the set of parameters in the mEIF model (7) that we need to optimize in order to obtain the best approximation of the mHH model (1). Specifically, a jump constant, j, is added to the muscarinic activation variable, n, immediately following each action potential. The dynamics of the activation variable, taking into account the jumps at the action potentials, are therefore described by the equation

$$ \frac{dn}{dt} = \frac{n_{\infty} - n}{\tau_{n}} + j \sum_{i} \delta(t-t_i) $$

(8)

where t _i denotes the i-th action potential of the mEIF neuron.

In all of our simulations, the activation variable, regardless of the choice of slow current, fluctuates beneath the maximal value of 1. Only at very high firing rates would n approach 1, in which case the HH jump size would decrease. As throughout most of our simulations this is not the case, we simply set 0.99 as the saturation value for the activation variable n. Biologically, the rapid transition in the activation of the muscarinic current modeled by the jump occurs because the large number of calcium-dependent ionic channels that open during an action potential allows a surge in the muscarinic current passing through the neuron. Similar phenomena occur for other concentration-dependent currents (Koch 1999).

Away from the action potentials, we solve the mEIF system of differential equations (7) using a standard second-order Runge-Kutta algorithm. Since the voltage begins to increase monotonically to arbitrarily large values before an action potential, we assume that an action potential will take place when the mEIF neuron’s voltage increases up to a sufficiently high prescribed value V _{s w i t c h} . As in Fourcaud-Trocme et al. (2003), we evolve the voltage numerically until it first reaches a value above V _{s w i t c h} , and choose this value as the initial condition V(t ₀) = V ₀ for an analytical solution of Eq. (7a) with the exponential term alone,

$$ C\frac{dV}{dt} \approx g_{L}\Delta_{T}e^{(V - V_{T})/ \Delta_{T}}. $$

(9)

This solution is

$$ V(t)=V_T-\Delta_{T}\ln\left[\exp\left(-\frac{V_0-V_{T}}{\Delta_{T}}\right)+\frac{g_{L}}{C}(t_0-t)\right], $$

(10)

and from it we compute the spike time as the time at which the argument in the logarithm vanishes.

Simple analysis shows that if we want to preserve second-order numerical accuracy of the mEIF model, we must choose V _{s w i t c h} so that the ratio between the exponential and the rest of the terms in Eq. (7a) is of order 1 / Δ t, where Δ t is the time-step size. In practice, following Fourcaud-Trocme et al. (2003), we take V _{s w i t c h} ≈ − 30m V, so that the exponential term in Eq. (7a) is approximately two orders of magnitude larger than the rest of the terms when we switch from the numerical to the analytical solution.

In the forthcoming section, we discuss how to extract the parameter values for Eq. (7) that will render the most accurate approximation of the mHH system (1). We remark that this approximation is not uniform, since it also depends on the type and strength of the external or synaptic input current that drives the neuron as explained below. We carry out the parameter fitting in two steps. First, we fit the parameters of the EIF part of the model using current-voltage (I-V) curves, and then the jumps in the muscarinic current.

2.4 Parameter optimization

Integrate-and-Fire (IF) models are phenomenological in the sense that there appears to be no systematic derivation of them, in general, from the HH model using a small parameter (Burkitt 2006a). (The linear IF model can be, however, obtained from the HH model using a systematic, perturbation-theory-like approximation procedure (Abbott and Kepler 1990), and also as the first-order truncation in a Wiener-kernel expansion of the HH model (Kistler et al. 1997).) Nevertheless, as was discussed in Kistler et al. (1997) and Fourcaud-Trocme et al. (2003), with appropriately chosen parameter values, versions of the IF model provide an excellent approximation of the HH model and even some experimental data (Carandini 1996; Rauch et al. 2003; Badel et al. 2008a, b). At the beginning of the Section 3, we show that the voltage traces, muscarinic current, and firing times of an appropriately parametrized mEIF model are virtually indistinguishable from those of the corresponding mHH model. Below, we show the same results for the HH model with a slow AHP current, and also a combination of the two currents. In this section, we discuss the procedure we use to fit the mEIF model parameters so as to optimally reproduce the mHH dynamical behavior. Note that the majority of the parameters used in the mHH model, including those with known physiological values, are fitted in the mEIF model and thus may be reparameterized for new settings.

The parameter optimization procedure we describe follows Badel et al. (2008a, b) and and begins by fitting the parameters g _L , V _L , Δ _T and V _T . We take the neuronal-membrane capacitance to be fixed at the typical physiological value C = 0. 29n F. Initially, we fit only the EIF model (6) to the HH model (17). Once the first fit is complete, we consider the analogous fit for the mEIF model. We write both the HH and EIF voltage equations in the form

$$ C\frac{dV}{dt} = - I_{ionic} + I_{syn}, $$

(11)

where $I^{HH}_{ionic}=I_L+I_{Na} + I_{K}$ in the mHH model and $I^{EIF}_{ionic} = C F\left ( V\right )$ in the EIF model, with

$$ F\left( V\right) = g_{L} \left[ V_{L} - V + \Delta_{T} \exp\left( \frac{V - V_{T}}{\Delta_{T}}\right) \right]. $$

(12)

To best approximate the HH model by the EIF equations, we minimize the function

$$L\left( g_{L} , V_{L} , \Delta_{T} , V_{T} \right) = \max_{V} \left| I^{HH}_{ionic} (V) -I^{EIF}_{ionic}(V) \right|. $$

We compute $I^{HH}_{ionic}$ using a pulse train of the form (4) for I _{s y n} and then choose parameters to find minL g _L , V _L , Δ _T , V _T .We use averaging to approximate the mean HH current-voltage dependence, i.e., $I^{HH}_{ionic}(V)$ as a function of V . In particular, first, we sort the computed values of $I^{HH}_{ionic}$ for which the voltage is below threshold into bins according to their corresponding values of V . Then, we calculate $\tilde {I}_{k}$, the average value of $I^{HH}_{ionic}$ within the k ^th bin. This process gives us a list of discrete points $\left \{\left (\tilde {V}_{k} , \tilde {I}_{k}\right )\right \}$ which represent the average voltage dependence of $I^{HH}_{ionic}$. Now we use least squares to fit an equation of the form F V = α + β V + γ expδ V to the points $\left \{\left (\tilde {V}_{k} , -\frac {1}{C}\tilde {I}_{k}\right )\right \}$. From the fit α, β, γ, δ we can solve for g _L , V _L , Δ _T , V _T .

Once the EIF parameters are optimized, we only need to fit the jump constant, j. We do this by minimizing the van Rossum metric difference between the spike trains of the mHH and mEIF models (Van Rossum 2001). The size of the jump j that gives the minimal difference is chosen in our model. For the van Rossum metric, we let $\{t^{f}_{j}\}$ and $\{t^{g}_{j}\}$ denote the mHH and mEIF spike trains, respectively. We define the smeared spike-train function f(t) used in the van Rossum metric by

$$f(t) = \displaystyle \sum _{i} H(t-t^{f}_i) \exp\left(-\frac{t-t^{f}_{i}}{t_{c}}\right), $$

where H denotes the Heaviside function, $t^{f}_{i}$ denotes a given spike time of the mHH model, and t _c an appropriately chosen time constant. We define the function g(t) analogously. In this way, we represent spikes by exponential tails, which gives us a means to estimate spike-time differences. In particular, the van Rossum metric we utilize defines the difference between the spike trains as

$$D^{2}(f,g)_{t_{c}} = \frac{1}{t_{c}} \displaystyle \int_{0}^{\infty} [f(t)-g(t)]^2dt. $$

Assuming that firing rates of the optimized mEIF model and corresponding mHH model will approximately agree, we choose a small time constant, t _c = 5m s, to measure coincidence of spikes as in Van Rossum (2001). Note that we choose a small t _c , as opposed to a larger value, in order to measure the similarity of the timing of the spikes rather than the difference in firing rate, as indicated by using large values of t _c . A time constant specifically of size t _c = 5m s reflects a time scale that is generally less than the average interspike interval (ISI), the amount of time between successive firing events, we simulate for both models, but greater than the average difference in respective spike times. After optimizing all other model parameters, we minimize the van Rossum metric difference to obtain the jump size, j. We remark that an alternative to fitting the jump constant from the spike train distance in this way is minimizing the voltage trace difference as in Mensi et al. (2012), which yields a similarly effective optimization.

3 Results

In order to examine the accuracy of our approximation and its optimization, we perform numerical simulations of both the mEIF and mHH neurons, given the same driving current, and then compare their resulting dynamics. Our simulated neurons are driven either by constant or time-periodic external currents, or by AMPA-type excitatory post-synaptic potentials (EPSPs), as described in Eq. (4), induced by a Poisson spike train, which reflect the random nature of the spikes received by neurons in a large network. We let ν denote the expected number of spikes a neuron will receive per unit time and ḡ _syn the strength of the post-synaptic conductances, as in Eq. (4). Our optimally chosen parameter values are listed in Table 1. The parameters entering the exponential term and the jump constant for the mEIF model are listed in Table 2. Unless specifically stated otherwise, the time step Δ t = 0. 001m s was used throughout this work. In Table 3, we list the parameters used for the external synaptic drive.

Table 1 mEIF model parameters

Table 2 mEIF exponential term parameters

Table 3 Synaptic current parameters

3.1 Comparison of voltage traces, slow current dynamics, and spike times

Using the parameter values given in Tables 1 and 2, we now compare the dynamics of the mEIF model to those of the mHH model. The voltage traces corresponding to simulations of the mEIF and mHH models over a time interval of 1000m s are depicted in Fig. 2a. In the caption of the voltage trace plot, we include the van Rossum metric difference between the traces for further comparison. The traces of the muscarinic activation variable for both models are compared in Fig. 2b over the same time interval.

As can be seen in Fig. 2, the subthreshold voltage trace of the mEIF model provides an excellent approximation to that of the mHH model. In addition, the spikes times are also reproduced almost perfectly. Capturing every spike in Fig. 2, we note that the mEIF model exhibits accuracy comparable to the aEIF model. For a longer, 2 second simulation time, the mEIF model misses only 2 % of mHH spikes and emits 4 % extra spikes, which compares well to the approximately 4 % of spikes missed and 3 % extra spikes produced by the aEIF model (Brette and Gerstner 2005). Moreover, using the same input current as for the mEIF and mHH models, we plot in Fig. 2 the corresponding voltage trace for the aEIF model. To appropriately choose the aEIF parameters, we have optimized the EIF parameters using the procedure described in the Parameter Optimization Section, and chose the remaining parameters, a = 0. 003μ S, b = 0. 06n A, and τ _w = 120m s, that minimized the van Rossum metric difference between the aEIF and mHH spike trains. In this particular case, the aEIF model misses one spike and exhibits one additional firing event, whereas every spike is captured by the mEIF model. For a further comparison of the aEIF and mHH dynamics, see the Comparison of Bifurcation Diagrams under Time-Periodic Driving Section.

It is important to stress that the Poisson spike train with which we have driven the models to produce the results shown in Fig. 2 is not the same as the one used in our optimization procedure; while it has the same rate ν and EPSC amplitude $\bar g_{syn}$, it is not the same realization. The mEIF muscarinic activation variable dynamics, which include the fitted jump constant at each spike, follow the shape of its mHH counterparts very closely, however they do experience a small error generally less than approximately 5 %. We remark that we simulated both neuron models using the same small fixed time-step size, which is kept at a small value Δ t = 0. 001m s to ensure we fully resolve the stiffness of the mHH model, and that the computational savings afforded by the mEIF model were only about 50 % of the mHH model runtimes.

To further address the efficiency of the mEIF versus mHH simulations, we compare the solutions of the two models using the largest time-step size for the mHH model that allows it to be fully resolved at all action potentials, Δ t _{m H H} = 0. 08m s, and an increasing sequence of step sizes for the mEIF model. We use the model parameters listed in Tables 1 and 2. For the stepsize Δ t _{m E I F} = 0. 5m s, we display the comparison between the model runtimes with these respective time-steps for several simulations of long duration in Table 4. In this case, the mEIF model still captures the mHH firing events with a coincidence rate of 96 % relative to the mHH spikes, where we consider any mHH and corresponding mEIF action potential to be coincident if they occur within a time interval of size 3. 0m s. Even when taking time-steps of size Δ t _{m E I F} = 1. 0m s and Δ t _{m E I F} = 2. 0m s, we observe that the coincidence rate remains no lower than 95 % . In each case, the mEIF model is significantly more efficient than its mHH counterpart, decreasing runtimes by over 85%. All computations in this comparison were performed using a Lenovo T420 laptop with a 2.7 GHz Intel Core i7-2620M Processor and 8GB of RAM. Moreover, simulations were run with a C++ based code on a 64-bit Windows 7 Operating system.

Fig. 2

Comparison between mHH and mEIF neuron dynamics. Comparison between mHH and mEIF (a) voltage traces and (b) muscarinic activation variables. Also included in (a) is a comparison with the aEIF voltage trace using a=0.003 μS, b=0.06nA, and τ_w = 120ms. Simulation time was 1000ms. The Van-Rossum Metric Difference is 0.003489, with t_c = 5ms. The parameters are given by Tables 1, 2 and 3

Table 4 Model efficiency comparison

The mEIF step-size used in the above comparison is significantly shorter than the time-scale of the AMPA conductance, which contributes to the high coincidence rate observed even though the mEIF time-step size is almost an order of magnitude larger than the corresponding mHH step-size. However, we have observed that even if we increase the mEIF time-step size to $\Delta t_{mEIF} =2.0ms$, which is only slightly shorter than the AMPA time-scale, we still note reasonable agreement between the solutions of the two models. To demonstrate the surprising accuracy of the mEIF approximation even for such a large time-step, in Fig. 3, we magnify the voltage traces near a single spike using $\Delta t_{mEIF} =2.0ms$. We observe agreement in both the subthreshold voltage dynamics and the timing of firing events. This large time-step yields a coincidence rate of $95 \%$ within a maximal spike-time distance of $3ms$, indicating that taking relatively large time-steps with the mEIF model increases the computational efficiency of the mEIF model while still maintaining a good level of accuracy relative to the mHH model. Figure 3 also includes for comparison the voltage trace of the mEIF model using the smaller stepsize $\Delta t_{mEIF} =0.5ms$, which exhibits nearly the same subthreshold dynamics as the mEIF model using the larger stepsize. We note that the larger stepsize does induce a larger spike width, but after the action potential is completed, both voltage traces agree quite well.

Fig. 3

Voltage dynamics of mHH and mEIF neurons computed with several time-step sizes. Comparison between mHH and mEIF voltage dynamics over the duration of a single firing event using a time-step of size Δt _mHH = 0.08ms for the mHH model, and also time-steps Δ t _mEIF = 0.5ms and Δt _mEIF = 2.0ms for the mEIF model. Parameter choices are given by Tables 1, 2 and 3

3.2 Comparison of voltage and firing-rate statistics

Tables 5 and 6 show a comparison of the firing rates, mean subthreshold voltages, and subthreshold voltage variances between the mHH and mEIF model neurons with optimized parameters under the same Poisson-train drive over relatively long time scales. The results of the two models are statistically nearly identical, with the subthreshold voltage means and variances approximately equal and differences largely remaining within a few percent.

Table 5 Long-Time firing-rate comparison

Table 6 Long-Time statistics comparison

3.3 Comparison of phase-response curves

A further indicator of closeness between the mHH and mEIF systems is the phase-response curve, which measures the sensitivity of a neuronal model to impulse-type perturbations in its input current (Gutkin et al. 2005). To construct a phase-response curve, we first inject a given neuron with a strong constant driving current, and then wait until time $t_{0}$ when the voltage trace undergoes periodic motion upon attaching to a stable limit cycle. Next, we compute the neuron’s time-to-spike $T_{0}$, i.e., the time necessary for completing an action potential following reset to the neuronal resting potential. We then measure the change in $T_{0}$ under an additional short injection of a weak depolarizing current at any given time $t_{s} = t_0+\phi _{s} T_{0}$, with $0\leq \phi _{s} \leq 1$ being the phase. In other words, the phase $\phi _{s}$ is the fraction of the initial time-to-spike completed before the additional current injection. For each $\phi _{s}$, we find the perturbed time-to-spike, $T_{1}(\phi _s)$, and plot the relative change in the time-to-spike, $R(\phi _s)$, where

$$R(\phi_s) = \frac{T_{1}(\phi_s) - T_{0}}{T_{0}}, $$

as a function of the phase $\phi _{s}$. This gives the phase-response curve.

We have computed the phase-response curves for the mEIF and mHH neurons, depicted in Fig. 4, using the base injected-current value $0.8nA$ and waiting until time $t_0=300ms$ before computing the time-to-spike, $T_{0}$. The additional injected-current has a value of $0.08nA$ and an injection duration of $\Delta t = 2ms$, with this current injected at times $t_s=t_0+ \phi _{s} T_{0}$ for $\phi _s=0,\ldots ,1$. The similarity in the concave structure and scale of the two curves suggests that both neuronal models respond very similarly to short impulses perturbing a strong constant driving current, revealing good qualitative agreement between the models.

Fig. 4

Phase-response curves. Comparison between the phase-response curves for the mEIF and mHH models given a constant driving current of 0.8nA and a perturbative current of 0.08nA injected for 2ms after time t₀ = 300ms. The injection times are specified in the text. The remaining model parameters are given in Tables 1 and 2

3.4 Comparison of spike-frequency adaptation

As the phenomenon of spike-frequency adaptation initially motivated our inclusion of the muscarinic current in the mEIF model (7), we now examine the quality of its approximation by the mEIF model versus the corresponding adaptation dynamics of the mHH model (1). We induce this type of dynamical behavior in our simulations by injecting, on a long time scale, either a Poisson-distributed AMPA-type pulse train of the form (4) or a weak constant current, and compare the dynamics of both the mHH and mEIF models. As time progresses, we expect an increase in the length of the interspike intervals for both model neuron types.

Figure 2 displays the results of our simulation using the AMPA-type synaptic drive injected for $1000ms$. We notice that the interspike intervals increase in length until approximately $500ms$ elapse. Then, both models appear to reach a steady state in which they continue to fire periodically. Similar dynamics occur for neurons with an injected constant current. Figure 5 depicts this second scenario by exhibiting the mHH and mEIF firing rates over simulation times of different lengths. From Fig. 5, it is clear that the decrease in the firing rate with increasing runtime is very close for both models, which indicates their close degree of spike-frequency adaptation.

Fig. 5

Spike-frequency adaptation. Comparison of firing rates for mHH and mEIF neurons for several simulation durations under an injected constant driving current of strength 0.83nA. The additional model parameters are given in Tables 1 and 2

3.5 Comparison of critical exponents

We now gauge the agreement of our computational mEIF reduction with the more complex mHH neuron by studying two types of bifurcations of neurons augmented with the slow muscarinic current, both of which had been previously discussed for the standard HH neurons (Roa et al. 2007; Jin et al. 2006).

The first bifurcation we discuss is the transition between a finite number of spikes fired after the current injection and infinite number of spikes (i.e., repetitive firing) with the increasing strength of the constant injected current $I_{ext}$ and sufficiently high initial depolarization of the neuronal voltage. For the classic, type-II, HH neuron (17), this transition results from a saddle-node bifurcation of limit cycles (the unstable of which merges with a stable equilibrium in a subcritical Hopf bifurcation at a yet higher strength of the driving current). In the simulations of a model HH neuron, there exist three different firing scenarios in three different driving-current regimes. When the injected current $I_{ext}$ is sufficiently far below the bifurcation value, $I_{c}$, and in fact below the rheobase, the neuron will fail to fire regardless of its initial membrane potential value. If the strength of the input current is raised above the bifurcation value $I_{c}$, the same neuron will be attracted to a stable limit cycle and thus fire periodically. In between, above the rheobase but below $I_{c}$, the neuron with a sufficiently large initial membrane potential value will fire a finite number of times and then remain at its resting potential (Hassard 1978); this number increases with the proximity to $I_{c}$. In this middle regime, the amount of time until the neuron undergoes its final action potential before settling back into the equilibrium scales as

$$ T_{fire}= A (I_c-I_{ext})^{-\Delta} $$

(13)

for some critical exponent $\Delta$ (Roa et al. 2007).

Through simulation, we observe that the mHH and mEIF neurons behave in a similar fashion. Beginning near the rheobase of $I_{ext}\equiv I_{T}\approx 0.7nA$, both the mHH and mEIF neurons will spike at least once and then reach a stable equilibrium which is close to the resting potential. This bifurcation scenario is complicated by the spike-frequency adaptation: in fact, there are two bifurcations, one from a finite number of spikes to an infinite number but with ever increasing interspike intervals, and then another to periodic firing. We find the scaling (13) for the first. The regimes with no spike, one spike, many, most likely infinitely many, spikes firing at an attenuating rate, and spikes firing in a periodic-like pattern are depicted for the mEIF and mHH neurons in Fig. 6. Both models are seen to share approximately the same rheobase $I_{T}$ and spiking behavior above and below the critical threshold $I_{c}$, indicating a shared transition structure.

Fig. 6

Passage through the rheobasis and bifurcation to infinitely many spikes for the mHH and mEIF neurons. Comparison between the dynamics of the mHH and mEIF models under constant driving currents I _ext , increasing through the rheobase I _T ≈ 0. 7n A: (a) I _ext = 0. 65n A < I _T , (b) I _ext = I _T , (c) I _{e x t} = 0. 77n A > I _c > I _T , (d) I _{e x t} = 0. 83n A ≫ I _c > I _T . The mEIF model parameters were chosen so that I _T = 0. 68n A for both models, and are Δ _T = 4. 1, V _T = − 44. 9m V, V _R = − 70m V, j = 0. 014. The initial membrane potential was − 70m V. Note that the neuron oscillates periodically for sufficiently large values of I _{e x t} , as depicted in panel (d). For smaller I _{e x t} > I _c , it appears that adaptation slows down the neuron’s firing indefinitely, as depicted in panel (c)

We list the values for the rheobase $I_{T}$, the bifurcation point $I_{c}$, and critical exponent Δ via numerical simulations and fitting of formula (13) in Table 7. The maximal error among the three parameters, which is in the exponent Δ, is approximately 10 %. This error confirms that the mHH model is rather well approximated by the properly fitted mEIF model for describing bifurcation phenomena. However, for the comparison of the specific firing times of the spikes in transients in the bifurcation scenario, agreement between the mHH and mEIF models appears to be qualitative. It should be pointed out that comparison of transient dynamics is a far more stringent measure than that of limit cycles.

Table 7 Critical exponent and bifurcation comparison

3.6 Comparison of bifurcation diagrams under time-periodic driving

Since appropriately chosen Poincaré-type maps in periodically-driven models generate highly model-specific bifurcation diagrams, at least a qualitative agreement between the bifurcation diagrams of the mHH and mEIF models presents a rather stringent test of the accuracy of the approximation by the mEIF model. We use the driving frequency as the bifurcation parameter, and construct the Poincaré map by plotting consecutive interspike intervals corresponding to various simulations using specific driving frequencies.

We drive our model neurons with the sinusoidal input current

$$ I = I_0+I_{1} \sin(2 \pi f_{0} t), $$

(14)

where I ₀ is the average current, I ₁ the amplitude of the periodic perturbation, and f ₀ is the frequency. To construct our ISI bifurcation diagrams, we vary the driving frequency f ₀, letting I ₀ = 1. 5n A and I ₁ = 1n A, and plot the duration of all ISIs in each simulation. For all such diagrams, we use a simulation time of 1000m s for each driving frequency.

First, we display the comparison between the resulting ISI bifurcation diagrams for the pure HH and EIF neurons without any additional adaptation current over a range of frequencies in Fig. 7. For the frequencies we have examined (as indicated in Fig. 7), we observe that both model neurons immediately settle into what appears to be an attracting, bounded firing pattern. This is to be expected since the primary driving current, I ₀, is far above the rheobase and thus the neurons’ dynamics are in a repetitive firing regime. It is important to note the remarkably strong structural and even quantitative agreement between the two diagrams, reaching down to fine bifurcation details.

Fig. 7

Bifurcation diagrams for HH and EIF neurons under periodic drive. Comparison between bifurcation diagrams of (a) HH and (b) EIF models, plotting the duration of each interspike interval as a function of the frequency of the oscillatory driving current used in the simulation. The driving current is described in Eq. (14), and the total run-time for each simulation is 1000m s. The remaining EIF model parameters are listed in Tables 1 and 2

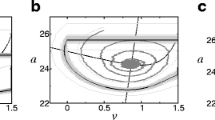
The corresponding ISI bifurcation diagrams for the mHH and mEIF neurons are depicted in Fig. 8, from which we again see a strong, detailed qualitative and quantitative agreement between the mEIF and mHH diagrams. This confirms that the same agreement between the models with the added slow currents is not simply due to the inclusion of those currents. For comparison, we also include the corresponding aEIF diagram, which exhibits the same overall qualitative bifurcation structure, but clearly does not match the finer mHH structure as well as the mEIF model, differing the most in the high frequency regime.

Fig. 8

Bifurcation diagrams for mHH, mEIF, and aEIF neurons under periodic drive. Comparison between bifurcation diagrams of the (a) mHH, (b) mEIF, and (c) aEIF models, plotting the duration of each interspike interval as a function of the frequency of the oscillatory driving current used in the simulation. The driving current is described in Eq. (14), and the total run-time for each simulation is 1000m s. The remaining mEIF model parameters are listed in Tables 1 and 2

3.7 Comparison of network dynamics

Since the primary reason for developing our computational reduction is to use it in network simulations, we now compare the network dynamics generated by the respective mEIF and mHH models. We compare two characteristic features of the network output, the raster plots depicting the time-dependence of each neuron’s firings, and the gain curves depicting the dependence of the network firing rate on the strength of the external drive. We use a small all-to-all coupled network of N = 10 excitatory neurons, in which all the neuron-to-neuron couplings have the same strength. Each neuron in the mHH and mEIF networks is still governed by Eqs. (1) and (7) respectively, but now the synaptic current of the j-th neuron $g^{j}_{syn}$ has the form

$$ g^{j}_{syn} = f \displaystyle \sum\limits_{i} G(t-t^{j}_i) + \frac{S_{N}}{N} \displaystyle \sum\limits_{k\neq j} \sum\limits _{l} G(t-t^{j}_{k,l}) $$

(15)

where the first sum denotes the Poisson-distributed external drive and the second the spikes arriving from all the other neurons in the network. In Eq. (15), f denotes the strength of the Poisson external drive and i labels the i-th spike, S _N denotes the coupling strength, k is the neuron index, and t _{k, l} is the l-th spike time of the k-th neuron. We still assume the postsynaptic conductance to follow time-course G as given in Eq. (5). In our simulation we choose f = 0. 05μ S, S _N = 1. 0μ S and N = 10. The spike times for each neuron are generated by independent Poisson spike trains with the same rate ν = 1000H z.

A comparison of the raster plots for each network is depicted in Fig. 9a, and while the spike times of the two models are not always indistinguishably close, the comparison shows good agreement not just in the total number of spikes but also in the relative delays among the firing times of different neurons. Moreover, the network firing rate shows close agreement between the two models, indicating close agreement in input-response.

Fig. 9

Network dynamics for mHH and mEIF models. Comparison between the raster plots and gain curves for the mHH and mEIF networks. Model parameters are listed in Tables 1 and 2. For the raster plots in (a), network parameters are N = 10, S _N = 1. 0μ S, f = 0. 05μ S, and ν = 1000H z. The average neuronal firing rates in the N = 10 neuron networks are 0. 0112s p i k e s / m s for the mHH model and 0. 0126s p i k e s / m s for the mEIF model.

The second measure we employ is a representation of the network firing rate, namely, the gain curve. For a given choice of the external-driving spike strength f , we analyze the relationship between the neuronal firing rate averaged over the network and a neuron’s external driving strength expressed as the product f ν of f and the Poisson rate ν. We vary ν while keeping f fixed. A comparison of the gain curves for both models is given by Fig. 9b, which shows good agreement as long as the firing rate does not become too large, indicating that the approximation of mHH neuron by the mEIF neuron is very good in a statistical sense, such that the firing rates averaged over the network agree for a broad range of the Poisson rate ν.

We remark that the mEIF model neuron parameters were only optimized for a single, uncoupled neuron and for only a single value of f and ν, f = 0. 05μ S and ν = 1000H z. As the model parameters were not optimized for the coupled network structure considered in this section, the pointwise comparison between the networks is not as good as that for an optimally-tuned single mEIF neuron. From the gain curves, it is clear that the fitting procedure is robust to network dynamics so long as firing rates do not grow so large that the fit is no longer valid, which would require a new optimization procedure for more accurate results. Since the mEIF model was optimized for a single neuron, it is expected that the error grows with the network firing rate. We notice a systematic overestimation in this case. Nevertheless, pointwise measures, including the relative delays among the firing times of different neurons and the Van Rossum distance, show good agreement, while the statistical measure given by the network firing rate shows excellent agreement even at values of ν for which the neuron parameters were not optimized. For example, the average van Rossum metric difference between the voltages traces of the neurons in the network displayed in Fig. 9 was 0.442, indicating close agreement in both the timing of spikes and subthreshold dynamics in the networks. In Table 8, we observe that using time-steps of size Δ t _{m H H} = 0. 08m s and Δ t _{m E I F} = 0. 5m s as in the single neuron case, similarly large computational savings, as in Table 4, in long-duration network simulations of N = 10 neurons are achievable using the mEIF neuronal model. Likewise, in Fig. 9c, we compare the raster plots of the mHH and mEIF models for a large network of N = 100 neurons, given the large time-step of size Δ t _{m E I F} = 2m s. We observe accuracy comparable to case of the N = 10 neuron network with small time-steps. This shows that the mEIF model is very well suited to approximate the mHH model in network simulations and yields at least very good statistical accuracy.

Table 8 Model network efficiency comparison

Table 9 Calcium current physiological parameters

3.8 After-hyperpolarization current

We now repeat the above approximation scheme for the HH neuron augmented by the AHP current using the equally augmented EIF model. Like the Muscarinic current, the AHP current introduces only one additional variable into the HH model (17), which is the time-dependent intracellular Calcium ion concentration, $\left [ Ca^{2+} \right ]$. The dynamics of the corresponding AHP current are described by the formula (Richardson 2009; Yamada et al. 1989)

$$ I_{AHP} = g_{AHP} \frac{\left[ Ca^{2+} \right]}{30+\left[ Ca^{2+} \right]} (V-V_K), $$

(16)

with the Calcium ion concentration $\left [ Ca^{2+} \right ]$ obeying the equation

$$\tau_{Ca} \frac{d \left[ Ca^{2+} \right]}{dt} = -0.16 I_{Ca}(V) - \left[ Ca^{2+} \right] $$

$$I_{Ca} = g_{Ca} s_{\infty} (V-V_{Ca}) $$

$$s_{\infty} = \frac{1}{1+ \exp(-(V-V_s)/ \Delta _s)}. $$

Our choice of parameters is unique to layer-II cortical neurons and is given in Table 9 (Richardson 2009).

Comparing Fig. 10 to Fig. 1, we notice that the increase in duration of the interspike intervals resulting from the AHP current is significantly larger than in the case of the Muscarinic current. However, since both currents play a similar role in decreasing firing rates, it is reasonable to expect we can utilize an analogous modeling approach using the EIF model with the added slow current(s) for neurons with either or both adaptation currents. Therefore, at each action potential, the dynamics of the Calcium concentration take the same form as Eq. (8).

Fig. 10

Comparison between the original HH neuron to an HH neuron including an additional AHP current. Both neurons are driven by the same constant external current I _ext = 2.0nA. Parameter values for the HH model are listed in the Appendix, and parameter values for the calcium current are listed Table 9

Carrying out the optimization procedure described in the Parameter Optimization Section above, we determine the best-fit parameter choices for two additional types of neurons: neurons incorporating only the AHP current and also those incorporating both currents. The values in either case, which differ from those described for the previous simulations for the mEIF neuron, are listed in Table 10. In our simulation of the neuron with both adaptation currents, we reuse the jump constants found optimal in each case when only one adaptation current was included in the neuron model. At the time of each action potential, we add the appropriate jump constants to their corresponding current variables. Comparing the adaptation variables for the EIF and HH neuron types in each set of models highlights a post action-potential jumping dynamics of the Calcium current which is even more pronounced than what was found earlier for the Muscarinic current, motivating a similar approach to updating at the action potentials.

Table 10 Calcium current exponential term parameters

To demonstrate the accuracy of the approximation scheme in these two new models, voltage traces for the cEIF neuron model, with only the Calcium current, and the bEIF neuron model, with both adaptation currents, are compared to their Hodgkin-Huxley counterparts, the cHH and bHH models, in Figs. 11a and 12a respectively. Figures 11b and 12b display the dynamics of the slow currents in these EIF and HH-type neurons using the fitted jump constants. Agreement comparable to the mEIF and mHH comparison described earlier is found in each case. Both models also exhibit the spike-frequency adaptation analogous to that of the mEIF model.

Fig. 11

Comparison between bHH and bEIF neuron dynamics. Comparison between (a) voltages traces and (b) the sum of the muscarinic and calcium ion activation variables for bHH and bEIF models. Simulation time was $1000ms$. The Van-Rossum Metric Difference is $0.000567$, with $t_{c} = 5ms$. The bEIF model parameters are listed in Tables 1, 3, 9, and 10

Fig. 12

Comparison between cHH and cEIF neuron dynamics. Comparison between (a) voltages traces and (b) calcium ion concentration for cHH and cEIF models. Simulation time was $1000ms$. The Van-Rossum Metric Difference is $0.001405$, with $t_{c} = 5ms$. The cEIF model parameters are listed in Tables 1, 3, 9, and 10

Finally, we compare several additional dynamical properties of the models analogous to the ones used above for the mHH and mEIF models to check for the accuracy of the approximation. The methodology used is identical to that used in those sections. In Fig. 13, we show that the cEIF and cHH neurons have approximately the same critical rheobase, $I_{T}\approx 1.2nA$, and critical current threshold, $I_{c}\approx 2nA$. Likewise, Fig. 14 displays ISI bifurcation diagrams for the bEIF and bHH neuron pair, which again show strong qualitative resemblance. Note also the similarity in structure to the diagrams for the mEIF and mHH neuron pair in Fig. 8.

Fig. 13

Passage through the rheobasis and bifurcation to infinitely many spikes for the cHH and cEIF neurons. Comparison between the dynamics of the cHH and cEIF models under constant driving currents I _ext , increasing through the rheobase I _T ≈ 1.2nA: (a) I _ext = 0.7nA < I _T , (b) I _ext = I _T , (c) I _ext = 4nA ≫ I _c > I _T . The initial membrane potential is $V=-70mV$. The cEIF model parameters are those listed in Table 1 and $\Delta _T=3.5mV$, $V_T=-46.52mV$, $V_R=-60mV$, and $j=0.148mM$.

Fig. 14

Bifurcation diagrams for bHH and bEIF neurons under periodic drive. Comparison between bifurcation diagrams of (a) bHH and (b) bEIF models under the periodic drive described in Eq. (14) with $I_0=2.5nA$, plotting the duration of each interspike interval as a function of the frequency of the oscillatory driving current used in the simulation. The bEIF model parameters are listed in Tables 1, 9, and 10. The total run-time for each simulation is $1000ms$

We conclude by studying the accuracy of our modeling scheme, using instead the AHP current, in the network setting. Using an all-to-all coupled network of $N=10$ neurons, we compare the synchronization and firing rates of the HH and EIF type networks in the presence of spike-frequency adaptation induced by the AHP current. The raster plots for each network, in Fig. 15a, show excellent agreement in the number of spikes and relative delays among the firing times of different neurons, with an average van Rossum metric difference of 0.378 in the voltage traces of the individual neurons. Similarly, the gain curves for the two models in Fig. 15b show that the cEIF computational reduction well approximates the cHH network in a statistical sense for a wide array of Poisson inputs. Like the mEIF model, since the cEIF model was optimized for a single neuron, it is expected that the error grows with the network firing rate. For the cEIF model, we notice a small systematic underestimation, but the gain curves remain relatively close together.

Fig. 15

Network dynamics for cHH and cEIF models. Comparison between the (a) raster plots and (b) gain curves for the cHH and cEIF networks. The cEIF model parameters are listed in Tables 1, 9, and 10. For the raster plots in (a), network parameters are $N=10$, $S_N=1.0\mu S$, $f=0.05\mu S$, and $\nu =1000Hz$. The average neuronal firing rates for the $N=10$ neuron networks are $0.0026spikes/ms$ for the cHH model and $0.0022spikes/ms$ for the cEIF model. For the gain curves in (b), the external spike strength was $f=0.05\mu S$, the coupling coefficient was $S_N=1.0\mu S$, and the number of neurons was $N=10$

4 Discussion

Through our extensive numerical simulations, we have shown that the dynamical behavior of the HH model with additional muscarinic and/or AHP current can be very accurately approximated by the EIF model with the same additional current(s) and appropriately optimized parameters. Not only can this approximation ensure the closeness of subthreshold neuronal voltage traces and spike times on finite-time intervals, but also a number of close bifurcation structures. In addition, network dynamics of HH neurons with slow currents can be well approximated by corresponding networks of EIF-like neurons. In the case of realistic, AMPA-like EPSCs, the EIF-like models can increase the speed of computation by at least an order of magnitude by using the maximal time-steps that still allow us to resolve spiking events, yielding especially large computational savings in large neuronal network simulations in which it would not be feasible to resolve the stiffness and high dimensionality of the corresponding HH neurons.

Detailed studies of bifurcations exhibited by the adaptive EIF model were presented in Touboul and Brette (2008), Naud et al. (2008), and Nicola and Campbell (2013). It would be interesting to investigate whether these bifurcations also occur for the EIF model that includes the two types of slow currents addressed here. Additionally, it would be informative to study the inclusion of the slow currents directly in the approximation of multi-compartment neurons, as in Clopath et al. (2007).

The EIF model has already been used in large-scale network simulations with considerable success to faithfully reproduce both the cortical conductance and subthreshold membrane-potential dynamics, as well as the neuronal firing rates, measured in experiments covering brain areas of tens of square millimeters (Tsodyks et al. 1999; Jancke et al. 2004), such as in the simulation of the Hikosaka line-motion illusion (Rangan et al. 2005). Our work indicates that the EIF model with additional slow currents has the potential to be equally useful as an efficient and accurate simplified point-neuron model incorporating spike-frequency adaptation.

An alternative approach to using the EIF model for approximating the HH dynamics and thus accelerating their computations is to use a precomputed library of HH spikes (Sun et al. 2009). This approach again avoids the costly evaluation of the membrane potential during the action potentials during the network simulation, and exhibits similar results relative to both the accuracy and computational efficiency of the EIF model by using the library-based updating scheme. While using significantly larger time-steps than with the traditional HH model, (Sun et al. 2009) demonstrated that the library-based updating scheme could reduce simulation time by at least a factor of 65 %. The same approach could be extended to include slow adaptation currents, which will be a good future project.

Appendix: Hodgkin-Huxley equations

The membrane potential in the Hodgkin-Huxley model is described by the equation

$$ C\frac{dV}{dt} = -I_{L}-I_{Na}-I_{K}+I_{syn}+I_{ext}. $$

(17)

The dynamics of both the sodium and potassium currents are governed by their respective kinetic equations. The choice of constants in the differential equations for the activation and inactivation variables were found experimentally and are elaborated on in Destexhe and Pare (1999).

The sodium current is described by the expression

$$I_{Na} = \bar{g}_{Na}m^3h(V-V_{Na}), $$

where the dynamics of the fast-acting sodium activation variable, m, are given by the equation

$$\frac{dm}{dt} = \frac{m_{\infty} - m}{\tau_{m}}, $$

with

$$m_{\infty}=\frac{\alpha_{m}(V)}{\alpha_{m}(V)+ \beta_{m}(V)} $$

$$\tau_m=\frac{1}{\alpha_{m}(V)+ \beta_{m}(V)} $$

$$\alpha_{m}(V)=\frac{-0.32(V+37)}{\exp(-(V+37)/4)-1} $$

$$\beta_{m}(V)=\frac{0.28(V+10)}{\exp((V+10)/5)-1} $$

and the dynamics of the sodium inactivation variable, h, are described by

$$\frac{dh}{dt} = \frac{h_{\infty} - h}{\tau_{h}}. $$

with

$$h_{\infty}=\frac{\alpha_{h}(V)}{\alpha_{h}(V)+ \beta_{h}(V)} $$

$$\tau_h=\frac{1}{\alpha_{h}(V)+ \beta_{h}(V)} $$

$$\alpha_{h}(V)=0.128 \exp(-(V+33)/18) $$

$$\beta_{h}(V)=\frac{4}{1+\exp((-V+10)/5)} $$

The expression for the delayed-rectifier potassium current is

$$I_{K} = \bar{g}_{K}n^{4}(V-V_{K}), $$

where the dynamics of the potassium activation variable, n, are described by

$$\frac{dn}{dt} = \frac{n_{\infty} - n}{\tau_{n}}. $$

with

$$n_{\infty}=\frac{\alpha_{n}(V)}{\alpha_{n}(V)+ \beta_{n}(V)} $$

$$\tau_n=\frac{1}{\alpha_{n}(V)+ \beta_{n}(V)} $$

$$\alpha_{n}(V)=\frac{-0.032(V+35)}{\exp(-(V+35))-1} $$

$$\beta_{n}(V)= 0.5 \exp(-(V+40)/40) $$