Minimum energy desynchronizing control for coupled neurons

Abstract

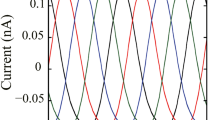
We employ optimal control theory to design an event-based, minimum energy, desynchronizing control stimulus for a network of pathologically synchronized, heterogeneously coupled neurons. This works by optimally driving the neurons to their phaseless sets, switching the control off, and letting the phases of the neurons randomize under intrinsic background noise. An event-based minimum energy input may be clinically desirable for deep brain stimulation treatment of neurological diseases, like Parkinson’s disease. The event-based nature of the input results in its administration only when it is necessary, which, in general, amounts to fewer applications, and hence, less charge transfer to and from the tissue. The minimum energy nature of the input may also help prolong battery life for implanted stimulus generators. For the example considered, it is shown that the proposed control causes a considerable amount of randomization in the timing of each neuron’s next spike, leading to desynchronization for the network.

Appendices

Appendix A: Essentially Non-Oscillatory (ENO) schemes

Finite difference approximations of derivatives of a function $\mathcal{V}: \mathbb{R}^n \mapsto \mathbb{R}$, are essentially equivalent to choosing an interpolation polynomial for the function $\mathcal{V}$, and performing exact differentiation. In traditional finite difference methods, the polynomial stencil is fixed, i.e., to approximate $\mathcal{V}_x \equiv \frac{\partial \mathcal{V}}{\partial x}$, at the grid point x _i , one assumes

$$ \left.\mathcal{V}_x\right|_i \approx f(\mathcal{V}_{i-m}, \mathcal{V}_{i-m+1}, \hdots, \mathcal{V}_i, \hdots, \mathcal{V}_{i+n-1}, \mathcal{V}_{i+n}), $$

where constants m and n are fixed in space and are the same for all points (except maybe at the boundaries). Here, the subscript indices refer to the grid points, i.e., $\mathcal{V}_i \equiv \mathcal{V}(x_i)$. Problems arise when the function $\mathcal{V}$ is not sufficiently smooth and this interpolation, when combined with time integration, results in spurious oscillations and even divergence.

To remedy this problem, Harten et al. (1987) first introduced the idea of essentially non-oscillatory (ENO) schemes. Unlike traditional finite difference methods, in ENO schemes the polynomial stencil is not fixed, and at each point, one chooses the smoothest possible polynomial. When combined with a TVD time integration method (see below), the scheme is guaranteed not to produce any spurious solutions.

This idea was further improved, from the implementation point of view, by Shu and Osher (1989) and later applied to the numerical solution of the HJ equation (Osher and Shu 1991). Here we merely consider the method in one spatial dimension. Extension of the method to higher spatial dimensions is possible through a dimension-by-dimension approach and we leave the details to the appropriate references mentioned above.

Consider the one-dimensional HJ equation written as

$$ \frac{\partial \mathcal{V}}{\partial t} + \mathcal{H}(\mathcal{V}_x) = 0, $$

where the explicit dependence on other variables have been dropped for brevity. To construct a polynomial function, $\mathcal{Q}_j^{j+\mathcal{M}}(x)$, of degree $\mathcal{M}$ that interpolates through points $x_j, x_{j+1} , \hdots, x_i, \hdots, x_{j+\mathcal{M}}$, one first needs to define the so-called mth-order Newton divided differences coefficients, $f_j^{j+m}$, for $m=0,1, \hdots, \mathcal{M}$. This is done via the recursive formula

$$ f_j^{j+m} = \frac{f_{j+1}^{j+m}-f_{j}^{j+m-1}}{x_{j+m} - x_j}, \label{eq:divdif} $$

with $f_j^j = \mathcal{V}_j = \mathcal{V}(x_j)$. Here the subscript index, j, and superscript index, j + m, refer to the lower and upper bounds of the interval used to compute the coefficient, i.e., to compute $f_j^{j+m}$, m + 1 grid points, x _j through x _j + m , are required. Using the divided differences coefficients, the polynomial $\mathcal{Q}_j^{j+\mathcal{M}}(x)$ may be written as,

$$ \mathcal{Q}_j^{j+\mathcal{M}} (x)= \sum_{m=0}^{\mathcal{M}} f_j^{j+m} \mathcal{\phi}_j^m(x), \label{eq:interpol} $$

(13)

where, by definition, $\mathcal{\phi}_j^0(x) = 1$ and, for m ≥ 1,

$$ \mathcal{\phi}_j^m (x) = \prod_{n=0}^{m-1} (x-x_{j+n}). $$

Once the interpolating polynomial, $\mathcal{Q}_j^{j+\mathcal{M}}(x)$, is known, Eq.  (13) may be differentiated with respect to x, to obtain the following approximation to the spatial derivative:

$$ \left.\mathcal{V}_x\right|_i= \left.\frac{d\mathcal{Q}_j^{j+\mathcal{M}}}{d x} \right|_{x_i} + \mathcal{O}\left(h^{\mathcal{M}}\right), $$

where $h \equiv \max_{1\le n \le \mathcal{M}} \left|x_{j+n}-x_{j+n-1}\right|$ is the maximum grid spacing in the interpolation interval and determines the order of truncation error.

Constructing the polynomial $\mathcal{Q}_j^{j+\mathcal{M}}(x)$ also requires the knowledge of the interpolation interval, $\mathcal{I} \equiv [x_j, x_{j+1},$ $\hdots, x_i, \hdots, x_{j+\mathcal{M}}]$. To build the interval, and starting at point x _i , one has two possible options for choosing the next point, x _i − 1 or x _i + 1. In fact, these are both valid, and as we shall see, required for the next step of the algorithm. Thus at each point, x _i , two different approximations for $\mathcal{V}_x$ exist which we denote as $\mathcal{V}_x^+$ and $\mathcal{V}_x^-$ based on whether x _i + 1 or x _i − 1 are chosen, respectively. In fact, if one chooses $\mathcal{M} = 1$, these are simply the classical first-order upwind methods.

What comes next is the core idea of the ENO scheme. At each remaining step, toward finding the interval, one will face two options in choosing the next point. The idea is to choose the point that will result in the smoothest polynomial. In fact, it is easy to note that the divided differences coefficients are a good measure of the variations in the interpolating function. A coefficient with a large magnitude alerts the existence of a rapid change, or even a discontinuity in the function $\mathcal{V}$ around point x _i , and thus should be avoided in constructing the polynomial.

For example, let’s consider the second-order correction to $\mathcal{V}_x^-$. The two possible options are x _i − 2 and x _i + 1. There are also two second-order divided differences coefficients, $f_{i-2}^{i}$ and $f_{i-1}^{i+1}$. As a result one either chooses x _i − 2 if

$$ \left|f_{i-2}^i\right| \leq \left|f_{i-1}^{i+1}\right|, $$

or x _i + 1 otherwise. This same idea is repeated for all higher-order coefficients until all remaining points in the interval are found, after which the interpolation polynomial is uniquely determined. Note that in this algorithm, one first determines the interval and then constructs the polynomial. It is possible to combine the two in one single pass as suggested in Osher and Fedkiw (2003).

Finally let us briefly mention that, since the ENO scheme always chooses the smoothest polynomial with minimal variations, it may dampen out even slightest gradients in the solution where no shock or discontinuity exist. To remedy this problem, Liu et al. (1994) introduced the idea of the weighted ENO (WENO) schemes in which one obtains a higher order numerical approximation to $\mathcal{V}_x$ by appropriate weighting of all possible $\mathcal{M}$th-order ENO schemes. The weighting coefficients are usually chosen so that they inversely depend on the smoothness of corresponding ENO scheme in a potential interval. This idea then results in a WENO scheme that automatically switches to an ENO scheme in parts of the domain that the solution is non-smooth while obtaining higher-order approximations in the smooth part of the domain. We do not present the algorithm in detail here and refer the interested reader to Osher and Fedkiw (2003) for a discussion of the implementation and also the literature review on WENO schemes.

Appendix B: Numerical Hamiltonian

The second part in constructing a high-order algorithm for solving the HJ equation is the high-order construction of a numerical Hamiltonian, $\hat{\mathcal{H}}$. As noted in the previous section, at each point there are two approximations to the gradient, denoted by $\mathcal{V}_x^+$ and $\mathcal{V}_x^-$, depending on the initial stencil bias. As such, in general, the numerical Hamiltonian may be written as

$$ \hat{\mathcal{H}} = \hat{\mathcal{H}}\left(\mathcal{V}_x^+, \mathcal{V}_x^-\right). $$

To get a numerical Hamiltonian that correctly accounts for the nonlinear shock and rarefaction phenomena (see Osher and Shu 1991), three criteria must be satisfied. First, the Hamiltonian needs to be Lipschitz continuous in both $\mathcal{V}_x^+$ and $\mathcal{V}_x^-$ . Second, the numerical Hamiltonian needs to be a non-increasing function of $\mathcal{V}_x^+$ and a non-decreasing function of $\mathcal{V}_x^-$. Symbolically, this is usually denoted as $\hat{\mathcal{H}}\left(\downarrow, \uparrow\right)$. Third, the numerical Hamiltonian needs to be consistent with the analytical Hamiltonian, i.e., $\hat{\mathcal{H}}(\mathcal{V}_x,\mathcal{V}_x) = \mathcal{H}(\mathcal{V}_x)$.

Usually, what makes one numerical Hamiltonian better than the other is the degree of numerical dissipation it adds to the problem. Different constructs have been proposed over the years that vary, not only in the degree of dissipation they add, but also how hard they are to implement. One of the easiest ones, though more dissipative, is the Lax-Friedrichs Hamiltonian. In one spatial dimension, this is written as

$$ \hat{\mathcal{H}}(\mathcal{V}_x^+,\mathcal{V}_x^-) = \mathcal{H}\left(\frac{\mathcal{V}_x^++\mathcal{V}_x^-}{2}\right) - \frac{1}{2}\alpha_x \left(\mathcal{V}_x^+-\mathcal{V}_x^-\right), $$

(14)

where $\alpha_x = \max \left|\partial \mathcal{H}/\partial \mathcal{V}_x \right|$. If the maximum is computed globally through the whole computational domain, the method is usually termed global Lax-Friedrichs (LF). This, however, is usually unnecessarily too restrictive and the maximum, at any point, is usually computed locally for adjacent grid points and the method is termed local Lax-Friedrichs (LLF).

Although both LF and LLF Hamiltonians are very easy to implement, they usually over-dampen the solution and distort sharp gradients. Better results may be obtained via the Godunov’s Hamiltonian. The Godunov’s Hamiltonian, unfortunately, is usually hard to obtain for complicated Hamiltonians and may be quite computationally expensive. We do not go into the details of finding these, and other, numerical Hamiltonians and refer the interested reader to Osher and Fedkiw (2003) and Osher and Shu (1991) for more details. Finally we note that to avoid the computational cost of evaluating the Godunov’s Hamiltonian, and to obtain solutions that are not overly damped when using the LLF Hamiltonian, one can generally use a high-order ENO scheme along with a high order TVD Runge-Kutta (see below) scheme and use a sufficiently refined grid.

Appendix C: Total Variation Diminishing (TVD) Runge-Kutta schemes

A TVD Runge-Kutta (TVD-RK) method is merely a Runge-Kutta method that is ensured to decrease the total variation (TV) in the solution as integrated in time. By definition, total variation of a differentiable function, f(x), is defined as,

$$ TV(f) = \int \left|f_x\right| dx, $$

while for a discrete function, u _j , this definition changes to

$$ TV(u) = \sum\limits_j \left|u_{j+1}-u_j\right|. $$

In both cases, TV of a function simply is a measure of the amount of variation in the function. To have a convergent solution, one requires a time integration method that decreases the total variation in the function since otherwise it may lead to non-physical oscillatory results. A TVD method is then any time integration scheme that satisfies the following condition:

$$ TV(u^{n+1}) \le TV(u^n). $$

Many different TVD methods exist in the literature, from both the Runge-Kutta (Shu and Osher 1988) and the linear multi-step families (Gottlieb et al. 2001). Without going into much detail, here we present the third-order TVD-RK method and leave other TVD methods to the references mentioned above.

Just like normal Runge-Kutta methods, the third-order TVD-RK method consists of three consecutive forward Euler parts. For the semi-discrete HJ equation, i.e., already discretized in the space variable, x, using the ENO scheme,

$$ \frac{\partial \mathcal{V}}{\partial t} = -\hat{\mathcal{H}}(\mathcal{V}_x^+, \mathcal{V}_x^-), \, $$

the third-order TVD-RK method is written as

$$ \begin{array}{rll} \mathcal{V}^{n+1/3} &=& \mathcal{V}^n - \Delta t \; \hat{\mathcal{H}}^n, \\ \mathcal{V}^{n+2/3} &=& \frac{3}{4}\mathcal{V}^n + \frac{1}{4}\mathcal{V}^{n+1/3} - \frac{1}{4}\Delta t \; \hat{\mathcal{H}}^{n+1/3}, \\ \mathcal{V}^{n+1} &=& \frac{1}{3}\mathcal{V}^n + \frac{2}{3}\mathcal{V}^{n+2/3} - \frac{2}{3}\Delta t \; \hat{\mathcal{H}}^{n+2/3}. \end{array} $$

Note that to ensure stability, and the TVD property, it is required to impose a restriction on the time step according to

$$ \frac{\Delta t}{h_{\rm min}} \alpha_{\rm max} \le c, $$

where $\alpha_{\rm max} = \max \left|\partial \mathcal{H} / \partial \mathcal{V}_x \right|$ and $h_{\rm min} = \min \left|x_{i+1}-x_{i}\right|$. These can also be local evaluations (i.e., for each grid point, x _i , within the stencil used to compute $\mathcal{V}_x^\pm$). Here, 0 < c ≤ 1 is called the CFL number (Osher and Shu 1991; Osher and Fedkiw 2003).