Bifurcation analysis applied to a model of motion integration with a multistable stimulus

Abstract

A computational study into the motion perception dynamics of a multistable psychophysics stimulus is presented. A diagonally drifting grating viewed through a square aperture is perceived as moving in the actual grating direction or in line with the aperture edges (horizontally or vertically). The different percepts are the product of interplay between ambiguous contour cues and specific terminator cues. We present a dynamical model of motion integration that performs direction selection for such a stimulus and link the different percepts to coexisting steady states of the underlying equations. We apply the powerful tools of bifurcation analysis and numerical continuation to study changes to the model’s solution structure under the variation of parameters. Indeed, we apply these tools in a systematic way, taking into account biological and mathematical constraints, in order to fix model parameters. A region of parameter space is identified for which the model reproduces the qualitative behaviour observed in experiments. The temporal dynamics of motion integration are studied within this region; specifically, the effect of varying the stimulus gain is studied, which allows for qualitative predictions to be made.

1 Introduction

The interesting and long-studied aperture problem constitutes an important ambiguity that must be resolved by the visual system in order to attribute an accurate direction of motion to moving objects (Wallach 1935; Wuerger et al. 1996). The motion of a uniform contour is consistent with many possible directions in the absence of terminator information provided by line endings. The ambiguous contour information is referred to as a 1D cue and the specific terminator information, which can be intrinsic to the object or produced by an occluding aperture, is referred to as a 2D cue.

In this article, we focus on a classical psychophysics stimulus used to probe the interactions between 1D and 2D motion cues, the so-called “barber pole” illusion (Chapter 4 Hildreth 1983). A a diagonally drifting grating viewed through an elongated rectangular aperture is perceived as drifting in the direction of the long edge of the aperture. The illusion is generated by the larger number of unambiguous (but misleading) 2D cues parallel to the long edges of the aperture. Mitigating the effect of the 2D cues can break the illusion as demonstrated in experiments by introducing a depth separation between grating and aperture (Shimojo et al. 1989), or, by introducing indentations on the aperture edges (Kooi 1993). More interesting is the fact that for certain stimulus parameters, the barber pole can elicit a multistable perceptual response. The effect of the ratio of the lengths of the aperture edges, or terminator ratio, was investigated in Castet et al. (1999) and Fisher and Zanker (2001). For large ratios the direction of the long aperture edge dominates perception. However, for ratios close to 1:1 the stimulus is multistable with a tri-modal response for the perceived direction; the main percepts either agree with the direction perpendicular to the grating’s orientation or with one of the two aperture edge directions. Another interesting aspect in resolving the aperture problem is the temporal dynamics of the integration of 1D and 2D cues. The barber pole illusion was studied in ocular following experiments (Masson et al. 2000); early tracking responses were shown to be initiated in the contour direction with a later response in the direction of the long axis of the aperture. The existence of an early response dominated by 1D cues, which is later refined when 2D cues are processed is supported by further studies in ocular following Barthélemy et al. (2010), psychophysics (Lorenceau et al. 1993) and physiology (Pack and Born 2001).

The middle temporal area (MT) of the visual pathway, that receives the majority of its synaptic inputs from the primary visual cortex (V1), plays a key role in the perception of moving objects and, more specifically, the solution of the aperture problem. MT is characterised by direction-selective neurons that are organised in a columnar fashion, similar to the organisation of orientation-selective neurons in V1 (Diogo et al. 2003). For an extensive discussion of the function of MT, see the following review articles (Britten 2003; Born and Bradley 2005). Cortical responses of MT have been linked specifically to perception of motion; see again the review article (Britten 2003) and, more recently, the paper (Serences and Boynton 2007).

Several models of motion integration have been proposed in the literature to solve the aperture problem, providing some insights into the underlying neural mechanisms. Building on the first linear/non-linear models (Chey et al. 1997; Simoncelli and Heeger 1998), several approaches added extensions to modulate the motion integration stages: feedback between hierarchical layers (Grossberg et al. 2001; Bayerl and Neumann 2004), inclusion of input form cues (Berzhanskaya et al. 2007; Bayerl and Neumann 2007), luminance diffusion gating (Tlapale et al. 2010b), or depth cues (Beck and Neumann 2010). Although these models reproduce the predominant percepts in a wide range of stimuli, in none of the articles describing them are multistable results depicted. Furthermore, although they show some limited individual case of dynamical behaviour just on the level of simulations, there is no rigorous analysis of the dynamical behaviour and no comprehensive parameter studies that fully explore all possible dynamical behaviour. In summary, the questions of what mechanisms are behind multistable motion perception and what dynamical processes are involved have largely been overlooked from the modelling point of view.

The focus of this paper will be the analysis of a mathematical model of motion integration with an input that generates a multistable perceptual response. To do so, we study cortical behaviour at the population level; see Pouget et al. (2000) for a discussion of how information can be encoded at a population level. We work within the neural fields formalism, a mathematical framework that was originally studied in Wilson and Cowan (1972) and Amari (1971, 1972); see Chapter 11 Ermentrout and Terman (2010) for various derivations of the equations. Instead of looking at the spiking behaviour of individual, interconnected neurons, the neural field approximation represents the mean firing rate of a neural population at the continuum limit and activity levels are represented in a spatially continuous way. Neural fields equations have been successfully applied to the study of motion in, e.g., Giese (1998), Deco and Roland (2010) and Tlapale et al. (2010a). In the later, the complex model presented, describing behaviour of multiple cortical layers and their feedforward and feedback connections, was capable of performing motion integration on both natural image sequences and classical psychophysics presentations. In terms of multistable stimuli, the 1:1 barber pole discussed above lead to coexisting steady states in the model, but the temporal dynamics of multistable perception were not investigated. We aim to develop a tractable model of manageable complexity that allows for a detailed study of the temporal dynamics of multistable motion perception using powerful tools from dynamical systems theory.

A natural tool for the study of dynamical systems for which multiple steady-state solutions co-exist is bifurcation analysis. Throughout the manuscript when the term solution is used this refers to a steady-state solution. In dynamical systems theory, a bifurcation is a critical point encountered under the variation of one or more parameters at which there is a change in the stability and number of solutions. Indeed, under the variation of a parameter a solution of a dynamical system will vary in state space; when the solution is plotted in terms of some norm against the parameter, it lies on a solution branch. A dynamical system may have multiple solution branches that are characterised by, for example, different spatial and stability properties. At special points when varying a parameter, solution branches can meet and bifurcate from each other. At these so-called bifurcation points, the number of solutions and their stability changes. In order to know what type of behaviour a model can produce it is necessary to gain full understanding of the type of bifurcations that occur, the types of solutions that are involved and at which parameter values. For a general introduction to bifurcation analysis of finite dimensional systems see Strogatz (1994) and Kuznetsov (1998), and of infinite dimensional systems with symmetries see Chossat and Lauterbach (2000) and Haragus and Iooss (2010). Bifurcation analysis has been used to study pattern formation in a number of different settings (Ermentrout and Cowan 1980; Bressloff and Kilpatrick 2008; Coombes and Owen 2005). More specifically, a spatialised model of V1 has been used to investigate hallucinatory visual patterns (Bressloff et al. 2001; Golubitsky et al. 2003; Bressloff and Kilpatrick 2008), localised patterns have been studied in models of working memory (Laing et al. 2002; Guo and Chow 2005; Faye et al. 2012) and in a model of texture perception (Faye et al. 2011). In all of these studies only spontaneous activity is studied, that is, in the absence of any cortical input.

In this article, we propose a spatialised ring model of direction selection, where the connectivity in the direction space and physical space is closely related to the Mexican-hat type connectivity typically used in the ring model of V1 (Ben-Yishai et al. 1995; Somers et al. 1995; Hansel and Sompolinsky 1997). We apply analytical tools such as stability analysis and normal form computations in order to identify and categorise bifurcations in our model. These tools have been used successfully to study the neural field equations, see, for example Curtu and Ermentrout (2004), Coombes et al. (2007) and Roxina and Montbrióa (2011). However, in the presence of an input to the model, these analytical tools are no longer applicable; although certain perturbation-type methods can be applied if the input is considered to have a specific, simple spatial structure and to be small (Veltz and Faugeras 2010; Ermentrout et al. 2010; Kilpatrick and Ermentrout 2012). Note that in the study (Veltz and Faugeras 2010), large inputs with a simple spatial structure were also studied with numerical continuation. In this paper, we first investigate the model’s behaviour in the absence of an input using analytical techniques. Then building on the knowledge gained we apply the tool of numerical continuation to track solution branches under parameter variation and detect bifurcation points; effectively continuation provides a computational tool for performing bifurcation analysis. For an introduction to continuation algorithms see Krauskopf et al. (2007). For the problem we study here the continuation module LOCA of the numerical tools package Trilinos is well suited (Heroux et al. 2005). Numerical bifurcation tools have not previously been used to study a neural fields model in the presence of a large, spatially complex input. Furthermore, the application of bifurcation analysis and numerical continuation to the study of a model of motion integration is new. These methods allow us to build a complete picture of the model’s possible dynamics in terms of parameter regions exhibiting qualitatively different behaviour and to identify the boundaries between these regions. In this way, we are able to ensure that parameter regions in which a desired behaviour is present are not isolated and that the behaviour is robust with respect to small changes in the model set up. The typical approach of a simple numerical search in parameter space often misses important parameter regions and does not provide information about robustness of behaviour with respect to parameter variation. The technical parts of this paper form the basis of the strategy employed to fix model parameters based on biological and mathematical constraints. We perform a systematic study of the model’s solution structure depending on key parameters including the stimulus strength and identify a parameter region for which the model has steady-state solutions corresponding to the three predominant percepts (diagonal, horizontal, vertical) observed in experiment (Fisher and Zanker 2001). An extended study of the system’s temporal dynamics allows for experimental predictions to be made regarding the distributions of the different percepts seen for different length presentations. In particular we predict that for long enough presentations only the horizontal and vertical percepts should be seen.

2 Model of direction selection

The model described here uses a neural fields description of the firing-rate activity of a population of neurons in middle temporal area (MT) over a physical (cortical) space and a feature space of motion direction. Two essential mechanisms are represented by the model: direction selectivity in the feature space and spatial diffusion of activity across the physical space. Stimulus input to the model is represented as preprocessed motion direction signals from V1 complex cells. Such a representation is comparable to classic motion detectors such as the output of elaborated Reichardt detectors (Van Santen and Sperling 1984; Bayerl and Neumann 2004) or of motion filters. The output of the model is the time evolution of activity levels across the physical-direction space.

The functionality of the model is encoded by the connectivity across direction-space and physical-space, which is processed by a nonlinearity. In the direction space, the connectivity is based on a narrowly tuned excitation with broadly tuned inhibition, as described for MT in Grunewald and Lankheet (1996). Such a Mexican-hat-type connectivity in the orientation-space has been used previously for the ring model of orientation selection (Ben-Yishai et al. 1995; Bressloff et al. 2001). Here, we assume that the inhibition tuning in MT is broad enough to be approximated by uniform lateral inhibition; with uniform lateral inhibition when cells selective for a particular direction are active, cells selective for the opposite direction are inhibited. This is consistent with known direction selectivity properties of MT (Albright 1984; Diogo et al. 2003) and with recordings from MT with transparent drifting dot patterns moving in opposite directions (Snowden et al. 1991). Furthermore, the uniform lateral inhibition connectivity has the convenient property of fixing the first non-trivial Fourier mode of the connectivity to be the largest, which is necessary for the model to produce tuning-curve solutions. In the physical space, diffusion is captured by an inverted Mexican hat connectivity, which has been used in a number of neural fields models with delays; see, for example, Hutt et al. (2003), Venkov et al. (2007) and Chapter 6 Veltz (2011). As motivated in Venkov et al. (2007), for cortical tissue the principal pyramidal cells are often surrounded by inhibitory interneurons and their long range connections are typically excitatory (Gilbert et al. 1996; Salin and Bullier 1995; McGuire et al. 1991). The inverted Mexican hat connectivity propagates activity outwards from stimulated regions and is consistent with a model output that describes a coherent motion across the physical space.

2.1 Representation of the stimulus

The stimulus that we consider here is a single drifting grating viewed through a square aperture, which has been shown to exhibit multistability of the viewer’s percept during the first 2 seconds of presentation (Castet et al. 1999; Fisher and Zanker 2001). For longer presentations, the stimulus is known to exhibit perceptual switching of the kind studied in, for example, binocular rivalry experiments (Blake 2001). However, the focus in this article will be the early dynamics after onset of the stimulus. The stimulus is shown in Fig. 1(a) and the three dominant percepts are labelled as diagonal D (the direction perpendicular to the grating’s orientation at 0°), horizontal H (in line with the horizontal aperture edge at − 45°) or vertical V (in line with the vertical aperture edge at 45°). Note that here in the description of the stimulus and later in the numerical results of Section 4 we give angles in degrees; however, for ease of presentation in the technical parts that follow in this section and in Section 3 angles are given in radians. One of the most significant simplifications in the model is that we consider a 1D approximation of the cortex for physical space, which restricts the way in which the stimulus can be represented as input to the model, as discussed below. We consider the different cues at different points on a 1D cut across the stimulus, as shown in Fig. 1(b). On the interior of the aperture the input is directionally ambiguous because 1D motion cues centred around the direction of the drifting grating are received. At the aperture edges the input is specific because 2D motion cues parallel to the aperture edges are received. It is the interplay between these two types of competing motion signals that produces the multistable percept. In this paper, we use the terms stable and unstable in the sense of dynamical systems theory to reflect whether a solution is attracting or repelling in state-space; the term multistable refers to the coexistence of different possible percepts for a visual stimulus.

Fig. 1

Description of the model stimulus. (a) A sinusoidal luminance grating viewed through a square aperture (grey); a large arrow indicates the diagonal grating direction D (v = 0°). Indicated by small arrows are the horizontal H (v = 45°) and vertical V (v = − 45°) directions corresponding to the aperture edges. (b) A cut across the aperture is used to represent the stimulus in the 1D physical space x (black line). At points on the interior of the aperture (black line is dashed) many directions are stimulated, on the edges of the aperture a single direction is stimulated parallel to the edge (black points) and outside the aperture no direction is stimulated (black line is solid). (c) Representation of the stimulus ${I_{\textrm{ext}}}$ in physical-direction space (x,v); at each point x each of the possible directions v ∈ ( − 180°,180°) is either stimulated (white) or not stimulated (black). Multiple directions are stimulated on the interior of the aperture x ∈ ( − 0.75,0.75), unique directions are stimulated at the aperture edges x = − 0.75 and x = 0.75. Note that the 1D cut in panel (b) is illustrative and the actual interior and exterior regions used in the model are those shown in panel (c)

The inclusion of 2D physical space would allow for many variations to the stimulus to be considered. However, there are a number modifications that are possible with the present 1D representation that we now discuss. For example, rectangular apertures are often considered with a specific ratio between the different edges (Fisher and Zanker 2001) and by taking a 1D cut across the stimulus this information would be lost. However, a similar effect could be achieved by giving a stronger weighting to the longer aperture edge. Another feature often investigated in psychophysics experiments is the angle of the grating with respect to the aperture edges (Castet et al. 1999). Again, although certain information is lost in the 1D cut, such a change to the stimulus could be considered by placing the 2D elements as shown in Fig. 1(c) asymmetrically about v = 0 (but still orthogonal to each other). Furthermore, the choice of the cut made Fig. 1(b) is quite arbitrary. For example, moving the cut closer to the line between the top left and bottom right corners would widen the stimulated region in x; in terms of the models response, we would expect the further separation of the 2D cue elements to delay the time it takes for the 2D cues to affect on the dynamics. The specific case where a cut is taken between two corners of the aperture would result in there being competition between 2D different cues at the aperture edge points. The stimulus shown in Fig. 1(c) could be modified to incorporate this by adding points at both v = ±45° at each aperture edge x = ±0.75 as opposed to v = 45° at x = − 0.75 and v = − 45° at x = 0.75 as is currently the case. Overall the 1D approximation used here is well suited to the specific stimulus studied with its particular symmetry properties, that is, with a square aperture and a grating that forms an equal angle with each aperture edge.

2.2 Neural field equation

We now introduce the neural field equation that describes the neuronal population’s activity, detailing how the different elements discussed so far enter into the model. The firing rate activity of a single population of neurons in MT is denoted

$$ p : (x,v,t) \in \Omega \times V \times \mathbb{R}^+ \rightarrow p(x,v,t) \in\mathbb{R}^+, $$

(1)

where Ω is the spatial domain (a bounded subset of ℝ) and V = ℝ/2πℤ is the direction space. Note that we impose the restriction that p ≥ 0, because it is not physically relevant to have a negative firing rate. We assume that x and v are independent variables: every direction v is represented at each physical position x. The neural field equation is given by

$$\label{eqn:nfield} \begin{cases} \hfill\displaystyle\frac{\partial p}{\partial t} &= -\mu p + S(\lambda\left[Jp+T+k{I_{\textrm{ext}}}\right]),\\[6pt] \hfill p(x,v,0)&=p_0(x,v), \end{cases} $$

(2)

where μ is the decay rate, J is the connectivity operator, k is the input gain (analogous to contrast) for the stimulus ${I_{\textrm{ext}}}$ (Fig. 1(c)) and T is the constant threshold parameter. The parameter λ is the stiffness (slope at x = 0) of the sigmoid nonlinearity $S(x)=\frac{1}{1+\exp(-x)}$. The choice of a sigmoid function, which is smooth and infinitely differentiable, facilitates the study of steady-state behaviour and allows for the application of numerical continuation (Veltz and Faugeras 2010). The initial condition at t = 0 is p ₀(x,v). The connectivity J has the following form

$$ Jp=\nu_1(G_E\star p)-\nu_2(G_I\star p)-\nu_3 p. $$

(3)

The first two terms represent a difference of 2D Gaussian functions G _E and G _I , where ν ₁ and ν ₂ represent the relative strength of excitation and inhibition, respectively. The convolutions G _E  ⋆ and G _I  ⋆ are defined by:

$$ G_E\star p=\int_\Omega\int_Vg^E_x(x-y)g^E_v(v-w)p(y,w,t){\textrm{d}}{w}{\textrm{d}}{y}, $$

(4)

$$ G_I\star p=\int_\Omega\int_Vg^I_x(x-y)b^I_v(v-w)p(y,w,t){\textrm{d}}{w}{\textrm{d}}{y},\quad $$

(5)

where $g^*_x(x)=\frac{1}{\sqrt{2\pi}\sigma^*_x}\exp(-\frac{|x|^2}{2\sigma^*_x})$ for $\sigma^*_x=\sigma^I_x,\sigma^E_x$ and similarly for $g^E_v(v)$. In physical space, we have an inverted Mexican hat type connectivity so $\sigma^E_x>\sigma^I_x$. The width of excitation in direction space is set by $\sigma^E_v$ and the uniform lateral inhibition is represented by the box-function $b^I_v(v)=\frac{1}{2\pi}$. In order to illustrate the shape of the connectivity function across (x,v)-space we first plot in Fig. 2(a) the function $M_x(x)=\nu_1g^E_x-\nu_2g^I_x$ with $\sigma^E_x>\sigma^I_x$ and ν ₂ > ν ₁ along with its Fourier transform $\hat{M}_x(j)$. Similarly in panel (b) we plot $M_v(v)=\nu_1g^E_v-\nu_2b^I_v$ and its Fourier transform $\hat{M}_v(k)$. Furthermore, the full connectivity $M(x,v)=\nu_1g^E_x(x)g^E_v(v)-\nu_2g^I_x(x)b^I_v(v)$ is plotted in panel (c); functions with the shape of M _x and M _v are recovered by taking 1D slices across this surface. The parameter ν ₃ is ignored here as this serves only to shift the surface up or down. Restrictions on the choice of parameters describing the connectivity function are discussed in Section 3.2.

Fig. 2

Profile of the connectivity function. (a) Form of the connectivity M _x in x-space and the corresponding Fourier transform $\hat{M}_x$. (b) Form of the connectivity M _v in v-space and the corresponding Fourier transform $\hat{M}_v$. (c) Full, coupled connectivity M. The functions M _x and M _v correspond to the 1D slices at v = 0 (black curve) and x = 0 (white curve), respectively

An additional linear threshold term ν ₃ p is used to tune the maximum firing rate of direction-selected solutions, whereas the constant threshold T is used to tune the firing rate of homogeneous, non-direction-selected solutions. It is convenient to include the linear threshold term in the connectivity operator as this simplifies the stability computations in Section 3.2. The choice of all parameters is discussed in Section 4.

3 Analytic results in the absence of stimulus, k = 0

In this section we discuss inherent properties of Eq. (2) and its solutions without a stimulus input. The results we obtain analytically provide a foundation of knowledge about the different types of solution the model can produce, the role of key parameters and a means to set appropriate values of parameters based on mathematical and biological constraints.

We begin our study by looking at the symmetry properties satisfied by the connectivity and the governing equation in Section 3.1. We show that Eq. (2) with the connectivity J as described above is equivariant with respect to a certain symmetry group. This important property dictates the types of solution that can be produced by the model. Furthermore, it determines the type of bifurcations that occur.

In the single population model that we consider here, the only types of solutions that we encounter are steady states (or, persistent states). Given an initial condition p ₀, the time evolution of the equations can be computed numerically; the particular initial condition chosen will determine which steady-state solution the system converges to. It is important to note that the transient dynamics encountered before the system converges to a steady state can also be greatly affected by the initial condition. In Section 3.2 we calculate analytically the steady states that have the additional property of being independent of both the physical and direction space. For these spatially independent solutions a constant level of activity persists across (x,v)-space; this type of solution can be thought of as the baseline activity that we would see in the absence of a stimulus (or below the contrast threshold). We give an expression that allows us to compute these solutions depending on the system parameters. Also in Section 3.2, we compute the eigenvalues and eigenvectors of the connectivity operator J (a spatial-mode decomposition), which allows us in turn to compute the stability of the steady-state solutions dependent on the nonlinearity stiffness λ. We show that for small enough λ the steady-state solutions are stable. As λ is increased, the most destabilising mode of J, as determined by its largest eigenvalue will become unstable at a critical value of λ. This critical value is the system’s principal bifurcation point.

We determine the type of the principal bifurcation in Section 3.3. Furthermore, given the mode of J that loses stability in this bifurcation, and given the symmetry properties of the governing equation, we are able to characterise the spatially dependent solutions produced by the model. A normal form computation determines the way in which the transition from spatially homogeneous solutions to spatially dependent solutions occurs in the model.

3.1 Symmetry group

Here we discuss the symmetry properties of Eq. (2), which will play an important role in determining the type of bifurcation that the model produces. The general concept is to specify the group of translations and reflections for which the governing equation is equivariant. The same group of translations and reflections, when applied to a solution of the equations, will produce coexisting solutions; for example, we will see in Section 3.3 that translational invariance in v means that a direction-selected solution associated with one specific direction can be translated by any angle to give direction-selected solutions associated with all other possible directions. Note that when a stimulus is introduced, the symmetry group of the equations will be in some way reduced and it is, therefore, important to first identify the full symmetry group before its introduction.

In order to simplify subsequent calculations we impose periodicity on the spatial domain so that Ω = ℝ/cℤ for some c ∈ ℝ; this simplification does not affect the stability properties of the system (Faugeras et al. 2008). Let us consider the group, denoted Γ, of translations of ℝ/cℤ: a one parameter group parametrised by α ∈ ℝ/cℤ. An element Γ _α of this group acts in the following way on the variables (x,v,t):

$$ {{\Gamma}_{\alpha}} \cdot (x,v,t) = (x+{\alpha},v,t). $$

(6)

In general the action of the group Γ on the function p is

$$ {\Gamma} \cdot p(x,v,t) \stackrel{\textrm{def}}{=} p\left({\Gamma}^{-1}(x,v,t)\right), $$

(7)

and more specifically for a translation in x:

$$ {{\Gamma}_{\alpha}} \cdot p(x,v,t) = p(x-{\alpha},v,t). $$

(8)

Let

$$\begin{array}{rll} F(p(x,v,t)) &=& \frac{\partial p(x,v,t)}{\partial t} + \mu p(x,v,t)\nonumber\\ &&-S(\lambda[Jp(x,v,t)+T]); \end{array}$$

(9)

it can be shown that F is equivariant with respect to the group Γ or, equivalently Γ _α F(p) = F(Γ _α p).

Furthermore, the function F is equivariant with respect to the reflection group generated by R which has the following action on the variables and activity:

$$ R\cdot (x,v,t) = (-x,v,t),$$

(10)

$$ R\cdot p(x,v,t) = p(-x,v,t). $$

(11)

If we denote H _x the group generated by Γ and R and since we have

$$ \begin{cases} {\Gamma}_{{\alpha}_1}{\Gamma}_{{\alpha}_2} = {\Gamma}_{{\alpha}_1+{\alpha}_2} \quad &\forall {\alpha}_1,{\alpha}_2, \in \mathbb{R}/c\mathbb{Z}, \\ R {{\Gamma}_{\alpha}} = {\Gamma}_{-{\alpha}} R \quad &\forall {\alpha} \in \mathbb{R}/c\mathbb{Z}, \\ {\Gamma}_0 = Id,\\ R^2= Id, \end{cases} $$

(12)

the group H _x is isomorphic to O(2), the group of two-dimensional orthogonal transformations. Furthermore, the equation F is equivariant with respect to the similarly defined group H _v generated by translation and reflection in v. Therefore, F is equivariant under the action of the symmetry group H = H _x ×H _v which is isomorphic to O(2)×O(2).

3.2 Spatially homogeneous solutions and their stability

Steady-state solutions are those for which $\frac{\partial p}{\partial t}=0$. We first consider solutions that are independent in both the physical space x and velocity space v and the level of activity across the population p is equal to a constant value $\bar{p}\in\mathbb{R}^+$. To find these solutions we set the right hand side of Eq. (2) equal to 0 and, thus, search for solutions $\bar{p}$ to the following equation

$$ \mu \bar{p}=S\left(\lambda\left[J\bar{p}+T\right]\right). $$

Given that for the normalised Gaussian functions we have $G_E\star\bar{p}=\bar{p}$ and $G_I\star\bar{p}=\bar{p}$, we can further write

$$ \mu\bar{p}= S\left(\lambda\left[(\nu_1-\nu_2-\nu_3)\bar{p}+T\right]\right),\label{eqn:pbar} $$

(13)

an implicit expression for $\bar{p}$.

Next, we wish to determine the linear stability of Eq. (2) at the solution $\bar{p}$ depending on system parameters. The first task is to compute the spectrum of the operator J. In order to do this we decompose J into Fourier modes by obtaining its eigenvalues and the associated eigenvectors; this information will determine exactly which (Fourier) modes of J have the greatest destabilising effect. The eigenvalues ζ _(j,k) of J are given by the following relation:

$$\label{eq:eigenvalues} \zeta_{(j,k)}=\nu_1\hat{g}^E_x(j)\,\hat{g}^E_v(k)-\nu_2\,\hat{g}^I_x(j)\,\hat{b}^I_v(k)-\nu_3, $$

(14)

where $\hat{g}^E_x(j)$, $\hat{g}^E_v(k)$ and $\hat{g}^I_x(j)$ are Fourier coefficients of the respective periodically extended Gaussian functions. The coefficients $\hat{b}^I_v(k)$ are defined as follows:

$$ \hat{b}^I_v(k)= \begin{cases} 1 & \text{for $k=0$}, \\ 0 & \text{otherwise}. \end{cases} $$

(15)

Due to the functions $g_x^E$, $g_x^I$, $g_v^E$ and $b_v^I$ being even, their Fourier coefficients are real positive and even. Hence we have ζ _{(±j, ±k)} = ζ _(j,k).

The dimension of the eigenspace E _(j,k) associated with each eigenvalue ζ _(j,k) depends on the indices j and k. Here we let the indices (j,k) be positive numbers. The eigenvectors χ _(j,k) are given by:

$$ \label{eqn:evecs} \chi_{(j,k)}= \left\{ \begin{array}{@{\!\!}c@{\quad}l} \{1\}\hfill & j=0, k=0, \\[6pt] \{e^{ikv},e^{-ikv}\} & j=0, k>0, \\[6pt] \left\{e^{\frac{2\pi ij x}{c}},e^{-\frac{2\pi ij x}{c}}\right\} & j>0, k=0, \\[6pt] \left\{e^{i\left(\frac{2\pi jx}{c}+kv\right)},e^{i\left(\frac{2\pi j x}{c}-kv\right)},\right.&\\[6pt] \,\,\,\left.e^{i\left(kv-\frac{2\pi jx}{c}\right)},e^{-i\left(\frac{2\pi jx}{c}+kv\right)}\right\} & j>0, k>0. \end{array} \right. $$

(16)

The eigenvectors could equivalently be represented as combinations of sin and cos functions.

Using the modal decomposition of J, we can obtain an expression for the eigenvalues associated with the solution $\bar{p}$, for each Fourier mode of J. The sign of the eigenvalue for each mode will tell us whether it is stable (−) or unstable (+). We define S ₁ to be the linear coefficient in the Taylor expansion of S at the fixed point $\bar{p}$; note that we Taylor expand about $\lambda[(\nu_1-\nu_2-\nu_3)\bar{p}+T]$ and S ₁ depends on the values of several other system parameters. By linearising about the solution $\bar{p}$ of Eq. (2), we obtain the following expression for the eigenvalues

$$\label{eqn:evals} \varrho_{(j,k)}=-\mu+\lambda S_1\zeta_{(j,k)}. $$

(17)

By identifying the mode of J with the largest eigenvalue ζ _(j,k), we can find the smallest value λ for which $\bar{p}$ is unstable. Indeed for small enough λ the solutions are stable as $\varrho_{(j,k)}\approx0$. For the values of ${\sigma}_{x}^{E}$, ${\sigma}_{x}^{I}$ and ${\sigma}_{v}^{E}$ used in this paper (see Table 1) and imposing certain restrictions on the values of ν ₁, ν ₂ and ν ₃, we can identify exactly which modes (j,k) are the most destabilising. If we impose ν ₁ > 0, 0 ≤ ν ₃ < ν ₁ and ν ₂ > ν ₁ then the following properties hold:

• The mode (0,0) is stable because ζ _(0,0) = ν ₁ − ν ₂ − ν ₃ < 0.

• The $\nu_2\,\hat{g}^I_x(j)\,\hat{b}^I_v(k)$ term ensures that all modes for which k = 0 are stable.

• The positive $\nu_1\hat{g}^E_x(j)\,\hat{g}^E_v(k)$ term produces the destabilising contribution, which is greatest for j = 0.

• Further, this destabilising contribution is greatest for k closest to 0 and then diminishes for increasing k.

Therefore, the largest eigenvalue ζ _(j,k) of J corresponds to the mode (0,1) followed by the subsequent modes with increasing k. Accordingly, in the analysis that follows it is convenient to drop the subscript j and to assume that it is zero, such that ζ _k  = ζ _(0,k). The largest eigenvalue is ζ ₁; therefore, the smallest value of λ for which $\varrho_{(j,k)}=0$ is given by

$$\label{eqn:lamc} \lambda_c=\frac{\mu}{S_1\zeta_1}. $$

(18)

This value λ _c is the system’s principal bifurcation point, which we study in the next section. The term S ₁ depends on λ and $\bar{p}$, but values of λ _c can be found by solving the following system for the pair $(\bar{p}_c,\lambda_c)$:

$$\label{eqn:plam} \left\{\begin{array}{@{}l} \bar{p}_c = \displaystyle\frac{S\left(\lambda_c\left[(\nu_1-\nu_2-\nu_3)\bar{p}_c+T\right]\right)}{\mu},\\[12pt] \lambda_c = \displaystyle\frac{\mu}{S_1(\lambda_c\left[(\nu_1-\nu_2-\nu_3)\bar{p}_c+T\right])\zeta_1}. \end{array}\right. $$

(19)

By taking advantage of the equality S′ = S(1 − S), it was proved in Veltz and Faugeras (2010) that given ζ ₀ < 0 and ζ ₁ > 0, the pair $(\bar{p}_c,\lambda_c)$ is unique. These two inequalities for the eigenvalues hold given the restrictions on ν ₁, ν ₂ and ν ₃ discussed above.

Table 1 Default parameter values used in the numerical studies in Sections 4.3 and 4.4

Bifurcation points associated with other modes that occur as λ is increased beyond λ _c can be found in a similar fashion, however, it is the branch of solutions that are born from the principal bifurcation that will determine the types of spatially dependent solutions that the model will produce.

3.3 Normal form of the principal bifurcation point

In this section we classify the principal bifurcation point by first, applying the center manifold theorem and secondly, giving the appropriate change of variables to reduce the system’s dynamics into a normal form; we now introduce these concepts. In the previous section we performed a modal decomposition of the connectivity and computed the linear stability of Eq. (2) with respect to perturbations in the different modal components. For the different modal components, or eigenvectors χ _(j,k) (Eq. (16)), the sign of the associated eigenvalue $\varrho_{(j,k)}$ (Eq. (17)) gives the linear stability. In the case when $\varrho_{(j,k)}=0$ the stability is neutral; the parameter value for which this occurs is the bifurcation point. At this bifurcation point it is necessary to also consider nonlinear terms in some parameter neighbourhood in order to capture the local dynamics. A center manifold reduction allows us to compute these nonlinear terms by means of a leading order Taylor approximation; the center manifold theorem allows us to prove rigorously that the computed reduced system accurately captures the local dynamics. A normal form computation is a change of variables that classifies the type of bifurcation present in our system and allows for the dynamics local to the bifurcation point to be seen clearly. The coefficients found in the normal form computation provide important information about the direction of bifurcating branches in terms of the bifurcation parameter and the stability of these branches.

We prove in Appendix A that the relevant hypotheses for the centre manifold hold in our case. This computation depends both on the symmetry properties discussed in Section 3.1 and the fixed point stability analysis from Section 3.2. Indeed, in the previous section we identified the system’s principal bifurcation point as given by the pair $(\bar{p}_c,\lambda_c)$, solutions to the system (19). We now define respectively the first, second and third order coefficients in the Taylor expansion of S at $\bar{p}_c$ to be S ₁, S ₂ and S ₃. We drop the subscript notation for the eigenvectors χ = e ^iv and $\overline{\chi}=e^{-iv}$, which span the two-dimensional eigenspace E ₁ associated with the eigenvalue ζ ₁. The eigenvalues ζ ₀ (for the homogeneous mode) and ζ ₂ (for the j = 0, k = 2 mode) will also appear in the analysis that follows.

Here we define a centre manifold on the two dimensional eigenspace of ζ ₁. This centre manifold will be independent of physical space x, therefore, the manifold must be equivariant with respect to the reduced symmetry group H _v , which is isomorphic to O(2). Here we introduce P the real valued solutions on the center manifold, which it is convenient to express in terms of a complex variable w. We decompose P into linear components on the eigenspace E ₁ and nonlinear components orthogonal to E ₁. We set

$$\label{eqn:pexp} P=\bar{p}_c+w\cdot\chi+\overline{w}\cdot\overline{\chi}+\Psi(w,\overline{w},\lambda-\lambda_c), \quad w(t)\in\mathbb{C}, $$

(20)

where Ψ is a grouping of nonlinear terms called the center manifold correction. A simple change of coordinates can be used to eliminate the constant term $\bar{p}_c$. From (Chapter 2 Haragus and Iooss 2010), we have in this case a pitchfork bifurcation with O(2) symmetry and the reduced equation for the dynamics of w has the following normal form equation

$$\label{eqn:dwdt} \frac{{\textrm{d}}{w}}{{\textrm{d}}{t}}= aw(\lambda-\lambda_c) + bw|w|^2 + O(|w|(|\lambda-\lambda_c|^2+|w|^4)), $$

(21)

together with the complex conjugated equation for $\overline{w}$. Indeed, due to the fact that the reduced equation for the dynamics of w must also be O(2)-equivariant, even powered terms in the reduced equation are prohibited. We define the parameter dependent linear operator L _λ  = − μId + λS ₁ J, which represents the linearisation of the right hand side of Eq. (2) at $\bar{p}_c$. The linear coefficient a can be determined by considering the action of L _λ on the eigenvector χ (equivalently, on the linear terms of P) at the bifurcation point given by Eq. (18):

$$\begin{array}{rll} L_\lambda\cdot\chi&=&(-\mu+\lambda S_1J)\cdot\chi,\\&=&(-\mu+\lambda S_1\zeta_1)\cdot\chi,\\&=&(-\mu+\lambda\frac{\mu}{\lambda_c})\cdot\chi,\\&=&\frac{\mu}{\lambda_c}(\lambda-\lambda_c)\cdot\chi,\\[-2pt] \end{array}$$

which, by comparing with Eq. (21), gives $a=\frac{\mu}{\lambda_c}>0$. The fact that a is positive means that the principal solution branch is stable before the bifurcation point. Note that the linear term disappears at the bifurcation point λ = λ _c and it is necessary to consider higher order terms in order to quantify the dynamics. The sign of the cubic coefficient b determines the direction of the bifurcating branch; see Fig. 3 for the two possibilities when a > 0. We now use the expression for solutions P on the center manifold to determine the coefficient b in terms of our model parameters. Substituting the expression (20) for P into Eq. (2) we obtain

$$\begin{array}{rll} \frac{{\textrm{d}}{P}}{{\textrm{d}}{t}}&=&\underbrace{(-\mu +\lambda_c S_1J)}_{L_{\lambda_c}}(P-\bar{p}_c)+\frac{\lambda_c^2 S_2}{2}(J(P-\bar{p}_c))^2\nonumber\\ &&+\,\frac{\lambda_c^3 S_3}{6}(J(P-\bar{p}_c))^3+O(P^4), \end{array}$$

(22)

where $J(P-\bar{p}_c)=\zeta_1 w\cdot\chi+\zeta_1\overline{w}\cdot\overline{\chi}+J\Psi$ and the linear terms are collected in the operator $L_{\lambda_c}$. Higher order terms in the Taylor expansion may be neglected given the form of Eq. (21) assuming that a and b are non-zero. It remains to determine the coefficient and b by matching terms between Eqs. (21) and (22).

Fig. 3

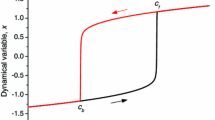
Sketch of bifurcation diagrams in λ for some norm |.| of a (a) supercritical or (b) subcritical pitchfork. Lower solution branch corresponds to spatially homogeneous solutions, upper solution branch corresponds to direction-selected solutions; stable parts are black, unstable parts are grey. Pitchfork occurs at λ _c and in (b) there is a fold bifurcation on the direction-selected branch λ _f ; arrows indicate temporal dynamics when passing λ _c on the lower branch

In order to compute b we Taylor expand Ψ at λ = λ _c :

$$ \Psi(w,\overline{w},0)=\sum\limits_{p,q=2}^\infty \psi_{pq}w^p\overline{w}^q, $$

where the coefficients Ψ _pq are orthogonal to the eigenvectors χ and $\overline{\chi}$. We identify terms with common powers in the Taylor expansion in order to obtain the following equation to be solved for b:

$$\begin{array}{rll} L_{\lambda_c}\Psi_{21}&+&\frac{\lambda_c^2 S_2}{2}(2J\Psi_{11}\zeta_1\chi+2J\Psi_{20}\zeta_1\overline{\chi})\\ &+&\frac{\lambda_c^3 S_3}{6}3\zeta_1^3\chi^2\overline{\chi}=b\chi. \end{array}$$

After some calculations given in Appendix B, we obtain the following expression for b:

$$\label{eqn:bfin} b=\lambda_c^3\zeta_1^3\left(\frac{S_3}{2}+\frac{\lambda_cS_2^2}{\mu}\left [ \frac{\zeta_0}{\left(1-\frac{\zeta_0}{\zeta_1}\right)}+ \frac{\zeta_2}{2\left(1-\frac{\zeta_2}{\zeta_1}\right)} \right]\right). $$

(23)

As we can see from Eq. (23), the criticality of the pitchfork bifurcation, as determined by the sign of b, depends on all system parameters in a complex way. We briefly discuss the implications of this criticality in our model.

• b < 0: The bifurcation is supercritical (Haragus and Iooss 2010). The new branch of solutions exist after the bifurcation, i.e. for λ > λ _c . Furthermore the branch of solutions will be stable (attracting) local to the bifurcation. In our model, for increasing λ passing the bifurcation point, there would be smooth transition (smooth change in activity levels) from spatially homogeneous solutions to a direction-selected solution.

• b > 0 The bifurcation is subcritical (Haragus and Iooss 2010). The new branch of solutions exist before the bifurcation, i.e. for λ < λ _c . Furthermore the branch of solutions will be unstable (repelling) local to the bifurcation. In our model, for increasing λ passing the bifurcation point, there would be non-continuous transition (jump in activity levels) from spatially homogeneous solutions to a direction-selected solution (see below for explanation).

Sketches of the bifurcation diagrams for the two cases are shown in Fig. 3. In the second case, and from the analysis in Veltz and Faugeras (2010), we know that the unstable branch existing for λ < λ _c must also have a fold bifurcation λ _f at some point 0 < λ < λ _c . Thus the unstable branch of solutions existing for λ < λ _c will change direction and stability at λ _f . For λ _f  < λ < λ _c there are coexisting stable solutions and for λ > λ _c the direction-selected solution is the only stable one. Therefore, passing the bifurcation at λ _c results in a jump from spatially homogeneous solutions to a direction-selected solution.

Ultimately we need to choose a value of λ such that

• 1. In the absence of a stimulus there are no direction selected solutions;

• 2. When a stimulus is introduced a solution is selected that is intrinsically present in the model.

For λ too large the model will produce direction-selected solutions in the absence of a stimulus. For λ too small the solutions will be purely driven by the stimulus once it is introduced, the connectivity that dictates the solutions intrinsically present in the model will not play a role. Therefore, for the case b < 0 we must choose a value close to but still less than λ _c . For the case b > 0 we must choose a value close to but still less than λ _f .

The bifurcating branch of solutions is characterised by the mode involved ((j,k) = (0,1)), that is, the solutions will be uniform in physical space and will have a single maximum in v-space; we can think of the maximal point as being centred at a selected direction. Hence, we refer to solutions on the bifurcated branch as direction-selected solutions. Secondly, due to the O(2) symmetry in the absence of a stimulus, taking a direction-selected solution, we know that it will still be a solution under any angular translation in v; i.e. there continuum (or ring) of solutions representing all possible selected directions.

4 Numerical results

In order to progress in the study of our model, we make use of computational tools. In Section 4.1 we take advantage of the analytical results from Section 3 in order to explore properties of the model dependent on parameters and to determine relevant ranges of the parameters. In Section 4.2 we build on the normal form computation from Section 3.3 by computing the bifurcated branch of solutions using numerical continuation. We compute the relationship between the activity levels along the bifurcated branch and certain parameters in order to fix their values. An in depth study of the solution structure of the model varying two parameters is given in Section 4.3. We identify a region of interest in parameters space, which we study in more detail in Section 4.4. In particular we investigate the temporal dynamics of the model which provides insight into the relation between the model’s solution structure and different stimulus driven responses.

The default parameter values that we use in Sections 4.3 and 4.4 are given in Table 1. We can arbitrarily set the decay parameter to μ = 2 and the diffusion parameter to ν ₁ = 3. Equally, these could be set to equal 1, however, the chosen values lead to all system parameters being of roughly the same order of magnitude, which facilitates the computations with Trilinos.

The activity levels for steady states of Eq. (2) are bounded by $[0,\frac{1}{\mu}]$. In order to simplify the presentation of the results it is convenient to give activity levels in terms of either the max-norm ${p_{\textrm{max}}}$ or L ₂-norm |p| as a percentage of the maximum value $\frac{1}{\mu}$. For the spatial connectivity, the surround width is set by ${\sigma}_{x}^{1}$ which is three times that of the centre width region ${\sigma}_{x}^{2}$ (Tadin et al. 2003). The spatial extent of the stimulus is roughly 1.5 times larger than the surround width. The width of the excitation in direction space is set by ${\sigma}_{v}^{1}$ to be about 20°. This relatively tight tuning allows for the model to produce direction selected solutions (tuning curves) of widths appropriate for distinguishing between the main percepts H, V and D; tuning widths are discussed further in Section 4.2. Finally, it remains to set values for T, ν ₂ and ν ₃, which we do in Sections 4.1 and 4.2.

4.1 Parameter tuning

Ultimately, we will operate the model at a value of λ close to the either λ _c or λ _f , depending on the coefficient b, as discussed in Section 3.3. We wish to determine an appropriate firing rate for the spontaneous activity. We do this by investigating the value of $\bar{p}_c$, which will be approximately the same as the activity before the bifurcation. In the experimental study (Sclar et al. 1990) the contrast response curves of neurons at various stages of visual processing, including MT, were found. The data were fitted with the standard Naka–Rushton function characterising low responsiveness at low contrast, followed by a region of high sensitivity where the firing increases rapidly, which eventually plateaus out at some maximal firing rate. From this data it appears that at very low contrast (in the absence of a stimulus), the firing rate is at approximately 5–20% of the maximum firing rate. It is therefore appropriate to set model parameters such that 5% $<\bar{p}_c<20$%. Figure 4(a) and (b) show the dependence of $\bar{p}_c$ and b on the threshold parameter T, used to set the spontaneous activity level, and ν ₂, the inhibition strength; all other parameters are set to the values in Table 1. Note that for each value of $\bar{p}_c$ there is an associated unique value of λ _c given by Eq. (19); it is possible vary T and ν ₂ linearly such that the argument of S in the first equation is fixed, which explains the affine relationship in Fig. 4(a). The same property carries through to the Taylor coefficients S ₂ and S ₃ and to the values of b given by Eq. (23).

Fig. 4

Tuning the parameters T and ν ₂. (a) Grey scale map of activity level $\bar{p}_c$ at bifurcation point λ _c ; plotted in both panels are the contours 5% and 20% (grey) along with the contour 99% (dashed black). (b) Grey scale map of the normal form coefficient b as given by Eq. (23); plotted in both panels are the contours b = 0 (black); positive values correspond to a subcritical bifurcation and negative values to a supercritical bifurcation. For |T| large (white region in bottom left of (a), grey region in bottom left of (b)) the activity level is saturated at $\bar{p}_c=100$% and b ≈ 0 because the Taylor coefficients S _* ≈ 0

For a given value of ν ₂, Fig. 4(a) provides the necessary range of T for which we have 5% $<\bar{p}_c<20$%. Furthermore, for values of (ν ₂,T) in this range, we always have the case b > 0 corresponding to a subcritical pitchfork bifurcation; this implies that it will be necessary to operate the model close to λ _f . In order to set the final values of T, ν ₂ and ν ₃, it is necessary to consider the level of activity and tuning width of the direction selected branch of solutions. In the next section we use the information presented here, along with the dependence of these solution properties on ν ₂ and ν ₃ to determine the final values of the parameters used.

4.2 Solution structure in the absence of stimulus

We now look at numerically computed solutions in the absence of stimulus (k = 0). In Section 3.3 it was shown that the system’s principal bifurcation is a pitchfork with O(2)-symmetry; furthermore, it was shown in the previous section that this pitchfork bifurcation is subcritical for the parameter values specified in Table 1. We now employ numerical continuation to compute directly the bifurcated solution branch under the variation of λ. We use the continuation package LOCA, part of the Trilinos package of numerical tools. We use a discretisation of 37 points for both the physical space x and direction space v, verifying that the integrals involved in the solution of the equations satisfy suitable error bounds; such a discretisation gives rise to a system of 1369 ordinary differential equations (ODEs), which resulted in manageable computations with Trilinos. Increasing the discretisation further results in a drastic increase in computation times.

Figure 5(a) shows a bifurcation diagram in the parameter λ in the absence of a stimulus. As predicted from the analytical results herein and Veltz and Faugeras (2010), the pitchfork bifurcation P ₁ from the homogeneous (lower) branch of solutions is subcritical and the bifurcated (upper) branch undergoes a fold bifurcation at F ₁. Here we have λ _c  = 22.1 and λ _f  = 15.4. Therefore, it will be necessary to operate the model with λ < 15.4 such that direction selected solutions do not exist in the absence of a stimulus. Due to the O(2)-symmetry properties of the solutions on the bifurcated branch, the direction selected solutions are invariant to translations in v (there is a continuum, or ring, of solutions corresponding to all possible directions). Panels (b) and (c) show a direction-selected solution from the upper branch centred at an arbitrary direction; the same solution exists for any translation in v. These direction-selected solutions are modulated in v, but are still uniform in physical space x; it is only later, with the introduction of an input, that the model produces responses that are also modulated in x (see Fig. 8).

Fig. 5

Model solutions in absence of stimulus. (a) A bifurcation diagram varying λ for k = 0 and the parameter values given in Table 1, where the solution norm is |p|; branches of steady-state solutions are plotted with stable sections black and with unstable sections grey. The lower branch of solutions are spatially uniform in both x and v; for increasing λ the branch loses stability in a subcritical pitchfork bifurcation at P ₁. The bifurcated branch represents direction-selected solutions (modulated in v but still uniform in x); a change in stability occurs at the fold bifurcation F ₁. (b) Activity p plotted over the (x,v)-plane for the direction selected solution indicated by a diamond marker on the upper branch in panel (a). (c) Cross section in v at an arbitrary value of x from panel (b)

In order to set values of the parameters ν ₂ and ν ₃ we investigate how certain properties of the direction-selected solutions change with respect to these parameters. Firstly, the solutions should have a suitable tuning width in v-space and, secondly, the activity should not be close to saturation. Given that we will operate the model at a value of λ close to λ _f , it is convenient to study these properties at the fold point F ₁, as shown in Fig. 5(a), and how they change under variation of the ν ₂ and ν ₃. Note that as we vary either ν ₂ or ν ₃, the value of λ for which the fold bifurcation occurs also changes. Therefore, we perform two-parameter continuation in λ and k, varying one parameter to satisfy the condition that the system be at a steady state and a second parameter to satisfy the condition that the system also be at a fold bifurcation.

We define $w_{\frac{1}{2}}$ to be the tuning width in v of the direction selected solutions at half-height. Figure 6(a) shows the variation of $w_{\frac{1}{2}}$ at the fold point F ₁ with respect to ν ₂, for convenience of presentation we do not show the variation of λ. As ν ₂ is increased (greater lateral inhibition) the tuning width decreases. Introducing the linear threshold term (ν ₃ = 1.5) does not change this characteristic, but shifts the curves up. It is necessary to set a value of ν ₂ such that the tuning width is less than 45° in order to make the distinction between solutions moving diagonally or vertically/horizontally as shown in Fig. 1. At ν ₂ = 66, which gives $w_{\frac{1}{2}}\in({30}^{\circ},{40}^{\circ})$, the maximum level of activity for the direction-selected solution is shown in Fig. 6(b). Imposing the condition that ${p_{\textrm{max}}}<50$% at F ₁, the system should still exhibit suitable sensitivity to changes in the input gain when the stimulus is introduced. We arrive at a choice of (ν ₂,ν ₃) = (66,1.5), which gives $w_{\frac{1}{2}}\approx{40}^{\circ}$ and ${p_{\textrm{max}}}\approx48$%.

Fig. 6

Tuning of parameters ν ₂ and ν ₃. (a) Dependence of velocity tuning half-width $w_{\frac{1}{2}}$ on ν ₂ at fold point F ₁; black curve computed for ν ₃ = 0, grey curve computed for ν ₃ = 1.5. (b) Dependence of maximum activity level for direction-selected solutions ${p_{\textrm{max}}}$ on ν ₃ computed for ν ₂ = 66

Overall, in the last two sections, we have explored the relationship between the three parameters T, ν ₂ and ν ₃ and properties of the homogeneous and direction-selected solutions. This has allowed us to set suitable values of these parameters such that the solutions produced by the model satisfy important biological and mathematical constraints; refer back to Table 1 for the parameter values used in the subsequent sections.

4.3 Introduction of stimulus and two-parameter analysis

From the results presented in the previous section we know that the sigmoidal slope λ should be set at a value for which the model cannot spontaneously produce direction-selected solutions. This gives rise to the requirement that λ < 15.4 so as to be at a λ-value less than the first fold point labelled F ₁ in Fig. 5. We now investigate the solutions when a stimulus is introduced to the model by increasing the stimulus gain parameter k from 0; this is analogous to increasing the stimulus contrast. Recall that the stimulus described in Section 1 has the form shown in Fig. 1(c) when represented in the (x,v)-plane.

Figure 7 shows one-parameter bifurcations diagrams in k initialised at the values of λ indicated in the panels. In order to see the solution structure clearly the diagrams are shown with k on a logarithmic scale. In panels (a), (b) and (c) solutions are plotted in terms of the the norm |p|; note that in panel (c) this allows the main solution branch at a lower activity level to be distinguished from the solution branch associated with the percept D. In panel (d) we plot solutions in terms of the average direction $\bar{v}$ in order to distinguish between the solutions associated the percepts H and V.

Fig. 7

Branches of steady-state solutions are plotted for varying bifurcation parameter k (shown on a logarithmic scale) as computed for different values of λ; stable sections of solution branches are black and unstable sections are grey. Changes in stability occur at fold bifurcations (black points) and pitchfork bifurcations (black stars). In panels (a), (b) and (c) solutions are plotted in terms of the L ₂-norm of the solution vector |p| for λ = {12.5,13,14}, respectively. The inset in panel (c) shows the largest eigenvalue $\zeta_{\textrm{max}}$ along the two upper solution branches from the main panel over the range of k as indicated by vertical dashed lines. Panel (d) shows the same solution branches as in panel (c), but in terms of the average direction $\bar{v}$

At λ = 12.5, as shown in panel (a), there is a single branch of stable solutions on which no bifurcations are encountered. The solutions effectively mimic the input stimulus along the solution branch and the level of activity increases with k.

At λ = 13, for increasing k bifurcations are encountered at the fold points labelled $F^H_1$ and $F^V_1$, the subcritical pitchfork P ₁ and the supercritical pitchfork P ₂. With the introduction of the stimulus, the O(2)-symmetry of the pitchfork for k = 0, as discussed in the previous section, is broken. We now find that the pitchfork bifurcation at P ₁ gives rise to a pair of direction-selected-solution branches, as opposed to a continuum of solutions at all possible directions when k = 0 as discussed in Section 4.2. The two branches are associated with the directions H and V and the branches undergo a fold bifurcations $F^H_1$ and $F^V_1$, respectively. These two fold points coincide when plotted in terms of the solution norm |p|. The pair of direction-selected branches reconnect at the supercritical (for k decreasing) pitchfork P ₂. The main solution branch (that mimics the input stimulus and has a lower level of activity than the bifurcated branch) is unstable between P ₁ and P ₂; it coexists with the direction-selected solutions.

At λ = 14, as shown in Fig. 7(c), the same bifurcations are encountered as for λ = 13, but with $F^H_1$, $F^V_1$ and P ₁ at lower values of k, and P ₂ at a larger value of k. The significant difference is the introduction of two pairs of fold bifurcations F ₂, F ₃ and F ₄, F ₅ on the main unstable branch of solutions. This series of bifurcations gives rise to an unstable direction-selected solution between F ₂ and F ₅. For values of k between F ₂ and F ₅ the inset shows the largest eigenvalue on the unstable direction-selected branch (grey) and the two symmetrical direction-selected branches (black). Close to F ₂, the largest eigenvalue is positive but very close to zero implying that the solution is weakly unstable in this region. Figure 7(d) shows the pair of symmetrical direction-selected branches with average direction $\bar{v}$ as the solution measure. The unstable solution corresponding to D ($\bar{v}={0}^{\circ}$) is shown in Fig. 8(a) and the stable solutions corresponding to V ($\bar{v}\approx{45}^{\circ}$) and H ($\bar{v}\approx-{45}^{\circ}$) are shown in Fig. 8(b) and (c), respectively. We note that a slightly elevated level activity persists outside of the aperture (stimulated region), which is a consequence of the underlying solutions encoded by the connectivity as shown in Fig. 5 that have a single direction selected across the entire physical space. It is suggested that this (subthresold) activity could facilitate further recruitment of direction selection beyond the aperture edges. See, for example, Shimojo et al. (1989) where experiments were carried out using gratings masked by multiple apertures.

Fig. 8

Three possible direction-selected solutions. Panels (a), (b) and (c) show, for λ = 14, k = 0.3, three possible direction-selected solutions corresponding to the unstable diagonal (D), stable vertical (V) and stable horizontal (H) percepts, respectively

The pitchfork and fold bifurcations encountered in the one-parameter bifurcation diagrams presented thus far are codimension-one bifurcations that lie on curves in the parameter plane and, can therefore, be tracked under variation of two parameters. Indeed, the necessary routines to achieve this are implemented in the package Trilinos. Figure 9 shows the locus of pitchfork bifurcation P and the loci of fold bifurcation F _H , F _V , F _D and F _T over the (λ,k)-plane; note that F _H and F _V coincide and that F _D is associated with the unstable D solution. In order to illustrate how solutions are organised we consider three one-parameter slices of the parameter plane. Indicated by vertical dashed lines in Fig. 9, the slices correspond to the three one-parameter cases shown in Fig. 7. Firstly, for the trivial case at λ = 12.5 the corresponding slice in Fig. 9 does not intersect the pitchfork or fold curves. At λ = 13, for increasing k the first (simultaneous) intersection is with F _H,V (corresponding to $F^H_1$ and $F^V_1$), followed by P (corresponding to P ₁), and P again (corresponding to P ₂); compare Figs. 9 and 7(b). Finally, at λ = 14, for increasing k the intersections occur in the following order F _H,V , F _D , P, F _T , F _T , F _D and P; these intersections correspond to the bifurcation points $F^{H,V}_1$, P ₁, F ₂, F ₃, F ₄, F ₅ and P ₂ in Fig. 7(c). We are now able to summarise the type of solutions that exist in different regions of the (λ,k)-plane. Outside of the region bounded by P and below F _H,V , there are no direction selected solutions. One can think of F _H,V representing a contrast threshold in k that changes with respect to λ. For λ too small, the solutions are purely stimulus driven. In the region between F _H,V and P the homogeneous solution is stable and coexists with the two direction selected solutions. Inside the area bounded by P, the system’s homogeneous solutions are unstable and there are always two direction selected solutions corresponding to H and V. For points in the region bounded by P and also to the right of F _D , there exists stable solutions associated with H and V, and an unstable solution associated with D. We identify this as a region of interest for which we expect the model to qualitatively reproduce the behaviour observed in experiment.

Fig. 9

A two-parameter bifurcation diagram is shown in the (λ,k)-plane where the locus of pitchfork bifurcation P is a black curve and the loci of fold bifurcations F _H,V , F _D and F _T are a grey curves. The point where the coinciding fold curves F _H,V terminate at an intersection with the pitchfork curve P is indicated by black point. One-parameter slices indicated by vertical dashed lines correspond to the bifurcation diagrams for fixed λ and varying k shown in Fig. 7; the labels along these slices correspond with the bifurcation points in Fig. 7

4.4 Temporal dynamics

By means of an in-depth, two-parameter bifurcation analysis we have identified a region of interest in parameter space for which the model produces two stable direction-selected solutions corresponding to the horizontal (H) and vertical (V) percepts, and one unstable direction-selected solution corresponding to the diagonal (D) percept. We know that in this parameter region the system will converge to one of the stable percepts; in this section we study how the unstable solution D plays a role in the temporal dynamics. At the chosen parameter values in Table 1 with λ = 14, the model produces a low level of homogeneous activity in the absence of stimulus k = 0. We take this homogeneous state as an initial condition for simulations with a random perturbation drawn from a standard uniform distribution in order to introduce a stochastic element. The equations remain deterministic, but we introduce variability in the initial conditions for each simulation. First, we present an example simulation and define some quantities that characterise the temporal dynamics; next, we study how the temporal dynamics change with respect to the strength of the input gain k. The reader may find it helpful to refer back to the bifurcation diagrams Fig. 7(c) and (d), which show the solution branches corresponding to H, D and V.

Figure 10 shows an example of the temporal dynamics produced by the model in the region of parameter space with solutions corresponding to H, D and V, (see Section 4.3). The behaviour can be broken into three phases: (1) initially no specific direction is selected but there is a slightly higher level of activity for stimulated directions, (2) the first direction-selected solution to appear corresponds to D but the system diverges from this unstable solution, (3) the final direction-selected solution corresponds to either H or V and the system will remain at this stable solution after convergence. The point in time of the transition from phase 1 to phase 2 is denoted t ₁, phase 2 to phase 3 is denoted t ₂ (see panels (b), (c) and accompanying caption for definition of t ₁ and t ₂. The time-mark t ₁ coincides with the first appearance of a direction-selected solution, in this case D. The time-mark t ₂ coincides with the convergence of the solution to either H or V. These two quantities characterise the temporal dynamics of the system as transitions are made between the solutions associated with the different percepts.

Fig. 10

Example of temporal dynamics for (λ,k) = (14,0.3) initialised from random initial conditions. (a) Grey scale map showing the evolution activity levels p(x,v,t) with time on the vertical axis. The state vector p is indexed locally by position in physical space x and globally by position in direction space v and it is, therefore, convenient to show v-position on the horizontal axis. At the time-point labelled t ₁ (horizontal white dashed line, star in panels (b) and (c)) there is a transition to the diagonal direction-selected solution. At the time-point labelled t ₂ (horizontal white line, point in panels (b) and (c)) there is a transition to the final steady-state, direction-selected solution. (b) Time-evolution of |p|; the time-mark t ₁ is the point of steepest increase for |p|. (c) Time evolution of the average direction $\bar{v}$ with horizontal dashed black lines indicating the two possible final steady-state solutions. The time-mark t ₂ is taken as the first point where the $\bar{v}$ is within 3° of the final selected direction

We now investigate the way in which the characteristic quantities t ₁ and t ₂ vary depending on initial conditions; as such we study their distribution in time based on many simulations initiated with random initial conditions. Furthermore, we study the dependence of these distributions on the parameter k. For a range of discrete values of k ∈ {0.2,0.7}, we run at each k-value N = 500 simulations. Figure 11 shows a summary of the statistics of the distributions of t ₁ and t ₂ depending on k. The results show that as k increases, the mean value of t ₁ decreases (D is perceived sooner) as does the mean value of t ₂-t ₁ (the switch from D to either H or V occurs sooner). Another important property is that for smaller values of k, there is a large spread for t ₂ with a long tail extending off to large values of t. This can be explained from the bifurcation results presented earlier, specifically, the unstable branch of solutions corresponding to D and the pair of stable solution branches corresponding to H and V as shown in Fig. 7(c), (d). The inset of Fig. 7(c) shows the largest eigenvalues along the solution branches for the parameter values considered here. For the unstable solution corresponding to D the largest eigenvalue is indeed positive, but still very close to 0. Therefore, very long transients can be observed resulting in a large time being spent at the D solution. As k increases the eigenvalue increases and the transient times decrease resulting in less time being spent near D. Finally, for large values of k the D solution is barely seen at all, there is convergence directly to H or V.

Fig. 11

Variability and skewness of the time-marks t ₁ and t ₂ dependent on the parameter k. At each k-value the data from N = 500 simulations with random initial conditions is shown. (a) Mean value of t ₁ is plotted in black and of t ₂ in grey over a range of values of k with error bars showing the standard deviation. (b) Similarly, the median is plotted with error bars showing the first and third quartile of the distributions. (c), (d) Example histograms of t ₁ in black and t ₂ in grey for k = 0.25 and k = 0.5, respectively

We now look more closely at how the unstable solution D affects the dynamics at k = 0.2 and k = 0.5, in particular in terms of the distributions of the average direction $\bar{v}$ taken at different time snapshots. At k = 0.2 the average $\bar{t}_1=280$ and at k = 0.5 the average $\bar{t}_1=34$; these two average times represent when the rate of change of the system’s activity is greatest. Figure 12 shows histograms of $\bar{v}$ for time snapshots before $\bar{t}_1$ (first row) at $\bar{t}_1$ (second row) and after $\bar{t}_1$ (third row). In the first case k = 0.2 there is a tri-modal short-term response dominated by D (panel (a)), there is a tri-modal medium-term response spread between H, D and V (panel (c)) and there is a late-term tri-modal response dominated by H and V (panel (e)). In the second case k = 0.5, we see a shift from a uni-modal, short-term response (panel (b)), that becomes a bimodal response for the medium- and late-term with no peak at $\bar{v}=0$ (panels (d), (f)). In the second case the unstable solution D does not have an distinguishable effect on the dynamics, there is a rapid convergence to one of the two stable solutions.

Fig. 12

Histograms of the average direction $\bar{v}$ taken at three different time snapshots for the two cases k = 0.2 and k = 0.5 for N = 500 trials

5 Discussion

In this paper we presented a spatialised model of direction selection that was used to study the dynamical behaviour of multistable responses to the 1:1 ratio barber pole (a diagonally drifting grating viewed through a square aperture). The aim was to reproduce, at the cortical level, firing rate activity that can be related to qualitative behaviour observed in psychophysics experiments: the stimulus exhibits multistability of perception for short presentations where the dominant percepts are either (1) the diagonal direction of the grating (D) (2) in agreement with horizontal (H) aperture edge, or (3) in agreement with the vertical (V) aperture edge (Castet et al. 1999; Fisher and Zanker 2001). The model reproduced this multistable behaviour, where the percepts H and V correspond to stable solutions and the percept D to an unstable solution. The temporal dynamics were investigated and it was shown that early responses were dominated by the diagonal percept, midterm responses were tri-modal between the three percepts and later responses were dominated by the two stable percepts H and V. This behaviour is consistent with experimental findings that show an early response dominated by 1D cues, which is later refined by 2D cues (Barthélemy et al. 2010; Lorenceau et al. 1993; Pack and Born 2001). One of the main predictions to be made from these results is that the percept D is only seen as a transient behaviour; for long term presentations on the order of seconds either H or V will be seen or perceived.

One of the main advantages of the model used here is its simplicity; the philosophy was to reproduce interesting behaviour observed in experiments with a minimalistic set of features to perform motion integration. Given the particular stimulus studied in this paper and its inherent symmetry properties, it was important to utilise a framework, such as neural fields, where these symmetry properties can be preserved. Another positive aspect of working with a relatively simple model is the small set of parameters that must be determined, in contrast to, for example, the study Chey et al. (1997) where a huge number of parameters must be determined heuristically. The strategy employed for setting model parameters took into account a number of important biological and mathematical constraints. One of the main ideas was to ensure that the model is operating close to its principal bifurcation where it will be most sensitive to subtleties of the stimulus input (Veltz 2011); the bifurcation analysis and other analytical results helped to ensure the model was operated in the right parameter regime. For the remaining parameters, we used numerical continuation to study the relationships between a given parameter and biologically relevant properties of the model’s solutions. We looked at these relationships over a wide range of parameter values and ensured that appropriate values were set. The general principles applied to tune parameters are applicable to a broad class of models that covers the various possible extensions proposed below. In existing studies of motion integration, behaviour was studied at fixed parameters (Chey et al. 1997; Simoncelli and Heeger 1998; Bayerl and Neumann 2004; Tlapale et al. 2010b); in certain cases the influence of a single term is tested by setting its weight to zero. Here the two-parameter continuation analysis allow us to determine an entire region of interest in parameter space. Further, the extended investigation in this region looked at the dynamical behaviour taking into account the effect of changing initial conditions. The two-parameter investigation also tells us that the behaviour produced is robust over entire regions of parameter space.

An important question in studies of motion perception is identifying exactly what happens in the first few hundred milliseconds of presentation. The most insightful work so far has come from ocular following experiments (Masson et al. 2000) and physiological recordings from individual neurons (Pack and Born 2001). In order to support the results in this paper we propose a psychophysics experiment that investigates the same stimulus described in this paper with incrementally increasing short presentation time in order to identify the qualitative change in percept distributions that were found in our model. We found a uni-modal distribution in the short-term dynamics and a tri-modal distribution for the medium-term dynamics. Furthermore, we predict that the D percept can only be seen as a transient and for long enough presentation times only the percepts H or V would be seen.

The model and results presented here not only captures a number of important aspects seen in experiment, but also forms a solid basis for further study of motion integration. One natural extension would be to lift the one dimensional approximation of the physical space. This would first of all allow for the validity of the original approximation to be tested, further, it would allow for other stimulus parameters such as the terminator ratio to be tested for further comparison with the results of Fisher and Zanker (2001). More complex aperture arrangements could also be considered such as the cross-shaped stimulus studied in Castet and Zanker (1999). A directional bias that varied from subject to subject but generally towards the horizontal (Fisher and Zanker 2001) is a feature of experimental results that was not captured by our model. The most straightforward way to investigate this would be to consider an asymmetry in the model’s input that assumes stronger (or more numerous) inputs at the preferred direction. The model in Tlapale et al. (2010b), implemented in a similar framework to the one studied here, considers a much more detailed description taking into account filtering stages applied to the input along with feedforward and feedback interactions between MT and V1. The methods used in this paper would be applicable to models of much greater complexity though at the cost of increasing the intricacy of analytical computations and scale of numerical computations. The focus of this article was multistable perception in the first few seconds after stimulus onset, a similar model and stimulus could be used to study perceptual switches that are known to occur for extended presentations by considering an adaptation dynamic on a slow timescale such as the one studied in Curtu and Ermentrout (2004).

Appendices

Appendix A: Centre manifold

Here, we show that the necessary hypotheses are satisfied in order to apply the centre manifold theorem as given in Chapter 2 Haragus and Iooss (2010). We introduce some functional spaces in which the problem defined by Eq. (2) is well-posed. We note ${\mathcal{F}}$ the Hilbert space L²(Ω×V, ℝ), where Ω = ℝ/cℤ and V = ℝ/2πℤ, endowed with the usual inner product

$$ \langle p_1,\,p_2 \rangle_{\mathcal{F}}=\int_{-c/2}^{c/2} \int_{-\pi}^\pi p_1(x,v)p_2(x,v)\,\frac{dx}{c}\,\frac{dv}{2\pi}. $$

We also note ${\mathcal{G}}$ the space ${\rm L}^\infty(\Omega \times V, {\mathbb{R}}) \subset {\mathcal{F}}$. It is then easy to show, using techniques similar to those in Faugeras et al. (2008) and Chapter 4 Veltz (2011), that for any initial condition $p_0(x,v) \in {\mathcal{F}}$ there is a unique solution p(x,v,t), defined for all times t ≥ 0 and continuously differentiable with respect to t for all t ≥ 0.

Regarding the applicability of the parameter dependent centre manifold theorem (Theorem 3.3, Chapter 2 Haragus and Iooss 2010), we consider the linear operator L _λ defined in Eq. (22):

$$ L_\lambda=-\mu{\rm Id}+\lambda S_1 J. $$

We note that J can be written K − ν ₃ Id, where K is a convolution operator (in effect a linear combination of two convolutions with bounded convolution kernels). From these remarks it follows that L _λ is in ${\mathcal{L}}({\mathcal{G}},{\mathcal{F}})$, the set of linear continuous operators from ${\mathcal{G}}$ to ${\mathcal{F}}$, and that it is a compact operator, hence that its spectrum is discrete and the eigenvalues have finite multiplicity.

It is also not difficult to prove that $\|(i\omega {\rm Id}-L_\lambda)^{-1}\|_{{\mathcal{L}}({\mathcal{F}})} \leq \frac{2}{|\omega|}$ and $\|(i\omega {\rm Id}-L_\lambda)^{-1}\|_{{\mathcal{L}}({\mathcal{G}})} \leq \frac{2}{|\omega|}$ for ω large enough.

The next technical step is to do the change of variables $p=\bar{p}_c+P$, λ = λ _c  + η and to write an equation for P as a function of the parameter η. In detail we have

$$\begin{array}{rll} \frac{\partial P}{\partial t}&=&\frac{\partial p}{\partial t}\\ &=&-\mu\left(\bar{p}_c+P\right)+S\left(\left(\lambda_c+\eta\right)\left[J\left(\bar{p}_c+P\right)+T\right]\right). \end{array}$$

We subtract from this equation

$$ 0=-\mu \bar{p}_c+S(\lambda_c[J\bar{p}_c+T]), $$

to obtain

$$\begin{array}{rll} \frac{\partial P}{\partial t}&=&-\mu P+S\left(\left(\lambda_c+\eta\right)\left[J\left(\bar{p}_c+P\right)+T\right]\right)\\ &&-\,S\left(\lambda_c\left[J\bar{p}_c+T\right]\right). \end{array}$$

We then write

$$\begin{array}{rll} \frac{\partial P}{\partial t}&=&L_{\lambda_c} P+S\left(\left(\lambda_c+\eta\right)\left[J\left(\bar{p}_c+P\right)+T\right]\right)\\ &&-\,S\left(\lambda_c\left[J\bar{p}_c+T\right]\right)-\lambda_cS_1JP. \end{array}$$

If we define G(p,λ) = S(λ[Jp + T]), it should be clear that $\lambda_cS_1JP=D_pG(\bar{p}_c,\lambda_c)P$. From this follows the fact that

$$\begin{array}{rll} R(P,\eta)&=&S\left(\left(\lambda_c+\eta\right)\left[J\left(\bar{p}_c+P\right)+T\right]\right)\\ &&-\,S\left(\lambda_c\left[J\bar{p}_c+T\right]\right)-\lambda_cS_1JP\\ &=&G\left(\bar{p}_c+P,\lambda_c+\eta\right)-G\left(\bar{p}_c,\lambda_c\right)\\ &&-\,D_pG\left(\bar{p}_c,\lambda_c\right)P, \end{array}$$

is such that (use first order Taylor’s expansion with integral remainder)

$$ R(0,0)=0,\quad D_pR(0,0)=0, $$

and R is infinitely differentiable, because the sigmoid S is.

Therefore, all hypotheses necessary for applying the parameter dependent centre manifold theorem (Haragus and Iooss 2010) are satisfied and the computation of the normal form Eq. (21) is justified.

Appendix B: Normal form coefficient

In order to compute b we need to solve:

$$\begin{array}{rll} \label{eqn:psi21} L_{\lambda_c}\Psi_{21}&+&\frac{\lambda_c^2 S_2}{2}\left(2J\Psi_{11}\zeta_1\chi+2J\Psi_{20}\zeta_1\overline{\chi}\right)\nonumber\\ &+&\frac{\lambda_c^3 S_3}{6}3\zeta_1^3\chi^2\overline{\chi}=b\chi. \end{array}$$

(24)

It is first necessary to obtain expressions for Ψ₁₁ and Ψ₂₀ by solving the following equations:

$$ L_{\lambda_c}\Psi_{20}+\frac{\lambda_c^2 S_2}{2}\zeta_1^2\chi^2=0,\label{eqn:psi20}$$

(25)

$$ L_{\lambda_c}\Psi_{11}+\lambda_c^2 S_2\zeta_1^2\chi\overline{\chi}=0.\label{eqn:psi11} $$

(26)

In order to solve Eq. (25) we decompose Ψ₂₀ into components on the eigenspace E ₁

$$ \Psi^{||}_{20}=\alpha_{20}\chi+\overline{\alpha_{20}\chi}, $$

for some arbitrary coefficients α ₂₀ and $\overline{\alpha_{20}}$, and components orthogonal to the eigenspace

$$ \Psi^{\vdash}_{20}= \sum\limits_{|k|\neq1}v_ke^{ikv}, $$

for coefficients v _k to be determined. From

$$ L_{\lambda_c}\Psi_{20}=-\frac{\lambda_c^2 S_2}{2}\zeta_1^2\chi^2, $$

we find that v _k  = 0 for k ≠ ±2 and that

$$ v_2=v_{-2}=-\frac{\lambda_c^2 S_2\zeta_1^2}{2(-\mu+\lambda_c S_1\zeta_2)}. $$

The ζ ₂ coefficient comes from the action of J on Ψ. Finally we have a general expression for Ψ₂₀:

$$ \Psi_{20}=-\frac{\lambda_c^2 S_2\zeta_1^2}{2(-\mu+\lambda_c S_1\zeta_2)}e^{i2v}+\alpha_{20}\chi+\overline{\alpha_{20}\chi}. $$

We obtain a similar expression for Ψ₁₁:

$$ \Psi_{11}=-\frac{\lambda_c^2 S_2\zeta_1^2}{-\mu+\lambda_c S_1\zeta_0}+\alpha_{11}\chi+\overline{\alpha_{11}\chi}. $$

The ζ ₀ coefficient comes from the action of J on Ψ. These expressions are further simplified by the fact that at the bifurcation point $\zeta_1=\frac{\mu}{\lambda_c S_1}$, so we have:

$$ \Psi_{20}=\frac{\lambda_c^2 S_2\zeta_1^2}{2\mu\left(1-\frac{\zeta_2}{\zeta_1}\right)}e^{i2v}+ \alpha_{20}\chi+\overline{\alpha_{20}\chi},$$

(27)

$$ \Psi_{11}=\frac{\lambda_c^2 S_2\zeta_1^2}{\mu\left(1-\frac{\zeta_0}{\zeta_1}\right)}+ \alpha_{11}\chi+\overline{\alpha_{11}\chi}. $$

(28)

Now to solve for b we take the inner product of Eq. (24) with $\overline{\chi}$ which gives

$$\begin{array}{rll} b&=&\underbrace{\langle L\Psi_{21},\overline{\chi}\rangle}_{=0} +\lambda_c^2 S_2\zeta_1\left(\langle J\Psi_{11}\chi,\overline{\chi}\rangle +\langle J\Psi_{20}\overline{\chi},\overline{\chi}\rangle \right)\\ &&+\,\frac{\lambda_c^3 S_3}{2}\zeta_1^3\underbrace{\langle\chi^2\overline{\chi},\overline{\chi}\rangle}_{=1}. \end{array}$$

Evaluating the remaining inner products we have

$$\begin{array}{rll} \langle J\Psi_{20}\chi,\overline{\chi}\rangle&=& \frac{\zeta_2\lambda_c^2 S_2\zeta_1^2}{2\mu(1-\frac{\zeta_2}{\zeta_1})} \underbrace{\langle e^{i2v}\overline{\chi},\overline{\chi}\rangle}_{=1} \\ &&+\,\alpha_{20}\underbrace{\langle \overline{\chi}\chi,\overline{\chi}\rangle }_{=0} \,+\,\overline{\alpha_{20}}\underbrace{\langle \overline{\chi}^2,\overline{\chi}\rangle}_{=0}\\ &=& \frac{\zeta_2\lambda_c^2 S_2\zeta_1^2}{2\mu(1-\frac{\zeta_2}{\zeta_1})}\\ \langle J\Psi_{11}\chi,\overline{\chi}\rangle&=& \frac{\zeta_0\lambda_c^2 S_2\zeta_1^2}{\mu(1-\frac{\zeta_0}{\zeta_1})} \underbrace{\langle \chi,\overline{\chi}\rangle}_{=1}\\ &&+\,\alpha_{11}\underbrace{\langle \chi^2,\overline{\chi}\rangle }_{=0} \,+\,\overline{\alpha_{11}}\underbrace{\langle \chi\overline{\chi},\overline{\chi}\rangle}_{=0}\\ &=& \frac{\zeta_0\lambda_c^2 S_2\zeta_1^2}{\mu(1-\frac{\zeta_0}{\zeta_1})}. \end{array}$$

Finally, we obtain the expression for b given in Eq. (23).