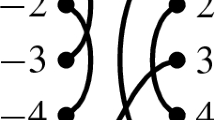1 Introduction

By the classical Schur–Weyl duality, the natural actions of the symmetric group \(\mathfrak{S}_{m}\) and the general linear group \(\operatorname{GL}_{N}=\operatorname {GL}_{N}(\mathbb{C})\) on the space of tensors

$$ \underbrace{\mathbb{C}^{N}\otimes\cdots\otimes \mathbb{C}^{N}}_m $$
(1.1)

centralize each other. This leads to the multiplicity free decomposition of the space (1.1) as a representation of the group \(\mathfrak{S}_{m}\times{\operatorname{GL}}_{N}\),

$$ \bigl(\mathbb{C}^N\bigr)^{\otimes m}\cong \bigoplus_{\lambda\vdash m,\, \ell(\lambda)\leq N}V_{\lambda }\otimes L(\lambda), $$
(1.2)

where V λ and L(λ) are the respective irreducible representations of \(\mathfrak{S}_{m}\) and \(\operatorname{GL}_{N}\) associated with a Young diagram λ which contains |λ|=m boxes, and the number of nonzero rows ℓ(λ) does not exceed N.

For any element \(X\in{}\operatorname{End}\mathbb{C}^{N}\) and a=1,…,m we denote by X a the corresponding element of the tensor product

An arbitrary element C of the group algebra \(\mathbb{C}[\mathfrak{S}_{m}]\) will be regarded as an operator in the space (1.1). We will identify the symmetric algebra \(\mathrm{S}(\mathfrak{gl}_{N})\) with the algebra of polynomial functions on the Lie algebra \(\mathfrak{gl}_{N}\). If we let X range over \(\mathfrak{gl}_{N}\) then the polynomial function \(X\mapsto{}\operatorname{tr}CX_{1}\dots X_{m}\) with the trace taken over all m copies of \(\operatorname{End}\mathbb{C}^{N}\) is a \(\operatorname{GL}_{N}\)-invariant element of the algebra \(\mathrm{S}(\mathfrak{gl}_{N})\). This follows easily by noting that for any matrix \(Z\in\operatorname {GL}_{N}\) we have

where we used the cyclic property of trace and the fact that the action of the element C commutes with the action of \(\operatorname{GL}_{N}\). The algebra of invariants \(\mathrm{S}(\mathfrak{gl}_{N})^{\operatorname {GL}_{N}}\) is isomorphic to the algebra of symmetric polynomials in N variables. An isomorphism is provided by the restriction of polynomial functions to the subspace of diagonal matrices in \(\mathfrak{gl}_{N}\). Hence, the function which takes a diagonal matrix X with eigenvalues x 1,…,x N to the trace \(\operatorname{tr}CX_{1}\cdots X_{m}\) is a symmetric polynomial in x 1,…,x N . Thus we define a linear map

$$ \operatorname{ch}:\mathbb{C}[\mathfrak{S}_m]\to\mathbb {C}[x_1,\dots,x_N]^{\mathfrak{S}_N},\quad C\mapsto \frac{1}{m!}\operatorname{tr}CX_1\cdots X_m. $$
(1.3)

Given any standard tableau T of shape λ consider the corresponding primitive idempotent \(E_{T}\in\mathbb{C}[\mathfrak{S}_{m}]\) and calculate its image under the map (1.3). To this end, we may assume without loss of generality that the matrix X is invertible so that X can be viewed as an element of the group \(\operatorname{GL}_{N}\). The space E T (ℂN)⊗m is an irreducible representation of \(\operatorname{GL}_{N}\) isomorphic to L(λ). Therefore, the trace \(\operatorname{tr}E_{T} X_{1}\cdots X_{m}\) coincides with the character of the representation L(λ) evaluated at the element X. This value is given by the Weyl character formula so that the trace equals the Schur polynomial s λ evaluated at the eigenvalues x 1,…,x N of the matrix X,

$$ \operatorname{tr}E_T X_1\cdots X_m=s_{\lambda}(x_1,\dots,x_N). $$
(1.4)

The trace does not depend on the choice of the standard tableau T of shape λ so that this relation allows us to calculate the image of the irreducible character χ λ under the map (1.3). Indeed,

$$ \chi_{\lambda}=\sum_{s\in\mathfrak{S}_m} \chi_{\lambda}(s)\cdot s^{-1} =\frac{m!}{\dim\lambda}\sum _{T} E_T, $$
(1.5)

where dimλ=dimV λ and the second sum is taken over the standard tableaux T of shape λ. Hence

$$ \operatorname{ch}:\chi_{\lambda}\mapsto s_{\lambda}(x_1, \dots,x_N). $$
(1.6)

This argument essentially recovers the characteristic map providing an isomorphism between the algebra generated by the irreducible characters of the symmetric groups and the algebra of symmetric functions; cf. [7, Sect. I.7].

Our goal in this paper is to extend the correspondence (1.6) to a map analogous to (1.3) involving the Brauer algebra and the respective orthogonal or symplectic group. Now we suppose that the orthogonal group O N or symplectic group \(\operatorname{Sp}_{N}\) acts on the space (1.1). The centralizer of this action in the endomorphism algebra of the tensor product space coincides with the homomorphic image of the Brauer algebra \(\mathcal{B}_{m}(\omega)\) with the parameter ω specialized to N and −N, respectively, in the orthogonal and symplectic case. This implies the tensor product decomposition analogous to (1.2),

(1.7)

where V λ and L(λ) are the respective irreducible representations of \(\mathcal{B}_{m}(N)\) and O N associated with the diagram λ, and we denote by λ′ the conjugate diagram so that \(\lambda'_{j}\) is the number of boxes in the column j of λ; see [16]. Given a diagram λ with \(\lambda'_{1}+\lambda'_{2}\leq N\) denote by λ ∗ the diagram obtained from λ by replacing the first column with the column containing \(N-\lambda'_{1}\) boxes. The corresponding representations L(λ) and L(λ ∗) of the Lie algebra associated with O N are isomorphic. In what follows we will only be concerned with the representations L(λ) corresponding to diagrams λ with at most n rows, i.e. \(\lambda'_{1}\leq n\), where N=2n or N=2n+1.

Similarly, in the symplectic case with N=2n,

(1.8)

where λ i denotes the number of boxes in row i of λ, V λ and L(λ′) are the respective irreducible representations of \(\mathcal{B}_{m}(-N)\) and \(\operatorname{Sp}_{N}\) associated with λ and λ′; see loc. cit.

We let \(\mathfrak{g}_{N}\subset\mathfrak{gl}_{N}\) denote the orthogonal Lie algebra \(\mathfrak{o}_{N}\) or symplectic Lie algebra \(\mathfrak{sp}_{N}\) which is associated with the corresponding Lie group G N =O N or \(\mathrm {G}_{N}=\operatorname{Sp}_{N}\). We will regard any element C of the respective Brauer algebra \(\mathcal{B}_{m}(N)\) or \(\mathcal{B}_{m}(-N)\) as an operator in the space (1.1). As with the Lie algebra \(\mathfrak{gl}_{N}\), we regard the polynomial function taking \(Y\in\mathfrak{g}_{N}\) to the trace \(\operatorname{tr}CY_{1}\cdots Y_{m}\) as an element of the symmetric algebra \(\mathrm{S} (\mathfrak{g}_{N})\). This element is G N -invariant which is verified by the same calculation as with the corresponding element of \(\mathrm{S}(\mathfrak {gl}_{N})\) above.

We will work with a particular presentation of the Lie algebra \(\mathfrak{g}_{N}\) so that its Cartan subalgebra consists of diagonal matrices. Suppose that y 1,…,y n ,−y 1,…,−y n are the eigenvalues of a diagonal matrix Y for N=2n and y 1,…,y n ,−y 1,…,−y n ,0 are the eigenvalues of Y for N=2n+1. Then the function which takes Y to the trace \(\operatorname{tr}CY_{1}\cdots Y_{m}\) is a symmetric polynomial in the variables \(y^{2}_{1},\dots,y^{2}_{n}\). Thus we get a linear map

$$ \operatorname{ch}:\mathcal{B}_m(\pm N)\to\mathbb{C} \bigl[y^2_1,\dots ,y^2_n \bigr]^{\mathfrak{S}_n},\quad C\mapsto \frac{1}{m!}\operatorname{tr}CY_1 \cdots Y_m. $$
(1.9)

The main result of this paper is the calculation of the image \(\operatorname{ch} (\phi_{\lambda})\) of the normalized central idempotent ϕ λ of the Brauer algebra associated with each partition λ of m satisfying the respective conditions \(\lambda'_{1}\leq n\) and λ 1≤n in the orthogonal and symplectic case. We show that \(\operatorname{ch}(\phi_{\lambda})=0\) if m is odd and give an explicit formula for the symmetric polynomial \(\operatorname{ch}(\phi_{\lambda})\) as a linear combination of the Schur polynomials \(s_{\nu}(y^{2}_{1},\dots,y^{2}_{n})\) where ν runs over partitions of l if m=2l.

The starting point of our arguments is the analogue of relation (1.4) for the classical group G N . Namely, suppose that T is a standard tableau of shape λ and let Z∈G N be a diagonal matrix such that detZ=1. We let E T denote the primitive idempotent of the respective Brauer algebra \(\mathcal{B}_{m}(N)\) or \(\mathcal{B}_{m}(-N)\), which we regard as an operator in the space (1.1). Due to the decompositions (1.7) and (1.8), the subspace E T (ℂN)⊗m is an irreducible representation of G N isomorphic to L(λ) in the orthogonal case and to L(λ′) in the symplectic case. Therefore, the trace \(\operatorname{tr}E_{T} Z_{1}\cdots Z_{m}\) equals the character of the respective representation L(λ) or L(λ′) so that

$$ \operatorname{tr}E_T Z_1\cdots Z_m=\chi^{\mathfrak{o}_N}_{\lambda }(z_1, \dots,z_n) $$
(1.10)

in the orthogonal case, and

$$ \operatorname{tr}E_T Z_1\cdots Z_m=\chi^{\mathfrak{sp}_N}_{\lambda '}(z_1, \dots,z_n) $$
(1.11)

in the symplectic case, where we denote by \(z_{1},\dots,z_{n},z^{-1}_{1},\dots,z^{-1}_{n}\) the eigenvalues of Z for N=2n and by \(z_{1},\dots,z_{n},z^{-1}_{1},\dots,z^{-1}_{n}, 1\) the eigenvalues of Z for N=2n+1. Explicit expressions for the characters are well known; they are implied by the Weyl character formula and can be found e.g. in [14]. Although relations (1.10) and (1.11) are analogous to (1.4), note a principal difference with the case of \(\operatorname{GL}_{N}\). In that case, the matrix X in (1.4) could be treated both as an element of the group \(\operatorname{GL}_{N}\) and as an element of the Lie algebra \(\mathfrak{gl}_{N}\). In contrast, the passage from the group G N to the Lie algebra \(\mathfrak{g}_{N}\) requires an additional step. To derive explicit formulas for the images of central idempotents of the Brauer algebra under the map (1.9) we use the Okounkov–Olshanski binomial formula [14, Theorem 1.2]. This allows us to express the characters occurring in (1.10) and (1.11) in terms of the Schur polynomials in \(y_{1}^{2},\dots,y_{n}^{2}\).

More precisely, by analogy with (1.5) set

$$ \phi_{\lambda}=\frac{1}{D(\lambda)}\sum _{T} E_T $$
(1.12)

in the orthogonal case, and

$$ \phi_{\lambda}=\frac{1}{D(\lambda')}\sum _{T} E_T $$
(1.13)

in the symplectic case, where D(λ)=dimL(λ) and the sums are taken over standard tableaux T of shape λ. Our main result (see Theorem 4.1 below) states that \(\operatorname{ch}(\phi_{\lambda})=0\) unless m is even, m=2l. In this case,

$$ \operatorname{ch}(\phi_{\lambda}) =\sum _{\nu\vdash l}\frac{s_{\nu}(y_1^2,\dots,y_n^2)}{C(\nu)} \sum_{\mu\subseteq\lambda}(-1)^{|\mu|} \frac{s_{\nu}(a_{\rho}|a)}{H(\mu)H(\lambda/\mu)}, $$
(1.14)

where ρ=μ and ρ=μ′ in the orthogonal and symplectic case, respectively, and we use the following notation. For any skew diagram θ we denote by dimθ the number of standard θ-tableaux with entries in {1,2,…,|θ|} and set

$$ H(\theta)=\frac{|\theta|!}{\dim\theta}. $$
(1.15)

If θ is normal (nonskew), then H(θ) coincides with the product of the hooks of θ due to the hook formula. Furthermore, the constant \(C(\nu)=C_{\mathfrak{g}_{N}}(\nu)\) equals the inner square of the Schur polynomial \(s_{\nu}(y_{1}^{2},\dots,y_{n}^{2})\) with respect to an invariant inner product on \(\mathrm{S}(\mathfrak{g}_{N})\) (see [14, Proposition 5.3]) and it is given by

$$ C(\nu)=\prod_{(i,j)\in\nu} 2 (n+j-i ) \bigl(N-1+2 (j-i+\varepsilon ) \bigr), $$
(1.16)

where

Finally, by s ν (x|a) we denote the double (or factorial ) Schur polynomial in the variables x=(x 1,…,x n ) associated with the particular parameter sequence a=(a i |i∈ℤ) with a i =(ε+i−1)2. The polynomial s ν (x|a) is symmetric in x 1,…,x n and it can be given by several equivalent formulas; see e.g. [7, Sect. I.3] (note that the sequence a there corresponds to our sequence −a). In particular,

$$ s_{\nu}(x|a)= \sum_{T}\prod _{\alpha\in\nu} (x_{T(\alpha)}-a_{T(\alpha )+c(\alpha)}), $$
(1.17)

summed over semistandard ν-tableaux T with entries in {1,…,n}, where c(α)=j−i denotes the content of the box α=(i,j). For any partition μ with at most n parts we denote by a μ the n-tuple

$$ a_{\mu}=(a_{\mu_1+n},a_{\mu_2+n-1},\dots, a_{\mu_n+1}). $$
(1.18)

We demonstrate below (Sect. 4.2) that the second sum in (1.14) simplifies if λ is a row or column diagram. However, we do not know whether shorter expressions for this sum exist for arbitrary λ.

The relation (1.14) is remarkably similar to the main result of Nazarov’s paper [12, Theorem 3.4] involving a different kind of characteristic maps.

As a consequence of our approach, we also demonstrate that the well-known hook dimension formulas for representations of the classical groups can be obtained directly from the properties of the primitive idempotents of the symmetric group and the Brauer algebra via relations (1.4), (1.10) and (1.11) implied by the Schur–Weyl duality.

We believe it is possible to extend the main results of the paper to the case where λ is a partition of m−2f with f≥1 and to calculate the images \(\operatorname{ch}(\phi_{\lambda})\) of the associated central idempotents ϕ λ under the map (1.9). This should involve more complicated combinatorics of paths in the Bratteli diagram corresponding to the Brauer algebras.

2 Idempotents in the Brauer algebra

Let m be a positive integer and ω an indeterminate. An m-diagram d is a collection of 2m dots arranged into two rows with m dots in each row connected by m edges such that any dot belongs to only one edge. The product of two m-diagrams d 1 and d 2 is determined by placing d 1 above d 2 and identifying the vertices of the bottom row of d 1 with the corresponding vertices in the top row of d 2. Let s be the number of closed loops obtained in this placement. The product d 1 d 2 is given by ω s times the resulting diagram without loops. The Brauer algebra \(\mathcal{B}_{m}(\omega)\) [1] is defined as the ℂ(ω)-linear span of the m-diagrams with the multiplication defined above. The dimension of the algebra is 1⋅3⋯(2m−1).

For 1≤a<b≤m denote by s ab and ϵ ab the respective diagrams of the form

figure a

and set s a =s aa+1 and ϵ a =ϵ aa+1 for a=1,…,m−1. The subalgebra of \(\mathcal{B}_{m}(\omega)\) generated over ℂ by the elements s ab is isomorphic to the group algebra of the symmetric group \(\mathbb{C}[\mathfrak{S}_{m}]\) so that s ab will be identified with the transposition (ab). The Brauer algebra \(\mathcal{B}_{m-1}(\omega)\) will be regarded as a natural subalgebra of \(\mathcal{B}_{m}(\omega)\).

The Jucys–Murphy elements x 1,…,x m for the Brauer algebra \(\mathcal{B}_{m}(\omega)\) are given by the formulas

$$ x_b=\frac{\omega-1}{2}+\sum _{a=1}^{b-1}(s_{ab}-\epsilon_{ab}), \quad b=1,\dots,m; $$
(2.1)

see [6] and [11], where, in particular, the eigenvalues of the x b in irreducible representations were calculated. We have followed [11] to include the shift by (ω−1)/2 in the definition to simplify the formulas below. The element x m commutes with the subalgebra \(\mathcal{B}_{m-1}(\omega)\). This implies that the elements x 1,…,x m of \(\mathcal{B}_{m}(\omega)\) pairwise commute. A complete set of pairwise orthogonal primitive idempotents for the Brauer algebra can be constructed with the use of these elements. Suppose that λ is a partition of m. We will identify partitions with their diagrams so that if the parts of λ are λ 1,λ 2,… then the corresponding diagram is a left-justified array of rows of unit boxes containing λ 1 boxes in the top row, λ 2 boxes in the second row, etc. The box in row i and column j of a diagram will be denoted as the pair (i,j). A standard λ-tableau is a sequence T=(Λ 1,…,Λ m ) of diagrams such that for each r=1,…,m the diagram Λ r is obtained from Λ r−1 by adding one box, where we set Λ 0=∅ (the empty diagram) and Λ m =λ. Equivalently, T will be viewed as the array obtained by writing r∈{1,…,m} into the box of the diagram λ which is added to the diagram Λ r−1 to get Λ r . To each standard tableau T we associate the corresponding sequence of contents (c 1,…,c m ), c a =c a (T), where

$$ c_a=\frac{\omega-1}{2}+j-i $$
(2.2)

if Λ a is obtained by adding the box (i,j) to Λ a−1. The primitive idempotents \(E_{T}=\nobreak E^{\lambda}_{T}\) can now be defined by the following recurrence formula (we omit the superscripts indicating the diagrams since they are determined by the standard tableaux). Set μ=Λ m−1 and consider the standard μ-tableau U=(Λ 1,…,Λ m−1) so that U can be viewed as the tableau obtained from T by removing the box containing m. Then

$$ E_{T}=E_{U}\frac{u-c_m}{ u-x_m} \bigg|_{u=c_m}. $$
(2.3)

Since the Brauer algebra is finite-dimensional, the fraction involving x m on the right hand side reduces to a polynomial in x m whose coefficients are rational functions in u. They turn out to be well-defined at u=c m and relation (2.3) states that the evaluation of the right hand side yields E T . This relation is essentially a version of the well-known Jucys–Murphy formula; see [5] and [8] for more details.

3 Hook dimension formulas for classical groups

Consider the vector space ℂN with its canonical basis e 1,…,e N . We will be using the involution on the set of indices {1,…,N} defined by i↦i′=N−i+1 and equip the space ℂN with the following nondegenerate symmetric or skew-symmetric bilinear form:

$$ \langle e_i,e_j\rangle=g_{ij}, $$
(3.1)

where N=2n is even in the skew-symmetric case, and

(3.2)

with ε i =1 for i=1,…,n and ε i =−1 for i=n+1,…,2n.

The classical group G N =O N or \(\mathrm{G}_{N}=\operatorname {Sp}_{N}\) is defined as the group of complex matrices preserving the respective symmetric or skew-symmetric form (3.1),

Observe that if Z=1 is the identity matrix, then the values provided by the expressions (1.10) and (1.11) coincide with the dimensions dimL(λ) and dimL(λ′) of the respective representations of the groups O N and \(\operatorname{Sp}_{N}\). It is well known by El Samra and King [4] that these dimensions are given by the hook formulas. We will consider the images of the idempotents E T under the action of the Brauer algebra in the tensor space (1.1) and calculate their partial traces with respect to the mth copy of the vector space ℂN. In particular, this will provide another proof of the hook dimension formulas of [4]; see also [15]. To make our arguments clearer, we first go over a technically simpler case of \(\operatorname{GL}_{N}\) to reproduce Robinson’s formula; see e.g. [4] and [7, Sect. I.3, Example 4] for other proofs.

3.1 Dimension formulas for \(\operatorname{GL}_{N}\)

The symmetric group version of the recurrence relation (2.3) takes exactly the same form [8] with the respective definitions of the objects associated with \(\mathfrak{S}_{m}\). Here, as above, T is a standard tableau of shape λ⊢m and U is obtained from T by removing the box occupied by m. The content c a =c a (T) of the box (i,j) of T occupied by a is now found by c a =j−i and the Jucys–Murphy elements x a are now given by x a =s 1a +⋯+s a−1a ; cf. (2.1). In the group algebra we have the relation s m−1 x m =x m−1 s m−1+1 which implies

$$ s_{m-1}+\frac{1}{u-x_m}=(u-x_{m-1})s_{m-1} \frac{1}{u-x_m}. $$
(3.3)

Hence,

Therefore, applying (3.3) once again we come to the identity

(3.4)

Consider the action of the symmetric group \(\mathfrak{S}_{m}\) in the space (1.1) so that the image of the element \(s_{ab}\in\mathfrak{S}_{m}\) with a<b is found by s ab ↦P ab ,

$$ P_{ab}=\sum_{i,j=1}^N 1^{\otimes(a-1)}\otimes e_{ij} \otimes1^{\otimes(b-a-1)}\otimes e_{ji}\otimes1^{\otimes(m-b)}, $$
(3.5)

where the \(e_{ij}\in\operatorname{End}\mathbb{C}^{N}\) denote the standard matrix units. From now on we use this action to regard elements of the group algebra \(\mathbb{C}[\mathfrak{S}_{m}]\) as elements of the algebra \(\operatorname{End} ((\mathbb {C}^{N})^{\otimes m} )\) which is naturally identified with the tensor product of the endomorphism algebras,

$$ \operatorname{End} \bigl(\bigl(\mathbb{C}^{N} \bigr)^{\otimes m} \bigr)\cong \underbrace{\operatorname{End} \mathbb{C}^{N}\otimes \cdots\otimes \operatorname{End} \mathbb{C}^{N}}_m. $$
(3.6)

The trace map \(\operatorname{tr}:\operatorname{End}\mathbb{C}^{N}\to \mathbb{C}\) is defined in a usual way as a linear map taking the matrix unit e ij to δ ij . For each a=1,…,m we will consider the partial trace \(\operatorname{tr}_{a}\) as a linear map \((\operatorname{End}\mathbb {C}^{N})^{\otimes m}\to(\operatorname{End}\mathbb{C}^{N})^{\otimes(m-1)}\) applied to the ath copy of the endomorphism algebra. Note that \(\operatorname{tr}_{a}(P_{ab})=1\). Furthermore, since

we get a recurrence relation for the rational functions

$$ A_m(u)=\operatorname{tr}_m \biggl( \frac{1}{u-x_m} \biggr) $$
(3.7)

in the form

that is,

Since for m=1 we have A 1(u)=N/u, solving the recurrence relation we find that

This calculation and the recurrence formula (2.3) allow us to find the partial trace \(\operatorname{tr}_{m} E_{T}\) of the idempotent E T regarded as an element of the algebra (3.6). By the properties of the Jucys–Murphy elements,

$$ x_aE_{U}=E_{U}x_a=c_aE_{U}, \quad a=1,\dots,m-1. $$
(3.8)

Therefore,

The evaluation of the rational function in u is well-defined and it depends only on the shape μ of the standard tableau U but does not depend on U. The result of the evaluation is easily calculated (cf. [8]); it gives

$$ \operatorname{tr}_m E_T=(N+c_m) \frac{H(\mu)}{H(\lambda)}E_{U}, $$
(3.9)

where H(μ) and H(λ) are the products of hooks of the diagrams μ and λ. By (1.4), the dimension of the irreducible representation L(λ) of \(\operatorname{GL}_{N}\) is found as the trace of E T taken over all m copies of the endomorphism space \(\operatorname {End}\mathbb{C}^{N}\). Hence, applying (3.9) we arrive at the well-known Robinson formula for this dimension. If λ is a partition with at most N parts, the dimension of the irreducible representation L(λ) of \(\operatorname{GL}_{N}\) is given by

3.2 Dimension formulas for O N and \(\operatorname{Sp}_{N}\)

To prove analogues of the hook dimension formula for the orthogonal and symplectic groups, consider the recurrence relation (2.3) in the Brauer algebra \(\mathcal{B}_{m}(\omega)\). The starting point will be an analogue of the identity (3.4) for \(\mathcal{B}_{m}(\omega)\) given in the next lemma. This identity goes back to [11, Sect. 4.1] where it is proved for the degenerate affine Wenzl algebra and used in the description of the center of that algebra; see also [2] for generalizations to the affine BMW algebras. Recall that now the Jucys–Murphy elements x a and the contents c a are defined by (2.1) and (2.2).

Lemma 3.1

We have the identity of rational functions in u,

Proof

Note the following relations in \(\mathcal{B}_{m}(\omega)\) satisfied by the Jucys–Murphy elements:

(3.10)
(3.11)

By (3.11) we have s m−1(u−x m )=(u−x m−1)s m−1−(1−ϵ m−1). Multiply both sides of this relation by (u−x m−1)−1 from the left and by (u−x m )−1 from the right and rearrange to get

$$ s_{m-1}\frac{1}{u-x_{m}}=\frac{1}{u-x_{m-1}}s_{m-1} +\frac{1}{u-x_{m-1}}(1-\epsilon_{m-1})\frac{1}{u-x_m} $$
(3.12)

which implies

The desired identity will follow after rewriting the second and third terms on the right hand side with the use of (3.10), (3.12) and the property that the elements x m−1 and x m commute. The second term takes the form

while for the third term we have

completing the proof. □

Now consider the natural action of the orthogonal group O N in the space of tensors (1.1) and the commuting action of the Brauer algebra \(\mathcal{B}_{m}(N)\) so that the parameter ω is specialized to N. The action of \(\mathcal{B}_{m}(N)\) in the space (1.1) is defined by the assignments

$$ s_{ab}\mapsto P_{ab},\quad \epsilon_{ab}\mapsto Q_{ab},\quad a< b, $$
(3.13)

where P ab is defined in (3.5), and

$$ Q_{ab}=\sum_{i,j=1}^N 1^{\otimes(a-1)}\otimes e_{ij} \otimes1^{\otimes(b-a-1)}\otimes e_{i'j'}\otimes1^{\otimes(m-b)}. $$
(3.14)

Note that \(\operatorname{tr}_{a}(Q_{ab})=1\) for 1≤a<b≤m, and for any element \(X\in\operatorname{End}\mathbb{C}^{N}\) we have the property \(Q_{ab}X_{a} Q_{ab}=\operatorname{tr}(X)Q_{ab}\). Now we use Lemma 3.1 and regard elements of the algebra \(\mathcal{B}_{m}(N)\) as elements of the algebra (3.6). Define the functions A m (u) by the same formula (3.7) as for the symmetric group, but with the new definition (2.1) of the Jucys–Murphy elements. Calculating the partial trace \(\operatorname{tr}_{m}\) on both sides of the identity of Lemma 3.1 we get the recurrence relation

which simplifies to

For m=1 we have A 1(u)=N/(u−c 1), where c 1=(N−1)/2 and the relation is easily solved by using the substitution

The solution reads (cf. closely related calculations in [3])

For any diagram λ with \(\lambda'_{1}\leq n\) set

$$ D(\lambda)=\frac{1}{H(\lambda)}\prod_{(i,j)\in\lambda} \bigl(N-1+d(i,j) \bigr), $$
(3.15)

where H(λ) is the product of hooks of λ (see (1.15)) and

Let T be a standard tableau of shape λ. Denote by U the standard tableau obtained from T by deleting the box occupied by m and let μ be the shape of U. As with the group algebra \(\mathbb{C}[\mathfrak{S}_{m}]\) in Sect. 3.1, the recurrence formula (2.3) allows us to find the partial trace \(\operatorname{tr}_{m} E_{T}\) of the idempotent E T regarded as an element of the algebra (3.6). The following proposition also recovers the hook dimension formula [4, (3.28)]. Note that it is given there in an equivalent form which amounts to a change in the definition of d(i,j): the inequalities i≤j and i>j are, respectively, replaced by i≥j and i<j.

Proposition 3.2

We have the relation

$$ \operatorname{tr}_m E_T=E_U \frac{D(\lambda)}{D(\mu)}. $$
(3.16)

Moreover, the dimension of the irreducible representation L(λ) of O N equals D(λ).

Proof

We have

and using the above formula for A m (u) we get

As we found in Sect. 3.1 (see (3.9)),

Furthermore, observe that

Hence, to complete the proof of (3.16) we need to verify the identity

(3.17)

where d λ (i,j) and d μ (i,j) denote the parameters d(i,j) associated with the diagrams λ and μ, respectively. The diagram λ is obtained from μ by adding one box. Let (k,l) be this box so that l=λ k and c m =λ k −k+c 1. First consider the case k≤l. The product on the left hand side does not depend on the standard tableau U and only depends on its shape μ. Therefore, the product can be written as

where c(i,j)=j−i+(N−1)/2 is the content of the box (i,j). We split the product into two parts by multiplying all terms corresponding to the subset of boxes (i,j) with i<l and those corresponding to the subset of boxes (i,j) with i≥l. After canceling common factors, the first part of the product will take the form

while the second part of the product can be written as

Therefore, the left hand side of (3.17) equals

$$ \frac{2c_m(c_m+c(l,\lambda_l)+1)}{2c_m-1} \prod_{i=1}^{l-1} \frac{c_m+c(i,\lambda_i)+1}{c_m+c(i,\lambda_i)} \prod_{j=1}^{\mu_l} \frac{c_m+c(\lambda'_j,j)-1}{c_m+c(\lambda'_j,j)}. $$
(3.18)

To see that this coincides with the right hand side of (3.17), note that for most of the pairs (i,j) the corresponding factors in the numerator and denominator of the fraction on the right hand side of (3.17) cancel. The remaining pairs are divided into five types: (i,k) with 1≤i<k; (k,k); (k,j) with k<j<l; (k,l); and (l,j) with 1≤j≤μ l . Examining the factors for each of the five types we conclude that their product coincides with (3.18). Indeed, taking the first type of pairs as an illustration, we obtain the product

which agrees with the corresponding factors in (3.18). The calculations for the other types and the argument in the case k>l are quite similar and will be omitted. This concludes the proof of the first part of the proposition. By (1.10), the dimension dimL(λ) equals the trace \(\operatorname{tr}_{1,\dots,m} E_{T}\) so that the second part follows from the first by an obvious induction. □

Now we turn to the symplectic group \(\operatorname{Sp}_{N}\), N=2n, acting in the space of tensors (1.1) and the commuting action of the Brauer algebra \(\mathcal{B}_{m}(-N)\). The action of \(\mathcal{B}_{m}(-N)\) in the space (1.1) is now defined by

$$ s_{ab}\mapsto-P_{ab},\quad \epsilon_{ab}\mapsto-Q_{ab},\quad a< b, $$
(3.19)

where P ab is defined in (3.5), and

$$ Q_{ab}=\sum_{i,j=1}^N \varepsilon_i\varepsilon_j1^{\otimes (a-1)}\otimes e_{ij} \otimes1^{\otimes(b-a-1)}\otimes e_{i'j'} \otimes1^{\otimes(m-b)}. $$
(3.20)

We use Lemma 3.1 in the same way as for the orthogonal group and write down a recurrence relation for the respective functions A m (u) defined by (3.7) with the definition (2.1) of the Jucys–Murphy elements. It takes the form

Noting that A 1(u)=N/(u−c 1) with c 1=(−N−1)/2 and using the substitution

we come to the solution

For any diagram ρ with at most n rows set

$$ D(\rho)=\frac{1}{H(\rho)}\prod_{(i,j)\in\rho} \bigl(N+1+d(i,j) \bigr), $$
(3.21)

where the parameters d(i,j) are now defined by

The following proposition recovers the symplectic version of the hook dimension formula [4, (3.29)]. We suppose that T is a standard tableau of shape λ⊢m such that the first row of λ does not exceed n, and U is the tableau obtained from T by removing the box occupied by m. The diagram μ is the shape of U.

Proposition 3.3

We have the relation

$$ \operatorname{tr}_m E_T=E_U \frac{D(\lambda')}{D(\mu')}. $$
(3.22)

Moreover, the dimension of the irreducible representation L(ρ) of \(\operatorname{Sp}_{N}\) equals D(ρ).

Proof

Applying again (2.3), we get

so that by the above formula for A m (u) we have

As with the orthogonal case (Proposition 3.2), the proof is reduced to verifying the identity

where d λ′(i,j) and d μ′(i,j) denote the respective parameters d(i,j) associated with the diagrams ρ=λ′ and ρ=μ′. This identity holds because after the replacement of N by −N it turns into (3.17), while the latter can be regarded as an identity of rational functions in a variable N. Finally, the dimension of L(λ′) equals \(\operatorname{tr}_{1,\dots,m} E_{T}\) by (1.11), so that an obvious induction yields dimL(λ′)=D(λ′). □

4 Images of central idempotents

We consider the cases of orthogonal group O N and symplectic group \(\operatorname{Sp}_{N}\) (the latter with N=2n), simultaneously, unless stated otherwise. Suppose that λ is a diagram with m boxes such that \(\lambda'_{1}\leq n\) in the orthogonal case and λ 1≤n in the symplectic case. Define the respective normalized central idempotents ϕ λ by (1.12) and (1.13) and regard them as elements of the algebra (3.6) under the action of the Brauer algebra defined by (3.13) and (3.19). We aim to calculate the images \(\operatorname{ch} (\phi_{\lambda})\) of ϕ λ under the characteristic maps (1.9).

4.1 Main theorem

We let Y run over the Cartan subalgebra of the Lie algebra \(\mathfrak{g}_{N}\) so that Y is a diagonal matrix

for N=2n or N=2n+1, respectively.

Consider the map \(F:\mathfrak{g}_{N}\to\mathrm{G}_{N}\) [14, Theorem 5.2], defined in a neighborhood of 0 by the formula

We let t be a complex variable and let Z=Z(t) be the image of the matrix tY under this map,

respectively. In particular, writing Z=F(tY) as a power series in t we have the following first few terms

Therefore, \(\operatorname{ch}(\phi_{\lambda})\) will be found from the coefficient of t m in the power series expansion

$$ \operatorname{tr}\phi_{\lambda}(Z_1-1)\cdots (Z_m-1)=m!t^m\operatorname{ch}(\phi_{\lambda })+ \cdots, $$
(4.1)

where the trace is taken over all m copies of \(\operatorname {End}\mathbb{C}^{N}\) in (3.6). We have

Each product \(Z_{a_{1}}\cdots Z_{a_{k}}\) can be written as PZ 1⋯Z k P −1, where P is the image in (3.6) of a permutation \(p\in \mathfrak{S}_{m}\) such that p(r)=a r for r=1,…,k. Since ϕ λ is proportional to a central idempotent, it commutes with P, and by the cyclic property of trace we bring the above expression to the form

Propositions 3.2 and 3.3 imply the formula for the partial trace,

summed over the diagrams μ obtained from λ by removing one box. Hence for any value of the parameter k=0,…,m we have the formula for multiple partial traces taken over the copies k+1,…,m of \(\operatorname{End}\mathbb{C}^{N}\),

where, as before, dimλ/μ is the number of standard tableaux with entries in {k+1,…,m} of the skew shape λ/μ. Therefore,

(4.2)

On the other hand, by (1.10) and (1.11),

in the orthogonal case, and

in the symplectic case. Now, using the notation (1.16), (1.17) and (1.18), we apply the binomial formula of [14, Theorem 1.2] which gives

$$ \frac{\chi_{\rho}(z_1,\dots,z_n)}{D(\rho)} =\sum_{\nu} \frac{s_{\nu}(a_{\rho}|a) s_{\nu}(t^2y_1^2,\dots,t^2y_n^2)}{C(\nu)}, $$
(4.3)

summed over partitions ν of length not exceeding n, where χ ρ (z 1,…,z n ) denotes any one of the characters \(\chi^{\mathfrak{o}_{N}}_{\rho}(z_{1},\dots,z_{n})\) or \(\chi^{\mathfrak {sp}_{N}}_{\rho }(z_{1},\dots,z_{n})\).

This formula implies that if m odd, then the coefficient of t m on the right hand side of (4.2) is zero. Now we assume that m is even, m=2l. Then the coefficient of t 2l in the right hand side of (4.3) can only come from the terms with the partition ν having exactly l boxes. Hence, using (4.1) and (4.2) we find that \(\operatorname{ch}(\phi_{\lambda})\) is the linear combination of the Schur polynomials \(s_{\nu}(y_{1}^{2},\dots,y_{n}^{2})\) with ν⊢l occurring with the respective coefficients

where ρ=μ and ρ=μ′ in the orthogonal and symplectic case, respectively. Thus, recalling the notation H(θ) in (1.15) we arrive at the main result.

Theorem 4.1

Suppose that λ is a diagram with m boxes such that \(\lambda'_{1}\leq n\) in the orthogonal case and λ 1≤n in the symplectic case. Then the image \(\operatorname{ch}(\phi_{\lambda})\) of the normalized central idempotent ϕ λ under the respective characteristic map (1.9) is zero if m is odd. If m=2l is even, then the image is found by

$$ \operatorname{ch}(\phi_{\lambda}) =\sum _{\nu\vdash l}\frac{s_{\nu}(y_1^2,\dots,y_n^2)}{C(\nu)} \sum_{\mu\subseteq\lambda}(-1)^{|\mu|} \frac{s_{\nu}(a_{\mu}|a)}{H(\mu)H(\lambda/\mu)} $$
(4.4)

in the orthogonal case, and

$$ \operatorname{ch}(\phi_{\lambda}) =\sum _{\nu\vdash l}\frac{s_{\nu}(y_1^2,\dots,y_n^2)}{C(\nu)} \sum_{\mu\subseteq\lambda}(-1)^{|\mu|} \frac{s_{\nu}(a_{\mu'}|a)}{H(\mu)H(\lambda/\mu)} $$
(4.5)

in the symplectic case.

Note that by the vanishing theorem [13] we have s ν (a ρ |a)=0 unless ν⊆ρ. Therefore, the first sum in (4.4) is restricted to the partitions ν contained in λ, while the second sum is restricted to the partitions μ containing ν. Similarly, the first sum in (4.5) is restricted to the partitions ν contained in λ′, while the second sum is restricted to the partitions μ containing ν′.

Example 4.2

Consider the orthogonal case with λ=(22). By (4.4), the image \(\operatorname{ch}(\phi_{(2^{2})})\) is a linear combination for the Schur polynomials \(s_{\nu}(y_{1}^{2},\dots,y_{n}^{2})\) with ν=(2) and ν=(12). Using [10, Proposition 3.2], we find

and

For the sequence a i =(ε+i−1)2 we have a n+i −a n+j =(i−j)(N+i+j−2). Hence the sums in (4.4) are found by

and

Thus,

4.2 Symmetrizers and antisymmetrizers

Now we consider the particular cases, where λ is a row or column diagram with 2l boxes. In each of these cases there is a unique standard tableau T of shape λ so that by (1.12) and (1.13), ϕ λ is proportional to the primitive idempotent E T . For λ=(2l) the primitive idempotent coincides with the symmetrizer S (2l), while for λ=(12l) it coincides with the antisymmetrizer A (2l) in the Brauer algebra. We will produce the images \(\operatorname{ch}(S^{(2l)})\) and \(\operatorname{ch}(A^{(2l)})\) in an explicit form. Suppose first that λ=(2l) in the orthogonal case. Then the first sum in (4.4) contains only one term with ν=(l), while the second sum is taken over row-diagrams μ=(k) with l≤k≤2l. By (1.17) we have

where the second relation holds since s (l)(x|a) is a symmetric polynomial. Recalling the definition (1.18), we find a (k)=(a k+n ,a n−1,…,a 1). Hence, taking x=a (k) we find that the only nonzero summand corresponds to i 1=⋯=i l =n,

$$ s_{(l)}(a_{(k)}|a)=(a_{k+n}-a_n) \cdots(a_{k+n}-a_{n+l-1}). $$
(4.6)

Furthermore, recalling that a i =(ε+i−1)2 we find

The sum in (4.4) then equals

Thus, taking into account the constants D(λ) for λ=(2l) and C(ν) for ν=(l) we come to the following corollary (for a different proof see [9, Proposition 3.4]).

Corollary 4.3

The image of the symmetrizer \(S^{(2l)}\in\mathcal{B}_{2l}(N)\) under the characteristic map is found by

Now let λ=(12l) with 2l≤n. The second sum in (4.4) is now taken over column-diagrams μ=(1k) with l≤k≤2l and ν=(1l). Using [10, Proposition 3.2], we find that

$$ s_{(1^l)}(a_{(1^k)}|a)=(a_{n-l+2}-a_{n-k+1}) \cdots(a_{n+1}-a_{n-k+1}). $$
(4.7)

Under the specialization a i =(ε+i−1)2 this simplifies to

so that the sum in (4.4) equals

thus leading to the image of the antisymmetrizer.

Corollary 4.4

The image of the antisymmetrizer \(A^{(2l)}\in\mathcal{B}_{2l}(N)\) under the characteristic map is found by

Note that this result also follows easily from the observation that A (2l) coincides with the antisymmetrizer in the group algebra \(\mathbb{C}[\mathfrak{S}_{2l}]\). Indeed, it suffices to apply (1.4) with λ=(12l) and replace X by the diagonal matrix Y.

The calculation in the symplectic case is quite similar. Suppose first that λ=(2l) with 2l≤n. Then ν=(1l) in (4.5) and μ runs over diagrams (k) with l≤k≤2l. Using (4.7) with the sequence a i =i 2 and performing the same calculations as in the orthogonal case we find the image of S (2l); see also [9, Proposition 3.5].

Corollary 4.5

The image of the symmetrizer \(S^{(2l)}\in\mathcal{B}_{2l}(-2n)\) under the characteristic map is found by

Finally, if λ=(12l) then ν=(l) in (4.5) and μ runs over diagrams (1k) with l≤k≤2l. Applying now (4.6), we calculate the image of A (2l).

Corollary 4.6

The image of the antisymmetrizer \(A^{(2l)}\in\mathcal{B}_{2l}(-2n)\) under the characteristic map is found by

This result also follows from the observation that A (2l) coincides with the symmetrizer in the group algebra \(\mathbb{C}[\mathfrak{S}_{2l}]\). It suffices to apply (1.4) with λ=(2l) and replace X by the diagonal matrix Y.