Inventory management of reusable surgical supplies

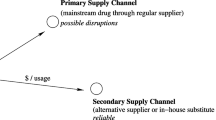
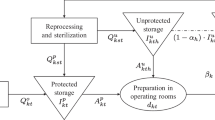
Abstract

We investigate the inventory management practices for reusable surgical instruments that must be sterilized between uses. We study a hospital that outsources their sterilization services and model the inventory process as a discrete-time Markov chain. We present two base-stock inventory models, one that considers stockout-based substitution and one that does not. We derive the optimal base-stock level for the number of reusable instruments to hold in inventory, the expected service level, and investigate the implied cost of a stockout. We apply our theoretical results to a dataset collected from a surgical unit at a large tertiary care hospital specializing in colorectal operations. We demonstrate how to implement our model when determining base-stock levels for future capacity expansion and when considering alternative stockout protocols. Our analysis suggests that the hospital can reduce the number of reusable instrument sets held in inventory if on-site sterilization techniques (e.g., flash sterilization) are employed. Our results will guide future procurement decisions for surgical units based on costs and desired service levels.

Appendices

Appendix A: Proofs

Proof Proof of Lemma 1:

Solving (6) for i = S and i=0 gives, respectively,

$$\begin{array}{@{}rcl@{}} \pi_{0}(S) &=& \pi_{S}(S)\mathbb{P}(D\geq S), \\ \pi_{S}(S) &=& \pi_{0}(S)\mathbb{P}(D\geq 0) +\mathbb{P}(D=0)\sum\limits_{i=1}^{S}\pi_{i}(S). \end{array} $$

Because $\mathbb {P}(D\geq 0)=1$,

$$\pi_{S}(S)=\pi_{0}(S) + \mathbb{P}(D=0)\sum\limits_{i=1}^{S}\pi_{i}(S). $$

Re-arranging the normalization condition, we get that ${\sum }_{i=1}^S\pi _i(S)=1-\pi _0(S)$, which implies

$$\pi_{S}(S)=\pi_{0}(S) + \mathbb{P}(D=0)(1-\pi_{0}(S)). $$

Substituting for π ₀(S) and re-arranging gives the desired result. We now show that, regardless of the demand distribution, both probabilities are monotone in S. Let Δπ _S (S) = π _S+1(S+1)−π _S (S). Substituting for the probabilities and simplifying gives

$$\begin{array}{@{}rcl@{}} &&{}{\Delta} \pi_{S}(S) \\ &=&\!\!\frac{\mathbb{P}(D\,=\,0)}{1\,-\,\mathbb{P}(D\!\geq\! S\,+\,1)\mathbb{P}(D\!\geq\! 1)}\,-\,\frac{\mathbb{P}(D\,=\,0)}{1\,-\,\mathbb{P}(D\!\geq\!S)\mathbb{P}(D\!\geq\! 1)} \\ &=&\mathbb{P}(D\,=\,0)\mathbb{P}(D\!\geq\! 1) \\ &&\times \left( \frac{\mathbb{P}(D\!\geq\! S\,+\,1)\,-\,\mathbb{P}(D\!\geq\!S)}{(1\,-\,\mathbb{P}(D\!\geq\!S+1)\mathbb{P}(D\!\geq\! 1))(1\,-\,\mathbb{P}(D\!\geq\!S)\mathbb{P}(D\!\geq\! 1))}\right)\\ &=&-\mathbb{P}(D\,=\,S)\mathbb{P}(D\,=\,0)\mathbb{P}(D\!\geq\! 1) \\ &&\times \left( \frac{1}{(1\,-\,\mathbb{P}(D\!\geq\! S\,+\,1)\mathbb{P}(D\!\geq\! 1))(1\,-\,\mathbb{P}(D\!\geq\! S)\mathbb{P}(D\!\geq\!1))}\right). \end{array} $$

Since all probability terms are positive, Δπ _S (S)<0. Now let Δπ ₀(S) = π ₀(S+1)−π ₀(S). Substituting for the probabilities and simplifying gives

$$\begin{array}{@{}rcl@{}} &&{} {\Delta} \pi_{0}(S) \\ &=&\! \frac{\mathbb{P}(D\,=\,0)\mathbb{P}(D\!\geq\! S\,+\,1)}{1\,-\,\mathbb{P}(D\!\geq\! S\,+\,1)\mathbb{P}(D\!\geq\! 1)}\,-\,\frac{\mathbb{P}(D\,=\,0)\mathbb{P}(D\!\geq\! S)}{1\,-\, \mathbb{P}(D\!\geq\! S)\mathbb{P}(D\!\geq\! 1)}\\ &=& \!-\mathbb{P}(D\,=\,S)\mathbb{P}(D\,=\,0) \\ && \times \left( \frac{1}{(1\,-\,\mathbb{P}(D\!\geq\! S\,+\,1)\mathbb{P}(D\!\geq\! 1))(1\,-\,\mathbb{P}(D\!\geq\! S)\mathbb{P}(D\!\geq\! 1))}\right). \end{array} $$

Again, since all probability terms are positive, Δπ ₀(S)<0. Thus, π _S (S) and π ₀(S) are monotone decreasing in the number of instruments, S. □

Proof Proof of Proposition 1:

From Lemma 1, we know π ₀(S) and π _S (S). For integer i, $1 \leq i \leq \lfloor \frac {S-1}{2} \rfloor$, assume we know π _j (S) for j<i and j>S−i. From Eq. 6, the system of equations for π _i (S) and π _S−i (S) are

$$\begin{array}{@{}rcl@{}} \pi_{S-i}(S) &=& \pi_{i}(S)\mathbb{P}(D\geq i) \\ &&+\mathbb{P}(D=i)\left( 1-\sum\limits_{k=0}^{i}\pi_{k}(S)\right), \\ \pi_{i}(S) &=& \pi_{S-i}(S)\mathbb{P}(D\geq S-i) \\ &&+\mathbb{P}(D=S-i)\sum\limits_{k=S-i+1}^{S}\pi_{k}(S). \end{array} $$

The above system only depends on π _j (S) for j≤i and j≥S−i. By the induction assumption, the set of equations define a linear system in two equations and two unknowns. Solving this system yields expressions for π _i (S) and π _S−i (S) as specified in Proposition 1. If S is odd, by induction on i, we are done. If S is even, there is an odd number of probability terms π _i (S). Using the normalization condition, $\pi _{\frac {S}{2}}(S)=1-{\sum }_{j \neq \frac {S}{2}}\pi _j(S)$. □

Proof Proof of Proposition 2:

To find the optimal S, consider the forward difference of C(S) defined as ${\Delta }\mathcal {C}(S)=\mathcal {C}(S+1)-\mathcal {C}(S)$. From Eq. 7,

$$\begin{array}{@{}rcl@{}} {\Delta} \mathcal{C}(S) &=& \frac{c}{T} + \left( \sum\limits_{i=0}^{S+1}\pi_{i}(S+1) \beta(i) \mathbb{E}\left[(D-i)^{+}\right] \right. \\ &&\qquad\qquad \left. - \sum\limits_{i=0}^{S} \pi_{i}(S) \beta(i)\mathbb{E}\left[(D-i)^{+}\right]\right). \end{array} $$

(14)

Substituting S=0 into Eq. 14,

$$\begin{array}{@{}rcl@{}} {\Delta} \mathcal{C}(0) & \,=\, & \frac{c}{T}\,+\,(\pi_{0}(1)\beta(0)\mathbb{E}[D]\,+\,\pi_{1}(1)\beta(1)\mathbb{E}\left[(D-1)^{+}\right] \\ &&\qquad\quad-\pi_{0}(0) \beta(0)\mathbb{E}[D])\\ & = & \frac{c}{T}+\; \pi_{1}(1) (\beta(1)\mathbb{E}\left[(D-1)^{+}\right]- \beta(0)\mathbb{E}[D]) \\ & \,=\, & \frac{c}{T}\,-\,\; \pi_{1}(1) ((\beta(0) \,-\, \beta(1))\mathbb{E}[D] \,+\, \beta(1) \mathbb{P}(D \!\geq\! 1) ) \end{array} $$

where $\mathbb {E}[D] = {\sum }_{i=0}^{\infty } \mathbb {P}(D > i) = {\sum }_{i=1}^{\infty } \mathbb {P}(D > i) + \mathbb {P}(D \geq 1)= \mathbb {E}[(D-1)^+] + \mathbb {P}(D \geq 1)$. Then because of our assumption of non-increasing stockout costs, $\mathbb {P}(D\geq 1)> \frac {c - (\beta (0)-\beta (1))\mathbb {E}[D]}{\beta (1) T - c}$. From Proposition 1 for S=1,

$$\pi_{0}(1) = 1 - \pi_{1}(1) \text{ and } \pi_{1}(1) = \frac{1}{1 + \mathbb{P}(D \geq 1)}. $$

Substituting for π ₁(1) and simplifying gives

$${\Delta} \mathcal{C}(0) = \frac{c}{T}- \frac{ (\beta(0) - \beta(1))\mathbb{E}[D] + \beta(1) \mathbb{P}(D \geq 1)}{1+\mathbb{P}(D \geq 1)}. $$

If $\mathbb {P}(D\geq 1)> \frac {c - (\beta (0)-\beta (1))\mathbb {E}[D]}{\beta (1) T - c}$, ${\Delta } \mathcal {C}(0) < 0$.

Now consider $\lim _{S \to \infty } {\Delta } \mathcal {C}(S)$.

$$\begin{array}{@{}rcl@{}} &&\underset{S \to \infty}{\lim} {\Delta} \mathcal{C}(S) \\ &=&\frac{c}{T} + \underset{S\to \infty}{\lim}\left( \sum\limits_{i=0}^{S+1} \pi_{i}(S+1) \beta(i)\mathbb{E}\left[(D-i)^{+}\right] \right. \\ &&\qquad\qquad\qquad\quad \left. -\sum\limits_{i=0}^{S} \pi_{i}(S)\beta(i)\mathbb{E}\left[(D-i)^{+}\right]\right), \\ &=& \frac{c}{T}+ \underset{S\to \infty}{\lim} \pi_{S+1} \beta_{S+1}(S+1)\mathbb{E}\left[(D-(S+1))^{+}\right] \\ &&\qquad + \underset{S\to \infty}{\lim} \sum\limits_{i=0}^{S} \beta(i) (\pi_{i}(S+1)-\pi_{i}(S))\mathbb{E}\left[(D-i)^{+}\right]. \end{array} $$

Using Lemma 1 and taking the limit as S→∞, we get

$$\begin{array}{@{}rcl@{}} &&\underset{S \to \infty}{\lim} {\Delta} \mathcal{C}(S) \\ &=& \frac{c}{T}+ \underset{S\to \infty}{\lim} \frac{\beta_{S+1}\mathbb{P}(D=0)\mathbb{E}\left[(D-(S+1))^{+}\right]}{1-\mathbb{P}(D\geq S)(1-\mathbb{P}(D=0))} \\ &&\qquad + \sum\limits_{i=0}^{\infty} \beta(i) (\pi_{i}(\infty)-\pi_{i}(\infty))\mathbb{E}\left[(D-i)^{+}\right]\\ &=& \frac{c}{T}+ \underset{S\to \infty}{\lim} \frac{\beta_{S+1}\mathbb{P}(D=0)\mathbb{E}\left[(D-(S+1))^{+}\right]}{1-\mathbb{P}(D\geq S)(1-\mathbb{P}(D=0))} \end{array} $$

Since β _S+1 is bounded below by zero or some positive constant, say $\underline {\beta }$,

$$\begin{array}{@{}rcl@{}} &&\underset{S \to \infty}{\lim} {\Delta} \mathcal{C}(S) \\ &\geq& \frac{c}{T}+ \; \underline{\beta}\mathbb{P}(D=0) \left( \underset{S\to \infty}{\lim}\mathbb{E}\left[(D-(S+1))^{+}\right] \right)\\ &=& \frac{c}{T}. \end{array} $$

Therefore, there exists some S ^∗ such that ${\Delta } \mathcal {C}(\hat {S}-1) < 0$ and ${\Delta } \mathcal {C}(\hat {S}) \geq 0$ for $S^{*}=\hat {S}$ or $\hat {S}-1$. □

Proof Proof of Proposition 3:

Let d=(d ₁,d ₂,…,d _τ ) represent a vector of demand realizations for t=1,…,τ. Let the expected conditional stockout cost for the base-stock level S, be defined as

$$ \bar{L}_{\tau}(S|D=\mathbf{d})=\frac{1}{\tau}\sum\limits_{t=1}^{\tau}\beta \left( {y_{t}^{S}}\right)\left( d_{t}-{y_{t}^{S}}\right)^{+}, $$

(15)

where $y_t^S$ is the amount of inventory available for use at the beginning of day t.

From Lemma 3.1 in [16] and for any set of demand realizations d, $y_t^S \leq y_t^{S+1} \leq y_t^S +1$ as long as the initial on-hand inventory is $y_1^S=S$ and $y_1^{S+1}=S+1$, respectively. Thus, at any time t, the difference in the number of units at the hospital using base-stock policy S+1 versus S is at most, one. From Lemma 3.2 in [16], for a constant lead-time of one period, two scenarios can occur.

• 1. If $y_t^S=y_t^{S+1}+1$ then the total number of shortages in period t−1 was not reduced using base-stock level S+1 instead of S.

• 2. If $y_t^S=y_t^{S+1}$ then the total number of shortages in period t−1 was reduced using base-stock level S+1 instead of S.

Lemmas 3.1 and 3.2 can be used in a similar induction proof on τ as Theorem 3.3 in [16] to demonstrate $\tau \bar {L}_{\tau }(S|D=\mathbf {d}) \geq \tau \bar {L}_{\tau }(S+1|D=\mathbf {d})$ for every τ≥1. Thus, $\bar {L}_{\tau }(S|D=\mathbf {d})$ is less than $\bar {L}_{\tau }(S+1|D=\mathbf {d})$ at every time point and on every sample path. Consider any set of random variables whose long-run distributions are the stationary distributions for the amount of inventory available for use at the beginning of day. For our system, this stationary distribution exists and is equal to π(S)=(π ₀(S),π ₁(S),…,π _S (S))). The monotonicity of the long-run average stockout cost (i.e., the expected stockout cost) is a direct consequence of the existence of this distribution and the finite-horizon monotonicity result. □

Proof Proof of Proposition 4:

Since $\mathcal {C}_U(S)$ and $\mathcal {C}_L(S)$ have state-independent stockout costs, they are both convex in S [16]. As a result, there exists base-stock levels S _L and S _U such that

$$\begin{array}{@{}rcl@{}} S_{L} &=& \min \left\{S \;\; \left| \;\; \mathcal{C}_{L}(S)\leq \mathcal{C}_{L}(j), \;\; \forall j\right.\right\},\\ S_{U} &=& \min \left\{S \;\; \left|\;\; \mathcal{C}_{U}(S)\leq \mathcal{C}_{U}(j), \;\;\forall j\right.\right\}. \end{array} $$

By definition, $\mathcal {C}_L(S) \leq C(S) \leq \mathcal {C}_U(S)$, ∀S and any S that minimizes $\mathcal {C}(S)$ satisfies 0≤S _L ≤S≤S _U <∞. □

Proof Proof of Proposition 5:

Consider IS1. Suppose that we do not allow substitution and assume that the demand for IS1 is actually $\overline {D} \equiv D_1+D_2$. That is, the demand for IS1 without substitution is equal to the sum of the demand for IS1 and IS2 in the original problem. It is apparent that $\overline {D}$ stochastically dominates the actual demand distribution for IS1 in a system with stockout-based substitution. Using $\overline {D}$ and setting $\beta _1^U=\beta _1(0)$, we solve (9) which is discretely convex in S ₁. The resulting optimal base-stock level, $S_1^U$, is an upper bound for the original problem where the demand for IS1 is D ₁ and substitution is allowed. A similar results holds for IS2. □

Appendix B: Sample path convexity counterexample

Let d=(d ₁,d ₂,…,d _τ ) represent a vector of demand realizations over time horizon t=1,…,τ. The average conditional stockout cost, dependent on the base-stock level S as defined in Eq. 15 is

$$\bar{L}_{\tau}(S|D=d)=\frac{1}{\tau}\sum\limits_{t=1}^{\tau}\beta \left( {y_{t}^{S}}\right)\left( d_{t}-{y_{t}^{S}}\right)^{+}, $$

where $y_t^S$ is the amount of inventory available for use at the beginning of day t when there are S total units in the system. Consider a system with 10, 11 and 12 instrument sets, respectively and a demand realization vector of d=(4,7,5,0). Table 8 presents the number of instrument sets at the sterilization facility, at the hospital and $t \bar {L}_t(\cdot |D=d)$ for each period.

Table 8 A counter example used to demonstrate that convexity cannot be proven using a sample path approach

To prove convexity for τ=5, we must show that

$$\begin{array}{@{}rcl@{}} &&\bar{L}_{5}(10|D=d) -\bar{L}_{5}(11|D=d) \geq \bar{L}_{5}(11|D=d)\\ &&-\bar{L}_{5}(12|D=d) \\ &&\Longrightarrow \beta(6) + \beta(4) - \beta(4) \geq \beta(4) - 0\\ &&\Longrightarrow \beta(6) \geq \beta(4) \end{array} $$

As we assumed β(i)≥β(i+1), we obtain a contradiction.

Appendix C: Transition matrix updating algorithm

Let the diagonal of a matrix refer to the entries from the lower left element to the upper right element. Let the sub-diagonal of a matrix refer to all entries below and to the right of the diagonal. As in Section 4.2, we assume two only only two instrument sets are available. The inventory state of instrument set 1 (IS1) and instrument set 2 (IS2) on day t is i=(i ₁,i ₂) and day t+1 is j=(j ₁,j ₂). Let Q _{i j} be the state transition matrix when stockout-based substitution is assumed to occur.

Lemma 2

Given base-stock levels S ₁ >0 and S ₂ >0, Q _{i j} is a (S ₁ +1)×(S ₁ +1) matrix composed of (S ₂ +1)×(S ₂ +1) sub-matrices. Further, the following four properties hold:

• 1. Sub-matrices above the diagonal of Q _{i j} are (S ₂ +1)×(S ₂ +1) zero-matrices.

• 2. Sub-matrices along and below the diagonal of Q _{i ji} are (S ₂ +1)×(S ₂ +1) matrices where all elements above the diagonal are zero.

• 3. For each sub-matrix along the diagonal of Q _ij :

  • The diagonal elements are associated with events where i ₁ +j ₁ =S ₁ and i ₂ +j ₂ =S ₂.

  • The sub-diagonal elements are associated with events where i ₁ +j ₁ =S ₁ and i ₂ +j ₂ >S ₂.

• 4. For each sub-matrix below the diagonal of Q _ij :

  • The diagonal elements are associated with events where i ₁ +j ₁ >S ₁ and i ₂ +j ₂ =S ₂.

  • The sub-diagonal elements are associated with events where i ₁ +j ₁ >S ₁ and i ₂ +j ₂ >S ₂.

Proof

The rows of Q _{i j} define the system state on day t and the columns day t+1. For each i ₁, the rows of Q _{i j} are organized as i=(i ₁,i ₂) for all i ₂=0,…,S ₂. For each j ₁, the columns of Q _{i j} are organized as j=(j ₁,j ₂) for all j ₂=0,…,S ₂. The properties discussed in the lemma follow directly from this representation of the transition matrix. □

Using Lemma 2, we propose an algorithm for updating Q _{i j} when the base-stock level for either IS1 or IS2 increases by one. Let the current base-stock levels be S ₁ and S ₂. Let the new base-stock levels be S1′ and S2′. Let Q _{i j} and Q i j′ represent the current and new transition matrix, respectively.

IS1 increases by one unit {( S1′, S2′) = ( S ₁ + 1 , S ₂ )}::

From Lemma 2, Q i j′ is now a (S1′+1)×(S1′+1) matrix composed of (S ₂+1)×(S ₂+1) sub-matrices.

• 1. Let C ₁ be a column vector of length S1′. Each entry of C ₁ is a (S ₂+1)×(S ₂+1) matrix calculated using (3) while fixing j ₁ = S1′ for i ₁=0,…,S ₁.

• 2. Let R ₁ be a row vector of length S1′. Each entry of R ₁ is a (S ₂+1)×(S ₂+1) matrix calculated using (3) while fixing i ₁ = S1′ for j ₁=0,…,S ₁.

• 3. Let E ₁ be a (S ₂+1)×(S ₂+1) matrix calculated using (3) fixing i ₁ = S1′ and j ₁ = S1′.

• 4. Let Q i j0 be equal to Q _{i j} except that the diagonal sub-matrices of Q _{i j} are replaced by (S ₂+1)×(S ₂+1) zero matrices.

The new transition matrix now becomes

$$Q_{\mathbf{i}\mathbf{j}}^{\prime} = \left( \begin{array}{cc} {Q_{\mathbf{i}\mathbf{j}}^{0}} & {\mathbf{C_{1}}}\\ {\mathbf{R_{1}}} & \mathbf{E_{1}} \end{array}\right). $$

IS2 increases by one unit {( S1′, S2′) = ( S ₁ , S ₂ + 1 )}::

Let $q_{\mathbf {i}_1\mathbf {j_1}}$ and $q_{\mathbf {i}_1\mathbf {j}_1}^{\prime }$ be sub-matrices, for a given i ₁ and j ₁, of Q _{i j} and Q i j′, respectively. From Lemma 2, Q i j′ is now a (S ₁+1)×(S ₁+1) matrix composed of (S2′+1)×(S2′+1) sub-matrices. Each sub-matrix is updated as follows.

• 1. Let C ₂ be a column vector of length S2′. Each entry of C ₂ is a (S ₁+1)×(S ₁+1) matrix calculated using (3) while fixing j ₂ = S2′ for i ₂=0,…,S ₂.

• 2. Let R ₂ be a row vector of length S2′. Each entry of R ₂ is a (S ₁+1)×(S ₁+1) matrix calculated using (3) while fixing i ₂ = S2′ for j ₂=0,…,S ₂.

• 3. Let E ₂ be a (S ₁+1)×(S ₁+1) matrix calculated using (3) fixing i ₂ = S2′ and j ₂ = S2′.

• 4. Let $q_{\mathbf {i}_1\mathbf {j}_1}^0$ be equal to $q_{\mathbf {i}_1\mathbf {j}_1}$ except that the diagonal entries of $q_{\mathbf {i}_1\mathbf {j}_1}$ are replaced by zeros.

The new sub-matrix matrix now becomes

$$q_{\mathbf{i}_{1}\mathbf{j}_{1}}^{\prime} = \left( \begin{array}{cc} {q_{\mathbf{i}_{1}\mathbf{j}_{1}}^{0}} & {\mathbf{C_{2}}}\\ {\mathbf{R_{2}}}& \mathbf{E_{2}} \end{array}\right). $$