1 Introduction

We consider a surgical department where elective, urgent and semi-urgent (synonym: semi-elective) patients are treated. An example of a department with such characteristics is a neurosurgery department. Urgent treatment is, among others, required for ruptured aneurysms, epidural or subdural hematomas, cauda equina syndrome, and (instable) spine fractures compromising the myelum or cauda equina. Semi-urgent pathologies include, among others, intracranial oncology, spine fractures with no or minimal neurological symptoms, drain dysfunctionalities, and disc herniations with unbearable pain or severe neurological deficits. Apart from these pathologies, the majority of neurosurgery patients do not require surgery within one or 2 weeks, and these are regarded as elective.

There is a definite trade-off between two major intertwined issues with respect to available surgical capacity: allocation of capacity to surgical departments and optimization of the surgical schedule within departments. On the one hand, when the target is minimal use of surgical resources, a more efficient surgical schedule may reduce the slack in the schedule, and therefore reduce the required capacity while keeping the societal costs due to patient cancellation and waiting constant. On the other hand, when the target is minimal societal costs due to patient cancellation and waiting, a more efficient surgical schedule may reduce these while keeping the allocated surgical resources constant. The trade-off is thus between societal costs and required surgical capacity. Allocating capacity to a surgical department usually is subject to additional constraints such as the restriction in the total available time, the time allocated to other departments, labor regulations (e.g., opening hours of the operating theater), staff restrictions (e.g., available number of surgeons), and the possibility to handle exceptions (e.g., in over-time).

In this paper we take the capacity allocated to a surgical department as a starting point. We aim for robust patient scheduling schemes. We focus on the setting of a neurosurgery department treating urgent, semi-urgent and elective patients. Urgent patients are usually treated in a separate operating room (OR), but semi-urgent patients need to be fitted in the regular OR schedule. When a semi-urgent patient arrives, an elective patient is canceled to accommodate this (prioritized) patient. The cancellation of a surgery negatively affects the patient [1]. Medical professionals tend to feel sorry for the canceled patient and aim to reschedule the surgery as soon as possible. Thus, a canceled elective patient receives a semi-urgent status, and rescheduling this surgery possibly causes the cancellation of another elective patient. This knock-on effect results in a clear dependency between semi-urgent patient arrivals and cancellation of elective patients in subsequent weeks.

Several strategies are known from literature to cope with non-elective patients. One strategy is to reserve a small amount of time for emergency patients for whom surgery is required on the day of arrival in each elective patient OR [2], instead of dedicating one or several ORs to emergent cases [3]. Another possibility is to determine the elective patient schedule given the expected number of emergencies [4]. In all papers reviewed in [5], acute cases have to be performed at least on the day of arrival, as opposed to the semi-urgent surgeries that are studied in this paper. In both [3] and [6] the authors distinguish between emergency surgeries (which have to be performed now) and urgent surgeries (which have to be performed within a day). In [4] and [7] stochastic programming is applied to support the scheduling of add-on cases, but in both papers these cases have to be completed on the day of arrival.

In [8] the authors start from a different viewpoint and determine, using a simulation model, how many elective cases can be performed in a dedicated orthopedic trauma OR. They state that when elective patients are willing to accept that their surgery might be canceled because of an incoming trauma patient, a higher throughput can be achieved. In [9] a trade-off is made between overtime and unused OR time. The paper has an operational viewpoint, by scheduling patients on an individual level. This is similar to the methodology presented in [10], where mathematical algorithms are used to schedule individual cases in available OR blocks.

The problem setting described here shows a similarity with the news vendor problem, where at the start of each decision period for that period the available capacity is matched with the required resources, and unmatched requests are discarded at the end of the period (see e.g. [9, 11–13] for news vendor problems applied to OR problems). The news vendor problem does not incorporate scheduling of discarded requests in subsequent periods, which is precisely the problem when elective surgeries are canceled and re-scheduled in subsequent periods. Modeling this knock-on effect is the natural domain of queuing theory. In this paper, we therefore invoke the powerful theory of queues to analyze the cancellation rate of elective patients given a pre-specified surgical capacity, and the influence of canceling patients on the cancellation rate in the future.

For a surgical department with given capacity handling elective, urgent and semi-urgent patients, this paper investigates reservation schemes of OR time for semi-urgent surgeries. As the arrival pattern of semi-urgent patients is unpredictable, the reserved OR may remain unused since elective patients cannot be scheduled so shortly before their surgery. We study the trade-off between cancellations of elective surgeries due to semi-urgent surgeries, and unused OR time due to excessive reservation of OR time for semi-urgent surgeries.

In the next section we first evaluate, using a queuing theory framework, the long run OR capacity needed to accommodate every incoming semi-urgent surgery. Second, we introduce another queuing model that enables a trade-off between the cancellation rate of elective surgeries and unused OR time. In Section 3 we develop a decision support tool, based on Markov decision theory, that assists the scheduling process of elective and semi-urgent surgeries. We demonstrate our results in Section 4 with actual data obtained from a department of neurosurgery, followed by the discussion and conclusion in Section 5.

2 Model and long term behavior

The goal of the strategic model presented in this section is to provide an estimate for the amount of OR time that should be reserved for all semi-urgent surgeries in the long run. Therefore, we do not distinguish between the 1- and 2-week streams or take overtime into account. These components of the problem are discussed in the tactical model presented in Section 3. Obviously, dynamically adjusting the amount of reserved OR time according to the effectuated inflow of semi-urgent surgeries would result in little unused OR time. However, given hospital policy that dictates that elective patients should be planned weeks in advance, such an adaptive policy would impose canceling the elective patients that were planned in the claimed slots. In order to make the trade-off between cancellation of surgeries and unused OR capacity, a constant amount of OR time is reserved for semi-urgent surgeries.

A summary of the notation used is listed in Table 1.

Table 1 Notation introduced in Section 2
Full size table

2.1 Assumptions and model parameters

The time available per OR day is divided into K slots of equal length. Surgeries can have a duration of 1,2,..,K slots (K < ∞), and are categorized according to this duration.

When a surgery has an expected duration of more than K slots, it is also included into the category of surgeries with length K slots. The total number of OR slots assigned to the department per week (m) equals the number of OR days per week multiplied by K. In order to accommodate semi-urgent patients, every week a fixed number of slots (s) is reserved (0 ≤ s ≤ m). Given the impact of the surgery on the patient and the undesirability of performing semi-urgent surgeries in overtime, we assume, in line with medical practice (see Section 1), that canceled elective patients become semi-urgent patients the following week. These patients need to undergo surgery within 1 week of their canceled surgery.

2.1.1 Progression of the number of semi-urgent slots

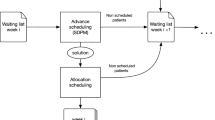
We focus on the number of semi-urgent slots waiting at the start of week n (W n ). This equals the amount of semi-urgent slots that arrived during the previous week (R n − 1) plus the elective slots that were canceled during the previous week in order to accommodate surplus semi-urgent slots. Elective slots are canceled if the reserved capacity for semi-urgent slots is insufficient. Recall that, in accordance with medical practice, the canceled elective slots from week n become semi-urgent slots in week n + 1. Therefore, for our analysis of W n , elective slots are not canceled, but instead the surplus semi-urgent slots from week n are transferred to week n + 1. An example of the progression in the number of semi-urgent slots waiting at the start of week n is given in Fig. 1.

Fig. 1
figure 1

An example of the progression of the number of semi-urgent slots waiting at the start of the week (s  =  3)

Full size image

2.1.2 The arrival process

The number of arriving semi-urgent slots per week is equal to the sum of the number of slots per arriving patient. Patients arrive independently according to a Poisson process, furthermore the number of slots per arriving patient is random. Therefore we can model the arrival process with the compound Poisson process [14]. The arrival rate of semi-urgent patients is λ. Let p k denote the probability that an arriving semi-urgent surgery is of size k slots, k = 1,..,K. The generating function of the arrival process is [14]:

$$ \begin{array}{rll} P_R(z) & = & \sum\limits_{j=0}^{\infty} \mathbb{P}(R=j)z^j = e^{-\lambda (1 - \sum_{k=1}^K p_k z^k)}, \quad \mbox{where} \\ \sum\limits_{k=1}^K p_k & = & 1, \quad \mbox{and} \quad |z| \leq 1. \end{array} $$
(1)

2.2 Stability of the system

From the description in Subsection 2.1.1 (see also Fig. 1) it is clear that the number of semi-urgent slots waiting at the start of week n + 1 equals the number of semi-urgent slots that arrived during week n plus the number of surplus semi-urgent slots of week n:

$$ W_{n+1} = R_n + \{W_n - s\}^+, \,\,\, n = 1,2,... \quad \mbox{and} \quad W_1 = R_0, $$

where {x} +  = 0 if x < 0 and x otherwise. This is the Lindley equation for the sojourn time in a GI/G/1 queue [15]. The limit for n → ∞ on W n + 1 converges in distribution to W if \(\mathbb{E}[R] < s\), and therefore we can conclude that as long as the expected weekly amount of semi-urgent slot arrivals, \(\mathbb{E}[R]\), is strictly smaller than the number of slots allocated to semi-urgent surgeries, s, the system is stable and the capacity reserved for these slots should be sufficient on average. It follows that there is a minimum amount of capacity (s min ) that should be reserved for semi-urgent surgeries: \(s_{min} = \left\lceil \mathbb{E}[R]\right\rceil\), where \(\left\lceil x \right\rceil\) equals x rounded up to the nearest integer.

2.3 Stationary distribution of the number of semi-urgent slots waiting

At the start of every week the state of the system is inspected. We represent the system by a slotted queuing model in discrete time [16]. We can distinguish between two situations: (1) more semi-urgent slots are waiting than can be completed in one week (epochs 2–6 and 9 in Fig. 1), and (2) less (epoch 7 in Fig. 1) or an equal amount of semi-urgent slots are waiting (epoch 8 in Fig. 1) than can be completed. We obtain the following expressions for the transition probabilities:

$$ \begin{array}{rll} \mathbb{P}(W_{n+1}&=&w_{n+1}|W_n=w_n) \\ &=& \left\{ \begin{array}{l l} \mathbb{P}(R_{n}=w_{n+1}-w_n+s) &\quad \mbox{if} \quad w_n - s > 0 \\ \mathbb{P}(R_{n}=w_{n+1}) &\quad \mbox{otherwise}. \\ \end{array} \right. \end{array} $$

Define P as the matrix with transition probabilities. Let \(\textbf{q} = \left( q_0 \quad q_1 \quad \cdots \right)\) denote the equilibrium distribution of W, the number of semi-urgent slots waiting at the start of a week, where q i  = ℙ(W = i). The q i ’s can be computed as \(\textbf{q} = \textbf{q}P\). An expression for the generating function of the equilibrium probabilities q i is [16]:

$$ P_{W}(z) = \frac{P_R(z) \sum_{i=0}^{s-1}q_i (z^s - z^i)}{z^s - P_R(z)}, \quad |z| \leq 1, $$
(2)

with P R (z) as given in (1). To obtain an exact expression for P W (z) we have to determine the s unknows q 0, q 1,...,q s − 1. By Rouché’s Theorem [17] it can be shown that the denominator of P W (z) has s − 1 zeros inside the unit disk [18]. Since P W (z) is a generating function and therefore bounded for all |z| ≤ 1, the zeros of the denominator are zeros of the numerator as well [16]. Thus we obtain s − 1 equations for the s unknowns q 0, q 1,...,q s − 1. To derive the last equation, we use that P W (1) = 1. In order to find the s − 1 zeros of the denominator of P W (z), we start by solving

$$ \begin{array}{rll} z^s - P_R(z) & = & 0, \quad \mbox{which is equivalent to} \\ z^s & = & e^{-\lambda\l\left(1 - \sum_{k=1}^K p_k z^k\right)}. \end{array} $$

We replace this equation by s − 1 equations, where each z j is a solution of the above equation [19]:

$$ z_j = F(z_j) e^{2\pi \tilde{\imath} \frac{j}{s}}, \quad \mbox{with} \quad F(z) = e^{-\frac{\lambda}{s}(1-\sum_{k=1}^K p_k z^k)}, $$

and \(\tilde{\imath} = \sqrt{-1}\). For each value of j (j = 1,2,...,s − 1), we numerically solve this equation by using fixed point iteration [20]:

$$ \begin{array}{rll} z_j^{(n+1)} &=& F\left(z_j^{(n)}\right) e^{2\pi \tilde{\imath} \frac{j}{s}}, \quad n=0,1,... \quad \mbox{and} \\ z_j^{(0)} &=& 0. \end{array} $$

The z j ’s that are found with this procedure are also zeros of the numerator of P W (z). We thus obtain s − 1 equations for the unknowns q 0,..,q s − 1 that with the added equation P W (1) = 1 define P W (z), |z| ≤ 1.

2.4 Performance measures

We are particularly interested in the expected number of canceled elective slots per work week (\(\mathbb{E}[N_{c}]\)), and the expected number of empty reserved semi-urgent slots per work week (\(\mathbb{E}[N_{e}]\)). For the latter it follows from (2) and P W (1) = P R (1) = 1 that

$$ \mathbb{E}[N_{e}] = \sum\limits_{i=0}^{s-1} (s-i) q_i = s - \mathbb{E}[R]. $$

The expected number of elective slots that are canceled per week equals

$$ \begin{array}{rll} \mathbb{E}[N_{c}] & = & \sum\limits_{i=s}^{\infty} (i-s) q_i = \sum\limits_{i=0}^{\infty} i q_i - s + \sum\limits_{i=0}^{s-1} (s-i) q_i \\ & = & P_{W}^{'}(1) - \mathbb{E}[R]. \end{array} $$

Since

$$ \begin{array}{rll} P_{W}^{'}(1) &=& \mathbb{E}[R] \\ &&+\, \frac{\sum_{i=0}^{s-1} q_i (s^2 - i^2 - s + i) - s^2 + s + P_R^{\prime\prime}(1)}{2(s-\mathbb{E}[R])}, \end{array} $$

where

$$ P_R^{\prime\prime}(1) = \lambda \sum\limits_{k=1}^K k(k-1) p_k + \mathbb{E}^2[R], $$

we see that

$$ \mathbb{E}[N_{c}] = \frac{\sum_{i=0}^{s-1} q_i (s^2 - i^2 - s + i) - s^2 + s + P_R^{\prime\prime}(1)}{2(s-\mathbb{E}[R])}. $$

2.5 Cost structure

Let C e and C c be the costs of one empty semi-urgent slot and one canceled elective slot. The expected total costs then equal

$$ \mathbb{E}[C_t] = \mathbb{E}[N_{e}] C_{e} + \mathbb{E}[N_{c}] C_{c}. $$

The optimal number of slots to reserve for semi-urgent surgeries (s *) depends on the choice of C e and C c , and is the value of s that minimizes \(\mathbb{E}[C_t]\).

3 Optimal allocation of surgery slots

Given the stochasticity of the arrival process of semi-urgent patients, there will be weeks when the allocated capacity s * is not sufficient. In this case the department can choose to perform the surplus semi-urgent patients this week, and cancel elective patients. On the other hand, the department can choose to postpone the semi-urgent surgeries until next week. A major drawback of this operational mode is that new semi-urgent patients arrive, who together with the postponed patients from this week, pose a huge demand on available resources. Furthermore, as mentioned in the introduction, if the number of semi-urgent slots waiting for treatment exceeds the weekly amount of OR slots available, semi-urgent surgeries have to be performed in overtime, which is very undesirable as well. In this section we describe a Markov decision model that provides a scheduling strategy for surplus semi-urgent slots, given the parameters obtained with the queuing model. A summary of the additional notation introduced in this section is given in Table 2.

Table 2 Additional notation introduced in Section 3
Full size table

3.1 Assumptions

In this model we employ a more detailed view of the process, and consider the inflow of the two types of semi-urgent surgeries separately: the first type of semi-urgent surgeries need to be performed within one week, the second type of semi-urgent surgeries need to be performed within two weeks. Given the system status at the beginning of week n, we decide how many 1- and 2-week semi-urgent slots should be performed this week. Since 1-week semi-urgent surgeries have to be performed this week, all incoming surgeries of this type are scheduled for this week. First the reserved slots (1,2,..,s *) are used, and if additional 1-week semi-urgent demand remains, elective slots are canceled.

One-week semi-urgent demand that is still unaccommodated is performed in overtime. There are several options for scheduling 2-week patients. A logical choice would be to first schedule all 1-week slots, then schedule 2-week slots in the reserved slots of this week that are still available. Subsequently, it has to be decided whether to perform the remaining 2-week slots either this or next week. If the remaining 2-week slots are scheduled for next week, no elective slots have to be canceled this week. On the other hand, postponed 2-week semi-urgent slots have evolved into 1-week semi-urgent slots the next week. The existence of these slots, together with newly arrived 1-week semi-urgent slots, can result in a vast amount of semi-urgent demand that possibly has to be treated in overtime. In this section, a Markov decision model is presented that enables a trade-off between these two factors. For an overview of Markov decision theory, see [21]. In the model, we make the following assumptions:

  • All 1-week semi-urgent slots are planned this week.

  • Two week semi-urgent slots not planned this week become 1-week semi-urgent slots next week.

  • Elective slots canceled this week become 2-week semi-urgent slots next week.

3.2 The Markov decision model

We use a Markov decision model with infinite planning horizon to support the department in deciding how many 2-week slots should be planned in a certain week (action a n ). The system state at the start of week n, (n = 0,1,..., ∞ ), is given by w n = (w1 n , w2 n ), where w1 n and w2 n are the number of 1- and 2-week semi-urgent slots waiting at that moment. The action chosen depends on the number of 2-week slots waiting and on the part of capacity that is already allocated to 1-week slots. Summarizing, the range for action a n is determined by \((0,1,..,\mbox{min}(w2_n,(m-w1_n)^+))\).

3.2.1 Transition probabilities

Let the random variables R1 n and R2 n denote the number of 1- and 2-week semi-urgent slot arrivals during week n, where R1 n  + R2 n  = R n . Similarly to the queuing model presented in Section 2, R1 and R2 follow a compound Poisson distribution, with arrival rates λ 1 and λ 2, and p 1k and p 2k the probability that a 1- and 2-week surgery is of length k slots.

Recall that m slots are available each week for both elective and semi-urgent surgeries. Therefore, when the number of 1-week semi-urgent slots waiting exceeds m, or when the sum of 1- and 2-week semi-urgent slots waiting exceeds 2m, the surplus semi-urgent slots are performed in overtime. Figure 2 shows how the number of slots performed in overtime is calculated. In our model, we take into account the overtime by including (high) costs for each overtime surgery slot. However, the slots performed in overtime do not affect the system state, as they have left the system in the subsequent week. Thus, the state space A of the system is described as follows:

$$ \begin{array}{rll} A&=&\{w=(w1,w2): w1,w2=0,1,\ldots; \\ &&w1\leq m; w1+w2\leq 2m\}. \end{array} $$

The state space is depicted in Fig. 3. The areas B,C and D and the arrows correspond to the three different cases of handling the overtime slots (see also Fig. 2). For notational purposes, let

$$ \begin{array}{lll} &&{\kern-6pt}\mathbb{P}(w_n|w_{n-1},a) \\ &&= \mathbb{P}(W1_n=w1_n,W2_n=w2_n \big| W1_{n-1}=w1_{n-1}, \\ &&\phantom{= \mathbb{P}(}W2_{n-1} = w2_{n-1}, a_{n-1}=a). \end{array} $$

Now we define these transition probabilities for each w n  ∈ A.

Fig. 2
figure 2

Number of semi-urgent slots performed in overtime: three different cases

Full size image
Fig. 3
figure 3

State space of the system

Full size image

If w1 n  < m and w1 n  + w2 n  < 2m then no slots are performed in overtime in week n and thus we have

$$ \begin{array}{rll} \mathbb{P}(w_n|w_{n-1},a) &= & \mathbb{P}(R1_{n-1}=w1_n-w2_{n-1}+a) \\ && \times \,\mathbb{P}(R2_{n-1}\! =\! w2_n - (w1_{n-1}-s+a)^+), \\ && w1_n<m, w1_n+w2_n<2m, \end{array} $$

and \((w1_{n-1}-s+a)^+\) is the number of canceled elective slots.

Now, assume that at the start of week n we have w1 1-week semi-urgent slots and w2 2-week semi-urgent slots waiting. If w = (w1,w2) ∈ B then some slots have to be performed in overtime as explained above. Thus, according to the overtime policy depicted in Fig. 2, the next state is given by w1 n  = w1, w2 n  = 2m − w1 n , a point on the boundary between A and B, as pointed out with arrows in Fig. 3. Including this into transition probabilities, we derive

$$ \begin{array}{rll} \mathbb{P}(w_n|w_{n-1},a) &=& \mathbb{P}(R1_{n-1}=w1_n-w2_{n-1}+a) \\ & &\times\,\mathbb{P}(R2_{n-1} \geq w2_n \!-\! (w1_{n-1}-s+a)^+), \\ w1_n&<&m, w1_n+w2_n=2m. \end{array} $$

Analogously, if at the start of week n the number of waiting semi-urgent slots is described by w ∈ C, then the next state is w n  = (m,m), and thus the transition probabilities for this state are given by

$$ \begin{array}{rll} \mathbb{P}(w_n|w_{n-1},a) &=& \mathbb{P}(R1_{n-1} \geq w1_n-w2_{n-1}+a) \\ && \times \,\mathbb{P}(R2_{n-1} \geq w2_n \!-\! (w1_{n-1}-s+a)^+), \\ w_n&=&(m,m). \end{array} $$

Finally, w ∈ D will result in the state with w1 n  = m, and we obtain

$$ \begin{array}{rll} \mathbb{P}(w_n|w_{n-1},a) &=& \mathbb{P}(R1_{n-1} \geq w1_n-w2_{n-1}+a) \\ && \times \,\mathbb{P}(R2_{n-1} = w2_n \!-\! (w1_{n-1}-s+a)^+), \\ w1_n&=&m, w2_n<m. \end{array} $$

Note that ℙ(R1 n  ≤ x) = ℙ(R2 n  ≤ x) = 0 if x < 0.

3.2.2 Performance measures

The performance measures that were introduced for the queuing model are calculated on a weekly basis. Given the state w n  = (w1 n ,w2 n ) and action a, the number of unused reserved semi-urgent slots and the number of canceled electives can be established as follows:

$$ \begin{array}{rll} N_{e,n} & = & (s - w1_n - a)^+, \quad \mbox{and} \\ N_{c,n} & = & (w1_n - s + a)^+. \end{array} $$

Besides, we introduce a new performance measure, \(\mathbb{E}[N_{o}]\) the expected number of semi-urgent slots that have to be performed in overtime next week as a consequence of the chosen action of this week. In week n, this amount depends on the number of slots at the start of week n, as described in Fig. 2. The formula for computing E[N o,n + 1|w n ,a] is given in Eq. 3.

$$ \begin{array}{rll} \label{EN1} \mathbb{E}[N_{o,n+1}|w_n,a] & = & \sum\limits_{\mathop{w1< m}\limits_{w1+w2>2m }} (w1 + w2 - 2m) \times \mathbb{P}(R1_{n}=w1-w2_{n}+a) \quad\mathbb{P}(R2_{n} = w2 - (w1_{n}-s+a)^+) \\ && + \sum\limits_{\mathop{w1 > m} \limits_{w1+w2>2m}} (w1 + w2 - 2m) \times \mathbb{P}(R1_{n}=w1-w2_{n}+a) \quad\mathbb{P}(R2_{n} = w2 - (w1_{n}-s+a)^+) \\ && + \sum\limits_{\mathop{w1>m} \limits_{w2<m}} (w1 - m) \times \mathbb{P}(R1_{n}=w1-w2_{n}+a) \quad\mathbb{P}(R2_{n-1} = w2 - (w1_{n}-s+a)^+). \end{array} $$
(3)

3.2.3 Cost structure

The costs incurred for unused semi-urgent slots (C e ) and canceled elective slots (C c ) are equivalent with those introduced in Section 2. An extra cost, C o , for performing 1- and 2-week slots in overtime is introduced. The expected total costs incurred in week n equal

$$ \mathbb{E}[C_{t,n}] = \mathbb{E}[N_{e,n}] C_{e} + \mathbb{E}[N_{c,n}] C_{c} + \mathbb{E}[N_{o,n+1}] C_{o}. $$

3.3 Determination of optimal policy

In the process of coming to an optimal policy δ * that defines an optimal action for each state w n , we want to take into account the costs incurred today and in the future. However, we consider the costs experienced today as being more important than those experienced in the future. Therefore we use discount factor α, α ∈ (0,1), in order to recalculate future costs to the cost level of today. Define V δ (w 0) as the expected discounted costs over an infinite horizon, given initial state w 0:

$$ V_{\delta}(w_0) = \mathbb{E}_{\delta} \left[ \sum\limits_{n=0}^{\infty} \alpha^n C_{t,n} \left(W_n,a_n \right) | w_0 \right]. $$

Let V(w 0) denote the minimal value of V δ (w 0):

$$ V(w_0) = \min\limits_{\delta} \quad V_{\delta}(w_0). $$

For each initial state w 0 and every action a, in an optimal policy it should hold that

$$ V(w_0) \leq C_{t,0} \left(w_0,a_0 \right) + \alpha \sum\limits_{w_1} \mathbb{P}(w_1|w_0,a) V(w_1). $$

This gives us the optimality equation

$$ V(w_0) = \min\limits_{a \in \delta} \, \left\{C_{t,0} \left(w_0,a_0 \right) + \alpha \sum\limits_{w_1} \mathbb{P} (w_1|w_0,a) V(w_1) \right\}. $$

The optimal policy δ * consists of the values of a that solve the optimality equation for each state. In order to find an optimal policy δ *, we use the policy iteration algorithm [22]. Since the state and action space are finite, the policy iteration algorithm converges in a finite number of steps.

Note that it is never optimal to perform 2-week slots in overtime, since even if they are postponed and then cannot be treated in regular time, they can be treated in overtime next week as well.

4 Capacity planning and scheduling at a Department of Neurosurgery

In this section we illustrate our modeling and optimization approach by considering a department of neurosurgery situated in an academic hospital in the Netherlands. Department staff feared that dedicating scarce OR time to the uncertain stream of semi-urgent patients would lead to an excessive amount of unused OR capacity, and therefore decided to plan almost only elective patients in the available OR time. As a consequence, in daily operation, a large portion of elective surgeries was canceled in order to accommodate semi-urgent surgeries. Furthermore, many ad hoc decisions were needed to ensure that all patients would receive the care they needed. Supported by our models, we show possibilities for improvement.

All surgeries performed by the department can be characterized by the estimated OR time as follows: a) one third of an OR day, b) two thirds of an OR day, c) one OR day, and d) more than one OR day. With this in mind the OR day is divided into three slots of equal length (K = 3). Type 1 surgeries have an estimated duration of one slot, type 2 of two slots, and type 3 surgeries an estimated duration of three or more slots. Therefore, it is either possible to perform in one OR day i) three type 1 surgeries, ii) one type 1 and one type 2 surgery, or iii) one type 3 surgery. The department is assigned eight OR days each week. With each day consisting of three slots, the department has 24 slots per week at its disposal (i.e. m = 24).

4.1 Data

The data needed for the model, semi-urgent patient arrivals, their expected surgery duration and semi-urgent state (i.e. surgery within one or two weeks) were recorded for a consecutive period of ten weeks. The characteristics of the arrival process are in line with the compound Poisson arrival process as outlined in [14]. Furthermore, the variance to mean ratio (vmr), defined as \(\frac{\sigma^2}{\mu}\), which equals 1 for the Poisson distribution, shows that modeling the patient arrival process at this department with a Poisson process gives a conservative estimate for the aggregated semi-urgent patient stream (vmr = 0.25, so the variance is lower than would be expected from the Poisson distribution), while it provides a good estimate for the 1-week semi-urgent patient flows (vmr = 1.03) and a slight conservative estimate for the 2-week semi-urgent patient flow (vmr = 0.76). Therefore we feel confident that the compound Poisson process is an appropriate choice for modeling the arrival process of semi-urgent surgeries at this department. Table 3 gives the parameter values derived from the data, used in the queuing model. Since in the Markov decision model a distinction is made between 1- and 2-week semi-urgent surgeries, different parameter values for the compound Poisson process apply (Table 4).

Table 3 Parameter values for queuing model (Section 2)
Full size table
Table 4 Parameter values for Markov decision model (Section 3)
Full size table

The cost parameters as defined in Sections 2 and 3 should be determined by the department, and depend on the emphasis the department wants to put on either canceling patients or having an empty OR. For example, when C e  = 10 and C c  = 1, having an empty semi-urgent slot is considered ten times worse than canceling one elective slot. Since the department considers performing semi-urgent slots in overtime as very undesirable, we emphasize on this by fixing C o on 100. We consider three combinations for C e and C c (Table 5). For the department under consideration, CC 1 is a reasonable cost configuration. To demonstrate our methodology we also use two other cost configurations.

Table 5 Cost combinations
Full size table

4.2 Determining the required number of semi-urgent slots

We start by calculating the minimal amount of semi-urgent slots required (s min ), which is equal to \(\left\lceil \mathbb{E}[R]\right\rceil\) (see Section 2.2). Since

$$ \mathbb{E}[R] = \lambda \sum\limits_{k=1}^K k p_k, $$

we have that \(s_{min} = \left\lceil 9.6 \right\rceil = 10\). The department estimated that approximately 40% of surgeries performed during regular OR days is of the semi-urgent type, which is supported by the data (\(\frac{9.6}{24} = 40\)%). Given that s may vary from s min to m, we obtain the results from Table 6. The optimal value of \(\mathbb{E}[C_t]\) for each cost combination is given in bold. Note the vast amount of canceled elective slots for s = 10. This shows that focusing on the average behavior of a system can result in unsatisfactory (and maybe unexpected) system outcomes. In Fig. 4 \(\mathbb{E}[N_{e}]\) and \(\mathbb{E}[N_{c}]\) are compared graphically. We see in Table 6 that for CC 1 the optimal value of s * equals 13 (\(4 \frac{1}{3}\) days), for CC 2, s * equals 11 (\(3 \frac{2}{3}\) days), and for CC 3, s * equals 17 (\(5 \frac{2}{3}\) days).

Table 6 Queuing model outcomes
Full size table
Fig. 4
figure 4

\(\mathbb{E}[N_{e}]\) (interrupted line) and \(\mathbb{E}[N_{c}]\) for \(s=(\left\lceil s_{min}\right\rceil,..,m)\)

Full size image

4.3 Allocation of 2-week semi-urgent slots

We now use the Markov decision model to schedule the 1- and 2-week semi-urgent slots. Our goal is to find an optimal policy that prescribes the number of 2-week semi-urgent slots to plan, given any possible system state.

4.3.1 Monotone policy

It is possible that in the optimal policy action a is not monotone increasing in w2 n . Although this form of the optimal policy is not uncommon in literature [23], it may be hard for medical professionals to implement. Therefore we proceed as follows. We determine an optimal policy δ *, as described in Section 3.3. We then check whether a is monotone increasing in w2 n . If this is the case, we maintain this optimal policy. Otherwise, we create a monotone policy, δ M , based on the optimal policy, where the number of 2-week slots to plan (the chosen action) is not allowed to decrease. Such a monotone policy is not necessarily optimal, even in the class of monotone policies.

4.3.2 Obtained policies

The cost combinations CC 1, CC 2, and CC 3 are used to obtain three policies from the Markov decision model. For cost combinations CC 1 and CC 3 we find monotone increasing optimal policies, given in Figs. 5 and 6. For cost combination CC 2 a monotone policy was created, given in Fig. 7. A discount factor of α = 0.95 is used in all cases. We find that \(\mathbb{E}[C_t] = 4.0093\) for CC 1, \(\mathbb{E}[C_t] = 20.2070\) for CC 2, and \(\mathbb{E}[C_t] = 7.4810\) for CC 3. The horizontal axes in the figures show the possible values of w 1 and w 2. When these are combined the system state is obtained. On the vertical axis the action that is chosen for each state is given. The set of actions for all possible states forms the policy δ. Recall that the action chosen consists only of the number of 2-week semi-urgent slots to plan this week, since 1-week semi-urgent slots are completed this week.

Fig. 5
figure 5

δ* for CC1 (s* = 13)

Full size image
Fig. 6
figure 6

δ M for CC2 (s* = 11)

Full size image
Fig. 7
figure 7

δ* for CC3 (s* = 17 )

Full size image

While δ * for CC 1 and CC 3 is straightforward—plan 2-week slots up to s * and postpone the remaining 2-week slots until next week, the policy obtained for CC 2 is quite different. In several states it occurs that even when the number of 1-week slots exceeds s *, elective slots are canceled in order to accommodate 2-week slots. This action is chosen to avoid overtime, a result of s * being close to s min . Similar to the queuing model outcomes, this shows that maintaining a cost structure similar to CC 2, which results in choosing an s * which is close to E[R], leads to the cancellation of elective slots.

5 Discussion and conclusion

In this paper we have developed a methodology to handle the semi-urgent patient flow at a surgical department. On a strategic level, we have determined the OR capacity needed to accommodate all semi-urgent patients on the long run, and we have described a queuing model that allows for a trade-off between the number of elective patients canceled and the amount of unused OR time. Given the amount of slots dedicated to semi-urgent patients, the distribution of the number of elective slots canceled, and the distribution of the number of unused semi-urgent slots can be derived with the queuing model, as is shown in Section 4. An insight that follows from these results is that focusing on only the average behavior of a system can result in undesired system outcomes, in this case the cancellation of many elective patients. Since semi-urgent patient arrivals and elective cancellations are dependent, even over consecutive periods, a natural modeling approach lies in the area of queuing theory.

On a tactical level, we have outlined a Markov decision model that supports the allocation of 1- and 2-week semi-urgent surgeries. This model provides a guideline for the weekly scheduling of semi-urgent patients. The policies obtained with the model can be transferred to a spreadsheet program and with little effort developed into a tool that is easy to use. The added value of the Markov decision model is that it simplifies the scheduling task substantially. Note that all models can be used for arbitrary parameter values.

In the methodology presented, both models involve the planning and scheduling of individual slots. It is not taken into account that when a surgery takes more than one slot, all slots must be scheduled adjacently in the same OR on the same day. To quantify this effect, we calculated the expected number of semi-urgent slots treated for the example in the case study where s * = 13. When considering all possible states, consisting of the number of one-, two- and three-slot semi-urgent surgeries waiting, this expectation equals 8.86 when taking into account the adjacency requirement (i.e. in the situation where we have four full OR days of three slots and a single slot on another OR day). Note that in these calculations we assumed that a rational planner would aim to maximize the number of semi-urgent slots treated in the available time. Given that we consider an instance of the problem where s * is relatively small, so there is little freedom to fill the OR days, the deviation of 7.7% from the value of 9.60 slots (calculated with the queuing model) will be smaller in most other (larger) instances of the problem. However, the adjency requirement results in a slightly higher demand for semi-urgent slots.

A topic for further research would be to extend the presented methodology with an operational model that schedules individual surgeries. We consider the total OR time allocated to a surgical department by OR management as given. Of course, it is possible to establish the optimal amount of allocated OR time, and doing so first could result in a better performance. One of our other aims is to carry out an extensive data analysis to support an implementation of our methodology at the neurosurgery department discussed in Section 4.