1 Introduction

Rock mass reinforcement by means of fully encapsulated rock bolts or cables is the most commonly adopted stabilization technique in underground mines and other excavations (Indraratna et al. 2000). The performance of any reinforcement system is limited by the efficiency of load transfer. Basically the load transfer process begins when the movement of a block of reinforced rock has occurred (Jalalifar 2006). Nowadays, fully encapsulated rock bolts have become a key element in the design of ground control systems. The main reason is they offer high axial resistance to bed separation (Jalaifar 2011). In fully encapsulated rock bolts, the load transfer mechanism is dependent on the shear stress on the bolt/resin and resin/rock interfaces. The peak shear stress capability of the interfaces and the rate of shear stress generation determine the reaction of the bolt to the strata behaviour. Load transfer is determined by measurement of the peak shear stress capacity and system stiffness (Jalalifar 2006). The interface shear stresses, rather than the grouting material itself, are of importance in the overall resistance of a rock bolt system. There are limitations to pull tests in determining the resistance of interfaces, as stress distribution in the system is affected by the geometry of the bolt, borehole and the embedment material properties. The characterization of the bolt surface has a major effect on the load transfer capacity of a fully grouted bolt, because surface roughness dictates the degree of interlocking between bolt and resin (Jalaifar 2011). To improve bolt load transfer through the steel rebar design, it is essential to research the details of the bolt profile shape and configuration. Analytical studies, laboratory tests and numerical modelling provide the tools that enable a better understanding of the rebar profile role in increasing the shear resistance during the working life of bolts (Cao et al. 2011). Blumel et al. (1997) was the first to report on the influence of profile spacing on load transfer capacity of the bolt. Blumel et al. (1997) carried out numerical simulation of the bolt load transfer characteristics with the main aspect of the analysis being to investigate the difference in the bolt behavior versus the rib geometry and in particular the spacing between the ribs. The numerical simulation, based on using finite element mesh to study the load transfer mechanisms, was aimed to be incorporated in future interface modeling (Blumel et al. 1997). Aziz and Jalalifar (2008) extended the work to include modelling of bolt profile configuration under axial and lateral loading conditions. Aziz and Jalalifar (2008) simulated short encapsulation pull and push tests and compared the results with the laboratory and field tests. Their findings outlined the refined techniques available to conduct sensitivity studies on various bolt rib profiles and their spacing to enable selection of the optimum bolt profile geometry (Aziz and Jalalifar 2008). Cao et al. (2010) presented advanced numerical modelling methods of rock bolt performance in underground mines. This study showed how numerical modeling methods could be successfully used to optimize the load transfer between the bolt and the surrounding strata. The study indicated that the standard rock bolt reinforcing elements which are, commonly used in the numerical simulation of the supported underground excavations cannot be used to optimize the load transfer capabilities of the bolt. A detailed model of the bolt profile must be constructed, loaded to failure and compared with other profiles to find the optimum bolt profile with maximum load transfer capabilities between the bolt and host strata (Cao et al. 2010). Further studies by Cao et al. (2011) were due to the improvement in profile rock bolt. The study of the bolt profile shape presented how the mathematical equations were derived. These equations are used to calculate the pull out force needed to fail the grout for different bolt profile configurations. The calculations can be applied to any plane of probable failure within the grout. The important outcome of their study was to show that there was another way to examine grout failure around the bolt for different profile configurations that could be compared with the laboratory tests and numerical modelling. This method could provide better understanding of the bolt-grout interaction with rock reinforcement (Cao et al. 2011). Das et al. ( 2011) presented an analytical model for fully grouted rock bolts considering movements of rock joints. The proposed analytical solution has been applied for evaluating the bolt displacements, axial load and shear stress along the bolt length when the bolt intersected single and multiple joint planes (Das et al. 2011). Aminaipour (2012) studied geometric parameters affecting the load transfer mechanism. Their studies showed that the most important parameter is the thickness of the resin (Aminaipour 2012). A typical steel bolt profile configuration is shown in Fig. 1. The work is presented here extended the analytical model fully encapsulated rock bolt based on bolt profile and jump plane. The analytical model is validated by ANSYS software. Finally, comparisons between the analytical solution and the numerical modeling are shown and the results discussed.

Fig. 1
figure 1

Steel bolt rib profile configuration (Cao et al. 2011)

Full size image

2 Fully Encapsulated Rock Bolt Failure

The type of axial failure depends on the properties of individual elements. The steel bar governs the axial behaviour of the bolt, which is much stiffer, and stronger than the resin and rock. If the bolt has sufficient length to transfer the entire bolt load to the rock, then the bolt will fail if the ultimate strength of the bolt is less than what it is necessary to support. The maximum capacity of the steel depends upon the bolt diameter and steel grade. It should be noted that it might be failure in the steel bolt under the shear load. The shear failure happens if a section along the bolt is subjected to a shear load, which exceeds its shear strength. The shear stress at the bolt-resin interface is greater than the shear stress at the resin-rock interface; because of the smaller effective area. It can be understood that if the resin and rock have similar strengths and if the required anchorage length is inadequate, then failure could occur at the bolt-resin interface. If the surrounding rock is softer, then the failure could happen at the resin–rock interface (Jalalifar 2006).

3 Analytical Approach

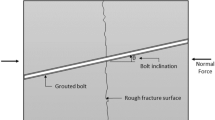
A bolt installed in a deformable rock mass is subjected to axial loading and it provides resistance to the movement of rock mass through shear stresses developed axially in the bolt–resin interfaces (Das et al. 2011). In all analytical models have been proposed, profiles of the rock bolt were ignored. Thus, in order to successfully determine it is essential that only a small part of the bolt, resin and joint rock is modelled as shown in Fig. 2. The new analytical model presented here, is the extension of work by Li and Stillborg (1999), Cao et al. (2011), Das et al. (2011).

Fig. 2
figure 2

Proposed research model (stress component along a fully encapsulated bolt)

Full size image

The authors presented new relationship to calculate the shear stress of the bolt, resin and joint rock based on bolt profile and jump plane, which are presented as follows:

3.1 Shear Stress in the Resin

To investigate where the resin failure will occur, several potential planes of failure can be trilled. The Mohr–Coulomb criterion of failure was used to calculate the maximum pull out force needed for the assumed plane of failure. To draw a link between the load transfer system and the bolt profile configuration, a single spacing between two bolts ribs is examined. When the bolt is loaded, the load is applied to the resin boundary as shown in Fig. 3. The location of these loads is dependent on the bolt geometry while their magnitudes depend on the bolt geometry and the resin-bolt interface properties (Cao et al. 2011).

Fig. 3
figure 3

Load transfer between the bolt, resin and jointed rock (Jalaifar 2011)

Full size image

The normal and shear force, resin displacement and shear stress to the failure plane are determined by Eqs. 1–5.

$$\begin{aligned} \int {\sigma_{n} \;dh} & = \frac{F}{\pi b\;sin\;\theta }\left[ {\left( {\frac{\pi }{2} - \theta } \right)\left( {a + 2b\;cos\;\theta + c} \right) - \left( {a + 2b\;cos\;\theta + c} \right)tan^{ - 1} \left( {\frac{(a + c)\;cos\;\theta + b\;cos\;2\theta }{m + (a + c)\;sin\;\theta + b\;sin\;2\theta }} \right)} \right. \\ & \quad \left. { + \left( {bcos\;\theta - m sin\;\theta } \right)\left[ {tan^{ - 1} \left( {\frac{a + b\;cos\;\theta + c + m\;sin\;\theta }{b\;sin\;\theta + m\;cos\;\theta }} \right) - tan^{ - 1} \left( {\frac{m\;sin \theta - b\;cos \theta }{b\;sin\;\theta + m\;cos\;\theta }} \right)} \right]} \right] \\ \end{aligned}$$
(1)
$$\int {\tau dh} = \frac{F}{\pi }\left[ {tan^{ - 1} \frac{a + b\;cos\;\theta + c}{b\;sin\;\theta } + \frac{\pi }{2} - \theta } \right]$$
(2)
$$u_{re} = \frac{F}{{\pi .L.K_{bond} }}\left[ {tan^{ - 1} \frac{a + b\;cos\;\theta + c}{b\;sin\;\theta } + \frac{\pi }{2} - \theta } \right]$$
(3)
$$\tau = u_{re} .L.K_{bond} /A_{in}$$
(4)

Thus:

$$\tau = \frac{F}{{\pi A_{in} }}\left[ {\text{tan}^{{\text{ - }1}} \left( {\frac{a + b\;cos \theta + c}{b\;sin \theta }} \right) + \frac{\pi }{2}\text{ - }\theta } \right]$$
(5)

where \(\int {\upsigma_{\text{n}} \;\text{dh}}\): Normal force in the resin—rock interface (KN); \(\int {\uptau\;\text{dh}}\): Shear force in the bolt—resin interface (KN); ure: Resin displacement (mm); τ: Shear stress in the resin (MPa); F: Axial bolt pull out force (KN); a: Rib width (mm); b sin θ: Rib height (mm); c: Rib spacing (mm); θ: Rib slope (degree); m: Resin thickness (mm); Ain: Area interface bolt and resin (mm2); L: Failure length (a + 2b cos θ + c) (mm); K bond : Bond shear stiffness (kg/mm2).

3.2 Shear Stress in Jointed Rock

In general, rock displacement is a monotonically decreasing function with radial distance x, measured from an excavation boundary. The form and rate of decrease of rock displacement u r depend on the size and shape of the opening, presence of a joint plane, the strength and structure of the rock mass, loading conditions, stress redistribution occurring around excavation due to the yield of rock mass, and the number of bolts installed at the excavation boundary (Das et al. 2011).

As mentioned in the previous section, rock displacement u r along the bolt axis has been represented by an analytical function depending on the above mentioned parameters of the excavation and joint movement. The distribution of rock displacement u r (x) is represented by a continuous function that contains (1) elastic part of rock deformation, and (2) displacement jump across the surface of the joint plane. Therefore, in case of a circular tunnel with a joint plane as shown in Fig. 4 (Das et al. 2011).

Fig. 4
figure 4

Distribution of rock displacement profile with a joint plane (Das et al. 2011)

Full size image

For a single joint plane, rock displacement along the bolt axis, can be written as:

$$U_{r} = \frac{{L_{b} Be^{ - nx} }}{f + 1}\left[ {2\left( {\frac{{L_{j} }}{{L_{b} }}} \right)^{f + 1} + \left( {f - 1} \right)} \right] +\Delta$$
(6)

Expression of B,\(\upsigma_{{\text{re}}}\), f, b and h are defined in Eqs. 7–11 respectively (Jalaifar 2011).

$$B = \frac{{1 + v_{r} }}{{E_{r} }}\left( {p_{0} - \sigma_{re} } \right)$$
(7)
$$\sigma_{re} = \frac{2}{1 + h}\left( {p_{0} + b} \right) - b$$
(8)
$$f = \frac{{tan\left( {45 + \varphi /2} \right)}}{{tan\left( {45 + \varphi /2 - \psi } \right)}}$$
(9)
$$b = \frac{c}{tan \varphi }$$
(10)
$$h = tan^{2} \left( {45 + \frac{\varphi }{2}} \right)$$
(11)

where Δ : Displacement of the joint plane (mm); n ∈(0, 1): Parameter controlling elastic part of rock deformation ; Lj: The length of the bolt up to at bolt intersect to the joint plane from the tunnel (mm); Lb: The length of the rock bolt (mm); Er: Modulus of elasticity of the rock mass (GPa); Vr: Poisson’s ratio of the mass; p0: In situ stress (MPa); σre: The radial stress at the elastic—plastic boundary (MPa); ψ: Dilatancy angle (degree); c: Cohesion (MPa); φ: Internal friction (degree) (Jalalifar 2006).

Li and Stillborg (1999) calculated the opening of a rock joint, by using Eq. 12 (Li and Stillborg 1999):

$$\Delta = \int {\varepsilon \;dh} = \frac{1}{{E_{b} }}\int {\sigma_{n} dh}$$
(12)

By substituting Eq. 1 into 12, displacement of the joint plane is:

$$\Delta = \int {\varepsilon \;dh} = \frac{1}{{E_{b} }}\int_{{L_{j} }}^{x} {\sigma_{n} dx} = \left( {\frac{{\sigma_{n} }}{{E_{b} }}} \right)\left( {x - L_{j} } \right)$$
(13)

where: σn: Normal stress in the resin—rock interface (MPa); Eb: Modulus of elasticity of the bolt (GPa); x−L j : Longitudianal distance from the joint (mm).

Therefore, jump plane is:

$$\begin{aligned}\Delta & = \frac{{F\left( {x - L_{j} } \right)}}{{\pi A_{in} E_{b} b\;sin\;\theta }}\left[ {\left( {\frac{\pi }{2} - \theta } \right)\left( {a + 2bcos\;\theta + c} \right) - \left( {a + 2b\;cos\;\theta + c} \right)tan^{ - 1} \left( {\frac{(a + c)\;cos\;\theta + b\;cos\;2\theta }{m + (a + c)\;sin\;\theta + bsin\;2\theta }} \right)} \right. \\ & \quad \left. { + \left( {bcos\;\theta - m sin\;\theta } \right)\left[ {tan^{ - 1} \left( {\frac{a + b\;cos\;\theta + c + m\;sin\;\theta }{b\;sin\;\theta + m\;cos\;\theta }} \right) - \tan^{ - 1} \left( {\frac{m\;sin \theta - b\;cos \theta }{b\;sin\;\theta + m\;cos\;\theta }} \right)} \right]} \right] \\ \end{aligned}$$
(14)

So rock displacement is:

$$\begin{aligned} u_{r} & = \frac{{L_{b}^{2} B}}{{(f + 1)(L_{b} + L_{j} )}}\left( {2\left( {\frac{{L_{j} }}{{L_{b} }}} \right) + (f - 1)} \right) \\ & \quad + \frac{{F\left( {x - L_{j} } \right)}}{{\pi A_{in} E_{b} \;sin \theta }}\left[ {\left( {\frac{\pi }{2} - \theta } \right)} \right.\;(a + 2b\;cos\;\theta + c) - (a + 2b\;cos\;\theta + c)\;tan^{ - 1} \;\left( {\frac{(a + c)cos\;\theta + b\;cos 2\theta }{m + (a + c)sin \theta + b\;sin 2\theta }} \right) \\ & \quad + (b\;cos \theta - m\;sin \theta )\left. {\left. {\left[ {tan^{ - 1} \left( {\frac{a + b\;cos\;\theta + c + m\;sin \theta }{bsin\;\theta + m\;cos\;\theta }} \right) - tan^{ - 1} \left( {\frac{m\;sin \theta - b\;cos\;\theta }{bsin\;\theta + m\;cos\;\theta }} \right)} \right.} \right]} \right] \\ \end{aligned}$$
(15)

u r : rock displacement (mm).

Ghadimi (2007) based on numerical modeling numerous pull out test in Tabas Coal Mine, calculated the bolt displacement by Eq. 16:

$$u_{b} = 2.8935u_{r} + u_{re}$$
(16)

where: u b : Bolt displacement (mm); u r : Rock displacement (mm); u re: Resin displacement (mm).

From Eq. 16 it can be understand that there is a linear relationship between rock and grout displacement versus bolt displacement. They change proportionally.

By substituting Eqs. 3 and 15 into 16, bolt displacement is:

$$\begin{aligned} u_{b} & = 2.8935\left[ {\frac{{L_{b}^{2} }}{{(f + 1)(L_{b} + L_{j} )}}\left( {2\left( {\frac{{L_{j} }}{{L_{b} }}} \right) + (f - 1)} \right)} \right. \\ & \quad + \frac{{F\left( {x - L_{j} } \right)}}{{\pi A_{in} E_{b} \;sin \theta }}\left[ {\left( {\frac{\pi }{2} - \theta } \right)} \right.\;(a + 2b\;cos\;\theta + c) - (a + 2b\;cos\;\theta + c)\;tan^{ - 1} \;\left( {\frac{(a + c)cos\;\theta + b\;cos 2\theta }{m + (a + c)sin \theta + b\;sin 2\theta }} \right) \\ & \quad \left. { + (b\;cos \theta - m\;sin \theta )\left. {\left. {\left[ {tan^{ - 1} \left( {\frac{a + b\;cos\;\theta + c + m\;sin \theta }{b\;sin\;\theta + m\;cos\;\theta }} \right) - tan^{ - 1} \left( {\frac{m\;sin \theta - b\;cos\;\theta }{b\;sin\;\theta + m\;cos\;\theta }} \right)} \right.} \right]} \right]} \right] \\ & \quad + F\frac{F}{{\pi L.K_{bond} }}\left[ {tan^{ - 1} \frac{a + b\;cos\;\theta + c}{b\;sin\;\theta } + \frac{\pi }{2} - \theta } \right] \\ \end{aligned}$$
(17)

By substituting Eqs. 14 and 17 into 18, joint-bolt normal stiffness is:

$$k_{n} = \frac{F}{{u_{b} +\Delta }}$$
(18)

Kn: bolt–joint normal stiffness (KN/mm).

Thus shear stress at joint plane could be calculated by:

$$\tau = \left( {\sigma_{re} + \frac{{\Delta .K_{n} }}{{A_{j} }}} \right).\tan \varphi$$
(19)

τ: shear stress in the jointed rock (MPa); Aj: area of joint plane (mm2).

3.3 Shear Stress in the Bolt

To gain a clear understanding of the pattern of buildup of loads and strains along the bolt, two tests were carried out on strain gauged instrumented bolts, the load and shear strain were incrementally recorded at every 0.2 KN until the failure occurred in bolt/grout interface.

By comparing the axial strain at each location along the bolt, the axial stress could be determined by Eq. 21:

$$\sigma_{aij} = E_{b} \left( {\varepsilon_{ai} - \varepsilon_{aj} } \right)$$
(20)

And the shear stress distribution can be give by:

$$\tau_{ij} = \frac{{\sigma_{aij} .A_{b} }}{2\pi rl} = E_{b} \left( {\varepsilon_{ai} - \varepsilon_{aj} } \right).\frac{r}{2l}$$
(21)

where: σaij: Change in axial stress between two adjacent gauges; E b : Bolt module of elasticity (MPa); εai: Axial strain at gauge (μs); εaj: Axial strain at gauge 2 (μs); l: Distance between gauges; r: Bolt radius (mm) (Jalalifar 2006).

Shear sress to tensile stress diagram in laboratory tests, shown this ratio could be calculated as follow:If rib spacing is fixed:

$$\frac{\tau }{\sigma } = 0.48 + 0.04b\sin \theta$$
(22)

And if rib height is fixed:

$$\frac{\tau }{\sigma } = 0.27 + 0.0208C$$
(23)

Rock bolt characteristics, material and joint properties are shown in Tables 1, 2, and 3 respectively. The results of the analytical method are shown in Table 4.

Table 1 Bolts characteristics (Aminaipour 2012)
Full size table
Table 2 Material properties (Aminaipour 2012)
Full size table
Table 3 Joint properties
Full size table
Table 4 The results of the analytical method (tension 330 MPa)
Full size table

Therefore, the shear stress of the interface exponentially decreases from the point of loading to the far end of the bolt before decoupling occurs.

4 Numerical Analysis

A three dimensional finite element model of the reinforced structure subjected to the tension loading was used to examine the behavior of a bolted rock joint. Three governing materials (steel, resin, rock) with three interfaces (bolt-resin, resin-rock and joint–joint) were considered for the 3D numerical simulation. A general purpose of finite element program (ANSYS, Version 12), specifically for advanced structural analysis, was used for 3D simulation of elasto-plastic materials and contact interfaces behavior. Due to the symmetry of the problem, only one-fourth of the system was considered here (Jalalifar 2006). Figure 5 shows the three dimensional model.

Fig. 5
figure 5

Three dimensional image numerical model

Full size image

The interface behavior of resin-rock as a perfect contacts, and was determined from the test results. However, the low value of cohesion (150 kPa) was adopted for resin–steel contact. 3D solid elements (solid 65 and solid 95) that have 8 nodes and 20 nodes were used for rock, resin and steel respectively, with each node having three translation degrees of freedom. That tolerates shapes without significant loss in accuracy. 3D surface to surface contact elements (contact 174) were used to represent the contact between 3D target surface (steel–resin and rock–resin). This element is applicable to 3D structural contact analysis and is located on the surface of 3D solid elements with midsize nodes. The numerical modeling was carried out at several sub steps and the middle block of the model was gradually loaded in the direction of shear (Jalalifar 2006).

4.1 Numerical Results

The numerical modelling in different bolt profile (T1, T2 and T3) and different axial bolt pull out forces (280, 330, 432, 475, and 528 KN) were carried out and the results were analyzed in the following sections. Because there are various graphs for each bolt profile, only the graphs of T3are presented here. For T1 and T2, just the results are reported.

4.1.1 Bolt Behaviour

Figure 6, shown the shear stress in the bolt under tensile stress (330 MPa), this value is in the order of one half of the elastic yield point strength of 600 MPa. This means the bolt behaves elastically and is unlikely to reach the yield situation.

Fig. 6
figure 6

The shear stress in the bolt under pulling test

Full size image

The maximum bolt displacement occurs at the top collar on the pulling side of the bolt, causing a reduction in bolt diameter. The shear stress in the bolt can be calculated by using various tensile stresses. The shear stresses in bolts T1, T2 and T3 were respectively 172.892, 183 and 256.834 MPa. The studies showed that bolt profile can affect the shear stress to tensile stress ratio. So shear stress to tensile stress ratio in the boltsT1, T2 and T3were respectively 0.52, 0.55 and 0.77. Increasing rib height caused shear stress to tensile stress ratio from 0.52 up to 0.55. By increasing rib spacing from 0.52 to 0.77, shear stress to tensile stress ratio is increased, too.

4.1.2 Resin Behaviour

The resin makes a mechanism for transferring the load between the rocks and reinforcing element. The redistribution of forces along the bolt is the result of movement in the rock mass, when movement occurs; the load is transferred to the bolt via shear resistance in the resin. This resistance could be the result of adhesion and or mechanical interlocking. Therefore, shear stresses in the resin of bolt T1, T2 and T3 respectively 27.822, 16.2 and 33.218 MPa. The maximum shear stress was approximately 49.5 % of the uniaxial compressive strength of the resin (Fig. 7).

Fig. 7
figure 7

Shear stress in resin

Full size image

4.1.3 Jointed Rock Behavior

Figure 8 shows shear stress in jointed rock. The maximum shear stress was concentrated in the vicinity of the bolt-joint intersection. There was an exponential relationship between the value of the shear stress and the distance from the joint rocks. This exponential reduction in shear stress is dependent on the material properties of the bolt, the resin and the rock interfaces. There are subscribing between found the authors with Serbouski and Singer (1987), Cai et al. (2004). The shear stresses in jointed rock are respectively 7, 7.02 and 9.081 MPa. The shear stresses are approximately 35, 35.1 and 45.4 % of the uniaxial compressive strength of the jointed rock. Bolt profile configuration is an important parameter in load transfer capacity of bolt, resin and jointed rocks. Profiles spacing increases the shear stress in the jump plane. So that increases high profiles, are not significant effects in jointed rocks. The results numerical methods are shown in Table 5.

Fig. 8
figure 8

Shear stress in jointed rock

Full size image
Table 5 The results of the numerical method (tension 330 MPa)
Full size table

5 Comparing the Results of Analytical and Numerical Methods

Comparing the results of numerical and analytical methods is shown in Figs. 9, 10, and 11 for three types of different bolts T1, T2 and T3. There are good agreements between the results of numerical and analytical methods. Therefore, the proposed analytical solution can be used as a useful tool for estimating the shear stress generated in the elements (rock, resin and bolt). Analytical techniques for physical modelling problems obviously do not understand profiles and so the combination of analytical techniques and realistic numerical modelling can provide better rock bolts profiles.

Fig. 9
figure 9

Comparison of analytical and numerical methods bolt T1

Full size image
Fig. 10
figure 10

Comparison of analytical and numerical methods bolt T2

Full size image
Fig. 11
figure 11

Comparison of analytical and numerical methods bolt T3

Full size image

6 Validation of Analytical Models Based on Pull-Out Tests

Using the values in Table 1, bond displacement against applied load was calculated. Figure 12 shows typical load displacement graphs of testing bolt by using analytical and fields. Experimental results issued from four examined bolts (bolt T1) in situ pull-out tests have been compared to the predictions of the new analytical approach and the results are very satisfactory. The results shown the load transfer capacity bolts (bolt T1) 165 KN.

Fig. 12
figure 12

Load versus displacement values of bolt

Full size image

7 Conclusions

This study proposes a new analytical solution to predict shear stress of a fully encapsulated rock bolt in jointed rock. This method is the extension of work by , Li and Stillborg (1999), Cao et al. (2011), Das et al. (2011). Analytical method has been validated numerically by ANSYS software and filed. The comparison methods show a good agreement between the results. So, the combination of analytical models and realistic numerical methods can improve bolt profile configuration.