Skip to main content
SpringerLink
Log in

Ontological Models, Preparation Contextuality and Nonlocality

  • Published:
Foundations of Physics Aims and scope Submit manuscript

Abstract

The ontological model framework for an operational theory has generated much interest in recent years. The debate concerning reality of quantum states has been made more precise in this framework. With the introduction of generalized notion of contextuality in this framework, it has been shown that completely mixed state of a qubit is preparation contextual. Interestingly, this new idea of preparation contextuality has been used to demonstrate nonlocality of some \(\psi \)-epistemic models without any use of Bell’s inequality. In particular, nonlocality of a non maximally \(\psi \)-epistemic model has been demonstrated from preparation contextuality of a maximally mixed qubit and Schrödinger’s steerability of the maximally entangled state of two qubits (Leifer and Maroney, Phys Rev Lett 110:120401, 2013). In this paper, we, show that any mixed state is preparation contextual. We, then, show that nonlocality of any bipartite pure entangled state, with Schmidt rank two, follows from preparation contextuality and steerability provided we impose certain condition on the epistemicity of the underlying ontological model. More interestingly, if the pure entangled state is of Schmidt rank greater than two, its nonlocality follows without any further condition on the epistemicity. Thus our result establishes a stronger connection between nonlocality and preparation contextuality by revealing nonlocality of any bipartite pure entangled states without any use of Bell-type inequality.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Fig. 1
Fig. 2

Similar content being viewed by others

Notes

  1. In [14], preparation contextuality has been shown for maximally mixed state of a qubit.

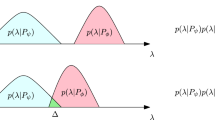
  2. The notion of contextuality is discussed more elaborately in the next section.

  3. This theorem states that every representation of a density matrix \(\rho _B\) can be prepared by acting on a different non-interacting system A if A and B share a pure entangled state \(|\psi _{AB}\rangle \) such that \(\rho _B=Tr_{A} (|\psi _{AB}\rangle \langle \psi _{AB}|)\).

  4. The scenario considered by Leifer and Maroney is more relaxed as it requires to satisfy Eq. (30) only for a single pair of \(\psi \) and \(\phi \).

  5. In [22], Maroney has shown that for every quantum state (in Hilbert spaces of dimension greater than two) there exists another quantum state such that the ontic overlap is strictly less than the quantum overlap and hence the ontological model cannot be maximally \(\psi \)-epistemic.

References

  1. Einstein, A., Podolsky, B., Rosen, N.: Can quantum-mechanical description of physical reality be considered complete? Phys. Rev. 47, 777–780 (1935)

    Article  MATH  ADS  Google Scholar 

  2. Bohr, N.: Can quantum-mechanical description of physical reality be considered complete? Phys. Rev. 48, 696–720 (1935)

    Article  MATH  ADS  Google Scholar 

  3. Popper, K.R.: In: Bunge, M. (ed.) Quantum Theory and Reality. Springer, Berlin (1967)

  4. Ballentine, L.E.: The statistical interpretation of quantum mechanics. Rev. Mod. Phys. 42, 358–381 (1970)

    Article  MATH  ADS  Google Scholar 

  5. Peres, A.: What is a state vector? Am. J. Phys. 52, 644–650 (1984)

    Article  ADS  Google Scholar 

  6. Caves, C.M., Fuchs, C.A., Schack, R.: Quantum probabilities as Bayesian probabilities. Phys. Rev. A 65, 022305 (2002)

    Article  MathSciNet  ADS  Google Scholar 

  7. Pusey, M.F., Barrett, J., Rudolph, T.: On the reality of the quantum state. Nat. Phys. 8, 476–478 (2012)

    Article  Google Scholar 

  8. Harrigan, N., Spekkens, R.W.: Einstein, incompleteness, and the epistemic view of quantum states found. Phys. Rev. 40(2), 125–157 (2010)

    MathSciNet  MATH  Google Scholar 

  9. Bohm, D.: A suggested interpretation of the quantum theory in terms of “Hidden” variables. I. Phys. Rev. 85, 166–179 (1952)

    Article  MathSciNet  MATH  ADS  Google Scholar 

  10. Bohm, D.: A suggested interpretation of the quantum theory in terms of “Hidden” variables. II. Phys. Rev. 85, 180–193 (1952)

    Article  MathSciNet  ADS  Google Scholar 

  11. Bell, J.S.: On the einstein podolsky rosen paradox. Physics 1(3), 195–200 (1964)

  12. Bell, J.S.: Speakable and Unspeakable In Quantum Mechanics. Cambridge University Press, Cambridge, England (2004)

  13. Kochen, S., Specker, E.P.: The problem of hidden variables in quantum mechanics. J. Math. Mech. 17, 59–87 (1967)

    MathSciNet  MATH  Google Scholar 

  14. Spekkens, R.W.: Contextuality for preparations, transformations, and unsharp measurements. Phys. Rev. A 71, 052108 (2005)

    Article  ADS  Google Scholar 

  15. Leifer, M.S., Maroney, O.J.E.: Maximally epistemic interpretations of the quantum state and contextuality. Phys. Rev. Lett. 110, 120401 (2013)

    Article  ADS  Google Scholar 

  16. Gisin, N.: Bell’s inequality holds for all non-product states. Phys. Lett. A 154, 201–202 (1991)

    Article  MathSciNet  ADS  Google Scholar 

  17. Schrödinger, E.: Discussion of probability relations between separated systems. Proc. Cambridge Philos. Soc. 31, 555–563 (1935)

  18. Schrödinger, E.: Discussion of probability relations between separated systems. Proc. Cambridge Philos. Soc. 32, 446–451 (1936)

  19. Hughston, L.P., Jozsa, R., Wootters, W.K.: A complete classification of quantum ensembles having a given density matrix. Phys. Lett. A 183, 14–18 (1993)

    Article  MathSciNet  ADS  Google Scholar 

  20. Gisin, N.: Stochastic quantum dynamics and relativity. Helv. Phys. Acta 62, 363–371 (1989)

    MathSciNet  Google Scholar 

  21. Aaronson, S., Bouland, A., Chua, L., Lowther, G.: \(\psi \)-epistemic theories: the role of symmetry. Phys. Rev. A 88, 032111 (2013)

    Article  ADS  Google Scholar 

  22. Maroney, O. J. E.: How statistical are quantum states? arXiv:1207.6906 (2012).

  23. Harrigan, N., Rudolph, T.: Ontological models and the interpretation of contextuality. arXiv:0709.4266 (2007).

  24. Peres, A.: Two simple proofs of the Kochen–Specker theorem. J. Phys. A: Math. Gen. 24, L175–L178 (1991)

    Article  MATH  ADS  Google Scholar 

  25. Mermin, N.D.: Hidden variables and the two theorems of John Bell. Rev. Mod. Phys. 65, 803–815 (1993)

    Article  MathSciNet  ADS  Google Scholar 

  26. Cabello, A., Estebaranz, J.M., Alcaine, G.G.: Bell–Kochen–Specker theorem: a proof with 18 vectors. Phys. Lett. A 212, 183–187 (1996)

    Article  MathSciNet  MATH  ADS  Google Scholar 

  27. Busch, P., Lahti, P.J., Mittelstaedt, P.: The Quantum Theory of Measurement (2nd Chapter). Springer, Berlin (1996)

  28. Cassinelli, G., De Vito, E., Levrero, A.: On the decompositions of a quantum state. J. Math. Anal. Appl. 210, 472–483 (1997)

    Article  MathSciNet  MATH  Google Scholar 

  29. Wiseman, H.M., Jones, S.J., Doherty, A.C.: Steering, entanglement, nonlocality, and the Einstein–Podolsky–Rosen paradox. Phys. Rev. Lett 98, 140402 (2007)

    Article  MathSciNet  ADS  Google Scholar 

  30. Cavalcanti, E.G., Jones, S.J., Wiseman, H.M., Reid, M.D.: Experimental criteria for steering and the Einstein–Podolsky–Rosen paradox. Phys. Rev. A. 80, 032112 (2009)

    Article  ADS  Google Scholar 

  31. Saunders, D.J., Jones, S.J., Wiseman, H.M., Pryde, G.J.: Experimental EPR-steering using Bell-local states. Nat. Phys. 6, 845–849 (2010)

    Article  Google Scholar 

  32. Leifer, M.S.: Is the quantum state real? A review of-ontology theorems. arXiv:1409.1570 (2014)

Download references

Acknowledgments

It is our great pleasure to acknowledge G. Kar for various discussions, suggestions and help in proving the results. M. B. acknowledges private communications with M. S. Leifer about stronger non-maximal \(\psi \)-epistemicity. Discussion with S. Ghosh is gratefully acknowledged. S. K. C. is thankful to the Physics and Applied Mathematics Unit, Indian Statistical Institute, Kolkata where a major part of this work was done when he was visiting the unit. A. M. acknowledges support from the CSIR Project 09/093(0148)/2012-EMR-I. S. K. C. acknowledges support from CSIR, Govt. of India. We also like to thank an anonymous referee for useful suggestions.

Author information

Authors and Affiliations

  1. Physics and Applied Mathematics Unit, Indian Statistical Institute, 203 B.T. Road, Kolkata, 700108, India

    Manik Banik, Some Sankar Bhattacharya, Amit Mukherjee & Arup Roy

  2. Institute of Physics, Sachivalaya Marg, Bhubaneswar, 751005, Orissa, India

    Sujit K. Choudhary

Authors
  1. Manik Banik
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Some Sankar Bhattacharya
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Sujit K. Choudhary
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Amit Mukherjee
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Arup Roy
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Manik Banik.

Additional information

Recently, M. S. Leifer have written a review on \(\psi \)-ontology theorems [32]. Among many open questions listed in there one is concerned about preparation contextuality proof for any mixed quantum state. This question is addressed in our paper and we have answered affirmatively.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Banik, M., Bhattacharya, S.S., Choudhary, S.K. et al. Ontological Models, Preparation Contextuality and Nonlocality. Found Phys 44, 1230–1244 (2014). https://doi.org/10.1007/s10701-014-9839-4

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10701-014-9839-4

Keywords

Search

Navigation