The Pauli Exclusion Principle. Can It Be Proved?

Abstract

The modern state of the Pauli exclusion principle studies is discussed. The Pauli exclusion principle can be considered from two viewpoints. On the one hand, it asserts that particles with half-integer spin (fermions) are described by antisymmetric wave functions, and particles with integer spin (bosons) are described by symmetric wave functions. This is a so-called spin-statistics connection. The reasons why the spin-statistics connection exists are still unknown, see discussion in text. On the other hand, according to the Pauli exclusion principle, the permutation symmetry of the total wave functions can be only of two types: symmetric or antisymmetric, all other types of permutation symmetry are forbidden; although the solutions of the Schrödinger equation may belong to any representation of the permutation group, including the multi-dimensional ones. It is demonstrated that the proofs of the Pauli exclusion principle in some textbooks on quantum mechanics are incorrect and, in general, the indistinguishability principle is insensitive to the permutation symmetry of the wave function and cannot be used as a criterion for the verification of the Pauli exclusion principle. Heuristic arguments are given in favor that the existence in nature only the one-dimensional permutation representations (symmetric and antisymmetric) are not accidental. As follows from the analysis of possible scenarios, the permission of multi-dimensional representations of the permutation group leads to contradictions with the concept of particle identity and their independence. Thus, the prohibition of the degenerate permutation states by the Pauli exclusion principle follows from the general physical assumptions underlying quantum theory.

Appendix: Short Necessary Knowledge on the Permutation Group

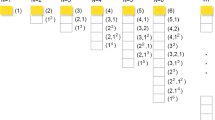
The permutation symmetry is classified according to the irreducible representations of the permutation group π _N .² The latter are labeled by the Young diagrams

$$[ \lambda ] = [ \lambda_{1} \lambda_{2} \cdots \lambda_{k} ], $$

$$ \lambda_{1} \geq \lambda_{2} \geq\cdots \geq \lambda_{k},\quad \sum_{i =1}^{k} \lambda_{i} = N , $$

(32)

where λ _i is represented by a row of λ _i cells. The presence of several rows of equal length λ _i is convenient to indicate by a power of λ _i . For example,

It is obvious that one can form from two cells only two Young diagrams:

For the permutation group of three elements, π ₃, one can form from three cells three Young diagrams:

The group π ₄ has five Young diagrams:

Each Young diagram [λ] uniquely corresponds to a specific irreducible representation Γ ^[λ] of the group π _N . The assignment of a Young diagram determines the permutation symmetry of the basis functions for an irreducible representation, i.e. determines the behavior of the basis functions under permutations of their arguments. A diagram with only one row corresponds to a function symmetrical in all its arguments. A Young diagram with one column corresponds to a completely antisymmetrical function. All other types of diagrams correspond to intermediate types of symmetry. There are certain rules that enable one to find the matrices of irreducible representations of the permutations group from the form of the corresponding Young diagram. Such rules are especially simple in the case of the so-called standard orthogonal representation (this is the Young-Yamanouchi representation; see Ref. [11]).

The basis functions for an irreducible representation Γ ^[λ] can be constructed by means of the so-called normalized Young operators [11],³

$$ \omega_{rt}^{ [ \lambda ]} = \sqrt{\frac{f_{\lambda}}{N !}} \sum _{P} \varGamma_{rt}^{ [ \lambda ]} ( P ) P, $$

(33)

where the summation over P runs over all the N! permutations in the group π _N , $\varGamma_{rt}^{ [ \lambda ]} ( P )$ are the matrix elements and f _λ is the dimension of the irreducible representation Γ ^[λ]. The application of operator (33) to a nonsymmetrized product of orthonormal one-particle functions φ _a

$$ \varPhi_{0} = \varphi_{1} ( 1 ) \varphi_{2} ( 2 ) \cdots \varphi_{N} ( N ) $$

(34)

produces a normalized function

$$ \varPhi_{rt}^{\lambda} = \omega_{rt}^{ [ \lambda ]} \varPhi_{0} = \sqrt{\frac{f_{\lambda}}{N !}} \sum _{P} \varGamma_{rt}^{ [ \lambda ]} ( P ) P \varPhi_{0} $$

(35)

transforming in accordance with the representation Γ ^[λ]. Let us prove this statement applying an arbitrary permutation Q of the group π _N to the function (35):

$$ Q\varPhi_{rt}^{ [ \lambda ]} = \sqrt{\frac{f_{\lambda}}{N !}} \sum _{P} \varGamma_{rt}^{ [ \lambda ]} ( P ) QP \varPhi_{0} = \sqrt{\frac{f_{\lambda}}{N !}} \sum _{R} \varGamma_{rt}^{ [ \lambda ]} \bigl( Q^{- 1} R \bigr) R \varPhi_{0}. $$

(36)

In this equation we have denoted the permutation QP by R and made use of the invariance properties of a sum over all group elements. Further, we write the matrix element of the product of permutations as products of matrix elements and make use of the property of orthogonal matrices:

$$ \varGamma_{rt}^{ [ \lambda ]} \bigl( Q^{- 1} R \bigr) = \sum _{u} \varGamma_{ru}^{ [ \lambda ]} \bigl( Q^{- 1} \bigr) \varGamma_{ut}^{ [ \lambda ]} ( R ) =\sum _{u} \varGamma_{ur}^{ [ \lambda ]} ( Q ) \varGamma_{ut}^{ [ \lambda ]} ( R ). $$

(37)

Substituting (37) in (36), we obtain finally

$$ Q \varPhi_{rt}^{ [ \lambda ]} = \sqrt{\frac{f_{\lambda}}{N !}} \sum _{u} \varGamma_{ur}^{ [ \lambda ]} ( Q ) \biggl( \sum_{R} \varGamma_{ut}^{ [ \lambda ]} ( R ) R \varPhi_{0} \biggr)= \sum_{u} \varGamma_{ur}^{ [ \lambda ]} ( Q ) \varPhi_{ut}^{[\lambda]}. $$

(38)

The function $\varPhi_{rt}^{ [ \lambda ]}$ transforms as the r-th column of the irreducible representation Γ ^[λ], and the set of f _λ functions $\varPhi_{rt}^{ [ \lambda ]}$ with fixed second index t forms a basis for the irreducible representation Γ ^[λ]. One can form altogether f _λ independent bases corresponding to the number of different values of t. This should be expected, since N! functions PΦ ₀ form a basis for the regular representation of π _N , and in the decomposition of the regular representation, each irreducible representation occurs as many times as its dimension. The first index, r, characterizes the symmetry of the function $\varPhi_{rt}^{ [ \lambda ]}$ under permutation of the arguments. It can be shown [11] that the second index, t, enumerating the different bases of Γ ^[λ], characterizes the symmetry of $\varPhi_{rt}^{ [ \lambda ]}$ under permutations of the one-particle functions φ _a .