Abstract
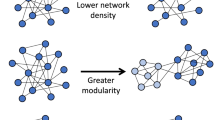
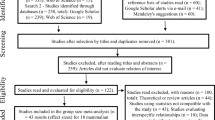
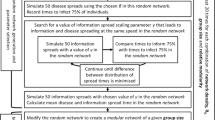
Living in a large social group is thought to increase disease risk in wild animal populations, but comparative studies have provided mixed support for this prediction. Here, we take a social network perspective to investigate whether patterns of social contact within groups influence parasite risk. Specifically, increased modularity (i.e. sub-grouping) in larger groups could offset the increased disease risk associated with living in a large group. We simulated the spread of a contagious pathogen in random social networks to generate theoretically grounded predictions concerning the relationship between social network connectivity and the success of socially transmitted pathogens. Simulations yielded the prediction that community modularity (Q) negatively impacts parasite success. No clear predictions emerged for a second network metric we considered, the eigenvector centralization index (C), as the relationship between this measure and parasite success depended on the transmission probability of parasites. We then tested the prediction that Q reduces parasite success in a phylogenetic comparative analysis of social network modularity and parasite richness across 19 primate species. Using a Bayesian implementation of phylogenetic generalized least squares and controlling for sampling effort, we found that primates living in larger groups exhibited higher Q, and as predicted by our simulations, higher Q was associated with lower richness of socially transmitted parasites. This suggests that increased modularity mediates the elevated risk of parasitism associated with living in larger groups, which could contribute to the inconsistent findings of empirical studies on the association between group size and parasite risk. Our results indicate that social networks may play a role in mediating pressure from socially transmitted parasites, particularly in large groups where opportunities for transmitting communicable diseases are abundant. We propose that parasite pressure in gregarious primates may have favored the evolution of behaviors that increase social network modularity, especially in large social groups.



Similar content being viewed by others
References
Ahumada JA (1992) Grooming behavior of spider monkeys (Ateles geoffroyi) on Barro Colorado Island, Panama. Int J Primatol 13(1):33–49
Akaike H (1974) A new look at the statistical model identification. IEEE Trans Autom Control 19(6):716–723
Altizer S, Nunn CL, Thrall PH et al (2003) Social organization and parasite risk in mammals: integrating theory and empirical studies. Ann Rev of Ecol Evol Syst 34:517–547
Arnold W, Lichtenstein AV (1993) Ectoparasite loads decrease the fitness of alpine marmots (Marmotamarmota) but are not a cost of sociality. Behav Ecol 4:36–39
Arnold C, Matthews LJ, Nunn CL (2010) The 10kTrees website: a new online resource for primate phylogeny. Evol Anthro 19:114–118
Boese GK (1975) Social behavior and ecological considerations of West African baboons (Papio papio). In: Tuttle RH (ed) Socioecology and psychology of primates. Mouton Publishers, The Hague, p 208
Bonacich P (1972) Factoring and weighting approaches to status scores and clique identification. J Math Sociol 2:113–120
Bonacich P (2007) Some unique properties of eigenvector centrality. Soc Netw 29(4):555–564
Bordes F, Morand S (2009) Parasite diversity: an overlooked metric of parasite pressure? Oikos 118:801–806
Butovskaya ML, Kozintsev AG, Kozintsev BA (1994) The structure of affiliative relations in a primate community: allogrooming in stumptailed macaques (Macaca arctoides). Hum Evol 9(1):11–23
Canright GS, Engo-Monson K (2006) Spreading on networks: a topographic view. Complexus 3:131–146
Chiarello AG (1995) Grooming in brown howler monkeys, Alouatta fusca. Am J Primatol 35:73–81
Clauset A (2005) Finding local community structure in networks. Phys Rev E 72:026132
Cooper MA, Bernstein IS, Hemelrijk CK (2005) Reconciliation and relationship quality in Assamese macaques (Macaca assamensis). Am J Primatol 65:269–282
Côté IM, Poulin R (1995) Parasitism and group size in social animals: a meta-analysis. Behav Ecol 6(2):159–165
Di Fiore A, Rendall D (1994) Evolution of social organization: a reappraisal for primates by using phylogenetic methods. Proc Nat Acad Sci USA 91:9941–9945
Diekmann O, De Jong MCM, Metz JJ (1998) A deterministic epidemic model taking account of repeated contacts between the same individuals. J Appl Prob 35(2):448–462
Dunbar RIM (1992) Time: a hidden constraint on the behavioural ecology of baboons. Behav Ecol Sociobiol 31(1):35–49
Dunbar RI, Dunbar EP (1976) Contrasts in social structure among black-and-white colobus groups. Anim Behav 24:84–92
Dunbar RIM, Dunbar P (1988) Maternal time budgets of gelada baboons. Anim Behav 36:970–980
Ezenwa VO, Price SA, Altizer S et al (2006) Host traits and parasite species richness in even and odd-toed hoofed mammals, Artiodactyla and Perissodactyla. OIKOS 115:526–536
Felsenstein J (1985) Phylogenies and the comparative method. Am Nat 125:1–15
Flack JC, Girvan M, de Waal FBM, Krakauer DC (2006) Policing stabilizes construction of social niches in primates. Nature 439:426–429
Freckleton RP, Harvey PH, Pagel M (2002) Phylogenetic analysis and comparative data: a test and review of evidence. Am Nat 160:712–726
Freeland WJ (1976) Pathogens and the evolution of primate sociality. Biotropica 8:12–24
Freeland WJ (1979) Primate social groups as biological islands. Ecol 60:719–728
Freeman LC (1979) Centrality in social networks: conceptual clarification. Soc Netw 1:215–239
Grimm V, Railsback SF (2005) Individual based modeling in ecology. Princeton University Press, Princeton
Hart BL (1990) Behavioral adaptations to pathogens and parasites: five strategies. Neurosci Biobehav Rev 14:273–294
Harvey PH, Pagel MS (1991) The comparative method in evolutionary biology. Oxford University Press, Oxford
Harvey PH, Rambaut A (1998) Phylogenetic extinction rates and comparative methodology. Proc R Soc Lond B Bio Sci 265:1691–1696
Hausfater G, Watson DF (1976) Social and reproductive correlates of parasite ova emissions by baboons. Nature 262:688–689
Hernandez AD, Macintosh AJ, Huffman MA (2009) Primate parasite ecology: patterns and predictions from an ongoing study of Japanese macaques. In: Huffman MA, Chapman CA (eds) Primate parasite ecology: the dynamics and study of host-parasite relationships. Cambridge University Press, Cambridge
Hess G (1996) Disease in metapopulation models: implications for conservation. Ecol 77:1617–1632
Hoogland L (1979) Aggression, ectoparasitism, and other possible costs of prairie dog (Sciuridae, Cynomys spp.) coloniality. Behav 69:1–35
Huang W, Li C (2007) Epidemic spreading in scale-free networks with community structure. J Stat Mech P01014
Huelsenbeck JP, Rannala B, Masly JP (2000) Accommodating phylogenetic uncertainty in evolutionary studies. Science 288:2349–2350
Huffman MA, Chapman C (2009) Primate parasite ecology: the dynamics and study of Host-Parasite relationships (Studies in biological and evolutionary anthropology series). Cambridge University Press, Cambridge
Hunkeler C, Bourliere F, Bertrand M (1972) Le comportement social de la Mone de Lowe (Cercopothecus campbelli lowei). Folia Primatol 17:218–236
Ives AR, Midford PE, Garland T (2007) Within-species variation and measurement error in phylogenetic comparative methods. Syst Biol 56(2):252–270
Izawa K (1980) Social behavior of the wild black-capped capuchin (Cebus apella). Primates 21(4):443–467
Kaplan JR, Zucker E (1980) Social organization in a group of free-ranging patas monkeys. Folia Primatol 34:196–213
Kasper C, Voelkl B (2009) A social network analysis of primate groups. Primates 50(4):343–356
Keele B, Jones J, Terio K, Estes J, Rudicell R, Wilson M, Li Y, Learn G, Beasley T, Schumacher-Stankey J (2009) Increased mortality and AIDS-like immunopathology in wild chimpanzees infected with SIVcpz. Nature 460:515–519
Keeling MJ (1999) The effects of local spatial structure on epidemiological invasions. Proc R Soc Lond B 266:859–867
Kohler TA, Gumerman GJ (2000) Dynamics of human and primate societies: agent-based modeling of social and spatial processes. Oxford University Press, Oxford
Krause J, Croft DP, James R (2007) Social network theory in the behavioural sciences: potential applications. Behav Ecol Socioecol 62(1):15–27
Kudo H, Dunbar RIM (2000) Neocortex size and social network size in primates. Anim Behav 62:711–722
Lindenfors P, Nunn CL, Jones KE et al (2007) Parasite species richness in carnivores: effects of host body mass, latitude, geographic range and population density. Global Biol Biogeo 16:496–509
Lloyd-Smith JO, Schreiber SJ, Kopp PE et al (2005) Superspreading and the effect of individual variation on disease emergence. Nature 438(17):355–359
Loehle C (1995) Social barriers to pathogen transmission in wild animal populations. Ecology 76:326–335
Lottker P, Huck M, Zinner DP, Heymann EW (2007) Grooming relationships between breeding females and adult group members in cooperatively breeding moustached tamarins (Saguinus mystax). Am J Primatol 69:1159–1172
Lusseau D, Newman MEJ (2004) Identifying the role that individual animals play in their social network. Proc R Soc Lond B Biol Sci 271:S477–S481
Marquardt DW (1970) Generalized inverses, ridge regression, biased linear estimation, and nonlinear estimation. Technometrics 12(3):591–612
Martins EP, Garland T (1991) Phylogenetic analysis of the correlated evolution of continuous characters: a simulation study. Evol 45:534–557
McGrew WC, Tutin CEG, Collins DA et al (1989) Intestinal parasites of sympatric Pan troglodytes and Papio spp. at two sites: Gombe (Tanzania) and Mt. Assirik (Senegal). Am J Primatol 17:147–155
Møller AP, Dufva R, Allander K (1993) Parasites and the evolution of host social behavior. Adv Study Behav 22:65–102
Morand S, Harvey PH (2000) Mammalian metabolism, longevity and parasite species richness. Proc R Soc Lond B Biol Sci 267:1999–2003
Newman MEJ, Girvan M (2004) Finding and evaluating community structure in networks. Phys Rev E 69(026113):1–15
Newman MEJ, Forrest S, Balthrop J (2002) Email networks and the spread of computer viruses. Phys Rev E 66:1–4
Nunn CL (2002a) A comparative study of leukocyte counts and disease risk in primates. Evol 56:177–190
Nunn CL (2002b) Spleen size, disease risk and sexual selection: a comparative study in primates. Evol Ecol Res 4:91–107
Nunn CL (2011) The comparative approach in evolutionary anthropology and biology. University of Chicago Press, Chicago
Nunn CL, Altizer S (2005) The Global Mammal Parasite Database: an online resource for infectious disease records in wild primates. Evol Anthro 14:1–2
Nunn CL, Altizer S (2006) Infectious diseases in primates: behavior, ecology and evolution. Oxford University Press, New York
Nunn CL, Gittleman JL, Antonovics J (2000) Promiscuity and the primate immune system. Science 290:1168–1170
Nunn CL, Altizer S, Jones KE et al (2003) Comparative tests of parasite species richness in primates. Am Nat 162(5):597–614
Nunn CL, Altizer S, Sechrest W, Jones KE, Barton RA, Gittleman JL (2004) Parasites and the evolutionary diversification of primate clades. Am Nat 164:S90–S103
Nunn CL, Altizer SM, Sechrest W, Cunningham A (2005) Latitudinal gradients of disease risk in primates. Divers Distrib 11:249–256
Nunn CL, Thrall PH, Stewart K (2008) Emerging infectious diseases and animal social systems. Evol Ecol 22:519–543
Nunn CL, Thrall PH, Leendertz FH, Boesch C (2011) The spread of fecally transmitted parasites in socially-structured populations. PLoS One (in press)
Pagel M, Lutzoni F (2002) Accounting for phylogenetic uncertainty in comparative studies of evolution and adaptation. In: Lässig M, Valleriani A (eds) Biological evolution and statistical physics. Springer, Berlin, pp 148–161
Pagel M, Meade A (2007) BayesTraits (www.evolution.rdg.ac.uk). Reading, UK
Pederson A, Altizer S, Poss M, Cunningham AA, Nunn CL (2005) Patterns of host specificity and transmission among parasites in wild primates. Int J Parasitol 35:547–657
Pederson A, Jones K, Nunn CL et al (2007) Infectious diseases and extinction risk in wild mammals. Conserv Biol 21:1269–1279
Petraitis PS, Dunham AE, Niewlarowski PH (1996) Inferring multiple causality: the limitations of path analysis. Funct Ecol 10:421–431
Poirier FE (1969) The Nilgiri langur (Presbytis johnii) troop: its composition, structure, function and change. Folia Primatol 10:20–47
Poulin R (1995) Phylogeny, ecology, and the richness of parasite communities in vertebrates. Ecol Monogr 65:283–302
Poulin R, Morand S (2004) Parasite biodiversity. Smithsonian Institution Press, Washington, DC
Purvis A, Gittleman JL, Luh H (1994) Truth or consequences: effects of phylogenetic accuracy on two comparative methods. J Theor Biol 167:293–300
Revell L (2010) Phylogenetic signal and linear regression on species data. Methods Ecol Evol 1:319–329
Rowe N (1996) The pictorial guide to the living primates. Pogonias Press, East Hampton
Ruhnau B (2000) Eigenvector centrality- a node centrality? Soc Netw 22:357–365
Sade SD (1971) Sociometrics of Macaca mulatta I. Linkages and cliques in grooming matrices. Folia Primatol 18:196–223
Salathé M, Jones JH (2010) Dynamics and control of diseases in networks with community structure. PLoS Comp Biol 6:e1000736
Semple S, Cowlishaw G, Bennett PM (2002) Immune system evolution among anthropoid primates: parasites, injuries and predators. Proc R Soc B Biol Sci 269:1031–1037
Shields WM, Crook JR (1987) Barn swallow coloniality- a net cost for group breeding in the adirondacks. Ecol 68:1373–1386
Smith KF, Sax DF, Lafferty KD (2006) Evidence for the role of infectious disease in species extinction and endangerment. Conserv Biol 20:1249–1357
Snaith T, Chapman C, Rothman J et al (2008) Bigger groups have fewer parasites and similar cortisol levels: a multi-group analysis in red colobus monkeys. Am J Primatol 70:1072–1080
Stoner KE (1996) Prevalence and intensity of intestinal parasites in mantled howling monkeys (Alouatta palliata) in northeastern Costa Rica: implications for conservation biology. Conserv Biol 10:539–546
Strier KB (1992) Causes and consequences of non-aggression in the woolly spider monkey, or Miriqui. In: Silverberg J, Gray JP (eds) Aggression and peacefulness in humans and other primates. Oxford University Press, USA, p 109
Sugiyama Y (1971) Characteristics of the social life of bonnet macaques (Macaca radiata). Primates 12:247–266
Tabachnick BG, Fidell LS (1989) Using multivariate statistics, 2nd edn. Harper and Row, Cambridge
Takahashi H, Furuichi T (1998) Comparative study of grooming relationships among wild Japanese macaques in Kinkazan A troop and Yakushima M troop. Primates 39(3):365–374
van Hooff JARAM, van Schaik CP (1992) Cooperation in competition: the ecology of primate bonds. In: Harcourt AH, De Waal FBM (eds) Coalitions and alliances in humans and other animals. Oxford University Press, Oxford, pp 357–389
van Schaik CP (1989) The ecology of social relationships amongst female primates. In: Standen V, Foley RA (eds) Comparative socioecology. Blackwell, Oxford, pp 195–218
Vital C, Martins EP (2009) Using graph theory metrics to infer information flow through animal social groups: a computer simulation analysis. Ethology 115:347–355
Vitone ND, Altizer SM, Nunn CL (2004) Body size, diet and sociality influence the species richness of parasitic worms in anthropoid primates. Evol Ecol Res 6:1–17
Vogt JL (1978) The social behavior of a marmoset (Saguinus fuscicollis) group II: behavior patterns and social interaction. Primates 19:287–300
Walther BA, Cotgreave P, Gregory RD et al (1995) Sampling effort and parasite species richness. Parasitol Today 11:306–310
Wasserman S, Faust K (1994) Social network analysis: methods and applications. Cambridge University Press, Cambridge
Watve MG, Jog MM (1997) Epidemic diseases and host clustering: an optimum cluster size ensures maximum survival. J Theor Biol 184:165–169
Wey T, Blumstein DT, Shen W et al (2008) Social network analysis of animal behaviour: a promising tool for the study of sociality. Anim Behav 75:33–344
Whitehead H (2008) Analyzing animal societies: quantitative methods for vertebrate social analysis. University of Chicago Press, Chicago
Wilkinson GS (1985) The social-organization of the common vampire bat. 1. Pattern and cause of association. Behav Ecol Sociobiol 17:111–121
Wilson K, Knell R, Boots M et al (2003) Group living and investment in immune defense: an interspecific analysis. J Anim Ecol 72:133–143
Acknowledgments
We thank Luke Matthews, Michael Mitzenmacher, Amanda Lobell, Natalie Cooper, Jamie Jones, Charles Mitchell, members of the Comparative Primatology Research Group at Harvard University, and anonymous reviewers for helpful comments. This research was supported by Harvard University, a Summer Undergraduate Research Fellowship (SURF) from the Harvard Initiative in Global Health (HIGH), and the National Science Foundation (BCS-0923791).
Author information
Authors and Affiliations
Corresponding author
Electronic supplementary material
Below is the link to the electronic supplementary material.
Rights and permissions
About this article
Cite this article
Griffin, R.H., Nunn, C.L. Community structure and the spread of infectious disease in primate social networks. Evol Ecol 26, 779–800 (2012). https://doi.org/10.1007/s10682-011-9526-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10682-011-9526-2