1 Introduction

Graphene is a single atomic layer of graphite. This allotrope of carbon is made up of very tightly bonded carbon atoms organized into a hexagonal lattice. Single-layered graphene sheet (SLGS) is the basic structural element of many carbon nanostructures such as carbon nanotubes (CNTs), carbon nanocones, nanorings, fullerenes etc. Hence, it is one of the most promising materials for widespread potential applications in nanotechnology, for example, sensors [1, 2], nanosheet resonators [3], composite materials [4, 5], nanoactuators [6], and memory devices [7]. In this regard, study on vibration and instability of nano-mechanical systems made of graphene have been conducted by many researches some of which are presented in this paper.

The mechanical properties of nanostructures can be analysed using three major procedures known as molecular dynamics (MD) simulations [8, 9], experimental study [10, 11], and the continuum mechanics approach [12]. The first two methods have some drawbacks that confine their usage under some conditions. MD method consumes much time, and it is economically inefficient for analysing large-scale systems. Also, it is very difficult to perform a controlled experiment at nanometer scales. Thus, because of these limitations, continuum mechanics-based approaches have been known as powerful and effective methods to study mechanical characteristics of nanostructures. Since the classical continuum mechanics have no ability in capturing the small-scale effect, it cannot be regarded as a reliable theory to predict the mechanical behaviour of nanomaterials. So far, several nonclassical continuum theories have been formulated to incorporate the small-scale size effects [13–15]. Among these theories, the nonlocal elasticity theory introduced by Eringen is the most often used theory [16–19]. Based on this theory, the nonlocal stress tensor at a reference point in a body depends not only on the strain tensor at that point, but also on the strain tensor at all other points in the body. The application of Eringen’s nonlocal theory to the nanoplate’s problems has been investigated in several research works. In this regard, Aghababaei and Reddy [20] reformulated the third-order shear deformation theory (TSDT) for bending and vibration of the simply supported nanoplate based on the Eringen’s nonlocal theory. A finite element model (FEM) based on the nonlocal theory was reported by Ansari et al. [21] to investigate the small-scale effect on the vibration analysis of multilayered graphene sheets (MLGSs) with various boundary conditions embedded in an elastic medium. Malekzadeh et al. [22] investigated the free vibration of orthotropic arbitrary straight-sided nanoplate via Eringen’s theory. They employed the differential quadrature method (DQM) to solve the governing equations of motion based on the first-order shear deformation theory (FSDT). A semi-inverse method based on the nonlocal continuum model was developed in [23] to derive variational principle for vibration and buckling analyses of orthotropic graphene sheets under biaxial compression resting on an elastic foundation. Free vibration of orthotropic graphene sheets with various boundary conditions was performed by Pradhan and Kumar [24] based on the nonlocal elasticity theory using DQM. Navier’s approach was applied in [25] to study vibration analysis of Kirchhoff and Mindlin nanoscale plates with consideration of surface effects using nonlocal theory. Ghorbanpour Arani et al. [26] researched the vibration response of the coupled double-layered graphene sheets (DLGSs) systems with different boundary conditions embedded on visco-Pasternak foundation using DQM on the basis of the nonlocal theory. Besides, other investigations in the vibration domain on the graphene sheet based on the Eringen’s theory have been presented in the open literature [27–30]. As mentioned, there are several exploratory researches on the nonlocal continuum models for free vibration of graphene sheets. On the contrary, a few works appear to have been done, associated with the bending behaviour of graphene sheets based on the nonlocal elasticity theory. Wang and Li [31] studied static bending of nanoplate embedded on elastic foundation for a simply supported boundary conditions using nonlocal elasticity theory. In recent years, the nonlinear bending response of a bilayer rectangular graphene sheets subjected to a transverse uniform load in thermal environments, using the nonlocal classical plate theory including the van der Waals interactions, was investigated by Xu et al. [32]. Also more recently, Sobhy [33] reformulated the sinusoidal shear deformation theory (SSDT) based on the nonlocal continuum model to analyse the bending and vibration of the SLGSs with different boundary conditions, where the nanoplates were supposed to be resting on Pasternak’s elastic foundations subjected to mechanical and thermal loads.

In the field of dynamic analysis of graphene sheet, dynamic response of the finite periodic SLGSs with different boundary conditions were investigated by Liu and Chen [34] using the wave method on the basis of the nonlocal Mindlin plate theory.

A literature survey indicates that there are a few static and dynamic analyses of graphene sheets based on the nonlocal elasticity theory, in contrast to their free vibration. However, close scrutiny of previous researches certifies that, up to now, the static and dynamic bendings of SLGS resting on the visco-Pasternak foundations subjected to sinusoidal and uniform loads have not been studied, especially in an analytical formulation. Hence, in this work an entirely analytical method to study the static bending and dynamic responses of SLGS with considering foundation effects is developed with foundation effects included using the Fourier series–Laplace transform. The SLGS resting on the viscoelastic medium is simulated by visco-Pasternak type as spring, shear and damping foundations. Based on the TSDT, equations of motion are derived utilizing Hamilton’s principle. Furthermore, the nonlocal elasticity theory is applied to capture the small-scale effects, unlike the classical theory. Using Laplace transform, the time dependency of the governing equations is eliminated and then an analytical strategy is employed to invert the results into the time domain. The results of this research can be used as a benchmark test for the static analysis and dynamic response of the SLGS.

2 Fundamental formulation

2.1 Description of the mathematical of model

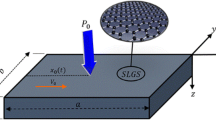
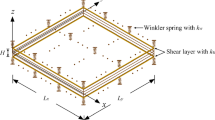
Consider a typical graphene sheet with length a, width b and thickness h as depicted in Fig. 1a, and the right-handed coordinate system (x, y, z) is located at the left corner of the mid-plane of the graphene sheet, in which \(x,\, y\) and z axes are taken along the length, width and thickness directions, respectively. Figure 1b shows that the top surface of the SLGS is subjected to dynamic transverse uniform and sinusoidal loads and the bottom one is continuously in contact with an elastic medium which is simulated by a visco-Pasternak foundation.

Fig. 1
figure 1

a Coordinate system and geometry of the SLGS embedded in visco-Pasternak foundation. b Schematic of SLGS under uniform and sinusoidal loads

Full size image

2.2 Nonlocal continuum theory

Unlike the conventional local elasticity theory, in the nonlocal theory, it is assumed that the stress at a reference point is a function of the strain field at every point in the body [16–19]. This is attributed by Eringen to the atomic theory of lattice dynamics and experimental observations on phonon dispersion. Using nonlocal elasticity theory, the constitutive equation for a linear homogenous nonlocal elastic body neglecting the body forces is given as

$$\begin{aligned} \sigma _{ij} ^\mathrm{nl}(x)=\int _v {\alpha \left( | {x-{x}'}|,\tau \right) \sigma _{ij} ^\mathrm{l}\;\mathrm{d}V({x}')}\quad \forall x\in V, \end{aligned}$$
(1)

where \(\sigma _{ij}^\mathrm{nl} \) and \(\sigma _{ij}^\mathrm{l}\) are the nonlocal and local stress tensors, respectively. The term \(\alpha (| {x-{x}'}|,\tau )\) is the nonlocal modulus (attenuation function), which incorporates nonlocal effects into the constitutive equation at the reference point x produced by the local strain at the source \({x}'; |{x-{x}'}|\) represents the distance between x and \({x}'\) in the Euclidean form, and \(\tau ={e_0 a}/l\) in which l is the external characteristic length (e.g. crack length, wavelength), \(e_0\) indicates constant appropriate to each material, and a is an internal characteristic length of the material (e.g. length of C–C bond, lattice parameter, granular distance). For more detail see [17]. The differential form of Eq. (1) can be written as

(2)

In the above equation, the parameter \({\mu } =(e_0 a)^{2}\) denotes the small-scale effect on the response of structures in nanosize, and \(\nabla ^{2}=({\partial ^{2}}/{\partial x^{2}}+{\partial ^{2}}/{\partial y^{2}})\) is the Laplacian operator in a Cartesian coordinate system. Also, C is the fourth-order stiffness tensor, ‘:’ represents the double dot product and \(\varepsilon \) is the strain tensor. Choice of the value of parameter \(e_0 \) is crucial to ensure the validity of nonlocal models. This parameter is determined such that the nonlocal model calibrated with the experimental observations or MD simulation results. Eringen [16] proposed \(e_0 \) as 0.39 by matching of the dispersion curves via nonlocal theory for plane wave and Born–Karman model of lattice dynamics at the end of the Brillouin zone. Sudak [35] used the length of C–C bond equal to 0.142 nm as internal characteristics length in CNTs’ stability analysis. Wang and Hu [36] used strain gradient method to propose an estimate of the value \((e_0)\) around 0.288. According to Duan et al. [37], nonlocal parameter \(e_0\) is not unique and depends on the length-to-diameter ratio, boundary conditions and mode shapes of the nanostructures. In another work, Duan and Wang [15] used the value of \(e_0 a\) ranging from 0 to 2 nm for bending analysis of circular plates at micro and nanoscale levels. A conservative estimate of the effect \(e_0 a\le 2\) nm for CNTs and graphene sheets have been proposed in [31, 38].

In the view of aforementioned studies on the nonlocal parameter, it is clear that the magnitudes of \(e_0 \) extremely depends on various parameters. Therefore, hitherto no specific values have been obtained for this parameter. In this research, the small-scale effect \({\mu } \) is chosen similar to [21, 26–28], namely, we assumed \(0\le {\mu } \le 3~\mathrm{nm}^{2}\) to investigate the nonlocal effects on the bending analysis of a monolayer graphene sheet. It should be noted that when \(e_0 a\) is equal to zero, the nonlocal elasticity reduces to the local (classical) elastic model.

Using Eq. (2), the stress nonlocal constitutive relations can be written as

$$\begin{aligned} \left( {{\begin{array}{l} {\sigma _{xx}^\mathrm{nl} } \\ {\sigma _{yy}^\mathrm{nl} } \\ {\sigma _{yz}^\mathrm{nl} } \\ {\begin{array}{l} \sigma _{xz}^\mathrm{nl} \\ \sigma _{xy}^\mathrm{nl} \\ \end{array}} \\ \end{array} }} \right) -{\mu } \nabla ^{2}\left( {{\begin{array}{l} {\sigma _{xx}^\mathrm{nl} } \\ {\sigma _{yy}^\mathrm{nl} } \\ {\sigma _{yz}^\mathrm{nl} } \\ {\begin{array}{l} \sigma _{xz}^\mathrm{nl} \\ \sigma _{xy}^\mathrm{nl} \\ \end{array}} \\ \end{array} }} \right) =\left( {{\begin{array}{ccccc} {Q_{11}} &{}\quad {Q_{12} }&{}\quad 0&{}\quad 0&{}\quad 0 \\ {Q_{21} }&{}\quad {Q_{22} }&{}\quad 0&{}\quad 0&{}\quad 0 \\ 0&{}\quad 0&{}\quad {Q_{44} }&{}\quad 0&{}\quad 0 \\ 0&{}\quad 0&{}\quad 0&{}\quad {Q_{55} }&{}\quad 0 \\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad {Q_{66} } \\ \end{array} }} \right) \left( {{\begin{array}{l} {\varepsilon _{xx} } \\ {\varepsilon _{yy} } \\ {\gamma _{yz} } \\ {\begin{array}{l} \gamma _{xz} \\ \gamma _{xy} \\ \end{array}} \\ \end{array} }} \right) . \end{aligned}$$
(3)

The plane-stress-reduced stiffness \(Q_{ij} \) is defined as [39]:

$$\begin{aligned} Q_{11} =Q_{22} =\frac{E}{1-\nu ^{2}},\quad Q_{12} =Q_{21} =\nu Q_{11} , \quad Q_{44} =Q_{55} =Q_{66} =\frac{E}{2 (1+\nu )}, \end{aligned}$$
(4)

where E and \(\nu \) denote Young’s modulus and Poisson’s ratio, respectively.

2.3 Third-order shear deformation theory

According to the TSDT, the mid-surface displacements \((u_0 ,v_0 ,w_0 )\), mid-surface rotations \((\psi _x ,\psi _y )\) and the displacement components of an arbitrary point (u, v, w) are related as [39, 40]

$$\begin{aligned} \begin{aligned} u\left( {x,y,z,t} \right)&=u_0 \left( {x,y,t} \right) +z\psi _x \left( {x,y,t} \right) -c_1 z^{3}\left( {\psi _x +w_{0,x} } \right) , \\ v\left( {x,y,z,t} \right)&=v_0 \left( {x,y,t} \right) +z\psi _y \left( {x,y,t} \right) -c_1 z^{3}\left( {\psi _y +w_{0,y} } \right) , \quad w\left( {x,y,z,t} \right) =w_0 \left( {x,y,t} \right) , \end{aligned} \end{aligned}$$
(5)

in which, the constant \(c_1 \) is given by \(c_1 ={4 }/{3h^{2}}\), the comma in subscript represents the partial differentiation and t denotes the time variable. Setting \(c_1 =0\) in Eq. (5), the displacement field relevant to FSDT is obtained. The linear strain–displacement relations are derived as follows [39]:

$$\begin{aligned} \left( {\begin{array}{l} \varepsilon _{xx} \\ \varepsilon _{yy} \\ \gamma _{xy} \\ \end{array}} \right)= & {} \left( {\begin{array}{l} \varepsilon _{xx}^{\left( 0 \right) } \\ \varepsilon _{yy}^{\left( 0 \right) } \\ \gamma _{xy}^{\left( 0 \right) } \\ \end{array}} \right) +z\left( {\begin{array}{l} \varepsilon _{xx}^{\left( 1 \right) } \\ \varepsilon _{yy}^{\left( 1 \right) } \\ \gamma _{xy}^{\left( 1 \right) } \\ \end{array}} \right) +z^{3}\left( {\begin{array}{l} \varepsilon _{xx}^{\left( 3 \right) } \\ \varepsilon _{yy}^{\left( 3 \right) } \\ \gamma _{xy}^{\left( 1 \right) } \\ \end{array}} \right) ,\quad \left( {\begin{array}{l} \gamma _{yz} \\ \gamma _{xz} \\ \end{array}} \right) =\left( {\begin{array}{l} \gamma _{yz}^{\left( 0 \right) } \\ \gamma _{xz}^{\left( 0 \right) } \\ \end{array}} \right) +z^{2}\left( {\begin{array}{l} \gamma _{yz}^{\left( 2 \right) } \\ \gamma _{xz}^{\left( 2 \right) } \\ \end{array}} \right) , \end{aligned}$$
(6)

where:

$$\begin{aligned} \begin{array}{l} \left( {\begin{array}{l} \varepsilon _{xx}^{\left( 0 \right) } \\ \varepsilon _{yy}^{\left( 0 \right) } \\ \gamma _{xy}^{\left( 0 \right) } \\ \end{array}} \right) =\left( {{\begin{array}{c} {u_{0,x} } \\ {v_{0,y} } \\ {u_{0,y} +v_{0,x} } \\ \end{array} }} \right) , \quad \left( {\begin{array}{l} \varepsilon _{xx}^{\left( 1 \right) } \\ \varepsilon _{yy}^{\left( 1 \right) } \\ \gamma _{xy}^{\left( 1 \right) } \\ \end{array}} \right) =\left( {{\begin{array}{c} {\psi _{x,x} } \\ {\psi _{y,y} } \\ {\psi _{x,y} +\psi _{y,x} } \\ \end{array} }} \right) ,\quad \left( {\begin{array}{l} \varepsilon _{xx}^{\left( 3 \right) } \\ \varepsilon _{yy}^{\left( 3 \right) } \\ \gamma _{xy}^{\left( 3 \right) } \\ \end{array}} \right) =-c_1 \left( {{\begin{array}{c} {\psi _{x,x} +w_{0,xx} } \\ {\psi _{y,y} +w_{0,yy} } \\ {\psi _{x,y} +\psi _{y,x} +2 w_{0,xy} } \\ \end{array} }} \right) , \\ \left( {\begin{array}{l} \gamma _{yz}^{\left( 0 \right) } \\ \gamma _{xz}^{\left( 0 \right) } \\ \end{array}} \right) =\left( {{\begin{array}{l} {\psi _y +w_{0,y} } \\ {\psi _x +w_{0,x} } \\ \end{array} }} \right) , \quad \left( {\begin{array}{l} \gamma _{yz}^{\left( 2 \right) } \\ \gamma _{xz}^{\left( 2 \right) } \\ \end{array}} \right) =-{c}'_1 \left( {{\begin{array}{l} {\psi _y +w_{0,y} } \\ {\psi _x +w_{0,x} } \\ \end{array} }} \right) . \\ \end{array} \end{aligned}$$
(7)

Here, \({c}'_1 =3 c_1 =4/{h^{2}}\).

2.4 Equations of motion

To derive the equations of motion for embedded SLGS, the dynamic version of principle of virtual work, i.e. Hamilton’s principle is utilized, which is defined as follows [26, 41]:

$$\begin{aligned} \int _0^t {\left( {\delta U+\delta V_\mathrm{f} +\delta V_\mathrm{e} -\delta K} \right) } \mathrm{d}t=0, \end{aligned}$$
(8)

where \(\delta U\) is the virtual strain energy, \(\delta K\) is the virtual kinetic energy, and \(\delta V_\mathrm{f}\) and \(\delta V_\mathrm{e}\) are the virtual works done by the elastic medium and external applied forces, respectively.

The virtual strain energy can be expressed in the following form [39]:

$$\begin{aligned} \delta U=\int _A {\int _{- h/2}^{h/2} { (\sigma _{xx} \delta \varepsilon _{xx} +\sigma _{yy} \delta \varepsilon _{yy} +\sigma _{yz} \delta \gamma _{yz} +\sigma _{xz} \delta \gamma _{xz} +\sigma _{xy} \delta \gamma _{xy} )} } \mathrm{d}z\, \mathrm{d}A. \end{aligned}$$
(9)

The virtual kinetic energy can be written as [39]:

$$\begin{aligned} \delta K=\int _A {\int _{- h/2}^{h/2} { \rho \left( {\dot{u} \delta \dot{u}+\dot{v} \delta \dot{v}+\dot{w} \delta \dot{w}} \right) \mathrm{d}z\, \mathrm{d}A} } , \end{aligned}$$
(10)

where \(\rho \) is the density of the graphene sheet, and the dot-superscript convention indicates the differentiation with respect to the time variable.

The graphene sheet is subjected to the external applied loads and embedded on a visco-Pasternak elastic medium. Therefore, the following two distinct forces should be considered to obtain the energy of virtual works:

  • Visco-Pasternak foundation

  • External Loads

Based on the visco-Pasternak foundation, the work done by the elastic medium on the graphene sheet is given by the following relation:

$$\begin{aligned} \delta V_\mathrm{f} =\int _A {\left[ {K_\mathrm{w} w\delta w-K_\mathrm{g} \left( {w_{,xx} +w_{,yy} } \right) \delta w+C_\mathrm{d} \dot{w} \delta w} \right] } \mathrm{d}A, \end{aligned}$$
(11)

in which \(K_\mathrm{w} \) is the spring constant of the Winkler type corresponding to normal pressure, and \(K_\mathrm{g} \) is the Pasternak type relevant to transverse shear stress. Also, \(C_\mathrm{d} \) stands for damping coefficient of the elastic foundation.

The virtual work done by external applied forces can be written as [42, 43]:

$$\begin{aligned} \delta V_\mathrm{e} =\int _A {-p \delta w}\; \mathrm{d}A. \end{aligned}$$
(12)

Here, the magnitude of the distributed transverse load is indicated by p.

Substituting Eqs. (9), (10), (11) and (12) into Eq. (8), integrating by parts and setting the coefficients of \(\delta u_0 , \delta v_0 , \delta w_0 , \delta \psi _x\) and \(\delta \psi _y\) to zero yields the following system of equations of motion:

$$\begin{aligned} \delta u_0&: N_{xx,x} +N_{xy,y} =I_0 \ddot{u}_0 +J_1 \ddot{\psi }_x -c_1 I_3 \ddot{w}_{0,x} ,\end{aligned}$$
(13a)
$$\begin{aligned} \delta v_0&: N_{xy,x} +N_{yy,y} =I_0 \ddot{v}_0 +J_1 \ddot{\psi }_y -c_1 I_3 \ddot{w}_{0,y} ,\end{aligned}$$
(13b)
$$\begin{aligned} \delta w_0&: \bar{{Q}}_{x,x} +\bar{{Q}}_{y,y} +c_1 \left( {P_{xx,xx} +2P_{xy,xy} +P_{yy,yy} } \right) +p+K_\mathrm{g} \left( {w_{0,xx} +w_{0,yy} } \right) -K_\mathrm{w} w_0 \nonumber \\&=I_0 \ddot{w}_0 +C_\mathrm{d} \dot{w}_0 -c_1 ^{2}I_6 \left( {\ddot{w}_{0,xx} +\ddot{w}_{0,yy} } \right) +c_1 \left[ {I_3 \left( {\ddot{u}_{0,x} +\ddot{v}_{0,y} } \right) +J_4 \left( {\ddot{\psi }_{x,x} +\ddot{\psi }_{y,y} } \right) } \right] ,\end{aligned}$$
(13c)
$$\begin{aligned} \delta \psi _x&: \bar{{M}}_{xx,x} +\bar{{M}}_{xy,y} -\bar{{Q}}_x =J_1 \ddot{u}_0 +K_2 \ddot{\psi }_x -c_1 J_4 \ddot{w}_{0,x} ,\end{aligned}$$
(13d)
$$\begin{aligned} \delta \psi _y&: \bar{{M}}_{xy,x} +\bar{{M}}_{yy,y} -\bar{{Q}}_y =J_1 \ddot{v}_0 +K_2 \ddot{\psi }_y -c_1 J_4 \ddot{w}_{0,y} , \end{aligned}$$
(13e)

where

$$\begin{aligned}&\bar{{M}}_{\alpha \beta } =M_{\alpha \beta } -c_1 P_{\alpha \beta } , \quad \bar{{Q}}_\alpha =Q_\alpha -{c}'_1 R_\alpha ,\end{aligned}$$
(14a)
$$\begin{aligned}&I_i = \int _{-h/2}^{h/2} { \rho z^{i}\,\mathrm{d}z\quad (i=0,1 , 2,\dots ,6) } ,\end{aligned}$$
(14b)
$$\begin{aligned}&J_i =I_i -c_1 I_{i+2} ,\quad K_2 =I_2 -2 c_1 I_4 +c_1 ^{2} I_6 ,\end{aligned}$$
(14c)
$$\begin{aligned}&\left( {N_{\alpha \beta } , M_{\alpha \beta } , P_{\alpha \beta } } \right) =\int _{-h/2}^{h/2} \left( {1, z, z^{3}} \right) \sigma _{\alpha \beta }\; \mathrm{d}z,\end{aligned}$$
(14d)
$$\begin{aligned}&\left( {Q_\alpha , R_\alpha } \right) =\int _{-h/2}^{h/2} \left( {1, z^{2}} \right) \sigma _{\alpha z} \;\mathrm{d}z. \end{aligned}$$
(14e)

In the above equations, \(N_{\alpha \beta } , M_{\alpha \beta },\,P_{\alpha \beta },\, Q_\alpha \) and \(R_\alpha \) are the resultant forces, moments, higher-order moments, shear forces and higher-order shear forces, respectively.

Substituting Eq. (3) into Eqs. (14), the stress resultants can be obtained as follows:

$$\begin{aligned}&\left( {{\begin{array}{l} {\begin{array}{l} N \\ M \\ \end{array}} \\ {P } \\ \end{array} }} \right) -{\mu } \nabla ^{2}\left( {{\begin{array}{l} {\begin{array}{l} N \\ M \\ \end{array}} \\ {P } \\ \end{array} }} \right) =\left( {{\begin{array}{lll} { A}&{}\quad {B }&{}\quad {E } \\ {B }&{}\quad {D }&{}\quad {F } \\ {E }&{}\quad {F }&{}\quad {H } \\ \end{array} }} \right) \left( {\begin{array}{l} {\begin{array}{l} {{\varepsilon ^{(0)}} } \\ {{\varepsilon ^{(1)}} } \\ {\varepsilon ^{(3)}} \\ \end{array} } \\ \end{array}} \right) ,\end{aligned}$$
(15a)
$$\begin{aligned}&\left( {{\begin{array}{l} { Q } \\ {R } \\ \end{array} }} \right) -{\mu } \nabla ^{2}\,\left( {{\begin{array}{l} {Q } \\ {R } \\ \end{array} }} \right) =\left( {{\begin{array}{ll} {A}&{}\quad {D } \\ {D}&{}\quad {F } \\ \end{array} }} \right) \,\left( {{\begin{array}{l} {{\gamma ^{(0)}} } \\ {{\gamma ^{(2)}} } \\ \end{array} }} \right) , \end{aligned}$$
(15b)

in which, the plate stiffness coefficients, i.e. \(A_{ij} , B_{ij} , D_{ij} , E_{ij} , F_{ij}\) and \(H_{ij}\), are defined by [44]

$$\begin{aligned} \left( {A_{ij} , B_{ij} , D_{ij} , E_{ij} , F_{ij} , H_{ij} } \right) =\int _{-h/2}^{h/2} { Q_{ij} } \left( {1, z, z^{2}, z^{3}, z^{4}, z^{6}} \right) \mathrm{d}z. \end{aligned}$$
(16)

Substituting relations (3), (4), (14) and (16) into the equations of motion (13), the governing equations of SLGS in terms of displacements and rotations are obtained as

$$\begin{aligned}&\bar{{A}}_1 u_{0,xx} +\bar{{A}}_2 u_{0,yy} +\bar{{A}}_3 v_{0,xy} +\left( {1-{\mu } \nabla ^{2}} \right) \left( {\bar{{A}}_4 \ddot{u}_0 +\bar{{A}}_5 \ddot{w}_{0,x} +\bar{{A}}_6 \ddot{\psi }_x } \right) =0,\end{aligned}$$
(17a)
$$\begin{aligned}&\bar{{B}}_1 u_{0,xy} +\bar{{B}}_2 v_{0,xx} +\bar{{B}}_3 v_{0,yy} +\left( {1-{\mu } \nabla ^{2}} \right) \left( {\bar{{B}}_4 \ddot{v}_0 +\bar{{B}}_5 \ddot{w}_{0,y} +\bar{{B}}_6 \ddot{\psi }_y } \right) =0,\end{aligned}$$
(17b)
$$\begin{aligned}&\bar{{C}}_1 w_{0,xx} +\bar{{C}}_2 w_{0,xxxx} +\bar{{C}}_3 w_{0,xxyy} +\bar{{C}}_4 w_{0,yy} +\bar{{C}}_5 w_{0,yyyy} +\bar{{C}}_6 \psi _{x,x} +\bar{{C}}_7 \psi _{x,xxx} +\bar{{C}}_8 \psi _{x,xyy} \nonumber \\&\quad +\,\bar{{C}}_9 \psi _{y,xxy} +\bar{{C}}_{10} \psi _{y,y} +\bar{{C}}_{11} \psi _{y,yyy}\nonumber \\&\quad +\left( {1-{\mu } \nabla ^{2}} \right) \left( {\begin{array}{l} \bar{{C}}_{12} \ddot{u}_{0,x} +\bar{{C}}_{13} \ddot{v}_{0,y} +\bar{{C}}_{14} \ddot{w}_0 +\bar{{C}}_{15} \ddot{w}_{0,xx} \\ +\bar{{C}}_{16} \ddot{w}_{0,yy} +\bar{{C}}_{17} \ddot{\psi }_{x,x} +\bar{{C}}_{18} \ddot{\psi }_{y,y} +p(x,y,t) \\ +K_\mathrm{g} (w_{0,xx} +w_{0,yy} )-K_\mathrm{w} w_0 -C_\mathrm{d} \dot{w}_0 \\ \end{array}} \right) =0, \end{aligned}$$
(17c)
$$\begin{aligned}&\bar{{D}}_1 w_{0,xxx} +\bar{{D}}_2 w_{0,xyy} +\bar{{D}}_3 w_{0,x} +\bar{{D}}_4 \psi _{x,xx} +\bar{{D}}_5 \psi _{x,yy} +\bar{{D}}_6 \psi _x +\bar{{D}}_7 \psi _{y,xy} \nonumber \\&\quad +\left( {1-{\mu } \nabla ^{2}} \right) \left( {\bar{{D}}_8 \ddot{u}_0 +\bar{{D}}_9 \ddot{w}_{0,x} +\bar{{D}}_{10} \ddot{\psi }_x } \right) =0,\end{aligned}$$
(17d)
$$\begin{aligned}&\bar{{E}}_1 w_{0,xxy} +\bar{{E}}_2 w_{0,yyy} +\bar{{E}}_3 w_{0,y} +\bar{{E}}_4 \psi _{x,xy} +\bar{{E}}_5 \psi _{y,xx} +\bar{{E}}_6 \psi _{y,yy} +\bar{{E}}_7 \psi _y \nonumber \\&\quad +\left( {1-{\mu } \nabla ^{2}} \right) \left( {\bar{{E}}_8 \ddot{v}_0 +\bar{{E}}_9 \ddot{w}_{0,y} +\bar{{E}}_{10} \ddot{\psi }_y } \right) =0, \end{aligned}$$
(17e)

where the coefficients \(\bar{{A}}_i,\,\bar{{B}}_i,\,\bar{{C}}_i ,\bar{{D}}_i ,\) and \(\bar{{E}}_i\) are given as

$$\begin{aligned} \bar{{A}}_1= & {} \frac{Eh}{1-\nu ^{2}} ,\quad \bar{{A}}_2 =\frac{Eh}{2(1+\nu )} ,\quad \bar{{A}}_3 =\frac{Eh}{2(1-\nu )}, \quad \bar{{A}}_4 =-I_0 ,\quad \bar{{A}}_5 =c_1 I_3 ,\quad \bar{{A}}_6 =-J_1,\end{aligned}$$
(18a)
$$\begin{aligned} \bar{{B}}_1= & {} \bar{{A}}_3 ,\quad \bar{{B}}_2 =\bar{{A}}_2 ,\quad \bar{{B}}_3 =\bar{{A}}_1, \quad \bar{{B}}_4 =\bar{{A}}_4 ,\quad \bar{{B}}_5 =\bar{{A}}_5 ,\quad \bar{{B}}_6 =\bar{{A}}_6, \end{aligned}$$
(18b)
$$\begin{aligned} \bar{{C}}_1= & {} \frac{E}{2(1+\nu )} \int _{-h/2}^{h/2} { (1-2{c}'_{1} z^{2}+{{c}{'}_{1}^{2}}z^{4}) \mathrm{d}z} ,\quad \bar{{C}}_2 =-\frac{Ec_1 ^{2}}{1-\nu ^{2}} \int _{-h/2}^{h/2} { z^{6} \mathrm{d}z},\nonumber \\ \bar{{C}}_3= & {} 2 \bar{{C}}_2 ,\quad \bar{{C}}_4 =\bar{{C}}_1 ,\quad \bar{{C}}_5 =\bar{{C}}_2 ,\quad \bar{{C}}_6 =\bar{{C}}_1, \quad \bar{{C}}_7 =\bar{{C}}_8 =\bar{{C}}_9 =\frac{Ec_1 }{1-\nu ^{2}} \int _{-h/2}^{h/2} { (z^{4}-c_1 z^{6}) \mathrm{d}z}, \nonumber \\ \bar{{C}}_{10}= & {} \bar{{C}}_1 ,\quad \bar{{C}}_{11} =\bar{{C}}_7 ,\quad \bar{{C}}_{12} =\bar{{C}}_{13} =-c_1 I_3, \quad \bar{{C}}_{14} =-I_0 ,\quad \bar{{C}}_{15} =\bar{{C}}_{16} =c_1 ^{2}I_6 ,\quad \bar{{C}}_{17} =\bar{{C}}_{18} =-c_1 J_4, \end{aligned}$$
(18c)
$$\begin{aligned} \bar{{D}}_1= & {} \bar{{D}}_2 =\frac{Ec_1 }{1-\nu ^{2}} \int _{-h/2}^{{h}/{2}} { (-z^{4}+c_1 z^{6}) \mathrm{d}z},\quad \bar{{D}}_3 =\frac{E}{2(1+\nu )} \int _{-h/2}^{{h}/{2}} { (-1+2{c}'_{1} z^{2}-{c}_{1}^{{\prime }2}z^{4}) \mathrm{d}z},\nonumber \\ \bar{{D}}_4= & {} \frac{E}{1-\nu ^{2}} \int _{-h/2}^{{h}/{2}} { (z^{2}-2c_1 z^{4}+c_1 ^{2}z^{6}) \mathrm{d}z} ,\quad \bar{{D}}_5 =\frac{E}{2(1+\nu )} \int _{-h/2}^{{h}/{2}} { (z^{2}-2c_1 z^{4}+c_1 ^{2}z^{6}) \mathrm{d}z}, \nonumber \\ \bar{{D}}_6= & {} \bar{{D}}_3 ,\quad \bar{{D}}_7 =\bar{{D}}_4 ,\quad \bar{{D}}_8 =-J_1 ,\quad \bar{{D}}_9 =c_1 J_4 ,\quad \bar{{D}}_{10} =-k_2, \end{aligned}$$
(18d)
$$\begin{aligned} \bar{{E}}_1= & {} \bar{{E}}_2 =\frac{Ec_1 }{1-\nu ^{2}} \int _{-h/2}^{{h}/{2}} { (-z^{4}+c_1 z^{6}) \mathrm{d}z} ,\quad \bar{{E}}_3 =\frac{E}{2(1+\nu )} \int _{-h/2}^{{h}/{2}} { (-1+2{c}'_1 z^{2}-{c}_1^{{\prime }2}z^{4}) \mathrm{d}z}, \nonumber \\ \bar{{E}}_4= & {} \frac{E}{2(1-\nu )} \int _{-h/2}^{{h}/{2}} { (z^{2}-2c_1 z^{4}+c_1 ^{2}z^{6}) \mathrm{d}z} ,\quad \bar{{E}}_5 =\frac{E}{2(1+\nu )} \int _{-h/2}^{{h}/{2}} { (z^{2}-2c_1 z^{4}+c_1 ^{2}z^{6}) \mathrm{d}z}, \nonumber \\ \bar{{E}}_6= & {} \frac{E}{1-\nu ^{2}} \int _{-h/2}^{{h}/{2}} { (z^{2}-2c_1 z^{4}+c_1 ^{2}z^{6}) \mathrm{d}z} ,\quad \bar{{E}}_7 =\bar{{E}}_3 ,\quad \bar{{E}}_8 =-J_1,\quad \bar{{E}}_9 =c_1 J_4, \quad \bar{{E}}_{10} =-k_2. \end{aligned}$$
(18e)

3 Solution procedure

It is assumed that the graphene sheet has simply supported boundary conditions at all edges. Mathematical expressions of this kind of conditions can be written in the following form [39]:

$$\begin{aligned}&u_0 \left( {x,0,t} \right) =0, \quad \psi _x \left( {x,0,t} \right) =0 ,\quad u_0 \left( {x,b,t} \right) =0, \quad \psi _x \left( {x,b,t} \right) =0 ,\end{aligned}$$
(19a)
$$\begin{aligned}&v_0 \left( {0,y,t} \right) =0, \quad \psi _y \left( {0,y,t} \right) =0, \quad v_0 \left( {a,y,t} \right) =0, \quad \psi _y \left( {a,y,t} \right) =0 ,\end{aligned}$$
(19b)
$$\begin{aligned}&w_0 \left( {x,0,t} \right) =0, \quad w_0 \left( {x,b,t} \right) =0, \quad w_0 \left( {0,y,t} \right) =0, \quad w_0 \left( {a,y,t} \right) =0 ,\end{aligned}$$
(19c)
$$\begin{aligned}&N_{xx} \left( {0,y,t} \right) =0, \quad N_{xx} \left( {a,y,t} \right) =0, \quad N_{yy} \left( {x,0,t} \right) =0, \quad N_{yy} \left( {x,b,t} \right) =0 ,\end{aligned}$$
(19d)
$$\begin{aligned}&\bar{{M}}_{xx} \left( {0,y,t} \right) =0, \quad \bar{{M}}_{xx} \left( {a,y,t} \right) =0, \quad \bar{{M}}_{yy} \left( {x,0,t} \right) =0, \quad \bar{{M}}_{yy} \left( {x,b,t} \right) =0 . \end{aligned}$$
(19e)

This set of boundary conditions can be obtained by Navier’s approach. Based on the Navier solution theory, the mid-plane displacements and mid-plane rotations are solved by the following Fourier series as [39]:

$$\begin{aligned} u_0 \left( {x,y,t} \right)= & {} \sum _{m=1}^\infty { \sum _{n=1}^\infty { U_{mn} } } (t)\cos \left( {\alpha x} \right) \sin \left( {\beta y} \right) ,\end{aligned}$$
(20a)
$$\begin{aligned} v_0 \left( {x,y,t} \right)= & {} \sum _{m=1}^\infty { \sum _{n=1}^\infty { V_{mn} } } (t)\sin \left( {\alpha x} \right) \cos \left( {\beta y} \right) ,\end{aligned}$$
(20b)
$$\begin{aligned} w_0 \left( {x,y,t} \right)= & {} \sum _{m=1}^\infty { \sum _{n=1}^\infty { W_{mn} } } (t)\sin \left( {\alpha x} \right) \sin \left( {\beta y} \right) ,\end{aligned}$$
(20c)
$$\begin{aligned} \psi _x \left( {x,y,t} \right)= & {} \sum _{m=1}^\infty {\sum _{n=1}^\infty { X_{mn} } } (t)\cos \left( {\alpha x} \right) \sin \left( {\beta y} \right) ,\end{aligned}$$
(20d)
$$\begin{aligned} \psi _y \left( {x,y,t} \right)= & {} \sum _{m=1}^\infty {\sum _{n=1}^\infty { Y_{mn} } } (t)\sin \left( {\alpha x} \right) \cos \left( {\beta y} \right) , \end{aligned}$$
(20e)

where \(\alpha ={(m\pi )/a}, \beta =(n \pi )/b,\) and \(m,\,n\) are the half wave numbers in the x and y directions, respectively. Moreover, the transverse mechanical load may be written in the double Fourier sine expansion as follows:

$$\begin{aligned} p\left( {x,y,t} \right) =\sum _{m=1}^\infty { \sum _{n=1}^\infty { p_{mn} (t)} } \sin \left( {\alpha x} \right) \sin \left( {\beta y} \right) . \end{aligned}$$
(21)

Here, the coefficients \(p_{mn} (t)\) for two types of dynamic load distribution at the top surface of SLGS are presented as

$$\begin{aligned} \begin{aligned}&p_{mn} (t)=\frac{16 P(t)}{mn\pi ^{2}} \quad (m,n=1, 3,5, \dots )\quad \hbox {for uniform load}, \\&p_{mn} (t)=P(t) \quad (m=n=1)\quad \hbox {for sinusoidal load}, \end{aligned} \end{aligned}$$
(22)

where \(P(t) =P_0 H(t)\), and \(P_0\) is the intensity of distributed applied load, and H(t) is the Heaviside step function defined as \(H(t)=\left\{ {{\begin{array}{l} {1 \quad t\ge 0,} \\ {0 \quad t<0}. \\ \end{array} }} \right. \)

Substituting Eqs. (20) and (21) into the governing Eqs. (17), the following system of equations is obtained in a matrix form as

$$\begin{aligned} {M_{mn} } {\ddot{\Delta }_{mn} } + {C_{mn} } {\dot{\Delta }_{mn} } +{K_{mn} } {\Delta _{mn} } ={F_{mn} }, \end{aligned}$$
(23)

where \( {\Delta _{mn} } = ({U_{mn} V_{mn} W_{mn} X_{mn} Y_{mn} }) ^\mathrm{T}\) is the displacement vector. In addition, the \(M,\, C\) and K are the mass, damping and stiffness matrices, respectively, which are obtained as follows:

$$\begin{aligned} \begin{aligned} M_{11}&=\bar{{A}}_4 (1+{\mu } \alpha ^{2}+{\mu } \beta ^{2}), \quad M_{13} =\bar{{A}}_5 \alpha (1+{\mu } \alpha ^{2}+{\mu } \beta ^{2}),\quad M_{14} =\bar{{A}}_6 (1+{\mu } \alpha ^{2}+{\mu } \beta ^{2}),\\ M_{22}&=\bar{{B}}_4 (1+{\mu } \alpha ^{2}+{\mu } \beta ^{2}), \quad M_{23} =\bar{{B}}_5 (1+{\mu } \alpha ^{2}+{\mu } \beta ^{2}), \quad M_{25}=\bar{{B}}_6 (1+{\mu } \alpha ^{2}+{\mu } \beta ^{2}), \\ M_{31}&=M_{13} , \quad M_{32} =M_{23} , \quad M_{33}=(\bar{{C}}_{14} - \alpha ^{2}\bar{{C}}_{15} -\beta ^{2}\bar{{C}}_{16} )(1+{\mu } \alpha ^{2}+{\mu } \beta ^{2}),\\ M_{34}&=-\alpha \bar{{C}}_{17} (1+{\mu } \alpha ^{2}+{\mu } \beta ^{2}), \quad M_{35} =-\beta \bar{{C}}_{18} (1+{\mu } \alpha ^{2}+{\mu } \beta ^{2}),\\ M_{41}&=M_{14} , \quad M_{43} =M_{34}, \quad M_{44} =\bar{{D}}_{10} (1+{\mu } \alpha ^{2}+{\mu } \beta ^{2}),\\ M_{52}&=M_{25} , \quad M_{53} =M_{35}, \quad M_{55} =\bar{{E}}_{10} (1+{\mu } \alpha ^{2}+{\mu } \beta ^{2}). \end{aligned} \end{aligned}$$
(24a)

Other \(M_{ij}\)’s are equal to zero.

$$\begin{aligned} C_{33} =-C_\mathrm{d} (1+{\mu } \alpha ^{2}+{\mu } \beta ^{2}). \end{aligned}$$
(24b)

Other \(C_{ij}\)’s are equal to zero.

$$\begin{aligned} \begin{aligned} K_{11}&=-\alpha ^{2}\bar{{A}}_1 -\beta ^{2}\bar{{A}}_2 , \quad K_{12} =-\alpha \beta \bar{{A}}_3,\quad K_{21} =K_{12} , \quad K_{22} =-\alpha ^{2}\bar{{B}}_2 -\beta ^{2}\bar{{B}}_3,\\ K_{33}&=-\alpha ^{2} \bar{{C}}_1 +\alpha ^{4} \bar{{C}}_2 +\alpha ^{2}\beta ^{2} \bar{{C}}_3 -\beta ^{2} \bar{{C}}_4 +\beta ^{4} \bar{{C}}_5 -K_\mathrm{w} (1+{\mu } \alpha ^{2}+{\mu } \beta ^{2}) -K_\mathrm{g} (\alpha ^{2}+\beta ^{2} ) (1+{\mu } \alpha ^{2}+{\mu } \beta ^{2}) ,\\ K_{34}&=-\alpha \bar{{C}}_6 +\alpha ^{3}\bar{{C}}_7 +\alpha \beta ^{2}\bar{{C}}_8 , \quad K_{35} =\alpha ^{2}\beta \bar{{C}}_9 -\beta \bar{{C}}_{10} +\beta ^{3}\bar{{C}}_{11},\\ K_{43}&=K_{34} , \quad K_{44} =-\alpha ^{2} \bar{{D}}_4 -\beta ^{2} \bar{{D}}_5 +\bar{{D}}_6 , \quad K_{45} =-\alpha \beta \bar{{D}}_7,\\ K_{53}&=K_{35} , \quad K_{54} =K_{45} , \quad K_{55} =-\alpha ^{2} \bar{{E}}_5 -\beta ^{2} \bar{{E}}_6 +\bar{{E}}_7. \end{aligned} \end{aligned}$$
(24c)

In static analysis, the displacement vector is time independent. Hence, both mass and damping matrices should be neglected. The solution of the system \( {K_{mn} } {\Delta _{mn} } = {F_{mn} } \) leads to the close-form expressions for each element of the displacement vector. When the displacement vector is known, rotations and displacements of SLGS are obtained using Eqs. (20).

For the purpose of the dynamic bending analysis, Eq. (23) must be solved by using the Laplace transformation. Performing the Laplace transform on Eq. (23) and considering zero initial conditions at the initial time (namely, \({\Delta _{mn} } = {\dot{\Delta }_{mn} } =0\) at \(t=0\)) yields a new system of equations in which time dependency is eliminated as follows:

$$\begin{aligned} {K_{mn} +sC_{mn} +s^{2}M_{mn} } {\bar{{\Delta }}_{mn} } = {\bar{{F}}_{mn} }. \end{aligned}$$
(25)

Here, s is the Laplace transform parameter, and the bar superscript indicates transformed quantities.

Solving the system of equations (25), each component of the displacement vector is derived in the Laplace domain. Analytical Laplace inversion technique is employed to return the displacement vector from Laplace domain into the real-time domain.

Table 1 Geometrical and material properties of the SLGS [24]
Full size table

A function \(\hat{{f}}(s)={A(s)/B(s)}\) can be used to find the unknown variables in Eq. (25) in the Laplace transformation domain. Both functions A(s) and B(s) are in the form of polynomials. Let us suppose that the roots of the function B(s)are known. Some of the roots are real roots which are denoted by \(r_{i,}\), and the others are complex and indicated by \(c_{i}\). Number of \(r_{i}\) and \(c_{i}\) are shown as \(n_{r}\) and \(n_{c}\), respectively. When all roots are simple, the inverse of the function \(\hat{{f}}(s)\), that is f(t), is obtained as [45]

$$\begin{aligned} f(t)={\mathrm {Re}}\left( {\sum _{i=1}^{n_c } {\frac{A(c_i )}{{B}'(c_i )}\mathrm{e}^{c_i t}} } \right) +\sum _{j=1}^{n_r } {\frac{A(r_j )}{{B}'(r_j )}\mathrm{e}^{r_j t}}, \end{aligned}$$
(26)

where Re(x) denotes the real part of the complex number, x and the prime specifies a derivative with respect to s . Following the mentioned approach, each component of the displacement vector is derived analytically. Carrying out the above inverse method, the natural frequencies of the system are obtained exactly when the damping is absent. As \(c_j ={\mathrm {Re}} (c_j )+\mathrm{i~Im} (c_j ), j=1, 2, \dots , n_c\) are calculated, the absolute magnitude of the imaginary parts, i.e. \(\left| {\mathrm{Im} (c_j )} \right| \)are the natural frequencies.

4 Results and discussion

Based on the procedure outlined in the previous sections, the numerical results and detailed discussion are explained in this section to study the static and dynamic bendings of SLGS. The effects of various parameters such as small-scale parameter, kind of the applied load, surrounded medium, length-to-thickness ratio (a / h) and aspect ratio (a / b) of nanoplate are investigated. In this study, boundary conditions of the plate are assumed to be simply supported in all edges. Geometrical and material properties of the SLGS are chosen from Table 1. The values of the length to thickness ratio and aspect ratio are assumed to be 10 and 1, respectively, except those that are being stated in the text. Also, magnitude of the applied load is \(P_0 =10^{6}\,\hbox {N/m}^{2}\).

4.1 Static analysis

Neglecting the small-scale effect, Table 2 gives the comparison of non-dimensional deflection of classical plates under uniformly distributed load versus the shear and Winkler parameters and length-to-thickness ratio. Same as [6], the dimensionless Winkler and Pasternak (shear) parameters are \(k_\mathrm{w} ={(K_\mathrm{w} b^{4})}/{D}\) and \(k_\mathrm{g} ={(K_\mathrm{g} b^{2})}/{D}\), respectively, in which \(D={E h^{3}}/[{12 (1-\nu ^{2})}]\) is the bending rigidity of the nanoplate. The present results have been compared to those reported by [46] based on simple refined shear deformation theory in Table 2. As seen, a good agreement between the results is found. Based on the results in this table, it can be concluded that for constant a / h, when each parameter of elastic foundation increases, deflection decreases. Because increasing the Winkler or Pasternak coefficients augments the resistance of springs against plate bending.

Table 2 Comparison of the non-dimensional deflection \(\bar{{w}}=({10^{3} w_\mathrm{c} D})/{P_0 a^{4}}\) for square plate versus the Pasternak and Winkler parameters subjected to uniform loads
Full size table
Table 3 Dimensionless deflection \((\bar{{w}}=({10^{3} w_\mathrm{c} D})/{P_0 a^{4}})\) of the SLGS versus the Pasternak and Winkler foundations subjected to uniform loads for different nonlocal parameters
Full size table

Table 3 illustrates the obtained results of the non-dimensional deflection \(\bar{{w}}\) of the SLGS versus the nonlocal parameter for various values of the elastic foundation parameters subjected to uniform load. It can be realized that the deflection increases when the nonlocal parameter increases. This is because of the fact that increasing small-scale parameter makes the SLGS more flexible and thus the deflection increases. Also, it can be seen that with presence of elastic foundation, the difference between the local (i.e. \(\mu =0\)) and nonlocal (i.e. \(\mu \ne 0\)) results starts to decline. Moreover, increasing the stiffness constants decreases the size dependency of the bending deflection. It is also worth mentioning that the Pasternak foundation (i.e. \(K_\mathrm{g}\ne 0\) and \(K_\mathrm{w}\ne 0\)) is more effective than the Winkler foundation (i.e. \(K_\mathrm{g}=0\) and \(K_\mathrm{w}\ne 0\)) to reduce the deflection of the nanoplate. This is due to the fact that the Winkler foundation considers the normal stresses, while Pasternak elastic foundation considers not only the normal stresses, but also the transverse shear deformation.

Table 4 Effect of the aspect ratio, length-to-thickness ratio and nonlocal parameter on the non-dimensional central deflections \((\bar{{w}}=({10^{2} w_\mathrm{c} Eh^{3}})/{P_0 a^{4}})\) of SLGSs subjected to sinusoidal and uniform loads
Full size table

Finally, Table 4 presents the results of non-dimensional maximum deflection for different values of nonlocal parameter and thickness of square and rectangular nanoplates subjected to uniform and sinusoidal loads. It is observed that when the aspect ratio increases, the non-dimensional maximum deflection decreases, significantly. Also, the results show that the difference between the solutions of the nonlocal and local theory is more distinguished in greater values of aspect ratio. As the aspect ratio increases, the SLGSs become smaller for a specified length of the nanoplates. This leads to an increase in the small-scale effect because size dependency plays an essential role in the nonlocal elasticity theory. Herein, to investigate the effect of nonlocal parameter, the relative error percent is defined as

$$\begin{aligned} \mathrm{Relative\,Error\,Percent}=\frac{\left| {\mathrm{{Local\,Result}}-\mathrm{{Nonlocal\,Result}}} \right| }{\left| \mathrm{Local\,Result} \right| }\times 100. \end{aligned}$$
(27)

For example, the relative error percent for aspect ratios 1 and 2 with \({\mu } =2\,\mathrm{nm}^{2}\) and \(a/h =50\) are 13.66 and 34.15 %, respectively. This shows the noticeable influence of the nonlocal parameter on the deflection of SLGS in the higher aspect ratios. Moreover, it can be observed that the deflection of SLGS with lower length-to-thickness ratio (i.e. \(a/h=20\)) are strongly affected by the nonlocal parameter than those of the nanoplates with relatively higher length-to-thickness ratios. In other words, the small-scale parameter has a slight effect on the deflection as the length-to-thickness ratio increases. As one should notice, the deflection not only depends on the small-scale parameter, length-to-thickness ratio and aspect ratio, but also on the external load type. Finally, it can be seen that the central deflection of the nanoplate subjected to uniform loading is more than sinusoidal loading, as found by [39].

4.2 Dynamic response analysis

To the best of the authors’ knowledge no published literature is available for dynamic response of SLGS resting on the visco-Pasternak foundation. In the absence of similar publications in the literature covering the same scope of the problem, one cannot directly validate the results found here. However, partially comparison can be carried out by Reddy [44] for analysing functionally graded material (FGM) plate under a uniformly distributed load based on the finite elements method. For this purpose, the geometric properties are assumed to be \(a=b=0.2\,\hbox {m}\), \(h=0.01\,\hbox {m}\) and loading intensity is \(P_0 =10^{6}\, \hbox {N/m}^{2}\). Also, material properties of the FGM are chosen similar to those adopted in [44], namely, for metal and ceramic were assumed to be \(E_\mathrm{m} =70\, \mathrm{GPa}, \nu _\mathrm{m} =0.3, \rho _\mathrm{m} =2707\,\mathrm{kg}/{\mathrm{m}^{3}}\) and \(E_\mathrm{c} =151\, \mathrm{GPa}, \nu _\mathrm{c} =0.3, \rho _\mathrm{c} =3000 \,\mathrm{kg}/{\mathrm{m}^{3}}\), respectively. Moreover, the central deflection and time are normalized as \(w^{{*}}=({w_\mathrm{c} hE_\mathrm{m} })/({a^{2}P_0 })\) and \(t^{{*}}=t\sqrt{{E_\mathrm{m} }/({a^{2}\rho _\mathrm{m} })}\). In Fig. 2, the results of the present method for the central deflection - have been compared to those reported in [44] using FEM for a simply supported FG square plate subjected to the uniformly load. As observed, in this case, our outcomes agree excellent with the finite elements results.

Fig. 2
figure 2

Comparison between deflection time-history of the centre of FG square plate under the uniform load

Full size image
Fig. 3
figure 3

Deflection history of a SLGS subjected to uniform load for various nonlocal parameters

Full size image

In order to perform dynamic analysis, non-dimensional form of the central deflection and time are defined as \(w^{{*}}=({w_\mathrm{c} hE})/({a^{2}P_0 })\) and \(t^{{*}}=t\sqrt{{E}/({a^{2}\rho })}\), respectively. Also, a thick SLGS with \(a/h=10\) is considered, except those that are being specifically stated in the text.

As a first example, Fig. 3 depicts the effect of small-scale parameter for SLGS subjected to a uniformly applied load. It is obvious that the small-scale parameter is a significant parameter in the analysis of nanomaterials and should not be neglected. Therefore, if the local elasticity theory \((\mu =0)\) is used, then the value will be under-predicted. As can be observed, an increase in small-scale parameter causes the higher amplitude of deflection in the plate.

Fig. 4
figure 4

The influence of load type on the dimensionless dynamic deflection of the SLGS with various nonlocal parameters

Full size image
Fig. 5
figure 5

Deflection history of the SLGS subjected to uniform load for various a / h ratios \((\mu =1\,\hbox {nm}^{2})\)

Full size image

In Fig. 4, the SLGS is illustrated under sinusoidal and uniform loadings for different values of the small-scale parameters. It can be seen that the response to a uniform load is higher than that to a sinusoidal load at the same nonlocal parameter. Moreover, the influence of the small-scale parameters for nanoplate subjected to uniform load is more than sinusoidal load.

Fig. 6
figure 6

Central deflection versus time for different Pasternak and Winkler foundations for the SLGS under uniform load. a \(\mu =1\,\hbox {nm}^{2}\) and b \(\mu =2\,\hbox {nm}^{2}\)

Full size image
Fig. 7
figure 7

Time–displacement curve of the SLGS under uniform load for various damping coefficients \((\mu =1\,\hbox {nm}^{2})\)

Full size image

Dynamic responses of the SLGS for various values of length-to-thickness ratio (i.e. \(a/h=10,\, 20,\, 50\)) is demonstrated in Fig. 5 in which the nonlocal parameter \((\mu )\) is assumed to be \(1\,\hbox {nm}^{2}\). It is interesting to note that as a / h decreases, the lateral deflection decreases. It is due to the fact that when a / h decreases, the nanoplate becomes thicker. Consequently, the lateral deflection decreases.

Influences of the elastic medium, including Winkler and Pasternak foundations in different nonlocal parameters, on the dynamic response of the SLGS are displayed in Fig. 6a and b. It can be seen that the difference between the dynamic responses with and without foundation increases with increasing the value of the small-scale parameter. It means that the elastic foundation is a significant factor for decreasing the dynamic response of the nanoplate and must be considered, particularly in the higher small-scale parameters. Also, an elastic foundation diminishes the dynamic response of the nanoplate in comparison with the contactless conditions. Besides, when the Pasternak foundation (\(K_\mathrm{g}\ne 0\) and \(K_\mathrm{w}\ne 0\)) is present, the deflection amplitude of SLGS is more reduced in comparison with the Winkler foundation (\(K_\mathrm{g}=0\) and \(K_\mathrm{w}\ne 0\)). Because Pasternak elastic foundation is modelled by adding a shear layer to the Winkler foundation. Therefore, the influence of Pasternak foundation on the reduction of dynamic response is considerable and should be investigated in bending analysis.

Figure 7 demonstrates the effect of damping on the dynamic response of contactless SLGS. As seen, the damping coefficient is found to have remarkable effect on the dynamic response of SLGS, especially for large damping parameters, where forced vibration response of the plate is damped quickly. It means that increasing the damping constant causes to decrease in the deflection.

5 Conclusion

In this study, an analytical method for static bending and dynamic response analysis of a simply supported SLGS resting on the visco-Pasternak foundation subjected to uniform and sinusoidal loads was presented. The effect of small scale was included by the nonlocal elasticity constitutive relations. The governing equations of motion were derived based on the TSDT and solved by means of Fourier series–Laplace transform technique. Several parametric studies were performed to show the effects of various parameters such as small-scale parameter, length-to-thickness ratio, aspect ratio, types of loading, the Winkler and Pasternak coefficients and damping parameter. The following main results were concluded:

  • Since increasing the small-scale parameter increases the non-dimensional midpoint deflection of nanoplate, this parameter is quite significant and should not be neglected for analysis of nanostructures. In addition, it can be seen that the central deflection of the SLGS subjected to uniform loading is more than sinusoidal loading.

  • The presence of the elastic foundation has an effective role on the stability of the SLGS. Increasing the Winkler and Pasternak constants leads to decrease the central deflection. Also, increasing the Winkler and Pasternak coefficients reduces the size dependency of the bending deflection. The results indicate that Pasternak foundation has more effect on reducing the deflection than the Winkler foundation.

  • The nonlocal effect on the deflection of SLGS is more prominent as the length-to-thickness ratio decreases (i.e. the nanoplate becomes thicker) and the aspect ratios increases.

  • Since the elastic foundation increases the stiffness of the nanoplate, it is a significant factor for decreasing the dynamic response of the nanoplate and must be considered, especially in the higher small-scale parameters.

  • The damping coefficient has a remarkable effect on the dynamic response of SLGS, particularly for large damping values, where forced vibration response of the plate is damped quickly. It means that increasing the damping constant causes to decrease deflection of nanoplate.

It is hoped that this work can be employed for optimum design and analysing of nanoscale devices.