Dynamics of a high speed coned thrust bearing with a Navier slip boundary condition

Abstract

A modified Reynolds equation for flow dynamically represented as incompressible is used to model the dynamics of a thin film bearing with slip flow and a rapidly rotating coned rotor. Previous studies including a Navier slip length shear condition on the bearing faces are extended to investigate applications with a coned bearing gap. A modified Reynolds equation for the film flow is coupled, through the pressure exerted by the fluid film, to the dynamic motion of the stator. Introducing a new variable leads to explicit analytical expressions for the pressure field and force on the stator with the equation for the time-dependent face clearance transformed to a nonlinear second-order non-autonomous ordinary differential equation. The face clearance for periodic axial motion of the coned rotor is obtained using a stroboscopic map solver; a focus is investigating bearing behaviour under extreme conditions. The coupled fluid flow and unsteady bearing dynamics are examined for a range of configurations to evaluate potential face contact over a range of bearing surface conditions.

1 Introduction

Thrust bearing technology typically utilises a thin fluid film to maintain a face clearance between the rotor and stator, when subjected to external axial loads through generating changes in local film pressure from the differential motion of the rotating and stationary elements.

Typical bearing geometries include a journal bearing with a supporting cylindrical sleeve containing a rotating cylindrical shaft separated by a thin air film, as studied by Belforte et al. [1]; a slider bearing comprising two non-parallel moving plates separated by a thin lubricating air film, as considered by Witelski [2]; and a thrust bearing which has an important significance dynamically in turbomachinery applications operating with very high rotational speeds.

In advanced engineering applications, an increased lubrication force on the stator can be obtained by incorporating a coned rotor. In early stability studies of coned bearings, Etison [3] studied the stability and response of a coned-face seal in the presence of rotor axial runout and assembly misalignment. An optimal coning angle was identified, as the one at which the stability is maximised. While examining a similar coned seal under a range of pressurisations, Green and Etison [4] concluded that axial stability exists if the film converges in the direction of the pressure drop or if there is a sufficiently high support stiffness in a divergent film. A divergent air film can lead to seal failure in cases of low support stiffness, low pressure gradient or large coning angles. Green [5] extended the bearing study, examining positive and negative coning angles consistent with a convergent air gap. To avoid face contact and maintain positive stiffness, a critical angle exists depending on geometric restrictions. Green and Barnsby [6] showed negative coning is resilient against hydrostatic instabilities, although still prone to dynamics instabilities.

Additional centrifugal inertia effects, which can be important in turbomachinery applications requiring operation at higher rotational speeds, were studied by Garratt et al. [7] for a thrust bearing. The bearing dynamics were investigated when one face undergoes prescribed periodic axial oscillations of amplitude smaller than the equilibrium film thickness, and the other face moves axially in response to the film dynamics. Considering similar geometry with incompressible flow and incorporating a coned rotor, Bailey et al. [8] provided more extensive analytical investigations and examined the effect of prescribed axial oscillations with amplitude larger than the equilibrium film thickness. Results indicated that the fluid film thickness can become very small causing the classical no-slip velocity condition to become invalid. Therefore, a slip condition on the bearing faces is included in the analysis of a parallel bearing with a small face clearance by Bailey et al. [9], with results giving no face contact, although the bearing gap can become very thin. In this work, the case of a coned bearing with a small face clearance is analysed to evaluate if contact can occur.

Fluid flows confined to micro- and nano scales are subject to surface effects beginning to dominate over volume-related phenomena, requiring accurate details of the fluid–solid interaction. In the case of a gas film, the Knudsen number $\text {Kn} = l / \hat{h}_0$, with $l$ as the mean free path and $\hat{h}_0$ the characteristic fluid thickness, is usually used to classify mathematical models for thin gas-flow regimes. The fluid is regarded as continuum for small Knudsen number ($\text {Kn} \le 10^{-3}$) where the no-slip boundary condition is valid. For larger Knudsen number between $10^{-3}$ and $10^{-1}$, a continuum model is still valid, but slip boundary conditions are usually implemented, which is the flow regime of interest in the present work. The flow is in a transition region for a Knudsen number between $10^{-1}$ and $10$, where a modified continuum model is required and in the case of a larger Knudsen number ($\text {Kn} \ge 10$), the free molecular flow can be modelled by molecular dynamics [10]. When classifying very thin flow regimes for a liquid, the Knudsen number can be used, but with the mean free path replaced by the intermolecular distance between molecules, giving exceedingly small fluid thickness using the above classification. When considering liquid flow over a hydrophilic surface, even on a nano scale, the classical no-slip boundary condition appears to hold; however, when considering a hydrophobic surface an apparent slip velocity has been observed just above the solid surface.

Slip flow has been studied in an inclined plain slider bearing by Burgdorfer [11] who devised a first-order slip model where the boundary slip velocity was identified at a mean free path distance from the wall. A non-axisymmetric thrust bearing with foil pads on the rotor face was examined by Park et al. [12] where the gas flow is coupled to the bearing structure. A Reynolds equation with slip was derived, and the bearing dynamics were investigated for rotor displacement of small amplitude in comparison to the film thickness, using existing perturbation analysis with results given for the no-slip and slip conditions. More extensive details on previous bearing studies incorporating slip flow are given in Bailey et al. [9].

The increasing performance advantages for bearings to operate with reduced gap between the rotor and stator motivated the study of a thin film model valid for slip flow. This study extends the formulation, analysis and predictions of the previous study of Bailey et al. [8] in which a coned thrust bearing is considered within a classical no-slip condition which predicts that face contact will not occur, although a period of very close proximity may exist. New bearing technologies are requiring bearing gap thicknesses to become very small and maintain appropriate dynamic properties to sufficiently resist the possibility of face contact and maintain a minimum gap thickness. A focus of this work is to incorporate a more general slip condition more relevant to modelling the fluid film under extreme operating conditions and evaluating the corresponding film flow and bearing behaviour. A slip length model is developed which couples the thrust bearing structure to flow dynamics induced by the fluid force exerted. An extended bearing model incorporates high-speed rotational bearing operation through centrifugal fluid inertia. The formulation of the coupled governing equations is presented in Sect. 2, including the Reynolds equation in terms of a slip boundary condition characterised by a slip length parameter, and the stator displacement equation. A representative single nonlinear second-order non-autonomous ordinary differential equation for the face clearance is derived in Sect. 3. To solve for the periodic bearing face clearance iteratively, a stroboscopic map solver is formulated and numerical procedure identified with an extension to the solver, identifying the value of slip length corresponding to a prescribed minimum face clearance (MFC) in the period. Detailed evaluation of the steady coned bearing is given in Sect. 4 and for the dynamic bearing in Sect. 5 to explore the dynamical behaviour and influence of increasing effects of slip boundary conditions through selected parameter studies. The possibility of contact through a parameter study, including the slip length and coning angle is examined in Sect. 6. To verify the numerical solution in the limit of small face clearance asymptotic analysis is carried out, and two different symbolic computations were used to verify the correctness of the lengthy algebra.

2 Geometric configuration

A simplified mathematical model of a fluid lubricated bearing containing a coned rotor, such as developed in Bailey et al. [8], is extended by incorporating a slip condition on the bearing faces. The coaxial annular rotor and stator have inner and outer dimensional radii of $\hat{r}_\mathrm{I}$ and $\hat{r}_\mathrm{O}$, respectively, and the rotor has angular rotation $\hat{\Omega }$. The rotor has a fixed coning angle, assumed to be small giving $\cos \hat{\beta }\simeq 1$ and $\sin \hat{\beta }\simeq \hat{\beta }$, with cases of a positively and negatively coned bearings considered, referred to as PCB and NCB, respectively. Pressures $\hat{p}_\mathrm{I}$ and $\hat{p}_\mathrm{O}$ are imposed at the inner and outer radii of the bearing, respectively, allowing a pressure gradient to drive the radial flow.

The axisymmetric rotor–stator clearance is defined with reference to the point of minimum film thickness; at the inside, radius for a PCB given by

$$\begin{aligned} \hat{h}(\hat{r},\hat{\beta },\hat{t})=\hat{h}_\mathrm{s}(\hat{t})-\hat{h}_\mathrm{r}(\hat{r}_\mathrm{I},\hat{t})+(\hat{r}-\hat{r}_\mathrm{I})\tan \hat{\beta }= \hat{h}_\mathrm{s}(\hat{t})-\epsilon \hat{h}_0\sin (\hat{\omega } \hat{t})+(\hat{r}-\hat{r}_\mathrm{I})\tan \hat{\beta }, \end{aligned}$$

(1)

and at the outer, radius for an NCB is given by

$$\begin{aligned} \hat{h}(\hat{r},\hat{\beta },\hat{t})=\hat{h}_\mathrm{s}(\hat{t})-\hat{h}_\mathrm{r}(\hat{r}_\mathrm{O},\hat{t})+(\hat{r}-\hat{r}_\mathrm{O})\tan \hat{\beta }= \hat{h}_\mathrm{s}(\hat{t})-\epsilon \hat{h}_0\sin (\hat{\omega } \hat{t})+(\hat{r}-\hat{r}_\mathrm{O})\tan \hat{\beta }. \end{aligned}$$

(2)

Here $\hat{h}_\mathrm{s}$ is the stator height, and the rotor height is given by $\hat{h}_\mathrm{r} = \hat{h}_\mathrm{r}(\hat{r}_j,\hat{t})-(\hat{r}-\hat{r}_j)\tan \hat{\beta }$ with $j$ = I, O for the PCB and NCB, respectively, with a temporal dependence $\hat{h}_\mathrm{r}(\hat{r}_j,\hat{t})$ at the reference height and a spatial dependence $(\hat{r}-\hat{r}_j)\tan \hat{\beta }$. The prescribed axial motion of the rotor is modelled by $\hat{h}_\mathrm{r}(\hat{r}_j,\hat{t})=\epsilon \hat{h}_0\sin \left( \hat{\omega }\,\hat{t}\,\right)$, with amplitude $\epsilon \hat{h}_0$ where $\hat{h}_0$ is the equilibrium film thickness at the inner and outer radii for a PCB, NCB, respectively.

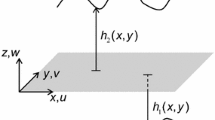
Deriving the velocity boundary conditions for a slip bearing requires the normal and tangential velocities on the rotor and stator to be specified, due to the additional slip component on the bearing face. Both PCB and NCB are considered separately in the coordinate system $(\hat{z}, \hat{r}, \hat{\theta })$ with velocities $(\hat{w}, \hat{u},\hat{v})$. Configurations of the PCB and NCB are shown in Fig. 1.

Fig. 1

Axially symmetric geometry and notation of a bearing with a PCB $\hat{\beta }>0$ and NCB $\hat{\beta }<0$ with normal vector $\hat{n}^\mathrm{r}$ and two orthogonal tangential components $t_1$ and $t_2$ on the face of the rotor with the origin of the coordinate system at the inner radius of the annulus

The PCB and NCB have the same normal and azimuthal tangent given by

$$\begin{aligned} \hat{n}^\mathrm{r}=(\cos \hat{\beta },\sin \hat{\beta },0), \quad \hat{t}_2=(0,0,1), \end{aligned}$$

(3)

respectively, whereas the axial tangents are given by

$$\begin{aligned} \hat{t}_{1,+}=(-\sin \hat{\beta },\cos \hat{\beta },0),\quad \hat{t}_{1,-}=(\sin \hat{\beta },-\cos \hat{\beta },0), \end{aligned}$$

(4)

for the PCB and NCB, respectively, requiring separate radial velocity boundary conditions to be derived.

The stator lies parallel to the radial direction, giving the normal vector $\hat{n}^\mathrm{s}$ in the negative $\hat{z}$ direction and two orthogonal tangential components, $t_3$ and $t_4$ on the face of the stator in the radial and azimuthal directions, respectively.

A first-order Navier formulation slip model is implemented as used by Burgdorfer [11] for the case of an inclined, plain slider bearing, where the slip velocity is proportional to the tangential component of the face shear. The velocity boundary conditions comprise a jump in the tangential velocity across the fluid–solid interface, which is equal to the slip velocity induced due to wall shear, and continuity of the normal velocity with a no flux condition. Thus, the velocity boundary conditions on the rotor and stator are given by

$$\begin{aligned} \begin{aligned}&\hat{u} \cdot \hat{t}_1-\hat{u}^{r} \cdot \hat{t}_1=2\hat{l_\mathrm{s}}\hat{e}_{ij}\hat{n}_j\hat{t}_{1,i},\quad \hat{u} \cdot \hat{t}_2-\hat{u}^\mathrm{r} \cdot \hat{t}_2=2\hat{l_\mathrm{s}}\hat{e}_{ij}\hat{n}_j\hat{t}_{2,i},\quad \hat{u} \cdot \hat{n}^\mathrm{r}-\hat{u}^\mathrm{r} \cdot \hat{n}^\mathrm{r}=0\quad \text {at} \quad \hat{z}=\hat{h}_\mathrm{r},\\&\hat{u} \cdot \hat{t}_3-\hat{u}^\mathrm{s} \cdot \hat{t}_3=2\hat{l_\mathrm{s}}\hat{e}_{ij}\hat{n}_j\hat{t}_{3,i},\quad \hat{u} \cdot \hat{t}_4-\hat{u}^\mathrm{s} \cdot \hat{t}_4=2\hat{l_\mathrm{s}}\hat{e}_{ij}\hat{n}_j\hat{t}_{4,i},\quad \hat{u} \cdot \hat{n}^\mathrm{s}-\hat{u}^\mathrm{s} \cdot \hat{n}^\mathrm{s}=0\quad \text {at} \quad \hat{z}=\hat{h}_\mathrm{s}. \end{aligned} \end{aligned}$$

(5)

The rotor velocity components denoted by superscript r, are given by $\hat{\mathbf {u}}^\mathrm{r}=(\partial \hat{h_\mathrm{r}}/\partial \hat{t}, 0,\hat{\Omega }\hat{r})$ corresponding to prescribed axial motion and fixed azimuthal rotation. The stator is allowed to move axially due to the interaction with the fluid, giving the stator velocity, denoted by superscript $s$, as $\hat{\mathbf {u}}^\mathrm{s}=(\partial \hat{h_\mathrm{s}}/\partial \hat{t}, 0,0)$.

Velocity boundary conditions on the rotor in (5) are given by

$$\begin{aligned} \hat{u}\cos \hat{\beta } - \hat{w}\sin \hat{\beta }= & {} - \frac{\partial \hat{h_\mathrm{r}}}{\partial \hat{t}}\sin \hat{\beta } + \hat{l_\mathrm{s}} \left( \left( \frac{\partial \hat{u}}{\partial \hat{z}} + \frac{\partial \hat{w}}{\partial \hat{r}}\right) \left( \cos ^2\hat{\beta }-\sin ^2\hat{\beta }\right) + 2\left( \frac{\partial \hat{u}}{\partial \hat{r}} - \frac{\partial \hat{w}}{\partial \hat{z}}\right) \cos \hat{\beta }\sin \hat{\beta }\right) \!,\nonumber \\ \hat{v} - \hat{\Omega }\hat{r}= & {} \hat{l_\mathrm{s}}\left( \hat{r}\frac{\partial }{\partial \hat{r}}\left( \frac{\hat{v}}{\hat{r}}\right) \sin \hat{\beta } + \frac{\partial \hat{v}}{\partial \hat{z}}\cos \hat{\beta }\right) \!,\nonumber \\ \hat{w}\cos \hat{\beta } + \hat{u}\sin \hat{\beta }= & {} \frac{\partial \hat{h_\mathrm{r}}}{\partial t}\cos \hat{\beta }, \end{aligned}$$

(6)

using the normal and tangent vectors given in (3) and (4) and the rate of strain tensor components as given in Batchelor [13], p. 602]. In an axisymmetric configuration, the azimuthal derivatives do not appear.

The velocity boundary conditions on the stator (5), give

$$\begin{aligned} \hat{u}= -\hat{l}_\mathrm{s}\left( \frac{\partial \hat{u}}{\partial \hat{z}} + \frac{\partial \hat{w}}{\partial \hat{r}}\right) ,\quad \hat{v}=-2\hat{l}_\mathrm{s}\frac{\partial \hat{v}}{\partial \hat{z}},\quad \hat{w}=\frac{\partial h_\mathrm{s}}{\partial \hat{t}}. \end{aligned}$$

(7)

A model for the incompressible fluid flow through the bearing is derived from the Navier–Stokes momentum and continuity equations in axisymmetrical coordinates. Variables are non-dimensionalized with respect to the typical bearing radius $\hat{r}_0$, rotor velocity $\hat{\Omega } \hat{r}$ and time scale $\hat{T} = 1/\hat{\omega }$, with dimensionless time variable $t = \hat{\omega }\hat{t}$ where $\hat{\omega }$ is the angular frequency. Dimensionless velocities are taken to be $\hat{u}/\hat{U}$, $\hat{v}/\hat{\Omega } \hat{r}_0$ and $\hat{w}/\hat{h}_0\hat{T}^{-1}$ with dimensionless radius and height given by $r=\hat{r}/\hat{r}_0$ and $z=\hat{z}/\hat{h}_0$, respectively. The dimensionless slip length is given by $l_\mathrm{s}=\hat{l}_\mathrm{s}/\hat{h}_0$.

The associated radial and azimuthal Reynolds numbers and relative ratio are given, respectively, by

$$\begin{aligned} \text {Re}_U = \frac{\hat{\rho } \hat{r}_0\hat{U}}{\hat{\mu }}, \quad \text {Re}_\Omega = \frac{\hat{\rho } \hat{r}_0^2\hat{\Omega }}{\hat{\mu }} \quad \text {and}\quad \text {Re}^* = \frac{\text {Re}_\Omega }{\text {Re}_U} = \frac{\hat{\Omega }\hat{r}_0}{\hat{U}}. \end{aligned}$$

(8)

The aspect ratio $\delta _0$, squeeze number $\tilde{\sigma }$ and Froude number Fr are defined as

$$\begin{aligned} \delta _0 = \frac{\hat{h}_0}{\hat{r}_0},\quad \tilde{\sigma }=\frac{\hat{r}_0}{\hat{U}\hat{T}}\quad \text {and}\quad \text {Fr}=\frac{\hat{U}}{\sqrt{\hat{g}\hat{h}_0}}, \end{aligned}$$

(9)

respectively, where $\hat{g}$ is the acceleration due to gravity, $\hat{\rho }$ the density and $\hat{\mu }$ the dynamic viscosity.

For thin film bearings $\delta _0 \ll 1$ and to ensure that the effects of viscosity are retained at leading order, the pressure is scaled as $\hat{P}=\hat{\mu } \hat{r}_0\hat{U}/\hat{h}_0^2$. Classical lubrication theory neglects inertia due to the reduced Reynolds number $\text {Re}_U\delta _0^2\ll 1$; however, as was done in Garratt et al. [7], the centrifugal inertia is retained to include cases of high rotational-speed bearing operations for which terms of the order $\text {Re}_U\delta _0^2 (\text {Re}^*)^2$ are considered to be of $O(1)$, with $(\text {Re}^*)^2\gg 1$. The squeeze number $\tilde{\sigma }$ characterises any time-dependent effects, whilst the Froude number Fr parameterises the importance of the gravitational effects relative to the radial flow although gravity can be neglected with $\text {Re}_U\delta _0^2\text {Fr}^{-2}\ll 1$; this is consistent with lubrication theory provided that the Froude number is $O(1)$. Importantly for more general application, it can be shown that under the present approximation, the flow field with a very thin film air bearing (nano scale gap) the usual incompressible solenoidal condition remains valid for compressible flow when the following conditions are satisfied:

$$\begin{aligned} \frac{\hat{U}^2}{{\hat{c}_0}^2}\frac{1}{\text {Re}_U{\delta _0}^2}\tilde{\sigma } \ll 1,\quad \frac{ \hat{g} \hat{h}_0}{{\hat{c}_0}^2}\tilde{\sigma } \ll 1,\quad \frac{\hat{\Omega }^2{\hat{r}_0}^2}{{\hat{c}_0}^2}\frac{1}{\text {Re}_{U}\delta _0^2}\ll 1, \end{aligned}$$

(10)

as found in Bailey et al. [9].

To leading order, where terms of $O(\delta _0)$ are neglected, the governing lubrication equations become

$$\begin{aligned}&-\frac{\partial p}{\partial r} + \frac{\partial ^2 u}{\partial z^2}=-\eta \frac{v^2}{r},\quad \frac{\partial ^2 v}{\partial z^2}=0,\quad \frac{\partial p}{\partial z}=0, \end{aligned}$$

(11)

$$\begin{aligned}&\frac{1}{r}\frac{\partial }{\partial r}(r u)+\tilde{\sigma }\frac{\partial w}{\partial z}=0, \end{aligned}$$

(12)

where the speed parameter $\eta =\text {Re}_U\delta _0^2 (\text {Re}^*)^2=\hat{\rho } \hat{r}_0 \hat{h}_0^2 \hat{\Omega }^2/\hat{\mu } \hat{U}$ characterises the importance of centrifugal inertia. For the derivation, see Bailey et al. [8]. Using (11) and (12) and (63)–(65) from Appendix 1, analytic expressions can be found for $u$, $v$ and $w$ in terms of the unknown stator position $h_\mathrm{s}(t)$.

In the case of a small coning angle $\beta$ with prescribed periodic oscillations, the dimensionless film thickness is given by

$$\begin{aligned} \begin{aligned} h(r,\beta ,t)&=h_\mathrm{s}(t)-\epsilon \sin t+(r-a)\beta \quad \text {for}\quad \beta >0,\\ h(r,\beta ,t)&=h_\mathrm{s}(t)-\epsilon \sin t+(r-1)\beta \quad \text {for}\quad \beta <0, \end{aligned} \end{aligned}$$

(13)

where $h_\mathrm{s}(t)$ is the height of the axially displaced stator and $a=\hat{r}_\mathrm{I}/\hat{r}_0$ is a measure of the bearing width, $0<a<1$. The coning angle is assumed small, giving $\sin \hat{\beta }\simeq \hat{\beta }=O(\delta _0)$ and $\cos \hat{\beta }=1+O(\delta _0)$ leading to the scaling $\hat{\beta }=\beta \delta _0$ with $\beta =O(1)$, giving consistency with the lubrication condition, such that $\partial h_\mathrm{r}/\partial r \simeq -\beta$.

Under these conditions, the leading-order non-dimensional rotor and stator velocity boundary conditions given in (6) and (7), respectively, become

$$\begin{aligned} \begin{aligned}&u=l_\mathrm{s}\frac{\partial u}{\partial z},\quad v=r +l_\mathrm{s}\frac{\partial v}{\partial z},\quad w=\frac{\partial h_\mathrm{r}}{\partial t} - \frac{u}{\tilde{\sigma }}\beta \quad \text {at}\quad z=h_\mathrm{r},\\&u=-l_\mathrm{s}\frac{\partial u}{\partial z},\quad v=-l_\mathrm{s}\frac{\partial v}{\partial z},\quad w=\frac{\partial h_\mathrm{s}}{\partial t} \quad \text {at} \quad z=h_\mathrm{s}. \end{aligned} \end{aligned}$$

(14)

The only dependence on the coning angle is given in the axial rotor velocity boundary condition.

The governing equation for flow in the bearing is obtained by integrating the continuity equation (12) between the rotor and the stator, and applying the Leibniz integral rule gives

$$\begin{aligned} w(h_\mathrm{s})-w(h_\mathrm{r})=-\frac{1}{\sigma r}\left( \frac{\partial }{\partial r}\int ^{h_\mathrm{s}}_{h_\mathrm{r}(r)}(ru)\partial z + \left( ur\frac{\partial h_\mathrm{r}}{\partial r}\right) _{z=h_\mathrm{r}}\right) . \end{aligned}$$

(15)

To leading order, imposing the velocity boundary conditions from (14) and using the expression for the radial velocity (63) gives the modified Reynolds equation

$$\begin{aligned} \sigma \frac{\partial h}{\partial t}-\frac{1}{r}\frac{\partial }{\partial r}\left( r\frac{\partial p}{\partial r}(h^3+6l_\mathrm{s}h^2)\right) + \frac{\lambda }{r}\frac{\partial }{\partial r}\left( \frac{r^2}{(h+2l_\mathrm{s})^2}\left( h^5+10h^4l_\mathrm{s}+\frac{70}{3}h^3l_\mathrm{s}^2+20h^2l_\mathrm{s}^3\right) \right) =0, \end{aligned}$$

(16)

where $\lambda =3\eta /10$ and $\sigma =12\tilde{\sigma }$. The Reynolds equation (16) has no explicit dependence on the coning angle and expresses the relationship between the pressure $p$ and film thickness $h$. Pressure boundary conditions at the inner and outer radii of the bearing are defined in dimensionless variables as

$$\begin{aligned} p=p_\mathrm{I}\quad \text {at} \quad r = a \quad \text {and}\quad p=p_\mathrm{O} \quad \text {at} \quad r=1. \end{aligned}$$

(17)

Axial displacement of the stator is modelled using a spring-mass-damper model giving the axial position of the stator in dimensional variables as

$$\begin{aligned} \begin{aligned}&\frac{\text {d}^2h_\mathrm{s}}{\text {d} t^2}+D_\mathrm{a}\frac{\text {d} h_\mathrm{s}}{\text {d} t}+K_z(h_\mathrm{s}-1)=\alpha F(t)\quad \text {for}\quad \beta >0,\\&\frac{\text {d}^2h_\mathrm{s}}{\text {d} t^2}+D_\mathrm{a}\frac{\text {d} h_\mathrm{s}}{\text {d} t}+K_z(h_\mathrm{s}-(1-a)\beta -1)=\alpha F(t)\quad \text {for}\quad \beta <0, \end{aligned} \end{aligned}$$

(18)

with $h_\mathrm{s}(t)$ defined at the origin of reference as shown in Fig. 1 with the film thickness at the inner radius taken as $h=1$ to give the stator height $h_\mathrm{s}=1$ for PCB and $h_\mathrm{s}=1+(1-a)\beta$ for an NCB. In (18), $F(t)$ is the resultant dimensionless axial force on the stator defined by

$$\begin{aligned} F(t)=2\pi \int ^1_\mathrm{a}(p-p_\mathrm{a})r\;\text {d}r, \end{aligned}$$

(19)

where $p_\mathrm{a}$ is the ambient pressure above the stator and the force coupling dimensionless parameter given by $\alpha =\hat{\mu } \hat{U}/(\hat{m}\hat{\omega }^2\delta _0^3)$, considered to be of $O(1)$. Bearing quantities $D_\mathrm{a}=\hat{D}_\mathrm{a}/(\hat{m}\hat{\omega })$ and $K_z=\hat{K}_z/(\hat{m}\hat{\omega }^2)$ are coefficients or dimensionless linear damping and effective restoring force, respectively, with $\hat{D}_\mathrm{a}$ and $\hat{K}_z$ as their corresponding dimensional values and $\hat{m}$ the mass of the stator.

The corresponding radial flux through the bearing is obtained from the integration of the radial flow velocity over an azimuthal bearing cross section and is given in Appendix 1, Eq. (66). The steady-state streamfunction along a radial cross section is obtained from the integration of the velocity components $(u,w)$ and is given by (67).

3 Bearing gap equation

Displacement of the stator is coupled by the periodic forcing of the rotor through the fluid film flow. To solve the Reynolds equation (16) and stator equation (18) simultaneously, it is mathematically convenient to introduce a measure of the bearing gap through the time-dependent magnitude of the MFC as

$$\begin{aligned} g(t)=h_\mathrm{s}(t)-\epsilon \sin t, \end{aligned}$$

(20)

occurring at the inner radius for a PCB and outer radius for an NCB. It is shown the system-dependent quantities can be characterised by $g(t)$ which is given as the solution of an explicit integro-differential equation.

Integrating the modified Reynolds equation (16) and imposing the pressure boundary conditions (17) gives

$$\begin{aligned} p(g(t),r)= & {} p_\mathrm{I} + (p_\mathrm{O}-p_\mathrm{I})\frac{G(g(t),r)}{G(g(t),1)}+ \frac{\sigma }{2}\frac{\text {d}g}{\text {d}t}\left( H(g(t),r)-\frac{H(g(t),1)}{G(g(t),1)}G(g(t),r)\right) \nonumber \\&+ \lambda \left( L(g(t),r)-\frac{L(g(t),1)}{G(g(t),1)}G(g(t),r)\right) {,} \end{aligned}$$

(21)

where the integrals $G(g,r)$, $H(g,r)$ and $L(g,r)$, for a PCB, are calculated from

$$\begin{aligned} G(g,r)= & {} \int ^\mathrm{r}_\mathrm{a}\frac{1}{x((g+(x-a)\beta )^3+6l_\mathrm{s}(g+(x-a)\beta )^2)}\text {d}x,\end{aligned}$$

(22)

$$\begin{aligned} H(g,r)= & {} \int ^\mathrm{r}_\mathrm{a}\frac{x}{(g+(x-a)\beta )^3+6l_\mathrm{s}(g+(x-a)\beta )^2}\text {d}x,\end{aligned}$$

(23)

$$\begin{aligned} L(g,r)= & {} \int ^\mathrm{r}_\mathrm{a}\frac{x\left( (g+(x-a)\beta )^5 + 10(g+(x-a)\beta )^4l_\mathrm{s} \right) }{((g+(x-a)\beta )^3+6l_\mathrm{s}(g+(x-a)\beta )^2)(g+(x-a)\beta +2l_\mathrm{s})^2}\nonumber \\&+\frac{x\left( \frac{70}{3}(g+(x-a)\beta )^3l_\mathrm{s}^2 +20(g+(x-a)\beta )^2l_\mathrm{s}^3\right) }{((g+(x-a)\beta )^3+6l_\mathrm{s}(g+(x-a)\beta )^2)(g+(x-a)\beta +2l_\mathrm{s})^2} \text {d}x, \nonumber \\ \end{aligned}$$

(24)

with exact evaluations given in Appendix 2 as (69), (71) and (73). The pressure is a function of the parameters $\lambda$, $\beta$ and $l_\mathrm{s}$, and the functions $G$, $H$, and $L$ are functions of $\beta$ and $l_\mathrm{s}$. Similar expressions are derived for an NCB. In this way, a complex closed form solution of the pressure field is obtained as a function of unknown stator position $h_\mathrm{s}(t)$. Separate calculations are needed for the limiting case of no-slip due to an apparent numerical singularity at $l_\mathrm{s}=0$ in the expansion for $G$ and $H$ given in the Appendix. Full expressions for $G$, $H$ and $L$ are given in Appendix 2 as (70), (72) and (74).

The force on the stator is obtained from the integration of the pressure field (21) using the force integral in (19), giving

$$\begin{aligned} F(t)= & {} \pi \left( A(g(t)) + \frac{\text {d}g}{\text {d}t}B(g(t))\right) \!{.} \end{aligned}$$

(25)

Expressions for $A$ and $B$ are defined as

$$\begin{aligned}&A(g,\lambda ,\beta ,l_\mathrm{s})=(1-a^2)(p_\mathrm{I}- p_\mathrm{a}) + 2(p_\mathrm{O}-p_\mathrm{I})\frac{G_\mathrm{I}}{G(g,1)}+ 2\lambda \left( L_\mathrm{I}-\frac{L(g,1)}{G(g,1)}G_\mathrm{I}\right) \!,\end{aligned}$$

(26)

$$\begin{aligned}&B(g,\beta ,l_\mathrm{s})=\sigma \left( H_\mathrm{I}-\frac{H(g,1)}{G(g,1)}G_\mathrm{I}\right) \!. \end{aligned}$$

(27)

The integrals $G_\mathrm{I}$, $H_\mathrm{I}$ and $L_\mathrm{I}$ are given by

$$\begin{aligned} G_\mathrm{I}(g)=\int ^1_\mathrm{a}rG(g,r) \text {d}r,\qquad H_\mathrm{I}(g)=\int ^1_\mathrm{a}rH(g,r)\text {d}r,\qquad L_\mathrm{I}(g)=\int ^1_\mathrm{a}rL(g,r)\text {d}r, \end{aligned}$$

(28)

with exact evaluations for a PCB given in Appendix 2, Eqs. (75)–(80) which are functions of the parameters $\lambda$, $\beta$ and $l_\mathrm{s}$. Separate expressions are given for the limiting case of no-slip $l_\mathrm{s}=0$. Similar expressions are derived for an NCB.

Substituting the force expression (25) and stator height from (20) into Eq. (18) gives a nonlinear second-order non-autonomous ordinary differential equation for the periodic time-dependent minimum bearing gap as

$$\begin{aligned} \frac{\text {d}^2g}{\text {d} t^2}+D(g,\beta ,l_\mathrm{s})\frac{\text {d} g}{\text {d} t}+S(g,\lambda ,\beta ,l_\mathrm{s})=\Upsilon \sin (t+\phi ), \end{aligned}$$

(29)

where

$$\begin{aligned} \begin{aligned}&D(g,\beta ,l_\mathrm{s})=D_\mathrm{a}-\alpha \pi B(g,\beta ,l_\mathrm{s}),\\&S(g,\lambda ,\beta ,l_\mathrm{s})=K_z(g-1)-\alpha \pi A(g,\lambda ,\beta ,l_\mathrm{s}),\\&\Upsilon \sin (t+\phi )=\epsilon ((1-K_z)\sin t -D_\mathrm{a}\cos t), \end{aligned} \end{aligned}$$

(30)

for a PCB. An NCB only differs in the term; $S(g,\lambda ,\beta ,l_\mathrm{s})=K_z(g-(1-a)\beta -1)-\alpha \pi A(g,\lambda ,\beta ,l_\mathrm{s})$. In this way, a simple ordinary differential equation is defined for the minimum bearing gap, as a function of the unknown stator height, $h_\mathrm{s}(t)$. Dynamically Eq. (29) corresponds to a harmonically forced oscillator with nonlinear damping coefficient $D(g,\beta ,l_\mathrm{s})$ and effective restoring force $S(g,\lambda ,\beta ,l_\mathrm{s})$.

The total stiffness of the system is defined as

$$\begin{aligned} K_{zT}=\frac{\text {d}S}{\text {d} g}=K_z - \alpha \pi \frac{\text {d} A}{\text {d} g}, \end{aligned}$$

(31)

comprising a structural component $K_z$ and a fluid stiffness term

$$\begin{aligned} K_{zf}= & {} -\alpha \pi \frac{\text {d} A(g,\lambda ,\beta ,l_\mathrm{s})}{\text {d}g}\nonumber \\= & {} -\alpha \pi \left( 2\lambda \left( \frac{\partial L_\mathrm{I}}{\partial g} -\frac{\partial L(g,1)}{\partial g}\frac{G_\mathrm{I}}{G(g,1)}-\frac{\partial G_\mathrm{I}}{\partial g}\frac{L(g,1)}{G(g,1)}\right. +\frac{\partial G(g,1)}{\partial g}\frac{L(g,1)}{G(g,1)^2}G_\mathrm{I}\right) \nonumber \\&\left. +2(P_\mathrm{O}-P_\mathrm{I})\left( \frac{\partial G_\mathrm{I}}{\partial g}\frac{1}{G(g,1)}-\frac{G_\mathrm{I}}{G(g,1)^2}\frac{\partial G(g,1)}{\partial g}\right) \right) \!, \end{aligned}$$

(32)

using the expression for $A(g,\lambda ,\beta ,l_\mathrm{s})$ in (26).

Details on solving Eq. (29) are given in the next subsection where a stroboscopic map solver is formulated, using Newton’s method to find periodic solutions. To compute solutions for an increased value of the slip length $l_\mathrm{s} + \bigtriangleup l_\mathrm{s}$, an Euler–Newton scheme (parameter continuation) is developed. The Euler procedure can be directly extended to find threshold values of the slip length corresponding to a minimum value of the MFC over the period, with the limiting case of contact given by $g_{\min }=0$.

3.1 Numerical method

Solutions to Eq. (29) for a fixed bearing configuration are denoted by the vector $\mathbf {g}(g(t),z(t))$, for a given initial conditions $g(t_0)=g_0$, $z(t_0)=z_0$ and fixed value of slip length $l_\mathrm{s}$, and are sought from the equivalent system of two first-order differential equations,

$$\begin{aligned} \frac{\text {d}g}{\text {d}t} = z\quad \text {and}\quad \frac{\text {d}z}{\text {d} t}=-D(g)z-S(g)+ Y\sin (t+\phi ). \end{aligned}$$

(33)

It is anticipated that for a fixed value of slip length $l_\mathrm{s}$ and period of prescribed rotor oscillation $T$, the system of equations (33) has periodic solutions. Thus, a mapping is constructed which advances any initial condition $\mathbf {g}_0$ at time $t_0$ by a time $T$, defining a stroboscopic map $\phi (T;\mathbf {g}_0,t_0)$. This $\mathbb {R}^2\rightarrow \mathbb {R}^2$ map, integrates the system of equations (33) forward through one period of the forcing term. To identify periodic solutions, the fixed points of the stroboscopic map $\mathbf {g}(t)=\mathbf {g}(t+T)$ are found iteratively, corresponding to the condition

$$\begin{aligned} \mathbf {g}(T)-\mathbf {g}(t_0)=\mathbf {\phi }(T;\mathbf {g_0},t_t)-\mathbf {g_0}=\mathbf {G}(\mathbf {\phi }(T;\mathbf {g_0},t_t),\mathbf {g_0})=0, \end{aligned}$$

(34)

giving periodic solutions $\mathbf {g}(g(t),z(t))$.

Solutions are found numerically from an iterative Newton’s method, given an initial guess value $\tilde{g}_0$. Successively improved iterates $\mathbf {g}_0$ are given from the numerical iterative scheme

$$\begin{aligned} \mathbf {g_0}_{n+1} = {\tilde{\mathbf{g_0}}}_n-J(T)^{-1}(\mathbf {g}(T)-{\tilde{\mathbf{g_0}}}_n), \end{aligned}$$

(35)

where the Jacobian matrix is given by

$$\begin{aligned} J(T)=\frac{\partial \mathbf {G}(\mathbf {\phi },\mathbf {g_0})}{\partial \mathbf {g_0}}= \left( \begin{array}{cc} \dfrac{\partial g(T)}{\partial g_0}-1 &{} \quad \dfrac{\partial g(T)}{\partial z_0}\\ \dfrac{\partial z(T)}{\partial g_0}&{} \quad \dfrac{\partial z(T)}{\partial z_0}-1 \end{array}\right) . \end{aligned}$$

(36)

To find the elements of the Jacobian matrix $J(T)$, the following auxiliary system of first-order differential equations is defined;

$$\begin{aligned} \begin{aligned}&\frac{\partial }{\partial t}\left( \frac{\partial g}{\partial g_0}\right) =\frac{\partial z}{\partial g_0},\quad \quad \quad \frac{\partial }{\partial t}\left( \frac{\partial z}{\partial g_0}\right) =-\frac{\partial D}{\partial g}\frac{\partial g}{\partial g_0}z -D\frac{\partial z}{\partial g_0} -\frac{\partial S}{\partial g}\frac{\partial g}{\partial g_0},\\&\frac{\partial }{\partial t}\left( \frac{\partial g}{\partial z_0}\right) =\frac{\partial z}{\partial z_0},\quad \quad \quad \frac{\partial }{\partial t}\left( \frac{\partial z}{\partial z_0}\right) =-\frac{\partial D}{\partial g}\frac{\partial g}{\partial z_0}z -D\frac{\partial z}{\partial z_0} -\frac{\partial S}{\partial g}\frac{\partial g}{\partial z_0}, \end{aligned} \end{aligned}$$

(37)

with initial conditions

$$\begin{aligned} \frac{\partial g}{\partial g_0}=1,\quad \frac{\partial z}{\partial g_0}=0,\quad \frac{\partial g}{\partial z_0}=0,\quad \frac{\partial z}{\partial z_0}=1. \end{aligned}$$

(38)

The values of the elements of the Jacobian matrix are given by the values of the auxiliary variables at the end of the forcing period, $t=T$, corresponding to the time at which periodicity is tested for.

Thus, for any given initial condition, a solution of the system of equations (33) and (37) for $t_0\le t \le T$ can be found using MATLAB’s ode15s routine. This procedure is repeated recursively, with the improved value of $\mathbf {g_0}$ used in the system of equations (33). The scheme is successively repeated until a prescribed tolerance, $tol$, is achieved, i.e. $\mid \mathbf {g}(T)-\mathbf {g_0}(t_0)\mid \le \text {tol}$ and a periodic solution is obtained.

To find a periodic solution for increasing slip lengths $l_\mathrm{s} + \bigtriangleup l_\mathrm{s}$, a new initial condition is needed. This is done via parameter continuation, which means the solution is now defined with the slip length as a parameter; $\mathbf {g}(T)=\mathbf {\phi }(T;\mathbf {g_0},t_0,l_{s0})$.

To define a new initial condition $\mathbf {g_0}$ for $l_\mathrm{s} + \bigtriangleup l_\mathrm{s}$, first, the derivative of $\mathbf {G}(\mathbf {\phi }(T;\mathbf {g_0},t_t),\mathbf {g_0})= \mathbf {\phi }(T;\mathbf {g_0},t_t)-\mathbf {g_0}=0$ is taken with respect to the slip parameter $l_\mathrm{s}$, i.e.

$$\begin{aligned} \frac{\partial \mathbf {G}}{\partial \mathbf {g_0}}\frac{\partial \mathbf {g_0}}{\partial l_\mathrm{s}} + \frac{\partial \mathbf {\phi }}{\partial l_\mathrm{s}} = J(T)\frac{\partial \mathbf {g_0}}{\partial l_\mathrm{s}} + \frac{\partial \mathbf {g}(T)}{\partial l_\mathrm{s}}=0. \end{aligned}$$

(39)

Then an Euler predictor step is performed

$$\begin{aligned} \mathbf {g_0}(l_\mathrm{s}+\bigtriangleup l_\mathrm{s})=\mathbf {g_0}(l_\mathrm{s}) + \frac{\partial \mathbf {g_0}}{\partial l_\mathrm{s}}\bigtriangleup l_\mathrm{s} = \mathbf {g_0}(l_\mathrm{s}) -J(T)^{-1}\frac{\partial \mathbf {g}(T)}{\partial l_\mathrm{s}}\bigtriangleup l_\mathrm{s}, \end{aligned}$$

(40)

and a new initial condition $\mathbf {g_0}$ for $l_\mathrm{s} + \bigtriangleup l_\mathrm{s}$ is defined. The inverse of the Jacobian matrix is as found previously, at the value of $l_\mathrm{s}$ for which a periodic solution was obtained.

To find the values of $\partial \mathbf {g}(T)/\partial l_\mathrm{s}$ the following auxiliary system of first-order differential equations is defined;

$$\begin{aligned} \frac{\partial }{\partial t}\left( \frac{\partial g}{\partial l_\mathrm{s}}\right)= & {} \frac{\partial z}{\partial l_\mathrm{s}},\qquad \frac{\partial }{\partial t}\left( \frac{\partial z}{\partial l_\mathrm{s}}\right) = -\frac{\partial D}{\partial l_\mathrm{s}}z -\frac{\partial D}{\partial g}\frac{\partial g}{\partial l_\mathrm{s}}z-D\frac{\partial z}{\partial l_\mathrm{s}}-\frac{\partial S}{\partial l_\mathrm{s}}-\frac{\partial S}{\partial g}\frac{\partial g}{\partial l_\mathrm{s}}, \end{aligned}$$

(41)

with initial conditions

$$\begin{aligned} \frac{\partial g}{\partial l_\mathrm{s}}=0,\quad \frac{\partial z}{\partial l_\mathrm{s}}=0. \end{aligned}$$

(42)

This system of equations can be coupled with the previous augmented system of equations and solved using the same MATLAB routine.

The above Newton procedure is iterated until convergence is achieved and a periodic solution for $l_\mathrm{s} +\bigtriangleup l_\mathrm{s}$ is found. To ensure Newton’s method converges it may be necessary to reduce the value of $\bigtriangleup l_\mathrm{s}$; typically the initial value of $\bigtriangleup l_\mathrm{s}$ was successively divided by two until a convergent solution was found.

A major advantage of the above numerical (Euler) procedure is that it can be directly extended to find threshold values of the slip length $l_\mathrm{s}$ corresponding to a minimum value of the MFC over the period, $g_{\min }$, with the limiting case of contact given by $g_{\min }=0$. In this approach, the slip length $l_\mathrm{s}$ is taken as a new dependent variable in the Newton scheme to determine the value of the unknown vector $\mathbf {g}=(g(T),z(T),l_\mathrm{s})$ given an initial guess value $\mathbf {g}_0=(g_0,z_0,l_{s0})$. Correspondingly additional constraint equation $g_{\min }-g^*=0$ is added, with $g^*$ as the prescribed $g_{\min }$ and the corresponding Jacobian matrix given by

$$\begin{aligned} J=\left( \begin{array}{ccc} \frac{\partial g(T)}{\partial g_0}-1 &{} \quad \frac{\partial g(T)}{\partial z_0} &{} \quad \frac{\partial g(T)}{\partial l_\mathrm{s}}\\ \frac{\partial z(T)}{\partial g_0} &{} \quad \frac{\partial z(T)}{\partial z_0}-1 &{} \quad \frac{\partial z(T)}{\partial l_\mathrm{s}}\\ \frac{\partial g_{\min }}{\partial g_0}-1 &{} \quad \frac{\partial g_{\min }}{\partial z_0} &{}\quad \frac{\partial g_{\min }}{\partial l_\mathrm{s}}\\ \end{array}\right) \!. \end{aligned}$$

(43)

The additional terms in the Jacobian matrix (43) with respect to (36), i.e. the last row and column in (43), are obtained from the solution of the augmented system of first-order differential equation (37) and (41). The values in the last row are determined at the time when $g_{\min }$ is achieved. The threshold slip length value, at the specified $g_{\min }$, can be stepped down successively to the point of contact, $g^*=0$. Continuation is used for a new value of the specified $g^*$ to get

$$\begin{aligned} \mathbf {g_0}(g^*+\bigtriangleup g^*)= \mathbf {g_0}(g^*) -J^{-1}\frac{\partial \mathbf {g}}{\partial g^*}{\bigtriangleup }g^*, \end{aligned}$$

(44)

with the Jacobian matrix as defined in (43) and $\bigtriangleup g^*<0$. The value of $\partial \mathbf {g}/ \partial g^*$ is evaluated numerically by a first-order forward finite difference approximation, in terms of the obtained solution $\mathbf {g}(g^*)$ and a new auxiliary solution $\mathbf {g}(\tilde{g}^*)$, corresponding to a specified $g_{\min }$, $\tilde{g}^*=g^* + \epsilon \bigtriangleup g^*$, with $\epsilon \ll 1$. This leads to a new initial condition being defined, allowing a periodic solution for a decreased $g_{\min }$ value $g^*+\bigtriangleup g^*$ to be found.

4 Effects of slip on steady-state bearing flow

In this section, the influences of the slip effects on the fluid flow in a steady-state bearing are examined. The stator is fixed axially at $h_\mathrm{s}=1$ and rotor axially fixed at $h_\mathrm{r}=0$ at the inner or outer radius for a PCB or NCB, respectively, with $g=1$ and $\epsilon =0$. The rotor has constant azimuthal velocity. Two classes of bearing pressurisation with typical values are used: internal pressurisation with $p_\mathrm{I}=2$, $p_\mathrm{O}=1$ and external pressurisation $p_\mathrm{I}=1$, $p_\mathrm{O}=2$. Results reported here correspond to $a=0.2$, i.e. a wide bearing of width $1-a=0.8$. Similar results occur for other values of $a$, with smaller variations on the pressure profile and larger variations on the velocity profiles as the value of $a$ increases.

The pressure is investigated for the presence of non-monotonic behaviour by examining the derivative of the pressure (21) with respect to $r$,

$$\begin{aligned} \frac{\partial p}{\partial r} =\frac{(p_\mathrm{O}-p_\mathrm{I})}{G(1,1)}\frac{\partial G(1,r)}{\partial r} - \lambda \left( \frac{L(1,1)}{G(1,1)}\frac{\partial G(1,r)}{\partial r} - \frac{\partial L(1,r)}{\partial r}\right) \!. \end{aligned}$$

(45)

A bearing with negligible inertia effects $\lambda =0$, under ambient pressure ($p_\mathrm{I}=p_\mathrm{O}$) has pressure gradient $\partial p/\partial r=0$, while under internal and external pressurisation the pressure field minima are dictated by $\partial G/ \partial r=0$, with

$$\begin{aligned} \frac{\partial G(1,r)}{\partial r} = \frac{1}{(1+(r-a)\beta )^2(1+(r-a)\beta +6l_\mathrm{s})r}. \end{aligned}$$

(46)

Thus, both PCB and NCB have a monotonic pressure field for finite slip lengths, as a minimum occurs only at $r=\infty$. The location of the minima when including inertia effects $\lambda \ne 0$ is given by $\partial p/\partial r=0$, requiring the numerical evaluation of

$$\begin{aligned} \frac{1}{G(1,1)}\left( \frac{p_\mathrm{O}-p_\mathrm{I}}{\lambda } + L(1,1)\right) = \frac{r^2(Wr^3 +Xr^2+Yr+Z)(1+(r-a)\beta )^2}{(1+(r-a)\beta +2l_\mathrm{s})^2}, \end{aligned}$$

(47)

with

$$\begin{aligned}&W=\beta ^3,\quad X=\beta ^2(3+10l_s-3a\beta ),\qquad Y=\beta \left( 3+20l_s+\frac{70}{3}{l_s}^2-\beta (6a+20l_sa)+3a^2\beta ^2\right) \!,\nonumber \\&Z=1+10l_s+\frac{70}{3}{l_s}^2+20{l_s}^3-\beta \left( 20al_s-3a-\frac{70}{3}{l_s}^2a\right) +\beta ^2(10a^2ls+3a^2-a^3\beta ^3), \end{aligned}$$

(48)

and $G(1,1)$ and $L(1,1)$ as given in Appendix 2. Figure 2 shows the minimum position $r_{\min }$ with the increasing speed parameter for the case of a PCB under external and internal pressurisations. A monotonic pressure field exists when inertia effects are negligible, i.e. $\lambda =0$, independent of the slip length. Increasing the speed parameter, $\lambda \ne 0$, causes a minimum to develop at the inner and outer radii, for external and internal pressurisation respectively, before moving into the bearing. The value of $r_{\min }$ decreases or increases with the increasing slip length in the case of external or internal pressurisations, respectively. Substituting the location of the minimum $r_{\min }$ into the pressure equation (21) gives the minimum pressure decreasing monotonically with the increasing speed parameter, which can become negative. Increasing the slip length causes the pressure to increase, tending to the large finite slip length limit.

Fig. 2

The radial position $r_{\min }$ and pressure value $p_{\min }$ at the minimum in the pressure field for increasing speed parameter $0\le \lambda \le 10$ and slip length $0\le l_\mathrm{s}\le 10^6$ in the case of a PCB under a external and b internal pressurisation; $\epsilon =0$, $\sigma =1$

The radial flux in a steady bearing can be examined by integrating the steady-state Reynolds equation from (16) to give

$$\begin{aligned} \!-r\frac{\partial p}{\partial r}h^2(h+6l_\mathrm{s}) + \lambda \frac{r^2h^2}{(h+2l_\mathrm{s})^2}(h^3+10h^2l_\mathrm{s}+\frac{70}{3}h{l_\mathrm{s}}^2+20{l_\mathrm{s}}^3) = C. \end{aligned}$$

(49)

where the left-hand side of (49) is proportional to the flux (66). The constant $C$ is obtained by substituting the steady pressure field (21) into (49), giving the steady flux as

$$\begin{aligned} Q=\frac{\pi }{6G(1,1,\beta ,l_\mathrm{s})}\left( p_\mathrm{I}-p_\mathrm{O}+\lambda L(1,1,\beta ,l_\mathrm{s})\right) . \end{aligned}$$

(50)

A bearing with negligible inertia effects $\lambda =0$ and ambient pressure has zero flux, corresponding to azimuthal flow only, as can be identified from velocity field expressions (63)–(65). Imposing internal or external pressurisation across the bearing gives the radial flux as being unidirectional outward or inward flow, respectively. For non-zero speeds $\lambda \ne 0$, a critical value $\lambda _c$ can arise where zero flux through the bearing is achieved; the flow driven by the pressure gradient exactly balances the flow due to high speed rotation. The critical speed parameter $\lambda _c$, found from (50), is given by

$$\begin{aligned} \lambda _c=\frac{p_\mathrm{O}-p_\mathrm{I}}{L(1,1,\beta ,l_\mathrm{s})}, \end{aligned}$$

(51)

with $L(1,1,\beta ,l_\mathrm{s})$ in (73). Numerical evaluations give $L(1,1,\beta ,l_\mathrm{s})>0$ for the range of parameters used, giving zero flux existing for an externally pressurised bearing only, with low speed parameters $\lambda <\lambda _c$ having negative flux and high speed parameters $\lambda >\lambda _c$ having positive flux.

The streamlines in Fig. 3 give the radial path of the fluid flow through the bearing for an externally pressurised PCB and NCB. Choosing the critical speed parameter for a no-slip bearing, which is consistent with the estimated value, $\lambda _c(l_\mathrm{s}=0)$, gives zero flux through the bearing. Increasing the slip length, but keeping the same speed parameter, results in a negative flux in the bearing, increasing in magnitude as the slip length increases. In Fig. 3, a comparison for slip length $l_\mathrm{s}=1$, shows that an NCB has unidirectional flow but a PCB retains some recirculation.

Fig. 3

Streamlines for increasing slip length a $l_\mathrm{s}=0$, b $l_\mathrm{s}=0.5$ and c $l_\mathrm{s}=1$ in the case of (1) PCB $\beta =0.2$, and (2) NCB $\beta =-0.2$, under external pressurisation; $\epsilon =0$, $\lambda =\lambda _c(l_\mathrm{s}=0)=2.0833$, $\sigma =1$

Due to the algebraic complexity of the equations, the fluid flow is studied by examining the velocity field in the asymptotic limit of a large finite slip length. To leading order the radial, azimuthal and axial velocity components are given by

$$\begin{aligned} u= & {} \frac{1}{12 r h(r,\beta ) G_{l_\mathrm{s}}(1,1,\beta ,l_\mathrm{s})}\left( -p_\mathrm{O} + p_\mathrm{I} + \frac{5\lambda }{12}(1-a^2)\right) \!,\qquad v=\frac{r}{2}\!, \nonumber \\ w= & {} -\frac{r\beta (z-h_\mathrm{s})}{\sigma ^2 r^2 h(r,\beta )^2 G_{l_\mathrm{s}}(1,1,\beta ,l_\mathrm{s})}\left( -p_\mathrm{O} + p_\mathrm{I} + \frac{5\lambda }{12}(1-a^2)\right) \!, \end{aligned}$$

(52)

with $G_{l_\mathrm{s}}$ given by

$$\begin{aligned} G_{l_\mathrm{s}+}(1,1,\beta ,l_\mathrm{s})= & {} \frac{1}{6l_\mathrm{s}(1-a\beta )}\left( \frac{1}{(1-a\beta )}\ln \left( \frac{1}{a(1+(1-a)\beta )}\right) +\frac{1}{1+(1-a)\beta }-1\right) \!, \end{aligned}$$

(53)

$$\begin{aligned} G_{l_\mathrm{s}-}(1,1,\beta ,l_\mathrm{s})= & {} \frac{1}{6l_\mathrm{s}(1-\beta )}\left( \frac{1}{(1-\beta )}\ln \left( \frac{1-(1-a)\beta }{a}\right) +1-\frac{1}{1-(1-a)\beta }\right) \!, \end{aligned}$$

(54)

where subscripts $+$ and $-$ denote a PCB and NCB, respectively. Expressions in (53) and (54) have dependence on $\beta$ and $l_\mathrm{s}$ and are non-negative. The azimuthal velocity has rigid body motion taking the value of the average between the azimuthal velocity of the rotor and the stationary stator. The radial and axial velocity are proportional to the slip length, with the radial velocity independent of the axial coordinates and the axial velocity the only component to change sign with a PCB and NCB, since $G_{l_\mathrm{s}}>0$ always. These limits match the numerical analysis of the full expressions.

Examining the flux in the limit of large slip length gives

$$\begin{aligned} Q=\frac{\pi }{6G_{l_\mathrm{s}}(1,1,\beta ,l_\mathrm{s})}\left( -p_\mathrm{O} + p_\mathrm{I} + \frac{5\lambda }{12}(1-a^2)\right) \!, \end{aligned}$$

(55)

which gives the flux proportional to slip length through $G_{l_\mathrm{s}}$, as given in (53) and (54) for PCB and NCB, respectively. The corresponding critical speed parameter is given by

$$\begin{aligned} \lambda _c=\frac{12(p_\mathrm{O}-p_\mathrm{I})}{5(1-a^2)}, \end{aligned}$$

(56)

confirming only an externally pressurised bearing as having zero flux. Equation (56) is consistent with (51) in the limit of large $l_\mathrm{s}$, with the limit of $L$ as $L_{l_\mathrm{s}}=5(1-a^2)/12$, which has been verified by the use of two different symbolic computations.

5 Parametric study of the bearing motion dynamics

This section investigates a parameter study of the dynamical behaviour of a bearing with slip effects for large amplitudes of the prescribed rotor oscillations and with the stator free to move axially in response to the fluid film dynamics; dynamical results for a bearing with a no-slip condition $l_\mathrm{s}=0$, are given in Bailey et al. [8].

Fig. 4

Fluid stiffness, total damping, force, stator height and MFC for varying coning angle $-0.2 \le \beta \le 0.2$ in the case of external pressurisation and wide annulus $1-a=0.8$; $l_\mathrm{s}=0.1$, $\epsilon =1.2$, $a=0.2$, $\lambda =1$, $\alpha =1$, $K_z=10$, $\sigma =1$ and $D_\mathrm{a}=1$

Figure 4 shows the periodic fluid stiffness, total damping, force, stator height and MFC for varying coning angle under external pressurisation in the case of a wide annulus $1-a=0.8$ with parameter values $l_\mathrm{s}=0.1$, $\epsilon =1.2$, $\lambda =1$, $\alpha =1$, $K_z=10$, $\sigma =1$ and $D_\mathrm{a}=1$. An NCB has smaller $g_{\min }$ than a PCB, with all cases having a very small MFC which is approximately constant during the time interval $1<t<2.5$, where the total damping and fluid stiffness have a local maximum and extrema, respectively. The fluid stiffness has a maximum of small magnitude for a PCB and minimum of large magnitude for an NCB. The damping has a maximum, with largest amplitude in the case of an NCB. We note that the stator has larger amplitudes of oscillation for a NCB than a PCB of the same value of coning angle and the force extrema occurring when the MFC is small, with an NCB having larger oscillations than a PCB. Increasing the bearing parameters, such as the amplitude of the rotor oscillations, slip length or bearing width give appropriate modified values but overall similar dynamics.

A main focus of this work is to examine the MFC $g_{\min }$ with a selection of values for the main bearing characteristics of parameters coning angle, slip length, speed parameter. Table 1 shows the obtained values of $g_{\min }$ for a wide $a=0.2$ and narrow $a=0.8$ annulus in the case of external pressurisation and large amplitude rotor oscillations, $\epsilon = 1.2$. A corresponding table for internal pressurisation is given in Appendix 4, Table 4. Under all pressurisations considered, values of $g_{\min }$ are larger in a bearing with a wide annulus than with a narrow annulus for a given bearing configuration. An exception is the case of a PCB under internal pressurisation with large coning angle and speed parameter, as is the case of $\beta =0.3$, $l_\mathrm{s}=0$ and $\lambda =5$ in Table 4. In this last case, for sufficiently large coning angle and speed parameter values, and since inertial effects are more significant in a wide annulus than a narrow one, it follows that $g_{\min }$ is smaller in the case of a wide annulus. In all cases, increasing the magnitude of coning angle and slip length decreases the value of $g_{\min }$; face contact is possible for some parameter choices, denoted by $*$. Under external pressurisation a PCB generally has larger values of $g_{\min }$ than a NCB for a given set of parameters, an exception is a wide annulus with large speed parameter is considered, as shown in Table 1 for $\lambda =5$. In this case, the increased inertia effects dominates over the differential pressure, giving larger values of $g_{\min }$ for an NCB. This effect is minimal in a narrow annulus. In contrast with the case of external pressurisation, a bearing under internal pressurisation gives an NCB having a larger value of $g_{\min }$ than a PCB.

Table 1 Values of $g_{\min }$ for an NCB and PCB under external pressurisation in the case a narrow $a=0.8$ and wide $a=0.2$ annulus with increasing speed parameter $0 \le \lambda \le 5$ and slip length $0\le l_\mathrm{s}\le 0.1$; $\epsilon =1.2$, $\sigma =1$, $K_z=10$, $\alpha =1$ and $D_\mathrm{a}=1$

Increasing the speed parameter for a narrow annulus causes an NCB to have increasing $g_{\min }$, while a PCB has the situation reversed. In the case of a wide annulus, a similar trend occurs. However, an NCB with small angle has decreasing $g_{\min }$ for the increasing speed parameter; this is italicised in Tables 1 and 4. Results are consistent with the expectation that, for the decreasing coning angle, both PCB and NCB should have common dynamics. A bearing with narrow annulus follows a similar trend to the wide annulus, but inertia effects are less pronounced. The change in behaviour with the increasing speed parameter occurs for smaller coning angle than those shown in Table 1.

6 Influence of slip effects on $g_{\min }$

An important aspect in bearing operation is the impact of a slip effect on maintaining a face clearance when the rotor is subjected to axial disturbances. Bearing gap behaviour has been investigated by Bailey et al. [8] to identify no contact occurs with a no-slip condition for amplitudes of the axial rotor displacement similar to or larger than the equilibrium MFC. Additional consideration is given to the dynamics of a parallel bearing to investigate if contact occurs for a wide range of slip lengths. Figure 5 shows a log–log plot of $g_{\min }$ against increasing slip length within the range $10^{-4}\le l_\mathrm{s}\le 10^{6}$, relative to a typical bearing gap, for axial rotor oscillations of amplitude $1.0\le \epsilon \le 1.2$. The bearing has two distinctly different asymptotic behaviours for increasing slip length depending on the magnitude of axial rotor oscillations $\epsilon$. In region I, $\epsilon <1.05325$, $g_{\min }$ approaches a constant value for increasing slip length values. In region II $\epsilon >1.05325$, the plot of $g_{\min }$ decreases approximately linearly as the slip length increases with gradient $-1$, giving contact occurring only in the limit of $l_\mathrm{s}\rightarrow \infty$. The values for $g_{\min }$ are obtained from the stroboscopic map solver at each value of the rotor oscillation $\epsilon$, with increasing discrete values of the slip length between $10^{-4}\le l_\mathrm{s}\le 10^{6}$. Investigation is extended to evaluate if, in general, contact can occur with a slip effect.

Fig. 5

$g_{\min }$ against increasing slip lengths $10^{-4}\le l_\mathrm{s}\le 10^{6}$ for increasing rotor amplitudes $1.00\le \epsilon \le 1.10$ in the case of a parallel bearing with a wide annulus under internal pressurisation; $a= 0.2$, $\lambda =1$, $\alpha =1$, $K_z=10$, $\sigma =1$ and $D_\mathrm{a}=1$

Figure 6 compares $g_{\min }$ against slip length for varying coning angle $-0.2\le \beta \le 0.2$ in the case of a wide and narrow bearing under external pressurisation. A narrow bearing has contact in all cases, with an NCB having contact at smaller slip lengths than a PCB of the same angle, and coning angles of larger magnitude give contact at smaller slip lengths. A wide bearing has contact only in an NCB for $l_\mathrm{s}\le 4.5$, as a PCB has $g_{\min }\sim 0.03$ at $l_\mathrm{s}=4.5$ for all angles.

Fig. 6

$g_{\min }$ against slip length for various coning angles $\beta =-0.3,-0.2,-0.1,0.1,0.2,0.3$ in the case of a narrow; $a=0.8$ and b wide; $a=0.2$ bearing under external pressurisation; $\epsilon =1.2$, $\lambda =1$, $\sigma =1$, $\alpha =1$, $K_z=10$ and $D_\mathrm{a}=1$

The values of slip length associated with face contact are examined for a PCB and an NCB in the case of a wide $a=0.2$ and narrow $a=0.8$ annulus with the increasing speed parameter $0\le \lambda \le 5$ are shown in Tables 2 and 3 for external and internal pressurisations, respectively. For values of $l_\mathrm{s}$ larger than these values, contact will always occur. It is interesting to observe that a bearing under external pressurisation can have no contact for a PCB in the case of a wide annulus, denoted by $o$ in Table 2. In all the cases considered, a bearing with wide annulus has contact at larger slip lengths than the one with a narrow annulus. An exception is a wide PCB under internal pressurisation with large speed parameter, italicised in Table 3. In this case, the large inertia effect is more significant in a wide annulus than a narrow annulus, giving $g_{\min }$ smaller in a wide annulus for a sufficiently large coning angle. Increasing the magnitude of the coning angle decreases the values of slip length at contact and increasing the speed parameter gives the increase in the slip length value at contact in an NCB, but a decreased one in the case of a PCB.

Table 2 Slip length values when face contact first occurs for an NCB and a PCB under external pressurisation in the case of a wide $a=0.2$ and narrow $a=0.8$ annulus with the increasing speed parameter $0\le \lambda \le 5$; $\epsilon =1.2$, $\sigma =1$, $K_z=10$, $\alpha =1$ and $D_\mathrm{a}=1$

Table 3 Slip length values when face contact first occurs for an NCB and a PCB under internal pressurisation in the case of a wide $a=0.2$ and narrow $a=0.8$ annulus with increasing speed parameter $0\le \lambda \le 5$; $\epsilon =1.2$, $\sigma =1$, $K_z=10$, $\alpha =1$ and $D_\mathrm{a}=1$

As expected in the case of internal pressurisation, an NCB has a larger slip length value at contact than a PCB, while for external pressurisation this situation is reversed, except for the case of a wide bearing with large values of $\lambda$ where inertial effects dominate the pressure gradient effects, italicised in Table 2.

7 Small face clearance in limit $g(t)\ll 1$

To further investigate the case when the MFC is small and also verify the numerical solution, an asymptotic analysis is undertaken. At near contact, it is assumed that $g\ll \beta$ in the limit $g(t)\ll 1$, so a new variable $f=g/\beta$ is introduced, giving the limit to be examined for $f\ll 1$. Rewriting the equations in term of $f$ gives $G$ and $H$ of $O(f^{-1})$ and $L$ and $L_\mathrm{I}$ of $O(1)$ for both a PCB and NCB, whilst $G_\mathrm{I}$ and $H_\mathrm{I}$ are of $O(f^{-1})$ for a PCB and $O(1)$ for an NCB.

The damping coefficient $D$ as defined in (30) in the limit of $f\ll 1$, is given for a PCB, denoted by subscript $+$ and NCB, denoted by subscript $-$, by

$$\begin{aligned} D_+= & {} D_\mathrm{a}-\frac{\alpha \pi \sigma }{2\beta ^4(6l_\mathrm{s}-a\beta )}\left( \ln \left( \frac{(1-a)\beta +6l_\mathrm{s}}{6l_\mathrm{s}}\right) (36{l_\mathrm{s}}^2-24l_\mathrm{s}\beta a+4\beta ^2a^2)+a^2\beta ^2\ln a +\beta (1-a)(a\beta -6l_\mathrm{s})\right) ,\nonumber \\ D_-= & {} D_\mathrm{a}-\frac{\alpha \pi \sigma }{2\beta ^4(6l_\mathrm{s}-\beta )}\left( \ln \left( \frac{6l_\mathrm{s}}{-(1-a)\beta +6l_\mathrm{s}}\right) (36{l_\mathrm{s}}^2-24l_\mathrm{s}\beta +4\beta ^2)+\beta ^2\ln a +\beta (1-a)(\beta -6l_\mathrm{s})\right) , \end{aligned}$$

(57)

which are both of $O(1)$ to leading order.

The effective restoring force $S$ as defined in (30), in the limit of $f\ll 1$ to leading order is given by

$$\begin{aligned} S=A_\pm = \left\{ \begin{array}{ll} K_z+\alpha \pi \left( (1-a^2)(p_\mathrm{O}-p_\mathrm{a})+2\lambda \bar{L}\right) \quad &{} \text {if}\; \beta >0,\\ K_z(1+(1-a)\beta )+\alpha \pi \left( (1-a^2)(p_\mathrm{I}-p_\mathrm{a})+2\lambda L_{-I}\right) \quad &{} \text {if}\; \beta <0. \end{array}\right. \end{aligned}$$

(58)

In the above, $\bar{L}$ and $L_{-I}$ are given in Appendix 3, by Eqs. (81) and (82), respectively, which are of $O(1)$, giving the effective restoring force of $O(1)$.

In the limit of small face clearance $g/\beta \ll 1$, the nonlinear second-order non-autonomous ordinary differential equation (29) becomes a linear ordinary differential equation with constant coefficients, given to leading order by

$$\begin{aligned} \frac{\text {d}^2 g}{\text {d}t^2}+D_\pm \frac{\text {d}g}{\text {d}t}-A_\pm =\epsilon ((1-K_z)\sin t -D_\mathrm{a}\cos t)). \end{aligned}$$

(59)

Solving Eq. (59) in the limit $g/\beta \ll 1$ with initial conditions $g(t_0)=g_0$ and $\text {d}g(t_0)/\text {d}t=-\xi$, with $\xi >0$ say, gives

$$\begin{aligned} g(t) = C_1+C_2\mathrm{e}^{-D_\pm t}+\frac{A_\pm }{D_\pm }t- \epsilon \left( \frac{({D_\pm }D_\mathrm{a}+1-K_z)}{{D_\pm }^2+1}\sin t -\frac{(D_\pm (1-K_z)-D_\mathrm{a})}{{D_\pm }^2+1}\cos t\right) {,} \end{aligned}$$

(60)

with constants of integration

$$\begin{aligned} C_1= & {} g_0-\frac{\xi }{D_\pm }-\frac{A_\pm }{D_\pm }\left( t_0+\frac{1}{D_\pm }\right) +\epsilon \frac{D_\mathrm{a}}{D_\pm }\sin t_0+\epsilon \frac{(1-K_z)}{D_\pm }\cos t_0,\nonumber \\ C_2= & {} \frac{\mathrm{e}^{D_\pm t_0}}{D_\pm }\left( \xi +\frac{A_\pm }{D_\pm }-\epsilon \frac{({D_\mathrm{a}}D_\pm +1-K_z)}{{D_\pm }^2+1}\cos t_0+\epsilon \frac{(D_\pm (1-K_z)-D_\mathrm{a})}{{D_\pm }^2+1}\sin t_0\right) {.} \end{aligned}$$

(61)

The dependence of $l_\mathrm{s}$ on the MFC is given by the coefficients $D_\pm$ and $A_\pm$ only.

An NCB under internal pressurisation is examined since a PCB under external pressurisation does not have contact for large amplitude and slip lengths $l_\mathrm{s}\le 4.5$, see Fig. 6b. Rotor amplitude $\epsilon =1.2$ and slip length $l_\mathrm{s}=0.13$ are used, giving a close comparison of the numerical solution and the asymptotic composite solution of the MFC as shown in Fig. 7, in the region $0.8<t<2.2$. The composite solution has increasing discrepancy with the numerical solution as the gap grows, consistent with the asymptotics approximations; region III was not included in the analysis.

Fig. 7

Numerical and composite solutions of the MFC for rotor amplitude $\epsilon =1.20$ in the case of an NCB with a wide annulus under internal pressurisation; $a= 0.2$, $\beta =-0.2$, $\lambda =1$, $\alpha =1$, $K_z=10$, $\sigma =1$, $D_\mathrm{a}=1$, $l_\mathrm{s}=0.13$, $g_0=0.03$ and $t_0=1.194$

On the other hand, in the limit of increasing $l_\mathrm{s}$ an asymptotic evaluation for $g(t)\ll 1$ gives the same form as the asymptotic equation in (59). In this case, the damping coefficient $D$ and the effective restoring force $S$ are given, respectively, as

$$\begin{aligned}&D=D_\mathrm{a},\nonumber \\&S=A_\pm =\left\{ \begin{array}{l@{\quad }l} K_z+\alpha \pi \left( (1-a^2)(p_\mathrm{O}-p_\mathrm{a})-\frac{5\lambda }{24}(1-a^2)^2\right) &{} \text {if}\; \beta >0, \\ K_z(1+(1-a)\beta )+\alpha \pi \left( (1-a^2)(p_\mathrm{I}-p_\mathrm{a})+\frac{5\lambda }{24}(1-a^2)^2\right) &{} \text {if}\; \beta < 0, \end{array}\right. \end{aligned}$$

(62)

to leading order.

In this limit, the solution takes the same form as Eq. (60) with constants given by (61), and using $D_\pm =D_\mathrm{a}$ and modified values for $A_\pm$ as given in (62), which are all independent of $l_\mathrm{s}$. In consequence in the limit, the value of the MFC cannot depend on the slip length. This behaviour is shown in Fig. 6 when $g_{\min }$ asymptotes of to a constant value when contact does not occur.

8 Summary and conclusions

Previous work by Bailey et al. [8] for a coned thrust bearing showed for axial disturbances a fluid film gap was maintained when subject to a no-slip condition, although this gap may become extremely small. This work identifies for a more general case, where a slip flow is relevant, that contact may occur, and for more practical purposes, maintaining a minimum gap thickness will depend on the coning angle, slip length, amplitude of rotor oscillations disturbance amplitude and direction of pressurisation.

A modified Reynolds equation is derived for a bearing containing a rigid coned rotor and a slip boundary condition imposed on the bearing faces characterised by a slip length, $l_\mathrm{s}$. An axisymmetric lubrication approximation is used and leading-order effects of centrifugal inertia are retained, which is relevant for very high-speed bearing rotation and flows that are dynamically incompressible. Axial structural response of the rotor are formulated corresponding to the stator motion, induced by periodic axial displacement of the rotor, through the fluid flow, acting as a spring-mass-damper structure.

The fully coupled unsteady bearing motion is examined where the stator displacement is coupled to the film dynamics via the axial force exerted on the stator by the fluid film. Rewriting the modified Reynolds equation and the stator equation in terms of the time-dependent MFC $g(t)$ allows for explicit analytic expressions for the pressure field and force on the stator. Bearing solutions are obtained from solving a nonlinear second-order non-autonomous ordinary differential equation using a stroboscopic map to find periodic solutions. Subsequent calculations give the force on the stator, stator height, total damping and fluid stiffness.

A steady bearing case with axially fixed rotor and stator was investigated to examine the existence of non-monotonic behaviour in the pressure field for increasing slip length. Results tending to the limit of large slip length are given for representative bearing parameter choices, showing an externally pressurised bearing can exist with no overall flux through the bearing at a critical speed parameter, corresponding physically to pressure effects directly balancing inertial effects.

The dynamics of the bearing are investigated for rotor displacement, in particular with amplitude larger than the equilibrium gap between a coupled rotor and stator system, simulating possible destabilising behaviour. Results show that if the rotor is forced into close proximity of the stator and a very thin fluid film is maintained, as the rotor continues on its forced path, the stator follows the rotor closely for a significant part of the periodic motion, preserving the fluid film. Dynamically the total damping, fluid stiffness and force are effectively constant for most of the time period, unless the MFC becomes small. Here, an enhanced localised force and a maximum in the total damping resist plate contact. Numerical solution of bearing dynamics is supported by asymptotic analysis.

Evaluation of possible contact occurring in a bearing is carried out when the rotor is subject to large axial disturbances. Increasing the coning angle decreases the value of slip length when contact first occurs, whereas increasing the speed parameter gives the slip length values at contact increasing for NCB but decreasing for a PCB. In general, a wide annulus has contact at larger slip lengths than a narrow annulus, with a wide annulus under external pressurisation having no contact for certain bearing configurations.

Appendices

Appendix 1: Velocities, flux and streamfunction

The radial, azimuthal and axial velocities are

$$\begin{aligned} u= & {} \frac{1}{2}\frac{\partial p}{\partial r}(z^2-(h_\mathrm{s}+h_\mathrm{r})z+h_\mathrm{s}h_\mathrm{r}-l_\mathrm{s}h)\nonumber \\&-\frac{5\lambda r}{18(h+2ls)^2}\left( (z-h_\mathrm{r})(z-h_\mathrm{s})(z^2+(h_\mathrm{r}-3h_\mathrm{s})z+3h_\mathrm{s}^2-3h_\mathrm{s}h_\mathrm{r}+h_\mathrm{r}^2)\right. \nonumber \\&+ l_\mathrm{s}((z-h_\mathrm{s})(-4(z-h_\mathrm{s})^2+6h^2)-h^3)+l_\mathrm{s}^2(6(z-h_\mathrm{s})(z-h_\mathrm{r})-6h^2),\left. - 6hl_\mathrm{s}^3 \right) \!, \end{aligned}$$

(63)

$$\begin{aligned} v= & {} -\frac{r}{(h+2l_\mathrm{s})}(z-h_\mathrm{s}-l_\mathrm{s}), \end{aligned}$$

(64)

$$\begin{aligned} w= & {} \frac{\partial h_\mathrm{r}}{\partial t}-\frac{1}{\sigma r}\left( \left( \frac{\partial p}{\partial r} + r\frac{\partial ^2 p}{\partial r^2}\right) (2(z-h_\mathrm{r})^3-3(z-h_\mathrm{r})^2h-6(z-h_\mathrm{r})hl_\mathrm{s})\right. \nonumber \\&+\,r\frac{\partial p}{\partial r} \left( (6(z-h_\mathrm{r})^2-6(z-h_\mathrm{r})h-6hl_\mathrm{s})\beta \left. - (3(z-h_\mathrm{r})^2+6(z-h_\mathrm{r})l_\mathrm{s})\beta \right) \right) \nonumber \\&+ \frac{\lambda }{3\sigma r}\left( \left( \frac{2r}{(h+2l_\mathrm{s})^2}-\frac{2r^2}{(h+2l_\mathrm{s})^3}\beta \right) \left( 2(z-h_\mathrm{r})^5-10(z-h_\mathrm{r})^4h\right. \right. +20(z-h_\mathrm{r})^3h^2-15(z-h_\mathrm{r})^2h^3\nonumber \\&+ 10l_\mathrm{s}(-(z-h_\mathrm{r})^4+4(z-h_\mathrm{r})^3h-3(z-h_\mathrm{r})^2h^2-3(z-h_\mathrm{r})h^3)+ 10l_\mathrm{s}^2(2(z-h_\mathrm{r})^3\nonumber \\&-\left. 3(z-h_\mathrm{r})^2h-6(z-h_\mathrm{r})h^2)+10l_\mathrm{s}^3(-6(z-h_\mathrm{r})h))\right) \nonumber \\&+\frac{r^2\beta }{(h+2l_\mathrm{s})^2}\left( (15(z-h_\mathrm{r})^2h^2-30(z-h_\mathrm{r})h^3+10l_\mathrm{s} (6(z-h_\mathrm{r})^2h\right. \nonumber \\&-15(z-h_\mathrm{r})h^2-3h^3)+10l_\mathrm{s}^2(3(z-h_\mathrm{r})^2-18(z-h_\mathrm{r})h-6h^2)-\left. \left. 60l_\mathrm{s}^3((z-h_\mathrm{r})+h\right) \right) \!, \end{aligned}$$

(65)

respectively.

The radial flux through the bearing is given by

$$\begin{aligned} Q=2\pi \int _{h_\mathrm{r}}^{h_\mathrm{s}} r u \text {d}z=\frac{\pi }{6}\left( \frac{\lambda r^2}{(h+2l_\mathrm{s})^2}(h^5+10h^4l_\mathrm{s}+\frac{70}{3}h^3{l_\mathrm{s}}^2+20h^2{l_\mathrm{s}}^3)-r\frac{\partial p}{\partial r}h^2(h+6l_\mathrm{s})\right) \!. \end{aligned}$$

(66)

The steady-state streamfunction is

$$\begin{aligned} \Psi (r,z)= & {} \frac{r}{12}\frac{\partial p}{\partial r}(2(z-h_\mathrm{r})^3-3(z-h_\mathrm{r})^2h-6(z-h_\mathrm{r})hl_\mathrm{s})\nonumber \\&-\frac{\lambda r^2}{36(h+2l_\mathrm{s})^2}\left( 2(z-h_\mathrm{r})^5-10(z-h_\mathrm{r})^4h+20(z-h_\mathrm{r})^3h^2-15(z-h_\mathrm{r})^2h^3)\right. \nonumber \\&+\left. 10l_\mathrm{s}(-(z-h_\mathrm{r})^4+4(z-h_\mathrm{r})^3h-3(z-h_\mathrm{r})^2h^2-3(z-h_\mathrm{r})h^3)\right. \nonumber \\&+\left. 10l_\mathrm{s}^2(2(z-h_\mathrm{r})^3-3(z-h_\mathrm{r})^2h-6(z-h_\mathrm{r})h^2)+10l_\mathrm{s}^3(-6(z-h_\mathrm{r})h)\right) \!, \end{aligned}$$

(67)

found using Eqs. (63) and (65).

The film thickness in terms of the variable $g(t)$ is given by

$$\begin{aligned} \begin{aligned}&h(r,\beta ,t) = g(t) +(r-a)\beta \quad \text {for}\quad \beta >0,\\&h(r,\beta ,t)= g(t)+(r-1)\beta \quad \text {for}\quad \beta <0. \end{aligned} \end{aligned}$$

(68)

Appendix 2: Analytical evaluation of integral functions

Expressions for $G$, $H$ and $L$ are given, with separate equations for no slip $l_\mathrm{s}=0$, denoted by subscript $l_\mathrm{s}=0$;

$$\begin{aligned} G(r)= & {} \int ^\mathrm{r}_\mathrm{a}\frac{1}{x((g+(x-a)\beta )^3+6l_\mathrm{s}(g+(x-a)\beta )^2)}\text {d}x\nonumber \\= & {} \frac{1}{g-a\beta +6l_\mathrm{s}} \left( \frac{1}{(g-a\beta )^2}\ln \left( \frac{gr}{a(g+(r-a)\beta }\right) +\frac{1}{g-a\beta }\left( \frac{1}{g}-\frac{1}{g+(r-a)\beta }\right) \right. \nonumber \\&+ \left. \frac{1}{36l_\mathrm{s}^2}\left( \ln \left( \frac{g(g+(1-a)\beta +6l_\mathrm{s})}{(g+(1-a)\beta )(g+6l_\mathrm{s})}\right) +6l_\mathrm{s}\left( \frac{1}{g+(r-a)\beta }-\frac{1}{g}\right) \right) \right) , \end{aligned}$$

(69)

$$\begin{aligned} G_{(l_\mathrm{s}=0)}(r)= & {} \int ^\mathrm{r}_\mathrm{a}\frac{1}{x(g+(x-a)\beta )^3}\text {d}x=\frac{1}{(g-a\beta )^3}\ln \left( \frac{gr}{a(g+(r-a)\beta )}\right) \nonumber \\&+\frac{1}{2(g-a\beta )^2}\left( \frac{3g+(2r-3a)\beta }{(g+(r-a)\beta )^2 }-\frac{3g-a\beta }{g^2}\right) , \end{aligned}$$

(70)

$$\begin{aligned} H(r)= & {} \int ^\mathrm{r}_\mathrm{a}\frac{x}{(g+(x-a)\beta )^3+6l_\mathrm{s}(g+(x-a)\beta )^2}\text {d}x\nonumber \\= & {} \frac{1}{\beta ^2} \left( \left( \frac{1}{g}-\frac{1}{g+(r-a)\beta } \right) +\frac{g-a\beta +6l_\mathrm{s}}{36l_\mathrm{s}^2}\left( \ln \left( \frac{g(g+(1-a)\beta +6l_\mathrm{s})}{(g+(1-a)\beta )(g+6l_\mathrm{s})}\right) \right. \right. \nonumber \\&\left. \left. +6l_\mathrm{s}\left( \frac{1}{g+(r-a)\beta }-\frac{1}{g}\right) \right) \right) , \end{aligned}$$

(71)

$$\begin{aligned} H_{(l_\mathrm{s}=0)}(r)= & {} \int ^\mathrm{r}_\mathrm{a}\frac{x}{(g+(x-a)\beta )^3}\text {d}x=\frac{1}{\beta ^2}\left( -\frac{1}{g+(r-a)\beta }+\frac{g-a\beta }{2(g+(r-a)\beta )^2}+\frac{g+a\beta }{2g^2}\right) , \end{aligned}$$

(72)

and

$$\begin{aligned} L(r)= & {} \int ^\mathrm{r}_\mathrm{a}\frac{x\left( (g+(x-a)\beta )^5 + 10(g+(x-a)\beta )^4l_\mathrm{s} \right) }{((g+(x-a)\beta )^3+6l_\mathrm{s}(g+(x-a)\beta )^2)(g+(x-a)\beta +2l_\mathrm{s})^2}\nonumber \\&+\frac{x\left( \frac{70}{3}(g+(x-a)\beta )^3l_\mathrm{s}^2 +20(g+(x-a)\beta )^2l_\mathrm{s}^3\right) }{((g+(x-a)\beta )^3+6l_\mathrm{s}(g+(x-a)\beta )^2)(g+(x-a)\beta +2l_\mathrm{s})^2} \text {d}x\nonumber \\= & {} \frac{r^2-a^2}{2}+\frac{l_\mathrm{s}}{\beta ^2} \left( \frac{4}{3}l_\mathrm{s} (g-a\beta +2l_\mathrm{s})\left( \frac{1}{g+(r-a)\beta +2l_\mathrm{s}}-\frac{1}{g+2l_\mathrm{s}} \right) \right. \nonumber \\&+\frac{3}{2}(g-a\beta +6l_\mathrm{s})\ln \left( \frac{(g+6l_\mathrm{s})(g+(r-a)\beta +2l_\mathrm{s})}{(g+2l_\mathrm{s})(g+(r-a)\beta +6l_\mathrm{s})}\right) \nonumber \\&-\left. \frac{14}{3}l_\mathrm{s}\ln \left( \frac{g+(r-a)\beta +2l_\mathrm{s}}{g+2l_\mathrm{s}}\right) \right) , \end{aligned}$$

(73)

$$\begin{aligned} L_{(l_\mathrm{s}=0)}(r)= & {} \int ^\mathrm{r}_\mathrm{a}\frac{x(g+(x-a)\beta )^5}{(g+(x-a)\beta )^3(g+(x-a)\beta )^2}\text {d}x=\frac{r^2-a^2}{2}. \end{aligned}$$

(74)

The integrals $G_\mathrm{I}$, $H_\mathrm{I}$ and $L_\mathrm{I}$ are given below with those for no slip denoted with subscript $l_\mathrm{s}=0$;

$$\begin{aligned} G_\mathrm{I}= & {} \int ^1_\mathrm{a}rG(r)\;\text {d}r\nonumber \\= & {} \frac{1}{g-a\beta +6l_\mathrm{s}} \left( -\frac{1}{2(g-a\beta )^2}\ln \left( \frac{a(g+(1-a)\beta )}{g} \right) + \frac{(1-a)(g-a\beta -\beta )}{2\beta g((g-a\beta )}\right. \nonumber \\&+\frac{1}{72\beta ^2l_\mathrm{s}^2}\left( 6l_\mathrm{s}(1-a)\beta \left( \frac{g-a\beta -\beta }{g}\right) \right. \nonumber \\&\left. \left. +\left( (g-a\beta +6l_\mathrm{s})^2-\beta ^2\right) \ln \left( \frac{g(g+(1-a)\beta +6l_\mathrm{s})}{(g+(1-a)\beta )(g+6l_\mathrm{s})} \right) \right) \right) , \end{aligned}$$

(75)

$$\begin{aligned} G_{(l_\mathrm{s}=0)I}= & {} \int ^1_\mathrm{a}rG_{(l_\mathrm{s}=0)}(r)\text {d}r\nonumber \\= & {} \frac{1}{2(g-a\beta )^3}\ln \left( \frac{g}{a(g+(1-a)\beta )}\right) +\frac{1}{2(g-a\beta )^2}\left( \frac{(1-a)}{\beta }-\frac{(1-a^2)(3g-a\beta )}{2g^2}\right) \nonumber \\&+\frac{1}{2\beta ^2}\left( \frac{1}{g+(1-a)\beta }-\frac{1}{g}\right) , \end{aligned}$$

(76)

$$\begin{aligned} H_\mathrm{I}= & {} \int ^1_\mathrm{a}rH(r)\text {d}r\nonumber \\= & {} \frac{1}{\beta ^2} \left( -\frac{(1-a)(2g-(1+a)\beta )}{2\beta g} +\frac{3(g-a\beta +2l_\mathrm{s})}{2\beta ^2}\ln \left( \frac{g+(1-a)\beta }{g} \right) \right. \nonumber \\&+\frac{g-a\beta +6l_\mathrm{s}}{72\beta ^2l_\mathrm{s}^2}\left[ \frac{6l_\mathrm{s}(1-a)\beta (g-(1+a)\beta )}{g}\right. \nonumber \\&\left. \left. + \left( (g-a\beta +6l_\mathrm{s})^2-\beta ^2 \right) \ln \left( \frac{g(g+(1-a)\beta +6l_\mathrm{s})}{(g+(1-a)\beta )(g+6l_\mathrm{s})}\right) \right] \right) , \end{aligned}$$

(77)

$$\begin{aligned} H_{(l_\mathrm{s}=0)I}= & {} \int ^1_\mathrm{a}rH_{(l_\mathrm{s}=0)}(r)\text {d}r\nonumber \\= & {} \frac{1}{\beta ^2}\left( \frac{a-1}{\beta }+\frac{(1-a^2)(g+a\beta )}{4g^2}+\frac{3(g-a\beta )}{2\beta ^2}\ln \left( \frac{g+(1-a)\beta }{g}\right) \right. \nonumber \\&+\left. \frac{(g-a\beta )^2}{2\beta ^2}\left( \frac{1}{(g+(1-a)\beta )}-\frac{1}{g}\right) \right) , \end{aligned}$$

(78)

and

$$\begin{aligned} L_\mathrm{I}= & {} \int ^1_\mathrm{a}rL(r)\text {d}r\nonumber \\= & {} \frac{(1-a^2)^2}{8}+\frac{2{l_\mathrm{s}}^2a(1-a^2)}{3\beta (g+2l_\mathrm{s})}+\frac{{l_\mathrm{s}}^2}{2\beta ^2}(8a+1-9a^2)-\frac{4(1-a){l_\mathrm{s}}^2}{\beta ^3}(g+5l_\mathrm{s})\nonumber \\&+\ln \left( \frac{g+6l_\mathrm{s}}{g+(1-a)\beta +6l_\mathrm{s}}\right) \left( -\frac{3l_\mathrm{s}a(1-a^2)}{4\beta }\frac{3l_\mathrm{s}}{4\beta ^2}(g+6l_\mathrm{s})(1-3a^2)\right. \nonumber \\&+\left. \frac{9l_\mathrm{s}a}{4\beta ^3}(g+6l_\mathrm{s})^2-\frac{3l_\mathrm{s}}{4\beta ^4}(g^3+18{l_\mathrm{s}}g^2+108{l_\mathrm{s}}^2g+216{l_\mathrm{s}}^3)\right) \nonumber \\&+\ln \left( \frac{g+(1-a)\beta +2l_\mathrm{s}}{g+2l_\mathrm{s}}\right) \left( -\frac{3l_\mathrm{s}a(1-a^2)}{4\beta }\frac{l_\mathrm{s}}{12\beta ^2}(9g+26l_\mathrm{s})(1-3a^2)\right. \nonumber \\&-\frac{l_\mathrm{s}a}{4\beta ^3}(9g^2+52gl_\mathrm{s}+68{l_\mathrm{s}}^2)+\left. \frac{l_\mathrm{s}}{4\beta ^4}(3g^3+26l_\mathrm{s}g^2+68{l_\mathrm{s}}^2g+56{l_\mathrm{s}}^3)\right) , \end{aligned}$$

(79)

$$\begin{aligned} L_{(l_\mathrm{s}=0)I}= & {} \int ^1_\mathrm{a}rL_{(l_\mathrm{s}=0)}(r)\;\text {d}r=\frac{1}{8}(1-2a^2+a^4). \end{aligned}$$

(80)

The asymptotic limit as $l_\mathrm{s}\rightarrow 0$ in all the equations has been found and matches those for the no-slip condition.

Appendix 3: Asymptotic equations in the limit $g\ll 1$

The asymptotic equation includes either $\bar{L}$ or $L_{-I}$ for a PCB or NCB, respectively, which are given by

$$\begin{aligned} \bar{L}= & {} -\frac{(1-a^2)^2}{8}+\frac{l_\mathrm{s}a(1-a^2)}{3\beta }+\frac{{l_\mathrm{s}}^2(8a+1-9a^2)}{2\beta ^2}-\frac{20{l_\mathrm{s}}^3(1-a)}{\beta ^3}\nonumber \\&+\ln \left( \frac{6l_\mathrm{s}}{(1-a)\beta +6l_\mathrm{s}}\right) \left( \frac{3l_\mathrm{s}a(1-a^2)}{4\beta }-\frac{9{l_\mathrm{s}}^2(1+a^2)}{2\beta ^2}+\frac{81{l_\mathrm{s}}^3a}{\beta ^3}-\frac{162{l_\mathrm{s}}^4}{\beta ^4}\right) \nonumber \\&+\ln \left( \frac{(1-a)\beta +2l_\mathrm{s}}{2l_\mathrm{s}}\right) \left( \frac{3l_\mathrm{s}a(1-a^2)}{4\beta }-\frac{13{l_\mathrm{s}}^2(1+a^2)}{6\beta ^2}+\frac{17{l_\mathrm{s}}^3a}{\beta ^3}-\frac{14{l_\mathrm{s}}^4}{\beta ^4}\right) \nonumber \\&-\frac{l_\mathrm{s}(1-a^2)}{3\beta ^2}(8l_\mathrm{s}-4\beta a)\left( \frac{1}{(1-a)\beta +2l_\mathrm{s}}-\frac{1}{2l_\mathrm{s}}\right) , \end{aligned}$$

(81)

$$\begin{aligned} L_{-I}= & {} \frac{(1-a^2)^2}{8}+\frac{2{l_\mathrm{s}}^2a(1-a^2)}{3\beta (-(1-a)\beta +2l_\mathrm{s})}+\frac{{l_\mathrm{s}}^2}{2\beta ^2}(8a+1-9a^2)-\frac{4(1-a){l_\mathrm{s}}^2}{\beta ^3}\left( -(1-a)\beta +5l_\mathrm{s}\right) \nonumber \\&+\ln \left( \frac{-(1-a)\beta +6l_\mathrm{s}}{6l_\mathrm{s}}\right) \left( -\frac{3l_\mathrm{s}a(1-a^2)}{4\beta }+\frac{3l_\mathrm{s}}{4\beta ^2}\left( -(1-a)\beta +6l_\mathrm{s}\right) (1-3a^2)\right. \nonumber \\&+\left. \frac{9l_\mathrm{s}a}{4\beta ^3}\left( -(1-a)\beta +6l_\mathrm{s}\right) ^2-\frac{3l_\mathrm{s}}{4}\left( -\frac{(1-a)^3}{\beta }+\frac{18{l_\mathrm{s}}(1-a)^2}{\beta ^2}\right. \right. +\left. \left. \frac{-108{l_\mathrm{s}}^2(1-a)}{\beta ^3}+\frac{216{l_\mathrm{s}}^3}{\beta ^4}\right) \right) \nonumber \\&+\ln \left( \frac{2l_\mathrm{s}}{-(1-a)\beta +2l_\mathrm{s}}\right) \left( -\frac{3l_\mathrm{s}a(1-a^2)}{4\beta }\right. +\frac{l_\mathrm{s}}{12\beta ^2}\left( -9(1-a)\beta +26l_\mathrm{s}\right) (1-3a^2)\nonumber \\&+\frac{l_\mathrm{s}a}{4}\left( \frac{9(1-a)^2}{\beta }-\frac{52l_\mathrm{s}(1-a)}{\beta ^2}+\frac{68{l_\mathrm{s}}^2}{\beta ^3}\right) \nonumber \\&-\left. \frac{l_\mathrm{s}}{4}\left( -\frac{3(1-a)^3}{\beta }+\frac{26l_\mathrm{s}(1-a)^2}{\beta ^2}-\frac{68{l_\mathrm{s}}^2(1-a)}{\beta ^3}+\frac{56{l_\mathrm{s}}^3}{\beta ^4}\right) \right) . \end{aligned}$$

(82)

Appendix 4: Additional table

Table 4 Values of $g_{\min }$ for an NCB and a PCB under internal pressurisation in the case of a narrow $a=0.8$ and wide $a=0.2$ annulus with the increasing speed parameter $0\le \lambda \le 5$ and slip length $0\le l_\mathrm{s}\le 0.1$; $\epsilon =1.2$, $\sigma =1$, $K_z=10$, $\alpha =1$ and $D_\mathrm{a}=1$