Area-preserving azimuthal shear deformation of an incompressible tube reinforced by radial fibres

Abstract

The principal problem of interest in this paper is that of the area-preserving azimuthal shear strain of an incompressible transversely isotropic hyper-elastic circular cylindrical tube subjected to homogeneous radial tractions on both its inner and outer boundaries. A considerable part of the solution to this problem is achieved numerically. A comparison is made between the stress distributions obtained here when fibres are very strong and their counterparts obtained in the limiting case of an ideal fibre-reinforced material [Soldatos, J Eng Math 68(1):99–127, 2010]. Pure azimuthal shear strain may be considered as a particular case of the present deformation. However, in the present case, equilibrium requires a change of the inner and outer tube boundaries which, due to the incompressibility constraint, may take place only in a manner which preserves the area of the tube cross section. Another particular case is the isotropic material counterpart of the present problem, which was considered previously [Dagher and Soldatos, J Eng Math 78(1):131–142, 2013].

Appendix: Inextensible fibres

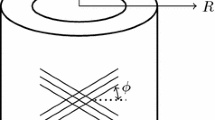
Using the components of $\mathbf {a}$ defined in (5.2), the equation of the deformed fibres (the so-called $a$-curves) is found to be

$$\begin{aligned} \theta - \Theta = \int \frac{a_\theta }{r a_r} \mathrm{d}r = \mathrm{sec}^{-1}\left( \frac{r}{\sqrt{c}}\right) - \mathrm{sec}^{-1}\left( \frac{\hat{b}_0}{\sqrt{c}}\right) . \end{aligned}$$

(8.1)

The orthogonal trajectories of the $a$-curves in the plane of the deformed cross section define the so-called $n$-curves [6], having unit tangent

$$\begin{aligned} \mathbf {n} = (n_r, n_\theta ,0)^\mathrm{T} = (a_\theta , -a_r,0)^\mathrm{T} = (\gamma , -\chi ,0)^\mathrm{T}. \end{aligned}$$

(8.2)

The equation of those curves is therefore

$$\begin{aligned} \theta - \Theta = \int \frac{n_\theta }{r n_r} \mathrm{d}r = \left( \frac{r^2}{c} - 1\right) ^{1/2} - \mathrm{sec}^{-1}\left( \frac{r}{\sqrt{c}}\right) - \left( \frac{\hat{b}_0^2}{c} - 1\right) ^{1/2} + \mathrm{sec}^{-1}\left( \frac{\hat{b}_0}{\sqrt{c}}\right) . \end{aligned}$$

(8.3)

These two families of curves define a local, orthogonal, curvilinear co-ordinate system, which will be found useful when equilibrium is considered.

Due to the plane-strain nature of the problem, the constraints of material incompressibility and fibre inextensibility leave independent only one of the invariants (2.12) [6]. This may be chosen to be $J_1$, and the strain energy density should be regarded a general function of it, namely

$$\begin{aligned} W = W(J_1). \end{aligned}$$

(8.4)

The corresponding constitutive equations can then be deduced directly from [4] by neglecting the fibre bending stiffness terms considered there.

Hence, considering that the implied inextensible fibres are perfectly flexible, one obtains

$$\begin{aligned} t_{\alpha \beta }&= -p \delta _{\alpha \beta } + T a_\alpha a_\beta + s_{\alpha \beta }, \quad t_{zz} = -p, \nonumber \\ s_{\alpha \beta }&= 2W_1 B_{\alpha \beta } - 2W_1 \delta _{\alpha \beta } - 2(J_1 - 3) W_1 a_\alpha a_\beta , \\ s_{zz}&= 0,\nonumber \end{aligned}$$

(8.5)

where $T$ is the arbitrary tension that represents the reaction of the material to the constraint of fibre inextensibility. Moreover, $s_{\alpha \beta }$ are the components of the so-called extra stress tensor (with the exception of $r$, $\theta$ and $z$, as well as $a$ and $n$ below, Latin indices operate in three dimensions, Greek indices in two dimensions). In addition, consistency with the imposed material constraints requires that the components of the extra stress tensor satisfy the following conditions [4, 6]:

$$\begin{aligned} s_{ii} = 0, \qquad s_{ij} a_i a_j = 0, \end{aligned}$$

(8.6)

where repeated indices imply summation over the range of their values.

In the aforementioned local curvilinear co-ordinate system, the components of the extra stress tensor are described as follows [4, 6, 12]:

$$\begin{aligned} s_{\alpha \beta } = s_a a_\alpha a_\beta + s_n n_\alpha n_\beta + \tau (a_\alpha n_\beta + a_\beta n_\alpha ), \end{aligned}$$

(8.7)

where $s_a$ and $s_n$ are the normal components of the extra stress tensor, and hence

$$\begin{aligned} \tau = s_{\alpha \beta } a_\alpha n_\beta \end{aligned}$$

(8.8)

represents the local shear stress component. Thus, when the constraint Eqs. (8.6) are combined with (8.5d), (8.7) reduces to

$$\begin{aligned} s_{\alpha \beta }=\tau (a_\alpha n_\beta + a_\beta n_\alpha ), \end{aligned}$$

(8.9)

in which $\tau$ is to be determined using constitutive equations as soon as the form of the strain energy density of the material becomes available.

For consistency with the application detailed in Sect. 4, it is now assumed that the strain energy density is that of the standard neo-Hookean material, namely

$$\begin{aligned} W(J_1) = \frac{\mu }{2}(J_1 - 3), \qquad W_1 = \frac{\partial W}{\partial J_1} = \frac{\mu }{2}, \end{aligned}$$

(8.10)

where, after (2.12a) and (5.1), $J_1$ necessarily takes the form

$$\begin{aligned} J_1 = \mathrm{tr}(\mathbf {B}) = \chi ^{-2} + 2. \end{aligned}$$

(8.11)

The constitutive Eq. (8.5c) then yields the non-zero components of the extra stress tensor as follows:

$$\begin{aligned} s_{rr}=2\mu (\chi ^2-1)=-\frac{2\mu c}{r^2}, \quad s_{\theta \theta }=2\mu \gamma ^2=\frac{2\mu c}{r^2},\quad s_{r\theta }=\mu \chi \gamma (2-\chi ^{-2})=\frac{\sqrt{c}(r^2-2c)}{r^2\sqrt{r^2-c}}, \end{aligned}$$

(8.12)

and hence (8.8) leads to

$$\begin{aligned} \tau = -\frac{\mu \gamma }{\chi } = -\frac{\mu \sqrt{c}}{\sqrt{r^2 - c}}. \end{aligned}$$

(8.13)

Equations (8.5) thus reveal that the only remaining stress unknowns are the functions $p$ and $T$, which must be determined by solving the two simultaneous equations of static equilibrium.

Those equilibrium equations obtain a standard form in the local co-ordinate system of the $a$- and $n$-curves [4, 6, 12], which, in the absence of body forces, is as follows:

$$\begin{aligned} \frac{\partial t_a}{\partial l_a} + \kappa _n (t_a - t_n) = 2\kappa _a \tau - \frac{\partial \tau }{\partial l_n}, \quad \frac{\partial t_n}{\partial l_n} + \kappa _a (t_a - t_n) = -2\kappa _n \tau - \frac{\partial \tau }{\partial l_a}. \end{aligned}$$

(8.14)

Here, $p$ and $T$ are replaced by the new pair of unknowns

$$\begin{aligned} t_a = -p + T, \qquad t_n = -p, \end{aligned}$$

(8.15)

and therefore the in-plane Cauchy stress components (8.5a) take the following alternative form:

$$\begin{aligned} t_{\alpha \beta } = t_a a_\alpha a_\beta + t_n n_\alpha n_\beta + \tau (a_\alpha n_\beta + a_\beta n_\alpha ). \end{aligned}$$

(8.16)

In (8.14), $l_a$ and $l_n$ denote the arc length along the $a$- and $n$-curves respectively, while $\kappa _a$ and $\kappa _n$ are the curvatures of those curves defined as follows:

$$\begin{aligned} \kappa _a = -\nabla \cdot \, \mathbf {n}, \qquad \kappa _n = \nabla \cdot \, \mathbf {a}. \end{aligned}$$

(8.17)

Thus, using (5.2) and (8.2), it is seen that

$$\begin{aligned} \kappa _a = 0, \qquad \kappa _n = R^{-1} =\frac{1}{\sqrt{r^2 - c}}, \end{aligned}$$

(8.18)

making it immediately clear that the fibres remain straight and, in accordance with theoretical expectations [6], the $n$-curves maintain their curvature after deformation. Moreover, the use of (8.1) and (8.3) provides the necessary relationship between the deformed cylindrical polar co-ordinates and the co-ordinates of the curvilinear local co-ordinate system; this is as follows:

$$\begin{aligned} \mathrm{d}l_a = \frac{r}{\sqrt{r^2 - c}} \mathrm{d}r=\mathrm{d}R, \qquad \mathrm{d}l_n = \frac{r}{\sqrt{c}} \mathrm{d}r. \end{aligned}$$

(8.19)

Using these results, the equilibrium equations (8.14) reduce to

$$\begin{aligned} \frac{\partial t_a}{\partial l_a} + l_a^{-1} t_a = l_a^{-1} t_n - \frac{\partial \tau }{\partial l_n}, \qquad \frac{\partial t_n}{\partial l_n} = -\frac{2\tau }{\sqrt{r^2 - c}} - \frac{\partial \tau }{\partial l_a}. \end{aligned}$$

(8.20)

Equation (8.20b) can be integrated immediately along the $n$-curves to give

$$\begin{aligned} t_n = - \int _{\hat{b}_0}^r \left[ \frac{-2 \mu \sqrt{c}}{r^2 - c} + \mu \sqrt{c} r (r^2 -c)^{-3/2} \frac{\sqrt{r^2-c}}{r} \right] \frac{r}{\sqrt{c}} \mathrm{d}r + f_1(l_a) = \mu \ln \left( \frac{\sqrt{r^2-c}}{B_0} \right) + f_1(l_a), \end{aligned}$$

(8.21)

where $f_1(l_a)$ is an arbitrary function of integration. Equation (8.20a) can also be integrated subsequently along the $a$-curves to yield

$$\begin{aligned} t_a = l_a^{-1} \int _{\hat{b}_0}^r \left( t_n - l_a \frac{\partial \tau }{\partial l_n} \right) \frac{{\text {d}}l_a}{{\text {d}}r} \mathrm{d}r + f_2(l_n), \end{aligned}$$

(8.22)

where $f_2(l_n)$ is a second arbitrary function of integration.

Use of the boundary conditions (2.17a) and (2.18a) in connection with (8.16) yields the pair of algebraic equations [4, 5]

$$\begin{aligned} t_a\Bigg |_{r=\hat{b}_k} + \frac{c}{B_k^2} t_n\Bigg |_{r=\hat{b}_k} = -\frac{2\sqrt{c}}{B_k} \tau \Bigg |_{r=\hat{b}_k} \qquad (k=0,1), \end{aligned}$$

(8.23)

which are used in connection with (8.21b) and (8.22) to determine the arbitrary functions $f_1(l_a)$ and $f_2(l_n)$. Application of the first of these boundary conditions $(k=0)$ yields

$$\begin{aligned} f_2(l_n)+\frac{c}{B_0^2}f_1(l_a)=\frac{2\mu c}{B_0^2}. \end{aligned}$$

(8.24)

Since $l_a$ and $l_n$ are independent variables, (8.24) can be satisfied only if $f_1(l_a)$ and $f_2(l_n)$ are both constant; these constants are denoted in what follows by $f_1$ and $f_2$ respectively.

Application of the boundary condition (8.23) at the outer tube boundary $(k=1)$ further yields

$$\begin{aligned} f_2+\frac{c}{B_1^2}f_1=\frac{2\mu c}{B_1^2}-\frac{\mu c}{B_1^2}\ln \left( \frac{B_1}{B_0}\right) -\frac{M}{B_1}, \end{aligned}$$

(8.25)

where the constant $M$ is given as follows:

$$\begin{aligned} M = \int _{\hat{b}_0}^{\hat{b}_1} \left( t_n - l_a \frac{\partial \tau }{\partial r}\frac{\partial r}{\partial l_n} \right) \frac{{\text {d}}l_a}{{\text {d}}r} {\text {d}}r = (B_1-B_0) \left[ f_1 - \mu \left( 1+ \frac{c}{B_0 B_1} \right) \right] + \mu B_1 \ln \left( \frac{B_1}{B_0} \right) . \end{aligned}$$

(8.26)

Solving (8.24) and (8.25) simultaneously, we obtain the values of $f_1$ and $f_2$ as

$$\begin{aligned} f_1&= \mu - \frac{\mu B_0 \hat{b}_1^2}{(B_1-B_0)(B_0 B_1-c)} \ln \left( \frac{B_1}{B_0} \right) , \quad f_2 = \frac{\mu c}{B_0} + \frac{\mu c \hat{b}_1^2}{(B_1-B_0)(B_0 B_1-c)} \ln \left( \frac{B_1}{B_0} \right) . \end{aligned}$$

(8.27)

Hence, performing the integration presented in (8.22), one finds

$$\begin{aligned} t_a = \mu \ln \left( \frac{\sqrt{r^2-c}}{B_0} \right) + \frac{\mu c}{r^2-c} + \frac{\mu \hat{b}_0^2 \hat{b}_1^2 \ln (B_1/B_0)}{(B_1-B_0)(B_0 B_1-c)}\frac{1}{\sqrt{r^2-c}} + f_1 -\mu . \end{aligned}$$

(8.28)

With $t_a$ and $t_n$ now known, the unknown functions $p$ and $T$ can also be determined; using (8.15), we find them to be

$$\begin{aligned} p(r)&= -\mu \ln \left( \frac{\sqrt{r^2-c}}{B_0} \right) - f_1, \quad T(r) = \frac{\mu c}{r^2-c} + \frac{\mu \hat{b}_0^2 \hat{b}_1^2 \ln (B_1/B_0)}{(B_1-B_0)(B_0 B_1-c)} \frac{1}{\sqrt{r^2-c}} -\mu . \end{aligned}$$

(8.29)

Thus, the components of the Cauchy stress tensor can be deduced from the constitutive Eqs. (8.5), which lead to their final explicit form (5.3).