Abstract
We consider the problem of characterizing the smooth, isometric deformations of a planar material region identified with an open, connected subset \({\mathcal{D}}\) of two-dimensional Euclidean point space \(\mathbb{E}^{2}\) into a surface \({\mathcal{S}}\) in three-dimensional Euclidean point space \(\mathbb{E}^{3}\). To be isometric, such a deformation must preserve the length of every possible arc of material points on \({\mathcal{D}}\). Characterizing the curves of zero principal curvature of \({\mathcal{S}}\) is of major importance. After establishing this characterization, we introduce a special curvilinear coordinate system in \(\mathbb{E}^{2}\), based upon an à priori chosen pre-image form of the curves of zero principal curvature in \({\mathcal{D}}\), and use that coordinate system to construct the most general isometric deformation of \({\mathcal{D}}\) to a smooth surface \({\mathcal{S}}\). A necessary and sufficient condition for the deformation to be isometric is noted and alternative representations are given. Expressions for the curvature tensor and potentially nonvanishing principal curvature of \({\mathcal{S}}\) are derived. A general cylindrical deformation is developed and two examples of circular cylindrical and spiral cylindrical form are constructed. A strategy for determining any smooth isometric deformation is outlined and that strategy is employed to determine the general isometric deformation of a rectangular material strip to a ribbon on a conical surface. Finally, it is shown that the representation established here is equivalent to an alternative previously established by Chen, Fosdick and Fried (J. Elast. 119:335–350, 2015).
Similar content being viewed by others
1 Introduction
Recently, we [1] established an explicit necessary and sufficient representation for a three-times continuously differentiable, isometric deformation of a planar material region identified with an open, connected region \({\mathcal{D}}\) in two-dimensional Euclidean point space \(\mathbb{E}^{2}\) into a surface \({\mathcal{S}}\) in three-dimensional Euclidean point space \(\mathbb {E}^{3}\). Each such deformation is determined by a sufficiently smooth space curve \({\mathcal{C}}\), the directrix, and a family of straight lines, the generators. A condition necessary, but not sufficient, for the deformation to be isometric is that the generator at each point of \({\mathcal{C}}\) lies in the plane orthogonal to \({\mathcal{C}}\) at that point, with its precise orientation within that plane being determined by the cumulative torsion of \({\mathcal{C}}\). Additionally, however, each ordered combination \((u,v)\) of arclength \(u\) along the directrix and distance \(v\) along the generators must correspond isometrically to a unique material point \(\boldsymbol{x}\) in \({\mathcal{D}}\). That correspondence takes the form of an implicit relation, involving convoluted dependence on the curvature and torsion of \({\mathcal{C}}\), and admits a closed-form solution only in very simple examples, encountered for instance in the construction of the isometric deformation that bends a half disk into a conical surface.
In the present paper, we describe an alternative strategy designed to mitigate the aforementioned difficulties. This strategy produces a different, but equivalent, necessary and sufficient representation for the class of isometric deformations of planar material regions and it corrects a fundamental misunderstanding concerning an interpretation of the coordinate representation that has circulated in the mainstream literature on the subject. We consider only kinematical issues, leaving questions surrounding the variational characterization of equilibrium configurations for future consideration.
Our primary objective is to determine a representation for the most general smooth isometric deformation \(\tilde{\boldsymbol{y}}\) that takes each point \(\boldsymbol{x}\) in an open, connected subset \({\mathcal{D}}\) of \(\mathbb{E}^{2}\) to a point \(\boldsymbol{y}\) on a surface \({\mathcal {S}}\) in \(\mathbb{E}^{3}\):
Our approach hinges on a characterization, provided in Sect. 3, of the generators of any surface \({\mathcal{S}}\) determined by such a deformation. This characterization leads naturally to the introduction, in Sect. 4, of curvilinear coordinates \((\eta^{1},\eta^{2})\) for \({\mathcal{D}}\) that correspond to an à priori chosen form for the pre-images of the generators. Relative to a fixed orthonormal basis \(\{\boldsymbol{\imath}_{1},\boldsymbol {\imath}_{2}\}\) for the translation space \(\mathbb{V}^{2}\) of \(\mathbb {E}^{2}\), each generator of \({\mathcal{S}}\) is the rotated and translated ‘rigid image’ of a straight line in \({\mathcal{D}}\) with orientation
where \(\theta(\eta^{1})\) is the angle that the \(\eta^{2}\)-coordinate line passing through the point \(\boldsymbol{x}=\eta^{1}\boldsymbol {\imath}_{1}\) makes with a line parallel to \(\boldsymbol{\imath }_{1}\). The \((\eta^{1},\eta^{2})\)-coordinate system is of central importance to our construction. In particular, defining a parametrization \(\hat{\boldsymbol{y}}\) that maps \({\mathcal{D}}\) to \({\mathcal{S}}\), but depends on position in \({\mathcal{D}}\) through the curvilinear coordinates \((\eta^{1},\eta^{2})\), by
we establish the representation
where \(\hat{\boldsymbol{y}}_{0}\)—which is defined such that \(\hat {\boldsymbol{y}}_{0}(\eta ^{1})=\tilde{\boldsymbol{y}}(\eta^{1}\boldsymbol{\imath}_{1})\) parametrizes the image of the \(\eta^{2}= 0\) coordinate line, namely the directrix \({\mathcal{C}}\) of \({\mathcal{S}}\)—is determined by integrating \(\dot{\hat{\boldsymbol{y}}}_{0}=\boldsymbol{Q}\boldsymbol{\imath }_{1}\) with \(\hat{\boldsymbol{y}} _{0}(0)\) prescribed, where a superposed dot denotes differentiation with respect to \(\eta^{1}\), and \(\boldsymbol{Q}(\eta^{1})\) is an element of the collection \(\mathrm{Orth}^{+}\) of proper orthogonal linear transformations from \(\mathbb{V}^{3}\), the translation space of \(\mathbb{E}^{3}\), into itself. We then prove that the condition
is both necessary and sufficient to ensure that \(\tilde{\boldsymbol {y}}\) defined via (1.3)–(1.4) in conjunction with a ruled parametrization of \({\mathcal{D}}\) in terms of the curvilinear coordinates \((\eta^{1},\eta^{2})\) is an isometric deformation. The representation (1.4) for the component \(\hat{\boldsymbol {y}}\) of the isometric deformation \(\tilde{\boldsymbol{y}}\) admits various alternative forms described in Sect. 5. Suppose, in particular, that the directrix parametrized by \(\hat{\boldsymbol{y}}_{0}\) has nonvanishing curvature \(\kappa\) and, thus, possesses a well-defined Frenet frame with unit tangent \(\boldsymbol{t}=\dot{\hat{\boldsymbol{y}}}_{0}\), unit binormal \(\boldsymbol {b}\), and torsion \(\tau\). The mapping \(\hat{\boldsymbol{y}}\) can then be expressed as
where \(\lambda\) is a scalar field related to the curvature and orientation of \({\mathcal{S}}\) and satisfies
with \(\mbox{ax}(\dot{\boldsymbol{Q}}\boldsymbol{Q}^{{\top}})\) being the axial vector of the skew linear transformation \(\dot {\boldsymbol{Q}}\boldsymbol{Q}^{{\top}}\). If, without regard for the overall consequences that are considered in Sect. 5, we naively set \(\theta(\eta^{1})\equiv\pi/2\), so that the generators of \({\mathcal{S}}\) must be orthogonal to its directrix, and additionally stipulate that \(\lambda>0\), then the right-hand side of (1.6) can be recognized as the parametric form of the rectifying developable of the directrix parametrized by \(\hat {\boldsymbol{y}}_{0}\). Hangan [3], Sabitov [4], Starostin and van der Heijden [2], Kurono and Umehara [5], Chubelaschwili and Pinkall [6], Naokawa [7], Kirby and Fried [8], Shen et al. [9], and others have used rectifying developable mappings to describe nominally isometric deformations of planar rectangular material material strips into ribbons and Möbius bands. These workers do not explain how to identify material points in the reference rectangle with the curvilinear coordinates \((\eta^{1},\eta^{2})\). Nor do they provide a condition such as (1.5) which ensures that the parametric representation of the underlying deformation is indeed isometric to the extent that it preserves the length of every possible arc of material points on the reference retangle. Importantly, these omissions undermine a dimensional reduction argument that is used to ostensibly obtain the bending energy of a rectangular strip that is isometrically deformed into a curved ribbon in terms of an integral over its midline. Moreover, they lead to variational strategies that involve comparing the energies of differently shaped, generally nonrectangular, planar reference regions that are mapped, with stretching, into developable surfaces instead of with the isometric deformations of a single rectangular material strip that cannot withstand stretching. See, also, the discussion of Chen and Fried [10].
Expressions for the curvature tensor and potentially nonvanishing principal curvature of a general smooth surface \({\mathcal{S}}\) determined by an isometric deformation of a rectangular material strip are derived on the basis of our representation in Sect. 6. In Sect. 7, we specialize our results to obtain the most general smooth isometric deformation of a planar material region to a cylindrical form and provide two elementary examples involving isometric deformations of rectangular material strips. A summary of our strategy for determining any smooth isometric deformation of a planar material region is provided in Sect. 8. This strategy is then used, in Sect. 9, to determine the isometric deformation of a rectangular material strip to a conical form. Next, in Sect. 10, we show the equivalence of the representation given in our [1] previous work and that obtained here. In particular, that equivalence rests on working with orthogonal curvilinear coordinates \((\zeta ^{1},\zeta^{2})\). Finally, in Sect. 11, we briefly review the conceptual position we have taken in this work regarding the isometric mappings of planar material regions. We contrast our position with a few other notable works that do not regard the surfaces as material entities and, rather, apply the concept of isometry as it is defined in differential geometry.
2 Notion of an Isometric Deformation
Consider a three times continuously differentiable, deformation \(\tilde{\boldsymbol{y}}\) that maps each point \(\boldsymbol{x}\) in a planar material region identified with an open, connected subset \({\mathcal{D}}\) of two-dimensional point space \(\mathbb{E}^{2}\) to a point
on a surface \({\mathcal{S}}\) in three-dimensional Euclidean point space \(\mathbb{E}^{3}\). We say that such a deformation is isometric if in taking \({\mathcal{D}}\) to \({\mathcal{S}}\) it preserves the length of every possible arc of material points on \({\mathcal{D}}\). This is the case if and only if the gradient
of \(\tilde{\boldsymbol{y}}\) on \({\mathcal{D}}\), the values of which are linear mappings from the translation space \(\mathbb{V}^{2}\) of \(\mathbb {E}^{2}\) to the translation space \(\mathbb{V}^{3}\) of \(\mathbb{E}^{3}\), preserves the lengths of vectors in \(\mathbb{V}^{2}\) in the sense that
for each \(\boldsymbol{u}\in\mathbb{V}^{2}\). On this basis, we see that
for all \(\boldsymbol{u}\in\mathbb{V}^{2}\) and \(\boldsymbol{v}\in \mathbb{V}^{2}\). Equivalently, \(\boldsymbol{F}\) must obey
where \(\boldsymbol{I}\) denotes the identity linear transformation on \(\mathbb{V}^{2}\). The requirement that (2.3) holds for all \(\boldsymbol{u}\in\mathbb{V}^{2}\) is also sufficient for \(\tilde {\boldsymbol{y}}\) to be an isometric deformation, as is the requirement that the gradient \(\boldsymbol{F}\) of \(\tilde{\boldsymbol{y}}\) satisfies (2.5).
It is important to distinguish between our notion of an isometric deformation and an alternative notion that is encountered in differential geometry—a notion that has been applied naively when dealing with deformations of two-dimensional bodies which cannot withstand stretching. Such bodies are referred to as “inextensional” in the classical theories of plates (see, for example, Simmonds and Libai [11, 12]) and shells (see, for example, Libai and Simmonds [13, 14]) but are often referred to as “inextensible” in recent works on ribbon-like forms.
In differential geometry, it is commonly understood that a mapping of a part \({\mathcal{D}}\) of a surface \({\mathcal{A}}\subset\mathbb{E}^{3}\) onto a part \({\mathcal{S}}\) of a surface \({\mathcal{B}}\subset \mathbb {E}^{3}\) is isometric, or length-preserving, if the length of any arc on \({\mathcal{S}}\) is the same as the length of the inverse image of the arc on \({\mathcal{D}}\). If such a mapping exists, then the surfaces \({\mathcal{D}}\) and \({\mathcal{S}}\) are said to be isometric. In the differential geometric concept of isometry, the surfaces \({\mathcal {A}}\) and ℬ are considered as given and the objective is to determine conditions which ensure that a length-preserving mapping exists between the corresponding parts \({\mathcal{D}}\subset{\mathcal {A}}\) and \({\mathcal{S}}\subset{\mathcal{B}}\). Statements to the effect that “isometric surfaces must have the same Gaussian curvature at corresponding points of such a mapping” and “if the Gaussian curvatures of \({\mathcal{D}}\) and \({\mathcal{S}}\) are constant and equal to one another then the surfaces are isometric” are commonplace.Footnote 1 So also is the statement “corresponding curves on isometric surfaces have the same geodesic curvature at corresponding points”. Furthermore, it is well-known that if \({\mathcal{D}}\) and \({\mathcal{S}}\) are developable then the Gaussian curvatures of both are zero and thus, in particular, \({\mathcal{D}}\) and \({\mathcal{S}}\) are isometric to one another from the differential geometric point of view.
In the kinematics of continuous two-dimensional material bodies, as is the concern of this paper, it is commonly understood that a mapping considered as a deformation of a given material surface \({\mathcal{D}}\subset\mathbb{E}^{3}\) into a surface \({\mathcal {S}}\subset\mathbb{E}^{3}\) is isometric (i.e., length-preserving, unstretchable, or inextensional), if the length of any arc of material points on \({\mathcal{D}}\) is the same as the length of the image of this material arc on the surface \({\mathcal{S}}\subset\mathbb{E}^{3}\) under the deformation. Any such mapping is considered to be a deformation of the surface \({\mathcal{D}}\subset\mathbb{E}^{3}\), which is identified as a given reference configuration, and the objective is to determine conditions on the deformation necessary and sufficient to ensure that it is length-preserving. If, for example, the material surface \({\mathcal{D}}\) is planar and its mapping, considered as a deformation of \({\mathcal{D}}\mapsto{\mathcal{S}}\), produces a developable image \({\mathcal{S}}\), then the Gaussian curvatures of both \({\mathcal{D}}\) and \({\mathcal{S}}\) are zero but the mapping is not necessarily an isometric deformation. To illustrate, \({\mathcal {D}}\subset\mathbb{E}^{2}\) could be an undistorted, rectangular material ribbon which is mapped to \({\mathcal{S}}\subset{\mathcal {T}}_{c}\), where \({\mathcal{T}}_{c}\subset\mathbb{E}^{3}\) is a circular cylindrical surface. In this case, both \({\mathcal{D}}\) and \({\mathcal{S}}\) have zero Gaussian curvature, but the mapping need not be an isometric deformation because stretching of material filaments may have taken place. To be an isometric deformation, the developability of the reference surface \({\mathcal{D}}\) and its target image \({\mathcal{S}}\) is not sufficient, as we show later in Sect. 4 of this paper.
The notions of isometry that arise in differential geometry and in the kinematics of continuous two-dimensional material bodies are fundamentally different. Importantly, however, only the second of these notions is relevant when studying the deformation of a two-dimensional body that cannot withstand stretching.
In the setting of differential geometry, the surfaces \({\mathcal{A}}\) and ℬ in \(\mathbb{E}^{3}\) are preconceived and given a priori without regard for how one is obtained from the other, and the central question concerns whether lengths measured on a part \({\mathcal{D}}\subset{\mathcal{A}}\) can be made to correspond to (i.e., be equal to) lengths measured on a part \({\mathcal{S}}\subset {\mathcal{B}}\) for any mapping in the collection of all mappings of \({\mathcal{D}}\mapsto{\mathcal{S}}\). When such a mapping exists then the surfaces \({\mathcal{D}}\) and corresponding \({\mathcal{S}}\) are said to be geometrically isometric. From this standpoint, no surface is considered to be a two-dimensional continuous material region and no mapping is considered to be the deformation of such a body. Suppose, for example, that \({\mathcal{A}}\) and ℬ are planar surfaces in \(\mathbb{E}^{3}\). Then, it is clear that a square part \({\mathcal{D}}\subset{\mathcal{A}}\) and a square part of equal size \({\mathcal{S}}\subset{\mathcal{B}}\) are isometric in the differential geometric sense. However, from the standpoint of the kinematics of two-dimensional continuous material regions, if \({\mathcal{D}}\subset {\mathcal{A}}\) is considered to be an undistorted material reference configuration and if \({\mathcal{S}}\subset{\mathcal{B}}\) is a distorted (i.e., stretched) image of \({\mathcal{D}}\), then no square parts of equal size in \({\mathcal{D}}\) and \({\mathcal{S}}\), respectively, are related by an isometric deformation.
If \({\mathcal{A}}\) and ℬ are developable surfaces in \(\mathbb{E}^{3}\), then in the differential geometric sense there generally exists an isometric image \({\mathcal{S}}\subset{\mathcal {B}}\) of a part \({\mathcal{D}}\) of \({\mathcal{A}}\). But, in the kinematics of two-dimensional continuous material regions there need not exist an isometric deformation which maps the same part \({\mathcal {D}}\subset{\mathcal{A}}\) to \({\mathcal{S}}\subset{\mathcal{B}}\). The differential geometric isometric image of \({\mathcal{D}}\) does not necessarily represent a deformation of the relevant points of \({\mathcal {A}}\) into the part \({\mathcal{S}}\subset{\mathcal{B}}\). In general, it is simply an image or overlay that defines a region \({\mathcal{S}}\) on ℬ in which lengths can be measured in the same way that they were measured in \({\mathcal{D}}\subset{\mathcal{A}}\). From the standpoint of the kinematics of two-dimensional continuous material region, if \({\mathcal{A}}\) is developable then an isometric deformation of a part \({\mathcal{D}}\subset{\mathcal{A}}\) in \(\mathbb{E}^{3}\) will produce a developable surface \({\mathcal{S}}\) which has the additional property that the length between material points on \({\mathcal{D}}\) and the length between corresponding material points on \({\mathcal{S}}\) under the deformation mapping are equal. From this point of view, the requirement that a deformation maps a developable surface to a developable surface is necessary for the underlying mapping to be an isometric deformation but it does not suffice to ensure that material lengths are preserved. Thus, when considering the characterization of the deformation (i.e., bending and twisting) of a rectangular material ribbon under the constraint that material lengths cannot be changed—which, for example, is the common hypothesis in deforming a rectangular strip of paper into a Möbius band—deformations are the only physically relevant class of mappings.
3 General Analysis and Set-up: Isometric Deformation of \({\mathcal{D}}\subset\mathbb{E}^{2}\) to \({\mathcal{S}}\subset \mathbb{E}^{3}\)
Let \(\{\boldsymbol{\imath}_{1},\boldsymbol{\imath}_{2}\}\) denote a fixed orthonormal basis in the translation space \(\mathbb{V}^{2}\) of \(\mathbb{E}^{2}\), let \(x_{i}\) denote the component of \(\boldsymbol{x}\) relative to \(\boldsymbol{\imath}_{i}\), \(i=1,2\), so that \(\boldsymbol {x}=x_{i}\boldsymbol{\imath}_{i}\),Footnote 2 and define \(\boldsymbol{\imath}_{3}:=\boldsymbol {\imath}_{1}\times\boldsymbol{\imath}_{2}\), so that \(\{\boldsymbol {\imath}_{1},\boldsymbol{\imath}_{2},\boldsymbol{\imath}_{3}\}\) provides a fixed positively-oriented orthonormal basis for the translation space \(\mathbb{V}^{3}\) of \(\mathbb{E}^{3}\). With a slight abuse of notation, we may then write \(\tilde{\boldsymbol {y}}(\boldsymbol {x})=\tilde{\boldsymbol{y}}(x_{1},x_{2})\) and define a basis \(\{ \boldsymbol {e}_{i},\boldsymbol{e}_{2}\}\) at each point \(\boldsymbol{y}=\tilde {\boldsymbol{y}} (\boldsymbol{x})\) of \({\mathcal{S}}\) by
for each material point \(\boldsymbol{x}\) of \({\mathcal{D}}\). The base vectors \(\boldsymbol{e}_{1}(\boldsymbol{x})\) and \(\boldsymbol {e}_{2}(\boldsymbol{x})\) are of course tangent to \({\mathcal{S}}\) at \(\boldsymbol{y}\). With reference to (2.4), the requirement that \(\tilde{\boldsymbol{y}}\) is an isometric deformation may then be expressed as
By differentiating we thus have
along with two similar equations obtained by cyclically permuting the indicies \(\{i, j, k\}\). By adding two of these equations and subtracting the other we easily arrive at
Now, on introducing the oriented unit vector normal
to \({\mathcal{S}}\), we infer from (3.4) that, for each \(\boldsymbol{x}\in{\mathcal{D}}\),
Observing that \(\tilde{\boldsymbol{y}},_{ijk}=\tilde{\boldsymbol {y}},_{ikj}\) by the assumed smoothness of the mapping \(\tilde{\boldsymbol{y}}\), we readily see from (3.6) that
Thus, because \(\boldsymbol{n},_{i}\) is orthogonal to \(\boldsymbol{n}\), we find from (3.7) that
which, with the symmetry condition (3.6)2, yields
This shows that at points where the mapping \(\tilde{\boldsymbol{y}}\) is smooth we may introduce a scalar field \(\phi\) satisfying
Consequently, (3.6) becomes
Moreover, (3.7) reduces to
which is equivalent to
where \({\varepsilon}_{ij}\) is the usual alternator symbol for \(\mathbb {E}^{2}\). Thus,
Now, because \(\boldsymbol{n},_{k}\cdot\boldsymbol {e}_{m}=-\boldsymbol {n}\cdot\boldsymbol{e}_{m},_{k}\) and because (3.1) and (3.11) imply that \(\boldsymbol{e}_{m},_{k}=\tilde{\boldsymbol {y}},_{mk}=\phi ,_{mk}\boldsymbol{n}\), this last relation may be written as
Recognizing that the expression on the left-hand side of the above relation is skew in the indices \(i\) and \(m\), we have equivalently
which gives
Now let us recall some elementary differential geometry. Consider a smooth curve
in \({\mathcal{D}}\). The image ℒ of this curve in \({\mathcal{S}}\) is then given by
with \(\check{\boldsymbol{y}}(\beta):=\tilde{\boldsymbol{y}}(\check {\boldsymbol{x}}(\beta))\) for \(0<\beta <\beta_{*}\), and, because \(\tilde{\boldsymbol{y}}\) is an isometric deformation, we see that the natural tangent vector \(\boldsymbol{e}\) to ℒ given by
satisfies
Also, the arclength parameter \(s\) is common to both \({{\mathcal {L}}}_{0}\) and ℒ, and we have
Clearly, \(\boldsymbol{\sigma}:= {\boldsymbol{e}}/ |{\boldsymbol{e}}|\) is a unit tangent vector to \({\mathcal{L}}\subset{\mathcal{S}}\). Finally, we record for later use that the chain rule gives
from which it follows that
The Frenet formula for ℒ may be written as
where \({\kappa}\) and \({\boldsymbol{m}}\) denote the curvature of ℒ and the unit normal of ℒ, respectively. The normal curvature of \({\mathcal{S}}\) at \(\boldsymbol{y}\) in the direction of \(\boldsymbol{\sigma}\) on ℒ is thus given by
where \(\mbox{grad}_{s}\boldsymbol{n}= (\mbox{grad}_{s}\boldsymbol {n})^{{\top}}\) denotes the surface gradient of the unit normal field in \({\mathcal{S}}\) and its negative represents the “curvature tensor” of \({\mathcal{S}}\).Footnote 3
In passing, if we let \({\mathcal{L}}_{0}\) be, respectively, an \(x_{1}\) or an \(x_{2}\) coordinate line in \({\mathcal{D}}\), and associate, alternatively, the orthonormal base vectors \(\boldsymbol{e}_{1}\) or \(\boldsymbol{e}_{2}\) with \(\boldsymbol{\sigma}\) then, because \(\boldsymbol{e}_{i}\cdot\boldsymbol{n}= 0\) we have \(\boldsymbol {e}_{i},_{j}\cdot\boldsymbol{n}+ \boldsymbol{e}_{i}\cdot\boldsymbol {n},_{j} = 0\) and similar to (3.26) we may write
Thus, because of (3.1) and (3.11) we have for an isometric deformation the special result
for all \(\boldsymbol{x}\) in \({\mathcal{D}}\), which implies that
Now, if we couple (3.29) with (3.17) we may conclude that, for an isometric deformation \(\tilde{\boldsymbol{y}}\) with \(\boldsymbol {n}\) given by (3.1) and (3.5),
at all points of \({\mathcal{S}}\) where the mapping \(\tilde {\boldsymbol{y}}\) is smooth. This, of course, implies that a principal curvature of \({\mathcal{S}}\) must vanish at all such points.
Now, let us associate the curve \({\mathcal{L}}\subset{\mathcal{S}}\) with a curve of zero principal curvature of \({\mathcal{S}}\). That is, let us suppose the natural tangent vector \(\boldsymbol{e}=\mbox{d}\check {\boldsymbol{y}} /\mbox{d}\beta\) is an eigenvector of \(\mbox{grad}_{s}\boldsymbol{n}\) on ℒ with zero eigenvalue. Thus, along ℒ we have
Further, the chain rule gives
which, with (3.11), yields
But, (3.29) and (3.23) show that
and so, using the symmetry of \(\mbox{grad}_{s}\boldsymbol{n}\), we see that
for \(0<\beta<\beta_{*}\). This means that
wherever ℒ is smooth. As a consequence, the unit normal field \(\boldsymbol{n}\) is also constant along ℒ wherever ℒ is smooth, from which we infer that if ℒ is smooth then it must lie on a fixed plane and the space curve ℒ must consequently be planar. Moreover, from (3.23), we have
where we emphasize that \(\boldsymbol{e}_{i}\) is constant along ℒ. Thus, on integrating with respect to \(\beta\) we find that, for smooth ℒ,
where \(\boldsymbol{c}\) is a constant vector in \(\mathbb{V}^{3}\). Finally, we observe that for smooth ℒ there is an element \(\boldsymbol{Q}\) of the collection \(\mathrm{Orth}^{+}\) of proper orthogonal linear transformations from \(\mathbb{V}^{3}\) to \(\mathbb {V}^{3}\) such that \(\boldsymbol{e}_{i}=\boldsymbol{Q}\boldsymbol {\imath }_{i}\), \(i=1,2\), at each point on ℒ. This then gives
and
the latter of which shows that \({\mathcal{L}}\subset{\mathcal{S}}\) is a rotated and translated “rigid image” of \({\mathcal{L}}_{0} \subset {\mathcal{D}}\). Since ℒ is planar, then if it is straight in \({\mathcal{S}}\) its pre-image, \({\mathcal{L}}_{0}\), is straight in \({\mathcal{D}}\) and is of the same length; if it is curved in \({\mathcal {S}}\) its pre-image, \({\mathcal{L}}_{0}\), being an exact copy in \({\mathcal{D}}\), must have chord lengths that are equal to those of ℒ for points which correspond under the isometric deformation \(\tilde{\boldsymbol{y}}\). Moreover, because all points on a chord of \({\mathcal{L}}_{0}\) must lie in \({\mathcal{D}}\) and ℒ is planar, then due to the isometry of \(\tilde{\boldsymbol{y}}\) all points on the corresponding chord of ℒ must lie in \({\mathcal{S}}\) and be governed by \(\tilde{\boldsymbol{y}}\). This shows that the plane region defined by the closure of the interior of the convex hull of the planar curve ℒ must be part of \({\mathcal{S}}\).
Now, if two smooth curves, \({\mathcal{L}}^{(1)}\subset{\mathcal{S}}\) and \({\mathcal{L}}^{(2)}\subset{\mathcal{S}}\), of zero principal curvature of \({\mathcal{S}}\) intersect then they intersect at a point on \({\mathcal{S}}\) where the (oriented) surface unit normal is either uniquely defined or the (oriented) surface has multiple unit normals. If the surface normal is unique then, arguing as above using the fact that in general the unit normal of \({\mathcal{S}}\) must be constant along both \({\mathcal{L}}^{(1)}\) and \({\mathcal{L}}^{(2)}\), we see that because of the common normal at the intersection point the two curves must then lie in a common plane and all points in the closure of the interior of the convex hull of these two curves must lie in a common planar part of \({\mathcal{S}}\). If the surface unit normal is not unique at the point of intersection then it has at least the two unit surface normals that are constant and propagated along \({\mathcal {L}}^{(1)}\) and \({\mathcal{L}}^{(2)}\), respectively; in this case the point of intersection is a “non-regular point” of \({\mathcal{S}}\). We shall not allow such situations in this work and consider only smooth surfaces \({\mathcal{S}}\) consisting solely of regular points. In this case, an elementary argument based on the conclusions just established shows that \({\mathcal{S}}\) is composed of only two categories of subregions:
-
Strips of \({\mathcal{S}}\) each of which contains a single one-parameter family of straight lines that do not intersect in \({\mathcal{S}}\) but run through \({\mathcal{S}}\). These families describe the bent regions of \({\mathcal{S}}\) in which only one principal curvature of \({\mathcal{S}}\) vanishes.
-
Planar strips of \({\mathcal{S}}\) each of which are bounded by straight lines of zero principal curvature of \({\mathcal{S}}\) that do not intersect in \({\mathcal{S}}\). Clearly, all continuous curves in such regions are curves of zero principal curvature of \({\mathcal{S}}\).
Even for the class of surfaces containing only regular points, as noted in the second of the above bullet items there may be continuous, non-differentiable curves of zero principle curvature of \({\mathcal {S}}\) that lie on \({\mathcal{S}}\). However, in this case such curves must again lie in a common planar part of \({\mathcal{S}}\) and the closure of the interior of its convex hull must also be in \({\mathcal {S}}\). Of course, on planar parts of \({\mathcal{S}}\) all curves are curves of zero principal curvature of \({\mathcal{S}}\).
To determine the form of the isometric deformation \(\tilde{\boldsymbol {y}}\), we must go further than simply the partial characterization (3.40). This requires the introduction of another parameter \(\alpha\), say, and a study of a one-parameter family \({\mathcal{L}}(\alpha)\) of straight lines of zero principal curvature in \({\mathcal{S}}\) with corresponding pre-image lines \({\mathcal{L}}_{0}(\alpha)\) in \({\mathcal{D}}\). Having taken this step, we may then replace the form (3.40) by
where \(\boldsymbol{c}(\alpha)\) is a constant vector in \(\mathbb {V}^{3}\) and \(\hat{\boldsymbol{x}}(\alpha,\cdot)\) is given by
with \(\hat{\boldsymbol{x}}_{0}(\alpha)\) parametrizing a specified curve in \({\mathcal{D}}\) and \({\boldsymbol{b}}(\alpha)\) a unit vector along the straight line \({\mathcal{L}}_{0}(\alpha)\). Alternatively, we may write (3.41) as
where \(\hat{\boldsymbol{y}}_{0}(\alpha):=\hat{\boldsymbol {y}}(\alpha, 0)=\tilde{\boldsymbol{y}}(\hat{\boldsymbol{x}} _{0}(\alpha))\) is the image in \({\mathcal{S}}\) of the curve \(\hat {\boldsymbol{x}} _{0}(\alpha)\) in \({\mathcal{D}}\). The remaining difficulty at this stage lies with guaranteeing that (3.43) is, indeed, an isometric mapping of \({\mathcal{D}}\) to \({\mathcal{S}}\subset \mathbb {E}^{3}\). Moreover, having achieved this, we must also transform from the parameters \((\alpha,\beta)\) to the coordinates \((x_{1},x_{2})\) and use (3.43) to determine the deformation \(\tilde{\boldsymbol{y}}\) in the form \(\boldsymbol{y}=\tilde {\boldsymbol{y}}(x_{1},x_{2})\).
4 Coordinate Representation of an Isometric Deformation: Necessary and Sufficient Condition
For convenience, let us introduce the curvilinear coordinates \((\eta ^{1}, \eta^{2}) := (\alpha, \beta)\) in \(\mathbb{E}^{2}\) and define the transformation \((x_{1},x_{2})\longleftrightarrow(\eta^{1},\eta ^{2})\) by
where
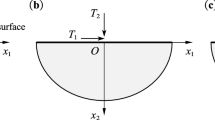
The \(\eta^{1}\)-coordinate line is coincident with the \(x_{1}\)-coordinate line at \(\eta^{2} = 0\) and the \(\eta ^{2}\)-coordinate lines run along straight lines in \({\mathcal{D}}\) that correspond to pre-images of the straight lines of zero principal curvature in \({\mathcal{S}}\). The \(\eta^{2}\)-coordinate line passing through \((\eta^{1},0)\) forms an angle \(\theta(\eta^{1})\in(0, \pi )\) with the \(x_{1}\)-axis as shown in Fig. 1.
Clearly, the \(\eta^{1}\)-coordinate lines corresponding to \(\eta ^{2}=\mbox{constant}\) are not straight unless \(\theta\) is constant, except for \(\eta^{2} = 0\), which then corresponds to the \(x_{1}\)-axis. The base vectors of \(\mathbb{V}^{2}\) through each \(\boldsymbol{x}\in {\mathcal{D}}\subset\mathbb{E}^{2}\) for the curvilinear system are given by
so that
where a superposed dot is used to denote differentiation with respect to \(\eta^{1}\) and the dependencies of \(\boldsymbol{b}_{1}\), \(\boldsymbol{b}_{2}\), and \(\theta\) on \(\eta^{1}\) are suppressed for brevity. Note, from (4.2b), that \(|\boldsymbol {b}_{2}|=1\) and that (4.1a) takes the explicit form
To ensure that \(\{\boldsymbol{b}_{1}, \boldsymbol{b}_{2}\}\) is an acceptable basis for representing the points of \({\mathcal{D}}\subset \mathbb{E}^{2}\), we restrict \(\theta\) and \(\eta^{2}\) so that
on \({\mathcal{D}}\).Footnote 4
Now, setting \(\alpha= \eta^{1}\), \(\beta= \eta^{2}\), \(\boldsymbol {b}(\alpha) = \boldsymbol{b}_{2}(\eta^{1})\), and \(\boldsymbol {Q}(\alpha) = \boldsymbol{Q}(\eta^{1})\) in (3.43), defining a mapping \(\hat{\boldsymbol{y}}\) of \((\eta^{1},\eta^{2})\) to \({\mathcal {S}}\) such that
and writing \(\hat{\boldsymbol{y}}_{0}=\hat{\boldsymbol{y}}(\cdot ,0)\) for the parametrization of the image in \({\mathcal{S}}\) of the \(\eta^{2} = 0\) coordinate line (i.e., the \(x_{1}\)-axis) in \({\mathcal{D}}\), we arrive at the representation
From here we easily see that
Thus, because (4.2a) implies that
and, because \(\boldsymbol{e}_{i}=\boldsymbol{Q}\boldsymbol{\imath }_{i}\), \(i=1,2\), we obtain the relations
which yield \(|\boldsymbol{a}_{i}| = |\boldsymbol{b}_{i}|\) for \(i=1,2\). In particular, we see that \(\boldsymbol{a}_{2}=\boldsymbol{Q}\boldsymbol {b}_{2}\) is a unit vector field which defines the straight lines of zero curvature in \({\mathcal{S}}\) that are associated with the straight lines given by \(\boldsymbol{b}_{2}\) in \({\mathcal{D}}\). Note that (4.6) implies that
where
and that from (4.2b) we have
Thus, recalling from (4.9) that \(\boldsymbol{a}_{1} = \boldsymbol{Q}\boldsymbol{b}_{1}\) we see from (4.10) that \(\boldsymbol{Q}\) must satisfy
which is a necessary condition on how the proper orthogonal transformation field \(\boldsymbol{Q}\) may be chosen so that the deformation \(\tilde{\boldsymbol{y}}\) of \({\mathcal{D}}\subset \mathbb{E}^{2}\) to \({\mathcal{S}}\subset\mathbb{E}^{3}\) defined implicitly through (4.3) and (4.6) is isometric. It readily follows that (4.13) is equivalent to \(\dot{\boldsymbol {Q}}\boldsymbol {Q}^{{\top}}\boldsymbol{a}_{2}=\boldsymbol{0}\) which means that the “angular velocity” corresponding to \(\boldsymbol{Q}\), namely the axial vector \(\mbox{ax}(\dot{\boldsymbol{Q}}\boldsymbol{Q}^{{\top}})\) of the skew linear transformation field \(\dot{\boldsymbol {Q}}\boldsymbol {Q}^{{\top}}\), must be parallel to \(\boldsymbol{a}_{2}\).Footnote 5 There thus exist a scalar field \(\lambda\) and a skew linear transformation \(\boldsymbol{A}\) with axial unit vector \(\boldsymbol{a}_{2}\), both generally dependent only on \(\eta^{1}\) but independent of \(\eta^{2}\), such that
Of course, \(|\lambda|=|\mbox{ax}(\dot{\boldsymbol{Q}}\boldsymbol {Q}^{{\top}})|\).
The condition (4.13) or, equivalently, (4.14) is not only necessary for the deformation \(\tilde{\boldsymbol{y}}\) of \({\mathcal{D}}\subset\mathbb{E}^{2}\) to \({\mathcal {S}}\subset\mathbb{E}^{3}\) defined implicitly through (4.3) and (4.6) to be isometric, but it is also sufficient. To verify this assertion, we first observe from (4.6) that
where \(\{\boldsymbol{b}^{1},\boldsymbol{b}^{2}\}\), with
is the basis of \(\mathbb{V}^{2}\) dual to \(\{\boldsymbol {b}_{1},\boldsymbol{b}_{2}\}\). Next, we observe that (4.11) and (4.12) allow us to write
and, because of (4.13), we arrive at
which is equivalent to
Thus, because \(\boldsymbol{Q}\in\mathrm{Orth}^{+}\),
and this ensures that the length between any two points in \({\mathcal {D}}\) is preserved under the deformation \(\tilde{\boldsymbol{y}}\) of \(\boldsymbol {x}\in{\mathcal{D}}\) to \(\boldsymbol{y}\in{\mathcal{S}}\) provided (4.13) holds.
5 Alternative Representative Forms of an Isometric Deformation
Note, from (4.11), that the unit tangent vector to the space curve parametrized by \(\hat{\boldsymbol{y}}_{0}\) is given by
and, granted that \(\dot{\boldsymbol{t}}\neq\boldsymbol{0}\), recall that the Frenet triad \(\{\boldsymbol{t},\boldsymbol{p},\boldsymbol {b}\} \) of tangent, normal, and binormal unit vectors, respectively, for this curve are related according to
Moreover, this triad satisfies the Frenet–Serret relations
where \(\kappa:= -\dot{\boldsymbol{p}}\cdot\boldsymbol{t}\) and \(\tau :=\dot{\boldsymbol{p}}\cdot\boldsymbol{b}\) denote, respectively, the curvature and torsion of the curve parametrized by \(\hat{\boldsymbol{y}}_{0}\).
From (4.14)2, we see that \(\dot {\boldsymbol{Q}}= \lambda\boldsymbol{A}\boldsymbol{Q}\), which yields
and with the second of (4.2b) we find, recalling that \(\theta\in(0, \pi)\), that
In view of (3.39) we thus have
which yields
and
from which we find that
and that
Thus, the curvature \(\kappa\) and torsion \(\tau\) of the curve parametrized by \(\hat{\boldsymbol{y}}_{0}\) are determined by
With these developments, it follows, with the aid of the second of (4.2b), that the component \(\hat{\boldsymbol{y}}\) of the parametric representation of the isometric deformation \(\tilde{\boldsymbol{y}}\) of \({\mathcal {D}}\subset\mathbb{E}^{2}\) to \({\mathcal{S}}\subset\mathbb{E}^{3}\) defined implicitly through (4.3) and (4.6) can be written in the following equivalent parametric forms:
The relationship between the point \(\boldsymbol{x}\in{\mathcal{D}}\) and the rectangular \((x_{1},x_{2})\) and curvilinear \((\eta^{1},\eta ^{2})\) coordinates used here is recorded in (4.1a)–(4.1b). The fourth form above, (5.12)4, is similar to a parametric representation often posited in the literature to represent the isometric deformation of a flat rectangular strip.Footnote 6 However, it is important to emphasize that in addition to (5.12)4 the necessary and sufficient condition (4.13) is an essential requirement that the representation describe an isometric deformation and it must be satisfied. As we have seen above, this condition places restrictions on the forms taken by the fields \(\hat{\boldsymbol{y}}_{0}\), \(\boldsymbol{t}\), \(\boldsymbol{b}\), \(\kappa\), and \(\tau\). Moreover, while it is clear from (4.1a), (4.1b) that \(\eta^{2}\sin\theta (\eta^{1})=x_{2}\) is the rectangular \(x_{2}\) coordinate of the point \(\boldsymbol{x}\in{\mathcal{D}}\), it is equally clear that \(\eta^{1}\) is not the rectangular \(x_{1}\) coordinate of that point. This distinction is not clearly described in the literature (see, for example, Hangan [3], Sabitov [4], Starostin and van der Heijden [2], Kurono and Umehara [5], Chubelaschwili and Pinkall [6], Naokawa [7], Kirby and Fried [8], and Shen et al. [9]) in which similar-looking representations are used, leading not only to confusion and error in interpreting the representation as an isometric deformation but also undermining an argument that is used to reduce the bending energy of the surface to a line integral over the midline of the surface.
Specializing the work of Dias and Audoly [16] to the case of a deformation of a flat rectangular strip of length \(L\) and width \(w\) to a deformed target surface, and with a change of notation from \((S, V)\) to \((s, v)\), we may rewrite their equation \((5)_{2}\) as the ruled surface
where, here, \(\boldsymbol{x}\) denotes the parametrized directrix on the target surface whose pre-image is the reference straight midline through the flat rectangular strip, \(\{\boldsymbol{d}_{1}, \boldsymbol {d}_{2}, \boldsymbol{d}_{3}\}\) is a positively oriented orthonormal frame attached to \(\boldsymbol{x}\), \(\boldsymbol{d}_{3} := \boldsymbol {x}^{\prime}\) is the unit tangent vector along the directrix on the target surface, \(\boldsymbol{d}_{2}\) is a normal to the target surface, \(\boldsymbol{d}_{1} := \boldsymbol{d}_{2}\times\boldsymbol{d}_{3}\), \(\eta\) is the tangent of the angle between \(\boldsymbol{d}_{1}\) and the generators spanned by \(\boldsymbol{d}_{1}+\eta\boldsymbol{d}_{3}\), \(s\in[0, L]\) is the length along the midline of the reference rectangular strip, and \(v\) is the coordinate along the generators measured from the directrix. Clearly, the length along \(\boldsymbol{x}\) and \(s\) are equivalent and in equation (8) of Dias and Audoly [16] it is noted that for the case of a rectangular ribbon \(v\in[-w/2, w/2]\), though this may be an oversight and needs some clarification.
In addition, Dias and Audoly [16] introduce the Darboux vector \(\boldsymbol{\omega}= \omega_{1}\boldsymbol{d}_{1} + \omega _{2}\boldsymbol{d}_{2} + \omega_{3}\boldsymbol{d}_{3}\) and write \(\boldsymbol{d}_{i}^{\prime}= \boldsymbol{\omega}\times\boldsymbol {d}_{i}\), (\(i = 1, 2, 3\)), where a prime denotes differentiation with respect to \(s\), and they show, by applying a classical theorem from differential geometry, that for the target surface in (5.13) to be developable and be associated with a flat rectangular pre-image the directors must satisfy
the latter of which follows from the fact that the geodesic curvature of \(\boldsymbol{x}\) in the target surface must equal the curvature of its straight pre-image. Accordingly, (5.14) is equivalent to \(\omega_{2} = 0\) and \(\omega_{3} = \eta\omega_{1}\), and we see that (5.14) holds if and only if the directors satisfy
Now, the representation (5.13) restricted by (5.14) is interpreted by Dias and Audoly [16] as an isometric deformation, but no strategy for constructing the deformation from the rectangular strip to the target (5.13) is given and the condition ensuing from the requirement that the distance between all pairs of material points is preserved is not checked. Further, while the representation appears to be distinct from those mentioned in (5.12) or \((\ast)\) of Footnote 6, we emphasize below, in agreement with a briefly noted observation of Dias and Audoly [16], that (5.13) restricted by (5.15) (the equivalent of (5.14)) amounts to a Frenet frame representation similar to that of (5.12)4 or \((\ast)\) of Footnote 6. To see this, let \(\{\boldsymbol{t}, \boldsymbol{p}, \boldsymbol{b}\}\) be the Frenet frame associated with space curve \(\boldsymbol{x}\), so that \(\boldsymbol{t}= \boldsymbol {x}^{\prime}\), \(\boldsymbol{p}= \boldsymbol{t}^{\prime }/|\boldsymbol {t}^{\prime}|\) and \(\boldsymbol{b}= \boldsymbol{t}\times\boldsymbol {p}\). It is then clear that
and we infer from (5.15)3 and the Frenet–Serret relation \(\boldsymbol{t}^{\prime}= \kappa\boldsymbol {p}\), where \(\kappa= |\boldsymbol{t}^{\prime}|\) is the curvature of the directrix \(\boldsymbol{x}\), that
We therefore have
and we see that, apart from a change of sign, the frame \(\{\boldsymbol {d}_{1}, \boldsymbol{d}_{2}, \boldsymbol{d}_{3}\}\) and the Frenet frame \(\{\boldsymbol{t}, \boldsymbol{p}, \boldsymbol{b}\}\) are identical.
We next observe that (5.15)1 may be written as
which represents the second Frenet–Serret relation \(\boldsymbol {b}^{\prime}= -\tau\boldsymbol{p}\), with
where \(\tau\) is the torsion of the directrix parametrized by \(\boldsymbol{x}\). With what has been shown above, it is in addition straightforward to see that (5.15)2 is equivalent to the third Frenet–Serret relation \(\boldsymbol {p}^{\prime }= -\kappa\boldsymbol{t}+ \tau\boldsymbol{b}\).
Finally, we observe that (5.13) may readily be transformed to the form
which, modulo an unambiguous interpretation of \(v\) and the multiplying sign \(\mbox{sgn}(\omega_{1})\), is similar to our (5.12)4 and \((\ast)\) of Footnote 6.
6 Curvature Tensor of \({\mathcal{S}}\)
To obtain an explicit expression for the curvature tensor \(-\mbox{grad}_{s}\boldsymbol{n}\) of \({\mathcal{S}}\), we first observe that, on using the curvilinear coordinates \((\eta^{1},\eta^{2})\) to locate points on \({\mathcal{S}}\) and recalling that \(\boldsymbol{Q}\) is independent of \(\eta^{2}\), the representation (3.39) for the unit normal \(\boldsymbol{n}\) of \({\mathcal{S}}\) yields
We also observe that \(\{\boldsymbol{a}_{1},\boldsymbol{a}_{2}\}\) provides a basis in the plane tangent to \({\mathcal{S}}\) which follows by noting, from (4.2b) and (4.9), that
and recalling, from (4.4), that \(\sin\theta- \eta ^{2}\dot{\theta}\neq0\) on \({\mathcal{D}}\).
Using the structure of the coordinate system \((\eta^{1}, \eta^{2})\) for locating the points \(\boldsymbol{x}\) on \({\mathcal{S}}\), we therefore find that
and determine the covariant components of \(\mbox{grad}_{s}\boldsymbol {n}\) as
Thus, we have
where \(\{\boldsymbol{a}^{1}, \boldsymbol{a}^{2}\}\) is the basis dual to \(\{\boldsymbol{a}_{1},\boldsymbol{a}_{2}\}\) and \(\boldsymbol {a}^{i}\cdot\boldsymbol{a}_{i}=\delta^{i}_{j}\). In addition, we see that
the last being due to (4.13). Relative to the basis \(\{ \boldsymbol{a}_{1},\boldsymbol{a}_{2}\}\) the covariant components of \(\mbox{grad}_{s}\boldsymbol{n}\) are thus given by
and this then yields
Then, because \(\boldsymbol{a}^{1}\) is perpendicular to \(\boldsymbol {a}_{2}\) and lies in the plane tangent to \({\mathcal{S}}\), and \(\boldsymbol{a}_{2}\) is a unit vector along a line of zero principal curvature of \({\mathcal{S}}\), the unit vector \(\boldsymbol{\nu }\equiv \boldsymbol{a}^{1}/|\boldsymbol{a}^{1}|\) defines the second principal direction of curvature on \({\mathcal{S}}\) and we may write
This last result is consistent with the intuitive expectation that the non-zero principal curvature of \({\mathcal{S}}\) should depend directly upon the angular ‘rate’ \(\boldsymbol{Q}^{{\top}}\dot{\boldsymbol{Q}}\) associated with \(\boldsymbol{Q}\) at which \({\mathcal{S}}\) is being mapped out as a local rotation about the axis \(\boldsymbol{a}_{2}\) of zero principal curvature.
To simplify (6.9) further, let us next note that
where, in accord with (4.14), we have used that \(\mbox{ax}(\dot{\boldsymbol{Q}}\boldsymbol{Q}^{{\top}})=\lambda \boldsymbol{a}_{2}\). Finally, recalling \(\boldsymbol{a}_{i}\cdot \boldsymbol{a}_{j} = \boldsymbol{b}_{i}\cdot\boldsymbol{b}_{j}\), it is not difficult to show that
Thus, using (6.9), we find that the curvature tensor has the form
and, thus, surmise that
is the second (possibly nonzero) principal curvature of \({\mathcal {S}}\). Of course, (4.4) ensures that the denominator common to (6.12) and (6.13) does not vanish due to the condition (4.4).
7 General Cylindrical Bending
Suppose that \(\theta=\theta_{0}\in(0,\pi)\) is an assigned constant. Then according to (4.2b) the curvilinear coordinates \((\eta^{1}, \eta^{2})\) correspond to a Cartesian coordinate system with constant base vectors \(\boldsymbol{b}_{1}=\boldsymbol{\imath }_{1}\) and \(\boldsymbol{b}_{2}=\boldsymbol{b}_{0}:= \cos\theta _{0}\boldsymbol{\imath}_{1}+\sin\theta_{0}\boldsymbol{\imath}_{2}\). The base vector \(\boldsymbol{b}_{0}\) defines a family of parallel lines cutting through \({\mathcal {D}}\subset\mathbb{E}^{2}\) at an angle of \(\theta_{0}\) with \(\boldsymbol{\imath}_{1}\), as depicted in Fig. 1. We then see from (4.9) that \(\dot{\boldsymbol{a}}_{2}=\dot {\boldsymbol{Q}}\boldsymbol{b}_{0}\) and with (4.13) we find that \(\boldsymbol{a}_{2}\) is a constant unit vector field in \(\mathbb{V}^{3}\) which, without loss of generality and for convenience, we may take as
Thus, \({\mathcal{S}}\) is of cylindrical form with generators parallel to \(\boldsymbol{\imath}_{3}\). Returning to (4.9), we have
Now, choose
where \(\boldsymbol{Q}_{0}\in\mathrm{Orth}^{+}\) is such that \(\boldsymbol{Q}_{0}\boldsymbol{b}_{0} = \boldsymbol{\imath}_{3}\) and, thus, corresponds to a rotation, by the angle \(\pi/2\), of \(\boldsymbol {b}_{0}\mapsto\boldsymbol{\imath}_{3}\) about the axis
and where \(\boldsymbol{R}\in\mathrm{Orth}^{+}\) satisfies \(\boldsymbol {R}(\eta^{1})\boldsymbol{\imath}_{3} = \boldsymbol{\imath}_{3}\). With this condition, it follows that (7.2) holds automatically. Specifically, note that \(\boldsymbol{Q}_{0}\) has the form
and, because of (4.14)2, that \(\boldsymbol{R}\) must obey the ordinary differential equation \(\dot {\boldsymbol{R}}\boldsymbol{R}^{{\top}}=\lambda\boldsymbol{A}_{0}\) or, equivalently,
where \(\boldsymbol{A}_{0}\in\mbox{Skew}\) is constant with \(\boldsymbol {a}_{2}=\boldsymbol{\imath}_{3}=\mbox{ax}(\boldsymbol{A}_{0})\) being its axial vector.
The solution of (7.6) which satisfies  , where
, where  denotes the identity linear transformation on \(\mathbb {V}^{3}\), is
denotes the identity linear transformation on \(\mathbb {V}^{3}\), is

with \(\omega\) given by
where \(b\) and \(\eta^{1}\) are arbitrary to the extent that for a given \(\lambda\) the integral exists. For each \(\eta^{1}\), (7.7a) clearly represents a rotation of angle \(\omega(\eta^{1})\) about the \(\boldsymbol{\imath}_{3}\)-axis. Thus, \(\boldsymbol{R}\boldsymbol {\imath}_{3}=\boldsymbol{\imath}_{3}\) and (7.2) is, indeed, satisfied. With this, we see from the last of (5.12) and (4.11) that the component \(\hat {\boldsymbol{y}}\) of the corresponding parametric representation of the isometric deformation \(\tilde{\boldsymbol{y}}\) of \({\mathcal{D}}\subset \mathbb{E}^{2}\) to \({\mathcal{S}}\subset\mathbb{E}^{3}\) is of the form
where the space curve parametrized by \(\hat{\boldsymbol{y}}_{0}\) is to be determined by integrating
once the point \(\boldsymbol{y}_{0}\in\mathbb{E}^{3}\) is specified.Footnote 7
Thus, from (7.3), (7.5), and (7.7a), we see that

with
Finally, after integration and simplification we arrive at
which, with (7.8), gives the general form of the component \(\hat{\boldsymbol{y}}\) of the parametric representation of the isometric deformation \(\tilde{\boldsymbol{y}}\) corresponding to the special case of \(\theta =\theta _{0}=\mbox{constant}\) considered in this section. Note, from (6.13), that the novanishing principal curvature \(k\) of the deformed surface \({\mathcal{S}}\) is given by
and, because \(\boldsymbol{a}_{2} = \boldsymbol{\imath}_{3}\), the surface \({\mathcal{S}}\) lies on a surface \({\mathcal{T}}\) of cylindrical form, the generators of which are parallel to \(\boldsymbol {\imath}_{3}\).
In the following two examples, it suffices, and is representative, to restrict \(\theta_{0}\) so that
and, moreover, to suppose that \({\mathcal{D}}\subset\mathbb{E}^{2}\) is a rectangle of length \(l\) and width \(w\) located such that the rectilinear coordinates \(x_{1}\) and \(x_{2}\) of each point \(\boldsymbol {x}=x_{i}\boldsymbol{\imath}_{i}\) belonging to \({\mathcal{D}}\) satisfy,
as depicted in Fig. 2.
7.1 Example 1: Circular Cylindrical Bending. Helical Forms
For the case \(\lambda=\lambda_{0}>0\) with \(\lambda_{0}\) constant we see from (7.13) that the nonvanishing principal curvature \(k\) of the deformed surface \({\mathcal{S}}\) is constant and given by
Thus, \({\mathcal{S}}\) lies on a circular cylindrical surface \({\mathcal{T}}_{c}\) of radius
From (7.7b) it follows that \(\omega(\eta^{1}) = \lambda _{0} (\eta^{1} - b )\). For this example, it is convenient to take \(b=0\), in which case, with the aid of (7.12) we find that
Clearly, \(\hat{\boldsymbol{y}}_{0}(0)=\boldsymbol{y}_{0}\).
To describe this curve, it is convenient to introduce the right-handed basis \(\{\boldsymbol{\jmath}_{1},\boldsymbol{\jmath }_{2},\boldsymbol {\imath}_{3}\}\) with \(\boldsymbol{\jmath}_{i}\), \(i=1,2\), defined by
and to take
Then, it follows that
which, for \(\theta_{0} <\pi/2\), is the graph of a helix on the circular cylindrical surface \({\mathcal{T}}_{c}\) with generators parallel to \(\boldsymbol{\imath}_{3}\) and radius \(r_{0}\). In accord with (7.8), the flat planar domain \({\mathcal{D}}\) is thus deformed isometrically to the form \({\mathcal{S}}\) which lies on \({\mathcal{T}}_{c}\) such that the parallel straight lines originally through \({\mathcal{D}}\) at angle \(\theta_{0}\) with the base vector \(\boldsymbol{\imath}_{1}\) coincide with the generators of \({\mathcal {T}}_{c}\), which are, of course, parallel to \(\boldsymbol{\imath }_{3}\). The helical space curve (7.21) is the image of the \(\eta ^{2} = 0\) coordinate line on \({\mathcal{T}}_{c}\).
From (4.1b) and (7.14), we see that \(\eta^{1}\) and \(\eta^{2}\) are related to \(x_{1}\) and \(x_{2}\) by
To cover all the points of \({\mathcal{D}}\) \(\eta^{1}\) and \(\eta^{2}\) must, consistent with (7.15), also satisfy
as is best seen in Fig. 2. With reference to (7.8) and (7.21), the isometric deformation \(\tilde{\boldsymbol {y}}\) from \({\mathcal {D}}\subset\mathbb{E}^{2}\) to \({\mathcal{S}}\subset{\mathcal {T}}_{c}\subset\mathbb{E}^{3}\) is thus given by
Note that the centerline \(x_{2}\to0\) is mapped to the helix on \({\mathcal{T}}_{c}\) parametrized by \(\hat{\boldsymbol{y}}_{0}\) and the end \(x_{1}\to 0\) is mapped to the curve on \({\mathcal{T}}_{c}\) given by
If, in particular, \(\theta_{0}<\pi/2\), then the rectangle \({\mathcal {D}}\) is wrapped isometrically onto the circular cylindrical surface \({\mathcal{T}}_{c}\) into a right-handed helical ribbon \({\mathcal{S}}\) according to the direction of \(\boldsymbol{\imath}_{3}\). If \(\theta _{0}=\pi/2\), the centerline \(x_{2} = 0\) is mapped to a circle and the form of \({\mathcal{S}}\) is right circular cylindrical. In Fig. 3, we show \({\mathcal{S}}\) for the case \(\theta_{0}=\pi/4\), \(r_{0} = 1\) (\(\lambda_{0} = \sin\theta_{0}/r_{0} = 1/\sqrt{2}\)), \(w = 1/2\) and \(l = 10\).
7.2 Example 2: Spiral Cylindrical Bending. Helical Forms
For this example, we take \({\mathcal{D}}\) to be the rectangle defined in (7.15) and shown in Fig. 2, and, again, for convenience assume that \(\theta_{0}\) is fixed in the interval \((0,\pi /2]\). Moreover, we choose \(\lambda\) to be of the form
where \(\eta^{1}\) obeys the restriction
Then, we see from (7.13) that the nonvanishing principal curvature \(k\) of the deformed surface \({\mathcal{S}}\) is given by
which is negative but not constant for each \(\eta^{1}>-a\). Thus, \({\mathcal{S}}\) lies on a spiral cylindrical surface \({\mathcal {T}}_{s}\) whose generators are parallel to \(\boldsymbol{\imath}_{3}\). Recalling, from (4.1b) and (7.14), that
it follows from (7.15) that for each \(\boldsymbol{x}\in {\mathcal{D}}\), we must have \(\eta^{1}>-w\cot\theta_{0}/2=-a\) and that \(x_{1}\to0\) and that \(x_{2}\to w/2\) as \(\eta^{1}\to-w\cot \theta_{0}/2=-a\), from which we infer that \(\eta^{2}\to w\csc\theta _{0}/2\). Thus, the top left corner of the rectangle \({\mathcal{D}}\) will have a infinitely negative nonvanishing principal curvature in its isometrically mapped configuration \({\mathcal{S}}\) and all other points of \({\mathcal{S}}\) will have a bounded, strictly negative nonzero principal curvature.
From (7.7a,b) and granted that \(\eta^{1}>-a\), it follows that
where, to be meaninful, \(b\) is a constant satisying \(b >-a\). To obtain a concise expression for \(\hat{\boldsymbol{y}}_{0}\), we introduce the right-handed basis \(\{\boldsymbol{l}_{1},\boldsymbol{l}_{2},\boldsymbol{\imath }_{3}\}\), with
Direct calculations using (7.12) and (7.14) then yield
Thus, choosing \(\boldsymbol{y}_{0}\) such that
we find that
where \(\eta^{1}\) must satisfy \(\eta^{1}>-a\).
For \(\theta_{0} < \pi/2\), \(\hat{\boldsymbol{y}}_{0}\) defined by (7.34) parametrizes a helical spiral on the spiral cylindrical surface \({\mathcal{T}}_{s}\) with generators parallel to \(\boldsymbol{\imath }_{3}\). For \(\theta_{0} = \pi/2\), we see from (7.26) that \(a = 0\) in which case (7.34) corresponds to a logarithmic spiral lying in the plane spanned by \(\boldsymbol{l}_{1}\) and \(\boldsymbol{l}_{2}\) and, of course, \(\hat{\boldsymbol {y}}_{0}(0)=\boldsymbol{0}\).
To explain further, we first observe that, on using (7.29)1 to express \(\eta^{1}\) in terms of \(x_{1}\) and \(x_{2}\), (7.34) can be written as
With reference to (7.8) and (7.35) we thus see that the isometric deformation \(\tilde{\boldsymbol{y}}\) of \({\mathcal {D}}\subset\mathbb {E}^{2}\) to \({\mathcal{S}}\subset{\mathcal{T}}_{s}\subset\mathbb {E}^{3}\) is given by
Note that the nonvanishing principal curvature \(k\) of \({\mathcal{S}}\) can now be expressed in terms of \(x_{1}\) and \(x_{2}\) by
In particular, the centerline of \({\mathcal{D}}\) at \(x_{2}=0\) is mapped to the helical spiral determined by
which lies on \({\mathcal{T}}_{s}\) and has the specific form of (7.34) with \(\eta^{1}\) replaced by \(x_{1}\), as also is seen in (7.35) with \(x_{2} = 0\), and the nonzero curvature of \({\mathcal {S}}\) on the midline parametrized by \(\hat{\boldsymbol{y}}_{0}\) is
Recall that \(\hat{\boldsymbol{y}}_{0}(0)=\boldsymbol{y}_{0}\), as defined in (7.33).
According to (7.36), the edge of \({\mathcal{D}}\) corresponding to \(x_{1}\to0\) is mapped to the curve determined by
which lies on \({\mathcal{T}}_{s}\) and, for which \(\hat{\boldsymbol {y}}_{0}\) has the specific form (7.34), with \(\eta^{1}\) replaced by \(-x_{2}\cot \theta_{0}\), as seen also in (7.35) with \(x_{1}\to0\). The nonvanishing principal curvature of \({\mathcal{S}}\) on this curve is given in terms of \(x_{1}\) and \(x_{2}\) by
Note that this curve runs through the point \(\boldsymbol{y}_{0}=\hat {\boldsymbol{y}} _{0}(0)\) as defined in (7.33) at \(x_{2}=0\) and that \(\tilde {k}(0,x_{2})<0\) for all \(x_{2}\in(-w/2,w/2)\) and that \(\tilde {k}(0,x_{2})\to-\infty\) as \(x_{2}\to w/2\). Note, also, that the corner of the rectangle \({\mathcal{D}}\) at \(\boldsymbol{x}\to (w/2)\boldsymbol{\imath}_{2}\) is mapped to the point
on the boundary of \({\mathcal{S}}\subset{\mathcal{T}}_{s}\subset \mathbb{E}^{3}\) and that \(\boldsymbol{\imath}_{3}\) is the axis of the spiral cylindrical surface \({\mathcal{T}}_{s}\).
In words, according to (7.36) the rectangle \({\mathcal{D}}\) is deformed isometrically to the form \({\mathcal{S}}\) which lies on \({\mathcal{T}}_{s}\) such that the parallel straight lines originally through \({\mathcal{D}}\) at angle \(\theta_{0}\) with the base vector \(\boldsymbol{\imath}_{1}\) are coincident with the generators of \({\mathcal{T}}_{s}\), which are, of course, parallel to \(\boldsymbol{\imath}_{3}\). The helical spiral on \({\mathcal{T}}_{s}\) given in (7.38) is the image of the \(x_{2} = 0\) coordinate centerline of \({\mathcal{D}}\) and runs through the point \(\boldsymbol {y}_{0}=\hat{\boldsymbol{y}}_{0}(0)\) on \({\mathcal{T}}_{s}\). The ‘left upper corner’ of the rectangle \({\mathcal{D}}\) at \(\boldsymbol{x}\to (w/2)\boldsymbol {\imath}_{2}\) is mapped to the point (7.42) on the boundary of \({\mathcal{S}}\subset{\mathcal{T}}_{s}\subset\mathbb {E}^{3}\), which is on the axis, \(\boldsymbol{\imath}_{3}\), of the spiral cylindrical surface \({\mathcal{T}}_{s}\). This corresponds to a limiting corner ‘tip’ of the domain \({\mathcal{S}}\) into which \({\mathcal{D}}\) is mapped. The remainder of the rectangle \({\mathcal {D}}\) is wrapped onto the spiral cylindrical surface \({\mathcal {T}}_{s}\) into a right-handed helical spiral form \({\mathcal{S}}\) according to the direction of \(\boldsymbol{\imath}_{3}\).
In the case \(\theta_{0}<\pi/2\), we know that \(a:= w\cot\theta _{0}/2\neq0\) and, to simplify, we may set \(b=0\) in all of the equations developed in this sub-section. For example, \(\boldsymbol {y}_{0}\) in (7.33) becomes \(\boldsymbol{y}_{0}=(a/\sqrt {2})\sin\theta_{0}\boldsymbol{l}_{1}\). In the case \(\theta _{0}=\pi/2\), we have \(a = 0\) and the rectangle \({\mathcal{D}}\subset \mathbb{E}^{2}\) is deformed isometrically into a logarithmic spiral cylindrical form \({\mathcal{S}}\subset{\mathcal{T}}_{s}\subset \mathbb {E}^{3}\). In this case, the constant \(b\) may be chosen as any number such that \(b>0\).
In Fig. 4, we use (7.35) and (7.36) to show the spiral cylindrical form \({\mathcal{S}}\subset{\mathcal {T}}_{s}\) for the case: \(\theta_{0}=\pi/4\), \(b=0\), \(w=1\) and \(l=10\). In this case, it follows that \(a=1/2\) and \(\boldsymbol {y}_{0}=(1/8)\boldsymbol{l}_{1}\). Also, according to (7.42), the ‘upper left corner’ point of the boundary of \({\mathcal{D}}\) is mapped to the point \((1/4\sqrt{2})\boldsymbol {\imath }_{3}\) on the (singular) axis of \({\mathcal{T}}_{s}\), at which the nonzero principal curvature of \({\mathcal{S}}\) obeys \(\tilde{k}(0, w/2)\to-\infty\).
8 Summary: Strategy for Determining an Isometric Deformation of \({\mathcal{D}}\subset\mathbb{E}^{2}\) to \({\mathcal{S}}\subset \mathbb{E}^{3}\)
The major problem related to the characterization of all (smooth) isometric deformations \(\tilde{\boldsymbol{y}}\) from \({\mathcal {D}}\subset\mathbb {E}^{2}\) to \({\mathcal{S}}\subset\mathbb{E}^{3}\) stems from the necessary and sufficient condition (4.14), which requires the determination of \(\boldsymbol{Q}:\mathbb{R}\mapsto\mathrm{Orth}^{+}\) as the solution of the following tensor initial-value problem:
where \(\boldsymbol{W}:\mathbb{R}\mapsto\mbox{Skew}\) is a given field for each \(\eta^{1}\in\mathbb{R}\) and a superposed dot denotes differentiation. Unfortunately, this problem has only been solved in closed form for special choices of the skew linear transformation \(\boldsymbol{W}\). If \(\eta^{1}\) is interpreted as time, (8.1) is a problem well-known in the field of rigid-body dynamics, in which case \(\boldsymbol{W}\) and \(\boldsymbol{Q}\) are the angular velocity tensor and the rotation tensor of the body.
Identifying the importance of problem (8.1) is one of the main conclusions of Sect. 4. Here, we shall summarize in six steps a strategy for the characterization of every isometric deformation from a region in \(\mathbb{E}^{2}\) to a surfaces in \(\mathbb {E}^{3}\) and illustrate how the solution to problem (8.1) is the key element:
-
1.
Recall from (4.14) that the fundamental proper orthogonal linear transformation \(\boldsymbol{Q}\), which is at the basis for constructing any isometric deformation, must satisfy
$$ \mbox{ax}\bigl(\dot{\boldsymbol{Q}}\boldsymbol{Q}^{{\top}}\bigr)= \lambda\boldsymbol{a}_{2}, $$where \(\lambda\) is scalar-valued and where the unit vector-valued field \(\boldsymbol{a}_{2}\) defines the direction of the straight lines of zero principal curvature on the deformed surface \({\mathcal{S}}\).
-
2.
Choose \(\lambda\) and \(\boldsymbol{a}_{2}\), and define \(\boldsymbol{w}\) by
$$ \boldsymbol{w}\bigl(\eta^{1}\bigr):=\lambda\bigl(\eta^{1}\bigr) \boldsymbol{a}_{2}\bigl(\eta^{1}\bigr). $$In addition, let \(\boldsymbol{W}\) be the skew linear transformation whose axial vector is \(\mbox{ax}(\boldsymbol{W}):=\boldsymbol{w}\) and note from Step 1 that \(\boldsymbol{Q}\) must satisfy
$$ \dot{\boldsymbol{Q}}\bigl(\eta^{1}\bigr)=\boldsymbol{W}\bigl( \eta^{1}\bigr)\boldsymbol{Q}\bigl(\eta^{1}\bigr), $$in which the field \(\boldsymbol{W}\) is now considered to be known. Clearly, if \(\boldsymbol{A}\) is the skew linear transformation whose axial vector is \(\mbox{ax}(\boldsymbol{A}):=\boldsymbol{a}_{2}\), then we may make the following replacement above: \(\boldsymbol{W}=\lambda \boldsymbol{A}\). Now, the initial condition \(\boldsymbol {Q}(0)=\boldsymbol{Q}_{0}\in\mathrm{Orth}^{+}\) must be chosen and the now-formulated tensor initial value problem for \(\boldsymbol{Q}\in \mathrm{Orth}^{+}\) must be solved. Note that this problem is equivalent to (8.1).
-
3.
Determine the unit vector-valued field \(\boldsymbol {b}_{2}\) using (4.9) according to
$$ \boldsymbol{b}_{2}\bigl(\eta^{1}\bigr) = \boldsymbol{Q}^{{\top}}\bigl(\eta^{1}\bigr)\boldsymbol{a}_{2} \bigl(\eta^{1}\bigr) $$and use (4.2b) to determine \(\theta\) with values in \((0,\pi)\) according to
$$ \boldsymbol{b}_{2}=\cos\theta\boldsymbol{ \imath}_{1}+\sin\theta\boldsymbol{\imath}_{2}. $$ -
4.
Interpret the two parameters \(\eta^{1}\) and \(\eta ^{2}\) such that all points \(\boldsymbol{x}\in{\mathcal{D}}\) are located according to (4.3), that is
$$ \boldsymbol{x}=\hat{\boldsymbol{x}}\bigl(\eta^{1},\eta^{2}\bigr)= \eta^{1}\boldsymbol{\imath}_{1}+\eta^{2} \boldsymbol{b}_{2}\bigl(\eta^{1}\bigr). $$Note, in particular, that this provides a definitive interpretation of the parameter \(\eta^{1}\) as the \(\eta^{1}\) (not \(x_{1}\)) coordinate of any point \(\boldsymbol{x}\in{\mathcal{D}}\).
-
5.
Determine \(\hat{\boldsymbol{y}}_{0}\) according to (4.11) by integrating
$$ \dot{\hat{\boldsymbol{y}}}_{0}\bigl(\eta^{1}\bigr)=\boldsymbol {Q}\bigl( \eta^{1}\bigr)\boldsymbol{\imath}_{1} \quad\mbox{subject to} \quad\hat{\boldsymbol{y}}_{0}(0)=\boldsymbol{y}_{0}\in \mathbb{E}^{3}. $$Here, \(\eta^{1}=0\) is the origin of the midline of the region \({\mathcal{D}}\) in \(\mathbb{E}^{2}\) and \(\boldsymbol{y}_{0}=\hat {\boldsymbol{y}} _{0}(0)\) is specified as the limit point in \(\mathbb{E}^{3}\) where \(\boldsymbol{x}\to\hat{\boldsymbol{x}}(0,0)=\boldsymbol{0}\) is to be transformed under the isometric deformation \(\tilde{\boldsymbol{y}}\) from \({\mathcal{D}}\) to \({\mathcal{S}}\).Footnote 8
-
6.
Determine the component \(\hat{\boldsymbol{y}}\) of the parametric representation of the isometric deformation \(\tilde{\boldsymbol{y}}\) defined implicitly through (4.3) and (4.6), in accord with
$$\begin{aligned} \hat{\boldsymbol{y}}\bigl(\eta^{1},\eta^{2}\bigr) &=\hat {\boldsymbol{y}}_{0} \bigl(\eta^{1}\bigr)+\eta^{2}{\boldsymbol{Q}}\bigl( \eta^{1}\bigr)\boldsymbol{b}_{2}\bigl(\eta^{1} \bigr) \\ &=\hat{\boldsymbol{y}}_{0}\bigl(\eta^{1}\bigr)+\eta^{2} \boldsymbol{a}_{2}\bigl(\eta^{1}\bigr). \end{aligned}$$
Finally, after determining the form of the isometric deformation \(\tilde{\boldsymbol{y}}\) by replacing \((\eta^{1},\eta^{2})\) in Step 6 with \((x_{1},x_{2})\) using Step 4, observe that the curvature tensor for \({\mathcal{S}}\) is given by (6.12).
9 Isometric Deformation of a Rectangular Material Strip \({\mathcal{D}}\subset\mathbb{E}^{2}\) to Portion \({\mathcal{S}}\) of a Conical Surface \({\mathcal{K}}\subset\mathbb{E}^{3}\)
Suppose that \({\mathcal{D}}\) is the rectangle of length \(l\) and width \(w\) consisting of all points \(\boldsymbol{x}=x_{i}\boldsymbol{\imath }_{i}\) with rectilinear coordinates \(x_{1}\) and \(x_{2}\) restricted as in (7.15) and shown in Fig. 2. Let \({\mathcal {K}}\subset\mathbb{E}^{3}\) denote a right conical surface with circular base of radius \(R\) in the plane spanned by \(\boldsymbol {\imath }_{1}\) and \(\boldsymbol{\imath}_{2}\) and tip located at \(H\boldsymbol {\imath}_{3}\). The tip angle of \({\mathcal{K}}\) is then equal to \(2\varphi\), where \(\varphi\in(0,\pi/2)\) satisfies
The cone \({\mathcal{K}}\) is allowed to extend without limit in the \(-\boldsymbol{\imath}_{3}\) direction but, for convenience and with a slight abuse of terminology, we continue to refer to its base as the plane spanned by \(\boldsymbol{\imath}_{1}\) and \(\boldsymbol{\imath}_{2}\). The objective of this section is to identify a general isometric deformation of \({\mathcal{D}}\subset\mathbb{E}^{2}\) to \({\mathcal {S}}\subset{\mathcal{K}}\subset\mathbb{E}^{3}\) using the strategy outlined above in Sect. 8.
9.1 General Case
To begin, following Steps 1 and 2 in Sect. 8, we suppose that there is a smooth family of distinct straight lines that foliate and intersect with \({\mathcal{D}}\), as generally illustrated in Fig. 1. The unit vector field \(\boldsymbol{b}_{2}\) that characterizes these straight lines was introduced in (4.2b) as
where \(\eta^{1}\boldsymbol{\imath}_{1}\) the point where each straight line cuts through the \(x_{1}\)-coordinate line and \(\theta(\eta ^{1})\in(0,\pi)\) is the angle of \(\boldsymbol{b}_{2}(\eta^{1})\) measured from \(\boldsymbol{\imath}_{1}\). These lines are the pre-images in \({\mathcal{D}}\) of the straight lines of zero curvature in \({\mathcal{S}}\subset{\mathcal{K}}\) to which \({\mathcal{D}}\) is isometrically deformed. According to (4.7) and (4.9), these lines are related to \(\boldsymbol{b}_{2}\) by
and we are to determine \(\boldsymbol{Q}\in\mathrm{Orth}^{+}\) such that
where \(\boldsymbol{Q}_{0}\in\mathrm{Orth}^{+}\) is prescribed, \(\boldsymbol{A}\in\mbox{Skew}\) is given with \(\boldsymbol {a}_{2}=\mbox{ax}(\boldsymbol{A})\) and the scalar-valued field \(\lambda\) is assumed known, but is to be determined later.
To analyze (9.4), we first need to characterize the skew tensor \(\boldsymbol{A}\) whose axial vector is \(\boldsymbol{a}_{2}\). Toward this end, note that since the straight line generators of the conical surface \({\mathcal{K}}\) are the lines of zero curvature on \({\mathcal {S}}\subset{\mathcal{K}}\) and that \(\boldsymbol{a}_{2}\) is parallel to these lines, we may write
where
is the direction of the specific generator from the point \(R\boldsymbol {\imath}_{1}\) on the base of \({\mathcal{K}}\) to the point \(H\boldsymbol {\imath}_{3}\) at its tip, and
represents a right-handed rotation of angle \(\omega\) about the \(\boldsymbol{\imath}_{3}=\mbox{ax}(\boldsymbol{A}_{1})\) axis. We set \(\omega(0) = 0\), so that  and \(\boldsymbol{a}_{2}(0)=\boldsymbol{a}\). An alternative representation for \(\boldsymbol{Q}_{1}\) is
and \(\boldsymbol{a}_{2}(0)=\boldsymbol{a}\). An alternative representation for \(\boldsymbol{Q}_{1}\) is
and we find, using (9.5), (9.6), and (9.8), that
Since \(\boldsymbol{a}_{2}\) is the axial vector of \(\boldsymbol{A}\), we see that
From (9.2) and (9.3), we note that
where \(\boldsymbol{Q}_{0} := \boldsymbol{Q}(0)\in\mathrm{Orth}^{+}\) and the angle \(\theta_{0} := \theta(0)\in(0, \pi)\) are yet to be prescribed. Clearly, \(\theta_{0}\) and \(\boldsymbol{Q}_{0}\) define how the particular line through \({\mathcal{D}}\) defined by \(\boldsymbol{b}_{2}(0)\) and the flat rectangular material strip \({\mathcal{D}}\) are attached with tangency to the conical surface \({\mathcal{K}}\) at the point \(R\boldsymbol{\imath}_{1}\) along the specific generator defined by \(\boldsymbol{a}\). Specifically, in view of (9.11), \(\boldsymbol{b}_{2}(0)\) is mapped to \(\boldsymbol{a}\) and all points in \({\mathcal{D}}\) that are along the line of \(\boldsymbol{b}_{2}(0)\) are deformed isometrically to points on the generator of \({\mathcal{K}}\) defined by \(\boldsymbol{a}\), as depicted in Fig. 5. If, for instance, \(\theta_{0} = \pi/2\), then \(\boldsymbol{b}_{2}(0) = \boldsymbol{\imath}_{2}\) and, in keeping with (9.11), the left-hand edge of the rectangle \({\mathcal{D}}\) is deformed isometrically to a section of length \(w\) of the generator of \({\mathcal{K}}\) which is centered on the periphery of its base and defined by \(\boldsymbol{a}\).
The conical surface \({\mathcal{K}}\) and the rectangle \({\mathcal{D}}\) shown attached at \(R\boldsymbol{\imath}_{1}\) and tangent to \({\mathcal{K}}\) along the generator defined by \(\boldsymbol{a}\). All points \(\boldsymbol{x}\in{\mathcal{D}}\) are translated by the constant vector \(R\boldsymbol{\imath}_{1}\) and then rotated about the point \(R\boldsymbol{\imath}_{1}\) by \(\boldsymbol{Q}_{0}\in \mathrm{Orth}^{+}\) so that \(\boldsymbol{b}_{2}(0)\) is mapped to the particular generator \(\boldsymbol{a}=\boldsymbol{Q}_{0}\boldsymbol{b}_{2}(0)\)
To explicitly determine \(\boldsymbol{Q}_{0}\), we first note that \(\{ \boldsymbol{\imath}_{2}, \boldsymbol{a}\}\) is an orthonormal basis for the tangent plane to the conical surface \({\mathcal{K}}\) at the point \(R\boldsymbol {\imath}_{1}\) and that the rectangle shown in Fig. 5 lies in this tangent plane. With this in mind, let \(\{\boldsymbol{\imath }_{1}^{\prime},\boldsymbol{\imath}_{2}^{\prime},\boldsymbol{\imath }_{3}'\}\) be an orthonormal basis for \(\mathbb{E}^{3}\) such that the basis \(\{\boldsymbol{\imath}_{1}^{\prime},\boldsymbol{\imath }_{2}^{\prime}\}\) with
lies in the tangent plane to \({\mathcal{K}}\) at \(R\boldsymbol{\imath }_{1}\), as indicated in Fig. 5. Of course,
Also, observe that \(\boldsymbol{\imath}_{i}^{\prime}=\boldsymbol {Q}_{0}\boldsymbol{\imath}_{i}\) for \(i=1,2\), that \(\boldsymbol {\imath }_{3}^{\prime}=\boldsymbol{Q}_{0}\boldsymbol{\imath}_{3}\), that \(\boldsymbol{Q}_{0}=\boldsymbol{\imath}_{i}^{\prime}\otimes \boldsymbol{\imath}_{i}+\boldsymbol{\imath}_{3}^{\prime}\otimes \boldsymbol{\imath}_{3}\in\mathrm{Orth}^{+}\), and that (9.11) holds. Specifically, we find that
On applying \(\boldsymbol{Q}_{0}\) to the rectangular material strip \({\mathcal{D}}\) and translating the origin of the strip at \(\boldsymbol {x}=\boldsymbol{0}\) to the point \(R\boldsymbol{\imath}_{1}\), the strip remains flat, the left-hand end becomes tangent to the conical surface \({\mathcal {K}}\) at the point \(R\boldsymbol{\imath}_{1}\), and the midline of the strip becomes coincident with \(\boldsymbol{\imath}_{1}^{\prime}\). The next step is to find \(\boldsymbol{Q}\) such that the strip is wrapped isometrically onto the conical surface \({\mathcal{K}}\), in agreement with the ‘initial condition’ \(\boldsymbol{Q}(0)=\boldsymbol{Q}_{0}\).
For convenience, we suppress dependence on the independent variable \(\eta^{1}\) whenever possible in the following development and rewrite (9.4), using (9.7)2 and (9.10), as
After some consideration, the structure of the right-hand side of (9.15) and the condition \(\boldsymbol{Q}(0) = \boldsymbol{Q}_{0}\) suggest that we look for \(\boldsymbol{Q}\) in the form
where \(\boldsymbol{Q}_{1}\) is as defined in (9.7) (see also (9.8)) and \(\boldsymbol{Q}_{2}\) is defined as
with \(\xi\) to be determined such that \(\xi(0)=0\) and, thus, that  . Following this proposition, we then see that
. Following this proposition, we then see that
and a short calculation using (9.6) and (9.14) yields
With the aid of (9.5), (9.8), and (9.9), it then follows that
Thus, with (9.15), (9.18), and (9.20) we find that
and, thus, that \(\lambda\) takes the form
and, moreover, that \(\dot{\xi}=-\dot{\omega}\sin\varphi\) which, when integrated subject to the requirement \(\omega(0)=\xi(0)=0\), gives
Finally, with the conclusions of (9.22), (9.23), and (9.14) we have found that \(\boldsymbol{Q}\) determined according to (9.16) with \(\boldsymbol{Q}_{1}\) and \(\boldsymbol{Q}_{2}\) given by
solves the tensor initial value problem (9.4), namely
with \(\lambda\) given by (9.22).
We now turn to Step 3 of Sect. 8 to determine the scalar field \(\theta\) and return to (9.3) and (9.5) to see that
from which it follows that we must have \(\boldsymbol{a}= \boldsymbol {Q}_{0}\boldsymbol{Q}_{2}\boldsymbol{b}_{2}\). Then, since (9.11) gives \(\boldsymbol{a}= \boldsymbol{Q}_{0} \boldsymbol{b}_{2}(0)\), we readily arrive at \(\boldsymbol{b}_{2}(0) = \boldsymbol{Q}_{2}\boldsymbol{b}_{2}\), or the equivalent relation
Now, observing from (9.24) that \(\boldsymbol{Q}_{2}\) corresponds to a rotation about \(-\boldsymbol{\imath}_{3}\) of angle \(\omega\sin \varphi\), it easily follows that
with the consequence that
This relationship (9.29) between \(\theta\) and \(\omega\) has a natural and clear interpretation. To express this, recall that the straight lines which intersect \({\mathcal{D}}\subset\mathbb{E}^{2}\) at the angle \(\theta_{0} = \theta(0)\) at the origin point \(\eta ^{1}\boldsymbol{\imath}_{1} = \boldsymbol{0}\) and at the angle \(\theta (\eta^{1})\) at the point \(\eta^{1}\boldsymbol{\imath}_{1}\) are supposed to correspond to two straight lines of zero curvature on \({\mathcal{S}}\subset{\mathcal{K}}\subset\mathbb{E}^{3}\). These, of course, are two straight line generators of the conical surface \({\mathcal{K}}\) on which \({\mathcal{S}}\) lies. Recall, also, that \(R\) is the radius of the base of \({\mathcal{K}}\) and \(H\) is its height. Thus, the length of the generator from the base of \({\mathcal{K}}\) to its tip is \(L := \sqrt {R^{2} + H^{2}}\) and the tip angle \(2\varphi\) satisfies \(\sin\varphi ={R}/{L}\). Accordingly, (9.29) may be written as
which implies that, for each choice of \(\eta^{1}\), the arc length of the sector of a circle of radius \(L\) in \(\mathbb{E}^{2}\) that spans the angle \(\theta(\eta^{1})-\theta_{0}\) is equal to the arc length of the sector of the circle of radius \(R\) in \(\mathbb{E}^{3}\) which lies on the base of \({\mathcal{K}}\) and spans the angle \(\omega(\eta ^{1})\). The arc of the circle in \(\mathbb{E}^{2}\) is therefore wrapped isometrically onto the arc of the base of \({\mathcal{K}}\subset \mathbb {E}^{3}\) which is necessary in order for \({\mathcal{D}}\in\mathbb {E}^{2}\) to be deformed isometrically onto the surface \({\mathcal{K}}\).
Note that (9.24) and (9.29) show that, for each choice of \(\eta ^{1}\), \(\boldsymbol{Q}_{2}(\eta^{1})\) corresponds to a rotation about \(-\boldsymbol{\imath}_{3}\) of angle \(\theta(\eta^{1}) - \theta _{0}\). Thus, \(\boldsymbol{b}_{2}(\eta^{1}) = \boldsymbol {Q}_{2}^{{\top}}(\eta^{1})\boldsymbol{b}_{2}(0)\) is a rotation of \(\boldsymbol{b}_{2}(0)\) by the angle \(\theta(\eta^{1}) - \theta_{0}\) about \(\boldsymbol{\imath}_{3}\). This means that the field of unit vectors \(\boldsymbol{b}_{2}(\eta^{1})\in\mathbb{E}^{2}\) that emanate from the centerline of \({\mathcal{D}}\) intersect at one point for all \(\eta^{1}\). Moreover, since \(\boldsymbol{a}= \boldsymbol {Q}_{0}\boldsymbol{b}_{2}(0)\) is the rotated image of \(\boldsymbol {b}_{2}(0)\) and, according to (9.6), \(L\boldsymbol{a}= -R\boldsymbol {\imath}_{1} + H\boldsymbol{\imath}_{3}\) is the vector generator of \({\mathcal{K}}\) from \(R\boldsymbol{\imath}_{1}\) on its base to \(H\boldsymbol{\imath}_{3}\) at its tip, then \(L\boldsymbol{b}_{2}(0)\) is the point of intersection of the field \(\boldsymbol{b}_{2}(\eta ^{1})\) in \(\mathbb{E}^{2}\). A triangle completed by the sides \(L\boldsymbol{b}_{2}(0)\) and \(\eta^{1}\boldsymbol{\imath}_{1}\) in \(\mathbb{E}^{2}\), which are at the angle \(\theta_{0}\) to one another, will have its third side parallel to \(\boldsymbol{b}_{2}(\eta^{1})\) and the angle opposite the side \(L\boldsymbol{b}_{2}(0)\) will be \(\pi- \theta(\eta^{1})\) and the angle opposite the side \(\eta ^{1}\boldsymbol{\imath}_{1}\) will be \(\theta(\eta^{1})-\theta_{0}\). See Fig. 6. Thus, by the ‘sine law’ for triangles we have
which, for any \(\eta^{1}\in(-\infty,+\infty)\), may be reduced to
Knowing that \(\theta_{0}\in(0,\pi)\), this yields a unique \(\theta (\eta^{1})\in(0, \pi)\) for all \(\eta^{1}\in(-\infty,+\infty)\) and gives
The reference rectangle \({\mathcal{D}}\subset\mathbb{E}^{2}\) showing the family of intersecting straight lines which become the lines of zero principal curvature on \({\mathcal{S}}\subset {\mathcal{K}}\subset\mathbb{E}^{3}\). Here, \(L\) is the length of a generator of the conical surface \({\mathcal{K}}\)
Following Step 4 in Sect. 8, we recall that each point \(\boldsymbol{x}\) of the rectangular material strip \({\mathcal{D}}\) is to be located by the coordinates \((\eta^{1},\eta^{2})\) by
with \(\boldsymbol{b}_{2}\) given by
as illustrated in Fig. 6. It is an exercise in trigonometry, using (9.32), to show that the \((\eta^{1},\eta^{2})\) coordinates of the bottom and top left corners on the boundary of \({\mathcal{D}}\) are \((d_{l}^{+},k_{l}^{+})\) and \((d_{l}^{-},k_{l}^{-})\), respectively, with
while, by (9.35), \(\boldsymbol{b}_{2}\) has corresponding values
Clearly, the values of \(\eta^{1}\) determined above make sense only if the width \(w\) of the rectangle is not too large compared to the length \(L\) of the generator of the conical surface \({\mathcal{K}}\)—that is, only if \(w < 2L\sin\theta_{0}\). Otherwise, the apex of \(\mathcal{K}\) is involved with the isometric deformation of \({\mathcal{D}}\) to \({\mathcal{S}}\) and the nonvanishing principal curvature of \({\mathcal{S}}\) is unbounded.Footnote 9
Similarly, the \((\eta^{1},\eta^{2})\) coordinates of the bottom and top right corners on the boundary of \({\mathcal{D}}\) are \((l+d_{r}^{+},k_{r}^{+})\) and \((l+d_{r}^{-},k_{r}^{-})\), respectively, with
while, by (9.35), \(\boldsymbol{b}_{2}\) has corresponding values
Referring to Step 5 in Sect. 8, we next determine the curve on the conical surface \({\mathcal{K}}\) that defines the midline of the rectangular material strip \({\mathcal{D}}\) under the isometric deformation of \({\mathcal{D}}\) to \({\mathcal{S}}\subset{\mathcal{K}}\). This is given by the field \(\hat{\boldsymbol{y}}_{0}\) determined by integrating
where \(\boldsymbol{Q}=\boldsymbol{Q}_{1}\boldsymbol {Q}_{0}\boldsymbol {Q}_{2}\) is given through (9.14) and (9.24)–(9.32).
Using \(\boldsymbol{Q}_{0}\) from (9.14) and the alternative form
of \(\boldsymbol{Q}_{2}\) from (9.24), we find, upon using (9.29), that
Thus,
and, with the alternative form (9.8) of \(\boldsymbol{Q}_{1}\), we have
Thus, integrating (9.40) yields
where, according to (9.29),
and, from (9.32),
In view of (9.33), we may change the variable of integration from \(x\) to \(\theta\), giving
However, it does not appear possible to integrate (9.48) in closed form for general choices of \(\theta_{0}\in(0, \pi)\) and \(\varphi\in (0, \pi/2)\).
Turning to Step 6 in Sect. 8, we next determine the component \(\hat{\boldsymbol{y}}\) of the isometric deformation \(\tilde {\boldsymbol{y}}\) of \({\mathcal{D}}\subset\mathbb{E}^{2}\) to \({\mathcal{S}}\subset {\mathcal {K}}\subset\mathbb{E}^{3}\) defined implicitly through (4.3) and (4.6), i.e.,
where \(\hat{\boldsymbol{y}}_{0}\) is given in (9.48) and, by (9.3), (9.9), and (9.29),
with
The angle \(\theta\) is determined from (9.32) and the monotonically increasing condition (9.33), from which we may write
Finally, to completely characterize the isometric deformation \(\tilde {\boldsymbol{y}} \), we need only to evaluate
for all \((\eta^{1},\eta^{2})\) that correspond to the points \(\boldsymbol{x}\in{\mathcal{D}}\) through (4.1b), which can be expressed as
With (9.32), the first of (9.54) gives
for all \((x_{1},x_{2})\in(0,l)\times(-w/2,w/2)\). Then, observing that (9.54) implies that \((\eta^{1} - x_{1})^{2} + (x_{2})^{2} = (\eta^{2})^{2}\) and knowing that \(0<\theta<\pi\), the second of (9.54) gives
for all \((x_{1},x_{2})\in(0,l)\times(-w/2,w/2)\), which, with (9.55), yields
for all \((x_{1},x_{2})\in(0,l)\times(-w/2,w/2)\). Clearly, (9.55) and (9.57) make sense only if \(w < 2L\sin\theta_{0}\), confirming what we reported earlier in the discussion following (9.34) concerning the location of the bottom and top corners on the boundary of \({\mathcal{D}}\) in terms of the coordinates \((\eta^{1},\eta ^{2})\).Footnote 10
The nonvanishing principal curvature \(k\) of the deformed surface \({\mathcal{S}}\) is obtained from (6.13), (9.22), (9.29), and (9.33) as
Thus, because (9.33) readily yields
it follows from (4.4) that the denominator in (9.58) is restricted away from zero. Since \(x_{2}\) is in the interval \((-w/2, w/2)\), it follows from (9.54)2 that this restriction is equivalent to \(w < 2L\sin\theta_{0}\). Consequently, \(k\) is strictly negative for all points \(\boldsymbol {x}\in{\mathcal{D}}\). With the additional use of (9.52)1, (9.55), and (9.58) we may represent \(k\) in terms of \((x_{1}, x_{2})\in(0,l)\times(-w/2,w/2)\) in the form
from which it is clear that the restriction \(w<2L\sin\theta_{0}\) keeps \(k\) bounded and negative for all \(\boldsymbol{x}\in{\mathcal{D}}\).
9.2 Particular Example
For illustrative purposes, we choose
in which case, the dimensions \(L\) and \(R\) of the conical surface \(\mathcal{K}\) satisfy
and from (9.29) we have
With (9.63) and the aid of common trigonometric identities we find that (9.48) yields
In addition, (9.53) reduces to
In these equations we need to substitute for the field \(\theta\) from (9.32), which in view of (9.61) and (9.62) reduces to
However, we may use the relations
arising from specializing (9.52) in accord with (9.61) and (9.62) to write (9.64) and (9.65) directly in terms of \((\eta^{1}, \eta^{2})\). Furthermore, to show explicit dependence on \((x_{1}, x_{2})\), we substitute for \((\eta ^{1},\eta^{2})\) from (9.55) and (9.57), which now have the reduced forms
for all \((x_{1},x_{2})\in(0,l)\times(-w/2,w/2)\). Note that for this example we must satisfy the restriction \(w<2\sqrt{2} R\). Note, also, that with (9.61) and (9.62), the relation (9.60) for the nonvanishing principal curvature \(k\) of \({\mathcal{S}}\) in terms of \((x_{1}, x_{2})\) becomes
which, with the restriction \(w<2\sqrt{2} R\) is bounded and negative for all \(\boldsymbol{x}\in{\mathcal{D}}\).
Now, to interpret \(\hat{\boldsymbol{y}}_{0}\) in (9.64): Clearly, at \(\eta^{1} = 0\), \(\theta(0) = \pi/4\), and \(\hat{\boldsymbol{y}}_{0}(0) = R\boldsymbol{\imath }_{1}\); at \(\eta^{1} = \sqrt{2} R\), \(\theta(\sqrt{2} R) = \pi/2\) and \(\hat{\boldsymbol{y}}_{0}(\sqrt{2} R) = (R/\sqrt{2})\boldsymbol {\imath}_{2} + \sqrt {3} R(1 - 1/\sqrt{2})\boldsymbol{\imath}_{3}\); at \(\eta^{1} =4R/\sqrt {2}\), \(\theta(4R/\sqrt{2}) = 3\pi/4\) and \(\hat{\boldsymbol {y}}_{0}(4R/\sqrt {2})=-R\boldsymbol{\imath}_{1}\). In words, the curve parametrized by \(\hat{\boldsymbol{y}}_{0}\) smoothly raises with increasing \(\eta ^{1}\) from the base of the conical surface \({\mathcal{K}}\) at \(R\boldsymbol{\imath}_{1}\) and crosses the plane spanned by \(\boldsymbol{\imath}_{2}\) and \(\boldsymbol {\imath }_{3}\) on \({\mathcal{K}}\) at the point \((R/\sqrt{2})\boldsymbol {\imath }_{2} + \sqrt{3} R(1 - 1/\sqrt{2})\boldsymbol{\imath}_{3}\). It then lowers on \({\mathcal{K}}\) with increasing \(\eta^{1}\) and intersects the base of \({\mathcal{K}}\) at the point \(-R\boldsymbol{\imath}_{1}\). It continues to lower on \({\mathcal{K}}\) with increasing \(\eta^{1}\) and as \(\eta^{1}\longrightarrow+\infty\), \(\theta(\eta^{1})\to\pi \) and, asymptotically, \(\hat{\boldsymbol{y}}_{0}(\eta^{1})\to-\sqrt {2} R\boldsymbol {\imath}_{1} -\infty\boldsymbol{\imath}_{2} - \infty\boldsymbol {\imath}_{3}\), never again crossing the \(\boldsymbol{\imath }_{2}\)-\(\boldsymbol{\imath}_{3}\) plane. The curve determined by \(\hat{\boldsymbol{y}}_{0}\) on \((-\infty,+\infty)\) is symmetric with respect to the plane spanned by \(\boldsymbol{\imath}_{2}\) and \(\boldsymbol{\imath}_{3}\).
In Fig. 7, we use (9.64), (9.65), (9.67), and (9.68) to show the form of \({\mathcal{S}}\subset{\mathcal{K}}\) for \(\theta_{0}=\pi/4\), \(\varphi=\pi/6\), \(R=1\), \(w=1/2\), and \(l=\pi\). The midline of the rectangle \({\mathcal{D}}\), which is defined by \(x_{1}\in(0,l)\), \(x_{2}\to0\), has coordinates \((\eta^{1},\eta ^{2})=(x_{1},0)\) and is mapped to the curve on \({\mathcal{K}}\) defined by (9.64). We show this curve for a substantial range of \(\eta ^{1}\in(-\infty,+\infty)\) to illustrate that it is symmetric with respect to the plane spanned by \(\boldsymbol{\imath}_{2}\) and \(\boldsymbol{\imath}_{3}\) and is asymptotic to the points \(\pm\sqrt {2}R\boldsymbol{\imath}_{1}-\infty(\boldsymbol{\imath }_{2}+\boldsymbol{\imath}_{3})\) on \({\mathcal{K}}\). The behavior of the mapped midline described above and shown in Fig. 7 is representative of all isometric deformations of the rectangular material strip \({\mathcal{D}}\subset\mathbb{E}^{2}\) to the conical surface \({\mathcal{K}}\subset\mathbb{E}^{3}\).
10 Orthogonal Coordinate Representation of an Isometric Deformation: Necessary and Sufficient Form
Here, we reconcile the component \(\hat{\boldsymbol{y}}\) of the parametric representation for an isometric deformation \(\tilde{\boldsymbol{y}}\) appearing in (4.6) and its alternatives in (5.12) with our [1] recently provided representation. To achieve that, we identify the curvilinear coordinates \((\zeta^{1}, \zeta ^{2})\) with the coordinate curves \((\alpha,\beta)\) introduced in Sect. 3, where the transformation \((x_{1},x_{2})\longleftrightarrow(\zeta^{1},\zeta^{2})\) is defined by
with
Here, \(\bar{\boldsymbol{x}}_{0}\) parametrizes a curve \({\mathcal {C}}_{0}\) that passes through the origin \(\boldsymbol{x}=\boldsymbol{0}\) and has unit tangent vector \(\bar{\boldsymbol{x}}^{\prime}_{0}\) given by
where a prime is used to denote differentiation with respect to \(\zeta ^{1}\). The \(\zeta^{1}\)-coordinate line is coincident with the curve \({\mathcal{C}}_{0}\) at \(\zeta^{2} = 0\) and the \(\zeta^{2}\)-coordinate lines run along straight lines in \({\mathcal{D}}\) that correspond to pre-images of the straight lines of zero principal curvature in \({\mathcal{S}}\). The \(\zeta^{2}\)-coordinate line passing through \((\zeta^{1},0)\) forms an angle \(\bar{\theta}(\zeta^{1})\in(0, \pi )\) with the \(x_{1}\)-axis as shown in Fig. 8.
The curve \({\mathcal{C}}_{0}\) is clearly orthogonal to the \(\zeta ^{2}\)-coordinate lines and the \(\zeta^{1}\)-coordinate lines corresponding to \(\zeta^{2}=\mbox{constant}\) are not straight unless \(\bar{\theta}\) is constant. The base vectors of \(\mathbb{V}^{2}\) through each \(\boldsymbol{x}\in{\mathcal{D}}\subset\mathbb{E}^{2}\) for the curvilinear system are given by
so that
where the dependencies of \(\boldsymbol{g}_{1}\), \(\boldsymbol{g}_{2}\), and \(\bar{\theta}\) on \(\zeta^{1}\) are suppressed for brevity. Note, from (10.3b), that \(|\boldsymbol{g}_{1}|=|1-\zeta ^{2}\bar{\theta}^{\prime}|\), \(|\boldsymbol{g}_{2}|=1\), and \(\boldsymbol{g}_{1}\cdot\boldsymbol{g}_{2}=0\), whereby \(\{ \boldsymbol {g}_{1},\boldsymbol{g}_{2}\}\) is an orthogonal basis. Moreover, (10.1a) takes the explicit form
To ensure that \(\{\boldsymbol{g}_{1},\boldsymbol{g}_{2}\}\) is an acceptable basis for representing the points of \({\mathcal{D}}\subset \mathbb{E}^{2}\), we restrict \(\bar{\theta}\) and \(\zeta^{2}\) so that
on \({\mathcal{D}}\).Footnote 11
Now, setting \(\alpha= \zeta^{1}\), \(\beta= \zeta^{2}\), \(\boldsymbol {b}(\alpha) = \boldsymbol{g}_{2}(\zeta^{1})\), and \(\boldsymbol {Q}(\alpha)=\bar{\boldsymbol{Q}}(\zeta^{1})\) in (3.43), defining a mapping \(\bar{\boldsymbol{y}}\) of \((\zeta^{1},\zeta ^{2})\) to \({\mathcal {S}}\) such that
and writing \(\bar{\boldsymbol{y}}_{0}=\bar{\boldsymbol{y}}(\cdot ,0)\) for the parametrization of the image in \({\mathcal{S}}\) of the \(\zeta^{2}=0\) coordinate line \({\mathcal{C}}_{0}\) in \({\mathcal{D}}\), we arrive at the representation
From here we easily see that
Thus, because (10.3a) implies that
and because \(\boldsymbol{e}_{m}=\bar{\boldsymbol{Q}}\boldsymbol {\imath}_{m}\), we obtain
which yields \(\bar{\boldsymbol{a}}_{1}\cdot\bar{\boldsymbol {a}}_{2} = 0\) and \(|\bar{\boldsymbol{a}} _{i}|=|\boldsymbol{g}_{i}|\). In particular, we see that \(|\bar {\boldsymbol{a}} _{1}|=|1-\zeta^{2}\bar{\theta}^{\prime}|\), \(|\bar{\boldsymbol {a}}_{2}|=1\) and that \(\bar{\boldsymbol{a}}_{2}\) defines the field of straight lines of zero curvature in \({\mathcal{S}}\) that associate with the straight lines given by \(\boldsymbol{g}_{2}\) in \({\mathcal{D}}\). Note that (10.7) implies that
where
and that from (10.3b) we have
Thus, recalling from (10.10) that \(\bar{\boldsymbol {a}}_{1}=\bar{\boldsymbol{Q}} \boldsymbol{g}_{1}\), we see from (10.11) that \(\bar {\boldsymbol{Q}}\) must satisfy
which is a necessary condition on how the proper orthogonal transformation field \(\bar{\boldsymbol{Q}}\) must be chosen to ensure that, in conjunction with (10.4), (10.7) provides a parametric representation of an isometric deformation \(\tilde {\boldsymbol{y}}\). It readily follows from (10.10) that (10.14) is equivalent to \(\bar{\boldsymbol{Q}}^{\prime }\bar{\boldsymbol{Q}}^{{\top} }\bar{\boldsymbol{a}}_{2}=\boldsymbol{0}\), which means that the “angular velocity” corresponding to \(\bar{\boldsymbol{Q}}\), namely the axial vector \(\mbox{ax}(\bar{\boldsymbol{Q}} ^{\prime}\bar{\boldsymbol{Q}}^{{\top}})\) of the skew linear transformation \(\bar{\boldsymbol{Q}} ^{\prime}\bar{\boldsymbol{Q}}^{{\top}}\), must be parallel to \(\bar {\boldsymbol{a}}_{2}\), the lines ℒ of zero principal curvature in \({\mathcal{S}}\). There thus exist a scalar field \(\bar{\lambda}\) and a skew linear transformation \(\bar{\boldsymbol{A}}\) with axial unit vector \(\bar {\boldsymbol{a}}_{2}\), both generally dependent only on \(\zeta^{1}\) but independent of \(\zeta ^{2}\), such that
Of course, \(|\bar{\lambda}|=|\mbox{ax}(\bar{\boldsymbol {Q}}^{\prime}\bar{\boldsymbol{Q}} ^{{\top}})|\).
The condition (10.14) is not only necessary for the parametric representation of the deformation \(\tilde{\boldsymbol{y}}\) of \({\mathcal{D}}\subset\mathbb{E}^{2}\) to \({\mathcal {S}}\subset{\mathcal{E}}^{3}\) as defined implicitly by (10.4) and (10.7) to be an isometric deformation, but it is also sufficient. To see this, first observe from (10.6), (10.7), and (10.11) that
where \(\{\boldsymbol{g}^{1},\boldsymbol{g}^{2}\}\), with
is the basis of \(\mathbb{V}^{2}\) dual to \(\{\boldsymbol{g}_{1}, \boldsymbol{g}_{2}\}\).
Next, we observe that (10.12)–(10.14) allow us to write
which is equivalent to
Thus, because \(\bar{\boldsymbol{Q}}\in\mathrm{Orth}^{+}\),
and this ensures that the length between any two points in \({\mathcal {D}}\) is preserved under the deformation \(\tilde{\boldsymbol{y}}\) provided (10.14) holds.
10.1 The Isometric Deformation \(\tilde{\boldsymbol{y}}\) in Terms of the Curve \({\mathcal{C}}\in{\mathcal{S}}\) and Its Coordinate Pre-image Curve \({\mathcal{C}}_{0}\in{\mathcal{D}}\)
Note, from (10.12), that the unit tangent vector to the space curve \({\mathcal{C}}\) parametrized by \(\bar{\boldsymbol {y}}_{0}\) is given by
and recall that the Frenet triad \(\{\bar{\boldsymbol{t}},\bar {\boldsymbol{p}},\bar{\boldsymbol{b}}\}\) of tangent, normal and bi-normal unit vectors, respectively, for this curve are related according to
for \(\bar{\boldsymbol{t}}^{\prime}\neq\boldsymbol{0}\). Moreover, this triad satisfies the Frenet–Serret relations
where \(\bar{\kappa}:= -\bar{\boldsymbol{p}}^{\prime}\cdot\bar {\boldsymbol{t}}\) and \(\bar{\tau }:= \bar{\boldsymbol{p}}^{\prime}\cdot\bar{\boldsymbol{b}}\) denote, respectively, the curvature and torsion of the curve \({\mathcal{C}}\) parametrized by \(\bar {\boldsymbol{y}}_{0}\).
Now, using \(\bar{\boldsymbol{Q}}^{\prime}= \bar{\lambda}\bar {\boldsymbol{A}}\bar{\boldsymbol{Q}}\) from (10.15)2 and employing (10.3b)2, (10.10), and the relation
which follows from (3.39) and our earlier replacement of \(\boldsymbol{Q}\) by \(\bar{\boldsymbol{Q}}\) in (3.43) to arrive at (10.7), we see that
Thus, it follows that \(|\bar{\boldsymbol{t}}^{\prime}| = \sqrt{\bar {\lambda}^{2} +(\bar{\theta}^{\prime})^{2}}\) and by introducing a field \(\bar {\varphi}\), with values in \([0,2\pi)\), defined such that
we may write
Also, because
and
we see that \(\{\bar{\boldsymbol{t}},\bar{\boldsymbol{a}}_{2},\bar {\boldsymbol{n}}\}\) provides a positively-oriented orthonormal basis for \(\mathbb{V}^{3}\) and, moreover, that the Frenet binormal of the curve parametrized by \(\bar{\boldsymbol{y}}_{0}\) is given by
As an immediate consequence of (10.27) and (10.30), we find that
Moreover, differentiating (10.27) and using (10.30), we obtain
Thus, as a consequence of the identities
and
it follows, using (10.26), that
from which we see that the curvature and torsion of the curve parametrized by \(\bar{\boldsymbol{y}}_{0}\) are given by
Then, again referring to (10.26), we see that
With these developments, it follows from (10.10) and (10.31) that the component \(\bar{\boldsymbol{y}}\) of the isometric deformation \(\tilde{\boldsymbol{y}}\) parametrized implicitly by (10.4) and (10.7) may be written as
In addition to the representation (10.37), we may use (10.1b) and (10.3b) to express the relationship (10.4) determining each point \(\boldsymbol{x}\in {\mathcal{D}}\) in terms of the curvilinear coordinates \((\zeta ^{1},\zeta^{2})\) as
where \(\{\boldsymbol{e},\boldsymbol{e}_{\scriptscriptstyle\perp}\}\) is an orthonormal basis for \(\mathbb{V}^{2}\) with
We thus see that the representation (10.37), along with (10.35) and the alternative relationship between \(\boldsymbol {x}\in{\mathcal{D}}\) and \((\zeta^{1}, \zeta^{2})\) given in (10.38) and (10.39), with \(\bar{\theta}\) defined up to an added constant in (10.36)1, is that proven recently by Chen, Fosdick and Fried [1] as a necessary and sufficient isometric smooth deformation of a planar region in \(\mathbb{E}^{2}\) to \(\mathbb{E}^{3}\).Footnote 12
It is noteworthy that while the representation (10.37) was derived assuming the existence of a \(\bar{\boldsymbol{Q}}\in \mathrm{Orth}^{+}\) that satisfies (10.14) or, equivalently (10.15), no remnant of this appears in (10.37). We now use the curvilinear coordinate system \((\zeta^{1}, \zeta^{2})\) to identify \(\bar{\boldsymbol{Q}}\) in terms of the properties of \({\mathcal{C}}\) and \({\mathcal{C}}_{0}\). First, recall (10.17) and note that
where
the first of which follows from (10.33b) and the second of which follows from (10.27) and (10.30). Thus,
which confirms that \(\nabla\tilde{\boldsymbol{y}}\) depends only upon the coordinate \(\zeta^{1}\), and it follows that
Making use of (10.27) and (10.30), we now define
Clearly, \(\det\bar{\boldsymbol{Q}}=1\) and

In the above, we have identified \(\bar{\boldsymbol{Q}}\in\mathrm {Orth}^{+}\) in terms of \({\mathcal{C}}\) and \({\mathcal{C}}_{0}\) and now we show that this field satisfies (10.14) or, equivalently (10.15). First, we observe that because of \(\bar{\boldsymbol {a}}^{\prime }_{2}=-\bar{\theta}\bar{\boldsymbol{t}}\) from (10.33b) we have
which, upon using the Frenet–Serret relation \(\bar{\boldsymbol{t}}^{\prime}= \bar{\kappa}\bar{\boldsymbol{p}}\) in conjunction with (10.27) and (10.36)1, we may write as
the latter being a consequence of (10.36)2. Thus, using the identity \(\bar {\boldsymbol{n}}^{\prime }=\bar{\lambda}\bar{\boldsymbol{t}}\) from (10.33a) we find that
and we see that \(\bar{\boldsymbol{Q}}^{\prime}\boldsymbol{g}_{2} = \bar{\boldsymbol{Q}}^{\prime }(\cos\bar{\theta}\boldsymbol{\imath}_{1} + \sin\bar {\theta}\boldsymbol{\imath}_{2}) \equiv\boldsymbol{0}\), i.e., (10.14) is identically satisfied. It is now easy to conclude that
with \(\bar{\lambda}= \bar{\kappa}\sin\bar{\varphi}\), and, because \(\{\bar{\boldsymbol{t}}, \bar{\boldsymbol{a}}_{2}, \bar {\boldsymbol{n}}\}\) is a positively-oriented orthonormal basis for \(\mathbb{V}^{3}\), we know that \(\bar {\boldsymbol{a}}_{2} = \mbox{ax}(\bar{\boldsymbol{t}}\otimes\bar{\boldsymbol{n}}- \bar {\boldsymbol{n}}\otimes\bar{\boldsymbol{t}})\) and, so, the tensor ordinary-differential equation (10.15)2 is satisfied by \(\bar{\boldsymbol{Q}}\in\mathrm{Orth}^{+}\) as defined in (10.42) and (10.44), with \(\bar{\boldsymbol{A}}:= \bar {\boldsymbol{t}}\otimes\bar{\boldsymbol{n}} - \bar{\boldsymbol{n}}\otimes\bar{\boldsymbol{t}}\).Footnote 13
10.2 Recovery of the Component \(\bar{\boldsymbol{y}}\), or Its Equivalent \(\hat{\boldsymbol{y}}\), of the Parametric Representation of an Isometric Deformation \(\tilde{\boldsymbol{y}}\)
With reference to (4.1a), (4.1b), (10.1a), and (10.1b), we find that the curvilinear coordinates \((\eta^{1},\eta^{2})\) and \((\zeta^{1},\zeta^{2})\) are related by
and
Thus, the representation (10.37) may be written in the form
where \(\bar{\boldsymbol{f}}\) is defined according to
Our aim is to show that the last of the representations (5.12) for the component \(\hat{\boldsymbol{y}}\) of the implicit parametric representation of an isometric deformation \(\tilde{\boldsymbol{y}}\) in terms of the curvilinear coordinates \((\eta^{1},\eta^{2})\), namely
follows from (10.51). Establishing this result amounts to using the coordinate transformation (10.50a) to show that, for \(\eta^{1}=\bar{\eta}^{1}(\zeta^{1})\),
where, recalling (4.11), \(\hat{\boldsymbol{y}}_{0}\) satisfies \(\dot {\hat{\boldsymbol{y}}}_{0}=\boldsymbol{Q}\boldsymbol{\imath}_{1}\) with \(\boldsymbol {Q}\) being related to \(\bar{\boldsymbol{Q}}\) of (10.44) by \(\boldsymbol {Q}(\eta^{1})=\bar{\boldsymbol{Q}}(\zeta^{1})\) for \(\eta^{1}=\bar {\eta }^{1}(\zeta^{1})\). To this end, we first define a field \(\boldsymbol {f}\) by
and apply the chain rule to yield
where, as in Sect. 4, a superposed dot denotes differentiation with respect to \(\eta^{1}\). Alternatively, since \(\bar{\boldsymbol{y}}^{\prime}_{0}=\bar{\boldsymbol{t}}\) and, by (10.33b), \(\bar{\boldsymbol{a}} ^{\prime}_{2}=-\bar{\theta}^{\prime}\bar{\boldsymbol{t}}\), computing the derivative of \(\bar{\boldsymbol{f}}\) with respect to \(\zeta^{1}\) directly from (10.52) and using the identity
where \(J\) is defined by \(J(\zeta^{1}):=\int_{0}^{\zeta^{1}}\cos\bar {\theta}(u)\,\mbox{d}u\), we obtain
To proceed further, we use (10.50a,b) to transform (10.57) to
which, since \(\bar{\theta}(\zeta^{1})=\theta(\eta^{1})\) for \(\eta ^{1}=\bar{\eta}^{1}(\zeta^{1})\) and, consequently, \(\bar{\theta }^{\prime}=(\mbox{d}\bar{\eta}^{1}/\mbox{d}\zeta^{1})\dot{\theta}\), can be written as
Recalling (10.5) and assuming that \(\sin\theta- \eta ^{2}\dot{\theta}\neq0\), which is (4.4), we thus find that
With (10.61), we infer from (10.56) and (10.58) that
Since \(\bar{\boldsymbol{Q}}\boldsymbol{\imath}_{1} = \sin\bar {\theta}\bar{\boldsymbol{t}}+ \cos\bar{\theta}\bar {\boldsymbol{a}}_{2}\) by (10.44) and since \(\boldsymbol{Q}(\eta^{1})=\bar{\boldsymbol {Q}}(\zeta^{1})\) for \(\eta^{1}=\bar{\eta}^{1}(\zeta^{1})\), it follows that \(\dot {\boldsymbol{f}}=\boldsymbol{Q}\boldsymbol{\imath}_{1}\), or, equivalently, that
which, because of (4.11), shows that \(\boldsymbol{f}=\hat {\boldsymbol{y}} _{0}\) and that \(\dot{\hat{\boldsymbol{y}}}_{0}=\boldsymbol {Q}\boldsymbol{\imath }_{1}\). Finally, we know from (10.10) that \(\bar {\boldsymbol{a}}_{2} = \bar{\boldsymbol{Q}}\boldsymbol{g}_{2}\) and from (10.3b)2, (4.2b)2, and the correspondence \(\bar{\theta}(\zeta ^{1})=\theta(\eta^{1})\), for \(\eta^{1} = \bar{\eta}^{1}(\zeta ^{1})\), that \(\boldsymbol{g}_{2}(\zeta^{1})=\boldsymbol{b}_{2}(\eta ^{1})\) for \(\eta^{1} = \bar{\eta}^{1}(\zeta^{1})\). In addition, we know that \(\bar{\boldsymbol{Q}}(\zeta^{1}) = \boldsymbol{Q}(\eta ^{1})\) and, from (4.9), that \(\boldsymbol{a}_{2}=\boldsymbol {Q}\boldsymbol {b}_{2}\). Thus, \(\bar{\boldsymbol{a}}_{2}(\zeta^{1}) = \boldsymbol {a}_{2}(\eta ^{1})\) for \(\eta^{1} = \bar{\eta}^{1}(\zeta^{1})\) and this finalizes the argument showing that (5.12)5 follows from (10.51).
In passing, to be complete, we need to determine the fields \(\lambda\) and \(\boldsymbol{A}\) that satisfy the tensor ordinary-differential equation (4.14). Clearly, since \(\boldsymbol{Q}(\eta ^{1})=\bar{\boldsymbol{Q}}(\zeta^{1})\) for \(\eta^{1}=\bar{\eta }^{1}(\zeta^{1})\),
so with the aid of (10.48) we may write
But, we know that \(\bar{\boldsymbol{a}}_{2}\) is the axial vector of \(\bar{\boldsymbol{A}}\in\mbox{Skew}\) and we have shown that \(\bar{\boldsymbol{a}}_{2}(\zeta ^{1})=\boldsymbol {a}_{2}(\eta^{1})\) for \(\eta^{1}=\bar{\eta}^{1}(\zeta^{1})\). Thus, \(\boldsymbol{A}(\eta^{1})=\bar{\boldsymbol{A}}(\zeta^{1})\) for \(\eta^{1}=\bar {\eta}^{1}(\zeta^{1})\), is Skew and has \(\boldsymbol{a}_{2}\) as its axial vector. With this, we see from the above that (4.14)1, namely \(\dot{\boldsymbol{Q}}\boldsymbol{Q}^{{\top} }= \lambda\boldsymbol{A}\), holds with \(\lambda\) given by
10.3 Curvature Tensor of \({\mathcal{S}}\)
Following the approach in Sect. 6, but now using the structure of the coordinate system \((\zeta^{1}, \zeta^{2})\) for locating the points \(\boldsymbol{y}\) on \({\mathcal{S}}\) and for evaluating the associated normal field \(\boldsymbol{n}\), we find, by using \(\boldsymbol{n}=\bar{\boldsymbol{n}}:=\bar{\boldsymbol {Q}}\boldsymbol{\imath}_{3}\) in the steps leading to (6.9), that
where \(\{\bar{\boldsymbol{a}}^{1},\bar{\boldsymbol{a}}^{2}\}\) is the basis dual to \(\{\bar{\boldsymbol{a}} _{1}, \bar{\boldsymbol{a}}_{2}\}\) in \(\mathbb{V}^{2}\). Since \(\{\bar {\boldsymbol{a}}_{1},\bar{\boldsymbol{a}} _{2}\}\) is orthogonal and \(\bar{\boldsymbol{a}}_{2}\) lies along the straight lines of zero curvature on \({\mathcal{S}}\), \(\{\bar{\boldsymbol {a}}^{1},\bar{\boldsymbol{a}}^{2}\}\) is orthogonal, with \(\bar{\boldsymbol{a}}^{1}\) being collinear with \(\bar{\boldsymbol{a}}_{1}\) but orthogonal to \(\bar{\boldsymbol{a}}_{2}\) and, moreover, that \(|\bar {\boldsymbol{a}} ^{1}|=1/|\bar{\boldsymbol{a}}_{1}|\). But, because \(\{\bar {\boldsymbol{t}}, \bar{\boldsymbol{a}}_{2}, \bar{\boldsymbol{n}}\} \) is an orthonormal basis for \(\mathbb{V}^{3}\), we may write \(\bar {\boldsymbol{a}} ^{1}\otimes\bar{\boldsymbol{a}}^{1}=|\bar{\boldsymbol {a}}^{1}|^{2}\bar{\boldsymbol{t}}\otimes\bar{\boldsymbol{t}}\). Thus, since \(|\bar{\boldsymbol{a}}_{1}|=|1-\zeta^{2}\bar{\theta}^{\prime }|\), (10.66) becomes
To go further, using (10.48) and (10.41), we may rewrite the numerator of (10.67) as
and obtain the curvature tensor of \({\mathcal{S}}\) in the form
the latter step following from (10.36). Hence, the second possibly nonvanishing principal curvature \(k\) of \({\mathcal{S}}\) is given by
which is equivalent to (80) of Chen, Fosdick and Fried [1].
Finally, note that by substituting (10.65) into (10.69)1 and using (10.60), we obtain
which is equivalent to the form derived earlier in (6.12) once it is recalled that \(\boldsymbol{\nu}\) in (6.12) and \(\bar{\boldsymbol{t}}\) are both unit vector fields in the tangent plane to \({\mathcal{S}}\) that are perpendicular to the straight lines of zero curvature on \({\mathcal{S}}\) and thus that \(\bar{\boldsymbol{t}}\) is collinear with \(\boldsymbol{\nu}\).
11 Discussion
It is common to find in the literature works in which two-dimensional continuous material regions in three-dimensional Euclidean point space \(\mathbb{E}^{3}\) are considered within the general class of surfaces that are related by being developable, namely the class of surfaces that are isometrically related in the differential geometric sense described in Sect. 3. For examples of this approach, see Hangan [3], Sabitov [4], Starostin and van der Heijden [2], Kurono and Umehara [5], Chubelaschwili and Pinkall [6], Naokawa [7], Kirby and Fried [8], and Shen et al. [9]. A somewhat different but related approach is taken by Dias and Audoly [16], who consider smooth mappings between flat reference surfaces and ruled target surfaces. It can be shown that a reference surface and a ruled target surface are related by an isometric deformation if arclength is measured identically along the directrix of the reference surface and the directrix of the target surface and the ruled target surface is assumed to be developable. Dias and Audoly [16] concentrate on developability but do not, however, provide a strategy for constructing such deformations. Nor do they explain how to identify material points in the reference surface and their coordinates, which measure distance along the directrices and the generators. We postpone further discussion of these issues and their bearing on the variational strategy proposed by Dias and Audoly [16] for future work. To ensure that the arc length of every curve of material points on an unstretchable material surface is preserved under a deformation, we have found in the present work that the generators, the curvature, and the rotation field of the deformed surface must satisfy a specific non-trivial relationship. Incompleteness in characterizing the isometric deformation is a common oversight in the literature concerned with the forms of ribbons in \(\mathbb{E}^{3}\).
Throughout this paper we have considered the kinematics related to the isomeric deformation of an unstretchable planar material region identified with an open, connected subset \({\mathcal{D}}\) of \(\mathbb {E}^{2}\) to a surface \({\mathcal{S}}\) in \(\mathbb{E}^{3}\). Such a deformation is a mapping which is restricted so that all material fibers of \({\mathcal{D}}\) remain unchanged in length. From this vantage point, a surface is a two-dimensional material object that is embedded in \(\mathbb{E}^{3}\) and the corresponding notion of isometry is fundamentally different from the differential geometric counterpart in which a surface is considered purely as two-dimensional non-Euclidean manifold that may be embedded in \(\mathbb{E}^{3}\) without regard to the identification of material points.
In differential geometry, surfaces are parametrically represented by coordinate systems and are endowed with first and second fundamental forms which describe their metric and curvature properties, respectively. The coordinate systems for different surfaces may, but are not required to, be taken as the ‘same’ in the sense that the values of the coordinates of an image point are the same as those of the corresponding inverse image point. According to Kreyszig [15, p. 161], given two surfaces, a portion of one is isometrically mapped onto a portion of the other if and only if at corresponding points of the two surfaces—when referred to the same coordinate systems on the two surfaces—the coefficients of the first fundamental forms for the two surfaces are the same. This has the consequence that for the isometric mapping of a portion of one surface onto a portion of another surface, the length of any arc on one surface must be the same as that of its inverse image. It is well-known in differential geometry that two surfaces which have the same constant Gaussian curvature may be isometrically mapped, one onto the other. It is also well-known in the kinematics of deformable two-dimensional continuous material regions that the isometric deformation of a planar, undistorted reference configuration must produce a surface with the same, vanishing, Gaussian curvature. However, it does not generally follow that a reference and a target surface that have the same constant Gaussian curvature from the differential geometric point of view represent the isometric deformation of a material reference configuration into its deformed image.
The first fundamental form of a deformed two-dimensional continuous material region characterizes its metric properties and is generated by the deformation itself. The deformation from a given reference configuration of the body is said to be isometric if the length of any arc of material fibers in the reference configuration and the length of the image of that arc in the deformed configurations is identical.
In differential geometry, an isometric mapping of a portion of one surface onto a portion of another surface requires that the length of any arc on one must be the same as that of its inverse image on the other. Since lengths on a surface are determined by the first fundamental form on that surface, and this depends on its parametrization, then there exists an isometric mapping if and only if when the same coordinates are used to parameterize the surfaces the coefficients of their first fundamental forms are equal. A test for this draws upon the important theorem that isometric surfaces necessarily have the same Gaussian curvature at corresponding points. This test is also sufficient if the surfaces have the same constant Gaussian curvature. Since developable surfaces are ruled surfaces of zero Gaussian curvature that characterize the class of all surfaces that are geometrically isometric to a plane, and since an isometric deformation of planar, undistorted material surfaces produces a developable image, the two distinct concepts of isometry from the differential geometric and the deformation points of view have become fuzzy and are sometimes mistaken to be equivalent. The characterization of an isometric deformation of a planar material region involves more than the geometric restriction of developability. All fibers of the material region must remain unchanged in length and this yields an additional restriction on the changing rotation field that is responsible for the bending that takes place around the generators of the ruled and developable deformed material surface.
In this paper, we have established several equivalent necessary and sufficient representations of a smooth, isometric deformation of a planar material region into a curved surface and we have emphasized the essential nature of the non-trivial tensorial ordinary-differential initial-value-problem that must be solved to properly relate the generators, the curvature, and the rotation field of the isometrically deformed material surface. For illustrative purposes, we have also provided examples involving isometric deformations of rectangular material strips into cylindrical and conical surfaces.
Notes
See, for example, Kreyszig [15, p. 164].
Throughout this work, Roman indicies range over \(\{1,2\}\), with summation over twice repeated indices being implicit, and a subscripted comma denotes partial differentiation.
The linear transformation \(-\mbox{grad}_{s}\boldsymbol{n}\) is also called the “Weingarten mapping” or the “shape operator” and its symmetry property is a fundamental theorem of differential geometry. The principal values of \(-\mbox{grad}_{s}\boldsymbol{n}\) are the principal curvatures of \({\mathcal {S}}\) at \(\boldsymbol{y}\).
In this regard, note that \(\boldsymbol{a}^{2}(\eta^{1})\) is the orientation of the line \({\mathcal{L}}(\eta^{1})\) of zero curvature in \({\mathcal{S}}\) which corresponds to the line \({\mathcal{L}}_{0}(\eta ^{1})\) that passes through the \(x_{1}\)-axis at \((\eta_{1}, 0)\) with orientation \(\boldsymbol{b}_{2}(\eta^{1})\) in \({\mathcal{D}}\).
For example, Starostin and van der Heijden [2] consider a parametrization
$$ \boldsymbol{y}(s,t)=\boldsymbol{r}(s)+t \bigl(\boldsymbol {b}(s)+\eta(s) \boldsymbol{t}(s) \bigr),\quad s\in[0, L],\ t\in[-w, w], $$(∗)of a strip of length \(L\) and width \(2w\), where \(\boldsymbol{r}\) is the centerline of the strip, \(s\) denotes the arc length along the centerline and \(\boldsymbol{t}\), \(\boldsymbol{b}\), \(\kappa\), \(\tau\) and \(\eta:= \tau/\kappa\) are as above in this section. They take this to be a representation that preserves all intrinsic distance. While this parametrization is similar to (5.12)4, Starostin and van der Heijden [2] do not explain how to correlate \(s\) and \(t\) with the corresponding material points of the flat reference rectangle. Since \(L\) and \(2w\) are designated as the length and width of the rectangular strip and the domains for \(s\) and \(t\) are given as \([0,L]\) and \([-w,w]\), respectively. it is natural to take \(s\) as \(x_{1}\) and \(t\) as \(x_{2}\). However, this would be incorrect, and this is what defines the ‘confusion’ noted in the text of the paragraph containing this footnote. Such a correlation is obtained in the present work through the use of (4.1) in \((5.1)_{4}\). Moreover, Starostin and van der Heijden [2] make no mention of any condition such as (4.13) which would ensure that their parametric representation is indeed isometric in the sense that it preserves distances between all pairs of material points. Without further restriction the parametrization does not represent an isometric deformation. See, also, the discussion of Chen and Fried [10].
We calculate the nonzero principal curvature of \({\mathcal{S}}\) in (9.58) and show how the inequality \(w < 2L\sin\theta_{0}\) arises from the condition that the curvature of \({\mathcal{S}}\) is bounded. Due to this inequality, the nonvanishing principal curvature is, in fact, everywhere negative on \({\mathcal{S}}\).
See also the interpretation of (9.58), below.
Of course, the initial value for (10.15)2 is \(\bar{\boldsymbol{Q}}_{0} := \bar {\boldsymbol{Q}}(0)\), which, according to (10.42) and (10.44), can be shown to depend upon the initial values of \({\mathcal{C}}\) through \(\bar {\boldsymbol{t}}(0)\), \(\bar{\boldsymbol{t}}^{\prime}(0)\), and \(\bar{\varphi}(0)\), and the initial value of \({\mathcal{C}}_{0}\) through \(\bar{\theta}_{0}\). Note, as an alternative, that \(\bar{\boldsymbol{R}}:= \bar{\boldsymbol{Q}}\bar {\boldsymbol{Q}}_{0}^{{\top} }\in\mathrm{Orth}^{+}\) satisfies
 (10.49)
(10.49)where, with reference to (10.36)2, \(\bar{\lambda}= \bar{\kappa}\sin\bar {\varphi}\).
References
Chen, Y.-C., Fosdick, R., Fried, E.: Representation for a smooth isometric mapping from a connected planar domain to a surface. J. Elast. 119, 335–350 (2015)
Starostin, E.L., van der Heijden, G.H.M.: The shape of a Möbius strip. Nat. Mater. 6, 563–567 (2007)
Hangan, T.: Elastic strips and differential geometry. Rend. Semin. Mat. (Torino) 63, 179–186 (2005)
Sabitov, I.K.: Isometric immersions and embeddings of a flat Möbius strip in Euclidean spaces. Izv. Math. 71, 1049–1078 (2007)
Kurono, Y., Umehara, M.: Flat Möbius strips of given isotopy type in \(\boldsymbol {R}^{3}\) whose midlines are geodesics or lines of curvature. Geom. Dedic. 134, 109–130 (2008)
Chubelaschwili, D., Pinkall, U.: Elastic strips. Manuscr. Math. 133, 307–326 (2010)
Naokawa, K.: Extrinsically flat Möbius strips on given knots in 3-dimensional spaceforms. Tohoku Math. J. 65, 341–356 (2013)
Kirby, N., Fried, E.: \(\varGamma\)-limit of a model for the elastic energy of an inextensible ribbon. J. Elast. 119, 35–47 (2015)
Shen, Z., Huang, J., Chen, W., Bao, H.: Geometrically exact simulation of inextensible ribbon. Comput. Graph. Forum 34, 145–154 (2015)
Chen, Y.-C., Fried, E.: Möbius bands, unstretchable material sheets, and developable surfaces. Proc. R. Soc. Lond., Ser. A, Math. Phys. Eng. Sci. 472, 20150760 (2016)
Simmonds, J.G., Libai, A.: Exact equations for the inextensional deformation of cantilevered plates. J. Appl. Mech. 46, 631–636 (1979)
Simmonds, J.G., Libai, A.: Alternate exact equations for the inextensional deformation of arbitrary, quadrilateral, and triangular plates. J. Appl. Mech. 46, 895–900 (1979)
Libai, A., Simmonds, J.G.: Nonlinear elastic shell theory. Adv. Appl. Mech. 23, 271–371 (1983)
Libai, A., Simmonds, J.G.: The Nonlinear Theory of Elastic Shells, 2nd edn. Cambridge University Press, Cambridge (1998)
Kreyszig, E.: Introduction to Differential Geometry and Riemannian Geometry. Mathematical Expositions, vol. 16. University of Toronto Press, Toronto (1968). Reprinted, 1975
Dias, M.A., Audoly, B.: “Wunderlich, meet Kirchhoff”: A general and unified description of elastic ribbons and thin rods. J. Elast. 119, 49–66 (2015)
Acknowledgements
The work of Eliot Fried was supported by the Okinawa Institute of Science and Technology Graduate University with subsidy funding from the Cabinet Office, Government of Japan. Yi-chao Chen thanks the Okinawa Institute of Science and Technology for hospitality and generous support during a sabbatical and several subsequent visits.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Chen, YC., Fosdick, R. & Fried, E. Representation of a Smooth Isometric Deformation of a Planar Material Region into a Curved Surface. J Elast 130, 145–195 (2018). https://doi.org/10.1007/s10659-017-9637-2
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10659-017-9637-2