1 Introduction

The modelling framework of mass-growth developed in [1–3] (i) is generally applicable to mass-growth processes related to large strain and deformation, and (ii) consists of elastic and inelastic stages that may take place (iii) successively and, therefore, independently [1] or (iv) simultaneously, in a manner that their effects are interconnected [2, 3]. These considerations enable that framework [1–3] to embrace modelling of mass-growth processes which are relevant to a large number of different classes of soft and hard tissue. Nevertheless, the complexity and generality of the obtained constitutive equations [1–3] suggest that mass-growth applications that may lead to physical and/or mathematic simplification should be welcomed.

Unlike, for instance, arterial wall, which is pre-stressed [4] and its mass-growth process may involve both elastic and plastic deformation features (e.g., [1–3, 5]), growth of hard tissue, such as bones, hair or nails, may be thought of as purely elastic to a considerable extent. Moreover, small growth rates observed in nature, such as those related to hair or nail elongation, justify introduction of a concept of mass-growth that takes place through periodically accumulating small elastic strain. The present study is accordingly interested to specialise the modelling framework developed in [1, 2] and relate it with possible mass-growth processes that are elastic in nature and take place at infinitesimally small strain.

Departing from the constitutive equations of hyper-elastic mass-growth developed in [1], Sect. 2 thus combines the concept of small strain mass-growth with postulates employed in conventional linear elasticity and arrives to some simpler set of relevant governing equations. It is seen though that, due to combined influence of the rate of mass-growth and the rate of volumetric strain, the obtained, simplified sets of constitutive and equilibrium equations are, in general, still non-linear.

Section 3 focuses next to mass-growth processes that can be characterised as either incompressible or slightly/moderately compressible and finds that further relevant simplification is still possible. It is recalled that, unlike conventional hyperelasticity where the constraint of incompressibility requires from deformations to be isochoric, and vice versa, mass-growth incompressibility refers to deformations that take place under constant mass density but, otherwise, are neither isochoric nor geometrically constrained (e.g., [1, 3]). Use of an auxiliary, proportionality relationship between the rate of mass-growth and the rate of growth dilatation enables thus Sect. 3 to establish a connection between conventional isotropic linear elasticity and mass-growth processes that may take place at infinitesimally small strain.

In a particular example, Sect. 4 considers that a specimen of the human nail apparatus (Fig. 1) can be thought of as comprising of two plate-like structures bonded in series (e.g., [6]). The first of those plates is the nail matrix and is made of “living”, growing soft tissue. The second is the partially visible nail plate which is made of hard, keratinous, unable to grow, dead tissue. Justification and use of certain simplifying considerations enables thus Sect. 4 to present a physically reasonable and mathematically tractable model of the nail growth process and elongation. Underpinned by a combination of the concept of periodically accumulating small strain with a nail-elongation criterion, that model enables the living, soft tissue part of the nail apparatus to add newly grown mass to, and thus push periodically forward its dead, hard tissue counterpart.

Fig. 1
figure 1

(a) General, and (b) cross-sectional schematic representation of the nail apparatus (reproduced from p. 2 of [A Text Atlas of Nail Disorders, Robert Baran and Ivan Bristow. © 2003 CRC Press, by permission of Taylor & Francis Books UK])

Full size image

The efficiency of the outlined model is tested in Sect. 5, which presents details of an analytical solution to a particular, example application. This considers that mass-growth of the living part of the nail apparatus is incompressible and grows, periodically, with a rate which is proportional to the principal (longitudinal) spatial co-ordinate parameter and inversely proportional to time. Geometric or material features of the nail apparatus are kept as simple as possible in this application. Incorporation of more advanced relevant features and concepts can be handled mathematically in a similar manner, at the expense of parts of the pursued analytical simplicity. Some of those advanced features and concepts are accounted for and discussed in Sect. 6, which also outlines the main conclusions of this investigation.

2 Basic Equations

In a Cartesian co-ordinate system \(Ox_{i}\), consider a growing solid continuum whose mass obeys the standard continuity equation with growing mass; namely

$$ \frac{d\rho}{dt} + \rho v_{i,i} = r_{g}, $$
(2.1)

where the mass density, \(\rho\), and the mass-growth rate, \(r_{g}\), are in general functions of the spatial co-ordinate parameters and the time, \(t\). Moreover, \(v_{i} = \dot{x}_{i}\) are the components of the velocity vector, \(\mathbf{v}\), and a dot denotes differentiation with respect to time. A suffix “\(g\)” will not assume numerical values and will always be associated with scalar quantities. Every other Latin suffix will assume the values 1, 2 and 3 while the usual summation convention applies, and a comma among suffices denotes partial differentiation.

It is assumed that the continuum of interest grows slowly, in the sense that \(\dot{v}_{i}\) and relevant mass-growth acceleration terms are negligibly small. Stress equilibrium prevails at all times and is accordingly described by the quasi-static version of the relevant equations of motion,

$$ \sigma_{ij,i} = 0, $$
(2.2)

where \(\boldsymbol{\sigma}\) is the Cauchy stress tensor and, for simplicity, action of body forces is considered also negligible.

2.1 Elastic Mass-Growth

Consideration of the set of constitutive equations which is already available for isotropic mass-growth at large deformation and strain [1] requires introduction of a general deformation rule

$$ x_{i} = x_{i} ( X_{R};t ), $$
(2.3)

which relates the current, \(O x_{i}\), with a reference configuration, \(OX_{R}\), that was pictured at \(t = t_{0}\). In the usual manner, low case and capital letters/suffices denote quantities or parameters referring to the implied spatial and material co-ordinates, respectively.

In the absence of initial stress, the set of the constitutive equations of interest is thus as follows [1]:

$$ \sigma_{ij} = 2\frac{\rho}{\rho_{0}}F_{iR}F_{jS} \bigl\{ ( W_{1} + I_{1}W_{2} + I_{2}W_{3} )\delta_{RS} - ( W_{2} + I_{1}W_{3} )C_{RS} + W_{3}C_{RP}C_{PS} \bigr\} + \frac{r_{g}}{\rho_{0}v_{k,k}}W\delta_{ij}, $$
(2.4)

where \(\rho_{0}\) denotes material density at \(t = t_{0}\). The components of the appearing deformation gradient and Cauchy-Green deformation tensors are respectively defined as follows:

$$ F_{iQ} = \frac{\partial x_{i}}{\partial X_{Q}}, \qquad C_{QS} = F_{iQ}F_{iS} = \frac{\partial x_{i}}{\partial X_{Q}}\frac{\partial x_{i}}{\partial X_{S}}. $$
(2.5)

The strain energy density, \(W\), is generally a function of the deformation invariants

$$ I_{1} = \operatorname{tr}\boldsymbol{C}, \qquad I_{2} = \frac{1}{2} \bigl[ ( \operatorname{tr}\boldsymbol{C} )^{2} -\operatorname{tr}\boldsymbol{C}^{2} \bigr], \qquad I_{3} = \det \boldsymbol{C}, $$
(2.6)

while (2.4) employs the standard notation

$$ W_{n} = \frac{\partial W}{\partial I_{n}} \quad ( n = 1,2,3 ). $$
(2.7)

The postulate \(v_{ k, k} \neq\) 0 is justified in (2.4) through the consideration that the mass-growth of interest is a non-isochoric process (see also [3]).

It is noted for later use that, because \(r_{g} \neq\) 0 and external mechanical loading may be limited or completely absent, incompressible mass-growth requires that volume change and mass-growth balance in a manner that \(d \rho /dt = 0\). Use of (2.1) then reveals that

$$ \rho = \rho_{0}, \quad v_{k,k} = r_{g}/ \rho_{0} \ne 0, $$
(2.8)

and, hence, incompressible mass-growth is necessarily non-isochoric.

2.2 Small Strain

The constitutive equations (2.4) apply regardless of the size of the mass-growth deformation of interest. However, infinitesimally small growth may appear in nature for different reasons and a relevant, simplified form of (2.4) can be of particular help in that case.

The linearisation process of the conventional version of (2.4), obtained for \(r_{g} = 0\), is well known. This may be completed in a number of different equivalent ways (e.g., [7–9]), and involves introduction and use of the displacement vector and the infinitesimal strain tensor

$$ u_{i} = x_{i} - X_{i},\qquad e_{ij} = \frac{1}{2} ( u_{i,j} + u_{j,i} ), $$
(2.9)

respectively. That linearisation process postulates that material and spatial co-ordinates coincide, while material density is unaffected by the infinitesimally small strain (\(\rho = \rho_{0}\)). When material isotropy prevails, that process leads to the standard form of Hooke’s law, the form of which may be derived as follows:

$$ \sigma_{ij} = \frac{1}{2}\frac{\partial W}{\partial e_{ij}}, \quad W = \frac{1}{2} \bigl( \lambda e_{kk}^{2} + 2\mu e_{ij}e_{ij} \bigr), $$
(2.10)

where \(\lambda\) and \(\mu\) are the well-known Lamé elastic moduli.

However, in the present case of interest where \(r_{g} \neq 0\), (2.1) reveals that \(\rho \neq \rho_{0}\) still holds and, therefore, the mass density varies in time even within the infinitesimal deformation regime. Thus, straight combination of (2.10) and (2.4) yields the simplified set of constitutive equations sought in the form

$$ \sigma_{ij} = \frac{\rho}{\rho_{0}} ( \lambda e_{kk} \delta_{ij} + 2\mu e_{ij} ) + \frac{r_{g}}{2\rho_{0}\dot{u}_{m,m}} \bigl( \lambda e_{kk}^{2} + 2\mu e_{k\ell} e_{k\ell} \bigr) \delta_{ij}, $$
(2.11)

which is still nonlinear, due to the appearing quadratic strains and their combination with the divergence of the rate of dilatation, \(\dot{u}_{k,k} = v_{k,k}\). Nevertheless, the next section shows that further simplification is still possible if the small strain growth of interest is either incompressible or slightly/moderately compressible.

3 Incompressible and Slightly/Moderately Compressible Mass-Growth at Small Strain

Consider a possible class of materials whose mass-growth dilatation, \(u_{k,k}\), stays infinitesimally small at all times while its rate, \(\dot{u}_{k,k}\), is regulated by a relationship of the form

$$ \dot{u}_{k,k} = s ( x_{i} )\frac{r_{g}}{\rho_{0}}. $$
(3.1)

The appearing non-dimensional proportionality factor, \(s(x_{i})\), is considered as an auxiliary parameter which is independent of time. This may be either specified a-priory, on the basis of existing theoretical/experimental evidence, or determined a-posteriori, by solving some well-posed mass-growth boundary value problem.

Introduction of (3.1) into the continuity condition (2.1) transforms the latter into the following:

$$ \frac{d\rho}{dt} + \biggl( s ( x_{i} )\frac{\rho}{\rho_{0}} - 1 \biggr)r_{g} = 0, $$
(3.2)

and yields further

$$ u_{k,k} = \frac{s ( x_{i} )}{\rho_{0}} \int_{t_{0}}^{t} r_{g} dt \ll 1. $$
(3.3)

The simplest possible value of the auxiliary parameter \(s(x_{i})\) is the constant

$$ s = 1, $$
(3.4)

and corresponds to cases of incompressible mass-growth that are discussed separately in Sect. 3.1 below. In the light of the inequality (3.3), (3.4) enables mass-growth to stay infinitesimally small for reasonably long periods, at least in cases that \(r_{g}\) is not a fast increasing function of time.

In addition to (3.4), cases in which

$$ s ( x_{i} ) \ne 1 $$
(3.5)

can still be associated with mass-growth that takes place under infinitesimally small strain. Such cases refer to compressible mass-growth and are considered in Sects. 3.2 and 3.3. They are associated with values or forms of \(s\) which are slightly or moderately perturbed from 1 and are, accordingly, referred to as cases of slight or moderate mass-growth compressibility. Mass-growth processes that either violate (3.1) or obey (3.1) through use of forms/values of \(s\) which are substantially perturbed from 1 are perceived as representing highly compressible mass-growth processes and, hence, are not considered further in this investigation.

3.1 Incompressible Mass-Growth

By virtue of (2.8) and (3.2), (3.4) and (3.1) hold simultaneously in cases of incompressible mass-growth and, hence, (3.3) reduces to

$$ u_{k,k} = \frac{1}{\rho_{0}} \int_{t_{0}}^{t} r_{g} dt \ll 1. $$
(3.6)

Moreover, (3.1) yields \(\rho_{0}\dot{u}_{i,i}/r_{g} = 1\) and, hence, the constitutive equation (2.11) simplifies to

$$ \sigma_{ij} = \lambda e_{kk}\delta_{ij} + 2\mu e_{ij} + \frac{1}{2} \bigl( \lambda e_{kk}^{2} + 2\mu e_{k\ell} e_{k\ell} \bigr)\delta_{ij}. $$
(3.7)

Validity of the inequality (3.6) suggests that quadratic strains are practically negligible if compared with their linear counterparts and, hence, (3.7) reduces to its conventional linear elasticity form

$$ \sigma_{ij} = \lambda u_{k,k}\delta_{ij} + \mu ( u_{i,j} + u_{j,i} ), $$
(3.8)

where use is also made of the kinematic relations (2.9b).

Introduction of (3.8) into the equations of motion (2.2) leads thus to the Navier equations

$$ ( \lambda + \mu )u_{k,ki} + \mu u_{i,jj} = 0, $$
(3.9)

which, with the use of (3.6), reduce to the following set of uncoupled Poisson’s equations

$$ u_{i,jj} = - \frac{ ( 1 + \lambda /\mu )}{\rho_{0}} \int_{t_{0}}^{t} \frac{\partial r_{g}}{\partial x_{i}} dt. $$
(3.10)

In a specific growth boundary value problem where the form of the mass-growth rate, \(r_{g}\), is known, each one of (3.10) may thus be solved independently for the corresponding displacement component, \(u_{i}\).

It is observed that if the rate of mass-growth is independent of one or more co-ordinate parameters, one or more of the Poisson differential equations (3.10) convert into corresponding Laplace’s equations. Thus, in a particular application in which \(r_{g}\) does not depend of the spatial co-ordinates, all three equations (3.10) convert into Laplace’s equations. It is recalled that relevant applications that employ constant mass-growth rate are already available [1, 2], though these refer to mass-growth under finite strain.

3.2 Slightly or Moderately Compressible Mass-Growth

In cases of mass-growth that (3.5), rather than (3.4), applies on (3.1), (3.2) implies that \(d \rho /dt \neq\) 0 and, hence, that mass-growth takes place in a compressible manner. If the form of \(r_{g}\) still guarantees that mass-growth stays infinitesimally small for reasonably long time, then the constitutive equation (2.11) takes the form

$$ \sigma_{ij} = \frac{\rho}{\rho_{0}} ( \lambda e_{kk} \delta_{ij} + 2\mu e_{ij} ) + \frac{1}{2s} \bigl( \lambda e_{kk}^{2} + 2\mu e_{k\ell} e_{k\ell} \bigr)\delta_{ij}, $$
(3.11)

and, provided that

$$ O \bigl( \vert s \vert \bigr) \ge O ( 1 ), $$
(3.12)

the contribution of the quadratic strains becomes again practically negligible; here, \(O(*)\) stands for the order of magnitude of “∗”. By dropping the appearing quadratic terms and using (2.9b), (3.11) then reduces to

$$ \sigma_{ij} = \frac{\rho}{\rho_{0}} \bigl\{ \lambda u_{k,k} \delta_{ij} + \mu ( u_{i,j} + u_{j,i} ) \bigr\} . $$
(3.13)

In the light of the reasoning outlined earlier, values or forms of \(s\) which are slightly perturbed from 1 can thus characterise (3.13) as a constitutive equation associated with slightly compressible, small strain mass-growth. For values or forms of \(s\) which are considerably distant from 1, a mass-growth process associated with (3.13) may be characterised as moderately compressible as long as (3.12) still holds.

In such cases of slight or moderate mass-growth compressibility, use of (3.13) converts the quasi-static equations of motion (2.2) into

$$ u_{i,jj} + ( 1 + \lambda /\mu )u_{k,ki} + \frac{\rho_{,j}}{\rho} \biggl( \frac{\lambda}{\mu} u_{k,k} + u_{i,j} + u_{j,i} \biggr) = 0, $$
(3.14)

which, in the particular case of incompressible mass-growth (\(s = 1\), \(\rho = \rho_{0}\)) reduce naturally to the set of uncoupled Poisson’s equations (3.10). It may alternatively be claimed that the employed concept of slight or moderate mass-growth compressibility converts (3.10) into the set (3.14) of coupled partial differential equations. This is complemented by and has to be solved simultaneously with the pair of additional Eqs. (3.2) and (3.3) because, unlike the case of incompressible mass-growth, neither the continuity equation (3.2) is now satisfied identically nor the proportionality factor, \(s\), is necessarily specified a-priori.

Thus, the principal system of simultaneous differential equations encountered in this case consists of the five, coupled, partial differential equations (3.2), (3.3) and (3.14), and is evidently nonlinear. For a well-posed boundary value problem where the form of \(r_{g}\) is given, this nonlinear set of equations has to be solved, analytically or numerically, for a total of five principal unknowns; namely the three displacement components, \(u_{i}\), the mass density, \(\rho\), and the auxiliary parameter \(s(x_{i})\). A potential solution to this set of equations may be considered physically admissible only if is consistent with the inequality shown in (3.6).

Nevertheless, further simplification of the system of simultaneous differential equations (3.2), (3.3) and (3.14) can still be sought, by looking for potential approximate solutions that might emerge through a-priori specification of the value or form of the auxiliary function \(s(x_{i})\).

3.3 Mass-Growth Compressibility Related with A-priori Specified Forms/Values of \(s (x_{i})\)

Consideration of a-priori specified values or forms of \(s(x_{i})\) which are slightly “perturbed” from \(s = 1\) is justified by a common continuum mechanics concept. Accordingly, solutions of (3.2), (3.3) and (3.14) that may result through slight violation of (3.4) should be expected to appear in the vicinity of relevant solutions of the corresponding incompressible mass-growth Eqs. (3.10).

For a-priori specified values/forms of \(s(x_{i})\) that diverge from \(s = 1\) and satisfy (3.12), (3.2) and (3.3) decouple from (3.14). In particular, (3.2) is regarded as a first order linear ordinary differential equation that admits the unique solution

$$ \rho = I^{ - 1} \int_{t_{0}}^{t} Ir_{g} dt,\quad I = \exp \biggl( \frac{s}{\rho_{0}} \int_{t_{0}}^{t} r_{g} dt \biggr). $$
(3.15)

Moreover, (3.3) yields

$$ u_{k,kj} = \frac{1}{\rho_{0}} \int_{t_{0}}^{t} \frac{\partial ( sr_{g} )}{\partial x_{j}} dt, $$
(3.16)

and (3.14) reduce to the following set of three, coupled, second-order linear partial differential equations:

$$ u_{i,jj} + \frac{\rho_{,j}}{\rho} ( u_{i,j} + u_{j,i} ) = - \frac{1}{\rho_{0}} \biggl\{ ( 1 + \lambda /\mu ) \int_{t_{0}}^{t} \frac{\partial ( sr_{g} )}{\partial x_{i}} dt + \frac{\lambda s\rho_{,i}}{\mu \rho} \int_{t_{0}}^{t} r_{g} dt \biggr\} , $$
(3.17)

for the three unknown displacement components.

In the particular case that mass-growth is incompressible, validity of (3.4) forces (3.2) to return \(\rho = \rho_{0}\) and, hence, (3.17) reduce again to the uncoupled system of Poisson’s equations (3.10). In the present case though, where (3.14) simplify to (3.17), solution of the latter is still required to satisfy (3.3) or, equivalently, (3.1). In other words, mass-growth dilatation predicted through a potential solution of (3.17) is required to match the a-priori provided value/form of \(s\); hence, to be consistent with (3.3).

Consider, for instance, that any given, constant value of \(s > 1/2\) can be represented in the following infinite power series form:

$$ s = 1 + \varepsilon + \varepsilon^{2} + \varepsilon^{3} +\cdots = \frac{1}{1 - \varepsilon},\quad \vert \varepsilon \vert < 1, $$
(3.18)

where \(\varepsilon\) is evidently also a constant. Provided that the selected constant value of \(s\) is such that (3.12) is satisfied, a solution of (3.2) and (3.17) that represents moderately compressible mass-growth at small strain may be sought in the following asymptotic series form:

$$\begin{aligned} \rho& = \rho^{(0)} + \rho^{(1)}\varepsilon + \rho^{(2)} \varepsilon^{2} + \rho^{(3)}\varepsilon^{3} +\cdots, \\ u_{i} &= u_{i}^{(0)} + u_{i}^{(1)} \varepsilon + u_{i}^{(2)}\varepsilon^{2} + u_{i}^{(3)}\varepsilon^{3} +\cdots, \\ u_{k,k}& = u_{k,k}^{(0)} + u_{k,k}^{(1)} \varepsilon + u_{k,k}^{(2)}\varepsilon^{2} + u_{k,k}^{(3)}\varepsilon^{3} +\cdots, \end{aligned}$$
(3.19)

where \(u_{i}^{(0)}\)and \(\rho^{(0)} \equiv \rho_{0}\) necessarily represent the incompressible mass-growth predicted by solving (3.10).

By inserting (3.18) and (3.19c) into (3.3) and, then, making equal same powers of \(\varepsilon\), one obtains

$$ u_{k,k}^{(0)} = u_{k,k}^{(1)} = u_{k,k}^{(2)} = u_{k,k}^{(3)} =\cdots = \frac{1}{\rho_{0}} \int_{t_{0}}^{t} r_{g} dt, $$
(3.20)

which, when inserted back into (3.19c), makes sure that, if the asymptotic series (3.19a,b) represent a convergent solution of (3.2) and (3.17), then that solution is also consistent with (3.3), regardless of the magnitude of the constant \(s > 1/2\).

However, confirmation of the validity of (3.3) does not seem possible in such generality when potential solutions of (3.2) and (3.17) are sought and obtained for variable forms of \(s(x_{i})\).

3.4 Example of Slight Mass-Growth Compressibility

Consider a particular case in which (3.18) is replaced by the exact representation

$$ s = 1 + \varepsilon, \quad \vert \varepsilon \vert \ll 1, $$
(3.21)

and (3.21b) justifies the growth of interest as slightly compressible such. A two-term truncation,

$$\begin{aligned} \rho& \cong \rho^{(0)} + \rho^{(1)}\varepsilon, \\ u_{i} &\cong u_{i}^{(0)} + u_{i}^{(1)} \varepsilon, \\ u_{k,k}& \cong u_{k,k}^{(0)} + u_{k,k}^{(1)} \varepsilon, \end{aligned}$$
(3.22)

of (3.19) may then be thought of as a reasonably accurate representation of the previously outlined solution.

By inserting (3.21a) and (3.22) into (3.2) and (3.17) and making equal same powers of \(\varepsilon\), one confirms that the basic approximation (\(\rho^{(0)}\), \(u_{i}^{(0)}\)) to the solution sought coincides with the incompressible mass-growth solution discussed in Sect. 3.1 \((\rho^{(0)}= \rho_{0})\). Moreover, the first correction term consists of

$$ \rho^{(1)} = - I^{(1) ^{- 1}} \int_{t_{0}}^{t} I^{(1)}r_{g} dt,\quad I^{(1)} = \exp \biggl( \frac{1}{\rho_{0}} \int_{t_{0}}^{t} r_{g} dt \biggr), $$
(3.23)

and the potential solution of the following set of uncoupled Poisson’s equations

$$ u_{i,jj}^{(1)} = - \frac{\rho^{(1)}}{\rho_{0}}u_{i,jj}^{(0)} - \frac{\rho_{,j}^{(1)}}{\rho_{0}} \biggl( u_{i,j}^{(0)} + u_{j,i}^{(0)} + \frac{\lambda}{\mu \rho_{0}} \int_{t_{0}}^{t} r_{g} dt \biggr) - \bigl( 1 + \rho^{(1)}/\rho_{0} \bigr)\frac{ ( 1 + \lambda /\mu )}{\rho_{0}} \int_{t_{0}}^{t} \frac{\partial r_{g}}{\partial x_{i}} dt. $$
(3.24)

For a given boundary value problem, where the form of \(r_{g}\), is provided, each of the three differential equations (3.24) may be solved independently for the corresponding unknown function \(u_{i}^{(1)}\), in a manner similar to that discussed in Sect. 3.1 for \(u_{i}^{(0)}\). Higher-order correction terms may similarly be determined, if at all necessary, by truncating appropriately (3.19) and, hence, retaining additional terms in (3.22).

4 A Simple Mathematical Model of Human Nail Growth and Elongation

Detailed information of the human nail apparatus is found in relevant medical sources and texts (e.g., [6]), and some of the relevant terminology is necessarily used here with the help of Fig. 1. Wherever lack of detailed clinical evidence requires implementation of assumptions in an essentially speculative manner, these are selected to serve mathematical simplicity. When new experimental or clinical evidence may become available, their refinement is hoped to lead to considerable improvement of the current version of the model.

4.1 Brief Description of the Nail Apparatus

Figure 1 shows schematically the main parts of the nail apparatus and illustrates the interconnected positions of the soft nail matrix and the hard nail plate. The first of those plate-like structures is made of so-called “living” soft tissue that grows and causes elongation of the nail by apparently pushing forward that second, partially visible nail plate. The latter is made of hard, dead tissue which is unable to grow and is mainly produced, and added to the nail plate by germinal activity of the proximal and distal matrix. “Proximal” is that part of the matrix that lies in Fig. 1 towards the left side of the nail plate. The term “distal” signifies the part of the matrix that lies underneath the nail plate and neighbours at its right the non-germinal nail bed.

The bottom boundary of the nail plate, formed by the nail bed and the distal matrix, is connected with the bone of the digit through a system of collagen fibres; see Fig. 1(b). The non-visible part of the nail plate is covered and bounded from above by the proximal nail fold which ends at the cuticle; see Fig. 1(a). The back edge of the nail plate emanates from the proximal matrix. Both its side edges are occluded by the lateral nail folds. The front edge of the nail plate is free and visible.

The proximal and lateral nail folds adapt themselves to a variety of different physiological situations. It is generally believed that the essentially unknown activity of the nail folds, along with that of the matrix and its orientation, enable a healthy nail plate to grow longitudinally rather than sidewise, as well as in the form of thin flat plate rather than as a bulky keratinous mass.

It is finally understood that the tissue transition from “living” to “dead” status takes place within a narrow transition zone. This lies between the nail matrix and nail plate and is only a few cells wide. Keratinocytes produced through matrix differentiation harden and apparently die within that transition zone, add their contribution to the nail plate and, hence, cause nail elongation.

4.2 Basic Modelling Postulates and Considerations

The fact that the nail plate is formed by layers of identical keratinous material, which are compacted together (e.g., [6]), is here perceived as evidence of temporary interruption in the nail growth and elongation process. This seems thus to be periodic rather than continuous in time. The occasional appearance of the so-called Beau’s lines (e.g., [10–12]) is also interpreted as clinical evidence of discontinuous nail growth. Beau’s lines are associated with traumatic and/or pathological, rather than healthy nail circumstances, but their appearance provides further evidence of the nail ability to grow in a discontinuous manner.

As a matter of fact, the living germinal matrix does generate and adds new keratinous hard tissue onto the nail plate but its anticipated deformation is necessarily confined within physical boundaries which have seemingly no reason and/or ability to deform substantially. By imposing restrictions on the magnitude of the matrix deformation, this observation reinforces the feeling that the implied “push forward” mechanism is activated periodically, at specific time instances, when the strain that mass-growth accumulates within the nail matrix enables the corresponding stress state to reach some critical intensity level.

That critical stress level should be high enough to (i) balance and/or negate the resultant frictions met at the edges and the lateral supports of the hard nail plate, and, hence, (ii) push the nail plate forward along its longitudinal direction. Material which is newly grown within the nail matrix and, during that push forward action, passes through the aforementioned narrow transition zone is keratinised and compressed/compacted within the nail plate to which it is evidently added.

Along with the fact that nails elongate slowly, these considerations endorse the previously outlined framework of small strain mass-growth as suitable for modelling the mechanism of human nail elongation.

4.3 Simplified Geometrical Representation of the Nail Apparatus

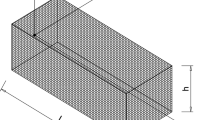
For simplicity, the thin nail plate is considered flat and rectangular in shape. Attention is thus restricted to a specimen of the nail apparatus which, at \(t = t_{0}\), has constant length \(L\), constant width \(2b < L\) and thickness \(h \ll b\). Figure 2 shows that the plane \(Ox_{1} x_{3}\) of the Cartesian co-ordinate system is placed horizontally, at the interface between the nail bed and the hard nail plate depicted in Fig. 1. The co-ordinate origin \(O\) is placed at the far left end of the proximal nail matrix; see also Fig. 1(a). The \(Ox_{2}\)-axis is directed upwards and the \(Ox_{1}\)-axis runs longitudinally, midway through the width of the specimen of the nail apparatus.

Fig. 2
figure 2

Simple geometrical representation, and nomenclature of a specimen of the human nail apparatus. The grey-shaded and unshaded parts represent the nail matrix (left) and the nail plate (right) respectively; see Sect. 4.3 for detailed description

Full size image

The left part of the specimen (\(0 \leq x_{1} \leq \ell\) in Fig. 2) is considered entirely within the “living” proximal matrix. Like the distal matrix, which lies underneath the hard nail plate and is not shown in Fig. 2, this proliferates and produces new material that may periodically die and add its contribution into the keratinous nail plate. The latter is represented by the right part of the specimen (\(\ell \leq x_{1} \leq L\) in Fig. 2) and, at \(t = t_{0}\), has thus constant and known longitudinal length, \(L -\ell\). The aforementioned narrow tissue transitional zone is thus approximated by the plane

$$ x_{1} = \ell. $$
(4.1)

Figure 1 implies that the hard nail plate emanates from the proximal matrix and that its thickness may vary with the longitudinal co-ordinate parameter \(x_{1}\). For simplicity, that nail plate thickness is here considered constant at all times and equal to the measurable, known thickness of the visible edge of the nail plate. This is accordingly noted as \(h_{\ell} \equiv h_{L}\), thus leading to the condition

$$ h\big\vert _{{\scriptstyle t \ge t_{0}\atop\scriptstyle x_{1} \ge \ell}} = h_{0} ( \ell ) = h_{\ell} \equiv h_{L}, $$
(4.2a)

where the role of the function \(h_{0}(x_{1})\) is explained in (4.2b) below.

Due to the germinal activity of the nail matrix, the thickness of the living part of the specimen is considered not known at \(t > t_{0}\). However, the upper boundary curve of the living nail part depicted in Fig. 2 and, hence, its time dependent thickness, is considered obeying an initial condition of the form

$$ h\big\vert _{{\scriptstyle t = t_{0} \atop\scriptstyle x_{1} \le \ell}} = h_{0} ( x_{1} ) , $$
(4.2b)

where \(h_{0}(x_{1})\) is a known smooth function of \(x_{1}\). If, for instance, \(h_{0}(x_{1})\) is assumed to be a constant function, then (4.2a) implies that \(h_{0} \equiv h_{\ell} \equiv h_{L}\). Otherwise, \(h_{0}(x_{1})\) may be selected in a manner that fits conveniently different sorts of initial cross-sectional nail plate features, such as those depicted in Fig. 1.

It is essentially considered that living tissue dies instantly, as soon as the mass-growth pressures and tractions built up in the matrix force it to cross the tissue transitional plane (4.1). Soft living tissue is thus assumed to harden on that plane, beyond which it is naturally incorporated into the hard keratinous tissue of the relatively inflexible nail plate. This is only a plausible simplification of the actual tissue hardening mechanism, which is not entirely understood; as neither is completely understood the manner in which the matrix and the nail plate are bonded along the narrow transitional zone represented by the plane (4.1).

In summary, the physical boundaries of the otherwise continuous nail apparatus specimen (Fig. 2) consist of (i) the depicted (left) edge of the proximal nail matrix at \(x_{1} = 0\) (\(0 \leq x_{2} \leq h\), \(-b \leq x_{3} \leq b\)); (ii) a fictitious interface at \(x_{2} = 0\) with \(x_{1} \leq \ell\) (\(-b \leq x_{3} \leq b\)), which distinguishes the depicted upper part of the proximal matrix from its lower part, to which is identical in nature and, hence, perfectly bonded; (iii) a real material interface at \(x_{2} = 0\) with \(x_{1} \ge \ell\) \((-b \leq x_{3} \leq b)\), which separates the nail plate form the distal matrix and the nail bed; (iv) the lateral nail folds at \(x_{3} = \pm b\) (\(0 \leq x_{1} \leq L\), \(0 \leq x_{2} \leq h\)), and (v) the proximal nail fold (at \(x_{2} = h\) if \(0 \leq x_{1} \leq \ell\), or \(x_{2} = h_{\ell}\) if \(x_{1} \geq \ell\)) which ends at the cuticle; see also Fig. 1.

4.4 Simplified Material and Mass-Growth Considerations

It is generally accepted that the layered nail plate is made through mass contributions of the proximal matrix, the distal matrix and the nail bed [6]. Whether the proximal and the distal matrix produce tissue of the same or different nature and constitution seems unclear, but the proximal matrix and its neighbourhood are perceived as heavier producers than their distal matrix counterpart. Beyond the distal matrix region, the dermal and epidermal parts of the nail bed seem to contribute at rather small, if not minimal rates through the standard cell production and differentiation observed in all parts of the skin and its epidermis.

Apart from the fact that the nail plate grows along a preferred direction, the nail apparatus does not seem to provide evidence of considerable anisotropic material behaviour. Combined with the previously outlined considerations, these observations allow someone to approximately perceive the living part of healthy nail tissue a macroscopically homogeneous, linearly elastic isotropic material which, however, may grow in some non-uniform manner. The rate of mass-growth, \(r_{g}\), seems thus certainly dependent on \(x_{1}\) and, possibly, on time. However, there is no evidence that the mass-growth rate depends substantially on the \(x_{3}\) co-ordinate parameter. Moreover, due to the small thickness of the plate, one may ignore possible non-uniform act of \(r_{g}\) in the \(x_{2}\) direction and, hence, claim that a choice of the form

$$ r_{g} = r_{g}(x_{1},t), $$
(4.3)

serves with reasonable accuracy the purposes of the present application.

Because the dead part of the nail tissue is a natural continuation of its living counterpart, its material may be considered also elastic, homogeneous and approximately isotropic. However, its considerable hardness suggests that the value of the associated Young’s modulus should be much higher than that of its neighbouring living part. That hardness difference between the two parts of the nail apparatus is exploited next to the limit, where the dead part of the nail is approximately perceived a rigid body that remains elastically unaffected from the pressures and tractions that develop within its living and growing counterpart.

4.5 Symmetry and Boundary Conditions

A combination of the symmetries of the adopted plate geometry with the potential deformation caused by a mass-growth rule of the form (4.3) suggests that \(u_{1}\) should be even while \(u_{3}\) odd in \(x_{3}\); namely,

$$ u_{1} ( x_{1},x_{2}, - x_{3} ) = u_{1} ( x_{1},x_{2},x_{3} ),\qquad u_{3} ( x_{1},x_{2}, - x_{3} ) = - u_{3} ( x_{1},x_{2},x_{3} ). $$
(4.4)

Moreover, the implied growth mechanism does not produce shear in the \(x_{3}\) direction and, hence, the identities

$$ e_{13} = e_{23} = 0, $$
(4.5)

hold necessarily throughout the matrix soft tissue at all times.

When combined with the small thickness of the nail apparatus specimen and the implied isotropy of the matrix material, (4.5) underpin the consideration that the nail tissue is essentially guided on and by the lateral nail folds. By postulating that movement of the nail tissue is accordingly prohibited across its lateral fold boundaries, one is led to employ the displacement boundary conditions

$$ u_{3}\vert _{x_{3} = \pm b/2} = 0. $$
(4.6)

In a similar manner, the rigid body role of the nail plate (\(x_{1} \geq \ell\)) prevents longitudinal expansion of the matrix across the tissue transitional plane (4.1) until the aforementioned critical stress state is reached, at some critical time instance \(t = t^{\mathit{cr}} > t_{0}\). This consideration leads then to the displacement boundary condition

$$ u_{1}\big\vert _{{\scriptstyle x_{1} = \ell\atop\scriptstyle t < t^{\mathit{cr}}}} = 0. $$
(4.7)

However, apart from the fact that (4.2a)–(4.2b) necessitate imposition of the “corner” displacement condition

$$ u_{2}\big\vert _{{\scriptstyle x_{1} = \ell \atop\scriptstyle x_{2} = h_{\ell}}} = 0, $$
(4.8)

the unknown manner in which the matrix tissue operates on the transition plane (4.1) implies that precise specification of further boundary conditions on \(x_{1} = \ell\) can only be a matter of speculation. In the same context, boundary conditions that may apply either at the bottom (\(x_{2} = 0\)) and the top (\(x_{2} = h\)) flat boundaries, or at the matrix left edge (\(x_{1} = 0\)) of the specimen (Fig. 2) cannot be specified precisely.

Simplicity allows thus someone to refrain from specifying precisely the remaining sets of boundary conditions. These are instead perceived as requiring from the matrix boundaries to support the deformation in a manner that is specified, a-posteriori, through a potential solution of the previously outlined governing equations. This, essentially semi-inverse solution method is not uncommon in solving fundamental, difficult finite elasticity problems (e.g., [1–3, 13–17]). It is thus employed in the present situation, and is demonstrated in Sect. 5 with an example application, although it is also emphasised that difficulty here is due to lack of accurate experimental information, rather than to inability of solving a relevant boundary value problem.

4.6 The Nail-Elongation Criterion

Attention is now turned to the postulate that nail-elongation at small length scale is triggered at a critical time instant \(t^{\mathit{cr}} > t_{0}\), when the relevant critical stress overpowers all frictional mechanisms that oppose the matrix expansion along the positive \(x_{1}\)-direction. It is accordingly anticipated that some measure, \(\boldsymbol{\sigma}^{\mathit{cr}}\), of that critical stress level can be determined or calculated with use of mechanics rules and principles, or experimental measurements which are independent of and, therefore, not immediately relevant with the matrix growth process.

Because the principal dimensions of the nail folds, and those of the nail matrix remain intact at all times, \(\boldsymbol{\sigma}^{\textit{cr}}\) should necessarily be negated by the stress level developing within the matrix towards the tissue transitional plane (4.1). When fully developed at \(t = t^{\mathit{cr}}\), such a critical stress state should dismiss/invalidate the boundary condition (4.7) and, by triggering a “push forward” move of the dead nail plate tissue, enable the matrix germinal tissue to relax and return back to its dimensions and stress state encountered at \(t = t_{0}\).

Potential availability of \(\boldsymbol{\sigma}^{\mathit{cr}}\) implies then that the following condition holds true at all times on the tissue transitional plane (4.1):

$$ \int_{ - b}^{b} \int_{0}^{h_{\ell}} \bigl( \sigma_{11} - \sigma_{11}^{\mathit{cr}} \bigr)\big\vert _{{\scriptstyle x_{1} = \ell\atop\scriptstyle t \leq t^{\mathit{cr}}}} dx_{2}dx_{3} \le 0. $$
(4.9)

If necessary, this condition may alternatively be expressed as follows:

$$ \int_{ - b}^{b} \int_{0}^{h_{\ell}} \sigma_{11}\big\vert _{{\scriptstyle x_{1} = \ell \atop\scriptstyle t \leq t^{\mathit{cr}}}} dx_{2}dx_{3} \le f_{1}^{\mathit{cr}}, $$
(4.10)

where \(f_{1}^{\mathit{cr}}\) is perceived as the resultant longitudinal force due to reaction tractions and friction mechanisms that oppose the movement of the nail plate in the positive \(x_{1}\)-direction.

It is emphasised that (4.9) or, equivalently (4.10), holds in the form of an equation only at \(t = t^{\mathop{cr}}\), at which instant of time it necessarily replaces the boundary condition (4.7). With (4.7) been thus dropped at \(t = t^{\mathit{cr}}\), the matrix tissue is enabled to release the elastic energy stored during mass-growth and, through an essentially spring-back type of action, to bounce/elongate into a new equilibrium state.

The part of the nail matrix that crosses the tissue transition plane (4.1) is associated with the non-zero value that the displacement components \(u_{1}\) attains at \(t = t^{\mathit{cr}}\) on that plane, and is considered as instantly dying at \(t^{\mathit{cr}}\). That part of the nail is thus incorporated into the hard nail plate, and enables it to elongate. As a result, the matrix stress state and size “relax” and return to their initial levels measured at \(t_{0}\).

Validity of (4.9) or, equivalently, (4.10) in the form of an equation becomes thus the nail elongation criterion. The implied elongation of the nail plate is the matrix longitudinal displacement, \(u_{1}\), calculated at, and averaged over the tissue transitional plane (4.1), at \(t^{\mathit{cr}}\). The total nail length increases at \(t^{\mathit{cr}}\) and becomes

$$ \hat{L} = L + \frac{1}{2bh_{\ell}} \int_{ - b}^{b} \int_{0}^{h_{\ell}} u_{1}\big\vert _{{\scriptstyle x_{1} = \ell\atop\scriptstyle t = t^{\mathit{cr}}}} dx_{2}dx_{3}, $$
(4.11)

while the described elongation process is set to repeat itself indefinitely, in an essentially periodical manner, after \(L\) and \(t^{\mathit{cr}}\) are replaced by \(\hat{L}\) and \(t_{0}\), respectively.

The outlined concept of periodically accumulated small elastic strain and the associated nail-elongation process imply that the nail matrix can be considered unstressed and un-deformed in its initial configuration. This consideration imposes thus naturally the initial conditions

$$ \boldsymbol{\sigma} \vert _{t = t_{0}} = \boldsymbol{u}\vert _{t = t_{0}} = \boldsymbol{0}. $$
(4.12)

The notation employed in (4.7) and (4.9) implies that \(u_{1}\) is expected to suffer a kind of spatial jump discontinuity at \(t^{\mathit{cr}}\). However, uniqueness of linear elasticity solutions suggests that the presented analysis is unable to predict another displacement field \(\hat{\boldsymbol{u}} \ne \boldsymbol{u}\vert _{t = t^{\mathit{cr}}} \), which matches exactly the stress field that satisfies (4.9) in the form of an equation while violates the alternative boundary condition (4.7). A search for the implied spring-back displacement field within the region of applicability of the theory of linear elasticity should accordingly involve additional considerations that include some concept of approximation. The example application discussed in the subsequent section clarifies further this issue.

5 Example Application of Incompressible Nail Growth

For an application, the proposed nail growth model requires a choice of the mass-growth rate that (i) enables the nail matrix to increase in volume; (ii) considers that mass-growth is more dominant at the beginning of and within the proximal matrix while (iii) declines towards and beyond the end of the distal matrix; and (iv) underpins the postulate that mass-growth strain stays infinitesimally small at all times. These requirements are fulfilled by the choice

$$ r_{g} = g ( 1 - x_{1}/\hat{m} ) ( t_{0}/t ),\quad g \ll \rho_{0}/t_{0},\ \hat{m} > \ell, $$
(5.1)

which decreases longitudinally and considers that \(g\) is a known, reasonably small positive constant.

If \(\hat{m} \leq L\), then this parameter may be perceived as a characteristic longitudinal length beyond which the mass-growth activity of the nail bed is negligible. However, values of \(\hat{m} > L\) are also admissible and, in this context, \(\hat{m}= \infty\) corresponds to a mass-growth rate that is independent of the spatial co-ordinate parameters. The choice of a value for \(\hat{m}\) may be considered a matter of future experimental evidence, but a manner in which \(\hat{m}\) can be determined analytically or numerically is also be revealed in what follows.

The form (5.1) of \(r_{g}\) is inversely proportional to and, hence, decreasing in time but enables the volumetric strain (3.3) to continually increase at logarithmic small time scale. The matrix volume is thus set to increase in time and enable the gradually increasing stress level to reach the expected critical stress level, \(\boldsymbol{\sigma}^{\mathit{cr}}\), at some finite time, \(t^{\mathit{cr}}\).

5.1 Incompressible Mass-Growth of the Nail Matrix

In the case of incompressible mass-growth, where \(\rho = \rho_{0}\) at all times, association of (5.1) with (3.6) yields

$$ u_{k,k} = \frac{gt_{0}}{\rho_{0}} ( 1 - x_{1}/\hat{m} )\ln (t/t_{0}), $$
(5.2)

while its combination with (3.10) reveals that determination of the displacement components requires solution of the three uncoupled differential equations

$$ u_{1,jj} = \frac{ ( 1 + \lambda /\mu )gt_{0}}{\rho_{0}\hat{m}}\ln (t/t_{0}), \qquad u_{2,jj} = u_{3,jj} = 0. $$
(5.3)

The form (5.2) of the volumetric strain reveals that solutions to (5.3) may be sought in the form of simple, low degree polynomials of the co-ordinate parameters. Moreover, (4.4b) and (4.5) require from \(u_{3}\) to be odd in \(x_{3}\) and to cause no out of plane shear deformation. These requirements are met only if a trial solution of (5.3c) has the form \(u_{3} = cx_{3}\), where \(c(t)\) is to be determined. However, the boundary condition (4.6) returns \(c = 0\) and, because this result leads to

$$ u_{3} = 0, $$
(5.4)

the problem in hand reduces to one of plane strain. It follows that \(u_{1}\) and \(u_{2}\) are necessarily functions of \(x_{1}\) and \(x_{2}\) only and, as a result, indices in (5.2) and (5.3a, b) may take the values 1 and 2 only.

Inspection of the right hand sides of (5.2) and (5.3) suggests next that the simple polynomial solutions sought need not be more complicated than

$$ \begin{aligned}[c] &u_{1} = a_{1}x_{1}^{2} + b_{1}x_{2}^{2} + c_{1}x_{1}x_{2} + d_{1}x_{1} + e_{1}x_{2}, \\ &u_{2} = c_{2}x_{1}x_{2} + d_{2}x_{1} + e_{2}x_{2}, \end{aligned} $$
(5.5)

where the appearing coefficients may depend only on time. During the pre-critical stage of matrix growth, (5.5a) should also satisfy the boundary condition (4.7), which is replaced by the equation form of (4.9) at \(t = t^{\mathit{cr}}\).

5.2 The Pre-critical Stage of Matrix Mass-Growth: \(t< t^{\mathit{cr}}\)

Introduction of (5.5) into (5.2) and (5.3a, b), as well as into the boundary condition (4.7) and the corner condition (4.8), yields the following intermediate results

$$\begin{aligned} &\begin{aligned}[c] &b_{1} = c_{1} = e_{1} = 0,\qquad a_{1} = \frac{ ( 1 + \lambda /\mu )gt_{0}}{2\rho_{0}\hat{m}}\ln (t/t_{0}),\qquad d_{1} = - a_{1}\ell, \\ &c_{2} = - 2a_{1} - \frac{gt_{0}}{\rho_{0}\hat{m}}\ln (t/t_{0}), \qquad e_{2} = - a_{1}\ell + \frac{gt_{0}}{\rho_{0}\hat{m}}\ln (t/t_{0}), \\ &d_{2} = - h_{\ell} ( c_{2} + e_{2}/\ell ), \end{aligned} \end{aligned}$$
(5.6)

use of which determines the non-zero displacement components as follows:

$$\begin{aligned} &\begin{aligned}[c] & u_{1} = \frac{ ( 1 + \lambda /\mu )gt_{0}}{2\rho_{0}\hat{m}}x_{1} ( x_{1} - \ell )\ln (t/t_{0}), \\ & \begin{aligned}[t] u_{2}& = \frac{gt_{0}}{2\rho_{0}\hat{m}} \biggl\{ - 2 \biggl( 2 + \frac{\lambda}{ \mu} \biggr)x_{1}x_{2} + \biggl( 3 - 2 \frac{\hat{m}}{\ell} + \frac{\lambda}{ \mu} \biggr)h_{\ell} x_{1} \\ &\quad {}+ \biggl( 1 + 2\frac{\hat{m}}{\ell} + \frac{\lambda}{\mu} \biggr)\ell x_{2} \biggr\} \ln (t/t_{0}). \end{aligned} \end{aligned} \end{aligned}$$
(5.7)

It is observed that, because

$$ u_{2}\vert _{x_{2} = 0} = \frac{gt_{0}}{2\rho_{0}\hat{m}} \biggl( 3 - 2\frac{\hat{m}}{\ell} + \frac{\lambda}{\mu} \biggr)h_{\ell} x_{1} \ln (t/t_{0}), $$
(5.8)

the nail matrix exerts its active mass-growth role by rising its bottom boundary if \(\hat{m}/\ell < ( 3 + \lambda /\mu )/2\), or forcing it to fall if \(\hat{m}/\ell > ( 3 + \lambda /\mu )/2\). That part of the specimen boundary remains thus intact through time only if \(\hat{m}/\ell = ( 3 + \lambda /\mu )/2 = 3K/2 \mu\), where \(K\) is the bulk modulus of the nail matrix material.

Some of the formulas that emerge in what follows obtain relatively simpler forms if the initial thickness of the nail matrix (Fig. 2) is assumed constant. In that case, in which \(h_{0} ( x_{1} ) \equiv h_{\ell}\) in (4.2b), the thickness of the growing, living part of the nail apparatus specimen is given as follows:

$$ h ( x_{1},t ) = h_{\ell} + u_{2}\vert _{x_{2} = h_{\ell}} = h_{\ell} \biggl\{ 1 + \frac{gt_{0}\ell}{2\rho_{0}\hat{m}} \biggl( 1 + 2\frac{\hat{m}}{\ell} + \frac{\lambda}{\mu} \biggr) ( 1 - x_{1}/\ell )\ln (t/t_{0}) \biggr\} . $$
(5.9)

In accordance with physical expectation, this is increasing with time, regardless of the direction that the bottom boundary of the matrix is forced to move. Thus the predicted, linearly decreasing longitudinal profile of the matrix thickness enables the corner condition (4.8) and, subsequently, (4.2a) to be satisfied at all times.

Combination of the displacement field (5.7) and Hooke’s law (3.8) yields next the non-zero stress components as follows:

$$ \begin{aligned}[c] &\sigma_{11} = \frac{gt_{0}\ell}{\rho_{0}\hat{m}} \biggl\{ \lambda \biggl( \frac{\hat{m}}{\ell} - 1 \biggr) + ( \lambda + 2\mu )\frac{x_{1}}{\ell} - \mu \biggr\} \ln (t/t_{0}), \\ &\sigma_{12} = \frac{gt_{0}}{\rho_{0}\hat{m}} \biggl\{ \biggl[ \lambda + \biggl( 3 - 2\frac{\hat{m}}{\ell} \biggr)\mu \biggr]\frac{h_{\ell}}{2} - ( \lambda + 2\mu )x_{2} \biggr\} \ln (t/t_{0}), \\ &\sigma_{22} = \frac{gt_{0}}{\rho_{0}} \biggl\{ ( \lambda + 2\mu ) + ( \lambda + \mu )\frac{\ell}{\hat{m}} - ( 3\lambda + 4\mu )\frac{x_{1}}{\hat{m}} \biggr\} \ln (t/t_{0}), \\ &\sigma_{33} = \frac{gt_{0}}{\rho_{0}} \biggl( 1 - \frac{x_{1}}{\hat{m}} \biggr)\ln (t/t_{0}). \end{aligned} $$
(5.10)

It may easily be verified that (5.10) satisfy the equilibrium conditions (2.2). This is evidently due to the fact that the expressions (5.2) and (5.3) obtained with the use of (3.6) and (3.10), respectively, ensure satisfaction of the Navier equations (3.9).

It is thus concluded that completeness and uniqueness of the obtained linear elasticity solution require further that:

  1. (a)

    the part of the digit that lies beyond the left edge boundary of the nail specimen (Fig. 2), namely at \(x_{1} \leq 0\), enables that boundary (\(x_{1} = 0\)) to support the shear stress (5.10b) and the normal stress

    $$ \sigma_{11}\vert _{x_{1} = 0} = \frac{gt_{0}\ell}{ \rho_{0}\hat{m}} \biggl[ \lambda \biggl( \frac{\hat{m}}{\ell} - 1 \biggr) - \mu \biggr]\ln (t/t_{0}); $$
    (5.11a)
  2. (b)

    the part of the proximal matrix that lies underneath the bottom boundary of the specimen (\(x_{2} \leq\) 0) enables that boundary (\(x_{2} = 0\)) to support the normal stress (5.10c) and the shear stress

    $$ \sigma_{12}\vert _{x_{2} = 0} = \frac{gh_{\ell} t_{0}}{2\rho_{0}\hat{m}} \biggl[ \lambda + \biggl( 3 - 2\frac{\hat{m}}{\ell} \biggr)\mu \biggr]\ln (t/t_{0}); $$
    (5.11b)
  3. (c)

    the proximal nail fold (\(x_{2} \geq h_{\ell}\)) enables the matrix top boundary (\(x_{2} = h_{\ell}\)) to support the normal stress (5.10c) and the shear stress

    $$ \sigma_{12}\vert _{x_{2} = h_{\ell}} = - \frac{gh_{\ell} t_{0}}{2\rho_{0}\hat{m}} \biggl[ \lambda + \biggl( 1 + 2\frac{\hat{m}}{\ell} \biggr)\mu \biggr]\ln (t/t_{0}); $$
    (5.11c)
  4. (d)

    combined action of the proximal nail fold (\(x_{2} \geq h_{\ell}\)) and the part of the proximal matrix that lies underneath the bottom boundary of the specimen (\(x_{2} \leq\) 0) balances the resultant shear traction caused by (5.10b) on the matrix right boundary, \(x_{1} = \ell\), where the boundary condition (4.7) is already satisfied;

  5. (e)

    the part of the digit that lies beyond the lateral fold boundaries of the nail specimen \((|x_{3}|\geq b)\) enables that boundary \((|x_{3}|=b)\) to be free of shear traction and to support the normal stress (5.10d).

If/when physically justified, potential modification of any of these boundary conditions, (a)–(e), will convert the mass-growth process considered in this section into a slightly or considerably different linear elasticity boundary value problem. This will need to be solved again and, hence, lead to displacement and stress distributions that necessarily differ from those detailed in (5.7) and (5.10), respectively. However, the principles that underpin the proposed nail elongation mechanism will still remain intact.

It is finally noted that, dependent on the value of the ratio \(\hat{m}/\ell\), \(\sigma_{11}\) may be negative and, therefore, compressive or positive and, therefore, tensile on the left edge of the matrix, \(x_{1} = 0\) (Fig. 2). However, \(\sigma_{11}\) is always positive in the neighbourhood of the tissue transitional plane (\(x_{1} = \ell\)), where it reaches its maximum value

$$ \sigma_{11}\vert _{x_{1} = \ell} = \frac{gt_{0}}{\rho_{0}} ( \lambda + \mu \ell /\hat{m} )\ln (t/t_{0}) > 0. $$
(5.12)

This is thus tensile within the soft living part and, therefore, compressive within the hard dead part of the nail tissue. Moreover, \(\sigma_{11}\) is increasing in time and, hence, is indeed set to reach, at some \(t = t^{\mathit{cr}} > t_{0}\), a value that will trigger nail elongation through satisfaction of (4.9) or, equivalently, (4.10).

5.3 The Critical Stage: \(t= t^{\mathit{cr}}\)

Equation (5.12) predicts that, at every instant of time, \(\sigma_{11}\) is constant throughout the tissue transition plane \(x_{1} = \ell\) and, hence, that either of (4.9) or (4.10) may conveniently obtain the simplified form

$$ \sigma_{11}\big\vert _{{\scriptstyle x_{1} = \ell \atop \scriptstyle t = t^{\mathit{cr}}}} = \sigma_{11}^{\mathit{cr}} = \frac{f_{1}^{\mathit{cr}}}{2bh_{\ell}}. $$
(5.13)

Connection of (5.12) with (5.13) yields then the time that the stress state reaches its critical level as

$$ t^{\mathit{cr}} = t_{0}\exp \biggl\{ \frac{\rho_{0}}{ ( \lambda + \mu \ell /\hat{m} )gt_{0}} \sigma_{11}^{\mathit{cr}} \biggr\} . $$
(5.14)

A subsequent substitution of this value back into (5.10) provides the non-zero stresses developing within the nail matrix at \(t^{\mathit{cr}}\) in terms of the known constant \(\sigma_{11}^{\mathit{cr}}\). These are as follows:

$$ \begin{aligned}[c] &\sigma_{11}\vert _{t = t^{\mathit{cr}}} = \biggl\{ \lambda \biggl( \frac{\hat{m}}{\ell} - 1 \biggr) + ( \lambda + 2\mu ) \frac{x_{1}}{\ell} - \mu \biggr\} \frac{\sigma_{11}^{\mathit{cr}}}{ ( \mu + \lambda \hat{m}/\ell )}, \\ &\sigma_{12}\vert _{t = t^{\mathit{cr}}} = \biggl\{ \biggl[ \lambda + \biggl( 3 - 2\frac{\hat{m}}{\ell} \biggr)\mu \biggr]\frac{h_{\ell}}{2\hat{m}} - ( \lambda + 2\mu )\frac{x_{2}}{\hat{m}} \biggr\} \frac{\sigma_{11}^{\mathit{cr}}}{ ( \lambda + \mu \ell /\hat{m} )}, \\ &\sigma_{22}\vert _{t = t^{\mathit{cr}}} = \biggl\{ ( \lambda + 2 \mu ) + ( \lambda + \mu )\frac{\ell}{\hat{m}} - ( 3\lambda + 4\mu ) \frac{x_{1}}{\hat{m}} \biggr\} \frac{\sigma_{11}^{\mathit{cr}}}{ ( \lambda + \mu \ell /\hat{m} )}, \\ &\sigma_{33}\vert _{t = t^{\mathit{cr}}} = \biggl( 1 - \frac{x_{1}}{\hat{m}} \biggr)\frac{\sigma_{11}^{\mathit{cr}}}{ ( \lambda + \mu \ell /\hat{m} )}. \end{aligned} $$
(5.15)

In a similar context, (5.7) reveals that the non-zero displacement components developing within the nail matrix when \(t\) approaches \(t^{\mathit{cr}}\), approach their limiting distributions

$$ \begin{aligned}[c] &\lim_{t \to t^{\mathit{cr}}}u_{1} = \frac{ ( 1 + \lambda /\mu )\sigma_{11}^{\mathit{cr}}}{2 ( \lambda \hat{m} + \mu \ell )}x_{1} ( x_{1} - \ell ), \\ & \begin{aligned}[t] \lim_{t \to t^{\mathit{cr}}}u_{2} &= \frac{\sigma_{11}^{\mathit{cr}}}{2 ( \lambda \hat{m} + \mu \ell )} \biggl\{ - 2 \biggl( 2 + \frac{\lambda}{\mu} \biggr)x_{1}x_{2} + \biggl( 3 - 2\frac{\hat{m}}{\ell} + \frac{\lambda}{\mu} \biggr)h_{\ell} x_{1} \\ &\quad {}+ \biggl( 1 + 2\frac{\hat{m}}{\ell} + \frac{\lambda}{ \mu} \biggr) \ell x_{2} \biggr\} . \end{aligned} \end{aligned} $$
(5.16)

However, those limiting displacement distributions will never be reached, because at \(t^{c r}\) the nail matrix will bounce into the aforementioned alternative equilibrium state, described by some different displacement field, \(\hat{\boldsymbol{u}}\).

The elastic energy that the nail matrix releases at \(t = t^{\mathit{cr}}\) through that bouncing effect is

$$ U^{\mathit{cr}} = \frac{2b}{\mu} \int_{0}^{\ell} \int_{0}^{h(x_{1})} \biggl[ \sigma_{\alpha \beta} \sigma_{\alpha \beta} - \frac{\lambda}{3\lambda + 2\mu} ( \sigma_{\gamma \gamma} )^{2} \biggr]_{t = t^{\mathit{cr}}} dx_{2}dx_{1} = \bigl( \sigma_{11}^{\mathit{cr}} \bigr)^{2}2b\bar{U}^{\mathit{cr}} ( \lambda,\mu,h_{\ell},\ell,\hat{m} ), $$
(5.17)

where Greek indices take the values 1 and 2 only, and \(h(x_{1})\) is evaluated by using (5.9) at \(t = t^{\mathit{cr}}\). It is noted that, because the critical stresses are proportional to \(\sigma_{11}^{\mathit{cr}}\), \(U^{\mathit{cr}}\) is proportional to \((\sigma_{11}^{\mathit{cr}})^{2}\) and, hence, \(\bar{U}^{\mathit{cr}} ( \lambda,\mu,h_{\ell},\ell,\hat{m} )\) is independent of \(\sigma_{11}^{\mathit{cr}}\). With use of the critical stress distributions (5.15), the form of \(\bar{U}^{\mathit{cr}} ( \lambda,\mu,h_{\ell},\ell,\hat{m} )\) may be found analytically, or its value can be determined numerically for given values of the appearing arguments. The form or value of the function \(\bar{U}^{\mathit{cr}} ( \lambda,\mu,h_{\ell},\ell,\hat{m} )\) is thus considered known in what follows.

5.4 Spring-Back Type of Nail Elongation

It is assumed that the anticipated spring-back action of the nail matrix takes place instantly at \(t^{c r}\); namely in a static manner, and without further interference of, or resistance from the hard nail plate. The nail matrix is thus temporarily perceived as an independent, strained and stressed elastic plate of length \(\ell\) which, by bouncing instantly into a new, unstrained and unstressed equilibrium state, increases its length and makes its thickness equal to that of its hard tissue counterpart; namely \(h_{\ell}\). The constant width of the plate, \(2b\), remains unchanged due to the prevailing plane strain conditions.

In a corresponding static equilibrium situation (\(t = t_{0}\)), an initially unstressed and unstrained elastic rectangular plate that possesses the same geometric and material properties with those of the undeformed nail matrix can undergo an equivalent, mechanically caused spring-back jump if, after (i) its \(x_{1} = 0\) edge is restrained against translation and (ii) its \(x_{1} = \ell\) edge is subjected to a uniform compression, \(- \sigma_{11}^{\mathit{cr}}\), that (iii) enables its stored energy to match the \(U^{\mathit{cr}}\)-level given in (5.17), (iv) it is allowed to bounce elastically back to its initial position through removal of the externally applied compression.

The relatively simple, exact elasticity solution to this reverse, linear elasticity plane strain problem is outlined in the Appendix with use of standard Airy stress function techniques (e.g., [18]). This shows that the bouncing type of displacements sought are averaged equivalents of

$$ \begin{aligned}[c] &u_{1}\vert _{t = t^{\mathit{cr}}} = \frac{\sigma_{11}^{\mathit{cr}}}{4\mu ( \lambda + \mu )} \bigl[ ( \lambda + 2\mu )x_{1} - \lambda h_{\ell} x_{2}/\ell \bigr], \\ &u_{2}\vert _{t = t^{\mathit{cr}}} = - \frac{\sigma_{11}^{\mathit{cr}}\lambda}{4\mu ( \lambda + \mu )} ( x_{2} - h_{\ell} x_{1}/\ell ), \end{aligned} $$
(5.18)

provided that their reverse counterparts (A.6) store into the plate a total of strain energy that equals \(U^{\mathit{cr}}\).

The elasticity solution obtained in the Appendix reveals that the strain energy associated with the displacement field (5.17) is

$$ U^{\mathit{cr}} = 2b\ell h_{\ell} \frac{ ( 1 + \lambda /\mu )}{2 + 3\lambda /\mu} \bigl( \sigma_{11}^{\mathit{cr}} \bigr)^{2}. $$
(5.19)

When compared with (5.17), this yields

$$ \bar{U}^{\mathit{cr}} ( \lambda,\mu,h_{\ell},\ell,\hat{m} ) = 2\ell h_{\ell} \frac{ ( 1 + \lambda /\mu )}{2 + 3\lambda /\mu}, $$
(5.20)

which can be perceived as a non-linear algebraic equation for the essentially unknown parameter \(\hat{m}\).

It is emphasised that the value of \(\hat{m}\) obtained by solving (5.20) depends on the elastic moduli and the geometric features of the living part of the nail tissue only. It is independent of, and, hence, irrelevant to the external frictions that caused \(\sigma_{11}^{\mathit{cr}}\).

By releasing an amount of energy equal to that stored previously into the grown nail matrix, the displacement field (5.18) brings the nail matrix into the unstressed and unstrained state described at the beginning of the Appendix. Combination of (5.18a) and (4.11) yields thus the nail elongation as follows:

$$ \hat{L} = L + \frac{\sigma_{11}^{\mathit{cr}}}{4\mu ( \lambda + \mu )} \bigl[ ( \lambda + 2\mu )\ell - \lambda h_{\ell}^{2}/2\ell \bigr]. $$
(5.21)

It is noted in passing that an estimate of the thickness reached at \(t = t^{\mathit{cr}}\) by the matrix part of the specimen depicted in Fig. 2 may similarly be obtained as follows:

$$ h^{\mathit{cr}} ( x_{1} ) = h_{\ell} + u_{2} \big\vert _{{\scriptstyle t = t^{\mathit{cr}}\atop\scriptstyle x_{2} = h_{\ell}}} = h_{\ell} \biggl\{ 1 + \frac{\sigma_{11}^{\mathit{cr}}\lambda}{4\mu ( \lambda + \mu )} ( 1 - x_{1}/\ell ) \biggr\} . $$
(5.22)

This approximate form of the critical thickness of the matrix may be used in this particular application for an estimate of the value of \(\hat{m}\) in an alternative manner. Instead of employing the previously described strain energy matching, someone could accordingly attempt to match the critical thickness (5.22) with the limiting expression obtained through (5.9) when \(t\) approaches \(t^{\mathit{cr}}\).

Such a matching, which is here possible because both (5.9) and (5.22) vary linearly in \(x_{1}\), yields

$$ \frac{\hat{m}}{\ell} = \frac{ ( \lambda + \mu )^{2} + \lambda \mu}{\lambda^{2} - 4\mu ( \lambda + \mu )}, $$
(5.23)

which, unlike its alternative estimate obtained by solving (5.20), may return a value of \(\hat{m}\) which does not depend on \(h_{\ell}\). It is thus seen that, for positive values of \(\lambda\) and \(\mu\) that satisfy

$$ \lambda > 2\mu ( 1 + \sqrt{2} )\quad \Leftrightarrow \quad \nu > \frac{1 + \sqrt{2}}{3 + 2\sqrt{2}} \cong 0.414, $$
(5.24)

(5.23) predicts that the ratio \(\hat{m}/\ell\) is greater than 1 and, by virtue of (5.1), it thus ensures that new mass is added within the nail matrix at all locations; here, \(\nu\) represents Poisson’s the ratio of the proliferating material of the nail matrix.

However, the noted convenient matching of (5.9) and (5.22) will not be necessarily present in more complicated nail mass-growth applications, where derivation of a simple formula like (5.23) may thus be not possible. In contrast, the energy release approach that leads to the algebraic Eq. (5.20) is likely to work successfully always and, either analytically or numerically, to provide some admissible value for \(\hat{m}\).

6 Conclusions

The complete analytical solution of the relatively simple example application detailed in the preceding section demonstrates that the present model enables interpretation of nail mass-growth and elongation in a mathematically reliable and physically sound manner. More advanced features of the mass-growth model itself and/or of the nail apparatus can accordingly be considered and handled mathematically in a similar manner, probably at the expense of some of the demonstrated analytical convenience.

The fact, for instance, that the nail supports and boundaries play a dictating role in the shape formation and growth of the nail apparatus (e.g., [6]), by appropriately absorbing and regulating all reaction pressures and tractions that develop in their neighbourhood, needs to be explored further both analytically and experimentally. It is recognised in this context that, at present, there is lack of experimental information and understanding regarding the precise manner in which those boundaries act, or react during mass-growth of the nail matrix.

On the other hand, the fact that the transitional tissue plane or zone is in general not perpendicular to the nail bed could also be seen as an advanced relevant feature that needs to be incorporated into a refined nail apparatus model. Moreover, the shape of the lunula (see Fig. 1) reveals that the end of the distal matrix is marked by a curved rather than a straight line and, hence, that the transitional plane concept employed is essentially a simplification. This feature may thus improve and become more pragmatic, if replaced by the advanced concept of some non-vertical transitional surface or a narrow transitional band. In the same context, resemblance of the nail geometrical features with those of a flat plate (Fig. 2) is also an approximation. This can be refined, by appropriately incorporating into the model the curved, shell-type features observed in an actual human nail plate.

Referring to the simplifications introduced on the material side of the model, some reconsideration and/or refinement of the longitudinally linear variation of the growth rate (5.1) might be desirable, though the current lack of relevant experimental information does not assist more pragmatic developments in that direction. The assimilation of the hard nail tissue constitution with that of a rigid plate can also be refined and replaced with the behaviour of an elastic plate that is much harder than its soft, living tissue counterpart.

These as well as additional potential refinements will, however, increase the mathematical complexity of the nail model presented in Sect. 4 and, hence, necessitate use of mathematical techniques that are considerably more advanced to those employed in the relatively simple application detailed in Sect. 5. In a similar context, consideration of the slight/moderate compressibility mass-growth features implied in the general model (Sect. 4) but not considered in the subsequent application (Sect. 5) is regarded as a straightforward application of the relevant analysis outlined previously in Sect. 3. These observations suggest that further examination and study of the advantages and/or limitations of the proportionality relationship (3.1) are also desirable, as validity of (3.1) underpins the applicability of linear elasticity concepts in mass-growth mechanics.

Finally, the relative simplicity of the outlined mass-growth analysis at small strain can serve as a compass towards mathematical modelling and treatment of mass-growth processes associated with large strain/deformation considerations; namely, mass-growth processes that need to make use of the lengthy, and more general constitutive equations derived in [1–3]. This study is accordingly introductory to a subject of small-strain mass-growth elasticity that relates to its large strain/deformation counterpart [1] in a manner analogous to the well-known connection of the conventional theories of linear elasticity and hyperelasticity.

In this context, mention is made again to the relevant semi-inverse mathematical methods employed already in the relevant literature, including [13–17]. Nevertheless, the asymptotic relationship that systematic development of second [19] and higher-order elasticity theories [20] establish between solutions of corresponding linear and non-linear elasticity boundary value problems should also be mentioned. Development of similar connections and relationships may be also possible in, and relevant to corresponding mass-growth processes that take place under small and large strain, despite the fact that the last term encountered in several versions of the present constitutive equations, namely (2.4), (2.11) or (3.7), might require some kind of special attention and treatment.