Skip to main content
SpringerLink
Log in

Asymptotic Analysis of a Linear Isotropic Elastic Composite Reinforced by a Thin Layer of Periodically Distributed Isotropic Parallel Stiff Fibres

  • Published:
Journal of Elasticity Aims and scope Submit manuscript

Abstract

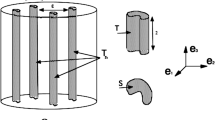
We present some mathematical convergence results using a two-scale method for a linear elastic isotropic medium containing one layer of parallel periodically distributed heterogeneities located in the interior of the whole domain around a plane surface Σ. The aim of this paper is to study the situation when the rigidity of the linearly isotropic elastic fibres is 1/ε m the rigidity of the surrounding linearly isotropic elastic material. We use a two-scale convergence method adapted to the geometry of the problem (layer of fibres). In the models obtained Σ behaves for m=1 as a “material surface” without membrane energy in the direction of the plane orthogonal to the direction of the fibres. For m=3 the “material surface” has no bending energy in the direction orthogonal to the fibres.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1

Similar content being viewed by others

Notes

  1. We thank an anonymous referee for his/her suggestions who permitted to notably simplify the original proof.

References

  1. Abdelmoula, R., Marigo, J.J.: The effective behavior of a fiber bridged crack. J. Mech. Phys. Solids 48, 2419–2444 (2000)

    Article  ADS  MATH  MathSciNet  Google Scholar 

  2. Allaire, G.: Homogenization and two-scale convergence. SIAM J. Math. Anal. 23, 1482–1518 (1992)

    Article  MATH  MathSciNet  Google Scholar 

  3. Arbogast, T., Douglas, J., Hornung, U.: Derivation of the double porosity model of single phase flow via homogenization theory. SIAM J. Math. Anal. 21, 823–836 (1990)

    Article  MATH  MathSciNet  Google Scholar 

  4. Bellieud, M.: Torsion effects in elastic composites with high contrast. SIAM J. Math. Anal. 41, 2514–2553 (2010)

    Article  MATH  MathSciNet  Google Scholar 

  5. Bellieud, M.: A notion of capacity related to elasticity. Applications to homogenization. Arch. Ration. Mech. Anal. 203, 137–187 (2012)

    Article  MATH  MathSciNet  Google Scholar 

  6. Bellieud, M.: Problèmes capacitaires en viscoplasticité avec effets de torsion. C. R. Math. Acad. Sci. Paris, Sér. I 351, 241–245 (2013)

    Article  MATH  MathSciNet  Google Scholar 

  7. Bellieud, M., Bouchitté, G.: Homogenization of a soft elastic material reinforced by fibres. Asymptot. Anal. 32, 153–183 (2002)

    MATH  MathSciNet  Google Scholar 

  8. Bellieud, M., Gruais, I.: Homogenization of an elastic material reinforced by very stiff or heavy fibers. Non local effects. Memory effects. J. Math. Pures Appl. 84, 55–96 (2005)

    Article  MATH  MathSciNet  Google Scholar 

  9. Bensoussan, A., Lions, J.-L., Papanicolaou, G.: Asymptotic Analysis for Periodic Structures. AMS Chelsea Publishing, Providence (2011). Corrected reprint of the 1978 original

    MATH  Google Scholar 

  10. Bessoud, A.L., Krasucki, F., Serpilli, M.: Plate-like and shell-like inclusions with high rigidity. C. R. Math. Acad. Sci. Paris, Sér. I 346, 697–702 (2008)

    Article  MATH  MathSciNet  Google Scholar 

  11. Bessoud, A.L., Krasucki, F., Michaille, G.: Multi-materials with strong interface: variational modelings. Asymptot. Anal. 61, 1–19 (2009)

    MATH  MathSciNet  Google Scholar 

  12. Bessoud, A.L., Krasucki, F., Serpilli, M.: Asymptotic analysis of shell-like inclusions with high rigidity. J. Elast. 103, 153–172 (2011)

    Article  MATH  MathSciNet  Google Scholar 

  13. Bouchitté, G., Fragalà, I.: Homogenization of thin structures by two-scale method with respect to measures. SIAM J. Math. Anal. 32, 1198–1226 (2001)

    Article  MATH  MathSciNet  Google Scholar 

  14. Cherednichenko, K.B., Cherdantsev, M.: Two-scale Γ-convergence of integral functionals and its application to homogenisation of nonlinear high-contrast periodic composites. Arch. Ration. Mech. Anal. 204, 445–478 (2012)

    Article  MATH  MathSciNet  Google Scholar 

  15. Cioranescu, D., Donato, P.: An Introduction to Homogenization. Oxford Lecture Series in Mathematics and Its Applications, vol. 17. Oxford University Press, New York (1999)

    MATH  Google Scholar 

  16. Cioranescu, D., Damlamian, A., Griso, G.: The periodic unfolding method in homogenization. SIAM J. Math. Anal. 40, 1585–1620 (2008)

    Article  MATH  MathSciNet  Google Scholar 

  17. Geymonat, G., Krasucki, F., Marigo, J.J.: Stress distribution in anisotropic elastic composite beams. In: Ciarlet, P.G., Sanchez-Palencia, E. (eds.) Applications of Multiple Scaling in Mechanics, pp. 118–133. Masson, Paris (1987)

    Google Scholar 

  18. Geymonat, G., Krasucki, F., Lenci, S.: Bonded joint with a soft thin adhesive. Math. Mech. Solids 4, 201–225 (1999)

    Article  MathSciNet  Google Scholar 

  19. Grisvard, P.: Singularities in Boundary Values Problems. Masson/Springer, Paris/Berlin (1992)

    Google Scholar 

  20. Krasucki, F., Lenci, S.: Analysis of interfaces of variable stiffness. Int. J. Solids Struct. 37, 3619–3632 (2000)

    Article  MATH  Google Scholar 

  21. Khruslov, E.Y.: Homogenized Models of Composite Media. Birkhäuser, Basel (1991)

    Book  Google Scholar 

  22. Lukkassen, D., Nguetseng, G., Wall, P.: Two-scale convergence. Int. J. Pure Appl. Math. 2, 35–86 (2002)

    MATH  MathSciNet  Google Scholar 

  23. Lukkassen, D., Wall, P.: Two-scale convergence with respect to measures and homogenization of monotone operators. J. Funct. Spaces Appl. 3, 125–161 (2005)

    Article  MATH  MathSciNet  Google Scholar 

  24. Murat, F., Sili, A.: Comportement asymptotique des solutions du système de l’élasticité linéarisée anisotrope hétérogène dans des cylindres minces. C. R. Math. Acad. Sci. Paris, Sér. I 328, 179–184 (1999)

    Article  ADS  MATH  MathSciNet  Google Scholar 

  25. Murat, F., Sili, A.: Effets non locaux dans le passage 3d–1d en élasticité linéarisée anisotrope hétérogène. C. R. Math. Acad. Sci. Paris, Sér. I 330, 745–750 (2000)

    Article  ADS  MATH  MathSciNet  Google Scholar 

  26. Marigo, J.J., Pideri, C.: The effective behavior of elastic bodies containing microcracks or microholes localized on a surface. Int. J. Damage Mech. 20, 1130–1150 (2011)

    Article  Google Scholar 

  27. Neukamm, S.: Rigorous derivation of a homogenized bending-torsion theory for inextensible rods from 3d elasticity. Arch. Ration. Mech. Anal. 206, 645–706 (2012)

    Article  MATH  MathSciNet  Google Scholar 

  28. Nguetseng, G.: A general convergence result for a functional related to the theory of homogenization. SIAM J. Math. Anal. 20, 608–623 (1989)

    Article  MATH  MathSciNet  Google Scholar 

  29. Nguetseng, G., Sanchez-Palencia, E.: Stress concentration for defects distributed near a surface. In: Ladevèze, P. (ed.) Local Effects in the Analysis of Structures, pp. 55–74. Elsevier, Amsterdam (1986)

    Google Scholar 

  30. Oleinik, O.A., Shamaev, A.S., Yosifian, G.A.: Mathematical Problems in Elasticity and Homogenization. North-Holland Publishing Co., Amsterdam (1992)

    MATH  Google Scholar 

  31. Pideri, C., Seppecher, P.: A second gradient material resulting from the homogenization of an heterogeneous linear elastic medium. Contin. Mech. Thermodyn. 9, 241–257 (1997)

    Article  ADS  MATH  MathSciNet  Google Scholar 

  32. Sanchez Palencia, E.: Non-homogeneous Media and Vibration Theory. Springer, Berlin (1980)

    MATH  Google Scholar 

  33. Stelzig, P.E.: On problems in homogenization and two-scale convergence. Ph.D. thesis, University of Trento, April 2012

  34. Tartar, L.: Cours Peccot, Collège de France (1977), unpublished, partially written in F. Murat, L. Tartar: H-convergence. In: Cherkaevand, L., Kohn, R.V. (eds.) Topics in the Mathematical Modelling of Composite Materials, Progress in Nonlinear Differential Equations and Their Applications, vol. 31, pp. 21–43. Birkhaüser, Boston (1998)

  35. Visintin, A.: Toward a two-scale calculus. ESAIM Control Optim. Calc. Var. 12, 371–397 (2006)

    Article  MATH  MathSciNet  Google Scholar 

  36. Zhikov, V.V.: On an extension and an application of the two-scale convergence method. Mat. Sb. 191(7), 31–72 (2000) (Russian), English translation in Sb. Math. 191(7), 973–1014 (2000)

    Article  MathSciNet  Google Scholar 

Download references

Acknowledgements

The work of G.G. and F.K. has been partially supported by the French Agence Nationale de la Recherche (ANR) under Grant ARAMIS (Project “Blanc”, ANR 12 BS01-0021) (Analysis of Robust Asymptotic Methods In numerical Simulation in mechanics).

Author information

Authors and Affiliations

  1. LMGC (Laboratoire de Mécanique et de Génie Civil de Montpellier) UMR–CNRS 5508, Université Montpellier II, Case courier 048, Place Eugène Bataillon, 34095, Montpellier Cedex 5, France

    Michel Bellieud

  2. Laboratoire de Mécanique des Solides, UMR–CNRS 7649, École Polytechnique, 91128, PALAISEAU Cedex, France

    Giuseppe Geymonat

  3. I3M, UMR–CNRS 5149, Université Montpellier II, Case courier 051, Place Eugène Bataillon, 34095, Montpellier Cedex 5, France

    Françoise Krasucki

Authors
  1. Michel Bellieud
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Giuseppe Geymonat
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Françoise Krasucki
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Françoise Krasucki.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Bellieud, M., Geymonat, G. & Krasucki, F. Asymptotic Analysis of a Linear Isotropic Elastic Composite Reinforced by a Thin Layer of Periodically Distributed Isotropic Parallel Stiff Fibres. J Elast 122, 43–74 (2016). https://doi.org/10.1007/s10659-015-9532-7

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10659-015-9532-7

Keywords

Mathematics Subject Classification

Search

Navigation