On the interplay of public and private law enforcement with multiple victims

Abstract

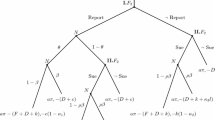
We analyze the interplay of public and private law enforcement when an infringement affects multiple parties, and where detection by just one party is sufficient to avoid the harm. Detection causes a positive externality on other victims, so that private effort incentives are inefficiently low. The public agency has might reduce its own inspection frequency in order to increase the number of private inspections (Peltzman-effect). However, due to the private parties’ incentive compatibility constraints, the agency can only trigger inspection by one more private party compared to the number of inspections when itself inspects with full frequency. Inspecting with full frequency is more likely to be second-best when the number of private parties affected is high.

Appendix

Proof of Lemma 1

Parts (i)–(iii). Taking the first partial derivatives gives $\frac{\partial \Delta }{\partial \alpha }=\frac{H}{n} q\left( 1-p\right) ^{m-1}>0$, $\frac{\partial \Delta }{\partial m}=-\frac{H}{ n}p\left( \ln \left( 1-p\right) \right) \left( 1-\alpha q\right) \left( 1-p\right) ^{m-1}>0$, and $\frac{\partial \Delta }{\partial n}= \frac{H}{n^{2}}p ( 1- \alpha q) ( 1-p) ^{m-1}>0$. Part (iv). For any given number of inspecting victims, the social benefit of an additional inspection is $X\equiv H\left( 1-\alpha q\right) \left( 1-p\right) ^{m}-H\left( 1-\alpha q\right) \left( 1-p\right) ^{m-1}$ while the private benefit is $Y\equiv \frac{H}{n}\left( 1-\alpha q\right) \left( 1-p\right) ^{m}-\frac{H}{n}\left( 1-\alpha q\right) \left( 1-p\right) ^{m-1}$. Thus, $Y<X$ for $n>1$. $\square$

Proof of Proposition 1

Part (i). Defining the non-detection probability as $P$, expected harm is $P\cdot H=H\left( 1-\alpha _{m}q\right) \left( 1-p\right) ^{m}$. Substituting $\alpha \left( m\right) =\left( \frac{1 }{q}-\frac{cn}{Hpq\left( 1-p\right) ^{m-1}}\right)$ and simplifying yields $P\cdot H=cn\frac{\left( 1-p\right) }{p}$.which is hence independent of $\alpha \left( m\right)$ and $m$. Part (ii). Define $\Delta \equiv SC_{m+1}-SC_{m}$ as the difference in social costs when the agency chooses $\alpha \left( m+1\right)$ instead of $\alpha \left( m\right)$, and recall that we restrict attention to the case where $m>\widehat{m}$. Then,

$$\begin{aligned} \Delta&= \left( cn\frac{\left( 1-p\right) }{p}+\left( \frac{1}{q}-\frac{cn}{ Hpq\left( 1-p\right) ^{m}}+\left( m+1\right) \right) c\right) \\&-\left( cn\frac{\left( 1-p\right) }{p}+\left( \frac{1}{q}-\frac{cn}{ Hpq\left( 1-p\right) ^{m-1}}+m\right) c\right) \\&= \frac{1}{H}\frac{c}{q}\left( \frac{Hq\left( 1-p\right) ^{m}-cn}{\left( 1-p\right) ^{m}}\right) , \end{aligned}$$

and thus $\Delta >0$ iff $Hq\left( 1-p\right) ^{m}>cn$. Recall from Assumption 1 that $Hp( 1-p) ^{n-1}( 1-q) >cn$. We show that this is a sufficient condition for $Hq\left( 1-p\right) ^{m}>cn$:

$$\begin{aligned} X&\equiv Hq\left( 1-p\right) ^{m}-\left( Hp\left( 1-p\right) ^{n-1}\left( 1-q\right) \right) \\&= H\left( q\left( 1-p\right) ^{m}-p\left( 1-p\right) ^{n-1}\left( 1-q\right) \right) >0: \end{aligned}$$

As $\frac{\partial X}{\partial m}=Hq\left( \ln \left( 1-p\right) \right) \left( 1-p\right) ^{m}<0$ and since we want to show that $X>0$, we insert the maximum $m=n$ to get

$$\begin{aligned} X&= H\left( q\left( 1-p\right) ^{n}-p\left( 1-p\right) ^{n-1}\left( 1-q\right) \right) \\&= H\left( 1-p\right) ^{n}\frac{q-p}{1-p}>0 \end{aligned}$$

since $q>p$. $\square$

Proof of Proposition 2

We know from Proposition 1 that the agency will never choose $\alpha <\alpha _{\widehat{m}+1}$. We start with part (ii) of the Proposition, and then we show that $\alpha =1$ and $\alpha _{\widehat{m}+1}$ can indeed both be optimal (part (i)). Proof of part (ii). First, note carefully that for the social costs with $\alpha =1$, we cannot make use of the binding (ICC) $\alpha \left( m\right) =\left( \frac{1}{q}-\frac{cn}{Hpq\left( 1-p\right) ^{m-1}}\right)$ as this is derived from the indifference condition which does not need to hold for $\alpha =1$.²⁰ For $\alpha =1$, social costs are

$$\begin{aligned} SC_{\widehat{m}}=H\left( 1-q\right) \left( 1-p\right) ^{\widehat{m}}+\left( 1+\widehat{m}\right) c \end{aligned}$$

(15)

by definition of $\widehat{m}$. For $\widehat{m}+1$, we know that social costs are

$$\begin{aligned} SC_{\widehat{m}+1}=cn\frac{\left( 1-p\right) }{p}+\left( \frac{1}{q}-\frac{cn }{Hpq\left( 1-p\right) ^{\widehat{m}}}+\widehat{m}+1\right) c. \end{aligned}$$

Define the difference in social costs as $D\equiv SC_{\widehat{m}+1}-SC_{ \widehat{m}}$ to get

$$\begin{aligned} D=cn\frac{\left( 1-p\right) }{p}+\left( \left( \frac{1}{q}-\frac{cn}{ Hpq\left( 1-p\right) ^{\widehat{m}}}\right) +\widehat{m}+1\right) c-\left( H\left( 1-q\right) \left( 1-p\right) ^{\widehat{m}}+\left( 1+\widehat{m} \right) c\right) . \end{aligned}$$

(16)

The partial derivative with respect to $n$ is

$$\begin{aligned} \frac{\partial D_{SC}}{\partial n}=-\frac{1}{H}\frac{c}{pq}\left( \frac{ c-Hq\left( 1-p\right) ^{m+1}}{\left( 1-p\right) ^{m}}\right) \end{aligned}$$

which is positive iff $Hq\left( 1-p\right) ^{m+1}>c$. Assumption 1 ensures that $\frac{Hp\left( 1-p\right) ^{n-1}\left( 1-q\right) }{n}>c$, so that a sufficient condition for $\frac{\partial D_{SC}}{\partial n}>0$ is that

$$\begin{aligned} Y\equiv Hq\left( 1-p\right) ^{m+1}-\frac{Hp\left( 1-p\right) ^{n-1}\left( 1-q\right) }{n}>0. \end{aligned}$$

As $\left( 1-p\right) ^{m+1}$ is decreasing in $m$ and increasing in $q$, we consider the maximum $m=n-1$ and the minimum $q=p$ to get

$$\begin{aligned} Y&= Hp\left( 1-p\right) ^{n}-\frac{Hp\left( 1-p\right) ^{n-1}\left( 1-p\right) }{n} \\&= \frac{H}{n}p\left( n-1\right) \left( 1-p\right) ^{n}>0. \end{aligned}$$

Part (i) is proven by an example where $\alpha =1$ is optimal for large $n$ and $\alpha _{\widehat{m}+1}$ is optimal for low $n$. This is sufficient to prove part (i) since we already know from Proposition 1 that $\alpha <\alpha _{\widehat{m}+1}$ cannot be optimal. In our example, we set harm $H=25$, inspection costs $c=0.4$, the victims’ detection probability $p=0.7$ and the agency’s detection probability $q=0.95$. Then, $\alpha =1$ is second best optimal for $n\ge 6$ and leads to $m=\widehat{m} =0$ private inspections while $\alpha <1$ is second best optimal for $n<6$. Social costs for $n=6$ are $SC=1.65$ with $\widehat{m}$ ($\alpha =1$) and $SC=1.79$ with $\widehat{m}+1$ (for $\alpha =0.908$). By contrast, for $n=5$, social costs are are $SC=1.65$ with $\widehat{m}$ ($\alpha =1$) and $SC=1.63$ with $\widehat{m}+1$ (for $\alpha =0.932$). Calculations are available on request.

In the discussion of Proposition 2 in the main body of the text, we claim that the agency may even prefer $\alpha _{\widehat{m}+1}$ to $\alpha =1$ when it has zero inspection costs. To show this, we consider the same example, but now assume that only private inspection costs are $c=0.4$, while the agency’s costs are zero. Then, $\alpha =1$ is second best optimal for $n\ge 5$, while $\alpha <1$ is second best optimal for $n<5$. $\square$