Skip to main content
SpringerLink
Log in

Dressler’s theory for curved topography flows: iterative derivation, transcritical flow solutions and higher-order wave-type equations

  • Original Article
  • Published:
Environmental Fluid Mechanics Aims and scope Submit manuscript

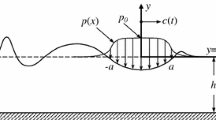
Abstract

The Dressler equations are a system of two non-linear partial differential equations for shallow fluid flows over curved topography. The theory originated from an asymptotic stretching method formulating the equations of motion in terrain-fitted curvilinear coordinates. Apparently, these equations failed to produce a transcritical flow profile changing from sub- to supercritical flow conditions. Further, wave-like motions over a flat bottom are excluded because the bed-normal velocity component is not accounted for. However, the theory was found relevant for several environmental flow problems including density currents over mountains and valleys, seepage flow in hillslope hydrology, the development of antidunes, the formation of geological deposits from hyper-concentrated flows, and shallow-water flow modeling in hydraulics. In this work, Dressler’s theory is developed in an alternative way by a systematic iteration of the stream and potential functions in terrain-fitted coordinates. The first iteration was found to be the former Dressler’s theory, whereas a second iteration of the governing equations results in velocity components generalizing Dressler’s theory to wave-like motion. Dressler’s first-order theory produces a transcritical flow solution over topography only if the total head is fixed by a minimum value of the specific energy at the transition point. However, the theory deviates from measurements under subcritical flow conditions, given that the bed-normal velocity component is significant. A second iteration to the velocity field was used to produce a second-order differential equation that resembles the cnoidal-wave theory. It accurately produces flow over an obstacle including the critical point and the minimum specific energy as part of the numerical solution. The new cnoidal-wave model compares well with the theory of a Cosserat surface for directed fluid sheets, whereas the Saint-Venant theory appears to be poor.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7

Similar content being viewed by others

References

  1. De Saint-Venant, A.B. (1871). Théorie du mouvement non permanent des eaux, avec application aux crues des rivières et à l’introduction des marrées dans leur lit (Theory of unsteady water movement, applied to floods in rivers and the effect of tidal flows). Comptes Rendus de l’Académie des Sciences 73: 147–154; 73: 237–240 (in French)

  2. Liggett JA (1994) Fluid mechanics. McGraw-Hill, New York

    Google Scholar 

  3. Sturm TW (2001) Open channel hydraulics. McGraw-Hill, New York

    Google Scholar 

  4. Toro EF (2002) Shock-capturing methods for free-surface shallow flows. Wiley, New York

    Google Scholar 

  5. Friedrichs KO (1948) On the derivation of the shallow water theory. Commun Pure Appl Math 1:81–87

    Google Scholar 

  6. Dressler RF (1978) New nonlinear shallow flow equations with curvature. J Hydraul Res 16(3):205–222

    Article  Google Scholar 

  7. Pudasaini SP, Hutter K (2007) Avalanche dynamics. Springer, Berlin

    Google Scholar 

  8. Hutter K, Wang Y (2014) Fluid and thermodynamics in geophysical context 1: Fluid mechanics. Springer, Berlin

    Google Scholar 

  9. Savage SB, Hutter K (1991) The dynamics of avalanches of granular materials from initiation to runout, part I. Analysis. Acta Mech 86(1–4):201–223

    Article  Google Scholar 

  10. Gray JMNT, Wieland M, Hutter K (1999) Gravity driven free surface flow of granular avalanches over complex basal topography. Proc R Soc Lond Ser A 455:1841–1874

    Article  Google Scholar 

  11. Pudasaini SP, Hutter K (2003) Rapid shear flows of dry granular masses down curved and twisted channels. J Fluid Mech 495:193–208

    Article  Google Scholar 

  12. Sivakumaran NS, Hosking RJ, Tingsanchali T (1981) Steady shallow flow over a spillway. J Fluid Mech 111:411–420

    Article  Google Scholar 

  13. Sivakumaran NS, Tingsanchali T, Hosking RJ (1983) Steady shallow flow over curved beds. J Fluid Mech 128:469–487

    Article  Google Scholar 

  14. Sivakumaran NS, Dressler RF (1986) Distribution of resistive body-force in curved free-surface flow. Math Methods Appl Sci 8(4):492–501

    Article  Google Scholar 

  15. Dressler RF, Yevjevich V (1984) Hydraulic-resistance terms modified for the Dressler curved-flow equations. J Hydraul Res 22(3):145–156

    Article  Google Scholar 

  16. Sivakumaran NS, Yevjevich V (1987) Experimental verification of the Dressler curved-flow equations. J Hydraul Res 25(3):373–391

    Article  Google Scholar 

  17. Sivakumaran NS, Dressler RF (1989) Unsteady density-current equations for highly curved terrain. J Atmos Sci 46:3192–3201

    Article  Google Scholar 

  18. Chapman TG, Dressler RF (1984) Unsteady shallow groundwater flow over a curved impermeable boundary. Water Resour Res 20(10):1427–1434

    Article  Google Scholar 

  19. Chapman TG, Ong G (2006) A new equation for shallow groundwater flow over a curved impermeable boundary: numerical solutions and laboratory tests. Water Resour Res 42:W03427. doi:10.1029/2005WR004437

    Google Scholar 

  20. Vesipa R, Camporeale C, Ridolfi L (2012) A shallow-water theory of river bedforms in supercritical conditions. Phys Fluids 24:094104

    Article  Google Scholar 

  21. Wooding RA (1991) Growth of natural dams by deposition from steady super-saturated shallow flow. J Geophys Res 96(B1):667–682

    Article  Google Scholar 

  22. Hager WH (2010) Comment on Steady open channel flow with curved streamlines: the Fawer approach revised. Environ Fluid Mech 10(4):491–494

    Article  Google Scholar 

  23. Steffler PM, Jin YC (1993) Depth-averaged and moment equations for moderately shallow free surface flow. J Hydraul Res 31(1):5–17

    Article  Google Scholar 

  24. Khan AA, Steffler PM (1996) Modelling overfalls using vertically averaged and moment equations. J Hydraul Eng 122(7):397–402

    Article  Google Scholar 

  25. Khan AA, Steffler PM (1996) Vertically averaged and moment equations model for flow over curved beds. J Hydraul Eng 122(1):3–9

    Article  Google Scholar 

  26. Castro-Orgaz O (2010) Steady open channel flow with curved streamlines: the Fawer approach revised. Environ Fluid Mech 10(3):297–310

    Article  Google Scholar 

  27. Benjamin TB, Lighthill MJ (1954) On cnoidal waves and bores. Proc R Soc Lond A 224:448–460

    Article  Google Scholar 

  28. Hager WH (1985) Equations for plane, moderately curved open channel flows. J Hydraul Eng 111(3):541–546

    Article  Google Scholar 

  29. Castro-Orgaz O, Hager WH (2009) Curved streamline transitional flow from mild to steep slopes. J Hydraul Res 47(5):574–584

    Article  Google Scholar 

  30. Berger RC, Carey GF (1998) Free-surface flow over curved surfaces. Part I: perturbation analysis. Int J Numer Methods Fluids 28:191–200

    Article  Google Scholar 

  31. Berger RC, Carey GF (1998) Free-surface flow over curved surfaces. Part II: computational model. Int J Numer Methods Fluids 28:201–213

    Article  Google Scholar 

  32. Dewalls BJ, Erpicum S, Archambeau P, Detrembleur S, Pirotton M (2006) Depth-integrated flow modelling taking into account bottom curvature. J Hydraul Res 44(6):785–795

    Article  Google Scholar 

  33. Naghdi PM, Vongsarnpigoon L (1986) The downstream flow beyond an obstacle. J Fluid Mech 162:223–236

    Article  Google Scholar 

  34. Van Dyke M (1975) Perturbation methods in fluid mechanics. Parabolic Press, Stanford

    Google Scholar 

  35. Matthew GD (1991) Higher order one-dimensional equations of potential flow in open channels. Proc ICE 91(3):187–201

    Google Scholar 

  36. Castro-Orgaz O, Giráldez JV, Robinson N (2012) Second order two-dimensional solution for the drainage of recharge based on Picard’s iteration technique: a generalized Dupuit-Forchheimer equation. Water Resour Res 48:W06516. doi:10.1029/2011WR011751

    Google Scholar 

  37. Castro-Orgaz O, Giráldez JV, Mateos L (2013) Second-order shallow flow equation for anisotropic aquifers. J Hydrol 501:183–185

    Article  Google Scholar 

  38. Ramamurthy AS, Vo ND (1993) Application of Dressler theory to weir flow. J Appl Mech 60:163–166

    Article  Google Scholar 

  39. Ramamurthy AS, Vo ND, Balachandar R (1994) A note on irrotational curvilinear flow past a weir. J Fluids Eng 116(2):378–381

    Article  Google Scholar 

  40. Hager WH (1991) Experiments on standard spillway flow. Proc ICE 91:399–416

    Google Scholar 

  41. Iwasa Y (1958) Hydraulic significance of transitional behaviours of flows in channel transitions and controls. Mem Fac Eng, Kyoto Univ 20(4):237–276

    Google Scholar 

  42. Ishihara T, Iwasa Y, Ihda K (1960) Basic studies on hydraulic performances of overflow spillways and diversion weirs. Bull Disaster Prev Res Inst 33:1–30

    Article  Google Scholar 

  43. Anh T, Hosoda T (2007) Depth-averaged model of open-channel flows over an arbitrary 3D surface and its applications to analysis of water surface profile. J Hydraul Eng 133(4):350–360

    Article  Google Scholar 

  44. Boussinesq, J. (1877). Essai sur la théorie des eaux courantes (Essay on the theory of flowing water). Mémoires présentés par divers savants à l’Académie des Sciences, Paris 23, 1-680 (in French)

  45. Engelund, F., Hansen, E. (1966). Investigations of flow in alluvial streams. Bull. 9, Hydraulic Laboratory, Technical University of Denmark, Copenhagen

  46. Bose SK, Dey S (2009) Reynolds averaged theory of turbulent shear flows over undulating beds and formation of sand waves. Phys Rev E 80(3):036304-1–036304-9

    Article  Google Scholar 

  47. Dey S (2014) Fluvial hydrodynamics: hydrodynamic and sediment transport phenomena. Springer, Berlin

    Book  Google Scholar 

  48. Press WH, Teukolsky SA, Vetterling WT, Flannery BP (2007) Numerical recipes: the art of scientific computing, 3rd edn. Cambridge University Press, Cambridge

    Google Scholar 

  49. Green AE, Naghdi PM (1976) Directed fluid sheets. Proc R Soc Lond A 347:447–473

    Article  Google Scholar 

  50. Green AE, Naghdi PM (1976) A derivation of equations for wave propagation in water of variable depth. J Fluid Mech 78:237–246

    Article  Google Scholar 

  51. Naghdi PM (1979) Fluid jets and fluid sheets: a direct formulation. In: Proceedings of the 12th Symposium on Naval Hydrodynamics, National Academy of Sciences, Washington, D.C, pp 505–515

  52. Marchi E (1992) The nappe profile of a free overfall. Rendiconti Lincei Matematica e Applicazioni Serie 9 3(2):131-140

  53. Marchi E (1993) On the free overfall. J Hydr Res 31(6):777–790; 32(5):794–796

  54. Montes JS (1998) Hydraulics of open channel flow. ASCE Press, Reston

    Google Scholar 

  55. Hager WH (1999) Wastewater hydraulics: theory and practice. Springer, Berlin

    Google Scholar 

  56. Chen J, Dracos T (1996) Water surface slope at critical controls in open channel flow. J Hydraul Res 34(4):517–536

    Article  Google Scholar 

  57. Iwasa Y, Kennedy JF (1968) Free surface shear flow over a wavy bed. J Hydraul Div 94(HY2):431–454

    Google Scholar 

  58. Jaeger, C. (1949). Technische Hydraulik (Technical hydraulics). Birkhäuser, Basel (in French)

Download references

Acknowledgments

This work was supported by the Spanish Project CTM2013-45666-R, Ministerio de Economía y Competitividad.

Author information

Authors and Affiliations

  1. University of Cordoba, Campus Rabanales, Leonardo Da Vinci Building, 14071, Córdoba, Spain

    Oscar Castro-Orgaz

  2. VAW, ETH Zurich, 8093, Zurich, Switzerland

    Willi H. Hager

Authors
  1. Oscar Castro-Orgaz
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Willi H. Hager
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Oscar Castro-Orgaz.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Castro-Orgaz, O., Hager, W.H. Dressler’s theory for curved topography flows: iterative derivation, transcritical flow solutions and higher-order wave-type equations. Environ Fluid Mech 16, 289–311 (2016). https://doi.org/10.1007/s10652-015-9418-z

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10652-015-9418-z

Keywords

Search

Navigation