Cooperation and Subgame Perfect Equilibria in Global Pollution Problems with Critical Threshold

Abstract

The paper examines the issue of international pollution control under a dynamic framework involving heterogeneous countries and a critical threshold. We propose an appealing specification for this type of problem, and its novelty is illustrated by the fact that countries use linear strategies in equilibrium, although their utility and damage functions are highly convex. The stock of pollution under cooperation is always lower. Surprisingly, emissions are always higher in distant periods under the cooperative scenario; and we show through examples that this is a significant finding rather than some marginal effect. It is also shown that the efficient allocation of pollution abatement is driven only by the respective technologies of the countries. Finally, a dynamic transfer scheme allowing to implement the cooperative solution is proposed.

1 Introduction

The mitigated results of global initiatives on climate change have recently shown (if further proof was needed) the difficulty of reaching effective international agreements on pollution control. As much as the countries at the negotiation table are concerned with keeping a clean environment, the pursuit of their individual economic performance constitutes a stumbling block to a consensus on enforcing binding emissions reduction targets.

Many papers on this issue use a cooperative approach by treating global warming as a single-agent problem [see for instance Tahvonen (1995), Folmer and Musu (1992) and Howarth (1998)].¹ Although these papers determine what the global emissions should be to achieve efficiency, they do not examine the strategic incentives that drive the countries’ emission decisions —which are crucial in implementing any regulation aiming at achieving global efficiency.

A second strand of works examines the issue of emission abatement in the context of international environmental agreements (IEAs): see for example Barrett (1994), Rubio and Ulph (2006). In order to determine the stable size of an IEA, these papers assume a framework where all countries are symmetric, which is rather restrictive given that the reality involves a diversity of countries with different characteristics and objectives. The dissimilarities of the negotiating countries have been illustrated (for instance) by the failure of the Copenhagen Conference on Climate Change, which has emphasized the diverging interests of developed economies and emerging ones.

Finally, a number of authors have modeled international pollution control as a non-cooperative issue involving strategic national interests. In particular, seminal works by Long (1992), van der Ploeg and de Zeeuw (1991, 1992), Dockner and Long (1993) propose differential game models allowing to study international pollution control with both open-loop and closed-loop strategies. Tolwinsky and Martin (1995) also propose a dynamic model where countries determine their emissions in a non-cooperative way. Nordhaus and Yang (1996) estimate and compare the emissions resulting from: the market approach, the cooperative approach and the non-cooperative approach. Dutta and Radner (2004) study dynamic treaties that are self-enforcing in the sense that they are subgame perfect.

The present paper examines a dynamic model with an arbitrary number of asymmetric countries which determine their respective levels of emissions in a strategic way. The respective damage functions are convex (in the pollution stock); and a key feature of the model is the assumption of a critical level of pollution which, if it was reached, would lead to a global environmental disaster. Recently, Barrett (2013) and Schmidt (2017) have studied the effects on climate treaties of a catastrophic pollution threshold. Unlike the present paper, Barrett (2013) considers symmetric countries and a static framework. His results show that, if the cost of the catastrophe is relatively high, the treaty can serve as a coordination device and help the countries avoid the threshold. Schmidt (2017) extends Barrett’s model by considering a dynamic framework. And he shows in particular that additional welfare gains make cooperation more likely. Our results are consistent with the findings of both authors. Indeed, the cost of the catastrophe in the present paper can be viewed as infinitely high;² and hence, in line with their results, the countries are able to coordinate and avoid it.

The objective of this paper is to solve for emission paths in both the cooperative and the non-cooperative approaches. In explaining the countries’ emissions, the paper specifically emphasizes the differences between the countries. These differences are materialized by the relative importance they give to a clean environment, their effectiveness in abating emissions and, finally, their respective discount factors for future utilities.³ We propose a novel and intuitive specification, which can be viewed as one of the main contributions of this paper. In this literature, it is well-known that quadratic or linear functions result in linear emission strategies. Using instead logarithmic utility and damage functions (to capture the extremely high costs of an approaching catastrophe), we prove that all countries use linear strategies under both the cooperative and non-cooperative scenarios. Our framework thus allows to model catastrophic scenarios without having to deal with complex equilibrium strategies.

The results show that emissions in each period are proportional to the gap between the critical level of pollution and its current stock. Ceteris paribus, countries with a lower discount factor (or a less efficient abatement technology) will emit more in the subgame perfect equilibrium than the others. Also, countries whose preferences give a high weight to a clean environment will emit less than the others. It is shown that the cooperative scenario entails a lower stock of pollution in each period.

Interestingly, the countries emit more (under the cooperative scenario) in periods that are distant in the future. This surprising result, which cannot be replicated in a static model, reinforces the importance of using a dynamic framework to study stock pollution. Let us provide an intuitive explanation for this result. Under our specification, the respective pollution stocks both converge to the critical level under both scenarios (this is not trivial, because they may have different limits for some other specification). This remark suggests that the two emission paths must cross at some point in time. We then proceed to prove that it is optimal for the international planner to adopt a stringent policy early on, so as to allow the countries to enjoy higher emissions in late periods

Finally, the paper proposes a Pigouvian transfer scheme allowing to sustain the socially efficient emission path. This scheme is based on the standard idea that the countries should receive the full benefit of any emission reduction they undertake. The implementation of Pigouvian transfers has been extensively studied in static pollution problems with externalities, but not so much in dynamic frameworks. One of the contributions of the present work is the design of such a transfer scheme in a dynamic setting with Markov strategies. In a seminal work on this issue, Hoel (1992, 1993) determines the conditions under which a uniform carbon tax can be used to achieve efficiency. The differences with the present work come from the facts that (i) we do not consider a uniform tax here, but rather bilateral transfers between countries and (ii) our transfer scheme always leads to the efficient solution, regardless of the values of the parameters. In particular, Hoel (1992, 1993) points out that a uniform tax may be used to attain the first best when, for any two countries, the ratio of their marginal damage functions equals that of their tax reimbursement shares.

The paper unfolds as follows. The following Sect. 2 presents the model and the strategic game that the n countries play in order to determine their respective levels of emission. Section 3 presents the general results that hold for an arbitrary specification of the model. In particular, the existence issue is discussed for both the Markov perfect equilibrium and the cooperative solution. Section 4 examines a particularly intuitive specification of the model, for which the Markov perfect equilibrium and the cooperative solution are explicitly derived. The evolution of the pollution stock is described in each case, and a comparison of global emissions under the two approaches is carried out. Finally, Sect. 5 concludes with some comments. All proofs are relegated to the Appendix.

2 The Model

Consider a global economy which consists of a finite number of countries, $n \ge 2$. The set of countries is $N=\{1,\ldots ,n\}$. In order to study the issue of strategic emission abatement, let us adopt the partial equilibrium framework in which country i enjoys the national product ${{\bar{y}}}_i$ in each period. The amount ${{\bar{y}}}_i$ is expressed in units of a composite good and is determined by what Nordhaus and Yang (1996) refer to as the “market approach”. Time is discrete and, in each period t, the production activity corresponding to ${{\bar{y}}}_i$ also generates the amount ${{\bar{e}}}_i$ of greenhouse gases (GHG) emissions. However, each country has the possibility to reduce its emissions to the level $e_{it}\in [0,{{\bar{e}}}_{i}]$ by incurring the abatement cost $c_i({{\bar{e}}}_i-e_{it})$ and hence consuming the amount $y_{it}={{\bar{y}}}_i-c_i({{\bar{e}}}_i-e_{it})$ of the composite good. Further on in this section, we state and explain the assumptions pertaining to the abatement cost functions $c_i(.), ~i=1,\ldots ,n$.

2.1 The Evolution of the Stock of Pollution

The stock of pollution, $S_t$, is subject to natural decay. From period t to period $t+1$, a constant proportion $\delta \in [0,1]$ of the stock survives this natural decay.⁴ On the other hand, the stock is increased by the sum of all the emissions produced by the n countries in period t. Precisely, the evolution of the state variable $S_t$ is given by:

$$\begin{aligned} S_{t+1}=\delta S_t+\sum \limits _{i=1}^n e_{it} \quad t=0,\ldots ,T, \end{aligned}$$

(1)

where $T\in {\mathbb {N}}\cup \{+\infty \}$ is the terminal period. We will give particular attention to the case where T is infinite. Note that the countries each choose their respective levels of emissions in every period $t=0,\ldots ,T$. Given these respective emissions and the initial stock of pollution $S_0$, the evolution of $S_t$ through time is completely determined by (1).

2.2 Preferences

The utility of country i in each period t is a function, $U_i(y_{it}, S_t)$, that depends on both i’s consumption ($y_{it}$) of the composite good and the global pollution stock ($S_t$). The overall utility of $i\in N$ is the sum of the discounted instantaneous utilities, $\beta _i$ being the discount factor specific to country i. Let us assume that each $U_i$ is twice continuously differentiable and satisfies the following properties.

Assumption 1

• (i) $U_{iy}>0, U_{iS}<0$, $U_{iyy}\le 0$ and $U_{iSS}<0$.

• (ii) $U_{i}(y,S)=-\infty$ and $S\ge {{\bar{S}}}$, with $\lim \limits _{S\rightarrow {{\bar{S}}}}U_{i}(y,S)=-\infty$, for any $y\ge 0$.

• (iii) $\lim \limits _{k\rightarrow +\infty } \sum \limits _{t=k}^{+\infty } \beta _i^t U_i(y_t,S_t)=0$, for any $(y_t,S_t)_{t \in {\mathbb {N}}}\in \left( [0,{{\bar{y}}}_i]\times [0,{{\bar{S}}})\right) ^{\mathbb {N}}$.

Property (i) says that the marginal utility of consumption is positive and non-increasing, while the utility decreases (at a decreasing rate) with the stock of pollution. Property (ii) states the fact that a pollution stock of ${{\bar{S}}}$ (or more) would cause an environmental catastrophe in each of the countries. Finally, property (iii) guarantees that one can compute (as a real number) the utility associated with any sequence $(y_t,S_t)_{t \in {\mathbb {N}}}$ such that the critical level of the stock ${{\bar{S}}}$ is never reached.

2.3 Emissions Abatement

As stated earlier on, country i’s emission abatement in period t is given by ${{\bar{e}}}_i-e_{it}$. The abatement cost incurred by i in t is then of the form $c_i({{\bar{e}}}_i-e_{it})$. Let us assume that the abatement cost functions of the respective countries are twice differentiable and meet the following requirements.

Assumption 2

• (i) $c_i(0)=0$;

• (ii) $c'_i({{\bar{e}}}_i-e_{it})>0$ and $c''_i({{\bar{e}}}_i-e_{it})>0$, for any $e_{it}\in [0,{{\bar{e}}}_i]$.

The requirement (i) states that a country which chooses not to abate (that is, $e_{it}={{\bar{e}}}_i$) pays nothing. Also, (ii) says that the abatement cost is increasing and convex. These features of the abatement cost functions are supported (in particular) by Nordhaus (1991)’s estimates as to the cost of reducing GHG emissions. Just as the country’s consumption $y_{it}$, the cost of abatement is expressed in units of the composite good.

2.4 The Strategic Emission-Abatement Game

Let us now define the dynamic game that the countries play in order to determine their respective levels of emission (abatement) in each period. The set of players $N=\{1,\ldots ,n\}$ is constituted of the n countries. Each country chooses its emission schedule $e_i=(e_{it})_{t=0,\ldots ,T}$ so as to maximize its sum of discounted utilities, $\sum \nolimits _{t=0}^T \beta _i^tU_{i} \left( {{\bar{y}}}_i-c_i({{\bar{e}}}_i-e_{it}), S_t\right)$, given the strategies $e_{-i}= (e_{j})_{j\in N \setminus \{i\}}$ of the other countries and the law of motion (1).

3 General Results

This section presents the results that hold regardless of the specification of the model, provided that Assumptions 1 and 2 are satisfied.

3.1 The Non-Cooperative Approach: Subgame Perfect Nash Equilibrium in Markov Strategies

Let us consider the case where the countries determine their emission levels in a non-cooperative way. In a Nash equilibrium, each of the n countries chooses the emission schedule $(e_{i})$ that is the best response to the strategies $(e_{-i})$ of the others. Given $e_{-i}$, country i therefore solves:

$$\begin{aligned} \max \limits _{(e_{it})_{t=0,\ldots ,T}}~ \sum \limits _{t=0}^T \beta _i^t U_{i}\left( {{\bar{y}}}_i-c_i({{\bar{e}}}_i-e_{it}), S_t\right) ~~~~~~~~~~~~~~~~~\nonumber \\ \text {s.t. }~S_{t+1}=\delta S_t+\sum \limits _{j=1}^n e_{jt}, ~\forall t\in \{0,\ldots ,T-1\}~~ (\text {with } S_0 \text { given}). \end{aligned}$$

(2)

Suppose that (for any T and any $S_0<{{\bar{S}}}$) there exists a subgame perfect equilibrium and denote by $V^T_i(S_0)$ country i’s payoff to the equilibrium emission profile, given the initial stock of pollution $S_0$ and the horizon T. Suppose in addition that, for any $T \in {\mathbb {N}}\cup \{+\infty \}$, the continuation functions $V^{T-t}_i(S)$ are known. Then, by using backward induction on this optimal path, we must have (for each country $i\in N$ and any period t such that $0\le t<T$):⁵

$$\begin{aligned} V^{T-t}_i(S_{t})=\max \limits _{{\small e_{it}\in [0,{{\bar{e}}}_i]}} \left[ U_{i}\left( {{\bar{y}}}_i-c_i({{\bar{e}}}_i-e_{it}), S_t\right) +\beta _iV^{T-t-1}_i\left( \delta S_t+\sum \limits _{j=1}^n e_{jt} \right) \right] .\qquad \end{aligned}$$

(3)

Equation (3) states the so-called principle of optimality —see for instance Leonard and Long (1992), on page 174. In the special case where $T=+\infty$, observe that we have $V^{T-t}_i=V^{T-t-1}_i=V^T_i=V_i^\infty$ and, therefore, (3) represents a Bellman equation.

Assuming an interior solution,⁶ one can write the first-order conditions of (3) as:

$$\begin{aligned} c_i '({{\bar{e}}}_i-e_{it})U_{iy}\left( {{\bar{y}}}_i-c_i({{\bar{e}}}_i-e_{it}),S_t\right) +\beta _i \left( V^{T-t-1}_i \right) '\left( \delta S_t+\sum \limits _{j=1}^n e_{jt} \right) =0,&\quad \forall i\in N, \end{aligned}$$

(4)

$~\forall t \text { such that } 0\le t<T.$

Equation (4) means that, given $S_t$ and the strategies of the other countries $(e_{-i})$, country i determines its emission abatement level by equating the marginal loss of utility (due to the cost of a one-unit reduction of emissions) to the discounted gain in future utility following that abatement. Using these first-order conditions, one can prove the following existence results.

Theorem 1

We have the following:

• (i) for any $T\in {\mathbb {N}}$, there exists a subgame perfect equilibrium in which each country uses a Markov strategy, $\left[ {{\hat{e}}}^T_{it}(S_t)\right] _{t=0,\ldots ,T}$;

• (ii) if there exists a sequence of Markov perfect equilibria $\{({{\hat{e}}}^T_{i})_{i\in N}, T\in {\mathbb {N}}\}$ that is convergent, then the infinite-horizon game ($T=+\infty$) possesses a Markov perfect equilibrium as well.

Proof

See Appendix “Proof of Theorem 1” $\square$

Theorem 1 shows that a subgame perfect equilibrium always exists when the horizon of the game is finite; this does not preclude the existence of multiple subgame perfect Nash equilibria in general. Furthermore, for the infinite-horizon case, Theorem 1 provides a sufficient condition: the convergence of any given sequence of finite-horizon equilibria guarantees the existence of an equilibrium when $T=+\infty$.⁷

3.2 The Cooperative Approach

Let us consider an international planner/agency whose objective is to maximize the sum of the countries’ utilities. Assuming that the utilities are transferable across countries, the optimal emission schedules are given by the solution to the problem:

$$\begin{aligned} W^T(S_{0})= & {} \max \limits _{(e_{it})_{i=1,\ldots ,n}^{t=0,\ldots ,T}} \sum \limits _{t=0}^T \sum \limits _{i=1}^n ~ \beta _i^t U_{i}\left( {{\bar{y}}}_i-c_i({{\bar{e}}}_i-e_{it}), S_t\right) \nonumber \\ \text {s.t. }~S_{t+1}= & {} \delta S_t+\sum \limits _{i=1}^n e_{it}, ~{\small \forall t\in \{0,\ldots ,T-1\}~~ (\text {with } S_0 \text { given})} \end{aligned}$$

(5)

The following theorem claims the existence of a unique solution for the finite-horizon problem. In addition, it provides a sufficient condition for the infinite-horizon problem to have a solution.

Theorem 2

The following hold true:

• (i) for any $T\in {\mathbb {N}}$, there exists a unique cooperative solution $\left[ {{\tilde{e}}}^T_{it}(S_0)\right] _{i=1,\ldots ,n}^{t=0,\ldots ,T}$;

• (ii) if $\lim \limits _{T\rightarrow \infty }{{\tilde{e}}}_{i0}^T(S_0)$ exists in ${\mathbb {R}}$ for any $i\in N$ and any $S_0\in [0,{{\bar{S}}})$, then the infinite-horizon game possesses a unique cooperative solution.

Proof

See Appendix “Proof of Theorem 2” $\square$

Denote by ${{\widetilde{W}}}^T _i$ the overall utility enjoyed by country i under the cooperative scenario, that is to say,

$$\begin{aligned} {{\widetilde{W}}}^T _i(S_0)= & {} \sum \limits _{t=0}^T ~ \beta _i^t U_{i}\left( {{\bar{y}}}_i -c_i({{\bar{e}}}_i-{{\tilde{e}}}^T_{it}(S_0), {{\widetilde{S}}}_t\right) , \end{aligned}$$

where ${{\widetilde{S}}}_{t+1}=\delta {{\widetilde{S}}}_t+\sum \limits _{j=1}^n {{\tilde{e}}}^T_{jt}(S_0) \text { and } {{\widetilde{S}}}_{0}=S_0.$

Using the continuation values ${{\widetilde{W}}}^k _j$ $(j\in N\text { and }k=0,\ldots ,T)$, one can rewrite (5) in the following recursive way:

$$\begin{aligned} W^{T-t}(S_t)=\max \limits _{(e_{it})_{i=1,\ldots n}} \sum \limits _{i=1}^n \left( U_i\left( {{\bar{y}}}_i-c_i({{\bar{e}}}_i-e_{it}), S_t\right) +\beta _i {{\widetilde{W}}}_i^{T-t-1}\left( \delta S_t+\sum \limits _{j=1}^n e_{jt}\right) \right) .\nonumber \\ \end{aligned}$$

(6)

Writing the first-order conditions of (5) for an interior solution, one obtains

$$\begin{aligned} c'_i({{\bar{e}}}_i-{{\widetilde{e}}}_{it})U_{iy} \left( {{\bar{y}}}_i-c_i\left( {{\bar{e}}}_i -{{\widetilde{e}}}_{it}\right) ,S_t\right) +\sum \limits _{j=1}^n \beta _j\left( {{\widetilde{W}}}^{T-t-1} _j\right) '\left( \delta S_t+\sum \limits _{j=1}^n {{\widetilde{e}}}_{jt}\right) =0,\qquad \end{aligned}$$

(7)

for any $i\in N$, and any t such that $0\le t<T$.

Equation (7) says that, unlike the individual countries, the international planner, when contemplating a reduction of country i’s emission level, compares the loss of utility caused by its cost to the sole country $i \left( \text {i.e. } c'_i({{\bar{e}}}_i-e_{it})U_{iy}\left( {{\bar{y}}}_i -c_i({{\bar{e}}}_i-e_{it}),S_t\right) \right)$ with the sum of the (discounted) gains in future utility obtained by the n countries (due to a cleaner environment). As seen in Eq. (4), each country cares only about their own gain in future utility (following a reduction of their current emissions) when determining their emissions non-cooperatively. This set of conditions will be useful in what follows.

Obviously, the cooperative solution yields the highest sum of utilities and typically differs from the Markov perfect equilibrium. One might think that global emissions are always lower under the cooperative scenario. Interestingly, it is shown in Sect. 4 that this is not the case for every period.

3.3 Enforcing the Cooperative Emission Schedules

This part proposes a scheme that would allow an international agency to enforce the cooperative emission schedules $({{\widetilde{e}}}_{1},\ldots ,{{\widetilde{e}}}_{n})$ which, as seen in the previous section, maximize global welfare. Without any action from the international agency, the countries behave in a non-cooperative way; that is to say, the status quo is the non-cooperative equilibrium ${{\hat{e}}}=({{\hat{e}}}_{1},\ldots , {{\hat{e}}}_{n})$. Assuming that the emission levels of the countries are perfectly observable, one way for the international agency to enforce cooperation is to make sure that each country gets the full global benefit of any emission abatement it undertakes. This objective can be achieved by fostering the Pigouvian transfer scheme defined as follows.

For any non-terminal period t (i.e. $t<T$) and any stock of pollution $S_{t+1}$ that may arise in period $t+1$, consider the sequence ${{\widetilde{S}}}'$ defined by

$$\begin{aligned} {{\widetilde{S}}}'_{t+1}=S_{t+1} \text{ and } {{\widetilde{S}}}'_{t+p}=\delta {{\widetilde{S}}}'_{t+p-1}+ \sum \limits _{k=1}^n {{\widetilde{e}}}_{k(t+p-1)} \left( {{\widetilde{S}}}'_{t+p-1}\right) ~ ~\forall p>1, \end{aligned}$$

where ${{\widetilde{e}}}()$ is the strategy profile introduced in Theorem 2. In words, given the stock $S_{t+1}$, ${{\widetilde{S}}}'_{t+p}$ is the pollution stock that will be reached in period $t+p$, provided the countries behave in a cooperative way in all the periods following $t+1$.

Next, let us define the transfer vector $\tau (t,S_{t+1}) = \left( \tau _{j}\left( t,S_{t+1} \right) \right) _{j=1,\ldots ,n}$ as follows:

$$\begin{aligned} \tau _{j}(t,S_{t+1})=-\sum \limits _{p=1}^{T-t}~ \beta ^{p}_j ~ U_{jS}\left( {{\bar{y}}}_j,{{\widetilde{S}}}'_{t+p}\right) >0 \end{aligned}$$

(8)

The amount $\tau _{j}(t,S_{t+1})$ represents the transfer that country j is willing to make (to any other country) in exchange for a one-unit reduction of emissions undertaken in period t, assuming cooperation in the future.⁸ Indeed, the right-hand side of (8) represents the sum of the discounted increases in country j’s future utilities following a one-unit reduction of global emissions in period t. Country j is better off paying the amount $({{\hat{e}}}_{it}(S_t) - {{\tilde{e}}}_{it}(S_t)) \tau _{j}(t,S_{t+1})$ to any country i that reduces its emissions, since this transfer is not higher than the benefit of the marginal reduction of emissions in terms of its utility. Observe that $\tau _{j}(t,S_{t+1})$ is expressed in current value at date t.

Under this scheme, for any pollution stock $S_{t+1}$ in period $t+1$, a country i that undertakes a one-unit reduction (in period t) receives from each country $j\ne i$ the transfer $\tau _{j}(t,S_{t+1})$. Therefore, the total amount received (from all other countries j) by country i in exchange for a one-unit reduction undertaken in period t is given by $\sum \limits _{j\ne i} \tau _{j}(t,S_{t+1})$. Also remark that, if country i’s emissions rather increase from the Markov equilibrium to cooperation, then $({{\hat{e}}}_{it}(S_t) - {{\tilde{e}}}_{it}(S_t)) \tau _{j}(t,S_{t+1})<0$: that is, country i has to pay to country j the amount $\tau _{j}$ per unit increased.

By putting in place these markets where the countries can make transfers to each other in exchange for emission reductions (or increases) at any given date, the international agency can enforce global efficiency as to the countries’ GHG emissions.

Theorem 3

Suppose that the cooperative solution exists (as is the case whenever T is finite). If the countries are allowed to solicit emission reductions from one another according to the transfer scheme $\tau$ defined in (8), then the unique equilibrium of the resulting dynamic game between the n countries is precisely ${{\tilde{e}}}$, the cooperative strategy profile.

Proof

See Appendix “Proof of Theorem 3” $\square$

The above results states that, by setting the right price for a marginal reduction of emissions by any given country in each period t, the international agency can achieve global efficiency. This result is not very surprising, mainly because it is well known in the static framework —see for example Chander and Tulkens (1997). A contribution of the current paper is the design a transfer scheme allowing to achieve efficiency in a dynamic framework with infinite horizon.⁹

Next, let us point out that cooperation, implemented using the transfers (8), is individually rational.¹⁰ Indeed, given the convexity of $c_i()$, one can check that each country i has a higher utility when changing its emissions (from ${{\hat{e}}}_{it}$ to ${{\tilde{e}}}_{it}$) and receiving the (per unit) transfer $\tau _{j}(t,S_{t+1})$ from every other country j.

Let us now explain why an international agency would be required to coordinate these transfers. To avoid false promises (of payment or emission abatement), any country soliciting emission reductions from others would have to transfer the corresponding amount to the international agency beforehand. Given the assumption of perfect observability, the agency would then monitor the respective countries’ emissions in order to make sure that emission reductions that have been paid for are indeed undertaken. Thus, the money would transit through the international agency and would be paid to beneficiary countries immediately after delivery of the required emission reductions. In case some countries fail to deliver the requested reductions, the agency would simply return the money to the different payers.

4 Specification of the Model

The object of this section is to solve explicitly for the emission schedules of the countries for a given specification of the model. Although specific forms are assumed, a reasonable level of generality is preserved as to the preferences, the abatement technologies and the discount factors of the countries.

Firstly, suppose that the utility of country i is given by

$$\begin{aligned} U_i(y_{it},S_t)=y_{it}+\alpha _i \ln ({{\bar{S}}}-S_t) ~ \forall ~ i\in N, \end{aligned}$$

(9)

with $\alpha _1>0,\ldots ,\alpha _n>0$. The term $-\alpha _i \ln ({{\bar{S}}}-S_t)$ can be viewed as the damage caused by pollution. Observe that this damage function is increasing and convex in $S_t$, the stock of pollution.¹¹ Across the n countries, the higher the parameter $\alpha _i$, the greater the importance given to a clean environment.

Secondly, consider the abatement cost functions:¹²

(10)

Notice that $c_i({{\bar{e}}}_i-e_{it})$ satisfies $c'_i>0$ and $c''_i>0$. The positive constants $\gamma _i~(i=1,\ldots ,n)$ represent technological parameters; and they could also reflect the respective sizes of the different countries.¹³ Of any two countries, the one with the lower value of $\gamma _i$ possesses the more efficient technology with regard to emission abatement. It is easy to check that these preferences and abatement cost functions satisfy Assumptions 1 and 2.

Finally, let us assume in this section that the natural decay of pollution is negligible (that is, $\delta =1$).¹⁴ This allows to derive the analytical form of the optimal emissions in both the strategic and the cooperative approaches. In addition, an insightful comparison of the two scenarios is provided.

4.1 The Strategic Emission Schedules

This part examines the non-cooperative solution for the specification we have assumed. Existence of the Markov perfect equilibrium is guaranteed by the result of Theorem 1 and, in the particular case at hand, this Markov equilibrium turns out to be unique. The following result characterizes the equilibrium.

Proposition 1

In the Markov perfect equilibrium of the emission abatement game, the countries’ emissions in period t are proportional to the gap ${{\bar{S}}}-S_t$ between the critical level of pollution and the current stock. Across countries, the higher the importance given to the environment $\alpha _i$ (respectively, the country’s discount factor $\beta _i$), the lower the emissions in every period. On the contrary, the higher the abatement-cost parameter $\gamma _i$, the higher the emissions in every period. Precisely, for each country $i \in N,$ we have:

$$\begin{aligned} \left\{ \begin{array}{ll} {{\hat{e}}}_{it}^T(S_{t})=\frac{\gamma _i \beta _i^{-1}\left( Z_{i(T-t)}\right) ^{-1}}{1+\sum \limits _{j =1}^n \gamma _j \beta _j^{-1}\left( Z_{j(T-t)}\right) ^{-1}}~ ({{\bar{S}}}- S_t) &{} {~~~} t=0,1,\ldots ,T-1~~ \text { if }~ T \text { is finite;} \\ {{\hat{e}}}_{it}^T(S_t)=\frac{\gamma _i \beta _i^{-1} (Z_{i\infty })^{-1}}{1+\sum \limits _{j=1}^n \gamma _j \beta _j^{-1} (Z_{i\infty })^{-1}}~ ({{\bar{S}}}- S_t) &{} \hbox {}~~~t=0,1,2,\ldots ~~~~~ \text { if }~ T \text { is infinite,} \end{array} \right. \end{aligned}$$

(11)

where $Z_{i}$ is the sequence defined by $Z_{ik}=\frac{1}{1-\beta _i}\left( \alpha _i+\gamma _i - \beta _i^{k-1}\left( \gamma _i+ \alpha _i \beta _i\right) \right)$ for any $k\in {\mathbb {N}}$, and $Z_{i\infty }=\frac{\alpha _i+\gamma _i}{1-\beta _i}$.

Proof

See Appendix “Proof of Proposition 1” $\square$

Note that the Markov perfect equilibrium in the infinite horizon case is precisely the limit of the sequence of equilibria obtained in the finite-horizon model (as the number of periods T approaches $+\infty$). This remark illustrates the result of Theorem 1-ii). Having shown that the emission levels are given by (11), one can easily check how they vary with the parameters $\alpha _i, \beta _i, \gamma _i$. Ceteris paribus, the countries which put a high weight on a clean environment (i.e. $\alpha _i$ is high) will produce less emissions than the others. The same can be said of the countries with a high discount factor $\beta _i$. Finally, all else equal, countries with a less efficient technology (relatively high $\gamma _i$) will produce more emissions in each period.

Also observe that, in each period t of the T-period game, the n optimal emission levels ${{\hat{e}}}_{it}^T(S_{t})$ depend solely on the stock of pollution at the beginning of period t. Hence, these strategies are optimal even off the equilibrium path. In the specific case where $T=+\infty$, notice that the optimal strategy profile is stationary, that is to say: ${{\hat{e}}}_{it}^T(S_{t})\equiv {{\hat{e}}}_{i}(S_{t}), \forall t \in {\mathbb {N}}$.

Given the equilibrium emission schedules derived earlier, a question of interest is the determination of the evolution of the stock of pollution. The following result addresses this issue.

Corollary 1

The evolution of the equilibrium stock of pollution over time is given by:

$$\begin{aligned} {{\hat{S}}}_t= {{\bar{S}}}-\left( {{\bar{S}}}-S_0\right) \prod \limits _{k=T-t+1}^T \left( 1+\sum \limits _{i=1}^n \gamma _i \beta _i^{-1} (Z_{i(T-k)})^{-1}\right) ^{-1}, ~\text { for }1\le t<T.\quad \end{aligned}$$

(12)

Proof

See Appendix “Proof of Corollary 1” $\square$

When $T=+\infty$, Corollary 1 shows that the stock of pollution increases towards the critical value ${{\bar{S}}}$, which is never reached in finite time. Furthermore, comparative dynamics on the parameters shows that the stock of pollution increases at a slower (faster) rate if the discount factor $\beta _i$ (the cost parameter $\gamma _i$) is higher in any given country. Also, the more the importance given to the environment in any given country (i.e. a higher $\alpha _i$), the slower the rate at which the stock increases.

4.2 The Cooperative Emission Schedules

The proposition hereafter describes the cooperative emission schedules that would be enforced by an international social planner. This schedule solves the problem stated in (5).

Proposition 2

Under the cooperative scenario too, the countries levels of emissions in period t are proportional to the difference ${{\bar{S}}}-S_t$ between the critical stock of pollution and its current stock. For any two countries, the relative difference between the emission levels is fully explained by their different abatement technologies (characterized by the $\gamma$s), regardless of their other characteristics $(\beta , \alpha )$, which account only for the overall level of emission. Explicitly, the emissions of country i are given by:

$$\begin{aligned} \left\{ \begin{array}{ll} {{\tilde{e}}}_{it}^T(S_{t})=\frac{\gamma _i }{\sum \nolimits _{j=1}^n \left( \gamma _j+\beta _j Z_{j(T-t)}\right) }({{\bar{S}}}- S_t) &{} {~~~} t=0,1,\ldots ,T-1 \quad \text { if } ~T \text { is finite,} \\ {{\tilde{e}}}_{it}^T(S_t)=\frac{\gamma _i }{\sum \nolimits _{j=1}^n \left( \gamma _j+\beta _j Z_{j \infty }\right) } ({{\bar{S}}}- S_t) &{} \hbox {}~~~t=0,1,2,\ldots \quad \text { if } ~T \text { is infinite;} \end{array} \right. \end{aligned}$$

(13)

where the sequence $Z_j$ is defined as in (11).

Proof

See Appendix “Proof of Proposition 2” $\square$

Let us provide some intuition as to the importance of the parameters $\gamma _i$ in explaining the countries’ emission levels. In a sense, solving for the cooperative emission schedules can be viewed as a two-stage process. In the first stage, through the preferences of the countries, the optimal level for global emissions $\left( \sum \nolimits _{i=1}^n e_{it}\right)$ is determined by the trade-off between production and pollution. In the second stage, given this optimal level of emissions in each period, the planner has to split the overall emission abatement $\left( \sum \nolimits _{i=1}^n {{\bar{e}}}_{i}-\sum \nolimits _{i=1}^n e_{it}\right)$ between the n countries in a way that minimizes the overall abatement cost. As explained by Baumol and Oates (1988), this is achieved through equating the marginal cost of abatement in the different countries. In other words, the planner has to assign more emissions reductions to the more efficient countries (low $\gamma _i$), which explains why countries that are less efficient (high $\gamma _i$) emit more under the cooperative scenario —no matter what their other characteristics.

Corollary 2

Under the cooperative scenario, the evolution of the stock of pollution is given by:

$$\begin{aligned} {{\widetilde{S}}}_t= {{\bar{S}}}-\left( {{\bar{S}}}-S_0\right) \prod \limits _{k=T-t+1}^T \frac{\sum \nolimits _{i=1}^n \beta _iZ_{i(T-k)}}{\sum \nolimits _{i=1}^n \gamma _i+ \beta _iZ_{i(T-k)}}, ~\text { for }1\le t<T. \end{aligned}$$

(14)

Proof

Omitted (similar to the proof of Corollary 1). $\square$

It is not difficult to see from Corollary 2 that, under the cooperative scenario too, the stock of pollution converges to the critical level ${{\bar{S}}}$ in the infinite-horizon game. In addition, performing some comparative statics, one can easily notice two intuitive results that hold under both the strategic scenario and the cooperative one: if the initial stock $S_0$ is lower, then the stock $S_t$ is lower for all t while emissions $e_{it}$ are higher for all t.

4.3 Comparing Global Emissions Under the Two Scenarios

Given the solutions derived in Propositions 1 and 2, it seems natural to compare the stocks of pollution and the countries’ emissions under the two scenarios. The following proposition provides an answer as to the stock of pollution and the per period overall emissions.

Proposition 3

• (i) All together, the countries emit less (under the cooperative scenario) in the sense that the stock of pollution is always lower than under the non-cooperative scenario: ${{\hat{S}}}_t>{{\widetilde{S}}}_t, \forall t=1,\ldots ,T-1$.

• (ii) However, it is not true that the countries emit less in every period. In the case where $T=+\infty$, there exist $T_1, T_2$ (with $0<T_1\le T_2$ ) such that:

  $$\begin{aligned} \sum \limits _{i=1}^n {{\tilde{e}}}_{it}&< \sum \limits _{i=1}^n {{\hat{e}}}_{it}, ~~~~\forall t \text { s.t. } 0\le t <T_1, \end{aligned}$$

  (15)
  $$\begin{aligned} \sum \limits _{i=1}^n {{\tilde{e}}}_{it}&> \sum \limits _{i=1}^n {{\hat{e}}}_{it}, ~~~~\forall t \text { s.t. } T_2\le t <+\infty . \end{aligned}$$

  (16)

Proof

See Appendix “Proof of Proposition 3” $\square$

Thus, although the stock of pollution is always lower under the cooperative scenario, there necessarily is a date $T_2$ (in the distant future) such that, from $T_2$ on, the countries globally emit more (than under the Markov perfect equilibrium) in every period. The intuition for this result can be explained as follows.

Fig. 1

Evolution of emissions per region (Markov)

Fig. 2

Evolution of emissions per region (cooperation)

Fig. 3

Evolution of the pollution stock (Markov vs cooperation)

We know from Corollaries 1 and 2 that, under our specification, the pollution stocks converge to the same limit ${{\bar{S}}}$ under both scenarios (note that, for some other specification, the respective limits under the two scenarios may differ). This observation suggests that the two emission paths must cross at least once. Note that the statement of Proposition 3-(ii) is stronger, since it tells us which scenario pollutes more in early (late) periods. More specifically, given the fact that the planner takes into account the global damage of emissions (as opposed to individual damage), overall emissions in early periods, and therefore the stock $S_t$, will be lower under cooperation. But then, as time goes by, the gap ${{\bar{S}}}-S_t$ between the critical level and the actual stock will become much larger under cooperation than under non-cooperation.¹⁵ As a result, since emissions under both scenarios have been shown to be a fixed fraction of this gap, there will eventually come a date when global emissions under cooperation will exceed those under non-ccoperation. Interestingly, this finding is consistent with that of another recent work by Schmidt (2017): in a two-period model the author finds that, without uncertainty about the threshold, global abatement in the last period is always much higher (and hence emissions are always much lower) under non-cooperation.

Also note that, as a consequence of Proposition 3, it is not true that each country emits less in every period under cooperation. This observation (that some countries may emit more under cooperation) highlights a well-known result due to Folmer and von Mouche (2000) in the static framework.¹⁶

4.4 Numerical Application with Three World Regions

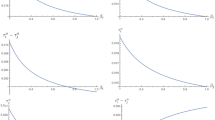
To illustrate the results of this section, let us consider the following example where there are three world regions (or countries): $R_1, R_2,R_3$. We assign the following numerical values to the parameters of the model (for the three respective regions): $\alpha _1=100$, $\alpha _2=60=\alpha _3$; $\gamma _1 = 4\simeq \gamma _2=4.1; \gamma _3=10$; $\beta _1=\beta _2=\beta _3=0.95$. Note that, for unambiguous comparisons, we have purposely chosen values such that the countries $R_1$ and $R_2$ differ in a single parameter. The same is true of $R_2$ and $R_3$. Indeed, Region 1 (industrialized countries) attaches a higher value to a clean environment than Region 2 (emerging economies). Region 3 (underdeveloped countries) has a much higher abatement cost function than Region 2. In addition, let us assume a critical threshold of ${{\bar{S}}}=1000$ parts per million for the pollution stock. For instance, developed western economies would be part of Region 1; China and India would belong to Region 2;¹⁷ and Region 3 would include the poorest nations. The following figures depict the evolution of the pollution stock, individual emissions and global emissions over the first 401 periods $(t=0,\ldots , 400)$.

Figure 1 illustrates the results of Proposition 1: Region 1 emits less than Region 2 due to a higher environmental valuation $(\alpha )$; and Region 2 emits less than Region 3, due to lower abatement costs $(\gamma )$. These differences in emissions are: (i) pronounced in early periods; and (ii) mitigated in late periods, as the countries’ emissions become very low.

Interestingly, in the following Fig. 2, the cooperative emission paths of Region 1 and Region 2 are very close, as predicted by Proposition 2. The international planner optimally assigns low abatement levels to Region 3 (due to its high abatement cost), which is why Region 3 emits the most under cooperation.

As for the pollution stock, Fig. 3 gives an illustration of Proposition 3-(i): starting in period $t=1$, the stock under cooperation is always below that under the Markov equilibrium. Under non-cooperation, it takes only 55 periods $(t=54)$ for the countries to emit half of the critical threshold $(S_t/{\bar{S}}=50\%)$, whereas the same level of pollution is reached after 180 periods under cooperation. After 401 years of non-cooperation, the countries have cumulatively emitted $99\%$ of the critical threshold. By contrast, the same countries have emitted only 80% of the threshold after 401 years of cooperation. These milestone dates are given in Table 1.

Table 1 Some important dates and ratios

Fig. 4

Evolution of global emissions (Markov vs cooperation)

In addition, Table 1 provides the evolution of the ratio of non-cooperative global emissions to cooperative ones $\left( \sum _i {{\hat{e}}}_{it}/\sum _i {{\tilde{e}}}_{it}\right)$. As shown by Fig. 4, global emissions are initially lower under cooperation. However, the gap between the two paths diminishes as time goes by and, at date $t=130$, the two paths intersect. From $T_2$ onwards, the cooperative emission path remains above the non-cooperative one. Figure 4 and Table 1 illustrate the fact that Proposition 3-(ii) (one of the main contributions of the paper) is not due to some second-order theoretical effect.¹⁸ Indeed, cooperation allows the countries to enjoy higher emissions for almost two-thirds of the 401-period horizon considered here. As can be seen from Table 1, global emissions under cooperation are ten times higher in period $t=400$. Moreover, looking carefully at Figs. 1, 2, one can see that every single region enjoys higher emissions under cooperation from $t=150$ onwards. These observations indicate that cooperation generates important gains for the countries (even more so in the presence of a critical threshold).

5 Concluding Comments

The object of this paper has been to model the incentives of the countries to abate their GHG emissions when there exists a critical pollution threshold, and to derive the subgame perfect equilibrium of the resulting strategic game. It has been shown that, whenever we consider a finite and possibly remote horizon, there exist both a subgame perfect equilibrium (in which the countries use Markov strategies) and a unique cooperative solution. Also, it has been proved that the cooperative solution (which maximizes global welfare) can be enforced by an international agency through side payments between the countries. The paper proposes a transfer scheme that, if implemented by this international agency, would result in the countries fostering the cooperative emission schedules while pursuing their individual interests. Furthermore, it has been established that all the results carry through to the infinite-horizon case if the solutions found in the finite case converge (as the horizon goes to infinity).

For the specification discussed in Sect. 4, the countries possibly differ with respect to three dimensions: the weight of a clean environment in their preferences $(\alpha _{i})$, the rate at which they discount the future $(\beta _{i})$ and their emission abatement technology $(\gamma _{i})$. In both the strategic and the cooperative scenarios, the emissions in each given period have been derived: they are proportional to the difference between the critical level and the current level of the stock of pollution. Under the non-cooperative framework, all else equal, the lower the $\alpha _{i}$ or the $\beta _{i}$ (the higher the $\gamma _i$), the greater the country’s emissions in every period. Under the cooperative scenario, countries that possess more efficient abatement technologies (i.e. $\gamma _i$ is relatively low) are allocated higher emission reductions by the international agency. It has been shown that, in every period, the stock of pollution is lower than under the non-cooperative scenario: cumulatively speaking, the countries globally emit less. In periods that are very remote in the future, however, global emissions are (rather surprisingly) higher under the cooperative scenario.

Even under the non-cooperative scenario, the critical level of the stock of pollution is never reached, and therefore the extreme version of the tragedy of the commons does not occur. Nevertheless, as seen in Sect. 3, the countries can reduce pollution and increase global welfare by acting in a concerted manner. The key to enforcing global efficiency through this optimal transfer scheme is the ability of the international agency to perfectly monitor the emissions of each of the n countries. Whether such an agency may be created and provided with the means to achieve its mandate is of course debatable; one of the contributions of this paper is the design of a transfer scheme that such an agency (if put in place) could use to efficiently compensate emission reductions.

Possible extensions of the present work include the examination of optimal transfer schemes under costly and/or imperfect monitoring of the countries’ emissions. In addition, as pointed out by the IPCC (2007), defining a real or implicit price of carbon emissions creates incentives for countries to invest in low-GHG technologies (corresponding to a lower $\gamma$). A variant of the model could be used to examine how countries should invest in cleaner technologies depending on the implicit carbon prices.

Appendix

1.1 Proof of Theorem 1

(i) Consider the case where T is finite ($T\in {\mathbb {N}}$). The proof proceeds by backward induction. Suppose that the stock in the terminal period is $S_T$. Since the overall payoff of each of the n countries is not affected by the level of pollution after date T, it is straightforward to see that the terminal conditions are $e_{iT}^T(S_T)={{\bar{e}}}_{i}$, for any $i\in N$ and $S_T\ge 0$. Therefore, given that $c_i({{\bar{e}}}_i-{{\bar{e}}}_i)=c_i(0)=0$, the continuation value of i in period $T-1$ is

$$\begin{aligned} V_i^0 \left( \delta S_{T-1}+\sum \limits _{j=1}^n e_{iT-1}\right) =U_i \left( {{\bar{y}}}_i,\delta S_{T-1}+\sum \limits _{j=1}^n e_{iT-1}\right) . \end{aligned}$$

Notice that for each country i, $V_i^0 \left( \delta S_{T-1}+\sum \nolimits _{j=1}^n e_{iT-1}\right)$ is continuous and concave in $e_{iT-1}$, since $U_i$ is concave by Assumption 1-(i).

Next, suppose that the continuation function $V^{T-t-1}_i$ of each country i is known and is concave (by the induction hypothesis). Then, given the stock $S_t$ in period t, the countries determine their optimal emissions in t by solving (3):

$$\begin{aligned} V^{T-t}_i(S_{t})= & {} \max \limits _{{\small e_{it}\in [0,{{\bar{e}}}_i]}} \left[ U_{i}\left( {{\bar{y}}}_i -c_i({{\bar{e}}}_i-e_{it}),S_t\right) +\beta _iV^{T-t-1}_i\left( \delta S_t+\sum \limits _{j=1}^n e_{jt} \right) \right] , \\&i=1,\ldots ,n. \end{aligned}$$

Observe that the countries’ emissions in period t solve this system of equations if and only they constitute a Nash equilibrium of the strategic game $\left[ N, (S_i)_{i\in N}, (v_i)_{i\in N}\right]$, where $S_i=[0,{{\bar{e}}}_i]$ and $v_i(e_{1t}, \ldots ,e_{nt})=U_i \left( {{\bar{y}}}_i-c_i({{\bar{e}}}_i-e_{it}), S_{t}\right) +\beta _iV^{T-t-1}_i\left( \delta S_t+\sum \nolimits _{j=1}^n e_{jt} \right)$. Note that $v_i$ is concave in $e_{it}$ by Assumption 1-(i), Assumption 2-(ii), and the fact that $V_i^{T-t-1}$ is concave. In addition, it is obviously continuous.

Since the payoff function of each country i is continuous and concave in $e_{it}$, and each strategy set is a compact, convex subset of ${\mathbb {R}}$, it follows that $\left[ N, (S_i)_{i\in N}, (v_i)_{i\in N}\right]$ has a pure-strategy Nash equilibrium.¹⁹ Let us denote by ${{\hat{e}}}_{1t}^T(S_t),\ldots , {{\hat{e}}}_{nt}^T(S_t)$ these equilibrium levels of emissions in period t. Replacing the right-hand side of (3) by the maximized value, one gets:

$$\begin{aligned} V^{T-t}_i(S_{t})=\left[ U_{i}\left( {{\bar{y}}}_i -c_i\left( {{\bar{e}}}_i-{{\hat{e}}}^T_{it}(S_t)\right) ,S_t\right) +\beta _iV^{T-t-1}_i\left( \delta S_t+\sum \limits _{j=1}^n {{\hat{e}}}_{jt}^T(S_t) \right) \right] . \end{aligned}$$

Using the envelope theorem along with Assumptions 1-(i), 2-(ii) and the fact that $V^{T-t-1}_i$ is concave, one can claim that $V^{T-t}$ is concave.

This ends the induction argument and proves the existence of a Markov perfect equilibrium when T is finite. Note that, in this equilibrium, the emissions ${{\hat{e}}}_{it}^T(S_t)$ in every period t are functions of the current stock pollution, which is why the subgame perfect equilibrium is in Markov strategies.

(ii) Next, let us examine the infinite-horizon case. Consider a sequence $\{({{{\hat{e}}}}^T_{i})_{i\in N}, T\in {\mathbb {N}}\}$ such that each $({{{\hat{e}}}}^T_{i})_{i\in N}$ is a Markov perfect equilibrium of the T-period truncated game. In addition, suppose that $\{({{{\hat{e}}}}^T_{i})_{i\in N}, T\in {\mathbb {N}}\}$ converges to some $\left( {{\hat{e}}}_{i}\right) _{i\in N}$, which is a Markov strategy profile in the infinite horizon game. From Theorem 3.3 in Fudenberg and Levine (1983), one can conclude that $\left( {{\hat{e}}}_{i} \right) _{i\in N}$ is a subgame perfect equilibrium of the infinite-horizon game. Observe that combining the continuity of U with Assumption 1-(iii) implies that the payoff function of the infinite-horizon game is uniformly continuous, as required by the aforementioned theorem by Fudenberg and Levine.

1.2 Proof of Theorem 2

(i) Suppose that the horizon is finite, i.e. $T\in {\mathbb {N}}$. Recalling that the planner has to solve the problem (5), note that the objective (which is a continuous function) has to be maximized over the set $\prod \limits _{i=1}^n[0,{{\bar{e}}}_i]^{T+1}$, which is compact and convex. This guarantees the existence of a solution to the maximization problem (5).²⁰ The uniqueness of this cooperative solution follows from the fact that the objective function is strictly concave -by Assumption 1-i) and Assumption 2-(ii)-. Let us denote by $[{{\tilde{e}}}^T_{it}(S_0)]_{i=1,\ldots ,n}^{t=0,\ldots ,T}$ this unique solution to the planner’s problem.

(ii) Next, consider the infinite-horizon case and suppose that $\lim \limits _{T\rightarrow \infty }{{\tilde{e}}}_{i0}^T(S_0)$ exists in ${\mathbb {R}}$ for any $S_0\in [0,{{\bar{S}}})$. Note that this implies: $\lim \limits _{T\rightarrow \infty }{{\tilde{e}}}_{it}^{T}(S_0)\in {\mathbb {R}}$, for any fixed $t\in {\mathbb {N}}$.²¹ Thus, the sequence of cooperative solutions converges (as T goes to infinity) to some strategy profile of the infinite-horizon game. Similarly to what was done for the proof of Theorem 1, one can claim that the limit of this sequence of cooperative emission schedules is a cooperative solution of the infinite-horizon game. The uniqueness, once again, comes from the fact that the objective function is strictly concave.

1.3 Proof of Theorem 3

Suppose that $T\in {\mathbb {N}}$ and consider the strategic game that takes place when the countries determine their emissions in the presence of the transfer scheme $\tau$ defined in (8). Denote by ${\check{e}}$ a subgame perfect equilibrium and by ${\check{V}}_i^{T}$ country i’s value function in this Markov perfect equilibrium, that is to say,

$$\begin{aligned} {\check{V}}^T _i(S_0)=\sum \limits _{t=0}^T ~ \beta _i^t U_{i}\left( {{\bar{y}}}_i-c_i({{\bar{e}}}_i -{\check{e}}_{it}),{\check{S}}_t\right) , \text { where } {\check{S}}_{t+1}= \delta {\check{S}}_t+\sum \limits _{j=1}^n {\check{e}}_{it} \text { and } {\check{S}}_{0}=S_0. \end{aligned}$$

One can use backward induction to see that ${\check{e}}^T_{it}={{\widetilde{e}}}^T_{it}$ and ${\check{V}}_i^{t}=W_i^t$, for any $t\in \{0,1,\ldots ,T\}$. Since the utilities of the countries do not depend on the stock after T, we must have ${\check{e}}^T_{it}(S_T)={{\bar{e}}}_i={{\widetilde{e}}}^T_{it}(S_T)$, for any $i\in N$ and $S_T< {{\bar{S}}}$. It follows that ${\check{V}}_i^0 \left( S_{T}\right) =U_i \left( {{\bar{y}}}_i, S_{T}\right) ={{\widetilde{W}}}_i^0(S_T)$.

By the induction hypothesis, suppose then that ${\check{V}}^{T-t-1}_i={{\widetilde{W}}}^{T-t-1}_i$ for any $i\in N$. The first-order conditions defining the equilibrium of the game with transfers are very similar to (4), except for the fact that the transfers received from the other countries must be added as a fallout of a marginal reduction of emissions by country i in period t:²²

$$\begin{aligned}&c_i'({{\bar{e}}}_i-e_{it})U_{iy}\left( {{\bar{y}}}_i -c_i({{\bar{e}}}_i-e_{it}),S_t\right) \nonumber \\&\quad +\, \beta _i \left( {\check{V}}^{T-t-1}_i \right) ' \left( \delta S_t+\sum \limits _{j=1}^n e_{jt}\right) - \sum \limits _{j\ne i} \tau _{j}\left( t,\delta S_t+\sum \limits _{j=1}^n e_{jt} \right) =0, \end{aligned}$$

(17)

$\forall i\in N, ~\forall t \text { such that } 0\le t<T$. Next, taking $S_{t+1}=\delta S_t+\sum \nolimits _{i=j}^{n}e_{jt}$, one has to notice from (8) that:

$$\begin{aligned} -\tau _{j}(t,S_{t+1})= & {} \sum \limits _{p=1}^{T-t} \beta ^{p}_j U_{jS}\left( {{\bar{y}}}_j,{{\widetilde{S}}}'_{t+p}\right) =\beta _j \sum \limits _{p'=0}^{T-t-1} \beta _j^{p'} U_{jS}\left( {{\bar{y}}}_j,{{\widetilde{S}}}'_{t+p'+1}\right) \\= & {} \beta _j \left( {{\widetilde{W}}}_j^{T-t-1}\right) '\left( \delta S_t+\sum \limits _{i=j}^{n}e_{jt}\right) . \end{aligned}$$

Note that we can use ${{\widetilde{W}}}_j^{T-t-1}$ above because the transfers (8) are defined using the cooperative stocks ${{\widetilde{S}}}'_{t+p}$: we thus get i’s value for the cooperative problem starting at $t+1$.

Since ${\check{V}}^{T-t-1}_i={{\widetilde{W}}}^{T-t-1}_i$ for any $i\in N$, it then follows that the tuple $(e_{1t},\ldots ,e_{nt})$ is a solution to the system (17) if and only if it satisfies:

$$\begin{aligned}&c_i'({{\bar{e}}}_i-e_{it})U_{iy}\left( {{\bar{y}}}_i-c_i({{\bar{e}}}_i-e_{it}),S_t\right) +\beta _i \left( {{\widetilde{W}}}^{T-t-1}_i \right) '\left( \delta S_t+\sum \limits _{j=1}^n e_{jt} \right) \end{aligned}$$

(18)

$$\begin{aligned}&\quad + \sum \limits _{j\ne i}\beta _j \left( {{\widetilde{W}}}^{T-t-1}_j \right) '\left( \delta S_t+\sum \limits _{j=1}^n e_{jt} \right) =0, \nonumber \\&\qquad \forall i\in N, ~\forall t \text { such that } 0\le t<T.~~~ \end{aligned}$$

(19)

To conclude the argument, one has to notice that (7) and (18) are identical. Hence, they have the same unique solution,²³ that is to say, ${\check{e}}^T_{it}(S_t)={{\widetilde{e}}}^T_{it}(S_t)$ and ${\check{V}}_i^{T-t}(S_t)={{\widetilde{W}}}_i^{T-t}(S_t)$ for any $t\in {\mathbb {N}}$ and any $S_t<{{\bar{S}}}$.

For the case where $T=+\infty$, looking at the common limit (when it exists) of the sequences $({\check{e}}^T_{i})_{T\in {\mathbb {N}}}$ and $({{\widetilde{e}}}^T_{i})_{T\in {\mathbb {N}}}$ and using once again the result by Fudenberg and Levine (1983) gives the desired result.

1.4 Proof of Proposition 1

Let us first examine the case where T is finite ($T\in {\mathbb {N}}$). Since the objective function of the problem (2) facing country i does not depend on the level of pollution after period T, it is straightforward to see that ${{\hat{e}}}_{it}^T(S_T)={{\bar{e}}}_{i}$. Given that $c_i(0)=0$, the continuation value of i in period $T-1$ is $V_i^0(S_{T-1}+\sum \nolimits _{j=1}^n e_{jt} )=U_{i}\left( {{\bar{y}}}_i, S_{T-1}+\sum \nolimits _{j=1}^n e_{jT-1}\right)$. Writing the first-order conditions (4), and using $U_i(y_{it},S_t)=y_{it}+\alpha _i \ln ({{\bar{S}}}-S_t)$ along with , one can form the following system of n linear equations with n unknowns:

$$\begin{aligned} e_{iT-1}=\gamma _i\alpha _i^{-1} \beta _i^{-1}\left( {{\bar{S}}}- S_{T-1}-\sum \limits _{j=1}^n e_{jT-1}\right) \quad i=1,\ldots ,n. \end{aligned}$$

(20)

Solving this system gives $e_{iT-1}=\frac{\gamma _i \beta _i^{-1}\alpha _i ^{-1}}{1+\sum \nolimits _{j =1}^n \gamma _j \beta _j^{-1}\alpha _i^{-1}}~ ({{\bar{S}}}- S_{T-1})$. The value $V_i^1\left( S_{T-1}\right)$ can then be derived. Proceeding backwards and using (4) likewise, one can derive ${{\hat{e}}}_{it}^T(S_{t})$, for $t=0,1,\ldots ,T-1$ and $i=1,\ldots ,n$. A fair amount of algebra shows that

$$\begin{aligned} \left\{ \begin{array}{ll} {{\hat{e}}}_{it}^T(S_{t})=\frac{\gamma _i \beta _i^{-1}\left( Z_{i(T-t)}\right) ^{-1}}{1+\sum \nolimits _{j =1}^n \gamma _j \beta _j^{-1}\left( Z_{j(T-t)}\right) ^{-1}}~ ({{\bar{S}}}- S_t) &{} ~~\hbox {for } t=0,1,\ldots ,T-1 \\ {{\hat{e}}}_{it}^T(S_{T})={{\bar{e}}}_{iT}, &{} \hbox {} \end{array} \right. \end{aligned}$$

(21)

where $Z_{i}$ is an arithmetico-geometric sequence satisfying $Z_{ik+1}=(\alpha _i+\gamma _i)+\beta _i Z_{ik}$, with $Z_{i1}=\alpha _i$. In other words, $Z_{ik}=\frac{1}{1-\beta _i} \left( \alpha _i+\gamma _i - \beta _i^{k-1}\left( \gamma _i+ \alpha _i \beta _i\right) \right) ,~ k=1,2,3,\ldots$

It is then easy to see that the values of the game can be written as $V_i^T(S)= \kappa _i \ln ({{\bar{S}}}- S)+\eta _i$, where $\kappa _i$ and $\eta _i$ are constants that depend on the parameters $T,~\alpha _i,~\beta _i,~ \gamma _i~ (i=1,\ldots ,n )$.

Deriving the equilibrium is somewhat easier when the horizon is infinite. Indeed, for the specific case $T=+\infty$, the continuation function $V^{T-t-1}_i$ is the same, regardless of the current period. One can therefore write the Bellman equation for every player $i\in N$ as:

$$\begin{aligned} V_i^\infty (S_{t})=\max \limits _{{\small e_{it}\in [0,{{\bar{e}}}_i]}} \left[ ~U_{i}\left( {{\bar{y}}}_i-c_i({{\bar{e}}}_i -e_{it}),S_t\right) +\beta _i V_i^\infty \left( S_t+\sum \limits _{j=1}^n e_{jt} \right) \right] \end{aligned}$$

(22)

The first-order conditions allowing to determine the current emission levels in the Nash equilibrium are then:

$$\begin{aligned} c_i '({{\bar{e}}}_i-e_{it})U_{iy}\left( {{\bar{y}}}_i -c_i({{\bar{e}}}_i-e_{it}),S_t\right) +\beta _i \left( V_i^\infty \right) '\left( S_t+\sum \limits _{j=1}^n e_{jt} \right) =0,~~{\tiny \forall i\in N, \forall t\in {\mathbb {N}}}\nonumber \\ \end{aligned}$$

(23)

In general, the solution to such a problem can be obtained by using the envelope theorem and solving the differential system obtained from (23). Based on the result derived in the finite case, let us instead conjecture that the value function of country i is of the form:²⁴ $V_i^\infty (S)= \sigma _i \ln ({{\bar{S}}}- S)+\epsilon _i$. Substituting this into (23) and solving for country i’s emission schedule yields:

$$\begin{aligned} {{\hat{e}}}_{it}^T(S_t)=\frac{\gamma _i \beta _i^{-1} \sigma _i^{-1}}{1+\sum \nolimits _{j=1}^n \gamma _j \beta _j^{-1} \sigma _j^{-1}} ({{\bar{S}}}-S_t),~~~t=0,1,2,\ldots \end{aligned}$$

(24)

Finally, substituting ${{\hat{e}}}_{it}^T(S_t)$ and the $n-1$ other emission levels in (22) shows that the guess is indeed right for $\epsilon _i=\frac{1}{1-\beta _i}\left[ {{\bar{y}}}_i+\gamma _i \ln \left( \gamma _i \beta _i^{-1} \sigma _i^{-1}\right) -(\gamma _i+\beta _i \sigma _i)\ln \left( 1+\sum \limits _{j=1}^n \gamma _j \beta _j^{-1} \sigma _j^{-1}\right) \right]$ and $\sigma _i= \frac{\alpha _i+\gamma _i}{1-\beta _i}=Z_{i\infty }.$

1.5 Proof of Corollary 1

From (11), it is easy to see that

$$\begin{aligned} \sum \limits _{i=1}^n{{\hat{e}}}_{ik}^T({{\hat{S}}}_{k}) =\frac{\sum \nolimits _{i=1}^n\gamma _i \beta _i^{-1} (Z_{i(T-k)})^{-1}}{1+\sum \nolimits _{i=1}^n \gamma _i \beta _i^{-1} (Z_{i(T-k)})^{-1}}({{\bar{S}}}-{{\hat{S}}}_k), \end{aligned}$$

in each period k such that $0\le k< T$. Next, define ${{\hat{r}}}_k=\frac{\sum \nolimits _{i=1}^n\gamma _i \beta _i^{-1} (Z_{i(T-k)})^{-1}}{1+\sum \nolimits _{i=1}^n \gamma _i \beta _i^{-1} (Z_{i(T-k)})^{-1}}$, that is to say

$$\begin{aligned} 1-{{\hat{r}}}_k=\left( 1+\sum \limits _{i=1}^n \gamma _i \beta _i^{-1} (Z_{i(T-k)})^{-1}\right) ^{-1}. \end{aligned}$$

From the law of motion (1), it then follows that ${{\hat{S}}}_{k+1}={{\hat{S}}}_{k}+{{\hat{r}}}_k ({{\bar{S}}}-{{\hat{S}}}_k)$. In other words, we have: ${{\bar{S}}}-{{\hat{S}}}_{k+1}=(1-{{\hat{r}}}_k) ({{\bar{S}}}-{{\hat{S}}}_k), ~k=0,\ldots ,T-1.$ It finally follows that, for each period t (with $1\le t<T$), we have:

$$\begin{aligned} {{\bar{S}}}-{{\hat{S}}}_{t}= & {} (1-{{\hat{r}}}_{t-1}) ({{\bar{S}}}-{{\hat{S}}}_{t-1})=(1-{{\hat{r}}}_{t-1}) (1-{{\hat{r}}}_{t-2})({{\bar{S}}}-{{\hat{S}}}_{t-2}) \\= & {} \ldots = (1-{{\hat{r}}}_{t-1})\ldots (1-{{\hat{r}}}_{0}) ({{\bar{S}}}-S_{0}). \end{aligned}$$

In the case where the terminal period T is finite, notice that Eq. (12) also holds in period T.

1.6 Proof of Proposition 2

First consider the case of a finite terminal date $T\in {\mathbb {N}}$. Once again, since the objective function of the planner’s problem [see (5)] does not depend on the stock of pollution after the terminal period T, the optimal levels of emissions in period T are ${{\tilde{e}}}_{it}^T(S_T)={{\bar{e}}}_i, ~\forall i\in N$. One can then write the continuation value of each of the n countries after period $T-1$ as: ${{\widetilde{W}}}_{i}^0(S_{T-1}+ \sum \nolimits _{j=1}^n e_{jT-1})=U_{i} \left( {{\bar{y}}}_i, S_{T-1}+\sum \nolimits _{j=1}^n e_{jT-1} \right)$. Similar to what was done in the non-cooperative case, the emissions of the countries in period $t\in \{0,1\ldots ,T-1\}$ can be derived from the first-order conditions (7) by backward induction. At the end of the procedure, the generic term of the emissions of country can be written as ${{\widetilde{e}}}_{it}(S_{t})=\frac{\gamma _i }{\sum \nolimits _{j=1}^n \left( \gamma _j+\beta _j Z_{j(T-t)}\right) }({{\bar{S}}}- S_t)$   (for $t=0,1,\ldots ,T-1)$, where Z is the sequence introduced in Proposition 2.

In the case where $T=+\infty$, the procedure “guess and verify”, once again, gives the emission levels described by (13).

1.7 Proof of Proposition 3

(i) Recall that ${{\hat{r}}}_{k}=\frac{\sum \nolimits _{i=1}^n \gamma _i \beta _i^{-1} (Z_{j(T-k)})^{-1}}{1+\sum \nolimits _{i=1}^n \gamma _i \beta _i^{-1} (Z_{i(T-k)})^{-1}}$ and define ${{\tilde{r}}}_k=\frac{\sum \nolimits _{i=1}^n\gamma _i}{\sum \nolimits _{i=1}^n \left( \gamma _i+\beta _i Z_{i(T-k)}\right) }$, for $k<T$.

From Corollaries 1 and 2, one can write

$$\begin{aligned} {{\hat{S}}}_t= & {} {{\bar{S}}}-\left( {{\bar{S}}}-S_0\right) \prod \limits _{k=T-t+1}^T (1-{{\hat{r}}}_{k}), ~\text { for }1\le t<T;\\ {{\widetilde{S}}}_t= & {} {{\bar{S}}}-\left( {{\bar{S}}}-S_0\right) \prod \limits _{k=T-t+1}^T (1-{{\tilde{r}}}_k), ~\text { for }1\le t<T. \end{aligned}$$

Showing that ${{\hat{r}}}_k>{{\tilde{r}}}_k$ (for every $k<T$) is then sufficient to guarantee the desired result, ${{\hat{S}}}_t<{{\widetilde{S}}}_t$.

First, observe that

$$\begin{aligned} {{\hat{r}}}_k=&\frac{\sum \nolimits _{i=1}^n \gamma _i \beta _i^{-1} (Z_{i(T-k)})^{-1}}{1+\sum \nolimits _{i=1}^n \gamma _i \beta _i^{-1} (Z_{i(T-k)})^{-1}}=\frac{1}{1+\left( \sum \nolimits _{i=1}^n \gamma _i \beta _i^{-1} (Z_{i(T-k)})^{-1}\right) ^{-1}} ;\\ {{\tilde{r}}}_k=&\frac{\sum \nolimits _{i=1}^n\gamma _i}{\sum \nolimits _{i=1}^n \left( \gamma _i+\beta _i Z_{i(T-k)}\right) }= \frac{1}{1+\left( \frac{\sum \nolimits _{i=1}^n \beta _i Z_{i(T-k)}}{\sum \nolimits _{i=1}^n \gamma _i}\right) }. \end{aligned}$$

Thus, we have ${{\hat{r}}}_k>{{\tilde{r}}}_k$ if and only if $\frac{1}{\sum \nolimits _{i=1}^n \gamma _i \beta _i^{-1} (Z_{i(T-k)})^{-1}}<\frac{\sum \nolimits _{i=1}^n \beta _i Z_{i(T-k)}}{\sum \nolimits _{i=1}^n \gamma _i}$, that is, if and only if

$$\begin{aligned} \sum \limits _{i=1}^n \gamma _i < \left( \sum \limits _{i=1}^n \gamma _i \beta _i^{-1} (Z_{i(T-k)})^{-1}\right) \left( \sum \limits _{i=1}^n \beta _i Z_{i(T-k)} \right) . \end{aligned}$$

(25)

Finally, observe that (25) indeed holds as a consequence of Hölder’s inequality (with $p=q=1$).²⁵ Notice that the inequality is strict because $\gamma _i, \beta _i, Z_i$ are all positive, for every $i\in N.$

(ii) From (11) and (13), one gets respectively

$$\begin{aligned} \sum \limits _{i=1}^n {{\hat{e}}}_{it}= & {} {{\hat{r}}}_t \left( {{\bar{S}}}-{{\hat{S}}}_t\right) ;\nonumber \\ \sum \limits _{i=1}^n{{\tilde{e}}}_{it}= & {} {{\tilde{r}}}_t \left( {{\bar{S}}}- {{\widetilde{S}}}_t\right) . \end{aligned}$$

(26)

For $T=+\infty$, we have ${{\hat{r}}}_t={{\hat{r}}}_\infty =\frac{\sum \nolimits _{i=1}^n \gamma _i \beta _i^{-1} (Z_{i\infty })^{-1}}{1+\sum \nolimits _{i=1}^n \gamma _i \beta _i^{-1} (Z_{i\infty })^{-1}}~$ and ${{\tilde{r}}}_t={{\tilde{r}}}_\infty =\frac{\sum \nolimits _{i=1}^n\gamma _i}{\sum \nolimits _{i=1}^n \left( \gamma _i+\beta _i Z_{i\infty }\right) }$, for any t. Similar to what was previously done with ${{\hat{r}}}_k$ and ${{\tilde{r}}}_k$, it can be shown that $1>{{\hat{r}}}_\infty>{{\tilde{r}}}_\infty >0$. Then, by using Corollaries 1 and 2 in (26), it follows that

$$\begin{aligned} \sum \limits _{i=1}^n {{\hat{e}}}_{it}= & {} {{\hat{r}}}_\infty \left( 1-{{\hat{r}}}_\infty \right) ^t({{\bar{S}}}-S_0);\nonumber \\ \sum \limits _{i=1}^n{{\tilde{e}}}_{it}= & {} {{\tilde{r}}}_\infty \left( 1-{{\tilde{r}}}_\infty \right) ^t({{\bar{S}}}-S_0). \end{aligned}$$

(27)

Define $f_t$ by $f_t(r)=r \left( 1-r\right) ^t$. The function $f_0(r)=r$ is increasing in r. Thus, in period $t=0$, since ${{\hat{r}}}_\infty >{{\tilde{r}}}_\infty$, we have $\sum \nolimits _{i=1}^n {{\hat{e}}}_{i0}=f_0({{\hat{r}}}_\infty )({{\bar{S}}}-S_0)> \sum \nolimits _{i=1}^n{{\tilde{e}}}_{i0}=f_0({{\tilde{r}}}_\infty )({{\bar{S}}}-S_0)$. Examining the variations of $f_t(r)$ for any $t\ge 1$, one can see that the unique maximum of $f_t$ in the interval [0, 1] is reached at $r=1/(t+1)$. It follows that for every period t such that ${{\hat{r}}}_\infty <1/(t+1)$, we have $f_t({{\tilde{r}}}_\infty )<f_t({{\hat{r}}}_\infty )$ and therefore, $\sum \nolimits _{i=1}^n{{\tilde{e}}}_{it}<\sum \nolimits _{i=1}^n {{\hat{e}}}_{it}$. On the other hand, when ${{\tilde{r}}}_\infty > 1/(t+1)$, we have $f_t({{\tilde{r}}}_\infty )>f_t({{\hat{r}}}_\infty )$ and hence, $\sum \nolimits _{i=1}^n{{\tilde{e}}}_{it}>\sum \nolimits _{i=1}^n {{\hat{e}}}_{it}$. Finally, given that $\frac{1}{t+1}$ decreases towards 0 (as t grows large), one can conclude that there exist $T_1, T_2$ as in Proposition 3.