Abstract
This paper analyses the effects of tax competition on environmental product quality, pollution and welfare in a two-country, vertically differentiated, international duopoly, in which consumers are environmentally conscious. The firm in each country chooses first the environmental quality of its product (which reflects the emissions generated in the production process) and then the price. In equilibrium one country will be more polluted than the other because firms choose different levels of environmental quality of their products. We find that a country’s optimal commodity tax is higher if the domestic firm is the more polluting supplier. Furthermore, non-cooperative commodity tax rates are inefficiently high in equilibrium. This is because, in this framework with environmentally aware consumers, commodity taxes affect the choice of firms regarding their emissions. Therefore, a domestic tax reduction not only raises the profits of the foreign firm but also lowers its emission levels, resulting in higher welfare for the other country. We also analyse the optimal cooperative and non-cooperative commodity and emission taxes with border tax adjustments. With these two policy instruments available, commodity taxes are higher.
Similar content being viewed by others
Notes
Shade-grown coffee is cultivated under a canopy of trees, providing a habitat for wildlife. Dolphin-safe tuna is tuna caught without harming or killing dolphins.
A paper that departs from a one country model in this literature is that of Petropoulou (2013) who, in a vertically differentiated international duopoly model, explores under international trade, the unilateral minimum quality standards and the global welfare-maximizing international standard.
The environmental product quality represents how environmentally friendly the product is. It is measured by the level of emissions that is generated during the production process.
Consider the example of cotton fabrics, that have their biggest environmental impact during manufacturing. Some firms choose to use environmentally-friendly methods in the processes of dyeing, printing, bleaching and finishing. In many other industries, firms adopt techniques that reduce the air, water, or land pollution during manufacturing or transportation.
Under an origin principle of taxation, taxes are levied by the country where the good is produced.
Under a destination principle of taxation, commodities are taxed in the country in which they are consumed.
A consumption-based emission tax is a production-based tax combined with BTAs.
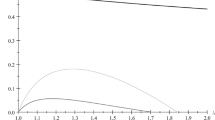
As we will see later on, in equilibrium the two firms will choose a different level of environmental quality, i.e., the one will pollute more than the other.
Although the tax per unit of emissions in each country is the same for both firms, the amount that each firm has to pay in emission taxation is not the same in that it is proportional to its emissions level.
The case in which countries have different degree of consumers’ environmental awareness is discussed in Sect. 4 of the paper.
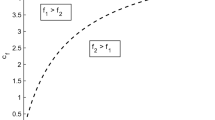
The following condition must hold for the optimal non-cooperative tax rates to be positive: \(a<1.\)
Following from (10), \(a>\frac{1}{4}\) so as \(q_{l}>0\).
Comparing (14) and (18) gives \(t_{CT}-t_{CT}^{c}=\frac{2\left( 228a+77+64a^{3}+144a^{2}\right) }{\left[ 16a\left( 1+a\right) +13\right] \left[ 16a\left( 1+a\right) +25\right] }>0,\) \(~t_{DT}-t_{DT}^{c}=\frac{ 2\left( 4a+5)(40a+16a^{2}+31\right) }{\left[ 16a\left( 1+a\right) +13\right] \left[ 16a\left( 1+a\right) +25\right] }>0.\)
It is straightforward to show that \(t_{CT}^{c}<t_{C}^{c}\) and \( t_{DT}^{c}<t_{D}^{c}.\)
This follows directly from Eq. (26) in “Appendix”.
Note that the tax rates are negative. The reason for this is that subsidies increase the consumption of the vertically differentiated product (note that the market in this case is not covered) and thus correct the distortion arising from imperfect competition.
References
Bansal S (2008) Choice and design of regulatory instruments in the presence of green consumers. Resour Energy Econ 30:345–368
Bansal S, Gangopadhyay S (2003) Tax/subsidy policies in the presence of environmentally aware consumers. J Environ Econ Manag 45:333–355
Brecard D (2013) Environmental quality competition and taxation in the presence of green network effect among consumers. Environ Resour Econ 54(1):1–19
Cremer H, Gahvari F (2005) Environmental taxation in open economies: unilateralism or partial harmonization. South Econ J 72:352–371
Cremer H, Gahvari F (2006) Which border taxes? Origin and destination regimes with fiscal competition in output and emission taxes. J Public Econ 90(10–11):2121–2142
Garella PG, Lambertini L (2014) Bidimensional vertical differentiation. Int J Ind Organ 32:1–10
Galera F, Mendi P, Molero JC (2014) Unit taxes and ad valorem taxes with vertically differentiated products. Appl Econ Lett 21(17):1221–1225
Haufler A, Pflüger M (2007) International oligopoly and the taxation of commerce with revenue constrained governments. Economica 74:451–473
Herguera I, Kujal P, Petrakis E (2002) Tariffs, quality reversals and exit in vertically differentiated industries. J Int Econ 58(2):467–492
Jakob M, Marschinski R, Hübler M (2013) Between a rock and a hard place: a trade-theory analysis of leakage under production- and consumption-based policies. Environ Resour Econ 56(1):47–72
Keen M, Kotsogiannis C (2013) Coordinating climate and trade policies: Pareto efficiency and the role of border tax adjustments. J Int Econ 94(1):119–128
Koonsed P (2015) Optimal policy under duopoly with environmental quality. Econ Bull 35(3):1976–1984
Lockwood B (2001) Tax competition and tax co-ordination under destination and origin principles: a synthesis. J Public Econ 81(2):279–319
Moraga-Gonzalez JL, Padron-Fumero N (2002) Environmental policy in a green market. Environ Resour Econ 22:419–447
Petropoulou D (2013) Vertical product differentiation, minimum quality standards and international trade. Oxf Econ Pap 65(2):372–393
Acknowledgements
The research project is implemented within the framework of the Action “Supporting Postdoctoral Researchers” of the Operational Program “Education and Lifelong Learning” (Action.s Bene.ciary: General Secretariat for Research and Technology) and is co-financed by the European Social Fund (ESF) and the Greek State.
Author information
Authors and Affiliations
Corresponding author
Appendix
Appendix
1.1 Proof of Equation (10)
Maximization of (5), after substituting (9) and (3), give the following first order conditions
Solving simultaneously the first order conditions for profit maximization gives the following three equilibria.
The last pair is the only one that satisfies the second order conditions.
1.2 Proof of Equations (14) and (18)
Substituting the Eqs. (4)–(7) in (8) gives
An analogous condition applies to the other country.
After using (2), (3), (9) and (10), the welfare becomes
We maximize the above expressions with respect to \(t_{C}\) and \(t_{D}.\) The solution of the first order conditions \(\frac{dW_{C}}{dt_{C}}=0\) and \(\frac{ dW_{D}}{dt_{D}}=0\) gives the non-cooperative taxes
By setting \(a_{C}=a_{D}=a\) in the above expression we get the non-cooperative taxes in (14).
Maximizing the joint welfare of the two countries i.e., \(\underset{ t_{C},t_{D}}{\max }(W_{C}+W_{D})\), gives
The cooperative taxes in (18) can be obtained by setting \(a_{C}=a_{D}=a.\)
1.3 Proof of Proposition 2
Suppose that both countries raise their commodity tax simultaneously. By the first order conditions \(\frac{dW_{C}}{dt_{C}}=0\) and \(\frac{dW_{D}}{dt_{D}} =0 \), a country’s increase in tax has a zero first-order impact on its welfare. However, its welfare changes from a rise in the neighboring country’s tax. As one can see from (17), \(\frac{dW_{C}}{ dt_{D}}=-\left[ \frac{3}{4}(1-t_{D})+\frac{1}{2}\left( a+\frac{5}{4}\right) \right] \) and \(\frac{dW_{D}}{dt_{C}}=-\left[ \frac{3}{4}(1-t_{C})+\frac{1}{2} \left( a-\frac{1}{4}\right) \right] .\) Since both tax rates are lower than one [as one can see from (14)] and \(a\geqslant \frac{ 1}{4}\), both \(\frac{dW_{C}}{dt_{D}}\) and \(\frac{dW_{D}}{dt_{C}}\) are negative. Therefore welfare in each country is strictly increased by a reduction in tax rates. Moreover, using (13) one can show that pollution in each country is decreased by a reduction in tax rates since \( \frac{\partial Z_{C}}{\partial t_{C}}+\frac{\partial Z_{C}}{\partial t_{D}} =a+\frac{5}{4}>0\) and \(\frac{\partial Z_{D}}{\partial t_{D}}+\frac{\partial Z_{D}}{\partial t_{C}}=a-\frac{1}{4}>0.\)
The second part of the proposition follows directly from the expressions (19) and (20).
1.4 Proof of Equation (21)
Substituting the Eqs. (4)–(7) in (8) gives
An analogous condition applies to the other country. After using (2), (3), (9) and (10 ), the welfare becomes
To obtain the non-cooperative emissions tax \(t_{i}^{e}\) and the non-cooperative commodity tax \(t_{i},\) each country solves \(\underset{t_{i},t_{i}^{e}}{\max }(W_{i})\). The first-order conditions for the choice of \(t_{C}\) and \(t_{C}^{e}\) are
The first-order conditions for the choice of \(t_{D}\) and \(t_{D}^{e}\) are
Solving simultaneously the first-order conditions we get
By setting \(a_{C}=a_{D}=a\) we can find the optimal non-cooperative taxes in (21).
1.5 Proof of Equations (22) and (25)
In the cooperative equilibrium both countries choose their taxes to maximize the joint welfare i.e., \(\underset{t_{C},t_{D},t_{C}^{e},t_{D}^{e}}{\max } (W_{C}+W_{D}).\) Adding (28) and (29) and maximizing it with respect to \(t_{C},t_{D},t_{C}^{e},t_{D}^{e}\) yields
We solve the first order conditions simultaneously to obtain Eq. (25)
and after setting \(a_{C}=a_{D}=a\) we get the cooperative taxes in (22).
1.6 Proof of Proposition 4
Using (21) and (22), we can show that
1.7 Partially Covered Market: Numerical Example
When the market is not covered there is a consumer in each country, denoted by \(\tilde{\theta }_{i}\), who is indifferent between buying the low-quality version of the product and not buying it at all, therefore \(u_{li}=0.\) Following (1), one obtains
The demand functions are given by
We denote \(\tau _{i}=\frac{1}{1-t_{i}}\) to simplify calculations. In the case of commodity tax competition, the profit functions for the high-and low-quality firms are given by
Maximizing profits with respect to prices, given quality levels and tax rates gives
Suppose now that \(a_{C}=a_{D}=0\) and \(E=2\). Maximizing profits with respect to qualities and solving simultaneously the first-order conditions gives the environmental product quality levels
Following the same steps as in Sect. 3.1, after using the equations above, we obtain the following optimal cooperative and non-cooperative tax rates: \( t_{DT}=-0.2,t_{CT}=-0.6\) and \(t_{DT}^{c}=t_{CT}^{c}=-1.5\).
1.8 Cournot Competition: Numerical Example
In the case of Cournot competition and non covered market we get the inverse demand functions, after using (31) and (2) in (32)
It can be easily shown that maximizing (33) with respect to quantities after using (36) gives
Suppose now that the parameters are \(a_{C}=a_{D}=0\) and \(E=2\). One can find the solution of the second stage of the game by substituting (37) in (33) and then maximizing with respect to the environmental product qualities. Solving simultaneously the first-order conditions gives
Following the same steps as in Sect. 3.1, after using the equations above, we obtain the following optimal cooperative and non-cooperative tax rates: \( t_{DT}=-0.15,t_{CT}=-0.09\) and \(t_{DT}^{c}=t_{CT}^{c}=-1.26\).
1.9 Case 1 Firms produce the high environmental quality good for domestic consumption and the low environmental quality good for their exports
Suppose that the two firms produce the high environmental quality good for domestic consumption and the low environmental quality good for their exports. Let \(\Pi _{C}\) denote the profits of the firm located in country C and \(\Pi _{D}\) the profits of the firm located in country D. Then the profits are
Moreover the total pollution that is generated by the production in each country is
The solution of the last stage, in which firms maximize profits with respect to prices, given quality levels and tax rates, is the same as in Eq. (9). In the second stage we maximize (39) with respect to the quality levels. Solving simultaneously the first order conditions \(\frac{\partial \Pi _{C}}{\partial q_{hC}}=0\), \(\frac{ \partial \Pi _{D}}{\partial q_{lC}}=0\) and \(\frac{\partial \Pi _{C}}{ \partial q_{lD}}=0\), \(\frac{\partial \Pi _{D}}{\partial q_{hD}}=0\) gives the same environmental product quality levels as in (10). The optimal non-cooperative tax rates are determined by maximizing national welfare, i.e., \(\underset{t_{C}}{\max }W_{C}\) and \(\underset{t_{D}}{\max } W_{D},\) after using (39), (40), (6) and (7)
By maximizing the joint welfare of the two countries, it is straightforward to derive the cooperative taxes which are the same as in (18).
1.10 Case 2 Firms produce the low environmental quality good for domestic consumption and the high environmental quality good for their exports
The profits in this case are
The total pollution that is generated by the production in each country is
Following the same steps as in Case 1, one can find the optimal non-cooperative tax rates
while the cooperative taxes are the same as in (18).
Rights and permissions
About this article
Cite this article
Karakosta, O. Tax Competition in Vertically Differentiated Markets with Environmentally Conscious Consumers. Environ Resource Econ 69, 693–711 (2018). https://doi.org/10.1007/s10640-016-0097-0
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10640-016-0097-0