Zero-correlation linear cryptanalysis of reduced-round LBlock

Abstract

Zero-correlation linear attack is a new method developed by Bogdanov et al. (ASIACRYPT 2012. LNCS, Springer, Berlin, 2012) for the cryptanalysis of block ciphers. In this paper we adapt the matrix method to find zero-correlation linear approximations. Then we present several zero-correlation linear approximations for 14 rounds of LBlock and describe a cryptanalysis for a reduced 22-round version of LBlock. After biclique attacks on LBlock revealed weaknesses in its key schedule, its designers presented a new version of the cipher with a revised key schedule. The attack presented in this paper does not exploit the structure of the key schedule or S-boxes used in the cipher. As a result, it is applicable to both variants of the LBlock as well as the block ciphers with analogous structures like TWINE. Moreover, we performed simulations on a small variant LBlock and present the first experimental results on the theoretical model of the multidimensional zero-correlation linear cryptanalysis method.

Appendices

Appendix 1: Lemmas

To describe the encryption or the decryption round, we can use the following lemmas:

Lemma 1

XOR operation: Let $f(x_1,x_2)=x_1 \oplus x_2$. Then the correlation of linear approximation $u_1\cdot x_1 + u_2 \cdot x_2= v \cdot f(x_1, x_2)$ is non-zero if and only if $u_1=u_2=v$.

Lemma 2

Branching operation: Let $f(x)=(x,x)$. Then the correlation of linear approximation $u_1 \cdot x+u_2 \cdot x= v \cdot f(x)$ is non-zero if and only if $v=u_1 + u_2$.

Lemma 3

Bijective function: Let $f(x)$ be a bijective function. If the correlation of a linear approximation $u\cdot x=v \cdot f(x)$ is non-zero then $u=v=0$, or both $u$ and $v$ are non-zero.

Appendix 2: Basic key recovery attack on 22 reduced-round LBlock

Appendix 3: Attack complexity

The time complexity of steps 3-11 in the described attack in Sect. 5 is as follows:

Step 3 requires $2^{12} \times 2^{32} \times 2^{32}=2^{76}$ memory accesses, because we should guess 12 bits for $SK_1$, and for $2^{32}$ values encrypt $x_0$ one round and then update $N_1$ for $2^{32}$ times.

Step 4 requires $2^{12} \times 2^{8} \times 2^{20} \times 2^{32}=2^{72}$ memory accesses, because for all of guessed $2^{12}$ keys in previous step, we should guess 8 bits for $SK_2$, and for $2^{20}$ values encrypt $x_1$ one round and then update $N_2$ for $2^{32}$ times.

Step 5 requires $2^{20} \times 2^4 \times 2^{12} \times 2^{32}=2^{68}$ memory accesses, because for all of guessed $2^{20}$ keys in previous steps, we should guess 4 bits for $SK_3$ and for $2^{12}$ values encrypt $x_2$ one round and then update $N_3$ for $2^{32}$ times.

Step 6 requires $2^{24} \times 2^4 \times 2^{8} \times 2^{32}=2^{68}$ memory accesses, because for all of guessed $2^{24}$ keys in previous steps, we should guess 4 bits for $SK_4$ and for $2^{8}$ values encrypt $x_3$ one round and then update $N_4$ for $2^{32}$ times.

Step 7 requires $2^{28} \times 2^{12} \times 2^{32} \times 2^{4}=2^{72}$ memory accesses, because for all of guessed $2^{28}$ keys in previous steps, we should guess 12 bits for $SK_{22}$ and for $2^{32}$ values decrypt $x_{22}$ one round and then update $N_5$ for $2^{4}$ times.

Step 8 requires $2^{40} \times 2^{8} \times 2^{20} \times 2^{4}=2^{72}$ memory accesses, because for all of guessed $2^{40}$ keys in previous steps, we should guess 8 bits for $SK_{21}$ and for $2^{20}$ values decrypt $x_{21}$ one round and then update $N_6$ for $2^{4}$ times.

Step 9 requires $2^{48} \times 2^{4} \times 2^{12} \times 2^{4}=2^{68}$ memory accesses, because for all of guessed $2^{48}$ keys in previous steps, we should guess 4 bits for $SK_{20}$ and for $2^{12}$ values decrypt $x_{20}$ one round and then update $N_7$ for $2^{4}$ times.

Step 10 requires $2^{52} \times 2^{4} \times 2^{8} \times 2^{4}=2^{68}$ memory accesses, because for all of guessed $2^{52}$ keys in previous steps, we should guess $2^{4}$ for $SK_{19}$ and for $2^{8}$ values decrypt $x_{19}$ one round and then update $N_8$ for $2^{4}$ times.

Step 11 requires $2^{56} \times 2^{8}= 2^{64}$ memory accesses, because for all of guessed $2^{56}$ keys in previous steps, we should read $2^8$ values of $N_8[x_4,x_{18}]$.

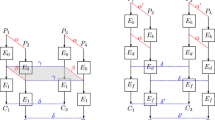
Appendix 4: Schematic of the key-recovery cryptanalysis