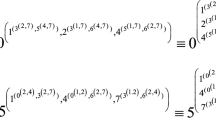1 Introduction

The ever-increasing complexity of embedded systems realized as Multi-Processor Systems-on-Chips (MPSoCs) is imposing several challenges on systems designers [18]. Two major challenges in designing streaming software for embedded MPSoCs are: (1) How to express parallelism found in applications efficiently?, and (2) How to allocate the processors to provide guaranteed services to multiple running applications, together with the ability to dynamically start/stop applications without affecting other already running applications?

Model-of-Computation (MoC) based design has emerged as a de-facto solution to the first challenge [10]. In MoC-based design, the application can be modeled as a directed graph where nodes represent actors (i.e., tasks) and edges represent communication channels. Different MoCs define different rules and semantics on the computation and communication of the actors. The main benefits of a MoC-based design are the explicit representation of important properties in the application (e.g., parallelism) and the enhanced design-time analyzability of the performance metrics (e.g., throughput). One particular MoC that is popular in the embedded signal processing systems community is the Cyclo-Static Dataflow (CSDF) model [5] which extends the well-known Synchronous Data Flow (SDF) model [15].

Unfortunately, no such de-facto solution exists yet for the second challenge of processor allocation [23]. For a long time, self-timed scheduling was considered the most appropriate policy for streaming applications modeled as dataflow graphs [14, 28]. However, the need to support multiple applications running on a single system without prior knowledge of the properties of the applications (e.g., required throughput, number of tasks, etc.) at system design-time is forcing a shift towards run-time scheduling approaches as explained in [13]. Most of the existing run-time scheduling solutions assume applications modeled as task graphs and provide best-effort or soft-real-time quality-of-service (QoS) [23]. Few run-time scheduling solutions exist which support applications modeled using a MoC and provide hard-real-time QoS [4, 11, 20, 21]. However, these solutions either use simple MoCs such as SDF/PGM graphs or use Time-Division Multiplexing (TDM)/Round-Robin (RR) scheduling. Several algorithms from the hard-real-time multiprocessor scheduling theory [9] can perform fast admission and scheduling decisions for incoming applications while providing hard-real-time QoS. Moreover, these algorithms provide temporal isolation which is the ability to dynamically start/run/stop applications without affecting other already running applications. However, these algorithms from the hard-real-time multiprocessor scheduling theory received little attention in the embedded MPSoC community. This is mainly due to the fact that these algorithms assume independent periodic or sporadic tasks [9]. Such a simple task model is not directly applicable to modern embedded streaming applications. This is because a modern streaming application is typically modeled as a directed graph where nodes represent actors, and edges represent data-dependencies. The actors in such graphs have data-dependency constraints and do not necessarily conform to the periodic or sporadic task models.

Therefore, in this paper we investigate the applicability of the hard-real-time scheduling theory for periodic tasks to streaming applications modeled as acyclic CSDF graphs. In such graphs, the actors are data-dependent. However, we analytically prove that they (i.e., the actors) can be scheduled as periodic tasks. As a result, a variety of hard-real-time scheduling algorithms for periodic tasks can be applied to schedule such applications with a certain guaranteed throughput. By considering acyclic CSDF graphs, our investigation findings and proofs are applicable to most streaming applications since it has been shown recently that around 90 % of streaming applications can be modeled as acyclic SDF graphs [30]. Note that SDF graphs are a subset of the CSDF graphs we consider in this paper.

1.1 Problem statement

Given a streaming application modeled as an acyclic CSDF graph, determine whether it is possible to execute the graph actors as periodic tasks. A periodic task τ i is defined by a 3-tuple τ i =(S i ,C i ,T i ). The interpretation is as follows: τ i is invoked at time instants t=S i +kT i and it has to execute for C i time-units before time t=S i +(k+1)T i for all k∈ℕ0, where S i is the start time of τ i and T i is the task period. This scheduling approach is called Strictly Periodic Scheduling ( SPS ) [22] to avoid confusion with the term periodic scheduling used in the dataflow scheduling theory to refer to a repetitive finite sequence of actors invocations. The sequence is periodic since it is repeated infinitely with a constant period. However, the individual actors invocations are not guaranteed to be periodic. In the remainder of this paper, periodic scheduling/schedule refers to strictly periodic scheduling/schedule.

1.2 Paper contributions

Given a streaming application modeled as an acyclic CSDF graph, we analytically prove that it is possible to execute the graph actors as periodic tasks. Moreover, we present an analytical framework for computing the periodic task parameters for the actors, that is the period and the start time, together with the minimum buffer sizes of the communication channels such that the actors execute as periodic tasks. The proposed framework is also capable of handling sporadic input streams. Furthermore, we define formally two classes of CSDF graphs: matched input/output (I/O) rates graphs and mis-matched I/O rates graphs. Matched I/O rates graphs constitute around 80 % of streaming applications [30]. We prove that strictly periodic scheduling is capable of delivering the maximum achievable throughput for matched I/O rates graphs. Applying our approach to matched I/O rates applications enables using a plethora of schedulability tests developed in the real-time scheduling theory [9] to easily determine the minimum number of processors needed to schedule a set of applications using a certain algorithm to provide the maximum achievable throughput. This can be of great use for embedded systems designers during the Design Space Exploration (DSE) phase.

The remainder of this paper is organized as follows: Sect. 2 gives an overview of the related work. Section 3 introduces the CSDF model and the considered system model. Section 4 presents the proposed analytical framework. Section 5 presents the results of empirical evaluation of the framework presented in Sect. 4. Finally, Sect. 6 ends the paper with conclusions.

2 Related work

Parks and Lee [25] studied the applicability of non-preemptive Rate-Monotonic (RM) scheduling to dataflow programs modeled as SDF graphs. The main difference compared to our work is: (1) they considered non-preemptive scheduling. In contrast, we consider only preemptive scheduling. Non-preemptive scheduling is known to be NP-hard in the strong sense even for the uniprocessor case [12], and (2) they considered SDF graphs which are a subset of the more general CSDF graphs.

Goddard [11] studied applying real-time scheduling to dataflow programs modeled using the Processing Graphs Method (PGM). He used a task model called Rate-Based Execution (RBE) in which a real-time task τ i is characterized by a 4-tuple τ i =(x i ,y i ,d i ,c i ). The interpretation is as follows: τ i executes x i times in time period y i with a relative deadline d i per job release and c i execution time per job release. For a given PGM, he developed an analysis technique to find the RBE task parameters of each actor and buffer size of each channel. Thus, his approach is closely related to ours. However, our approach uses CSDF graphs which are more expressive than PGM graphs in that PGM supports only a constant production/consumption rate on edges (same as SDF), whereas CSDF supports varying (but predefined) production/consumption rates. As a result, the analysis technique in [11] is not applicable to CSDF graphs.

Bekooij et al. presented a dataflow analysis for embedded real-time multiprocessor systems [4]. They analyzed the impact of TDM scheduling on applications modeled as SDF graphs. Moreira et al. have investigated real-time scheduling of dataflow programs modeled as SDF graphs in [20–22]. They formulated a resource allocation heuristic [20] and a TDM scheduler combined with static allocation policy [21]. Their TDM scheduler improves the one proposed in [4]. In [22], they proved that it is possible to derive a strictly periodic schedule for the actors of a cyclic SDF graph iff the periods are greater than or equal to the maximum cycle mean of the graph. They formulated the conditions on the start times of the actors in the equivalent Homogeneous SDF (HSDF, [15]) graph in order to enforce a periodic execution of every actor as a Linear Programming (LP) problem.

Our approach differs from [4, 20–22] in: (1) using the periodic task model which allows applying a variety of proven hard-real-time scheduling algorithms for multiprocessors, and (2) using the CSDF model which is more expressive than the SDF model.

3 Background

3.1 Cyclo-static dataflow (CSDF)

In [5], the CSDF model is defined as a directed graph G=〈V,E〉, where V is a set of actors and E⊆V×V is a set of communication channels. Actors represent functions that transform incoming data streams into outgoing data streams. The communication channels carry streams of data, and an atomic data object is called a token. A channel e u ∈E is a first-in, first-out (FIFO) queue with unbounded capacity, and is defined by a tuple e u =(v i ,v j ). The tuple means that e u is directed from v i (called source) to v j (called destination). The number of actors in a graph G is denoted by N=|V|. An actor receiving an input stream of the application is called input actor, and an actor producing an output stream of the application is called output actor. A path w a⇝z between actors v a and v z is an ordered sequence of channels defined as w a⇝z ={(v a ,v b ),(v b ,v c ),…,(v y ,v z )}. A path w i⇝j is called output path if v i is an input actor and v j is an output actor. \(\mathcal{W}\) denotes the set of all output paths in G. In this work, we consider only acyclic CSDF graphs. An acyclic graph G has a number of levels, denoted by \(\mathcal{L}\), which is given by Algorithm 1. The level of an actor v i ∈V is denoted by σ i . Each actor v i ∈V is associated with four sets:

  1. 1.

    The successors set, denoted by succ(v i ), and given by:

    $$ \mathsf{succ}(v_i) = \bigl\{ v_j \in V : \exists e_u = (v_i, v_j) \in E \bigr\} $$
    (1)
  2. 2.

    The predecessors set, denoted by prec(v i ), and given by:

    $$ \mathsf{prec}(v_i) = \bigl\{ v_j \in V : \exists e_u = (v_j, v_i) \in E \bigr\} $$
    (2)
  3. 3.

    The input channels set, denoted by inp(v i ), and given by:

    $$ \mathsf{inp}(v_i) = \left \{ \begin{array}{l@{\quad}l} \{ e_u \in E : e_u = (v_j, v_i) \}, & \mbox{if } \sigma_i >1 \\ \mbox{The set of channels delivering the input streams to } v_i & \mbox{if } \sigma_i = 1 \end{array} \right . $$
    (3)
  4. 4.

    The output channels set, denoted by out(v i ), and given by:

    $$ \mathsf{out}(v_i) = \left\{ \begin{array}{l@{\quad}l} \{e_u \in E : e_u = (v_i, v_j)\}, & \mbox{if } \sigma_i <\mathcal{L}\\ \mbox{The set of channels carrying the output streams from } v_i, & \mbox{if } \sigma_i = \mathcal{L} \end{array} \right. $$
    (4)
Algorithm 1
figure 1

Levels(G)

Full size image

Every actor v j ∈V has an execution sequence [f j (1),f j (2),…,f j (P j )] of length P j . The interpretation of this sequence is: The nth time that actor v j is fired, it executes the code of function f j (((n−1)modP j )+1). Similarly, production and consumption of tokens are also sequences of length P j in CSDF. The token production of actor v j on channel e u is represented as a sequence of constant integers \([x_{j}^{u}(1), x_{j}^{u}(2), \ldots, x_{j}^{u}(P_{j})]\). The nth time that actor v j is fired, it produces \(x_{j}^{u}(((n - 1) \bmod P_{j}) + 1)\) tokens on channel e u . The consumption of actor v k is completely analogous; the token consumption of actor v k from a channel e u is represented as a sequence \([y_{k}^{u}(1), y_{k}^{u}(2), \ldots, y_{k}^{u}(P_{j})]\). The firing rule of a CSDF actor v k is evaluated as “true” for its nth firing iff all its input channels contain at least \(y_{k}^{u}(((n - 1) \bmod P_{j}) + 1)\) tokens. The total number of tokens produced by actor v j on channel e u during the first n invocations, denoted by \(X_{j}^{u}(n)\), is given by \(X_{j}^{u}(n) = \sum_{l = 1}^{n} x_{j}^{u}(l)\). Similarly, the total number of tokens consumed by actor v k from channel e u during the first n invocations, denoted by \(Y_{k}^{u}(n)\), is given by \(Y_{k}^{u}(n) = \sum_{l = 1}^{n} y_{k}^{u}(l)\).

Example 1

Figure 1 shows a CSDF graph consisting of four actors and four communication channels. Actor v 1 is the input actor with a successors set succ(v 1)={v 2,v 3}, and v 4 is the output actor with a predecessors set prec(v 4)={v 2,v 3}. There are two output paths in the graph: w 1={(v 1,v 2),(v 2,v 4)} and w 2={(v 1,v 3),(v 3,v 4)}. The production sequences are shown between square brackets at the start of edges (e.g., [5,3,2] for actor v 1 on edge e 2), while the consumption sequences are shown between square brackets at the end of the edges (e.g., [1,3,1] for v 3 on e 2).

Fig. 1
figure 2

Example CSDF graph

Full size image

An important property of the CSDF model is its decidability, which is the ability to derive at compile-time a schedule for the actors. This is formulated in the following definitions and results from [5].

Definition 1

(Valid static schedule [5])

Given a connected CSDF graph G, a valid static schedule for G is a finite sequence of actors invocations that can be repeated infinitely on the incoming sample stream while the amount of data in the buffers remains bounded. A vector q=[q 1,q 2,…,q N ]T, where q j >0, is a repetition vector of G if each q j represents the number of invocations of an actor v j in a valid static schedule for G. The repetition vector of G in which all the elements are relatively primeFootnote 1 is called the basic repetition vector of G, denoted by \(\dot{\mathbf{q}}\). G is consistent if there exists a repetition vector. If a deadlock-free schedule can be found, G is said to be live. Both consistency and liveness are required for the existence of a valid static schedule.

Theorem 1

([5])

In a CSDF graph G, a repetition vector q=[q 1,q 2,…,q N ]T is given by

$$ \mathbf{q} = \mathbf{P} \cdot\mathbf{r}, \quad \mbox{\textit{with} } P_{jk} = \left\{ \begin{array}{l@{\quad}l} P_j, & \mbox{\textit{if} } j = k\\ 0, & \mbox{\textit{otherwise}} \end{array} \right. $$
(5)

where r=[r 1,r 2,…,r N ]T is a positive integer solution of the balance equation

$$ \varGamma\cdot\mathbf{r} = \mathbf{0} $$
(6)

and where the topology matrix Γ∈ℤ|E|×|V| is defined by

$$ \varGamma_{uj} = \left\{ \begin{array}{l@{\quad}l} X^u_j(P_j), & \mbox{\textit{if actor} } v_j \mbox{ \textit{produces on channel} } e_u \\ -Y^u_j(P_j), & \mbox{\textit{if actor} } v_j \mbox{ \textit{consumes from channel} } e_u \\ 0, & \mbox{\textit{Otherwise}} \end{array} \right. $$
(7)

Definition 2

For a consistent and live CSDF graph G, an actor iteration is the invocation of an actor v i ∈V for q i times, and a graph iteration is the invocation of every actor v i ∈V for q i times, where q i ∈q.

Corollary 1

(From [5])

If a consistent and live CSDF graph G completes n iterations, where n∈ℕ, then the net change to the number of tokens in the buffers of G is zero.

Lemma 1

Any acyclic consistent CSDF graph is live.

Proof

Bilsen et al. proved in [5] that a CSDF graph is live iff every cycle in the graph is live. Equivalently, a CSDF graph deadlocks only if it contains at least one cycle. Thus, absence of cycles in a CSDF graph implies its liveness. □

Example 2

For the CSDF graph shown in Fig. 1

3.2 System model and scheduling algorithms

In this section, we introduce the system model and the related schedulability results.

3.2.1 System model

A system Ω consists of a set π={π 1,π 2,…,π m } of m homogeneous processors. The processors execute a task set τ={τ 1,τ 2,…,τ n } of n periodic tasks, and a task may be preempted at any time. A periodic task τ i ∈τ is defined by a 4-tuple τ i =(S i ,C i ,T i ,D i ), where S i ≥0 is the start time of τ i , C i >0 is the worst-case execution time of τ i , T i ≥C i is the task period, and D i , where C i ≤D i ≤T i , is the relative deadline of τ i . A periodic task τ i is invoked (i.e., releases a job) at time instants t=S i +kT i for all k∈ℕ0. Upon invocation, τ i executes for C i time-units. The relative deadline D i is interpreted as follows: τ i has to finish executing its kth invocation before time t=S i +kT i +D i for all k∈ℕ0. If D i =T i , then τ i is said to have implicit-deadline. If D i <T i , then τ i is said to have constrained-deadline. If all the tasks in a task-set τ have the same start time, then τ is said to be synchronous. Otherwise, τ is said to be asynchronous.

The utilization of a task τ i is U i =C i /T i . For a task set τ, the total utilization of τ is \(U_{\mathrm{sum}} = \sum_{\tau_{i} \in\tau} U_{i}\) and the maximum utilization factor of τ is \(U_{\mathrm{max}} = \max_{\tau_{i} \in\tau} U_{i}\).

In the remainder of this paper, a task set τ refers to an asynchronous set of implicit-deadline periodic tasks. As a result, we refer to a task τ i with a 3-tuple τ i =(S i ,C i ,T i ) by omitting the implicit deadline D i which is equal to T i .

3.2.2 Scheduling asynchronous set of implicit deadline periodic tasks

Given a system Ω and a task set τ, a valid schedule is one that allocates a processor to a task τ i ∈τ for exactly C i time-units in the interval [S i +kT i ,S i +(k+1)T i ) for all k∈ℕ0 with the restriction that a task may not execute on more than one processor at the same time. A necessary and sufficient condition for τ to be scheduled on Ω to meet all the deadlines (i.e., τ is feasible) is:

$$ U_{\mathrm{sum}} \le m $$
(8)

The problem of constructing a periodic schedule for τ can be solved using several algorithms [9]. These algorithms differ in the following aspects: (1) Priority Assignment: A task can have fixed priority, job-fixed priority, or dynamic priority, and (2) Allocation: Based on whether a task can migrate between processors upon preemption, algorithms are classified into:

  • Partitioned: Each task is allocated to a processor and no migration is permitted

  • Global: Migration is permitted for all tasks

  • Hybrid: Hybrid algorithms mix partitioned and global approaches and they can be further classified to:

    1. 1.

      Semi-partitioned: Most tasks are allocated to processors and few tasks are allowed to migrate

    2. 2.

      Clustered: Processors are grouped into clusters and the tasks that are allocated to one cluster are scheduled by a global scheduler

An important property of scheduling algorithms is optimality. A scheduling algorithm \(\mathcal{A}\) is said to be optimal iff it can schedule any feasible task set τ on Ω. Several global and hybrid algorithms were proven optimal for scheduling asynchronous sets of implicit-deadline periodic tasks (e.g., [2, 3, 8, 16]). The minimum number of processors needed to schedule τ using an optimal scheduling algorithm, denoted by M OPT , is given by:

$$ M_{\textsf{OPT}}= \lceil U_{\mathrm{sum}} \rceil $$
(9)

Partitioned algorithms are known to be non-optimal for scheduling implicit-deadline periodic tasks [7]. However, they have the advantage of not requiring task migration. One prominent example of partitioned scheduling algorithms is the Partitioned Earliest Deadline First (P-EDF) algorithm. EDF is known to be optimal for scheduling arbitrary task sets on a uniprocessor system [6]. In a multiprocessor system, EDF can be combined with different processor allocation algorithms (e.g., Bin-packing heuristics such as First-Fit (FF) and Worst-Fit (WF)). López et al. derived in [17] the worst-case utilization bounds for a task set τ to be schedulable using P-EDF. These bounds serve as a simple sufficient schedulability test. Based on these bounds, they derived the minimum number of processors needed to schedule a task set τ under P-EDF, denoted by M P-EDF :

$$ M_{\textsf{P-EDF}}\ge \left\{ \begin{array}{l@{\quad}l} 1, & \mbox{if } U_{\mathrm{sum}} \le1 \\ \min( \lceil\frac{n}{\beta} \rceil, \lceil \frac{(\beta+ 1) U_{\mathrm{sum}} - 1}{\beta}\rceil), & \mbox{if } U_{\mathrm{sum}} > 1, \end{array} \right. $$
(10)

where β=⌊1/U max⌋. A task set τ with total utilization U sum and maximum utilization factor U max is always guaranteed to be schedulable on M P-EDF processors. Since M P-EDF is derived based on a sufficient test, it is important to note that τ may be schedulable on less number of processors. We define M PAR as the minimum number of processors on which τ can be partitioned assuming bin packing allocation (e.g., First-Fit (FF)) with each set in the partition having a total utilization of at most 1. M PAR can be expressed as:

$$ \displaystyle M_{\textsf{PAR}}= \min\{ x \in\mathbb{N} : B \mbox{~is~} x\mbox {-partition~of~} \tau\mbox{~and~} U_{\mathrm{sum}} \le1 \mbox{ for all } y \in B\} $$
(11)

M PAR is specific to the task set τ for which it is computed. Another task set \(\hat{\tau}\) with the same total utilization and maximum utilization factor as τ might not be schedulable on M PAR processors due to partitioning issues.

4 Strictly periodic scheduling of acyclic CSDF graphs

This section presents our analytical framework for scheduling the actors in acyclic CSDF graphs as periodic tasks. The construction it uses arranges the actors forming the CSDF graph into a set of levels as shown in Sect. 3. All actors belonging to a certain level depend directly only on the actors in the previous levels. Then, we derive, for each actor, a period and start time, and for each channel, a buffer size. These derived parameters ensure that a strictly periodic schedule can be achieved in the form of a pipelined sequence of invocations of all the actors in each level.

4.1 Definitions and assumptions

In the remainder of this paper, a graph G refers to an acyclic consistent CSDF graph. We base our analysis on the following assumptions:

Assumption 1

A graph G has a set \(I = \{ I_{1}, I_{2}, \ldots, I_{\mathcal{K}}\}\) of \(\mathcal{K}\) sporadic input streams connected to the input actors of G. The set of input streams to an actor v i is denoted by Z i . We make the following assumptions about the input streams:

  1. 1.

    Z i ∩Z j =∅ ∀v i ,v j ∈V.

  2. 2.

    The first samples of all the streams arrive prior to or at the same time when the actors of G start executing

  3. 3.

    Each input stream I j is characterized by a minimum inter-arrival time (also called period) of the samples, denoted by γ j . This minimum inter-arrival time is assumed to be equal to the period of the input actor which receives I j . This assumption indicates that the inter-arrival time for input streams can be controlled by the designer to match the periods of the actors.

Assumption 2

An actor v i consumes its input data immediately when it starts its firing and produces its output data just before it finishes its firing.

We start with the following definition:

Definition 3

(Execution time vector)

For a graph G, an execution time vector μ, where μ∈ℕN, represents the worst-case execution times, measured in time-units, of the actors in G. The worst-case execution time of an actor v j ∈V is given by

(12)

where P j is the length of CSDF firing/production/consumption sequences of actor v j , T R is the worst-case time needed to read a single token from an input channel, \(y_{j}^{l}\) is the consumption sequence of v j from channel e l , T W is the worst-case time needed to write a single token to an output channel, \(x_{j}^{r}\) is the production sequence of v j into channel e r , and \(T_{j}^{C}(k)\) is the worst-case computation time of v j in firing k.

Let \(\eta= \max_{v_{i} \in V}(\mu_{i} q_{i})\) and Q=lcm{q 1,q 2,…,q N } (lcm denotes the least-common-multiple operator). Now, we give the following definition.

Definition 4

(Matched input/output rates graph)

A graph G is said to be matched input/output (I/O) rates graph if and only if

$$ \eta\bmod Q = 0 $$
(13)

If (13) does not hold, then G is said to be mis-matched I/O rates graph.

The concept of matched I/O rates applications was first introduced in [30] as the applications with low value of Q. However, the authors did not establish exact test for determining whether an application is matched I/O rates or not. The test in (13) is a novel contribution of this paper. If ηmodQ=0, then there exists at least a single actor in the graph which is fully utilizing the processor on which it runs. This, as shown later in Sect. 4.3.3, allows the graph to achieve optimal throughput. On the other hand, if ηmodQ≠0, then there exist idle durations in the period of each actor which results in sub-optimal throughput. This is illustrated later in Example 3 which shows the strictly periodic schedule of a mis-matched I/O rates application.

Definition 5

(Output path latency)

Let w a⇝z ={(v a ,v b ),…,(v y ,v z )} be an output path in a graph G. The latency of w a⇝z under periodic input streams, denoted by L(w a⇝z ), is the elapsed time between the start of the first firing of v a which produces data to (v a ,v b ) and the finish of the first firing of v z which consumes data from (v y ,v z ).

Consequently, we define the maximum latency of G as follows:

Definition 6

(Graph maximum latency)

For a graph G, the maximum latency of G under periodic input streams, denoted by L(G), is given by:

$$ L(G) = \max_{w_{i \leadsto j}\in\mathcal{W}} L(w_{i \leadsto j}) $$
(14)

Definition 7

(Self-timed schedule)

A self-timed schedule (STS) is one where all the actors are fired as soon as their input data are available.

Self-timed scheduling has been shown in [28] to achieve the maximum achievable throughput and minimum achievable latency of a Homogeneous SDF (HSDF, [15]) graph. This results extends to CSDF graphs since any CSDF graph can be converted to an equivalent HSDF graph. For acyclic graphs, the STS throughput of an actor v i , denoted by R STS (v i ), is given by:

$$ R_{\textsf{STS}}(v_i) = q_i/\eta $$
(15)

Definition 8

(Strictly periodic actor)

An actor v i ∈V is strictly periodic iff the time period between any two consecutive firings is constant.

Definition 9

(Period vector)

For a graph G, a period vector λ, where λ∈ℕN, represents the periods, measured in time-units, of the actors in G. λ j ∈λ is the period of actor v j ∈V. λ is given by the solution to both

$$ q_1 \lambda_1 = q_2 \lambda_2 = \cdots= q_{N-1} \lambda_{N-1} = q_N \lambda_N $$
(16)

and

$$ \boldsymbol{\lambda} - \boldsymbol{\mu} \ge\mathbf{0}, $$
(17)

where \(q_{j} \in\dot{\mathbf{q}}\) (the basic repetition vector of G according to Definition 1).

Definition 9 implies that all the actors have the same iteration period. This is captured in the following definition:

Definition 10

(Iteration period)

For a graph G, the iteration period under strictly periodic scheduling, denoted by α, is given by

$$ \alpha= q_i\lambda_i\quad \mbox{for any } v_i \in V $$
(18)

Now, we prove the existence of a strictly periodic schedule when the input streams are strictly periodic. An input stream I j connected to input actor v i is strictly periodic iff the inter-arrival time between any two consecutive samples is constant. Based on Assumption 1-3, it follows that γ j =λ i . Later on, we extend the results to handle periodic with jitter and sporadic input streams.

4.2 Existence of a strictly periodic schedule

Lemma 2

For a graph G, the minimum period vector of G, denoted by λ min, is given by

$$ \lambda_i^{\min} = \frac{Q}{q_i} \biggl\lceil\frac{\eta}{Q} \biggr\rceil\quad\mbox{\textit{for} } v_i \in V $$
(19)

.

Proof

Equation (16) can be re-written as:

$$ \Delta \cdot\boldsymbol{\lambda} = \mathbf{0}, $$
(20)

where Δ∈ℤ(N−1)×N is given by

$$ \Delta_{ij} = \left\{ \begin{array}{l@{\quad}l} q_1, & \mbox{if } j = 1 \\ -q_j, & \mbox{if } j = i + 1 \\ 0, & \mbox{otherwise} \end{array} \right. $$
(21)

Observe that nullity(Δ)=1. Thus, there exists a single vector which forms the basis of the null-space of Δ. This vector can be represented by taking any unknown λ k as the free-unknown and expressing the other unknowns in terms of it which results in:

$$ \boldsymbol{\lambda} = \lambda_k [q_k/q_1, q_k/q_2, \ldots, q_k/q_N]^T $$

The minimum λ k ∈ℕ is

$$ \lambda_k = \mathsf{lcm}\{ q_1, q_2, \ldots, q_N \}/ q_k $$

Thus, the minimum λ∈ℕ that solves (16) is given by

$$ \lambda_i = Q /q_i\quad \mbox{for } v_i \in V $$
(22)

Let \(\boldsymbol{\hat{\lambda}}\) be the solution given by (22). Equations (16) and (17) can be re-written as:

(23)
(24)

where c∈ℕ. Equation (24) can be re-written as:

(25)

It follows that c must be greater than or equal to \(\max_{v_{i} \in V}(\mu_{i} q_{i}) /Q = \eta/ Q\). However, η/Q is not always guaranteed to be an integer. As a result, the value is rounded by taking the ceiling. It follows that the minimum λ which satisfies both of (16) and (17) is given by

$$ \lambda_i = Q/q_i\lceil\eta/ Q \rceil\quad\mbox{for } v_i \in V $$

 □

Theorem 2

For any graph G, a periodic schedule Π exists such that every actor v i ∈V is strictly periodic with a constant period λ i ∈λ min and every communication channel e u ∈E has a bounded buffer capacity.

Proof

Recall that in this proof we assume that the input streams to level-1 actors are strictly periodic with periods equal to the input actors periods. Therefore, it follows that level-1 actors can execute periodically since their input streams are always available when they fire. By Definition 2, level-1 actors will complete one iteration when they fire q i times, where q i is the repetition of v i ∈A 1. Assume that level-1 actors start executing at time t=0. Then, by time t=α, level-1 actors are guaranteed to finish one iteration. According to Theorem 1, level-1 actors will also generate enough data such that every actor v k ∈A 2 can execute q k times (i.e., one iteration) with a period λ k . According to (16), firing v k for q k times with a period λ k takes α time-units. Thus, starting level-2 actors at time t=α guarantees that they can execute periodically with their periods given by Definition 9 for α time-units. Similarly, by time t=2α, level-3 actors will have enough data to execute for one iteration. Thus, starting level-3 actors at time t=2α guarantees that they can execute periodically for α time-units. By repeating this over all the \(\mathcal{L}\) levels, a schedule Π 1 (shown in Fig. 2) is constructed in which all the actors that belong to A i are started at start time ϕ i given by

$$ \phi_i = (i - 1) \alpha $$
(26)
Fig. 2
figure 3

Schedule Π 1

Full size image

A j (k) denotes level-j actors executing their kth iteration. For example, A 2(1) denotes level-2 actors executing their first iteration. At time \(t = \mathcal{L}\alpha\), G completes one iteration. It is trivial to observe from Π 1 that as soon as level-1 actors finish one iteration, they can immediately start executing the next iteration since their input streams arrive periodically. If level-1 actors start their second iteration at time t=α, their execution will overlap with the execution of the level-2 actors. By doing so, level-2 actors can start immediately their second iteration after finishing their first iteration since they will have all the needed data to execute one iteration periodically at time t=2α. This overlapping can be applied to all the levels to yield the schedule Π 2 shown in Fig. 3.

Fig. 3
figure 4

Schedule Π 2

Full size image

Now, the overlapping can be applied \(\mathcal{L}\) times on schedule Π 1 to yield a schedule \(\varPi_{\mathcal{L}}\) as shown in Fig. 4.

Fig. 4
figure 5

Schedule \(\varPi_{\mathcal{L}}\)

Full size image

Starting from time \(t = \mathcal{L}\alpha\), a schedule Π ∞ can be constructed as shown in Fig. 5.

Fig. 5
figure 6

Schedule Π ∞

Full size image

In schedule Π ∞, every actor v i is fired every λ i time-unit once it starts. The start time defined in (26) guarantees that actors in a given level will start only when they have enough data to execute one iteration in a periodic way. The overlapping guarantees that once the actors have started, they will always find enough data for executing the next iteration since their predecessors have already executed one additional iteration. Thus, schedule Π ∞ shows the existence of a periodic schedule of G where every actor v j ∈V is strictly periodic with a period equal to λ j .

The next step is to prove that Π ∞ executes with bounded memory buffers. In Π ∞, the largest delay in consuming the tokens occurs for a channel e u ∈E connecting a level-1 actor and a level-\(\mathcal{L}\) actor. This is illustrated in Fig. 5 by observing that the data produced by iteration-1 of a level-1 source actor will be consumed by iteration-1 of a level-\(\mathcal{L}\) destination actor after \((\mathcal{L}- 1) \alpha\) time-units. In this case, e u must be able to store at least \((\mathcal{L}- 1) X^{u}_{1}(q_{1})\) tokens. However, starting from time \(t = \mathcal{L} \alpha\), both of the level-1 and level-\(\mathcal{L}\) actors execute in parallel. Thus, we increase the buffer size by \(X^{u}_{1}(q_{1})\) tokens to account for the overlapped execution. Hence, the total buffer size of e u is \(\mathcal{L} X^{u}_{1}(q_{1})\) tokens. Similarly, if a level-2 actor, denoted v 2, is connected directly to a level-\(\mathcal{L}\) actor via channel e v , then e v must be able to store at least \((\mathcal{L}-1) X^{v}_{2}(q_{2})\) tokens. By repeating this argument over all the different pairs of levels, it follows that each channel e u ∈E, connecting a level-i source actor and a level-j destination actor, where j≥i, will store according to schedule Π ∞ at most:

$$ b_u = (j - i + 1) X^u_k(q_k) $$
(27)

tokens, where v k is the level-i actor, and \(q_{k} \in \dot{\mathbf{q}}\). Thus, an upper bound on the FIFO sizes exists. □

Example 3

We illustrate Theorem 2 by constructing a periodic schedule for the CSDF graph shown in Fig. 1. Assume that the CSDF graph has an execution vector μ=[5,2,3,2]T. Given \(\dot{\mathbf{q}}= [3, 3, 6, 4]^{T}\) as computed in Example 2, we use (19) to find λ min=[8,8,4,6]T. Figure 6 illustrates the periodic schedule of the actors for the first graph iteration. \(\mathcal{L}= 3\) and the levels consist of three sets: A 1={v 1}, A 2={v 2,v 3}, and A 3={v 4}. A 1 actors start at time t=0. Since α=q i λ i =24 for any v i in the graph, A 2 actors start at time t=α=24 and A 3 actors start at time t=2α=48. Every actor v j in the graph executes for μ j time-units every λ j time-units. For example, actor v 2 starts at time t=24 and executes for 2 time-units every 8 time-units.

Fig. 6
figure 7

Strictly periodic schedule for the CSDF graph shown in Fig. 1. The x-axis represents the time axis.

Full size image

4.3 Earliest start times and minimum buffer sizes

Now, we are interested in finding the earliest start times of the actors, and the minimum buffer sizes of the communication channels that guarantee the existence of a periodic schedule. Minimizing the start times and buffer sizes is crucial since it minimizes the initial response time and the memory requirements of the applications modeled as acyclic CSDF graphs.

4.3.1 Earliest start times

In the proof of Theorem 2, the notion of start time was introduced to denote when the actor is started on the system. The start time values used in the proof of the theorem were not the minimum ones. Here, we derive the earliest start times. We start with the following definitions:

Definition 11

(Cumulative production function)

The cumulative production function of actor v i producing into channel e u during the interval [t s ,t e ), denoted by \(\mathsf{prd}_{[t_{s}, t_{e})} (v_{i},e_{u})\), is the sum of the number of tokens produced by v i into e u during the interval [t s ,t e ).

In case of implicit-deadline periodic tasks, \(\mathsf{prd}_{[t_{s}, t_{e})}(v_{i},e_{u})\) is given by:

$$ \mathop{\mathsf{prd}}_{[t_s,t_e)}(v_i,e_u) = \left\{ \begin{array}{l@{\quad}l} X_i^u ( \lfloor\frac{t_e - t_s}{\lambda_i} \rfloor ),& \mbox{if } (t_e - t_s) \ge\lambda_i \\ 0, & \mbox{if } (t_e - t_s) < \lambda_i \end{array} \right. $$
(28)

Similarly, we define the cumulative consumption function as follows:

Definition 12

(Cumulative consumption function)

The cumulative consumption function of actor v i consuming from channel e u over the interval [t s ,t e ], denoted by \(\mathsf{cns}_{[t_{s}, t_{e}]}(v_{i},e_{u})\), is the sum of the number of tokens consumed by v i from e u during the interval [t s ,t e ].

Similar to (28), \(\mathsf{cns}_{[t_{s}, t_{e}]} (v_{i},e_{u})\) is given by:

$$ \mathop{\mathsf{cns}}_{[t_s, t_e]}(v_i,e_u) = \left\{ \begin{array}{l@{\quad}l} 0, & \mbox{if } t_e < t_s \\ Y_i^u ( \lceil\frac{t_e - t_s}{\lambda_i} \rceil+ 1 ), & \mbox{if } (t_e - t_s) \bmod\lambda_i = 0\\ Y_i^u ( \lceil\frac{t_e - t_s}{\lambda_i} \rceil ), & \mbox{if } (t_e - t_s) \bmod\lambda_i \ne0\\ \end{array} \right. $$
(29)

Recall that prec(v i ) is the predecessors set of actor v i , \(Y_{i}^{u}\) is the consumption sequence of an actor v i from channel e u , and α is the iteration period. Now, we give the following lemma:

Lemma 3

For a graph G, the earliest start time of an actor v j ∈V, denoted by ϕ j , under a strictly periodic schedule is given by

$$ \phi_j = \left\{ \begin{array}{l@{\quad}l} 0, & \mbox{\textit{if} } \mathsf{prec}(v_j) = \emptyset\\ \displaystyle \max_{v_i \in\mathsf{prec}(v_j)} ( \phi_{i \rightarrow j} ), & \mbox{\textit{if} } \mathsf{prec}(v_j) \ne\emptyset \end{array} \right. $$
(30)

where

$$ \phi_{i \rightarrow j}= \min_{t \in[0,\phi_i + \alpha]} \Bigl\{ t : \mathop{\mathsf{prd}}_{[\phi_i, \max(\phi_i,t) + k)}(v_i,e_u) \ge\mathop{\mathsf{cns}}_{[t, \max(\phi _i,t)+k]}(v_j,e_u)~\forall k = 0, 1, \ldots, \alpha\Bigr\} $$
(31)

Proof

Theorem 2 proved that starting a level-k actor v j at a start time

$$ \phi_j = (k - 1) \alpha $$
(32)

guarantees strictly periodic execution of the actor v j . Any start time later than that guarantees also strictly periodic execution since v j will always find enough data to execute in a strictly periodic way.

Equation (32) can be re-written as:

$$ \phi_j = \left\{ \begin{array}{l@{\quad}l} 0, & \mbox{if } \mathsf{prec}(v_j) = \emptyset\\ \displaystyle \max_{v_i \in\mathsf{prec}(v_j)} (\phi_i) + \alpha, & \mbox{if } \mathsf{prec}(v_j) \ne\emptyset \end{array} \right. $$
(33)

The equivalence follows from observing that a level-k actor, where k>1, has a level-(k−1) predecessor. Hence, applying (33) to a level-k actor, where k>1, yields:

$$ \phi_j = \max\bigl((k - 2) \alpha, (k - 3) \alpha, \ldots, 0\bigr) + \alpha = (k - 1) \alpha $$

Now, we are interested in starting v j ∈A k , where k>1, earlier. That is:

$$ \phi_j \le\max_{v_i \in\mathsf{prec}(v_j)} (\phi_i) + \alpha $$
(34)

ϕ j has also a lower-bound by observing that an actor v j can not start before the application is started. That is:

$$ 0 \le\phi_j \le\max_{v_i \in\mathsf{prec}(v_j)} (\phi_i) + \alpha \quad\Rightarrow\quad0 \le\phi_j \le\max_{v_i \in \mathsf{prec}(v_j)}( \phi_i + \alpha) $$
(35)

If we select ϕ j such that

$$ \phi_j = \max_{v_i \in\mathsf{prec}(v_j)}(\phi_{i \rightarrow j}), \phi_{i \rightarrow j}= \hat{t},\quad \hat{t} \in[0, \phi_i + \alpha] $$
(36)

then this guarantees that ϕ j also satisfies (35).

In (36), a valid start time candidate ϕ i→j must satisfy extra conditions to guarantee that the number of produced tokens on edge e u =(v i ,v j ) at any time instant \(t \ge\hat{t}\) is greater than or equal to the number of consumed tokens at the same instant. To satisfy these extra conditions, we consider the following two possible cases:

Case I: \(\hat{t} \ge\phi_{i}\). This case is illustrated in Fig. 7. In this case, a valid start time candidate \(\hat{t}\) must satisfy:

$$ \mathop{\mathsf{prd}}_{[\phi_i, \hat{t} + k)}(v_i,e_u) \ge\mathop{\mathsf{cns}}_{[\hat{t}, \hat {t} + k]} (v_j,e_u)\quad \forall k = 0, 1, \ldots, \alpha $$
(37)
Fig. 7
figure 8

Timeline of v i and v j when \(\hat{t} \ge\phi_{i} \)

Full size image

Satisfying (37) guarantees that v j can fire at times \(t = \hat{t}, \hat{t} + \lambda_{j}, \ldots, \hat{t} + \alpha\). Thus, a valid value of \(\hat{t}\) guarantees that once v j is started, it always finds enough data to fire for one iteration. As a result, v j executes in a strictly periodic way.

Case II: \(\hat{t} < \phi_{i}\). This case is illustrated in Fig. 8. A valid start time candidate \(\hat{t}\) must satisfy:

$$ \mathop{\mathsf{prd}}_{[\phi_i, \phi_i + k)}(v_i,e_u) \ge \mathop{\mathsf{cns}}_{[\hat{t}, \phi _i + k]}(v_j,e_u)\quad \forall k = 0, 1, \ldots, \alpha $$
(38)
Fig. 8
figure 9

Timeline of v i and v j when \(\hat{t} < \phi_{i}\)

Full size image

This case occurs when v j consumes zeros tokens during the interval \([\hat{t},\phi_{i}]\). This is a valid behavior since the consumption rates sequence can contain zero elements. Since \(\hat{t} < \phi_{i}\), it is sufficient to check the cumulative production and consumption over the interval [ϕ i ,ϕ i +α] since by time t=ϕ i +α both v i and v j are guaranteed to have finished one iteration. Thus, \(\hat{t}\) also guarantees that once v j is started, it always finds enough data to fire. Hence, v j executes in a strictly periodic way.

Now, we can merge (37) and (38) which results in:

$$ \mathop{\mathsf{prd}}_{[\phi_i, \max(\phi_i,\hat{t}) + k)}(v_i,e_u) \ge \mathop{\mathsf{cns}}_{[\hat{t}, \max(\phi_i,\hat{t})+k]}(v_j,e_u)\quad\forall k = 0, 1, \ldots, \alpha $$
(39)

Any value of \(\hat{t}\) which satisfies (39) is a valid start time value that guarantees strictly periodic execution of v j . Since there might be multiple values of \(\hat{t}\) that satisfy (39), we take the minimum value because it is the earliest start time that guarantees strictly periodic execution of v j . □

4.3.2 Minimum buffer sizes

Lemma 4

For a graph G, the minimum bounded buffer size b u of a communication channel e u ∈E connecting a source actor v i with start time ϕ i , and a destination actor v j with start time ϕ j , where v i ,v j ∈V, under a strictly periodic schedule is given by

$$ b_u = \left\{ \begin{array}{l@{\quad}l} \displaystyle \max_{k \in[0,1, \ldots, \alpha]} (\mathsf{prd}_{[\phi_i, \phi_j + k)}(v_i,e_u) - \mathsf{cns}_{[\phi_j, \phi_j + k)}(v_j,e_u ) ), & \mbox{\textit{if} } \phi_i \le\phi_j \\ \displaystyle \max_{k \in[0,1, \ldots, \alpha]} (\mathsf{prd}_{[\phi_i, \phi_i + k)}(v_i,e_u) - \mathsf{cns}_{[\phi_j, \phi_i + k)}(v_j ,e_u) ), & \mbox{\textit{if} } \phi_i > \phi_j \end{array} \right. $$
(40)

Proof

Equation (40) tracks the maximum cumulative number of unconsumed tokens in e u during one iteration for v i and v j . There are two cases:

Case I: ϕ i ≤ϕ j . In this case, (40) tracks the maximum cumulative number of unconsumed tokens in e u during the time interval [ϕ i ,ϕ j +α). Figure 9 illustrates the execution time-lines of v i and v j when ϕ i ≤ϕ j . In interval A, v i is actively producing tokens while v j has not yet started executing. As a result, it is necessary to buffer all the tokens produced in this interval in order to prevent v i from blocking on writing. Thus, b u must be greater than or equal to \(\mathsf{prd}_{[\phi_{i}, \phi _{j})}(v_{i},e_{u})\). Starting from time t=ϕ j , both of v i and v j are executing in parallel (i.e., overlapped execution). In the proof of Theorem 2, an additional \(X^{u}_{i}(q_{i})\) tokens were added to the buffer size of e u to account for the overlapped execution. However, this value is a “worst-case” value. The minimum number of tokens that needs to be buffered is given by the maximum number of unconsumed tokens in e u at any time over the time interval [ϕ j ,ϕ j +α) (i.e., intervals B and C in Fig. 9). Taking the maximum number of unconsumed tokens guarantees that v i will always have enough space to write to e u . Thus, b u is sufficient and minimum for guaranteeing strictly periodic execution of v i and v j in the time interval [ϕ i ,ϕ j +α). At time t=ϕ j +α, both of v i and v j have completed one iteration and the number of tokens in e u is the same as at time t=ϕ j (Follows from Corollary 1). Due to the strict periodicity of v i and v j , the pattern shown in Fig. 9 repeats. Thus, b u is also sufficient and minimum for any t≥ϕ j +α.

Fig. 9
figure 10

Execution time-lines of v i and v j when ϕ i ≤ϕ j

Full size image

Case II: ϕ i >ϕ j . Figure 10 illustrates this case. According to Lemma 3, ϕ j can be smaller than ϕ i iff v i consumes zero tokens in interval A. Therefore, the intervals in which there is actually production/consumption of tokens are B and C. During interval B, there is overlapped execution and b u gives the maximum number of unconsumed tokens in e u during [ϕ i ,ϕ j +α) which guarantees that v i always have enough space to write to e u and v j has enough data to consume from e u . At time t=ϕ j +α, v j finishes one iteration and interval C starts. During interval C, v i is producing data to e u while v j is consuming zero tokens. Therefore, e u has to accommodate all the tokens produced during interval C and b u must be greater than or equal to \(\mathsf{prd}_{[\phi_{j} + \alpha,\phi_{i} + \alpha]}(v_{i},e_{u})\). As in Case I, b u is sufficient and minimum for guaranteeing strictly periodic execution of v i and v j in the interval [ϕ j ,ϕ i +α]. At time t=ϕ i +α, both of v i and v j have completed one iteration and e u contains a number of tokens equal to the number of tokens at time t=ϕ i . Due to the strict periodicity of v i and v j , their execution pattern repeats. Thus, b u is also sufficient and minimum for any t≥ϕ i +α.

Fig. 10
figure 11

Execution time-lines of v i and v j when ϕ i >ϕ j

Full size image

 □

Theorem 3

For a graph G, let τ G be a task set such that τ i ∈τ G corresponds to v i ∈V. τ i is given by:

$$ \tau_i = ( \phi_i, \mu_i, \lambda_i ), $$
(41)

where ϕ i is the earliest start time of v i given by (30), μ i ∈μ, and λ i ∈λ min is the period given by (19). τ G is schedulable on M processors using any hard-real-time scheduling algorithm \(\mathcal{A}\) for asynchronous sets of implicit-deadline periodic tasks if:

  1. 1.

    every edge e u ∈E has a capacity of at least b u tokens, where b u is given by (40)

  2. 2.

    τ G satisfies the schedulability test of \(\mathcal{A}\) on M processors

Proof

Follows from Theorem 2, and Lemmas 3 and 4. □

Example 4

This is an example to illustrate Lemmas 3, 4, and Theorem 3. First, we calculate the earliest start times and the corresponding minimum buffer sizes for the CSDF graph shown in Fig. 1. Applying Lemmas 3 and 4 on the CSDF graph results in:

$$ \left[ \begin{array}{c} \phi_1 \\ \phi_2 \\ \phi_3 \\ \phi_4 \end{array} \right] = \left[ \begin{array}{c} 0 \\ 8 \\ 8 \\ 20 \end{array} \right] \quad\mbox{and}\quad \left[ \begin{array}{c} b_1 \\ b_2 \\ b_3 \\ b_4 \end{array} \right] = \left[ \begin{array}{c} 3 \\ 5 \\ 3 \\ 5 \end{array} \right] , $$

where ϕ i denotes the earliest start time of actor v i , and b j denotes the minimum buffer size of communication channel e j . Given μ and λ min computed in Example 3, we construct a task set τ G ={(0,5,8),(8,2,8),(8,3,4),(20,2,6)}. We compute the minimum number of required processors to schedule τ G according to (9), (10), and (11):

τ G is schedulable using an optimal scheduling algorithm on 2 processors, and is schedulable using P-EDF on 3 processors.

4.3.3 Throughput and latency analysis

Now, we analyze the throughput of the graph actors under strictly periodic scheduling and compare it with the maximum achievable throughput. We also present a formula to compute the latency for a given CSDF graph under strictly periodic scheduling. We start with the following definitions:

Definition 13

(Actor throughput)

For a graph G, the throughput of actor v i ∈V under strictly periodic scheduling, denoted by R SPS (v i ), is given by

$$ R_{\textsf{SPS}}(v_i) = 1/\lambda_i $$
(42)

Definition 14

(Rate-optimal strictly periodic schedule [22])

For a graph G, a strictly periodic schedule that delivers the same throughput as a self-timed schedule for all the actors is called Rate-Optimal Strictly Periodic Schedule (ROSPS).

Now, we provide the following result.

Theorem 4

For a matched I/O rates graph G, the maximum achievable throughput of the graph actors under strictly periodic scheduling is equal to their maximum throughput under self-timed scheduling.

Proof

The maximum achievable throughput under strictly periodic scheduling is the one obtained when \(\lambda_{i} = \lambda_{i}^{\min}\). Recall from (19) that

$$ \lambda_i^{\min} = \frac{Q}{q_i} \biggl\lceil \frac{\eta}{Q} \biggr\rceil $$
(43)

Let us re-write η as η=pQ+r, where p=η÷Q (÷ is the integer division operator), and r=ηmodQ. Now, (43) can be re-written as

$$ \lambda_i^{\min} = \left\{ \begin{array}{l@{\quad}l} \eta/q_i, & \mbox{if } \eta\bmod Q = 0 \\ (p + 1)Q/q_i, & \mbox{if } \eta\bmod Q \ne0 \end{array} \right. $$
(44)

Recall from (15) that

$$ R_{\textsf{STS}}(v_i) = q_i/\eta $$
(45)

Now, recall from Definition 4 that a matched I/O rates graph satisfies the following condition:

$$ \eta\bmod Q = 0 $$
(46)

Therefore, the maximum achievable throughput of the actors of a matched I/O rates graph under strictly periodic scheduling is:

$$ R_{\textsf{SPS}}(v_i) = q_i / \eta= R_{\textsf{STS}}(v_i) $$
(47)

 □

Equation (44) shows that the throughput under SPS depends solely on the relationship between Q and η. Recall from Definition 3 that the execution time μ used by our framework is the maximum value over all the actual execution times of the actor. Therefore, if ηmodQ=0, then R SPS (v i ) is exactly the same as R STS (v i ) for SDF graphs and CSDF graphs where all the firings of an actor v i require the same actual execution time. If ηmodQ≠0 and/or the actor actual execution time differs per firing, then R SPS (v i ) is lower than R STS (v i ). These findings illustrate that our framework has high potential since it allows the designer to analytically determine the type of the application (i.e., matched vs. mis-matched) and accordingly to select the proper scheduler needed to deliver the maximum achievable throughput.

Now, we prove the following result regarding matched I/O rates applications:

Corollary 2

For a matched I/O rates graph G scheduled using its minimum period vector λ min, U max=1.

Proof

Recall from Sect. 3.2.1 that the utilization of a task τ i is defined as U i =C i /T i , where C i ≤T i . Therefore, the maximum possible value for U i is when C i =T i which leads to U i =1.0. Now, let v m be the actor with the maximum product of actor execution time and repetition. That is

$$ \mu_m q_m = \max_{v_i \in V} (\mu_i q_i) = \eta $$
(48)

The period of v m is λ m given by

$$ \lambda_m = \frac{Q}{q_m} \biggl\lceil\frac{\eta}{Q} \biggr \rceil $$
(49)

Now, let us write η as η=pQ+r, where p=η÷Q (÷ is the integer division operator), and r=ηmodQ. Then, we can re-write (48) as

$$ \lambda_m = \frac{Q}{q_m} \biggl\lceil p + \frac{r}{Q} \biggr\rceil $$
(50)

For matched I/O rates applications, r=0 (see Definition 4). Therefore, (50) can be re-written as

$$ \lambda_m = \frac{pQ}{q_m} $$
(51)

The utilization of v m is U m given by

$$ U_m = \frac{\mu_m}{\lambda_m} = \frac{\mu_m q_m}{pQ} $$
(52)

Since r=0 and η=pQ=μ m q m , (52) becomes

$$ U_m = \frac{\eta}{\eta} = 1.0 $$
(53)

 □

Recall from Sect. 3.2.2 that β=⌊1/U max⌋. It follows from Corollary 2 that β=1 for matched I/O rates applications scheduled using their minimum period vectors.

Let ϕ i be the earliest start time of an actor v i ∈V. Then, according to Definitions 5 and 6, the graph latency L(G) is given by:

$$ L(G) = \max_{w_{i \leadsto j}\in\mathcal{W}} \bigl(\phi_j + \bigl(g^C_j + 1\bigr) \lambda_j - \bigl(\phi_i + g^P_i \lambda_i\bigr)\bigr) $$
(54)

where ϕ j and ϕ i are the earliest start times of the output actor v j and the input actor v i , respectively, λ j and λ i are the periods of v j and v i , and \(g^{C}_{j}\) and \(g^{P}_{i}\) are two constants, such that for an output path w i⇝j in which e r is the first channel and e u is the last channel, \(g^{P}_{i}\) and \(g^{C}_{j}\) are given by:

(55)
(56)

where \(x_{i}^{r}\) and \(y_{j}^{u}\) are production/consumption rates sequences introduced in Sect. 3.

4.4 Handling sporadic input streams

In case the input streams are not strictly periodic, there are several techniques to accommodate the aperiodic nature of the streams. We present here some of these techniques.

4.4.1 De-jitter buffers

In case of periodic with jitter input streams, it is possible to use de-jitter buffers to hide the effect of jitter. We assume that a jittery input stream I i starts at time t=t 0 and has a constant inter-arrival time γ i equal to the input actor period (see Assumption 1-3) and jitter bounds \([\varepsilon_{i}^{-}, \varepsilon_{i}^{+}]\). The interpretation of the jitter bounds is that the kth sample of the stream is expected to arrive in the interval \([t_{0} + k\gamma_{i} - \varepsilon_{i}^{-}, t_{0} + k\gamma_{i} + \varepsilon_{i}^{+}]\). If a sample arrives in the interval \([t_{0} + k\gamma_{i} - \varepsilon_{i}^{-}, t_{0} + k\gamma_{i})\), then it is called an early sample. On the other hand, if the sample arrives in the interval \((t_{0} + k\gamma_{i}, t_{0} + k\gamma_{i} + \varepsilon_{i}^{+}]\), then it is called a late sample. It is trivial to show that early samples do not affect the periodicity of the input actor as the samples arrive prior to the actor release time. Late samples, however, pose a problem as they might arrive after an actor is released.

For late samples, it is possible to insert a buffer before each input actor v i receiving a jittery input stream I j to hide the effect of jitter. The buffer delays delivering the samples to the input actor by a certain amount of time, denoted by t buffer(I j ). t buffer(I j ) has to be computed such that once the input actor is started, it always finds data in the buffer. Assume that \(\varepsilon_{i}^{-}\) and \(\varepsilon_{i}^{+} \in[0, \gamma_{i}]\), then we can derive the minimum value for t buffer(I j ) and the minimum buffer size. In order to do that, we start with proving the following lemma:

Lemma 5

Let I j be a jittery input stream with \(\varepsilon_{i}^{-}, \varepsilon_{i}^{+} \in[0,\gamma_{i}]\). Then, the maximum inter-arrival time between any two consecutive samples in I j , denoted by t MIT(I j ), satisfies:

$$ t_{\mathrm{MIT}}(I_j) = 3\gamma_i $$
(57)

Proof

Based on the jitter model, t MIT occurs when the kth sample is early by the maximum value of jitter (i.e., arrives at time t=kγ i −γ i ), and the (k+1) sample is late by the maximum value of jitter (i.e., arrives at time t=(k+1)γ i +γ i ). This is illustrated in Fig. 11.

Fig. 11
figure 12

Occurrence of the maximum inter-arrival time

Full size image

 □

Lemma 6

An input actor v i ∈V is guaranteed to always find an input sample in each of its input de-jitter buffers if the following holds:

$$ t_{\mathrm{buffer}}(I_j) \ge2\gamma_j\quad\forall I_j \in Z_i $$
(58)

Proof

During a time interval (t,t+t MIT(I j )), v i can fire at most twice. Therefore, it is necessary to buffer up to 2 samples in order to guarantee that the input actor v i can continue firing periodically when the samples are separated by t MIT time-units. □

Lemma 7

Let v i be an input actor and I j be a jittery input stream to v i . Suppose that I j starts at time t=t 0 and v i starts at time t=t 0+t buffer(I j ). The de-jitter buffer must be able to hold at least 3 samples.

Proof

Suppose that the (k−1) and (k+1) samples arrive late and early, respectively, by the maximum amount of jitter. This means that they arrive at time t=t 0+kγ i . Now, suppose that the kth sample arrives with no jitter. This means that at time t=t 0+kγ i there are 3 samples arriving. Hence, the de-jitter buffer must be able to store them. During the interval [t 0+kγ i ,t 0+(k+1)γ i ), there are no incoming samples and v i processes the (k−1) sample. At time t=t 0+(k+1)γ i , the (k+2) sample might arrive which means that there are again 3 samples available to v i . By the periodicity of v i and I j , the previous pattern can repeat. □

The main advantage of the de-jitter buffer approach is that the actors are still treated and scheduled as periodic tasks. However, the major disadvantage is the extra delay encountered by the input stream samples and the extra memory needed for the buffers.

4.4.2 Resource reservation

For sporadic streams in general, we can consider the actors as aperiodic tasks and apply techniques for aperiodic task scheduling from real-time scheduling theory [6]. One popular approach is based on using a server task to service the aperiodic tasks. Servers provide resource reservation guarantees and temporal isolation. Several servers have been proposed in the literature (e.g., [1, 27]). The advantages of using servers are the enforced isolation between the tasks, and the ability to support arbitrarily input streams. When using servers, we can schedule each actor using a server which has an execution budget C s equal to the actor execution time and a period P s equal to the actor’s period.

One particular issue when scheduling the actors using servers is how to generate the aperiodic task requests. For the CSDF model, the requests can be generated when the firing rule of an actor is evaluated as “true” (see Sect. 3). Detecting when the firing rule is evaluated as “true” can be done in the following ways:

  1. 1.

    The underlying operating system (OS) or scheduler has a monitoring mechanism which polls the buffers to detect when an actor has enough data to fire. Once it detects that an actor has enough data to fire, it releases an actor job.

  2. 2.

    Modify the actor implementation such that the polling happens within the actor. In this approach, an actor job is always released at the start of the actor period. When the actor is activated (i.e., running), it checks its input buffers for data. If enough data is available, then it executes its function. Otherwise, it exhausts its budget and waits until the next period. This mechanism is summarized in Fig. 12.

    Fig. 12
    figure 13

    Polling within the actor to detect when the actor is eligible to fire

    Full size image

The first approach (i.e., polling by the OS) does not require modifications to the actors’ implementations. However, it requires an additional task which always checks all the buffers. This task can become a bottleneck if there are many channels. The second approach is better in terms of scalability and overhead. However, it might cause delays in the processing of the data.

5 Evaluation results

We evaluate our proposed framework in Sect. 4 by performing an experiment on a set of 19 real-life streaming applications. The objective of the experiment is to compare the throughput of streaming applications when scheduled using our strictly periodic scheduling to their maximum achievable throughput obtained via self-timed scheduling. After that, we discuss the implications of our results from Sect. 4 and the throughput comparison experiment. For brevity, we refer in the remainder of this section to our strictly periodic scheduling/schedule as SPS and the self-timed scheduling/schedule as STS.

The streaming applications used in the experiment are real-life streaming applications coming from different domains (e.g., signal processing, communication, multimedia, etc.). The benchmarks are described in details in the next section.

5.1 Benchmarks

We collected the benchmarks from several sources. The first source is the StreamIt benchmark [30] which contributes 11 streaming applications. The second source is the SDF3 benchmark [29] which contributes 5 streaming applications. The third source is individual research articles which contain real-life CSDF graphs such as [19, 24, 26]. In total, 19 applications are considered as shown in Table 1. The graphs are a mixture of CSDF and SDF graphs. The actors execution times of the StreamIt benchmark are specified by its authors in clock cycles measured on MIT RAW architecture, while the actors execution times of the SDF3 benchmark are specified for ARM architecture. For the graphs from [24, 26], the authors do not mention explicitly the actors execution times. As a result, we made assumptions regarding the execution times which are reported below Table 1.

Table 1 Benchmarks used for evaluation
Full size table

We use the SDF3 tool-set [29] for several purposes during the experiments. SDF3 is a powerful analysis tool-set which is capable of analyzing CSDF and SDF graphs to check for consistency errors, compute the repetition vector, compute the maximum achievable throughput, etc. SDF3 accepts the graphs in XML format. For StreamIt benchmarks, the StreamIt compiler is capable of exporting an SDF graph representation of the stream program. The exported graph is then converted into the XML format required by SDF3. For the graphs from the research articles, we constructed the XML representation for the CSDF graphs manually.

5.2 Experiment: throughput and latency comparison

In this experiment, we compare the throughput and latency resulting from our SPS approach to the maximum achievable throughput and minimum achievable latency of a streaming application. Recall from Definition 7 that the maximum achievable throughput and minimum achievable latency of a streaming application modeled as a CSDF graph are the ones achieved under self-timed scheduling. In this experiment, we report the throughput for the output actors (i.e., the actors producing the output streams of the application, see Sect. 3). For latency, we report the graph maximum latency according to Definition 6. For SPS, we used the minimum period vector given by Lemma 2. The STS throughput and latency are computed using the SDF3 tool-set. SDF3 defines R STS (G) as the graph throughput under STS, and R STS (v i )=q i R STS (G) as the actor throughput. Similarly, L STS (G) denotes the graph latency under self-timed scheduling. We use the sdf3analysis tool from SDF3 to compute the throughput and latency for the STS with auto-concurrency disabled and assuming unbounded FIFO channel sizes. Computing the throughput is performed using the throughput algorithm, while latency is computed using the latency(min_st) algorithm.

Now, Table 2 shows the results of comparing the throughput of the output actor for every application under both STS and SPS schedules. The most important column in the table is the last column which shows the ratio of the SPS schedule throughput to the STS schedule throughput (R SPS (v out)/R STS (v out)), where v out denotes the output actor. We clearly see that our SPS delivers the same throughput as STS for 16 out of 19 applications. All these 16 applications are matched I/O rates applications. This result conforms with Theorem 4 proved in Sect. 4. Only three applications (CD2DAT-(S,C) and Satellite) are mis-matched and have lower throughput under our SPS. Table 2 confirms also the observation made by the authors in [30] who reported an interesting finding: Neighboring actors often have matched I/O rates. This reduces the opportunity and impact of advanced scheduling strategies proposed in the literature. According to [30], the advanced scheduling strategies proposed in the literature (e.g., [28]) are suitable for mis-matched I/O rates applications. Looking into the results in Table 2, we see that our SPS approach performs very-well for matched I/O applications.

Table 2 Results of throughput comparison. v out denotes the output actor
Full size table

Figure 13 shows the ratios of the SPS latency (denoted by L SPS (G)) to the STS latency. For all the applications, the average SPS latency is 5× the STS latency. We also see that the mis-matched applications have large latency which conforms with their sub-optimal throughput. If we exclude the mis-matched applications, then the average SPS latency is 4x the STS latency. For latency-insensitive applications, this is acceptable as long as they can be scheduled using SPS to achieve the maximum achievable throughput. For latency-sensitive applications, reducing the latency can be done by, for example, using the constrained deadline model (see Sect. 3.2.1). The constrained deadline model assigns for each task τ i a deadline D i <T i , where T i is the task period. For example, the Vocoder application has ratio of L SPS (G)/L STS (G)≈13.5 under the implicit-deadline model. This ratio is reduced to 1.0 if the deadline of each task is set to its execution time. However, using the constrained-deadline model requires different schedulability analysis. Therefore, a detailed treatment of how to reduce the latency is outside the scope of this paper.

Fig. 13
figure 14

Results of the latency comparison

Full size image

5.3 Discussion

Suppose that an engineer wants to design an embedded MPSoC which will run a set of matched I/O rates streaming applications. How can he/she determine easily the minimum number of processors needed to schedule the applications to deliver the maximum achievable throughput? Our SPS framework in Sect. 4 provides a very fast and accurate answer, thanks to Theorems 3 and 4. They allows easy computation of the minimum number of processors needed by different hard-real-time scheduling algorithms for periodic tasks to schedule any matched I/O streaming application, modeled as an acyclic CSDF graph, while guaranteeing the maximum achievable throughput. Figure 14 illustrates the ability to easily compute the minimum number of processors required to schedule the benchmarks in Table 1 using optimal and partitioned hard-real-time scheduling algorithms for asynchronous sets of implicit-deadline periodic tasks. For optimal algorithms, the minimum number of processors is denoted by M OPT and computed using (9). For partitioned algorithms, we choose P-EDF algorithm combined with First-First (FF) allocation, abbreviated as P-EDF-FF. For P-EDF-FF, the minimum number of processors is computed using (10) (M P-EDF ) and (11) (M PAR ). For matched I/O applications scheduled using the minimum periods obtained by Lemma 2, Corollary 2 shows that β defined in Sect. 3.2.2 is equal to 1. This implies that for matched I/O applications, M P-EDF =⌈2U sum−1⌉ which is approximately twice as M OPT for large values of U sum. M PAR provides less resource usage compared to M P-EDF with the restriction that it is valid only for the specific task set τ G for which it is computed. Another task set \(\hat{\tau}_{G}\) with the same total utilization and maximum utilization factor as τ G may not be schedulable on M PAR due to the partitioning issues. Comparing M PAR to M OPT , we see that P-EDF-FF requires in around 44 % of the cases an average of 14 % more processors than an optimal algorithm due to the bin-packing effects.

Fig. 14
figure 15

Number of processors required by an optimal algorithm and P-EDF-FF

Full size image

Unfortunately, such easy computation as discussed above of the minimum number of processors is not possible for STS. This is because the minimum number of processors required by STS, denoted by M STS , can not be easily computed with equations such as (9), (10), and (11). Finding M STS in practice requires Design Space Exploration (DSE) procedures to find the best allocation which delivers the maximum achievable throughput. This fact shows one more advantage of using our SPS framework compared to using STS in cases where our SPS gives the same throughput as STS.

6 Conclusions

We prove that the actors of a streaming application, modeled as an acyclic CSDF graph, can be scheduled as periodic tasks. As a result, a variety of hard-real-time scheduling algorithms for periodic tasks can be applied to schedule such applications with a certain guaranteed throughput. We present an analytical framework for computing the periodic task parameters for the actors together with the minimum channel sizes such that a strictly periodic schedule exists. We also show how the proposed framework can handle sporadic input streams. We define formally a class of CSDF graphs called matched I/O rates applications which represents more than 80 % of streaming applications. We prove that strictly periodic scheduling is capable of delivering the maximum achievable throughput for matched I/O rates applications together with the ability to analytically determine the minimum number of processors needed to schedule the applications.