1 Introduction

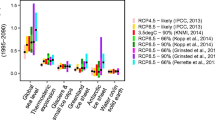
Anthropogenic greenhouse gas emissions are causing sea-level rise (SLR) (Church and White 2006; Jevrejeva et al. 2008). Because of the impacts SLR has on coastal flood risks (McGranahan et al. 2007; Houston 2013; Spanger-Siegfried et al. 2014), many studies focus on resolving future sea-level projections (e.g., Rahmstorf 2007; Grinsted et al. 2010; Church et al. 2013; Moore et al. 2013; Kopp et al. 2014, 2016). However, many of these studies generate ranges in projections that vary from study to study (Fig. SI 11) as they differ in methodology, model approach, and assumptions (Bakker et al. 2016).

Routinely, sea-level projections are constructed using both process-based and semi-empirical model approaches (e.g., Church et al. 2013; Moore et al. 2013). Process-based models of SLR describe the system of interest in the greatest detail available and are thus complex (Church et al. 2013). In contrast, semi-empirical models are typically simple models that trade off completeness (i.e., physical realism) for computational speed and calibration efficiency (e.g., Rahmstorf 2007; Grinsted et al. 2010; Moore et al. 2013). In both cases, projections rely heavily on assumptions, e.g., about the statistical model used for model fitting or lack of representing physical processes.

Key statistical challenges in projecting SLR include (i) the importance of interdependent (autocorrelated) data-model residuals, (ii) the representation of non-constant (heteroskedastic) observation errors, and (iii) tail probabilities far beyond the 90% credible interval (Von Storch 1995; Zellner and Tiao 1964; Ricciuto et al. 2008). Another issue includes spatial aggregation of the data (see, for example, Kopp et al. 2016). In recent years, studies have accounted for the complex error structure of the data including the heteroskedastic nature of the observation errors (Kemp et al. 2011; Kopp et al. 2016) because it is presumed that neglecting these properties of the observations and uncertainties can potentially lead to overconfidence (e.g., Zellner and Tiao 1964; Ricciuto et al. 2008; Donald et al. 2013). This quantitatively raises the question of how large the effect that neglecting or assuming too simple of an error structure is on projections, especially the upper tail projections.

Here, we quantify how explicitly accounting for autocorrelation and heteroskedastic residuals affects SLR projections (especially in the upper tail). We choose to use a semi-empirical sea-level model in our didactic analysis for two reasons: (1) calibration efficiency and (2) their use in informing risk-and-decision analyses (for example, Heberger et al. 2009; Dalton et al. 2010; Neumann et al. 2011; Dibajnia et al. 2012; McInnes et al. 2013). In our analysis, we implement a hierarchical model with a process-level model characterized by the Vermeer and Rahmstorf (2009) sea-level model (Eq. 1) and a data-level model (Eq. 2) where we fit the model in three different ways to the observational data (section 2). Additionally, we run the same analysis on two simpler models to assess the robustness of the conclusions (results in the SI). In section 3, we present the differences among the approaches, and in section 4, we discuss how our results can inform future sea-level projections.

2 Method

2.1 Sea-level model, observational data, and input data for projections

As described above, we adopt a semi-empirical model that predicts SLR on an annual time-step (Vermeer and Rahmstorf 2009):

$$ \delta H(t)/\delta (t)=\alpha \left(T-{T}_0\right)+b\times \delta T(t)/\delta (t), $$
(1)

where α is the sensitivity of the rate of SLR to temperature, T is the global mean surface air temperature, T 0 is the temperature when the sea-level anomaly equals zero, b is a constant corresponding to a rapid response term, H is the global mean sea-level, and t is time. We slightly expand on the model-fitting setup by including the initial value of SLR, H 0 , as an uncertain parameter (prior bounds based on measurement error; Church and White 2006). We use the global mean sea-level estimates, based on tide-gauge observations, of Church and White (2006). The sea-level anomalies are referenced to the average sea level from the 1980 to 2000 period. We use historical temperature anomalies (with respect to the twentieth century; Smith et al. 2008) for the model-fitting process. When the model is used in SLR projection mode, we use global-mean surface air temperature anomalies based on the CNRM-CM5 simulation of the RCP 8.5 scenario (Meinshausen et al. 2011; Riahi et al. 2011) as obtained from the CMIP5 model output archive (http://cmip-pcmdi.llnl.gov/cmip5/). As in Vermeer and Rahmstorf (2009), we apply the same smoothing process to estimate the rate of temperature.

2.2 Analyzed model-fitting methods

We compare parameter estimates and the SLR projections based on three model-fitting methods: a Bootstrap method (Solow 1985), a Bayesian method assuming homoskedastic errors, and a Bayesian method accounting for the time dependent (heteroskedastic) nature of the observation errors (details of the three methods are in the SI) (Zellner and Tiao 1964; Gilks 1997). The methods are described in detail in the SI. Here, we provide a brief overview. The methods approximate the observation dataset as the sum of the model output plus a residual term:

$$ \underset{\mathrm{observations}}{\underbrace{y_t}}=\underset{\mathrm{model}}{\underbrace{f\left(\theta, t\right)}}+\underset{\mathrm{residuals}}{\underbrace{R_t}}, $$
(2)
$$ \underset{\mathrm{model}\ \mathrm{parameters}}{\underbrace{\theta}}=\left(\alpha,\ {T}_0,\ {H}_0,\ b\right), $$
(3)

where the f(θ,t) (or H(t)) defines the portion of global mean sea-level related to temperature by the semi-empirical model and y t describe the noisy observations including the variability not explained by the semi-empirical model and the observational error. The model error accounts for effects such as unresolved internal variability or other structural errors. The observational error (often also referred to as measurement error) is the difference between a measured value (i.e., estimated global mean sea-level anomalies) and the true value. The residuals are the sum of the model error ωt and observational error εt:

$$ {R}_t={\omega}_t+{\varepsilon}_t, $$
(4)
$$ {\omega}_t=\rho \times {\omega}_{t-1}+{\delta}_t, $$
(5)
$$ {\omega}_0\sim N\left(0,\frac{\sigma_{AR1}^2}{1-{\rho}^2}\right),\kern0.5em {\delta}_t\sim N\left(0,{\sigma}_{AR1}^2\right),\kern0.5em {\varepsilon}_t\sim N\left(0,{\sigma}_{\varepsilon}^2\right). $$
(6)

Therefore, \( \overrightarrow{\omega}=\left({\omega}_1, \dots,\ {\omega}_N\right) \) is a time series from a multivariate normal distribution with variance \( {\upsigma}_{\mathrm{AR}1}^2 \) and the correlation structure given by the first-order autoregressive parameter ρ (this model is also recognized as AR1). The observational errors are given by the global mean sea-level data. In principle, they should be treated as correlated (see, for example, the Church and White (2006) analysis). However, for simplicity, we approximate the observational errors as uncorrelated.

Following the Bootstrap method implemented in Lempert et al. (2012), we fit the model according to the least absolute residual method and approximate the data-model residuals using a first-order autoregressive model assuming homoskedastic observational errors. The resulting residuals are superimposed to the original fit. Parameters are then re-estimated from the Bootstrap realizations. This method estimates parameters without the use of priors. For the two Bayesian methods, we estimate the posterior density using a Markov Chain Monte Carlo method and the Metropolis Hastings algorithm (Metropolis et al. 1953; Zellner and Tiao 1964; Hastings 1970; Gilks 1997; Vihola 2012). Both Bayesian methods approximate the residuals as normally distributed with zero mean. The homoskedastic method and the Bootstrap method assume the variance of the observational errors σε 2 to be constant in time, whereas the heteroskedastic method accounts for the time-varying observational error (Fig. 1). All three methods retain the autocorrelation structure of the residuals (Fig. 1). The Bootstrap method approximates the autoregression coefficient ρ with the most likely value, while the Bayesian methods account for uncertainty in the autocorrelation (as well as in the white noise variance \( {\upsigma}_{\mathrm{AR}1}^2 \)). All three methods use the same annual mean temperature and sea-level data covering the time period of 1880 to 2002.

Fig. 1
figure 1

Stochastic properties of the model residuals and observational errors in the global mean sea-level record. a Displays the residuals (observations—best-fit model simulation derived by differential evolution optimization). b Shows the observational errors are time-dependent. c Displays the autocorrelation coefficient for the residuals. When the vertical lines at the time lags exceed the dashed blue line (95% significance), then the residuals are considered to be statistically autocorrelated

Full size image

2.3 Method implementation

We implement a hierarchal model with a process-level model characterized by Eq. 1 and a data-level model characterized by Eq. 2. The Bayesian methods use uniform prior distributions for the physical model parameters (θ, including α, T 0 , H 0 , b) and the statistical model parameters (σAR1 and ρ) (Table 1). In the Bayesian (homoskedastic) approach, the observation errors are set to zero (merging the model error and observational error into one term) to represent the homoskedastic assumption. In the heteroskedastic Bayesian approach, the errors are set to the reported values (Zellner and Tiao 1964). We use 2∙104 (Bootstrap), 5∙106 (homoskedastic Bayesian), and 3∙106 (heteroskedastic Bayesian) iterations. For the Bayesian methods, we remove a 2% initial “burn-in” from the Markov chains (Gilks 1997). Additionally, we thin the chains in the Bayesian methods to subsets of 2∙104 for the analysis. To assess convergence, we use (i) visual inspection and (ii) the potential scale reduction factor (Gelman and Rubin 1992; Gilks 1997). Furthermore, we test the sea-level hindcasts from each method for reliability based on the reliability diagram and surprise index (see SI for details). A reliability diagram is a graph of the observed frequency (or the fraction of observations) that is covered by the hindcast credible interval versus the forecast probability. The surprise index is the deviation between the observed frequency and the forecast probability. The hindcasts and projections display the 90% confidence interval (Bootstrap) and the 90% credible interval (Bayesian methods) for comparison to other sea-level studies (comparison shown in Fig. SI. 11; for simplicity, we refer to these intervals as credible intervals in the remainder of this paper). The main conclusions are not sensitive to the random seed applied (tested with five seeds for each method) and not sensitive to the choice of SLR model applied (analysis run with Rahmstorf (2007) and the Grinsted et al. (2010) model; details shown in the SI).

Table 1 Prior uniform distributions and fitted median, mode, and 99% estimates for model and statistical parameters
Full size table

3 Results

3.1 Stochastic structure of sea-level observations

Accounting for the stochastic structure of sea-level observations can be important in hindcasting and projecting sea level (see Fig. 1). Sea-level observation errors vary through time (Fig. 1b). For example, the error estimates of global sea level generally decrease with time due to effects of improved measurement techniques and more frequent observations. By specifying the heteroskedastic observation error, the model-fitting method can account for years when measurements are less or more certain. Moreover, sea-level residuals are autocorrelated because deviations from the main trend often impact sea-level anomalies in the following years (Fig. 1c; the importance of autocorrelation representation is tested by performing a perfect model experiment in the SI, Fig. SI. 1). For example, the climate system is known for its many multi-year oscillations (such as the El Niño-Southern Oscillation (ENSO); Boening et al. 2012; Cazenave et al. 2012) that can cause long-term deviations of the observations from the long-term global sea-level trend (Rietbroek et al. 2016). These multi-year oscillations are often not well represented in the models, leading to structural model errors. Testing the observations and the model residuals for these properties is important, because they can impact the choice of the model-fitting method, parameter estimates, and projections.

3.2 Model evaluation and parameter uncertainty

The considered methods produce similar hindcasts and reliability diagrams, but different parameter distributions (Figs. 2 and 3; (nb: median fits are shown in Fig. SI. 10)). The methods predict well at low to intermediate credible intervals, yet perform relatively poorly at the high credible intervals (i.e., >90% credible level; the SI describes simple tests and results of investigating potential causes for poor performance, Fig. SI. 1–3) (Fig. 2b). Despite the arguably poor performance, each method produces a small average deviation from perfect reliability; this concept is known as the surprise index (Fig. 2b). The average surprise index for the Bootstrap, homoskedastic Bayesian, and heteroskedastic Bayesian methods are 2–7%. Choosing different methods causes differences in the estimated modes and tails of the model parameters (Fig. 3; Table 1). As we account for more known observational properties (i.e., moving from Bootstrap to homoskedastic Bayesian to heteroskedastic Bayesian), the distributions widen, the modes shift, and the tail areas increase for each parameter (Fig. 3; Table 1).

Fig. 2
figure 2

Comparison of sea-level rise hindcasts and projections and the reliability diagram. a, c, d Display the 90% credible interval for each method along with the synthesized observations (points) and their associated measurement error (Church and White 2006). The color ramp from light green to dark blue represents accounting for more known observational properties (Bootstrap to homoskedastic Bayesian to heteroskedastic Bayesian). b The reliability diagram analyzes the hindcast credible intervals produced from each method from 10 to 100% in increments of 10. If the method produces perfectly reliable credible intervals, then the points will plot on a 1:1 line (displayed as a dashed line) representing neither over—nor—underconfidence. b The subplot zooms in on the credible intervals from 90 to 100%

Full size image
Fig. 3
figure 3

Marginal probability density functions of the estimated model and statistical parameters. Shown are (α) sensitivity of sea-level to changes in temperature (a), (T 0 ) the equilibrium temperature (c), (b) a constant referring to a rapid response term (c), (H 0 ) the initial sea-level anomaly in the year 1880 (d), and (ρ) autoregression coefficient (e). The dashed lines are the prior parameter distribution used in the Bayesian methods. The prior distribution is not shown for parameters α and b because the prior is far larger than the posterior distribution

Full size image

3.3 Comparison of low probability sea-level estimates

The choice of model-fitting method and associated parameter uncertainty considerably impacts the probability density functions, and especially the upper tail-area estimates, of the SLR projections (Figs. 2 and 4). The projected 90% probability ranges in 2050 differ by up to 0.11 m; Bootstrap (0.23–0.33 m), homoskedastic Bayesian (0.19–0.32 m), to heteroskedastic Bayesian (0.14–0.35 m) (Fig. 2c). Depending on the choice of model-fitting method, the projected sea-level anomaly with a 1% (10−2) probability of being equaled or exceeded in the year 2050 (compared to the 1980–2000 period) varies from 0.35 to 0.46 m (Fig. 4e). The heteroskedastic Bayesian method gives a roughly 34% larger sea-level anomaly (associated with the 1% probability) in the year 2050 compared to the sea-level anomaly produced by the Bootstrap method. In 2100, the sea-level anomaly produced by the heteroskedastic Bayesian method with a 1% probability of being equaled or exceeded (1.49 m) differs from the Bootstrap method sea-level anomaly (1.07 m) by 0.42 m; this difference corresponds to a 40% increase (Fig. 4f).

Fig. 4
figure 4

Projections for global mean sea-level rise in 2050 (a, c, e) and 2100 (b, d, f) determined for the different methods presented as the probability density function (a, b), the cumulative density function (c, d), and the survival function (e, f). The horizontal dashed lines in the survival function represent the 1% (10−2) probability used in example studies to design sea-level rise adaptation strategies (IWR 2011; Houston 2013)

Full size image

The differences in the SLR projections and parameter distributions can be traced back to assumptions embedded in the model-fitting methods. The Bootstrap method neglects uncertainty in the autocorrelation coefficient, neglects the heteroskedastic nature of the observational errors, and is not informed by priors. The homoskedastic Bayesian method still neglects the heteroskedastic nature of the observational errors, but accounts for uncertainty about the autocorrelation coefficient. Lastly, the heteroskedastic Bayesian method best represents the error structure as it accounts for the heteroskedastic nature of the observation errors and uncertainty about the autocorrelation coefficient.

4 Discussion and conclusion

Semi-empirical SLR models have been used to project sea-level changes (e.g., Rahmstorf 2007; Grinsted et al. 2010; Church et al. 2013; Moore et al. 2013) and inform risk-and-decision analysis (e.g., Heberger et al. 2009; Dalton et al. 2010; Neumann et al. 2011; Dibajnia et al. 2012; McInnes et al. 2013). Here, we present results using a simple sea-level model (i.e., sea level responds only to changes in temperature) to quantify the effects of neglecting known observational properties (i.e., autocorrelated and heteroskedastic residuals). We have chosen a simple (and therefore transparent) framework to demonstrate how neglecting such properties leads to overconfident projections, which can impact how sea-level projections inform risk-and-decision analyses.

The performance of the model-fitting methods could be further analyzed using methods other than reliability diagrams and surprise indices (e.g., Brier 1950; Runge et al. 2016). Given the poor performance at the low probability estimates, extending the temperature and sea-level data with paleo-reconstructions (Hegerl et al. 2006; Kopp et al. 2016) could potentially improve underconfidence in the upper tails (the SI details this effect using a perfect model experiment, Fig. SI. 2). Additionally, this study could be extended to assess the impacts of neglecting error structure has on historical extremes or particular regions and comparing the results to previous studies (e.g., Kopp et al. 2014 and Menendez et al. 2009). Lastly, this study is silent on the impacts of measurement error in temperatures and only considers a single sea-level and temperature reconstruction to isolate the effects of autocorrelated and heteroskedastic residuals. Using different reconstructions and accounting for temperature measurement error would impact estimated parameters and projection probabilities (the SI details the impact different temperature scenarios have on probabilistic projections; Fig. SI. 12 and 13) (Kopp et al. 2016).

Given the caveats, we show that projections are overconfident when the process model neglects autocorrelation and accounts for too simple of an error structure. By considering known observational properties (i.e., heteroskedastic and autocorrelated data-model residuals), the parameter distributions widen and the upper tails increase. Moreover, we show that these effects are enhanced in the upper tail projections. For example, accounting for known observational properties increase the projected sea-level anomaly with a 1% probability of being equaled or exceeded in the year 2050 and the year 2100 (compared to the 1980–2000 period) by roughly 34 and 40%, respectively. This assessment demonstrates how neglecting known properties of the residuals can lead to low-biased sea-level projections and associated flood risk estimates.