An analytical solution for the swing-by problem

Abstract

The extension of Öpik’s theory of close encounters developed in the last decades allows a fully analytical, quantitative treatment of the motion of a small body encountering a massive perturber on a circular orbit. In this paper we derive explicit expressions for the initial values of the angular elements of the small body orbit, of given semimajor axis, eccentricity and inclination, in order to obtain a post-encounter orbit with prescribed values of semimajor axis, eccentricity and inclination. We describe the geometrical aspects of the algorithm, and give two examples of application; the first of them concerns the geometry of the 2029 Earth encounter of Apophis, while the second illustrates a sequence of close encounters with Callisto of the JUICE probe, aimed at changing the inclination of the spacecraft orbit. In the planning of complex space missions involving multiple encounters with planets or satellites, the algorithm described in the paper could provide a reliable initial guess to start the computationally intensive optimization process.

Appendices

Appendix 1: Notation

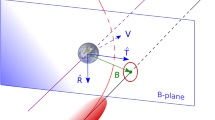
As noted in Valsecchi et al. (2003), the b-plane coordinate $\xi$ represents essentially the local minimum of the distance between the orbits of the secondary and of the small body, which results in $\xi =0$ if the two orbits cross. The theory holds also when they almost cross. On the other hand, $\zeta$ is related to the timing of the encounter, i.e. to how early, or how late, is the small body with respect to the secondary.

$a, e, i, \varOmega , \omega , f$	Pre-encounter orbital elements of the small body about the primary
$a', e', i', \varOmega ', \omega ', f'$	Post-encounter orbital elements of the small body about the primary
X-Y-Z	Reference frame centred on the secondary at the encounter
$\mathbf{U}$	Pre-encounter relative velocity vector in the X-Y-Z reference frame
$U_x, U_y, U_z$	Components of $\mathbf{U}$
$\theta , \phi$	Angles defining the direction of $\mathbf{U}$ in the X-Y-Z reference frame
$\mathbf { U}\varvec{'}$	Post-encounter relative velocity vector in the X-Y-Z reference frame
$U'_x, U'_y, U'_z$	Components of $\mathbf { U}\varvec{'}$
$\theta ', \phi '$	Angles defining the direction of $\mathbf { U}\varvec{'}$ in X-Y-Z
$\xi , \zeta$	b-plane coordinates
$\xi ', \zeta '$	Coordinates on the post-encounter b-plane (normal to $\mathbf { U}\varvec{'}$)
r	Distance from the primary
$\lambda , \beta$	Longitude and latitude of the small body
$a_p$	Radius of the circular orbit of the secondary about the primary
$\lambda _p$	Longitude of the secondary
d	Distance between the small body and the secondary
$t_b$	Time of b-plane crossing
c	Modulus of the semimajor axis of the hyperbola about the secondary
m	Mass of the secondary in units of that of the primary
b	Impact parameter
q, Q	Pericentre, apocentre

Appendix 2: Range of validity of the algorithms

The quantitative description of close encounter dynamics made by the theory presented in the paper can be reasonably accurate if a certain number of conditions are verified; we list them hereafter.

1.1 The encounter must be hyperbolic

The orbit of the small body about the secondary at encounter must be hyperbolic, otherwise $\mathbf{U}$ is undefined, implying that $U^2>0$; this, in turn, implies that

$$\begin{aligned} \frac{a_p}{a}+2\sqrt{\frac{a(1-e^2)}{a_p}}\cos {i}<3. \end{aligned}$$

1.2 The secondary and the small body must not be co-moving

Even for a hyperbolic encounter it can happen, if the pre-encounter orbit of the small body is characterized by a very small i, and either $q\approx {a}_p$ or $Q\approx {a}_p$, that $\sin \theta$ is very small; if this happens, $\phi$ becomes ill-determined, since $\sin \theta$ appears in the denominators of (1) and (2), and the quantitative results are likewise degraded.

1.3 The encounter must be close

As discussed in Section 3 and Appendix A.1 of Valsecchi et al. (2003), the formulae to pass from orbital elements to encounter-related variables are linearized in b, so cannot reliably used for very shallow encounters.

1.4 The mass of the secondary must be small

The encounter velocity U is in units of the velocity of the secondary about the primary, provided that the velocity of the secondary is computed as if its mass were 0; this introduces a small error, of order m. As a consequence, the encounter-related variables are linearized not only in b, as seen above, but also in m; therefore the theory cannot reliably used for encounters with very massive secondary bodies.