Atmospheric Flow over a Mountainous Region by a One-Way Coupled Approach Based on Reynolds-Averaged Turbulence Modelling

Abstract

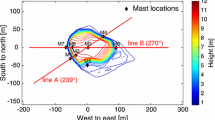
The atmospheric flow over a mountainous region has been simulated using a model-chain approach, whereby the flow in a larger region was simulated using a mesoscale model with three nesting levels, down to a 3-km horizontal resolution, within which a fourth nesting level was set with a microscale flow solver and a domain with varying horizontal resolution, around 300 m at the site of interest. Two periods in the summer (July) and autumn (November–December) 2005, each with a duration of two weeks, were selected to test the present approach. Two sites were chosen, comprising a total of seven meteorological masts with wind vanes and anemometers at two heights. The microscale solver improved the wind-speed prediction of the mesoscale model in 10 of the 14 anemometers and replicated the high wind speeds, which were under-predicted in the mesoscale model. The wind conditions in summer varied with the daily cycle, related to regional-scale sea breezes and their interaction with local circulations induced by the topography. Regarding the turbulence intensity, the predicted decay with wind-speed increase was in agreement with the measurements. This study shows the need of both models: the microscale model captures the details of the boundary-layer physics, which would not be possible without the boundary conditions provided by the mesoscale model.

Appendices

Appendix 1: Surface-Layer Stability Functions and Flow Near Walls

The vertical profiles of velocity and temperature across the surface layer are functions of stability, $\zeta$, defined as,

$$\begin{aligned} \zeta =\dfrac{z}{\mathcal {L}} =-\dfrac{g}{\varTheta }\dfrac{\kappa \, z\,q_{\mathrm {w}}}{\rho _{\mathrm {w}}\,c_\mathrm{p}\,u_*^3}, \end{aligned}$$

(22)

where z is the distance from the ground, $\mathcal {L}$ is the Obukhov length, $\rho _{\mathrm {w}}$ and $q_{\mathrm {w}}$ are the fluid density and the surface heat flux, $u_*$ is the friction velocity and $\varTheta$ is a temperature representative of the surface layer, taken as the wall value of $\theta _{\textsc {h}}$.

The stability functions are formulated as in Dyer (1974). Considering horizontal flow aligned with the longitudinal direction, we have

(23)

(24)

with the constants $b_\mathrm{mu}=b_\mathrm{hu}=16$ and $b_\mathrm{ms}=b_\mathrm{hs}=5$, $\kappa =0.4$ and the turbulent Prandtl number at neutral stratification $\sigma _{\textsc {n}}=1$.

For a surface layer characterized by constant fluxes of momentum and heat, the velocity and temperature, obtained by integration of $\phi _\mathrm{m}$ and $\phi _\mathrm{h}$, are

$$\begin{aligned} \overline{u}\,(z,\mathcal {L})&= \dfrac{u_*}{\kappa }\left[ \ln \left( \dfrac{z}{z_{\mathrm{m}0}}\right) -\psi _\mathrm{m}\left( \dfrac{z}{\mathcal {L}}\right) +\psi _\mathrm{m}\left( \dfrac{z_{\mathrm{m}0}}{\mathcal {L}}\right) \right] , \end{aligned}$$

(25)

$$\begin{aligned} \Delta \overline{\theta }\,(z,\mathcal {L})&= \dfrac{\sigma _{\textsc {n}}\,\theta _*}{\kappa }\left[ \ln \left( \dfrac{z}{z_{\mathrm{h}0}}\right) -\psi _\mathrm{h}\left( \dfrac{z}{\mathcal {L}}\right) +\psi _\mathrm{h}\left( \dfrac{z_{\mathrm{h}0}}{\mathcal {L}}\right) \right] , \end{aligned}$$

(26)

where $z_{\mathrm{m}0}$ and $z_{\mathrm{h}0}$ are roughness lengths for momentum and heat, with $z_{\mathrm{h}0} \approx 0.1\,z_{\mathrm{m}0}$ (Garratt 1992). The potential temperature difference, $\Delta \overline{\theta }$, is relative to the respective value at the wall and the turbulence temperature scale, $\theta _*$, is defined such that $q_{\mathrm {w}}=-\rho _{\mathrm {w}}\,c_\mathrm{p}\,u_*\,\theta _*$. Functions $\psi _\mathrm{m}$ and $\psi _\mathrm{h}$ are defined as,

$$\begin{aligned} \psi _\mathrm{m}\left( \zeta \right)= & {} {\left\{ \begin{array}{ll} \ln \left( \dfrac{[1+\eta ^2][1+\eta ]^2}{8}\right) -2\,\mathrm {atan}\left( \eta \right) +\dfrac{\pi }{2}, &{} \text {for}\; \zeta < 0,\\ -b_\mathrm{ms}\,\zeta ,&{} \text {for}\; \zeta \ge 0, \end{array}\right. } \end{aligned}$$

(27)

$$\begin{aligned} \psi _\mathrm{h}\left( \zeta \right)= & {} {\left\{ \begin{array}{ll} 2\,\ln \left( \dfrac{1+\chi }{2}\right) ,&{}\text {for}\; \zeta < 0,\\ -\dfrac{b_\mathrm{hs}}{\sigma _{\textsc {n}}}\,\zeta , &{}\text {for}\; \zeta \ge 0, \end{array}\right. } \end{aligned}$$

(28)

with and . From (25) and (26), the bulk transfer coefficients for momentum and heat, $C_\mathrm{m}$ and $C_\theta$, are defined as

$$\begin{aligned} C_\mathrm{m}\left( z,\mathcal {L}\right)= & {} \dfrac{u_*}{\overline{u}} =\kappa \,\left[ \ln \left( \dfrac{z}{z_{\mathrm{m}0}}\right) -\psi _\mathrm{m}\left( \dfrac{z}{\mathcal {L}}\right) +\psi _\mathrm{m}\left( \dfrac{z_{\mathrm{m}0}}{\mathcal {L}}\right) \right] ^{-1}, \end{aligned}$$

(29)

$$\begin{aligned} C_\theta \left( z,\mathcal {L}\right)= & {} \dfrac{\theta _*}{\overline{\Delta \theta }} =\dfrac{\kappa }{\sigma _{\textsc {n}}} \, \left[ \ln \left( \dfrac{z}{z_{\mathrm{h}0}}\right) -\psi _\mathrm{h}\left( \dfrac{z}{\mathcal {L}}\right) +\psi _\mathrm{h}\left( \dfrac{z_{\mathrm{h}0}}{\mathcal {L}}\right) \right] ^{-1}. \end{aligned}$$

(30)

1.1 Wall Laws from Known Velocity and Temperature Profiles

For microscale grid nodes below the first vertical mesoscale level, tri-linear interpolation from the $\text {WRF}$ model results is identical to assume that velocity and temperature profiles obey a linear law. To use logarithmic laws instead, the Obukhov length $\mathcal {L}$ should be consistent with (25) and (26) to compute both $u_*$ and $\theta _*$. From the definition of the bulk Richardson number and Eqs. 22, 29 and 30,

$$\begin{aligned} \dfrac{g}{\varTheta } \dfrac{z\,\Delta \overline{\theta }}{\left[ \overline{u}^2 + \overline{v}^2\right] } = \dfrac{z}{\mathcal {L}}\, \dfrac{C_\mathrm{m}^2}{\kappa \,\sigma _{\textsc {n}}\,C_\theta }, \end{aligned}$$

(31)

where the horizontal wind speed and temperature difference relative to the wall ($\Delta \overline{\theta }$) at height z are known, given by the mesoscale solution at the first vertical level above the wall. The value of $\mathcal {L}$ is computed by numerically solving Eq. 31 using a bisection root-finding method. Equations 29 and 30 are then used to obtain $u_*$ and $\theta _*$.

1.2 Prescribed Heat-Flux Condition at the Bottom Surface

The mesoscale model provides fields for both surface temperature and sensible heat flux. Although a prescribed temperature is straightforward to implement, e.g. using (31), it may introduce severe discrepancies due to the sensitivity of the temperature with height. As the microscale and mesoscale grids have different elevations for the same location, the temperature variation between both heights may be large. Instead, as the heat flux within the surface layer is expected to be nearly constant with height, it is preferable to use it as a boundary condition for the microscale.

This boundary condition may yield two solutions of $\mathcal {L}$ for the same surface heat flux, $q_{\mathrm {w}}$, known as the duality problem (van de Wiel et al. 2007). As one of these solutions leads to a collapse of turbulence, such that both turbulent and laminar states are possible, a limitation was imposed on the maximum value of $\zeta$ to force a continuous turbulent regime,

$$\begin{aligned} \max \left( \zeta \right) = \dfrac{z\,\ln \left( \left. { z}/{z_{\mathrm{m}0}}\right. \right) }{2\,b_\mathrm{ms}\left( z-z_{\mathrm{m}0}\right) }. \end{aligned}$$

(32)

This limit arises from the minimum value possible for $q_{\mathrm {w}}$ to attain,

$$\begin{aligned} \min \left( q_{\mathrm {w}}\right) = \dfrac{-4\,\kappa ^2\,\rho _{\mathrm {w}}\,c_\mathrm{p}\,\vert \mathbf {u}_\parallel \vert ^3}{ 27\,\dfrac{g}{\varTheta }\,b_\mathrm{ms}\left( z-z_{\mathrm{m}0}\right) \, \ln \left( z/z_{\mathrm{m}0}\right) ^2}, \end{aligned}$$

(33)

where $\vert \mathbf {u}_\parallel \vert$ is the magnitude of tangential velocity at the centre of the control volumes adjacent to the wall.

The stability parameter $\zeta$ is computed from the known values of $\vert \mathbf {u}_\parallel \vert$ and $q_{\mathrm {w}}$. The velocity is related to $u_*$ through the momentum bulk transfer coefficient (29),

$$\begin{aligned} u_* = \vert \mathbf {u}_\parallel \vert \, C_\mathrm{m}. \end{aligned}$$

(34)

A value for $\zeta$ is computed by numerically solving the implicit relation obtained by combining (22) and (29). This was done at each surface grid point for each iteration of the segregated solver, using a fixed-point iteration method which was verified to converge in the range of $\zeta$ for which the stability functions are valid, considering the limit imposed by Eq. 32.

Appendix 2: Error Measures

Considering the time series of a quantity X and $X_n$ as its sample at instant n, for $n=1,\,\ldots ,\,N$ records, the absolute error, $\Delta X$, is defined as,

$$\begin{aligned} \Delta X_n = X^\textsc {f}_n - X^\textsc {m}_n, \end{aligned}$$

(35)

where the superscripts $\textsc {f}$ and $\textsc {m}$ refer to the forecasted and measured values. A positive value indicates that the forecast over-predicts the observation and otherwise for a negative value. If X represents the wind direction, $\phi$, as this is a circular quantity in the interval $[0^{\circ },\,360^{\circ } [$, the azimuth difference between $\phi ^\textsc {f}$ and $\phi ^\textsc {m}$ was used to define the error, such that

$$\begin{aligned} \Delta X_n= \Delta \phi ^*_n -360\,{\text {sgn}}\big (\Delta \phi ^*_n\big )\, \max \Big (0,\,{\text {sgn}}\big (\vert \Delta \phi ^*_n\vert -180\big )\Big ), \end{aligned}$$

(36)

where $\Delta \phi ^*_n = \phi ^\textsc {f}_n - \phi ^\textsc {m}_n$. The azimuthal error will only take values in $[-180^{\circ },\,180^{\circ } ]$.

From $\Delta X$, the bias (B), mean-squared-error ($\textit{MSE}$) and its square-root ($\textit{RMSE}$) are defined as:

$$\begin{aligned} B(X^\textsc {f})= & {} \dfrac{1}{N}\sum ^{N}_{n=1}\Delta X_n, \end{aligned}$$

(37)

$$\begin{aligned} \textit{MSE}(X^\textsc {f})= & {} \dfrac{1}{N}\sum ^{N}_{n=1}\Delta X_n^2, \end{aligned}$$

(38)

$$\begin{aligned} \textit{RMSE}(X^\textsc {f})= & {} \sqrt{\textit{MSE}}. \end{aligned}$$

(39)

The linear correlation between $X^\textsc {f}$ and $X^\textsc {m}$ was estimated using the Pearson correlation coefficient,

$$\begin{aligned} r=\left[ \sum _{n=1}^{N} \left( X^\textsc {f}_n - \overline{X^\textsc {f}}\right) \, \left( X^\textsc {m}_n - \overline{X^\textsc {m}}\right) \right] \Bigg /\sqrt{ \sum _{n=1}^{N}\left( X^\textsc {f}_n-\overline{X^\textsc {f}}\right) ^2 \,\sum _{n=1}^{N}\left( X^\textsc {m}_n-\overline{X^\textsc {m}}\right) ^2},\nonumber \\ \end{aligned}$$

(40)

where the overbar denotes the sample mean.

If two forecasts for X exist, $X^\textsc {f}$ and $X^\textsc {r}$, the skill score (SS) may be used to estimate the improvement of one forecast over another (Murphy 1988). Choosing one of the forecasts as reference, $X^\textsc {r}$, the SS is obtained by comparing the respective mean squared errors:

$$\begin{aligned} \textit{SS} = 1 - \textit{MSE}(X^\textsc {f})/\textit{MSE}(X^\textsc {r}), \end{aligned}$$

(41)

where $\textit{MSE}(X^\textsc {f})$ and $\textit{MSE}(X^\textsc {r})$ refer to the mean squared error of $X^\textsc {f}$ and $X^\textsc {r}$. The SS is dimensionless and varies between $-\infty$ and 1, indicating that forecast $X^F$ has lower error than $X^R$ when $SS>0$.

Appendix 3: Statistics for Unsteady RANS Results

The flow fields of an unsteady RANS model refer to mean and turbulent quantities specific to a timestep $\Delta t$. The velocity field is regarded as either its ensemble or time average, $\overline{\mathbf {u}}$, while $k=\tfrac{1}{2}\sum _i\overline{u'_i\,u'_i}$. The overbar is here used to represent the mean field which is related to the simulation timestep $\Delta t$, whereas the operator $\langle \,\rangle$ represents an average over a larger integration time $\Delta T$, where $\Delta T \gg \Delta t$.

To compare unsteady RANS results with cup anemometer measurements, the former have to be resampled as as the latter refer to integrations over $\Delta T = 10\,\mathrm {min}$. Albeit the simulation mean fields vary in time, it is assumed that the mean and turbulent quantities are quasi-stationary, i.e. the time scale of turbulent motions is much smaller than that of the mean flow and at the timestep scale $\Delta t$, turbulent fluctuations become null when averaged. Breaking $\Delta T$ into $N\,\Delta t$ intervals, the average of quantity u over $\Delta T$ becomes,

$$\begin{aligned} \langle u\rangle =\dfrac{1}{\Delta T}\int \limits _0^{\Delta T}u\,\text {d}t =\dfrac{1}{N\,\Delta t}\sum \limits _{n=1}^{N} \left[ \overset{n\,\Delta t}{\underset{(n-1)\,\Delta t}{\int u\,\text {d}t}} \right] =\dfrac{1}{N}\sum \limits _{n=1}^{N} \overline{u}|_n \equiv \langle \overline{u} \rangle , \end{aligned}$$

(42)

where $\overline{u}|_n$ represents the mean field of u at timestep $n\Delta t$. Assuming that turbulent fluctuations are uncorrelated with the motions of the mean flow, $\langle \overline{u}\,u'\rangle \approx 0$, the variance of u over $\Delta T$ is

$$\begin{aligned} \sigma ^2_\mathrm{u} = \langle u^2\rangle - \langle u\rangle ^2 =\dfrac{1}{N}\sum \limits _{n=1}^{N} \left[ \overline{u}\big |_n^2 +2\,\overline{\overline{u}|\,u'}\Big |_n +\overline{u'u'}\Big |_n \right] -\langle \overline{u} \rangle ^2 =\langle \overline{u}{^2} \rangle +\langle \overline{u'u'}\rangle -\langle \overline{u} \rangle ^2.\nonumber \\ \end{aligned}$$

(43)

If u is a velocity component, the variance $\overline{u'u'}$ at timestep $n\Delta t$ is obtained applying the eddy viscosity hypothesis. From the definition of the turbulence stress tensor in Eq. 4,

$$\begin{aligned} \overline{u'_i u'_i} = -\dfrac{\tau '_{ii}}{\rho _{\textsc {h}}} = -2\,\nu _\mathrm{t}\,\dfrac{\partial \,\overline{u}_i}{\partial \,x_i} +\dfrac{2}{3}\,k. \end{aligned}$$

(44)

Cup anemometers measure the horizontal magnitude of the wind velocity and its variance, integrated over $\Delta T$, while the simulations return the average components of the velocity vector at time scale $\Delta t$. Averaging $\overline{u}$ and $\overline{v}$ over $\Delta T$ will not yield the same value as computing the average of the magnitude itself. Applying the average operator on the horizontal wind speed, s, then

$$\begin{aligned} s=\sqrt{u^2+v^2} \;\Rightarrow \; \left\{ \begin{array}{l} \langle {s}\rangle =\big \langle \sqrt{u^2+v^2}\,\big \rangle , \\ \langle {s^2}\rangle =\langle {u^2}\rangle +\langle {v^2}\rangle . \end{array}\right. \end{aligned}$$

(45)

Substituting in (45) the mean of the squares by the variance, i.e. $\langle {\chi ^2}\rangle = \sigma ^2_\chi +\langle {\chi }\rangle ^2$,

$$\begin{aligned} \sigma ^2_\mathrm{s} + \langle {s}\rangle ^2 =\sigma ^2_\mathrm{u} + \langle {u}\rangle ^2 +\sigma ^2_\mathrm{v} + \langle {v}\rangle ^2. \end{aligned}$$

(46)

This identity is equally valid for a smaller timestep, $\Delta t$, relating both $\overline{s}$ and $\overline{s's'}$ to $\overline{u}$, $\overline{u'u'}$, $\overline{v}$ and $\overline{v'v'}$. As the unsteady RANS model returns no information on $\overline{s}$ (only its components $\overline{u}$ and $\overline{v}$) the best assumption becomes

$$\begin{aligned} \overline{s}^2 \approx \overline{u}^2 + \overline{v}^2 \;\Rightarrow \; \overline{s's'} \approx \overline{u'u'} + \overline{v'v'}. \end{aligned}$$

(47)

Thus, for an integration time $\Delta T$, the mean and variance of the horizontal wind speed are estimated as

$$\begin{aligned} \langle {s}\rangle= & {} \langle \overline{s}\rangle =\big \langle \sqrt{\overline{u}{^2} + \overline{v}{^2}}\,\big \rangle , \end{aligned}$$

(48)

$$\begin{aligned} \sigma ^2_\mathrm{s}= & {} \langle \overline{u'u'}\rangle + \langle \overline{u}^2\rangle + \langle \overline{v'v'}\rangle + \langle \overline{v}^2\rangle - \langle \overline{s}\rangle ^2. \end{aligned}$$

(49)