Modification of Two-Equation Models to Account for Plant Drag

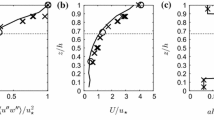
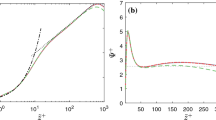
Abstract

A modification of the most popular two-equation (E–φ) models, taking into account the plant drag, is proposed. Here E is the turbulent kinetic energy (TKE) and φ is any of the following variables: El (product of E and the mixing length l), $\varepsilon$ (dissipation rate of TKE), and ω (specific dissipation of TKE, $\omega = \varepsilon\!/\!E$). The proposed modification is due to the fact that the model constants estimated experimentally for ‘free-air’ flow do not allow for adequate reconstruction of the ratio between the production and dissipation rates of TKE in the vegetation canopy and have to be adjusted. The modification is universal, i.e. of the same type for all E–φ models considered. The numerical experiments carried out for both homogeneous and heterogeneous plant canopies with E–φ models (and with the E–l model taken as a kind of reference) show that the modification performs well. They also suggest that E–$\varepsilon$ and E–ω schemes are more promising than the E–El scheme for canopy flow simulation since they are not limited by the need to use a wall function.

In addition, a new parameterization for enhanced dissipation within the plant canopy is derived. It minimizes the model sensitivity to C _μ, the key parameter for two-equation schemes, and whose estimates unfortunately vary considerably from experiment to experiment. The comparison of results of new modified E–$\varepsilon$ and E –ω models with observations from both field and wind-tunnel experiments shows that the proposed parameterization is quite robust. However, because of uncertainties with the turbulence Prandtl and Schmidt numbers for the E–$\varepsilon$ model within the canopy, the E–ω model is recommended for future implementation, with the suggested modifications.