Skip to main content
SpringerLink
Log in

When is the error in the \(h\)-BEM for solving the Helmholtz equation bounded independently of \(k\)?

  • Published:
BIT Numerical Mathematics Aims and scope Submit manuscript

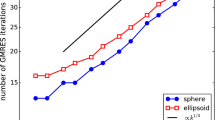
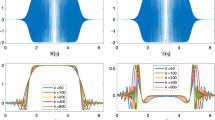
Abstract

We consider solving the sound-soft scattering problem for the Helmholtz equation with the \(h\)-version of the boundary element method using the standard second-kind combined-field integral equations. We obtain sufficient conditions for the relative best approximation error to be bounded independently of \(k\). For certain geometries, these rigorously justify the commonly-held belief that a fixed number of degrees of freedom per wavelength is sufficient to keep the relative best approximation error bounded independently of \(k\). We then obtain sufficient conditions for the Galerkin method to be quasi-optimal, with the constant of quasi-optimality independent of \(k\). Numerical experiments indicate that, while these conditions for quasi-optimality are sufficient, they are not necessary for many geometries.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Fig. 1
Fig. 2

Similar content being viewed by others

Notes

  1. Of course, if the goal is to compute the solution in (a subset of) the domain, then after using the \(h\)-BEM one must evaluate the integrals in Green’s integral representation (1.7) or the ansatz (1.12). This adds to the computational cost of the \(h\)-BEM, but the question “which of the \(h\)-BEM and \(h\)-FEM achieves the goal of computing the solution with the least cost?” is independent of the question “to what extent does each method suffers from the pollution effect?”.

References

  1. Abramowitz, M., Stegun, I.A.: Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. Dover, New York (1964)

    MATH  Google Scholar 

  2. Anselone, P.M.: Collectively Compact Operator Approximation Theory and Applications to Integral Equations. Prentice-Hall, Englewood Cliffs (1971)

    MATH  Google Scholar 

  3. Atkinson, K.E.: The numerical solution of integral equations of the second kind. In: Cambridge Monographs on Applied and Computational Mathematics. Cambridge University Press, Cambridge (1997)

  4. Banjai, L., Sauter, S.: A refined Galerkin error and stability analysis for highly indefinite variational problems. SIAM J. Numer. Anal. 45(1), 37–53 (2007)

    Article  MATH  MathSciNet  Google Scholar 

  5. Bayliss, A., Goldstein, C.I., Turkel, E.: On accuracy conditions for the numerical computation of waves. J. Comput. Phys. 59(3), 396–404 (1985)

    Article  MATH  MathSciNet  Google Scholar 

  6. Betcke, T., Chandler-Wilde, S.N., Graham, I.G., Langdon, S., Lindner, M.: Condition number estimates for combined potential boundary integral operators in acoustics and their boundary element discretisation. Numer. Methods Partial Differ. Equ. 27(1), 31–69 (2011)

    Article  MATH  MathSciNet  Google Scholar 

  7. Betcke, T., Spence, E.A.: Numerical estimation of coercivity constants for boundary integral operators in acoustic scattering. SIAM J. Numer. Anal. 49(4), 1572–1601 (2011)

    Article  MATH  MathSciNet  Google Scholar 

  8. Boubendir, Y., Turc, C.: Wave-number estimates for regularized combined field boundary integral operators in acoustic scattering problems with Neumann boundary conditions. IMA J. Numer. Anal. 33(4), 1176–1225 (2013)

    Article  MATH  MathSciNet  Google Scholar 

  9. Chandler, G.A.: Superconvergence for second kind integral equations. In: The Application and Numerical Solution of Integral Equations, pp. 103–117. Sijthoff and Nordhoff, Alphen aan den Rijn (1980)

  10. Chandler, G.A., Graham, I.G.: Uniform convergence of Galerkin solutions to non-compact integral operator equations. IMA J. Numer. Anal. 7(3), 327–334 (1987)

    Article  MATH  MathSciNet  Google Scholar 

  11. Chandler-Wilde, S.N., Graham, I.G., Langdon, S., Lindner, M.: Condition number estimates for combined potential boundary integral operators in acoustic scattering. J. Integral Equ. Appl. 21(2), 229–279 (2009)

    Article  MATH  MathSciNet  Google Scholar 

  12. Chandler-Wilde, S.N., Graham, I.G., Langdon, S., Spence, E.A.: Numerical-asymptotic boundary integral methods in high-frequency acoustic scattering. Acta Numerica 21(1), 89–305 (2012)

    Article  MATH  MathSciNet  Google Scholar 

  13. Chandler-Wilde, S.N., Hewett, D.P., Langdon, S., Twigger, A.: A high frequency boundary element method for scattering by a class of non-convex obstacles (2012, preprint)

  14. Chandler-Wilde, S.N., Langdon, S.: A Galerkin boundary element method for high frequency scattering by convex polygons. SIAM J. Numer. Anal. 45(2), 610–640 (2007)

    Article  MATH  MathSciNet  Google Scholar 

  15. Chandler-Wilde, S.N., Langdon, S., Mokgolele, M.: A high frequency boundary element method for scattering by convex polygons with impedance boundary conditions. Commun. Comput. Phys. 11, 573–593 (2012)

    MathSciNet  Google Scholar 

  16. Chandler-Wilde, S.N., Monk, P.: Wave-number-explicit bounds in time-harmonic scattering. SIAM J. Math. Anal. 39(5), 1428–1455 (2008)

    Article  MATH  MathSciNet  Google Scholar 

  17. Colton, D.L., Kress, R.: Integral Equation Methods in Scattering Theory. Wiley, New York (1983)

    MATH  Google Scholar 

  18. Domínguez, V., Graham, I.G., Smyshlyaev, V.P.: A hybrid numerical-asymptotic boundary integral method for high-frequency acoustic scattering. Numerische Mathematik 106(3), 471–510 (2007)

    Article  MATH  MathSciNet  Google Scholar 

  19. Elschner, J.: On spline approximation for a class of non-compact integral equations. Mathematische Nachrichten 146, 271–321 (1990)

    Article  MATH  MathSciNet  Google Scholar 

  20. Esterhazy, S., Melenk, J.M.: On stability of discretizations of the Helmholtz equation. In: Graham, I.G., Hou, Th.Y., Lakkis, O., Scheichl, R. (eds.) Numerical Analysis of Multiscale Problems. Lecture Notes in Computational Science and Engineering, vol. 83, pp. 285–324. Springer, Berlin (2012)

  21. Fabes, E.B., Jodeit, M., Riviere, N.M.: Potential techniques for boundary value problems on \(C^1\) domains. Acta Mathematica 141(1), 165–186 (1978)

    Article  MATH  MathSciNet  Google Scholar 

  22. Folland, G.B.: Real Analysis: Modern Techniques and Their Applications. Wiley, New York (1984)

  23. Hetmaniuk, U.: Stability estimates for a class of Helmholtz problems. Commun. Math. Sci 5(3), 665–678 (2007)

    Article  MATH  MathSciNet  Google Scholar 

  24. Hewett, D.P., Langdon, S., Melenk, J.M.: A high frequency \(hp\)-version boundary element method for scattering by convex polygons. SIAM J. Numer. Anal. 51(1), 629–653 (2013)

    Article  MATH  MathSciNet  Google Scholar 

  25. Ihlenburg, F.: Finite Element Analysis of Acoustic Scattering. Springer, Berlin (1998)

  26. Ihlenburg, F., Babuška, I.: Finite element solution of the Helmholtz equation with high wave number Part I: the h-version of the FEM. Comput. Math. Appl. 30(9), 9–37 (1995)

    Article  MATH  MathSciNet  Google Scholar 

  27. Lapinski, L.: Fast quadrature techniques for high order boundary element methods. Master’s thesis, Institut für Analysis und Scientific Computing, Technische Universität Wien (2007)

  28. Löhndorf, M., Melenk, J.M.: Wavenumber-explicit \(hp\)-BEM for high frequency scattering. SIAM J. Numer. Anal. 49(6), 2340–2363 (2011)

    Article  MATH  MathSciNet  Google Scholar 

  29. McLean, W.C.H.: Strongly Elliptic Systems and Boundary Integral Equations. Cambridge University Press, Cambridge (2000)

  30. Melenk, J.M.: On generalized finite element methods. PhD thesis, The University of Maryland (1995)

  31. Melenk, J.M.: Mapping properties of combined field Helmholtz boundary integral operators. SIAM J. Math. Anal. 44(4), 2599–2636 (2012)

    Article  MATH  MathSciNet  Google Scholar 

  32. Melrose, R.B., Taylor, M.E.: Near peak scattering and the corrected Kirchhoff approximation for a convex obstacle. Adv. Math. 55(3), 242–315 (1985)

    Article  MATH  MathSciNet  Google Scholar 

  33. Meyer, Y., Coifman, R.: Wavelets: Calderón–Zygmund and Multilinear Operators. Cambridge University Press, Cambridge (2000)

  34. Moiola, A., Spence, E.A.: Is the Helmholtz equation really sign-indefinite? SIAM Rev. 56(2), 274–312 (2014)

  35. Morawetz, C.S., Ludwig, D.: An inequality for the reduced wave operator and the justification of geometrical optics. Commun. Pure Appl. Math. 21, 187–203 (1968)

    Article  MATH  MathSciNet  Google Scholar 

  36. Nečas, J.: Les méthodes directes en théorie des équations elliptiques, Masson (1967)

  37. Nédélec, J.C.: Acoustic and Electromagnetic Equations: Integral Representations for Harmonic Problems. Springer, Berlin (2001)

  38. Oberhettinger, F., Badii, L.: Tables of Laplace Transforms. Springer, New York (1973)

    Book  MATH  Google Scholar 

  39. Olver, F.J.W.: Asymptotics and special functions. In: Computer Science and Applied Mathematics. Academic Press, New York (1974)

  40. Sauter, S.A., Schwab, C.: Boundary Element Methods. Springer, Berlin (2011)

    Book  MATH  Google Scholar 

  41. Schatz, A.H.: An observation concerning Ritz–Galerkin methods with indefinite bilinear forms. Math. Comput. 28(128), 959–962 (1974)

    Article  MATH  MathSciNet  Google Scholar 

  42. Spence, E.A.: Bounding acoustic layer potentials via oscillatory integral techniques. doi:10.1007/s10543-014-0506-0

  43. Spence, E.A.: Wavenumber-explicit bounds in time-harmonic acoustic scattering. SIAM J. Math. Anal. (2014, to appear)

  44. Spence, E.A., Chandler-Wilde, S.N., Graham, I.G., Smyshlyaev, V.P.: A new frequency-uniform coercive boundary integral equation for acoustic scattering. Commun. Pure Appl. Math. 64(10), 1384–1415 (2011)

    Article  MATH  MathSciNet  Google Scholar 

  45. Spence, E.A., Kamotski, I.V., Smyshlyaev, V.P.: Coercivity of combined boundary integral equations in high-frequency scattering. Commun. Pure Appl. Math. (2014, to appear)

  46. Wu, H.: Pre-asymptotic error analysis of CIP-FEM and FEM for the Helmholtz equation with high wave number. Part I: linear version. IMA J. Numer. Anal. (2014, to appear)

Download references

Acknowledgments

I.G.G and E.A.S were supported by EPSRC Grant EP/F06795X/1 and E.A.S by EPSRC Grant EP/1025995/1.

Author information

Authors and Affiliations

  1. Department of Mathematical Sciences, University of Bath, Bath, BA27, AY, UK

    I. G. Graham & E. A. Spence

  2. Kapsch TrafficCom, Am Europlatz 2, 1120 , Wien, Austria

    M. Löhndorf

  3. Institut für Analysis und Scientific Computing, Technische Universität Wien, 1040 , Wien, Austria

    J. M. Melenk

Authors
  1. I. G. Graham
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. M. Löhndorf
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. J. M. Melenk
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. E. A. Spence
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to E. A. Spence.

Additional information

Communicated by Ralf Hiptmair.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Graham, I.G., Löhndorf, M., Melenk, J.M. et al. When is the error in the \(h\)-BEM for solving the Helmholtz equation bounded independently of \(k\)?. Bit Numer Math 55, 171–214 (2015). https://doi.org/10.1007/s10543-014-0501-5

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10543-014-0501-5

Keywords

Mathematics Subject Classification

Search

Navigation