1 Introduction

When John Bell derived his famous inequalities in 1964 (Bell 1966), he referred to correlations of measurements made at two particles in an entangled state. However, Bell’s inequalities are derived from purely classical assumptions. Entangled states are used in order to relate correlation functions of non-commuting observables (which cannot be measured simultaneously) to correlation functions of commuting and hence compatible observables. In order to make this relation one has to assume that a measurement made at one particle has no influence onto the second measurement made at the other particle. In addition and often not mentioned explicitly is the assumption of induction: with respect to a particular observable which is measured for one particle, the second particle is (anti-) correlated to the first one (which has been tested in previous experiments) even when the corresponding observable is not measured for the second particle. Non-invasiveness was the essential argument in the famous 1935 article of Einstein et al. (1935): The first measurement should have no influence onto the state of the system for which the second measurement is performed. Otherwise one cannot distinguish between a (purely classical) indeterminism due to a “mechanical disturbance” [an expression used by Bohr in his answer to EPR (Bohr 1935)] induced by the first measurement and an intrinsic indeterminism due to the non-boolean character of the theory.

A very elegant proof of Bell’s inequalities can be found in d’Espagnat (1979) (see also David Mermin 1990). This derivation clearly distinguishes between inequalities which refer to correlation functions of certain observables and the way how to measure these inequalities using entangled stats. In the following we will often talk about Bell’s inequalities even when we actually refer to inequalities with respect to the correlation functions of (non-commuting) observables derived under the assumption of an underlying classical reality.

In general, a violation of Bell’s inequalities is considered as one of the peculiarities of quantum theory. Such a violation depends crucially on the existence of non-compatible observables, i.e., on observables which do not commute. In such a case, the predication space is non-boolean, and it is known that these types of non-boolean predication spaces cannot be obtained as a subset of a boolean predication space (see e.g., Giuntini 1991). In this sense one can interpret Bell’s inequalities as inequalities which hold for a boolean predication space, and the violation of these inequalities in quantum theory (Aspect et al. 1982) as an experimental verification that “nature” is based on a non-boolean predication space.

Generalized quantum theory (Atmanspacher et al. 2002) was developed in order to define a mathematical framework for observables which is fulfilled for any meaningful scientific context. It is not restricted to classical or quantum physics. The axiomatic setting is much more general, but both cases are included in the general formalism as special cases. In particular, generalized quantum theory was meant to be a framework which is also applicable when cognitive systems are involved, i.e. for the realm of psychology, neurosciences and even social sciences. The axioms of generalized quantum theory allow to define the concepts of non-commutativity and hence non-compatibility of observables (Atmanspacher et al. 2002, 2006, 2008b). Even the notion of entangled states can be formulated, but for our purpose this will be only of minor interest.

In this article we want to show that for cognitive systems a test of Bell’s inequalities may be possible even without reference to entangled states. The relevant idea will be that Bell’s inequalities are formulated in terms of correlations of non-commuting observables, and it is not possible to measure these observables separately and then determine their correlations. However, if the information about the correlation can be obtained in one single measurement, one can avoid the problem of invasiveness. Instead of obtaining the correlation function by making separate measurements of the non-commuting observables (which for quantum systems is not possible without changing the state of the system, i.e. invasive measurements) and determining the correlations from these results, the idea is to make one single measurement of the correlation (without referring to the observables separately).

Also in quantum theory it is in principle possible to measure (symmetrized or antisymmetrized) products AB, even if A and B are non-commuting, but one has to find a special experimental set-up for this measurement; knowing how to measure A and B separately gives no clue about how to measure AB. Furthermore, the spectrum of \({\frac{1}{2}}(AB+BA)\) or \({\frac{1}{2\hbox{i}}}(AB-BA)\) is generally not related to the products of the spectra of A and B. Under the assumption of an underlying classical behavior, however, we will show how certain observables allow to determine the correlations occurring in Bell’s inequalities.

A prerequisite for a system to violate Bell’s inequalities is that non-commuting observables exist. Correlation functions of compatible observables will never violate Bell’s inequalities. Finding such non-commuting observables (and, in particular, finding a measurement prescription for the correlation of such observables) will, in general, not be easy, in particular in the realm of cognitive systems.

This might, at first sight, seem surprising, because many effects are known in psychology (e.g., priming effects) where the order of “measurements” is relevant. However, also in classical physics, the order of processes is, in general, non-commutative, but in most cases such processes cannot serve as observables. For simple neural networks the non-commutativity of external influences which mimick pattern recognition (and, in this sense, measurements) has been shown explicitly (see e.g., Atmanspacher and Filk 2006). But this type of non-commutativity cannot be used for a violation of Bell’s inequalities. The question concerning the necessary conditions for processes to be observables which allow for a violation of Bell’s inequalities is presently investigated in the context of generalized quantum theory.

Therefore, in the present article, we take a slightly different approach. It was observed that in a particular model for bistable perception (Atmanspacher et al. 2004, 2008a, b), which will be explained in more detail in Sect. 3, a measurement of the same quantity at different time instances refers to non-commuting observables. In this case, the observable is not conserved, i.e., its value may change in time, or, in other words, the dynamics of the system (defined by a Hamiltonian) is not compatible with the observable. It is known from quantum theory, that in this case observables for the same measurement at different times may not commute.

The article is structured as follows. In the next section (Sect. 2) we indicate the derivation of Bell’s inequalities based on classical boolean predication space. As a particular example, we will formulate a temporal version of these inequalities for a two-state system. In Sect. 3, we will briefly review the Necker-Zeno model of bistable perception and show that according to the predictions of this model, Bell’s inequalities are violated for a particular experimental set-up. Finally, in Sect. 4, we will describe how in the case of two-state systems one may actually measure a violation of Bell’s inequalities. This will introduce the concept of temporally non-local measurements. We will conclude this article with some speculations about possible explanations of what a violation of Bell’s inequalities in cognitive systems may imply.

2 Classical Bell-Type Inequalities

Bell’s inequalities can be derived on the basis of a boolean predication space. Note that a boolean predication space is essentially equivalent to the algebraic structure of the set of subsets of a given set. The AND and OR combinations of predications are represented as the intersection (∩) and the union (∪) of sets, respectively. Furthermore, the NOT operation on predications is represented by taking the complement of a set.

We will first formulate the most general form of Bell’s inequalities based on set theory. This formulation will make no reference to temporality or particular structures of the observables. Then, in a second step, we will derive as a special case the temporal Bell’s inequalities for a two-state system involving one observable at three different time instances.

2.1 The General Form of Bell’s Inequalities

We will define a system to be classical, if the predication space of the system is boolean, and if every state can be considered to be a mixture of pure states which assume definite values with respect to any meaningful observable.

A predication about a physical system is a statement about the result of a possible measurement. We now define what we mean by a classical system: Let \(\Upomega\) be the set of all pure states of a classical system. For each observable A we define \(\hbox{spec}(A)=\{a\}\) (the spectrum of A) to be the set of all possible experimental outcomes, i.e., all possible results of a measurement of this observable. For simplicity, we take this set to be discrete. Now, each observable A defines disjoint subsets \(E_a \subset \Upomega\) such that

$$ \bigcup_a E_a = \Upomega \quad\hbox{and}\quad E_a \cap E_b = \emptyset \quad(\hbox{for}\, a \neq b). $$

For any pure state ω ∈ E a , we have ω(A) = a and \(\omega(A^2)=a^2\) (this last requirement implies that ω is non-dispersive). Therefore, we assume that for each pure state \(\omega \in \Upomega\) and each observable A there exists an \(a \in \hbox{spec} (A),\) such that ω  ∈ E a and \(\omega \not\in E_b\) for any b ≠ a. (This statement is not fulfilled for quantum states.)

Now let E 1 and E 2 be two subsets of \(\Upomega\) such that \(E_1 \subset E_2\) . For any ensemble of states {ω i } we define N 1 and N 2 to be the number of states in E 1 and E 2, respectively. We then have the inequality:

$$ N_1 \leq N_2. $$

Essentially one may say that this is the most general form of a Bell inequality, where, however, the non-trivial part is to represent the sets E i by certain unions and disjunctions of sets E a . To be fair one should mention that Bell derived his inequalities for entangled states, i.e., he included a way to measure the sets E 1 and E 2. This later part was the non-trivial achievement.

To give an idea of a “Bell inequality”, consider three coins which can only assume the values “head” and “tail”. There is a total of eight states depending on the visible side of the coins. Let N 12 count all the cases where coins 1 and 2 show unequal sides, and N 23 all the cases where coins 2 and 3 are unequal, and finally N 13 all cases where coins 1 and 3 are unequal. Obviously, \(N_{13} \leq N_{12}+N_{23},\) because in order that coin 1 shows a different side than coin 3, either coin 1 has to be unequal to coin 2, or coin 3 has to be unequal to coin 2. This example essentially is transformed into a temporal inequality in the next section.

As a sideremarkFootnote 1 I should mention, that this inequality can be interpreted as a triangle inequality in a counting space; this emphasizes the generality of the argument.

In order to experimentally verify this (trivial) inequality, one specifies the sets E 1 and E 2 by making certain measurements. However, we do not assume that measurements are compatible, i.e., measurements may change the state of a system (albeit in a classical “mechanical” sense). Hence, two successive measurements performed at the same physical system cannot be interpreted as two measurements made in the same state. (The assignment of definite measurement results for all observables to a state is purely ontological; epistemically we may only have access to the results for compatible observables.) This is the reason why Bell referred to entangled states.

2.2 A Temporal Inequality

In 1985, Leggett and Garg (1985, see also Mahler 1994) derived a temporal version of Bell’s inequalities. In this case it is possible to refer to only one observable which, however, does not commute with the dynamics, i.e., with the Hamiltonian of the system. In general, such quantum observables when measured at different times do not commute.

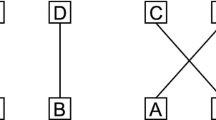
The following derivation (see also Atmanspacher and Filk 2010) of a temporal Bell inequality refers to a two-state system, i.e., a system which (classically) can only assume two different states. The classicality assumption now implies that at each moment t the system is in one of the two states. The “history” of the system is then given by a classical trajectory which, at each moment, assumes one of two possible values (Fig. 1).

Fig. 1
figure 1

A classical trajectory assumes at each moment in time a definite state (here one of two possible states). With respect to three instances \(t_1, t_2,\) and t 3 it falls into one of 23 = 8 possible classes (cf. Table 1, left). For the history shown this class is characterized by (−1,  +1,  +1)

Full size image

We specify three different moments \(t_1, t_2\) and t 3 and define s(t 1) to be the state of the system at time t 1 [and similarly s(t 2) and s(t 3)]. Now, any classical trajectory falls into one of 23 = 8 possible classes summarized in Table 1 (left).

Table 1 A classical trajectory for a two-state system falls into one of eight possible classes with respect to the states assumed at three different moments of time
Full size table

Let us consider an ensemble of classical trajectories, and we denote by \(N^-(t_1,t_3)\) the number of cases in which the system is in different states at t 1 and t 3 (i.e., where the product of the state values is −1). Similarly, we define \(N^-(t_1,t_2)\) and \(N^-(t_2,t_3)\) . From Table 1 (right) it is obvious that any of the four possibilities contained in \(N^-(t_1,t_3)\) is also contained in either \(N^-(t_1,t_2)\) or \(N^-(t_2,t_3)\) . Therefore, simple set-theoretical considerations provide the inequality:

$$ N^-(t_1,t_3) \leq N^-(t_1,t_2) + N^-(t_2,t_3). $$
(1)

We divide Eq. 1 by the total number of trajectories and we obtain an inequality for the corresponding probabilities:

$$ p^-(t_1,t_3) \leq p^-(t_1,t_2) + p^-(t_2,t_3). $$
(2)

Assuming time-translation invariance—i.e., these probabilities do not depend on absolute times but only on time differences—leads to:

$$ p^-(t_3-t_1) \leq p^-(t_2-t_1) + p^-(t_3-t_2). $$
(3)

In a last step we take \(\tau=t_2-t_1=t_3-t_2\) and, therefore, \(2\tau = t_3-t_1\) . For this particular choice of time intervals the inequality becomes:

$$ p^-(2\tau) \leq 2 p^-(\tau). $$
(4)

This inequality is a “sublinearity”-condition. For a linear dependence of p − on the time interval τ, the inequality becomes an equality, and if the dependence for some values of τ is stronger than linear the inequality is violated.

3 The Necker-Zeno Model

The Necker-Zeno model is a mathematical model describing the effective dynamics leading to the perception shifts in mental states when one observes an ambiguous figure like the Necker cube (Fig. 2, left).

The Necker cube is a two-dimensional drawing of a cube without fixing the perspective (Necker 1832). Two possible three-dimensional perspectives are consistent with the Necker cube, and mentally we usually perceive one of these three-dimensional perspectives (Fig. 2, right).

In experiments under controlled conditions, a subject is requested to look at a fixation cross in the middle of the drawing and to indicate (e.g., by pressing a bottom) when he or she perceives a perspective shift. What one obtains is a curve which looks similar to the one in Fig. 1.

Fig. 2
figure 2

The Necker cube (left) and the two ways in which it can be interpreted as a three dimensional cube (right)

Full size image

From such a curve one can determine the average dwell time T for a perceptive state and also distribution curves for dwell times or cumulative probabilities that a shift has occured. This distribution curve is schematically shown in Fig. 3, and it resembles an integrated gamma-distribution (see Brascamp et al. 2005; this article discusses in which way the measured results deviate from a gamma-distribution).

Fig. 3
figure 3

Schematic representation of the cumulative probability that a perceptive shift has occurred at time t

Full size image

The mathematical formalism of the Necker-Zeno model is identical to the mathematics of a two-state Quantum-Zeno model (Misra and Sudarshan 1977). However, it should be kept in mind, that this refers only to the mathematical framework: We do not consider a quantum phenomenon to be responsible for the switching dynamics. The details of the Necker-Zeno model have been described elsewhere (see Atmanspacher et al. 2004), so we will only review those features which are relevant for our later discussion on the violation of classical causation. We first summarize the ingredients of the quantum Zeno model and then make the transformation of the concepts to the Necker-Zeno model. Of course, the violation of Bell’s inequalities also occurs for the quantum Zeno model.

The quantum Zeno model describes a two-state system with two complementary processes:

  1. (D1)

    a continuous “rotation” in a 2-dimensional state space generated by a Hamiltonian H = gσ1 (where σ1 is one of the Pauli matrices), corresponding to the free evolution of the system without any external interference.

  2. (D2)

    a discontinuous reduction process onto one of the two eigenstates |+〉 or |−〉 of the Pauli matrix σ3 as the result of an “observation”.

Note that the two matrices σ1 and σ3 do not commute. One is interested in two different types of probabilities:

  1. (P1)

    The conditional probability w 1(t) that the system is measured in state |+〉 at time t under the condition that it has been in state |+〉 at time t = 0, and no measurement has been performed in between. This probability is:

    $$ w_1(t) = \cos^2 (gt). $$
    (5)

    Obviously t 0: = 1/g is a reference time for the “decay” of a state without any external influence.

  2. (P2)

    The conditional probability w N (t) that the system is measured in state |+〉 at time t under the condition that it has been in state |+〉 at time t = 0, and under the condition, that in time intervals \(\Updelta t\) further observations have been performed and the system has always been measured to be in state |+〉. This probability is given by:

    $$ w_N(t) = \left( \cos^2 (g \Updelta t)\right)^N \quad \hbox{with}\quad t = N \cdot \Updelta t . $$
    (6)

    The condition \(\Updelta t \ll t_0\) leads to the approximation:

    $$ w_N(t) \approx \exp (-g^2 \Updelta t^2 \cdot N) = \exp\left( - {\frac{\Updelta t}{t_0^2}} t \right) . $$
    (7)

From the last formula one obtains a relation for the average time T for the “decay” of the system under repeated observation (with observation intervals \(\Updelta t\)) expressed in terms of the reference time t0 of the unperturbed system:

$$ T = {\frac{t_0^2}{\Updelta t}} \quad \hbox{or}\quad t_0 = \sqrt{T \cdot \Updelta t}. $$
(8)

This formula describes the quantum Zeno effect: the smaller the observation intervals \(\Updelta t,\) the larger is the average time T for the system to undergo a transition from |+〉 to |−〉.

Now we summarize the essential results of the Necker-Zeno model for bistable perception by associating the cognitive counterparts to the mathematical structures of the quantum Zeno effect. First, we interpret the two dynamical processes of the quantum Zeno model in terms of cognitive processes:

  1. (D1)

    We assume a “decay” of a perceptual state under the condition that a person is not observing the ambiguous stimulus, i.e. when the external stimulus is turned off. The probability that the mental state is still associated with the subjective perspective perceived before the stimulus was turned off is (for small values of t) given by:

    $$ w_0(t) = 1 - {\frac{t^2}{t_0^2}} + O(t^4) \ldots $$
    (9)

    (Notice that this is the short term approximation of Eq. 5.) The reference time t 0 is associated to the P300 (300 ms) of cognitive processes. (For details of this interpretation, see Atmanspacher et al. 2004.).

  2. (D2)

    We assume a cognitive “update”-process which takes place whenever a person is actually looking at the stimulus. The mental state characterized by its perspective of the cube is not stationary during the observation period, but is updated in short time intervals \(\Updelta t\). This update-interval \(\Updelta t\) has been associated to the time-scale for which a sequentiality of stimuli is resolved cognitively. (Again, for details see Atmanspacher et al. 2004.)

Having associated the dynamics of the quantum Zeno effect and their time scales to the cognitive dynamics relevant for the perception of ambiguous stimuli, we now arrive at the main conclusion of the Necker-Zeno model. It provides a relation between the average dwell time T of a perceived perspective and the other cognitive time scales t 0 and \(\Updelta t,\) and, according to the model this relation is given by Eq. 8. For experimental tests and a refinement of the model (see Atmanspacher et al. 2008a, b).

Note that according to Eq. 9 the probability for a change of the perceptive state in a time interval τ during off-times (stimulus is turned off) is given by:

$$ w_0^{-}(\tau) \propto \tau^2. $$

This probability is “superlinear” and, hence, violates the temporal Bell inequality derived above (Eq. 4).

4 Experimental Tests of Bell’s Inequalities in Cognitive Systems

At first sight, the experimental test for a violation of Bell’s inequalities (in the form of Eq. 4) looks simple: take any two-state system, measure the probabilities that the system is in different states for time intervals τ and 2τ, respectively, and compare the measured probabilities with inequality (4). However, there is one problem: invasiveness! Most experimental set-ups which determine the correlations in p −(τ) involve two measurements: a measurement of the state of the system at t = 0 and one of the state of the system at t = τ. In this case it is impossible to guarantee that the first measurement has no influence onto the result of the second measurement.

Indeed, looking at the results of Brascamp et al. (2005) (schematically indicated in Fig. 3), this cumulative probability would, for small values of t where it behaves like a power-law, violate Eq. 4 and, therefore, a Bell inequality. But as two measurements are involved (or, to put it into a different language, as we have information about the state of the system at the two moments separately), we cannot conclude from this result that Bell’s inequalities are violated for bistable perception. (In addition, note that the prediction of the Necker-Zeno model refers to off-times, not to the dwell times during the presentation of the stimulus.).

In order to avoid any “mechanical disturbance” of the cognitive state due to the first measurement, we should look for a possibility to determine the correlation involved in p −(τ) in one single measurement and without any reference to the two states separately. Because such a measurement would yield information about the state of a system at two different moments t 1 and t 2 with \(\tau=t_2-t_1,\) we refer to such a measurement as being temporally non-local. A possible “measurement” would be the question: “Were the two states at t = 0 and t = τ different or not?” The two possible answers are “different” and “not different”. If we can get this information in such a way that the subject does not become aware of what the states at t = 0 and t = τ were, but only of their correlation, this could be considered as a single non-invasive measurement of the correlation.

In order to make the point even clearer, let me mention an experiment which has been done in the context of temporal stimulus resolution (Pöppel 1997). Two different stimuli were presented to a subject within a short time interval (of the order of 30–70 ms). The subjects recognized with large probability that the stimuli were not simultaneous, but they were not aware which one of the two stimuli was first (when asked, the answers coincided with the actual sequence only in roughly 50% of the cases). This is an example of a temporally non-local measurement: the temporally non-local information “not simultaneous” is known, but not the two separate informations which one of the stimuli was first and which second.

At present, several groups are designing experimental protocols along the lines indicated. Due to the fundamental problem of non-invasiveness, such experiments are extremely difficult and no conclusive results are to be expected in the immediate future.

5 Conclusions

Let’s suppose that a convincing experimental set-up (for which invasiveness of measurements can be ruled out) would indicate that in a cognitive system Bell’s inequalities are violated. What could be a possible explanation?

Of course, there is always the possibility that quantum effects actually do play a prominent role in cognitive processes and that a violation of Bell’s inequalities is due to a quantum effect. In general, such a possibility cannot be eliminated, but we consider this explanation as extremely unlikely in view of the size and decoherence times of systems involved in cognitive processes.

One of the central assumptions of the derivation of temporal Bell’s inequalities was that at any time the system is in one of the possible definite states characterized by the value of the observable (e.g., the perception of the perspective). In quantum mechanics this assumption is violated, and also for cognitive systems it is conceivable that there are states which do not relate to one of the “classical” observables, and that (say) a definite perspective is only assumed when the subject tries to realize in which state he or she is (which would correspond to a measurement). In a different context, such indefinite states have been referred to as “acategorial” (Atmanspacher 1992; Feil and Atmanspacher 2010), an expression which goes back to Jean Gebser (1986).

In my opinion, the existence of such acategorial states would be the most convincing explanation for a violation of Bell’s inequalities. For these states the assignment of a (hypothetical) result of measurement for any observable would not be possible. Similar to the interpretation in quantum theory, the result of a measurement is not predetermined but is generated during the measuring process.

Often the question has been raised what one would expect to observe if by future scanning techniques we could determine the perspective of the Necker cube perceived by a subject without any cognitive interference. If acategorial states exist, these measurements would indicate that they are not associated with a definite perspective of the cube, but that this perspective is generated during the process when the subject tries to become aware of his or her momentary perceptive state. These states could be compared with superposition states (may be even eigenstates of the time evolution operator) which cannot be measured by introspection or other psychological methods aiming at determining the perceived perspective. Any introspection will destroy these states and project onto one of the eigenstates of the observation operator (i.e., one of the definite perspectives). Of course, in view of the absence of experimental hints these considerations remain pure speculations.