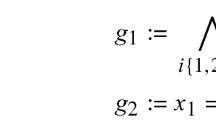Abstract
We present a verification methodology for analysing the decision-making component in agent-based hybrid systems. Traditionally hybrid automata have been used to both implement and verify such systems, but hybrid automata based modelling, programming and verification techniques scale poorly as the complexity of discrete decision-making increases making them unattractive in situations where complex logical reasoning is required. In the programming of complex systems it has, therefore, become common to separate out logical decision-making into a separate, discrete, component. However, verification techniques have failed to keep pace with this development. We are exploring agent-based logical components and have developed a model checking technique for such components which can then be composed with a separate analysis of the continuous part of the hybrid system. Among other things this allows program model checkers to be used to verify the actual implementation of the decision-making in hybrid autonomous systems.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
Autonomous systems are moving beyond industrial and military contexts, and are now being deployed in the home, in health-care scenarios, and in automated vehicles. In many cases there may be a human operator who directs the autonomous system, but increasingly the system must work on its own for long periods without such interventions. These systems must essentially decide for themselves what to do and when to do it. This might seem fraught with danger, but there is a clear need for such systems, particularly:
-
when deployed in remote or dangerous environments where direct and local human control is infeasible; or
-
when the complexity or speed of the environmental interactions is too high for a human to handle.
Examples of the former include deep sea exploration, space probes, and contaminated area cleanup; examples of the latter include automated stock trading systems, robot swarms, and unmanned air vehicle collision avoidance. In addition to the above reasons, autonomous systems are becoming popular as they can sometimes be much cheaper to develop and deploy than manned systems.
1.1 Hybrid autonomous systems
Autonomous systems, such as we are discussing, are constructed in a component-based fashion with an agent-based decision maker and a continuous control system. This means they have a natural decomposition at design time. In many cases the agent-based decision maker is viewed as the replacement for a human pilot or operator who would, otherwise, interact with the control system.
Systems that combine continuous control algorithms with any kind of discrete behaviour that forms jumps between different continuous states are called hybrid control systems. When the discrete component includes behaviour we would recognise as autonomous we refer to the system as a hybrid autonomous system. Traditionally, such hybrid autonomous systems have been engineered using the concept of a hybrid automaton (in which continuous aspects are encapsulated within a single state of an automaton while discrete jumps are represented as transitions between these states—see Sect. 2.4 for a more detailed description). However, as these systems have become more complex, combining discrete decision-making and continuous control within a hybrid automaton has faced challenges. It is difficult to separate the two concerns (decision-making and continuous control) when designing and implementing a system in this fashion—this has an impact on the understandability and reuse of both design and code. Furthermore many autonomous systems operate in environments where the users wish to access some high level account for why a decision was taken by the system (Fisher et al. 2013). Such an account can be difficult to extract from a hybrid automaton.
As a result, the practice developed of separating decision-making components from the underlying control system, often using the popular agent paradigm (Wooldridge 2002). A drawback of this approach, however, is that it is generally non-trivial to transform such a system back into a hybrid automaton based model and so well-developed techniques for verifying hybrid automata by model checking (Henzinger et al. 1997; Frehse 2005) become difficult to apply to these new systems. Moreover, verification of hybrid automaton based systems tends to scale badly as the reasoning processes become more complex. Since autonomous systems are frequently safety or mission critical this verification gap is a significant concern.
1.2 A methodology for verifying autonomous choices
In Fisher et al. (2013) we proposed a methodology for the verification of decision-making components in hybrid autonomous systems, where such a decision-making component is implemented as a rational agent. In this paper, we give a more detailed and technical explanation of the methodology and apply the approach to verify the implementation of agent-based decision-making in a variety of complex autonomous systems (see Sects. 3, 4, 5). We argue that one of the most crucial aspect of verifying complex decision-making algorithms for autonomous systems, for example concerning safety, is to identify that the controlling agent never deliberately makes a choice it believes to be unsafe.Footnote 1 In particular this is important in answering questions about whether a decision-making agent will make the same decisions as a human operator given the same information from its sensors.
How might we guarantee behaviour within such an autonomous system embedded in the real world? Following a decompositional approach we need not (and, indeed we argue that we can not) ensure that an autonomous system will certainly lead to a change in the real world.
Thus, rather than verifying agent behaviour within a detailed model of the system’s environment, we now verify the choices the agent makes given the beliefs it has. This approach is clearly simpler than monolithic approaches as we can state properties that only concern the agent’s internal decisions and beliefs, and so verification can be carried out without modelling the “real world”. At a logical level, the verification of safety properties changes from the checking ofFootnote 2
i.e., nothing bad can ever happen which involves verifying the state of the external world, to checkingFootnote 3
i.e., the agent never believes that something bad happens which involves only checking the internal state of the agent. Similarly, liveness properties change from checking \(\lozenge \mathsf {good}\) (eventually something good happens) to checking \(\lozenge \mathrm {\mathbf {B}}_{agent} \, \mathsf {good}\) (eventually the agent believes something good has happened). Thus, we verify the (finite) choices the agent has, rather than all the (typically infinite) “real world” effects of those choices.
Specifically, we propose model checking (and the model checking of programs, if possible) as an appropriate tool for demonstrating that the core rational agent always endeavours to act in line with our requirements and never deliberately chooses options that lead internally to bad states (e.g., ones where the agent believes something is unsafe). Since we are verifying only the core agent part we can use model checking approaches that do not consider the continuous behaviour of the system. These are easier to use in a modular/compositional fashion than approaches designed to cope with the continuous and real world aspects. Thus, we do not verify all the “real world” outcomes of the agent’s choices (but assume that analysis of the underlying control system has provided us with theorems about the outcomes of actions etc.), but do verify that it always tries to achieve its goals/targets to the best of its knowledge/beliefs/ability. Thus, the agent believes it will achieve good situations and believes it will avoid bad situations. Consequently, any guarantees here are about the autonomous system’s decisions, not about its external effects.
Efforts to model the entire system and its interaction with the real world with any degree of accuracy necessarily involve complex abstractions together with a number of assumptions. These abstractions and assumptions are embedded deep within an executable model and may not be explicit to end users, or even to the modellers. Therefore if we provide a guarantee, for example, that the autonomous system can definitely achieve or avoid something, there will be a number of pre-conditions (that the real world will behave in some particular way) to that guarantee that may be hard to extract. One of the aims of our approach is that the assumptions embedded in the modelling of the real world should be as explicit as possible to the end users of a verification attempt.
Obviously, some parts of an agent’s reasoning are triggered by the arrival of information from the real world and we must deal with this appropriately. So, we first analyse the agent’s program to assess what these incoming perceptions can be, and then explore, via the model checker, all possible combinations of these. This allows us to be agnostic about how the real world might actually behave and simply verify how the agent behaves no matter what information it receives. Furthermore, this allows us to use hypotheses that explicitly describe how patterns of perceptions might occur. Taking such an approach clearly gives rise to a large state space because we explore all possible combinations of inputs to a particular agent. However it also allows us to investigate a multi-agent system in a compositional way. Using standard assume-guarantee (or rely-guarantee) approaches (Misra and Chandy 1981; Jones 1983, 1986; Manna and Pnueli 1992; Lamport 2003), we need only check the internal operation of a single agent at a time and can then combine the results from the model checking using deductive methods to prove theorems about the system as a whole. Abstracting away from the continuous parts of the system allows us to use model checking in a compositional fashion.
It should be noted that, in many ways, our approach is the complement of the typical approach employed in the verification of hybrid automata and hybrid programs. We are primarily concerned with the correctness of the discrete algorithms and are happy to abstract away from the underlying continuous system, while the other approaches are more concerned with the verification of the continuous control and are happy to abstract away from the discrete decision-making algorithms.
1.3 Overview
In summary, we had two main aims in developing our verification methodology: to maintain the natural decomposition of the system design in the verification, allowing us to verify the symbolic (i.e., logical decision based) and non-symbolic (continuous) aspects separately; and to make any assumptions about the continuous/real world environment as explicit as possible. It is preferable to treat the verification and analysis in a compositional fashion, if at all possible, for a variety of reasons. It simplifies the verification task, encourages reuse, and allows appropriate domain specific analysis tools to be used. Compositional verification has its roots in the use of lemmas in the construction of proofs both by hand and, more recently, with mechanized theorem proving tools. In model checking settings care sometimes has to be taken to use sound composition rules, especially in cases where the reasoning contains circular elements (e.g., sub-system A requires sub-system B to be correct as an assumption while sub-system B requires sub-system A to be correct as a an assumption) (McMillan 1999; Barringer and Giannakopoulou 2003).
In many of the situations we are interested in, the control system is trusted and the primary concern is the extent to which the decision-making component conforms to the expectations about the behaviour of a human operator. This provides an additional motivation to verify the symbolic reasoning in detail and in isolation.
Thus, in summary, our overall approach (Fisher et al. 2013) involves:
-
1.
modelling/implementing the agent behaviour and describing the interface (input/output) to the agent;
-
2.
model checking the decision-making agent within a coarse over-approximation of the environment derived from the analysis of agent inputs (this will establish some property, \(\varphi \));
-
3.
if available, utilizing environmental hypotheses/assumptions, in the form of logical statements, to derive further properties of the system;
-
4.
if the agent is refined, then modify (1) while if environmental properties are clarified, modify (3); and
-
5.
deducing properties of multi-agent systems by model checking the behaviour of individual agents in a component-wise fashion and then combining the results deductively to infer properties of the whole system.
We will later examine three very different scenarios in order to exemplify the key features of the methodology.
Previous work (Fisher et al. 2013) presents a high level overview of the work described here. It concentrates primarily on outlining the methodology without any discussion of or comparison to alternative approaches. Two of the case studies (the Search and Rescue scenario and the Satellite example) are also presented in brief but without presentation of the actual code, any details on how the verification is set up, how the environmental assumptions are obtained, nor discussion of performance issues. The chief contributions of this paper are:
-
Extended and more detailed versions of the first two case studies,
-
Positioning our technique properly within the wider field of the verification of hybrid systems,
-
The new case study on adaptive cruise control.
These provide technical detail on how the methodology actually works, how it integrates with other systems, and where it exists in the field of the verification of hybrid systems. We believe this detail to be important to understanding the methodology and, critically, to any attempt to implement it.
The satellite system presented in our second case study has also been presented in Lincoln et al. (2013). This makes no reference to the verification at all and instead focuses on the implementation issues with considerable attention paid to the continuous control and the link between the agent and the control system.
2 Background and related work
The verification of decision-making in hybrid agent systems, where that decision-making takes place as part of a separate agent-based component, draws upon background and research from a range of areas, namely hybrid control systems, agent-based programming and verification approaches to hybrid systems and rational agents.
2.1 Hybrid control systems
A fundamental component of low-level control systems technology is the feedback controller. This measures, or estimates, the current state of a system through a dynamic model and produces subsequent feedback/feed-forward control signals. In many cases, difference equations can be used to elegantly manage the process. These equations of complex dynamics not only make changes to the input values of sub-systems and monitor the outcomes on various sensors, but also allow deeper understanding of system behaviour via analytical mathematical techniques.
As we move to autonomous systems, such controllers are increasingly required to work in situations where there are areas of discontinuity, where a distinct change in behaviour is required and where control needs to switch to the use of an alternative model and alternative control equations. This kind of control system often requires some decision-making system to be integrated with the feedback controller (Branicky et al. 1998; Varaiya 1999; Goebel et al. 2009). It may also be necessary for a system to take actions such as detecting that a fuel line has ruptured and switching valves to bring an alternative online: this falls outside the scope of monitoring and adjusting input and output values, and involves detecting that thresholds have been exceeded or making large changes to the system.
It is possible to encode all these choices in, often hierarchical, hybrid automata but this creates several problems from a software engineering perspective. Firstly, it does not allow a natural separation of concerns between the algorithms and procedures being designed or implemented for making decisions, and those which are being designed and implemented for continuous control, this reduces the understandability of the resulting code and therefore increases the risk of errors and bugs being present in the code. It can often also make the underlying code, particularly that of decision-making algorithms, harder to reuse since it becomes more difficult to identify the generic aspects of any decision algorithm from those that are specific to the continuous control. There is also evidence (Damm et al. 2007; Dennis et al. 2010b) that hybrid automata based implementations scale poorly with the complexity of decision-making when compared to agent-based control. This again impacts upon understandability.
In the autonomous systems we consider here, the control system usually follows fairly well defined functions, while the discrete decision-making process must make appropriate choices, often without human intervention; see Fig. 1. Increasingly, this discrete decision-making process will be a rational agent, able to make justifiable decisions, to reason about those decisions, and dynamically modify its strategy (Wooldridge and Rao 1999).
2.2 Agents and rational agents
At its most general, an agent is an abstract concept that represents an autonomous computational entity that makes its own decisions (Wooldridge 2002). Since its introduction in the 1980s, the agent abstraction has become very influential in practical situations involving complex flexible, autonomous, and distributed components (Bond and Gasser 1988; Bratman et al. 1988; Davis and Smith 1983; Cohen and Levesque 1990; Durfee et al. 1989; Shoham 1993).
A general agent is simply the encapsulation of some distributed computational component within a larger system. However, in many settings, something more is needed. Rather than just having a system which makes its own decisions in an opaque way, it is increasingly important for the agent to have explicit reasons (that it could explain, if necessary) for making one choice over another.
In the setting of autonomous systems, explicit reasoning assists acceptance. When queried about its choices an autonomous system should be able to explain them, thus allowing users to convince themselves over time that the system is reasoning competently. More importantly, where an autonomous system is likely to be the subject of certification, it may need to fulfill obligations to do with reporting, particularly in instances where an accident or “near miss” has occurred. It is desirable for such reporting to be presented at a high level which explains its choices in terms of what information it had, and what it was trying to achieve.
Rational agents (Bratman 1987; Rao and Georgeff 1992; Wooldridge and Rao 1999) enable the representation of this kind of reasoning. Such an agent has explicit reasons for making the choices it does. We often describe a rational agent’s beliefs and goals, which in turn determine the agent’s intentions. Such agents make decisions about what action to perform, given their current beliefs, goals and intentions.
The predominant view of rational agency is that encapsulated within the BDI model (Rao and Georgeff 1991, 1992, 1995). Here, ‘BDI’ stands for Beliefs, Desires, and Intentions. Beliefs represent the agent’s (possibly incomplete, possibly incorrect) information about itself, other agents, and its environment, desires represent the agent’s long-term goals while intentions represent the goals that the agent is actively pursuing.
There are many different agent programming languages and agent platforms based, at least in part, on the BDI approach. Particular languages developed for programming rational agents in a BDI-like way include AgentSpeak (Rao 1996), Jason (Bordini et al. 2005, 2007), 3APL (Hindriks et al. 1999; Dastani et al. 2005), Jadex (Pokahr et al. 2005), Brahms (Sierhuis 2001), GOAL (Hindriks et al. 2001; Boer et al. 2007), and Gwendolen (Dennis and Farwer 2008). Agents programmed in these languages commonly contain a set of beliefs, a set of goals, and a set of plans. Plans determine how an agent acts based on its beliefs and goals and form the basis for practical reasoning (i.e., reasoning about actions) in such agents. As a result of executing a plan, the beliefs and goals of an agent may change as the agent performs actions in its environment.
Agent based control of decision-making in hybrid systems has been an area of research since at least the 1990s. Kohn and Nerode’s MAHCA system (Kohn and Nerode 1992) uses multiple knowledge-based agents as planners which generate the actions performed by the underlying control system. While these agents are not based on the BDI paradigm, which was only in its infancy when MAHCA was originally developed, the approach is motivated by a desire to represent logical decision-making in a high-level declarative fashion. More recently agent based approaches have been explored in the control of spacecraft (Muscettola et al. 1998), Unmanned Aircraft (Karim and Heinze 2005; Webster et al. 2011; Patchett and Ansell 2010), and robotics (Wei and Hindriks 2013). Many of these approaches are explicitly BDI based and are motivated by the desire to separate the symbolic and non-symbolic reasoning and model the mission designer’s intent.
Generating appropriate abstractions to mediate between continuous and discrete parts of a system is the key to any link between a control system and a reasoning system. Abstractions allow concepts to be translated from the quantitative data derived from sensors (and necessary to actually run the underlying system) to the qualitative data needed for reasoning. For instance a control system may sense and store precise location coordinates, represented as real numbers, while the reasoning system may only be interested in whether a vehicle is within reasonable bounds of its desired position.
We have been exploring an architecture (Dennis et al. 2010a) in which the rational agents are partnered with an abstraction engine that discretizes the continuous information in an explicit fashion which we are able to use in verification. Currently the abstraction engine is implemented as a distinct rational agent, though we intend to move to a stream processing model in future. We describe this technique further in Sect. 4.
2.3 Formal verification and model checking
Formal verification is essentially the process of assessing whether a specification given in formal logic is satisfied on a particular formal description of the system in question. For a specific logical property, \(\varphi \), there are many different approaches to this (Fetzer 1988; DeMillo et al. 1979; Boyer and Moore 1981), ranging from deductive verification against a logical description of the system \(\psi _S\) (i.e., \(\vdash \psi _S\Rightarrow \varphi \)) to the algorithmic verification of the property against a model of the system, \(M\) (i.e., \(M\models \varphi \)). The latter has been extremely successful in Computer Science and Artificial Intelligence, primarily through the model checking approach (Clarke et al. 1999). This takes an executable model of the system in question, defining all the model’s possible executions, and then checks a logical property against this model (and, hence, against all possible executions).
Whereas model checking involves assessing a logical specification against all executions of a model of the system, an alternative approach is to check a logical property directly against all actual executions of the system. This is termed the model checking of programs (Visser et al. 2003) and crucially depends on being able to determine all executions of the actual program. In the case of Java, this is feasible since a modified virtual machine can be used to manipulate the program executions. The Java Pathfinder (JPF) system (Visser et al. 2003) carries out formal verification of Java programs in this way by analysing all the possible execution paths. This avoids the need for an extra level of abstraction and ensures that verification truly occurs on the real system.
All model-checking techniques have to deal with issues of scalability. In essence they all involve exhaustive search over all executions of a system and so, as the system increases in size, they run into combinatorial explosion. Many advanced techniques have been developed to combat these issues including checking for loops, limiting search branching in ways that do not compromise the result (partial order reduction), and abstracting the system in systematic ways, again to limit the number of states and branch points. Program model checking is typically much slower even than standard model checking because actual programs tend to contain more instructions, at a lower level (and hence involves either more branch points or more computation to generate each state of the system), than models of programs.
2.4 Verifying hybrid systems
Both theorem proving and model checking techniques have been applied to the verification of hybrid systems and there are several mature tools available (e.g., KeYmaera (theorem proving), HyTech and PHAVer (both model checking)).
As mentioned above, there are two major approaches to constructing hybrid systems. We have followed the methodology of providing two components, a decision making system that interacts with an underlying control system. The other major approach is that of hybrid automata and it is on that approach that most of the verification efforts have been focused.
An automaton consists of a set of states with transitions between them. Traditionally automata states are static but, in hybrid automata, the states are governed by differential inclusions which control the behaviour of the overall system while the automata is in that state. Each state therefore contains (state) variables whose value may evolve and change in a continuous fashion while the automata is in that state. Key aspects of a hybrid automaton state are the flow conditions; equations which express the evolution of continuous variables while in that state, and invariant conditions; a predicate over the state variables which must be satisfied in that state. If the invariant conditions are violated then the state is forced to transition to another. When a transition occurs, jump conditions determine the initial values of the state variables in the next state.
The model checking of hybrid automata involves first composing the implemented system with a model of the real world, also expressed as a hybrid automaton. Then the model checker explores trajectories within each automata state. Given (a set of) starting values for the variables in the state the system attempts to determine a bounded sub-region of \(\mathbb {R}^n\) which contains all possible values of the variables that can be reached within that state before it transitions to another. The possible values of the variables at the point of transition, together with the jump conditions, will form the starting values for the variables in the next state, and so on until all possible states of the system have been explored. (See Henzinger 1996; Alur et al. 2000; Henzinger et al. 1997 for detailed descriptions of the model checking of hybrid automata based systems.)
Since the real world can not be modelled in its full complexity, modelling it as a hybrid automaton requires some kind of abstraction. Abstraction has a long history in the formal modelling of “real world” phenomena for verification (Clarke et al. 1994) and abstractions for model checking hybrid systems have been extensively studied (Alur et al. 1995; Henzinger et al. 1997; Tiwari 2008; Tabuada 2009). Since the “real world” is inherently complex, often involving control systems, physical processes and human interactions, even defining appropriate abstractions is difficult. Often we either take a very coarse abstraction, which risks being very far away from a real system, or a very detailed abstraction leading to complex structures such as stochastic, hybrid automata (which are, themselves, often very hard to deal with (Bujorianu 2012)). We also face this problem in our agent-based approach which favours a coarse abstraction.
From our perspective: the verification of decision making code in agent-based hybrid control systems, with a particular interest in the verification of implementations of decision-making algorithms, the hybrid automata approach has several drawbacks, as follows.
-
1.
As noted earlier, it is difficult to decompose a hybrid automaton with a complex decision-making process into sub-systems (though approaches using concurrent automata are possible). However, even after such a decomposition, the model checking problem can not be easily decomposed to consider only some sub-set of the states of the system (e.g., just those involved with control algorithms). The calculation of a bounded region that limits the trajectories within a state is dependent upon the possible values of the variables on entering the state and these, in turn, depend upon the values of those variables in the previous state and the jump conditions. Therefore the region of possible trajectories may vary each time a state is visited. As a result, the algorithm needs to calculate all the potential sets of starting values for each state. It is not, in general, possible to determine in advance what the entry constraints will be for some sub-set of the automaton states without exploring the whole automaton. As a result the whole system must often be treated as a unit. This not only makes the model checking problem harder but also limits the reuse of results when changes are made to the system. Section 2.4.1 surveys some recent work to overcome this problem.
-
2.
The classes of hybrid automata that have decidable model checking problems are limited. While there are several possible decidable fragments, linear hybrid automata are most frequently used. The main restrictions on linear hybrid automata are that the formulæ describing the evolution of dynamic variables, their constraints, and the evolution to new discrete states must be finite conjunctions of linear inequalities, and the flow conditions may refer only to derivatives of state variables and not to the variables themselves. From the perspective of complex decision-making the restriction to conjunctions of inequalities, rather than more expressive formulæ forces logical reasoning to be modelled using sequences of discrete transitions where intuitively only one transition should take place.
-
3.
This in turn means that tools such as HyTech (Henzinger et al. 1997), and PHAVer (Frehse 2005) implemented for the model checking of linear hybrid automata also do not scale well in the presence of large discrete state spaces (Damm et al. 2007). Not only do complex logical computations have to be modelled as a set of states with the same continuous dynamics, but also the process of determining trajectories through individual discrete states tends to create multiple states in the model checking algorithm for each state in the hybrid automata (i.e., a state for each possible region of trajectories through the state).
-
4.
As noted above, a hybrid automaton models the behaviour of an entire system; both the computational and the real world parts. As a result, in general, hybrid automata do not provide a suitable implementation language for a programmer wishing to create the computational parts of some larger system. Consequently, hybrid automata model checking operates much like standard model checking, i.e., it verifies a model of the implemented system, rather than the system itself.
Particularly in certification contexts and especially when introducing a novel component such as an autonomous decision-maker, there is a need to verify the actual implemented system (or at least the implementation of the novel part). In these cases it is necessary to somehow compile the implemented system, together with a model of its environment, into an explicit hybrid automaton before analysis.
2.4.1 Solutions to compositionality and expressivity
In recent years there has been considerable work on overcoming the problems outlined in the previous section. In particular the issue of compositionality and abstraction has been tackled in a number of ways.
PHAVer (Frehse 2005) is a model-checking system for linear hybrid automata that uses assume-guarantee style reasoning to allow the model checking to be approached in a compositional fashion (Frehse et al. 2004). The approach takes a hybrid automaton that has been constructed from the parallel composition of smaller sub-systems (e.g., a physical system with its continuous dynamics, and a software controller). During model checking, these sub-systems can be replaced by abstractions which have certain features that retain the soundness of the approach. So a physical system can be model checked, composed with an abstraction of a software controller and vice versa. The more abstract systems constitute an over-approximation of the original sub-system and therefore it is possible for the verification process to return false negatives (i.e., it may disprove a conjecture that is actually true). The underlying verification continues to use hybrid automata based model checking and so remains constrained by many of the considerations above (e.g., PHAVer is restricted to linear hybrid automata). However the basic approach, abstracting away one sub-system, is substantially similar to the one we adopt here.
Platzer has developed a theorem proving approach for verifying hybrid automata which is implemented in the KeYmaera system (Platzer 2010). This benefits from many of the advantages of theorem proving including a naturally compositional approach to proof. Theorem proving also produces stronger, more general, results than model checking but has its disadvantages. Producing such verifications is generally time-consuming and requires highly skilled users although KeYmaera is linked to a number of automated systems for solving sub-problems.
KeYmaera verifies hybrid systems which are represented as hybrid programs written in a dedicated while-style programming language. There is a direct embedding of hybrid automata into hybrid programs. However hybrid programs are more expressive than, for instance, linear hybrid automata, and it is possible to represent complex logical formulæ as invariants on states. Unfortunately, the language remains at a low level, meaning that the implementation of complex decision-making is quite cumbersome.
2.4.2 Solutions to the modeling problem
While it is theoretically possible to represent all hybrid systems as hybrid automata or hybrid programs, it is time consuming to do so. In particular, as noted above, it is difficult to represent complex computations occurring at the discrete decision-making level in a compact fashion. As a result, where complex decision-making takes place the hybrid automaton (or hybrid program) that models the system for verification frequently abstracts away from the process and, instead, just represents all possible outcomes of the decision-making as non-deterministic choices.
There have been several attempts to produce systems that will compile higher level programming languages into hybrid automata for verification—thus allowing the full complexity of decision-making to be represented. These systems can also, potentially, employ abstraction techniques during the compilation process in order to reduce the search space. Such approaches have focused on synchronous languages such as Lustre (Briand and Jeannet 2009), and Quartz (Bauer 2012).
The agent paradigm, in particular, has been developed to address distributed asynchronous situations which makes it attractive in situations where a synchronous model of time is unhelpful. However, as yet, no system has been created to compile agent-based control into hybrid automata.
2.5 Model checking agent programs
There are a number of approaches to model checking and verifying multi-agent systems (Alechina et al. 2010; Lomuscio et al. 2009; Gammie et al. 2004). Most of these are not specifically geared towards BDI-style rational agents but provide more general tools for the analysis of agents. In general these have not been applied to the problem of hybrid systems although MCMAS has been used in the verification of hybrid automata (Ezekiel et al. 2011).
There are four systems that focus specifically on the model checking of BDI programs. Jongmans et al. (2010) describe a program model checker tailored specifically towards the GOAL programming language. Both Hunter et al. (2013) and Stocker et al. (2012) have investigated the model checking of Brahms (Sierhuis 2001) programs using SPIN (Holzmann 2004). Both systems re-implement Brahms in Java and then either export directly into SPIN (Stocker et al. 2012) or use Java Pathfinder (JPF) to generate a model which is then exported to SPIN (Hunter et al. 2013). Bordini et al. (2006) explores the model checking of AgentSpeak programs in both SPINand JPF but, as far as we aware, the system is no longer maintained.
The MCAPL framework (Dennis et al. 2012) (described in more detail below) provides access to model checking facilities to programs written in a wide range of BDI-style agent programming languages so long as those languages have a Java-based program interpreter. We chose to use the MCAPL framework in this work.
2.5.1 The MCAPL framework
In the examples discussed later in this paper we use the MCAPL framework which includes a model checker built on top of JPF. We do not consider the framework to be integral to our approach to the verification of agent-based decision-making in autonomous systems, though some general background on the system will be useful when reading the later examples. The framework is described in detail in Dennis et al. (2012), we therefore provide only a brief overview here. It has two main sub-components: the AIL-toolkit for implementing interpreters for rational agent programming languages and the AJPF model checker.
Interpreters for BDI languages are programmed by instantiating the Java-based AIL toolkit (Dennis et al. 2008). An agent system can be programmed in the normal way for a language but runs in the AIL interpreter which in turn runs on the Java Pathfinder (JPF) virtual machine. This is a Java virtual machine specially designed to maintain backtrack points and explore, for instance, all possible thread scheduling options (that can affect the result of the verification) (Visser et al. 2003).
Agent JPF (AJPF) is a customisation of JPF that is optimised for AIL-based language interpreters. Agents programmed in languages that are implemented using the AIL -toolkit can thus be model checked in AJPF. Furthermore if they run in an environment programmed in Java, then the whole agent system can be model checked. Common to all language interpreters implemented using the AIL are the AIL-agent data structures for beliefs, intentions, goals, etc., which are subsequently accessed by the model checker and on which the modalities of a property specification language are defined. Since we will be using this AJPF property specification language (PSL) extensively later in this paper, we here describe its syntax and semantics (from Dennis et al. 2012).
2.5.2 Temporal and modal logics and the MCAPL property specification language
In standard model checking, the logical formulæ are typically from some variety of temporal logic, such as PLTL (propositional linear temporal logic). Underlying this particular logic is a model of time based upon the natural numbers. Non-temporal formulæ are evaluated at a single moment in time. Thus, some proposition ‘\(\mathsf {raining}\)’ might be true at the current moment in time but false in the next moment. Temporal operators then allow us to move between moments in time within our formulæ. In PLTL, such operators are typically of the form ‘\(\square \)’ (at all future moments), ‘\(\lozenge \)’ (at some future moment), ‘ ’ (at the next moment), etc. Thus
’ (at the next moment), etc. Thus

means that if, at some moment in the future it will be raining, then at the next moment in time we should get our umbrella. Such a logical base provides well-understood and unambiguous formalism for describing the basic system dynamics (Fisher 2011). (Note that we do not define \(\lozenge \), \(\square \), etc, directly but give the semantics of the more expressive temporal operators \(\mathop {\mathrm {\fancyscript{U}}}\) and \(\mathop {\mathrm {\fancyscript{R}}}\), and then derive other temporal operators from these as needed.)
However, in order to describe the behaviour of, and requirements within, rational agents, we often need additional logical dimensions (Kurucz 2006). Thus we combine our basic temporal logic with logical modalities for describing beliefs (that represent the agent’s knowledge about its situation) and motivations (that represent the agent’s reasons for making choices).
As an example, consider the following formula, a variation of which we will use later:
meaning that if a robot believes it has found a trapped human then eventually either it believes the human is free or it intends to make the human free. Notice how this formula combines temporal operators with the belief operator, \(\mathbf {B}\), and the intention operator, \(\mathbf {I}\).
The AJPF property specification language is thus formally defined as follows:
PSL syntax The syntax for property formulæ \(\varphi \) is as follows, where \(ag\) is an “agent constant” referring to a specific agent in the system, and \(f\) is a ground first-order atomic formula:
Here, \(\mathrm {\mathbf {B}}_{ag} \, f\) is true if \(ag\) believes \(f\) to be true, \(\mathrm {\mathbf {G}}_{ag} f\) is true if \(ag\) has a goal to make \(f\) true, and so on with \(\mathrm {\mathbf {A}}\) representing actions, \(\mathrm {\mathbf {I}}\) representing intentions, and \(\mathrm {\mathbf {P}}\) representing percepts, i.e., properties that are true in the external environment (e.g., a simulation of the real world) in which the agent operates.
PSL semantics We next examine the specific semantics of our property formulæ. Consider a program, \(P\), describing a multi-agent system and let \( MAS \) be the state of the multi-agent system at one point in the run of \(P\). \( MAS \) is a tuple consisting of the local states of the individual agents and of the environment. Let \(ag\in MAS \) be the state of an agent in the \( MAS \) tuple at this point in the program execution. Then
where \(\models \) is logical consequence as implemented by the agent programming language.Footnote 4 The interpretation of \(\mathrm {\mathbf {G}}_{ag} f\) is given as:
where \(ag_{G}\) is the set of agent goals (as implemented by the agent programming language).Footnote 5 The interpretation of \(\mathrm {\mathbf {A}}_{ag} f\) is:
if, and only if, the last action changing the environment was action \(f\) taken by agent \(ag\). Similarly, the interpretation of \(\mathrm {\mathbf {I}}_{ag} f\) is given as:
if, and only if, \(f \in ag_{G}\) and there is an intended means for \(f\) (in AIL this is interpreted as having selected some plan that can achieve \(f\)). Finally, the interpretation of \(\mathrm {\mathbf {P}}(f)\) is given as:
if, and only if, \(f\) is a percept that holds true in the environment.
The other operators in the AJPF property specification language have standard PLTL semantics (Emerson 1990) and are implemented as Büchi Automata as described in Gerth et al. (1996), Courcoubetis et al. (1992)). Thus, the classical logic operators are defined by:
The temporal formulæ apply to runs of the programs in the JPF model checker. A run consists of a (possibly infinite) sequence of program states \( MAS _i\), \(i \ge 0\) where \( MAS _0\) is the initial state of the program (note, however, that for model checking the number of different states in any run is assumed to be finite). Let \(P\) be a multi-agent program, then
The common temporal operators \(\lozenge \) (eventually) and \(\square \) (always) are, in turn, derivable from \(\mathop {\mathrm {\fancyscript{U}}}\) and \(\mathop {\mathrm {\fancyscript{R}}}\) in the usual way (Emerson 1990).
For the future, we hope to incorporate modalities for knowledge (for describing information evolution) and coalitions (for describing cooperative systems) (Blackburn et al. 2006) as well as extending some or all of these modalities to a full logic. Investigating alternative logics for model checking autonomous systems is also the subject of further work.
In this section we have examined the history of agent-based control of hybrid systems and the separate strands of research into the verification in hybrid systems and verification of agent programs. We next begin to tackle a series of example systems, defining the controlling agent(s), describing the environmental assumptions and carrying out formal verification.
3 Scenario: urban search and rescue
Consider a (simplified) example based on the RoboCup Rescue, or “urban search and rescue”, scenario (Kitano and Tadokoro 2001). This is a widely used test scenario for autonomous mobile robots, providing not only a variety of environmental abstractions but also the potential for both individual and cooperative behaviours. A natural disaster (e.g., an earthquake) has caused buildings to collapse. Autonomous robots are searching for survivors buried in the rubble. There may be many of these robots, each with sensors for detecting buried humans. Let us model this scenario on a simple grid. A robot can move around spaces on the grid and at most one human is placed randomly on the grid. The robot’s sensors are such that a robot ‘detects’ a human if the human is in the same grid square.Footnote 6
3.1 Implementation
Listing 1 shows part of the agent code for a simple search robot written using the BDI-style agent programming language, Gwendolen (Dennis and Farwer 2008). The robot has the goal of reaching a state where it can leave the area. It can only achieve this goal if either it believes it has found the human or believes that the area is actually empty.

Syntax. Gwendolen uses many syntactic conventions from BDI agent languages: +!g indicates the addition of the goal g; +b indicates the addition of the belief b; while -b indicates the removal of the belief. Plans then consist of three parts, with the pattern

The ‘trigger’ is typically the addition of a goal or a belief (beliefs may be acquired thanks to the operation of perception and as a result of internal deliberation); the ‘guard’ states conditions about the agent’s beliefs (and, potentially, goals) which must be true before the plan can become active; and the ‘body’ is a stack of ‘deeds’ the agent performs in order to execute the plan. These deeds typically involve the addition and deletion of goals and beliefs as well as actions (e.g., move_to(X1,Y1)) which refer to code that is delegated to non-rational parts of the systems (in this case, motor systems). In the above, Prolog conventions are used, and so capitalised names inside terms indicate free variables which are instantiated by unification (typically against the agent’s beliefs). Programs may also perform deductive reasoning on their atomic beliefs as described in their reasoning rules. For instance

indicates that the agent deduces that the whole area is empty if it is not the case(i.e., \(\sim \)) that there is some square that is empty (the “closed world assumption” is usedto deduce that the agent does not believe something). When asked to check B area_empty then the agent will use the reasoning rule to deduce new beliefs based on predicates in its belief base. Reasoning rules can also be used to deduce new goals but this feature is not used in the work described here.
In Listing 1, the goal, +!leave[achieve], represents an achievement goal (Riemsdijk et al. 2009) meaning that the agent must continue attempting the plans associated with the goal (if they are applicable) until it has acquired the belief ‘leave’ (i.e., it wishes to achieve a state of the world in which it believes it can leave the area). Note that, in the above program, the agent cannot directly deduce “B human”, i.e., there is a human at the current position, as it requires its sensors to tell it if it can see a human. The underlying language interpreter polls the sensors for belief changes associated with perception once each reasoning cycle. The belief that the agent can see a human is not parameterised by the robot’s location because the sensors are presumed to simply register the presence or absence of a human in the robot’s immediate location, it then subsequently deduces the location of the human from its own current location.
In Listing 1 the agent picks an unchecked square in the grid to explore. It continues to do this until either its sensors tell it that it can see a human or until it believes the area is empty.
In this example the agent handles information about its location internally, i.e., it does not perceive its location by checking the environment but adds and removes beliefs about its location based on where it is in the execution (lines 9, 15 and 16 in Listing 1). This was adequate for the example here, and allowed us to minimize interaction with the environment in order to simplify the explanations of our methodology. Obviously, in practice, it would be dangerous to handle beliefs about location in this way and, in particular, to update such beliefs before any move action had taken place. A more complex example, which introduced more events for the agent to handle (which could potentially occur during movement and which required accurate location information) would have revealed the limitations of this implementation during verification (if not before).
3.2 Verification
Now, we wish to verify the robot’s reasoning is correct, independent either of the modelling of other parts of the system or any detail of its environment. So, we might wish to verify that
if the searching robot, s, believes it can leave the area, then it either believes the human is found or it believes the area is empty.
An abstract model for the incoming perceptions must be provided, otherwise we would only be able to check the robot’s behaviour when it does not believe it can see a human (since that belief arises from perception alone). Whenever the agent requests some perceptions we supply, randomly, all relevant inputs to the robot. In this case it either sees a human or does not see a human.
The choice of which perceptions to supply to the agent and the times at which these perceptions may change obviously represent an abstract model of the real world. However we believe that these are decisions that can be made explicit, avoiding the need for someone to inspect the code of the model in order to determine precisely what has been proved. Moreover it is a model that is extremely conservative in its assumptions about the real world.
Using this model of the environment we were successfully able to verify (1) automatically in AJPF. Similarly we also verified other parts of the agent reasoning for instance,
if the searching robot, s, never believes it sees the human then that means that eventually it will believe it has visited all squares in the grid.
NB. the AJPF property specification language is propositional and so the use of universal (\(\forall \)) quantifiers in these examples is just a shorthand for an enumeration over all possible values. In this case we used a \(3\times 3\) grid so the actual property checked was
Use of quantifiers in other AJPF property specification language expressions throughout the paper should be understood in a similar way.
3.2.1 Deduction using environmental assumptions
There is a great deal we can formally verify about an agent’s behaviour without reference to the agent’s environment. However there are still things we might reasonably wish to prove given simple assumptions about the behaviour of the real world. Thus, once we have shown \( System \models \varphi \), for some relevant property \(\varphi \), then we can use the fact that the environment satisfies \(\psi \) to establish \( System \models (\psi \wedge \varphi )\) and hence (if \((\psi \wedge \varphi )\Rightarrow \xi \)) that \( System \models \xi \). For instance, we might want to assume that the robot’s sensors accurately detect the human,Footnote 7 and that its motor control operates correctly. If we know these facts then we can prove a stronger property that the agent will actually find the human as well as believing it has found the human.
Let us define ‘\(\mathsf {found\_human}\)’ as the property that
the robot and the human are in the same grid square and the robot believes it can see the human.
We can characterise \(\mathsf {correct\_sensors}\) as:
the robot believes it can see a human if, and only if, it is in the same square as the human.
Similarly, we need to state, as an assumption, that the robot’s motors are working correctly.
the robot believes it has reached a grid square if, and only if, it is actually in that grid square.
Given this framework we might want to show that
if the robot’s sensors and motors are working correctly and if a human is stationary on the grid then eventually the robot will find the human.
We have already verified the agent’s internal reasoning by model checking to give us the property in (2) which tells us that either the robot believes it sees the human or it visits every square. From this (6) can easily be proved. This can be done by hand, or by using a suitable temporal/modal logic prover (Fisher 2011)—for instance we were easily able to prove this theorem on a three by three grid automatically in the online Logics Workbench (Heuerding et al. 1996) (see Appendix 3 for the input commands).
A key aspect here is that this ‘proof’ that the robot will find the human only works if the human does not move and, indeed, we have had to state that explicitly (via \(\square \mathsf {at(human,X,Y)}\))! Without this assumption the proof fails since there will be no way to prove that, eventually, the robot and human will be in the same square at the same time.
3.2.2 Multi-agent systems
In more sophisticated scenarios we not only want to check properties of single agents but of groups of agents working together. Thus, imagine that we now have another robot, capable of ‘lifting’ rubble. The aim is for the two robots to work as a team: the ‘searching’ robot, ‘\(s\)’, will find the human, then the ‘lifting’ robot, ‘\(l\)’, will come and remove the rubble. We will refer to the beliefs of the lifting robot as \(\mathbf {B}_l\). Ideally, if these two work together as expected then we would like to show that eventually the lifter believes the human is free:
However, this depends on several things, for example that any communication between the robots will actually succeed. We can adopt our previous approach and analyse each robot independently based on random perceptions and, in this case, messages being received from the environment. So we can establish that (we have slightly simplified the properties for presentational purposes):
the searcher will send a message to the lifter if it finds a human.
and
the lifter will free the human if it receives such a message
We can also express the assumption that messages sent by the searcher will always be received by the lifter and then use the model checker to prove properties of the combined system, e.g:
if messages sent by the searcher are always received by the lifter then if the searcher believes it has found a human, eventually the lifter will believe the human is free.
Potentially, using reasoning such as this, two autonomous robots could believe that they will together achieve a required situation given some joint beliefs about the environment. However if we reason about each agent separately to deduce properties (8) and (9) we reduce both the size of the automaton to be checked and the size of the search space. We can then combine these component properties with an appropriate statement about communication, i.e.
in order to reach the conclusion of (10) deductively.Footnote 8 This demonstrates one of the advantages of a compositional approach—namely that the complexity of model checking tasks can be kept to a minimum.

3.2.3 Goals and intentions
We have been verifying the beliefs agents acquire about their environment in lieu of verifying actual facts about the environment. However, we are also interested in verifying the choices that agents make. Suppose that our lifting agent does not deduce that the human is free (because it has moved some rubble), but continues to lift rubble out of the way until its sensors tell it the area is clear (see Listing 2). We cannot verify that the robot will eventually believe the human is free since we can not be sure that it will ever believe that the human is actually clear of rubble. However, we can establish (and have verified) that
if the lifting agent believes the human to be at position \(\mathsf {(X,Y)}\) then eventually it will form an intention to free the human.
As above, we can derive further properties under assumptions about the way perception behaves:
assuming that, whenever the lifter forms an intention to free the human it will eventually believe the rubble is clear, then receipt of a message from the searcher will eventually result in the lifter believing the human is free.
3.2.4 Performance
In this section we briefly outline performance results for the Robot Rescue Scenario. Performance issues will be discussed more fully in our next example. The verification was performed on a dual core 2.8 GHz Macbook with 8 GB of memory running \(\hbox {MacOS} \times 10.9.2\).
Table 1 shows the time taken and number of states generated when verifying theorem 1. In this instance we show performance for a \(3\times 3, 4\times 4, 5\times 5\) and \(6\times 6\) grid. While the number of states explored increases roughly linearly with the number of squares in the grid the time increase is much more severe. This is because of the time taken to execute the Prolog-style rules for area_empty and unchecked. This is indicative of inefficiency in the implementation of Gwendolen therefore, rather than in AJPF itself.
Table 2 shows the number of verification states and time taken for the other theorems discussed in this section on the \(3\times 3\) grid.
While much simplification has occurred here, it is clear how we can carry out compositional verification, mixing agent model checking and temporal/modal proof, and how the environmental abstractions we use can be refined in many ways to provide increasingly refined abstractions of the “real world”. Crucially, however, we can assess the choices the agent makes based on its beliefs about its environment and not what actually happens in its environment.
4 Scenario: rational hybrid agents for autonomous satellites
The previous example involved simple code developed to illustrate our methodology. We now turn to look at code developed as part of a project to investigate agent based control of satellite systems (Lincoln et al. 2013). The code was not initially developed with verification in mind.
Traditionally, a satellite is a large and very expensive piece of equipment, tightly controlled by a ground team with little scope for autonomy. Recently, however, the space industry has sought to abandon large monolithic platforms in favour of multiple, smaller, more autonomous, satellites working in teams to accomplish the task of a larger vehicle through distributed methods.
The nature of these satellite systems, having a genuine need for co-operation and autonomy, mission critical aspects and interaction with the real world in an environment that is, in many respects, simpler than a terrestrial one, makes them a good test-bed for our approach to analysing autonomous systems.
4.1 System architecture
We have built a hybrid system embedding existing technology for generating feedback controllers and configuring satellite systems within a decision-making part based upon a high-level agent program. The decision-making relies on discrete information (e.g., “a thruster is broken”) while system control tends to rely on continuous information (e.g., “thruster fuel pressure is 65.3”). Thus, it is vital to be able to abstract from the dynamic system properties and provide discrete abstractions for use by the agent program. It is for this reason that, as mentioned earlier, we have an explicit abstraction layer within our architecture that translates between the two information styles as data flows around the system.
Figure 2 shows the full architecture for our system (Dennis et al. 2010). \(R\) is a traditional BDI system dealing with discrete information, \(\varPi \) and \(\varOmega \) are traditional control systems, typically generated by MatLab/Simulink, while \(A\) provides the vital “glue” between all these parts. We will not discuss the implementation of \(\varPi \) and \(\varOmega \) in any detail; our concern is primarily with \(R\) and its interaction with \(A\).
Hybrid agent architecture. Real time control of the satellite is governed by a traditional feedback controller drawing its sensory input from the environment. This forms a Physical Engine (\(\varPi \)). This engine communicates with an agent architecture consisting of an Abstraction Engine (\(A\)) that filters and discretizes information. To do this \(A\) may use a Continuous Engine (\(\varOmega \)) to make calculations. Finally, the Reasoning Engine (\(R\)) contains a “Sense-Reason-Act” loop captured as a rational agent. Actions involve either calls to the Continuous Engine, \(\varOmega \), to calculate new controllers (for instance) or instructions to the Physical Engine, \(\varPi \), to change these controllers. These instructions are passed through the Abstraction Engine, \(A\), for reification
The agent programming language used to implement \(R\) (again, Gwendolen) encourages an engineer to express decisions in terms of the beliefs an agent has, what it wants to achieve, and how it will cope with any unusual events. This reduces code size so an engineer need not explicitly describe how the satellite should behave in each possible configuration of the system, but can instead focus on describing the factors relevant to particular decisions (Dennis et al. 2010b). The key aspect of deliberation within agent programs allows the decision-making part to adapt intelligently to changing dynamic situations, changing priorities, and uncertain sensors.
4.1.1 Semantics of interaction
We developed a semantics for interaction between the components of the architecture (Dennis et al. 2010a) which operates via shared sets of which, for our purposes, the most interesting is the set of shared beliefs, \(\Sigma \), used by both \(A\) and \(R\) to describe their shared, discrete, understanding of the world. \(R\) may also make specific requests for calculations to be performed by \(\varOmega \) or actions to be performed by \(\varPi \). These requests are sent via \(A\). Among other things, \(A\) takes any (potentially continuous) results returned by \(\varOmega \) and discretizes these as a shared belief for \(R\). Overall, the role of \(A\) is to interface between \(R\) and the other engines. This helps avoid data overload by replacing large ‘chunks’ of incoming data with key discrete predicates (Dennis et al. 2010a).
In this semantics all perceptions that arrive via sensors from the real world are filtered through \(A\), which converts them into discrete shared beliefs, \(\Sigma \). Therefore, from a model checking perspective, if we are interested in how the external world can affect the internal beliefs of the Reasoning Engine, \(R\), then we are primarily interested in the possible compositions of \(\Sigma \).
4.1.2 System implementation
This architecture and interaction semantics have been implemented within a simulation environment, where the Physical and Continuous engines (\(\varPi \) and \(\varOmega \)) are implemented in MatLab, while \(A\) and \(R\) are written in a customised variant of the Gwendolen programming language. This extended language includes constructs for explicitly calling \(\varPi \) and \(\varOmega \) and a Java environment interface that supports such calls. This Java environment handles the shared data sets, in particular the shared beliefs which are used by \(A\) and \(R\) and also controls communication with MatLab via sockets.
The architecture has been deployed on multiple satellites within a satellite hardware test facility as well as within a number of simulated environments. A range of satellite scenarios have been devised and tested, involving assuming and maintaining various formations, fault monitoring and recovery and collaborative surveying work in environments such as geostationary and low Earth orbits and among semi-charted asteroid fields. The system and scenarios are described more fully in Lincoln et al. (2013).
The focus of this example is upon the verification that took place after this initial implementation and testing. Given the verification was of the rational engine alone, it was obviously important that the behaviour of the whole system be tested separately but this paper does not examine these aspects.
4.2 Adapting the system for model checking
Our principal interest here is in the verification of the discrete reasoning parts of the system. These are represented by \(R\) and so we want to abstract away \(A\), \(\varOmega \) and \(\varPi \), yet do so in a coherent fashion. Since all communication with \(\varPi \) and \(\varOmega \) to and from \(R\) occurs via \(A\), we can ignore \(\varOmega \) and \(\varPi \) entirely and just focus on \(A\) and \(R\).
The architecture proved particularly conducive to the verification methodology proposed. Since programmers had to explicitly program up the abstractions to be used with the Abstraction Engine, \(A\), it became possible to “read off” from the code for an abstraction engine all the shared beliefs that could possibly be asserted in response to changing perceptions. This in turn allows us to pre-determine the possible configurations of \(\Sigma \), the set of shared beliefs. Similarly we were able to analyse the messages that agents sent to determine which messages might be received by other agents in the system. Since the only external inputs to the reasoning engine come from shared beliefs and messages it was easy to clearly define the set of inputs needed for verification.
We implemented specific verification environments that observed the Reasoning Engine’s interface requirements for the hybrid system. This consisted entirely of asserting and retracting these shared beliefs and messages. Each time an agent took an action in the environment a new set of shared beliefs and a new set of messages were generated at random. Each time the agent requested the shared beliefs a random shared belief set was sent to it (similarly with messages). During model checking the calls to random number generation caused the model checker to branch and to explore all possible outcomes that could be generated. In order to limit the search space we take the (simplifying) view that reasoning happens instantaneously, while action has a duration. Therefore the only times at which the system randomly changes the perceptions/shared beliefs and messages available to the reasoning engine are when the reasoning engine takes some form of action (i.e., a request for a calculation from \(\varOmega \)). The model checker will then explore all possible combinations of shared beliefs and messages that might be available at that point, modelling essentially both the times an action results in the expected outcome and those when it does not.
It is important to again emphasize that those aspects of the system relating to the Abstraction, Continuous and Physical engines were not required for model checking the system.
4.3 Example: autonomous satellites in low Earth orbit
A low Earth orbit (LEO) is an orbit with an altitude ranging between that of the Earth’s upper atmosphere, at approximately 250 km, and an upper bound of 2,000 km; the orbit may be inclined to the equator and may or may not be elliptical. LEOs are used predominantly by Earth observation missions that require high resolution imaging, including weather, Earth resource and military satellites.
Low Earth orbit based satellites travel at high speed, completing an orbit within approximately 90 min. Orbiting at such great speeds presents a secondary issue concerning the control and monitoring of LEO satellites: ground station visibility is restricted to between 5 and 15 min per overhead passage of a ground station. Whilst multiple ground stations, or space based relay satellites orbiting at higher altitudes, may be switched between to enable greater communication periods, the growth in infrastructure is a clear disadvantage. As a result there is a need to increase the autonomous control of such systems.
4.3.1 Scenario
We developed a model of satellite formations in low Earth orbit. The Continuous Engine, \(\varOmega \), was programmed to supply plans for moving to particular locations in a formation. The algorithm used to generate such plans was based on that in Lincoln and Veres (2006). Controls were made available in the Physical Engine, \(\varPi \), which could send a particular named activation plan (i.e., one calculated by \(\varOmega \)) to the feedback controller.
The satellite was provided with thrusters in three body axes (X, Y and Z) each of which contained two fuel lines. The agent was also able to control which fuel line was in use which enabled it to switch in the event of a rupture (detectable by a drop in fuel pressure).
In the simple case examined here, the satellites were expected to move to pre-generated locations in a formation, correcting for a single fuel line breakage, if it occurred.
4.3.2 Implementation and testing
The code for the abstraction and rational engines for these examples can be found in Appendix 1 together with a detailed description of its functionality.
The software was developed and tested both in simulation, using a Simulink implementation of \(\varPi \) and \(\varOmega \), and on a physical satellite simulation environment developed initially at the University of Southampton and then moved to the University of Sheffield (Fig. 3). In simulation a “gremlin” agent was introduced that could, at specified points, insert hardware failures into the satellite system. In physical testing it was possible to simulate failures in “path following” by physically moving the satellites from their chosen course. Having produced a working system the task was then to formally analyse it.
4.3.3 Analysis of a single satellite agent
We wish to verify the satellite’s Reasoning Engine is correct, independent of the modelling of other parts of the system and any detail of its environment.
We inspected the Abstraction engine code to determine the shared beliefs. A fragment of this code is shown in Listing 3 and the full listing can be found in Listing 6. \(+_{\Sigma }\) b and \(-_{\Sigma }\) b are used to indicate when the Abstraction engine asserts or removes a shared belief.

Simply reading off the uses of these constructs in the fragment tell us that the shared beliefs that can be asserted are, close_to(Pos) (meaning that the satellite is close to position, Pos), and broken(X) (meaning thruster X is broken). thruster_bank_line (X, B, L) (meaning thruster X, is currently in bank B and using fuel line L) and get_close_to(Pos, P) (meaning that P is a plan for moving to position, P) also appear in the full code shown in Listing 6. All of these have parameters. We knew from the physical satellite set-up that the thruster “name”, X, could be x, y or z and its bank, B (not used in these examples), and line, L, could be 1 or 2 respectively, depending upon the formation under consideration, \(Pos\), could be none, right, middle, left, topright, topleft, bottomright or bottomleft. get_close_to also had the name of a plan, \(P\), as a parameter. This name was generated and supplied by the Continuous Engine. This was more of a challenge since the name of the plan would be derived algorithmically inside the Continuous Engine. However the code, itself, never analysed this name simply passing it on to the Physical Engine and so a place-holder name, plan, was used.
Unfortunately, even with relatively few perceptions the combinatorial explosion associated with exploring all possibilities gets very large. For most experiments it is necessary therefore to limit the number of possibilities (we discuss this further in Sect. 6). However the analysis does allow us to state clearly which inputs are being considered, as is shown in Tables 3, 4, 5, and 6.
The choice of parameters for shared beliefs and the times at which these shared beliefs might change obviously represent an abstract model of the real world. However we believe that this choice can be made explicit (and show how in our presentation of performance results). This avoids the need for someone to inspect the code of the model in order to determine exactly what assumptions (parameters choices in this case) have been made and hence to determine precisely what has been proved. Moreover it is a model that is extremely conservative in its assumptions about the real world.
In Sect. 3.2.2 we modelled reliable communication via a hypothesis to our theorem. We will use the same technique to capture hypotheses about the workings of the Continuous and Physical engines. Thus, potentially, once we have shown \( R \models (\psi \rightarrow \varphi )\) then we can use the fact that, for instance \(\varPi \) satisfies \(\psi \) to establish \(\{ R , \varPi \} \models \varphi \)
As a result of this analysis a number of additional plans were introduced into the agent code to handle edge conditions where information was changing particularly rapidly. The code shown in Appendix 1 is the final code. The plans on line 50 and lines 56–58 in the Rational Engine in Appendix 1 (a) were introduced as a result of model-checking to cover cases where, for instance, an abort has already occurred but information arrives that a thruster is newly broken, or that a thruster had been successfully fixed but is now reporting it is broken again. This demonstrates the ability of verification to locate errors that were not found by simulation or testing.
Agent operation without thruster failure or outside communication
We first chose to investigate the operation of the agent in a situation where its thrusters do not fail and when no messages were received from outside. Therefore it started out with the goal of assuming its position in a formation, and that the position it was to assume was in the middle of a line. This was achieved by preventing the environment from sending the perception broken(X). The environment delivered no messages.
We define two assumptions about the environment:
if the agent requests a plan to get to some position, then it eventually believes it has received a plan.
if the agent executes a plan then eventually it believes it has reached the desired position.
We want to establish, using model checking, that:
if the agent receives a plan on request, and the execution of that plan takes it to the middle position in a line, then eventually the agent will believe it is maintaining a position in the middle of the line.
If we wish to relax our environmental assumptions, we can also show that
if plan execution always succeeds, then either the agent will eventually believe it is in its desired position, or it never believes it has a plan for getting there.
Table 3 shows the environment provided for each property (Inputs), and the size of the generated product automata (in states) and the time taken in hours, minutes and seconds on a dual core 2.8 GHz Macbook with 8 GB of memory running \(\hbox {MacOS}\times 10.9.2\) Footnote 9 (Results). The columns on the left of the Inputs chart show the arguments that were supplied to each of the potential percepts (i.e., every time it took an action the agent could either gain the perception get_close_to(middle, plan) or not, but could not, for instance, get the perception get_close_to(left,plan)). \(\times \) indicates that the percept was not supplied at all.
These results could be combined deductively with results about the correct performance of the Continuous and Physical engines to produce a proof that the the agent would eventually believe it was in position. Furthermore, with additional analysis to prove that the sensors always operated correctly:
if the agent believes it is in the middle then it really is in the middle
then the theorem could be extended to prove that the agent really could be guaranteed always to reach its position.
The important thing to note is that the theorem resulting from the model checking process explicitly states its assumptions about the real world (i.e., that plans are always produced and are always accurate) rather than concealing these assumptions within the coding of the model. Since it is, in reality, unlikely that you could ever guarantee that plan execution would always succeed it might be necessary to combine the model checking with probabilistic results to obtain an analysis of the likely reliability of the agent (see further work in Sect. 6).
Investigating the response to thruster failure
If we include the possibility of thruster failure into our analysis then we can show that
if the planning process succeeds then either the agent eventually believes it is maintaining the position or it believes it has a broken thruster.
We can improve on this result by adding extra assumptions about the way the environment behaves:
whenever the agent fixes a fuel line then eventually it believes the thruster is working again.
where \(T\) is the thruster effected. A second hypothesis is
broken thrusters never lead to an abort because of thruster failure.
Property (21) states that
if planning succeeds for the middle position, and the x thruster is always believed to be fixable and changing a fuel line means eventually the agent believes the thruster is no longer broken, then eventually the agent will believe it is maintaining its position.
This is obviously only true if the y and z thrusters do not also break. Unfortunately expressing the conditions for the additional thrusters made the automaton too large for construction in reasonable time (however, see ‘aside’ below). As a result this property was checked only with the option of sending the agent the predicate \(\mathsf {broken(x)}\) not with the option of \(\mathsf {broken(y)}\) or \(\mathsf {broken(z)}\). However this restriction is clear from the presentation of results in Table 4.
4.3.4 Analysis of multi-agent models and communication
We now extend the scenario into one which involves multiple agents and communication. In the previous scenario the agent knew which pre-determined position in a formation it was to assume. In this example a further “lead agent” is introduced. This is a purely software agent whose role is to decide which position in some formation each of four satellites are to assume and communicate that information to the agents controlling the spacecraft. It can place the satellites in a line or a square formation and can react to an abort from one of the satellites (e.g., because of thruster failure) to modify the formation if possible (i.e., moving from a square to a line). Appendix 1 (b) shows the code for this lead agent agent.
In the previous examples we were able to determine the appropriate random inputs to the verification by inspecting the shared beliefs asserted by the Abstraction Engines for each agent. The lead agent has no abstraction engine since it is not controlling a physical system directly and so does not actually receive any information from shared beliefs. It receives all its inputs as messages from other agents. We therefore have to analyse it in the light of the messages the other agents in the system (e.g., ag1) send rather than by analysis of the Abstraction Engine. Messages are passed directly between rational agents rather than being processed by the Abstraction Engines. Just as we “read off” the shared beliefs from the Abstraction Engine we can “read off” possible messages from the Reasoning Engine code of the other agents in the system by looking for uses of the send instruction. However, this does not allow us to verify the system against the presence of unknown agents, or message corruption. It is important to note, therefore, that we are explicitly not investigating this in the context of a system where malicious agents may send conflicting messages.
Using this analysis we determine the following messages that may be received by agents in the system. aglead may receive the message maintaining(AgName) in which agent, AgName, asserts that is is maintaining its position and the message aborted(thruster_failure, AgName) in which agent, AgName states that it has aborted its current maneouvre because of thruster failure. The satellite agents (as represented by ag1) can receive three messages, assuming_formation(F) which tells them that the group will be assuming some formation, F; position(Pos) which informs them that they should assume position, Pos within the formation; and the instruction drop_formation(F) which tells to abandon the attempt to assume the formation F. In the system under consideration, AgName can be ag1, ag2, ag3 or ag4. F is one of line or square, and Pos could be none, right, middle, left, topright, topleft, bottomright or bottomleft. For reasons of efficiency, we do not consider the issue of thruster failure in the multi-agent system so we will not use values of aborted(thruster_failure, AgName) in what follows.
Single formation
We verified the behaviour of both the leader agent and the follower agents in the situation where there is only one formation, a line, to be adopted. We needed a new assumption about the performance of the environment, stating that:
once the leader believes it has informed an agent that it should assume a position in a line formation then, eventually, it will believe it has received a message telling it that the (informed) agent is maintaining that position.
With this assumption we were able to verify that
if all agents respond, the lead agent eventually believes the agents have assumed a linear formation.
We also verified some safety properties, e.g.:
the leader never believes it has assigned an agent (ag1 in the case shown below) to two positions at the same time.
the leader never believes it has assigned two agents to the same position (the left in the case shown below).
The follower agent uses the code investigated in our single agent case, but when it is interacting with a multi-agent system we want to verify that the messages it sends to the leader agent accurately portray its beliefs. So, we show that
under the assumption that planning and plan execution are successful for the relevant formation and position, the follower will eventually believe it has informed the leader that it is maintaining its position.
We can also verify that
followers only send messages if they believes they are maintaining the positions they have been assigned.
The results of this analysis are shown in Table 5
Changing formations
Lastly we investigated the behaviour of the leader agent in situations where the formation could change.
if all agents respond, then eventually the leader agent will believe a square formation to have been achieved.
if all agents respond, then whenever the leader agent believes all the agents to be in square formation it will eventually believe them to be in a line formation.
The results of this are shown in Table 6
We can, of course, continue with further verification. However, it should be clear to the reader by now how this proceeds, combining model checking of behaviour for individual agents in the presence of a random environment, together with straight-forward temporal/modal reasoning that can be carried out by hand or by appropriate automated proof tools.
5 Scenario: adaptive cruise control
For our final example we demonstrate how our approach can integrate with approaches based on hybrid automata or hybrid programs which focus on the continuous dynamics of the system. We look at an example developed in KeYmaera by Loos et al. (2011). This example considers the problem of a car with adaptive cruise control that must maintain a safe distance between itself and the car in front and may only change lane when it is safe to do so. Loos et al., analyse this problem compositionally working up from the simple case of two cars in a single lane to an arbitrary number of cars on a motorway with an arbitrary number of lanes. The control system for the cars is modelled as a hybrid program.
It is outside the scope of this paper to describe the syntax and semantics of hybrid programs. But we reproduce a simple example from (Loos et al. 2011) to give a flavour of the language. In Fig. 4, \(x_f\) is the position of the follower car, \(v_f\) its velocity and \(a_f\) its acceleration. Similarly \(x_l, v_l\) and \(a_l\) represent the position, velocity and acceleration of the leader car. \(-B\) is a global constant for the maximum possible deceleration due to braking (so acts as a bound on the speed at which both the leader and follower may slow down, this allows the results to be composed into theorems about whole convoys of cars), \(-b\) is a global constant for the minimum deceleration and \(A\) is the maximum possible acceleration. \(\epsilon \) is an upper bound on the reaction time for all vehicles. \(\mathbf {Safe}_{\epsilon }\) is an equation used by the control system to determine the safe distance between cars. A key part of the verification effort reported is establishing this equation and proving that it does guarantee the system to be collision free. It is defined as
In Fig. 4, \(\mathsf {llc}\) defines a repeated sequence of a discrete control, \(ctrl\), followed by dynamic control, \(dyn\). The discrete control is the parallel composition of the control of the leader, \(l_{ctrl}\), and the follower, \(f_{ctrl}\). The leader has a simple control program—it may adopt any acceleration (\(a_l :{:}= *\)) within the available range. \(f_{ctrl}\) defines three possible states. In the first \((a_f :{:}= *; ?(-B \le a_f \le -b))\) the acceleration may be any negative value in the allowed range. In the second \( (?\mathbf {Safe}_{\epsilon }; a_f :{:}= *; ?(-B \le a_f \le A))\) the acceleration may be any possible value provided the car is a safe distance behind the leader, and in the final state \((?(v_f = 0); a_f :{:}= 0)\), the acceleration may be zero if the velocity is zero. The dynamic control, \(dyn\), states how position and velocity vary depending upon acceleration, using the standard differential equations for motion.
The control systems for the cars in the more complex examples follow a similar form—represented as a non-deterministic choice over legal states for the system. The decision-making represented by the constraints on each state is relatively simple here with no reference, for instance, to any goals of the system. It would be possible to represent more complex control in hybrid programs, particularly since the constraints have access to full first order logic (unlike the constraints in linear hybrid automata) as well as simple if-then control structures, but it would be cumbersome to do so since the language remains low level.
We implemented an agent for adaptive cruise control within the system described in Sect. 4. This adopted the above rules for safety but added in additional features involving goal-based and normative behaviour. We present the code for the Reasoning Engine here, the code for the Abstraction Engine can be found in Appendix 2.
The simple case of a car travelling in a single lane of a motorway is shown in Listing 4. The agent has a goal to drive at the speed limit. To achieve this goal it accelerates if it believes it can do so and then waits for a period before checking if the goal is achieved. If it can not accelerate then it waits until it believes it can. The construct \(*b\) causes an intention to suspend until \(b\) becomes true. can_accelerate is determined by a reasoning rule and is true if it is safe to accelerate and the driver is not currently taking any action. Once the car has reached the speed limit (line 18) it maintains its speed. At this point the goal will be dropped because it has been achieved. So if the speed drops below the speed limit the goal will be re-established (lines 20, 21). If it stops being safe to accelerate, the agent brakes (line 23). Actions by the driver override decisions by the agent, but it still will not accelerate unless it believes it is safe to do so.
We tested the agent in a simple Java environment which modelled the dynamics described by Loos et al. (2011) and performed the calculation of \(\mathbf {Safe}_{\epsilon }\) passing the perception, safe, to the Abstraction Engine if \(\mathbf {Safe}_{\epsilon }\) returned true.Footnote 10
We then used our agent based model checking to verify that the agent obeyed the constraints verified by Loos et al. (i.e., it only accelerated if it was safe to do so) We analysed the abstraction engine (shown in Appendix 2) to determine the possible incoming shared beliefs were safe, at_speed_limit, driver_accelerates, and driver_brakes. Then we proved that
whenever the agent accelerates then it believes itself to be a safe distance from the car in front:

We also investigated a more complex case (also analysed by Loos et al) in which cars could change lane. We implemented the normative rules of the UK highway code so that the agent would always attempt to drive in the leftmost lane unless it wished to overtake a car in front, in which case it would attempt to overtake on the right.
The code is shown in Listing 5. This code introduces further features of our Gwendolen language variant. The action ‘perf’ is interpreted by the environment as a message to the Abstraction Engine to adopt a goal which in turn causes the execution of some non-symbolic code. \(+_{\Sigma }\) b and \(-_{\Sigma }\) b are used to indicate when an agent adds b to, or removes b from, the set of shared beliefs. We introduce a new type of perform goal which is distinguished from an achieve goal by the fact that there is no check that it succeeds; once the actions in a plan associated with a perform goal have been executed then the goal vanishes. Lastly, .lock and .unlock are used to lock an intention to remain current, this ensures that the sequence of deeds are executed one after the other without interference from other intentions.
The code represents an agent which can be in one of two contexts, moving left or overtaking which are represented as beliefs. Lines 9–10 control switching between these contexts. The use of contexts allows us to control dropping goals as the situation changes even if they have not been achieved. The percepts car_ahead and car_ahead_in_left_lane are supplied by the Abstraction Engine and represent the detection of a car the agent wishes to overtake or pass on the right. The intention is that these beliefs are shared before the car would need decelerate in order to maintain a safe distance from the car in front (although we verified the more general case where the beliefs could appear in any order). Similarly clear_left is used by the agent to indicate whether there is no car in the left hand lane which the agent wants to overtake before moving left. Lines 13–15 control the assertion and removal of clear_left. Lines 16–17 control the adoption and abandonment of the goal, in_leftmost_lane. Lines 19–26 are the code for achieving this goal depending upon whether or not it is safe to move left, or there is a car in the left hand lane to be overtaken before moving left. Lines 28–45 work similarly for the overtaking context with the belief overtaken used by the agent to keep track of whether it has successfully overtaken a car.

Once again we analysed the abstraction engine (Appendix 2) to obtain the list of shared beliefs that might be sent to the rational engine: in_leftmost_lane, in_rightmost_lane, changed_lane, safe_right, safe_left, car_ahead_in_lane, car_ahead_in_left_lane.
In this system we were able to verify that
the car only changes lane to the right if it believes it is safe to do so and the car only changes lane to the left if it believes it is safe to do so:
It should be noted that our verification here shows that the implemented rational agent adheres to the constraints on the discrete control used in the verification of the full hybrid system by Loos et al. We assume, among other things, that ‘safe’ is calculated correctly. The point is not to redo the safety analysis but to show that the additional normative and goal-directed behaviours do not effect the agent’s ability to obey the safety constraints.
5.1 Performance
Verification of the adaptive cruise control example was performed on a dual core 2.8 GHz Macbook with 8 GB of memory running MacOS X 10.9.2. The number of states generated and time taken are shown in Table 7.
6 Concluding remarks
In this paper we have presented a compositional approach to the verification of the decision-making parts of hybrid autonomous systems, demonstrating both that such an approach is feasible and how it can be pursued. The methodology uses model checking to perform formal verification of the reasoning of a rational agent that is controlling a hybrid autonomous system. This approach avoids the necessity for complex and opaque models of the external system. At the same time our approach allows the results of model checking to be combined deductively (in a straight-forward way) with results about the full system, in order to provide formal analysis of the whole.
Our hypothesis is that different verification techniques are more suited to different aspects of hybrid system analysis. Program model checking is well-adapted to the analysis of rational agent code, but less well adapted to reasoning in continuous domains where probabilistic, analytical and deductive techniques may yield more accurate results. Our approach allows theorems about the rational agent to be combined deductively in a compositional fashion with results about the rest of the system. Our claim is that it is easier, under this methodology, to make explicit the assumptions we have utilized in order to allow verification to take place. While we have focused particularly on the program model checking of rational agent implementations, the methodology would also be suitable for general model checking of complex agent-based (and possibly other) models for discrete control of hybrid systems. This could be done in a specialised model checker for agent systems such as MCMAS (Lomuscio et al. 2009) or MCK (Gammie et al. 2004). In essence we believe approaches such as ours are suitable wherever there is significant complexity within the discrete reasoning required to control a hybrid system.
To exhibit this approach, we explored three examples in which verification was performed in this compositional manner. The first example used a simple program based on the RoboCup Rescue scenario. Our second example examined code actually developed separately for the control of satellites in low Earth orbit, and our third looked at an adaptive cruise control system already analysed in KeYmaera. In all examples we were able to prove properties about the efficacy of the system in the absence of a detailed formal analysis of real world (and continuous) aspects. Work of this kind enables us to provide accurate and clear analysis of the autonomous decisions made by agents in real world scenarios. It is made feasible by the ability for us to refer to the beliefs, goals and actions of the agent in the property specification language, which allow us to limit our theorems to the internals of the agent.
Our interest is primarily in the verification of discrete logic/agent based decision-making algorithms for controlling hybrid systems, rather than in the analysis of the underlying continuous control. As such our approach abstracts away from the continuous aspects entirely, much as many hybrid automata based analyses abstract away from the details of decision-making. This potentially leads to over-approximation, where we examine all the inputs that an agent could receive not just those that “make sense” from the continuous perspective—e.g., in our adaptive cruise control example we explored the case where the driver is reported to be both braking and accelerating at the same time. It is a matter of some debate whether this truly represents an over-approximation since it would potentially be possible for a malfunctioning sensor to transmit contradictory information. However it is clear that the over-approximation also has repercussions on the search space as the number of potential sensor inputs increases which, combined with the inefficiencies of program model checking currently limits the scope of the methodology.
There are a number of avenues for further work. The most urgent problem is that the agent verification technology is actually very slow (as can be seen from the times reported in Sect. 4.3). Program model checking, such as that provided by Java Pathfinder (JPF), analyzes the real code, often in an explicit way which increases the time taken to generate new states in the model. Improving the efficiency of AJPF, including the investigation of well-known abstraction techniques such as property-based slicing (Bordini et al. 2009), is the subject of on-going work. Following the work by Hunter et al. (2013), we have also investigated the use of AJPF to generate models of the program that can be exported into other model checking systems such as SPIN, NuSMV or MCMAS (Dennis et al. 2013b).
We have shown how agent decision-making can be formally verified in the presence of random environmental interactions. However, we would also like to incorporate a more refined probabilistic analysis of environmental interactions. For instance, it is highly probable that no guarantee can be supplied that data incoming from sensors is correct, yet it is highly likely that the sensor will come with a probabilistic guarantee of reliability. It is therefore desirable to extend the kind of analysis we have done here to theorems of the form “Assuming data from sensors is correct 98% of the time, and actions succeed 98% of the time, then 97% of the time the agent never believes it has reached a bad state”. Initial investigation of a link between AJPF and the probabilistic PRISM model checker (Kwiatkowska et al. 2002) reported in Dennis et al. (2013b) will allow us to explore this direction further.
We are also interested in formalising the composition of the environment used for this kind of analysis. We presented an informal overview of how incoming percepts could be chosen and in the examples we performed this selection was carried out by hand. However, we believe that much could be done to automate the process and so ensure that no potential inputs are overlooked.
As noted above, the non-deterministic modelling of sensor input places limits on the ability of our system to scale as the number of sensors, and more importantly sensor values, increase. It would therefore be beneficial to move in the direction of Frehse et al. (2004) and represent the continuous parts of the system as an abstract automata, or a similar formulation, which allowed us to control the number of possible states. This would draw on work such as (Lomuscio et al. 2010; Păsăreanu et al. 2008; Silva and Melo 2011).
Finally, we also wish to consider agent control systems that can co-operate together, exchange information (and, potentially, plans) and, in some cases, learn new plans for solving problems. Techniques such as those presented above, if embedded within an agent’s own reasoning capabilities, would allow individual agents to assess whether any new plan violated safety constraints imposed upon it, and would allow groups of agents to reason about whether their combined capabilities could ever achieve some goal.
Similarly we are interested in techniques for providing guarantees that an agent always operates within certain bounds no matter what new plans it is given or learns. Some initial steps towards this have been investigated in Dennis et al. (2013a).
Notes
Further discussion of this aspect is provided in Fisher et al. (2013).
‘\(\square \)’ and ‘\(\lozenge \)’ are temporal logic operators meaning “at all future moments” and “in some future moment”, respectively, while ‘\(\mathrm {\mathbf {B}}_{agent} \, \)’ is a logical operator describing the beliefs the agent has.
Alternatively: \(\mathrm {\mathbf {B}}_{agent} \, \square \lnot \mathsf {bad}\) if the agent can hold temporal beliefs.
Some agent languages may draw on more than just the belief base when determining logical consequence. Hence this is written as \(ag\models f\) not \({ag}_B \models f\). This does not mean that an agent can believe one of its goals is true (when it is not true but is simply a goal), but does mean that the agent can believe that it has some goal.
In some languages agents may deduce the existence of implicit goals they possess, based on the explicit goals in the Goal Base. At present the PSL semantics do not support verification of the existence of implicit goals, but it is an extension that we intend to consider. Our thanks go to the anonymous referee who raised this issue.
Relevant code for all the examples in this paper can be found in the examples package of the MCAPL Project, available at sourceforge: http://mcapl.sourceforge.net or can be supplied on request by the first author.
It should be noted that this includes a wider assumption that the programming of the language interpreter correctly adds information from sensors as beliefs at suitable times in the agent’s reasoning cycle. It would be possible to use the \(\mathrm {\mathbf {P}}(\phi )\) modality in the PSL to push these kinds of properties out to the java layer, i.e., to model check that if the percept was available in the software system then the agent together with the interpreter behaves appropriately and indeed we have used this technique in employing probabilistic reasoning about unreliable sensors (Dennis et al. 2013b). A similar technique would also be needed to verify that sensors were polled at appropriate points in languages which give the programmer control over such things. This technique requires an analysis of the larger software system beyond just the agent program in order to determine which percepts should be supplied at random.
Logics Workbench Commands, again in Appendix 3.
It can be seen (particularly, for instance, by comparison of Tables 4 and 6) that time taken does not scale consistently with the number of states in the product automata. This is because the time taken to generate the automata was sensitive to the complexity of generating new states within the agent code—for instance, as already noted, where a lot of Prolog-style reasoning was needed there was a significant slow down in the generation of new program states.
We could have had the Abstraction Engine calculate ‘safe’ but it seemed more in keeping with (Loos et al. 2011) to have this calculated centrally.
In our implementation interaction with shared beliefs is handled as an action by the underlying system, changes to the shared beliefs are then acquired by the perception mechanisms in the abstraction and reasoning engine.
References
Alechina, N., Logan, B., Nguyen, H.N., Rakib, A.: Automated verification of resource requirements in multi-agent systems using abstraction. In: Proceedings of the 6th International Workshop on Model-Checking AI, Springer, LNAI, vol. 6572, pp. 69–84 (2010)
Alur, R., Courcoubetis, C., Halbwachs, N., Henzinger, T.A., Ho, P.H., Nicollin, X., Olivero, A., Sifakis, J., Yovine, S.: The algorithmic analysis of hybrid systems. Theor. Comput. Sci. 138(1), 3–34 (1995)
Alur, R., Henzinger, T.A., Lafferriere, G., Pappas, G.J.: Discrete abstractions of hybrid systems. Proc. IEEE 88(7), 971–984 (2000)
Barringer, H., Giannakopoulou, D.: Proof rules for automated compositional verification through learning. In: Proceedings of SAVCBS Workshop, pp. 14–21 (2003)
Bauer, K.: A New Modelling Language for Cyber-Physical Systems. PhD thesis, Technische Universität Kaiserlautern (2012)
Blackburn, P., van Benthem, J., Wolter, F. (eds.): Handbook of Modal Logic. Elsevier, Amsterdam (2006)
Bond, A.H., Gasser, L. (eds.): Readings in Distributed Artificial Intelligence. Morgan Kaufmann, San Mateo, CA (1988)
Bordini, R.H., Hübner, J.F., Vieira, R.: Jason and the Golden Fleece of agent-oriented programming. In: Bordini, R.H., Dastani, M., Dix, J., El Fallah-Seghrouchni, A. (eds.) Multi-Agent Programming: Languages, Platforms and Applications, chap. 1, pp. 3–37. Springer, Berlin (2005)
Bordini, R.H., Fisher, M., Visser, W., Wooldridge, M.: Verifying multi-agent programs by model checking. J. Auton. Agents Multi Agent Syst. 12(2), 239–256 (2006)
Bordini, R.H., Hübner, J.F., Wooldridge, M.: Programming Multi-agent Systems in AgentSpeak Using Jason. Wiley, Hoboken, NJ (2007)
Bordini, R.H., Fisher, M., Wooldridge, M., Visser, W.: Property-based slicing for agent verification. J. Log. Comput. 19(6), 1385–1425 (2009)
Boyer, R.S., Moore, J.S. (eds.): The Correctness Problem in Computer Science. Academic Press, London (1981)
Branicky, M.S., Borkar, V.S., Mitter, S.: A unified framework for hybrid control: model and optimal control theory. IEEE Trans. Automat. Contr. 43(1), 31–45 (1998)
Bratman, M.E.: Intentions, Plans, and Practical Reason. Harvard University Press, Cambridge, MA (1987)
Bratman, M.E., Israel, D.J., Pollack, M.E.: Plans and resource-bounded practical reasoning. Comput. Intell. 4, 349–355 (1988)
Briand, X., Jeannet, B.: Combining control and data abstraction in the verification of hybrid systems. In: Formal Methods and Models for Codesign (MEMOCODE), pp. 141–150. IEEE Computer Society (2009)
Bujorianu, M.L.: Stochastic reachability analysis of hybrid systems. In: Communications and Control Engineering. Springer, London, UK (2012)
Clarke, E.M., Grumberg, O., Long, D.E.: Model checking and abstraction. ACM Trans. Program. Lang. Syst. 16(5), 1512–1542 (1994)
Clarke, E.M., Grumberg, O., Peled, D.: Model Checking. MIT Press, Cambridge, MA (1999)
Cohen, P.R., Levesque, H.J.: Intention is choice with commitment. Artif. Intell. 42, 213–261 (1990)
Courcoubetis, C., Vardi, M., Wolper, P., Yannakakis, M.: Memory-efficient algorithms for the verification of temporal properties. Form. Methods Syst. Des. 1, 275–288 (1992)
Damm, W., Disch, S., Hungar, H., Jacobs, S., Pang, J., Pigorsch, F., Scholl, C., Waldmann, U., Wirtz, B.: Exact state set representations in the verification of linear hybrid systems with large discrete state space. In: Proceedings of Automated Technology for Verification and Analysis, LNCS, vol. 4762, pp. 425–440. Springer (2007)
Dastani, M., van Riemsdijk, M.B., Meyer, J.J.C.: Programming multi-agent systems in 3APL. In: Bordini, R.H., Dastani, M., Dix, J., El Fallah-Seghrouchni, A. (eds.) Multi-Agent Programming: Languages, Platforms and Applications, chap. 2, pp. 39–67. Springer, Berlin (2005)
Davis, R., Smith, R.G.: Negotiation as a metaphor for distributed problem solving. Artif. Intell. 20(1), 63–109 (1983)
de Boer, F.S., Hindriks, K.V., van der Hoek, W., Meyer, J.J.C.: A verification framework for agent programming with declarative goals. J. Appl. Log. 5(2), 277–302 (2007)
DeMillo, R.A., Lipton, R.J., Perlis, A.J.: Social processes and proofs of theorems of programs. ACM Commun. 22(5), 271–280 (1979)
Dennis, L.A., Farwer, B.: Gwendolen: A BDI language for verifiable agents. In: Workshop on Logic and the Simulation of Interaction and Reasoning, AISB (2008)
Dennis, L.A., Farwer, B., Bordini, R.H., Fisher, M., Wooldridge, M.: A Common Semantic Basis for BDI Languages. In: Proceedings of the 7th International Workshop on Programming Multiagent Systems (ProMAS), LNAI, vol. 4908, pp. 124–139. Springer, Berlin (2008)
Dennis, L.A., Fisher, M., Lincoln, N., Lisitsa, A., Veres, S.M.: Declarative abstractions for agent based hybrid control systems. In: Proceedings of the 8th International Workshop on Declarative Agent Languages and Technologies (DALT), LNCS, vol. 6619, pp. 96–111. Springer, Berlin (2010a)
Dennis, L.A., Fisher, M., Lincoln, N., Lisitsa, A., Veres, S.M.: Reducing code complexity in hybrid control systems. In: Proceedings of the 10th International Symposium on Artificial Intelligence, Robotics and Automation in Space (i-Sairas) (2010b)
Dennis, L.A., Fisher, M., Lisitsa, A., Lincoln, N., Veres, S.M.: Satellite control using rational agent programming. IEEE Intell. Syst. 25(3), 92–97 (2010c)
Dennis, L.A., Fisher, M., Webster, M.P., Bordini, R.H.: Model checking agent programming languages. Autom. Softw. Eng. 19(1), 5–63 (2012)
Dennis, L.A., Fisher, M., Slavkovik, M., Webster, M.P.: Ethical choice in unforeseen circumstances. In: Proceedings Towards Autonomous Robotic Systems (TAROS), Oxford, UK (2013a)
Dennis, L.A., Fisher, M., Webster, M.P.: Using agent JPF to build models for other model checkers. In: Proceedings of Workshop on Computational Logic in Multi-Agent Systems (CLIMA), Corunna, Spain (2013b)
Durfee, E.H., Lesser, V.R., Corkill, D.D.: Trends in cooperative distributed problem solving. IEEE Trans. Knowl. Data Eng. 1(1), 63–83 (1989)
Emerson, E.A.: Temporal and modal logic. In: van Leeuwen, J. (ed.) Handbook of Theoretical Computer Science, pp. 996–1072. Elsevier, Amsterdam (1990)
Ezekiel, J., Lomuscio, A., Molnar, L., Veres, S.M., Peabody, M.: Verifying fault tolerance and self-diagnosability of an autonomous underwater vehicle. In: AI in Space: Intelligence beyond Planet Earth (IJCAI-11 Workshop) (2011)
Fetzer, J.H.: Program verification: the very idea. ACM Commun. 31(9), 1048–1063 (1988)
Fisher, M.: An introduction to practical formal methods using temporal logic. Wiley, Hoboken, NJ (2011)
Fisher, M., Dennis, L.A., Webster, M.P.: Verifying autonomous systems. ACM Commun. 56(9), 84–93 (2013)
Frehse, G.: PHAVer: algorithmic verification of hybrid systems past HyTech. In: Proceedings of Hybrid Systems: Computation and Control, LNCS, vol. 3414, pp. 258–273. Springer, Berlin (2005)
Frehse, G., Han, Z., Krogh, B.: Assume-guarantee reasoning for hybrid I/O-automata by over-approximation of continuous interaction. In: Proceedings of 43rd IEEE Conference on Decision and Control (CDC), vol. 1, pp. 479–484 (2004)
Gammie, P., van der Meyden, R.: MCK: model checking the logic of knowledge. In: Proceedings of the 16th International Conference on Computer Aided Verification (CAV), pp. 479–483. Springer, Berlin (2004)
Gerth, R., Peled, D., Vardi, M.Y., Wolper, P.: Simple on-the-fly automatic verification of linear temporal logic. In: Proceedings fo the 15th IFIP WG6.1 International Symposium on Protocol Specification, Testing and Verification, pp. 3–18. Chapman & Hall, London (1996)
Goebel, R., Sanfelice, R., Teel, A.: Hybrid dynamical systems. IEEE Control Syst. Mag. 29(2), 28–93 (2009)
Henzinger, T.A.: The theory of hybrid automata. In: Proceedings of the 11th Annual IEEE Symposium on Logic in Computer Science (LICS), pp. 278–292. IEEE Computer Society Press (1996)
Henzinger, T.A., Ho, P.H., Wong-Toi, H.: HYTECH: a model checker for hybrid systems. Int. J. Softw. Tools Technol. Transf. 1(1–2), 110–122 (1997)
Heuerding, A., Jäger, G., Schwendimann, M., Seyfried, M.: A logics workbench. AI Commun. 9(2), 53–58 (1996)
Hindriks, K.V., de Boer, F.S., van der Hoek, W., Meyer, J.J.: Agent programming in 3APL. Auton. Agent Multi Agent Syst. 2(4), 357–401 (1999)
Hindriks, K.V., de Boer, F.S., van der Hoek, W., Meyer, J.J.: Agent programming with declarative goals. In: Intelligent Agents VII (Proceedings of the 6th Workshop on Agent Theories, Architectures, and Languages), LNAI, vol. 1986, pp. 228–243. Springer, Berlin (2001)
Holzmann, G.: Spin Model Checker: Primer and Reference Manual. Addison-Wesley, Reading (2004)
Hunter, J., Raimondi, F., Rungta, N., Stocker, R.: A synergistic and extensible framework for multi-agent system verification. In: Proceedings of the 13th International Conference on Autonomous Agents and Multiagent Systems (AAMAS), pp. 869–876. IFAAMAS (2013)
Jones, C.B.: Tentative steps toward a development method for interfering programs. ACM Trans. Program. Lang. Syst. 5(4), 596–619 (1983)
Jones, C.B.: Systematic Software Development Using VDM. Prentice Hall Int, Englewood Cliffs (1986)
Jongmans, S.S.T.Q., Hindriks, K.V., van Riemsdijk, M.B.: Model checking agent programs by using the program interpreter. In: Proceedings of the 11th International Workshop on Computational Logic in Multi-Agent Systems (CLIMA), LNCS, vol. 6245, pp. 219–237. Springer, Berlin (2010)
Karim, S., Heinze, C.: Experiences with the design and implementation of an agent-based autonomous UAV controller. In: Proceedings of the 4th International Joint Conference on Autonomous Agents and Multiagent Systems (AAMAS), pp 19–26. ACM (2005)
Kitano, H., Tadokoro, S.: RoboCup rescue: a grand challenge for multiagent and intelligent systems. AI Mag. 22(1), 39–52 (2001)
Kohn, W., Nerode, A.: Multiple agent autonomous hybrid control systems. In: Proceedings of the 31st Conference on Decision and Control (CDC), Tucson, USA, pp. 2956–2964 (1992)
Kurucz, A.: Combining modal logics. In: Blackburn, P., van Benthem, J., Wolter, F. (eds.) Handbook of Modal Logic, pp. 869–924. Elsevier, Amsterdam (2006)
Kwiatkowska, M., Norman, G., Parker, D.: PRISM: probabilistic symbolic model checker. In: Proceedings of the 12th International Conference on Modelling Techniques and Tools for Computer Performance Evaluation (TOOLS), LNCS, vol. 2324. Springer, Berlin (2002)
Lamport, L.: Specifying Systems: The TLA+ Language and Tools for Hardware and Software Engineers. Addison Wesley, Reading (2003)
Lincoln, N.K., Veres, S.M.: Components of a vision assisted constrained autonomous satellite formation flying control system. Int. J. Adapt. Control Signal Process. 21(2–3), 237–264 (2006)
Lincoln, N.K., Veres, S.M., Dennis, L.A., Fisher, M., Lisitsa, A.: Autonomous asteroid exploration by rational agents. IEEE Comput. Intell. Mag. 8(4), 25–38 (2013)
Lomuscio, A., Qu, H., Raimondi, F.: MCMAS: a model checker for the verification of multi-agent systems. In: Proceedings of the 21st International Conference on Computer Aided Verification (CAV), LNCS, vol. 5643, pp. 682–688. Springer, Berlin (2009)
Lomuscio, A., Strulo, B., Walker, N., Wu, P.: Assume-guarantee reasoning with local specifications. In: Proceedings of the 12th International Conference on Formal Engineering Methods and Software Engineering (ICFEM), pp. 204–219. Springer, Berlin (2010)
Loos, S.M., Platzer, A., Nistor, L.: Adaptive cruise control: hybrid, distributed, and now formally verified. In: Proceeding of the FM, LNCS, vol. 6664, pp. 42–56. Springer, Berlin (2011)
Manna, Z., Pnueli, A.: The Temporal Logic of Reactive and Concurrent Systems: Specification. Springer, Berlin (1992)
McMillan, K.: Circular compositional reasoning about liveness. In: Pierre, L., Kropf, T. (eds.) Correct Hardware Design and Verification Methods, Lecture Notes in Computer Science, vol. 1703, pp. 342–346. Springer, Berlin, Heidelberg (1999). doi:10.1007/3-540-48153-2_30
Misra, J., Chandy, K.M.: Proofs of networks of processes. IEEE Trans. Softw. Eng. 7(4), 417–426 (1981)
Muscettola, N., Nayak, P.P., Pell, B., Williams, B.: Remote agent: to boldly go where no AI system has gone before. Artif. Intell. 103(1–2), 5–48 (1998)
Patchett, C., Ansell, D.: The development of an advanced autonomous integrated mission system for uninhabited air systems to meet UK airspace requirements. In: Proceedings of the International Conference on Intelligent Systems, Modelling and Simulation (ISMS), pp. 60–64 (2010)
Platzer, A.: Logical Analysis of Hybrid Systems: Proving Theorems for Complex Dynamics. Springer, Heidelberg (2010)
Pokahr, A., Braubach, L., Lamersdorf, W.: Jadex: a BDI reasoning engine. In: Bordini, R.H., Dastani, M., Dix, J., El Fallah-Seghrouchni, A. (eds.) Multi-Agent Programming: Languages, Platforms and Applications, pp. 149–174. Springer, Berlin (2005)
Păsăreanu, C.S., Giannakopoulou, D., Bobaru, M.G., Cobleigh, J.M., Barringer, H.: Learning to divide and conquer: applying the L* algorithm to automate assume-guarantee reasoning. Form. Methods Syst. Des. 32(3), 175–205 (2008)
Rao, A.: AgentSpeak(L): BDI agents speak out in a logical computable language. In: Agents Breaking Away: Proceedings of the 7th European Workshop on Modelling Autonomous Agents in a Multi-Agent World, LNCS, vol. 1038, pp. 42–55. Springer, Berlin (1996)
Rao, A.S., Georgeff, M.P.: Modeling agents within a BDI-architecture. In: Proceedings of the 2nd International Conference on Principles of Knowledge Representation and Reasoning (KR&R), pp. 473–484. Morgan Kaufmann, San Mateo, CA (1991)
Rao, A.S., Georgeff, M.P.: An abstract architecture for rational agents. In: Proceedings of the International Conference on Knowledge Representation and Reasoning (KR&R), pp. 439–449. Morgan Kaufmann, San Mateo, CA (1992)
Rao, A.S., Georgeff, M.P.: BDI agents: from theory to practice. In: Proceedings of the 1st International Conference on Multi-Agent Systems (ICMAS), San Francisco, USA, pp. 312–319 (1995)
Shoham, Y.: Agent-oriented programming. Artif. Intell. 60(1), 51–92 (1993)
Sierhuis, M.: Modeling and Simulating Work Practice. BRAHMS: a Multiagent Modeling and Simluation Language for Work System Analysis and Design. PhD thesis, Social Science and Informatics (SW), University of Amsterdam (2001)
Silva, P.S., Melo, A.C.: A formal environment model for multi-agent systems. In: Formal Methods: Foundations and Applications, LNCS, vol. 6527, pp 64–79. Springer, Berlin (2011)
Stocker, R., Dennis, L.A., Dixon, C., Fisher, M.: Verifying brahms human-robot teamwork models. In: Proceedings of the 13th European Conference on Logics in Artificial Intelligence (JELIA), LNCS, vol. 7519, pp. 385–397. Springer, Berlin (2012)
Tabuada, P.: Verification and Control of Hybrid Systems: A Symbolic Approach. Springer, Berlin (2009)
Tiwari, A.: Abstractions for hybrid systems. Form. Methods Syst. Des. 32, 57–83 (2008)
van Riemsdijk, M.B., Dastani, M., Meyer, J.J.: Goals in conflict: semantic foundations of goals in agent programming. Auton. Agent Multi Agent Syst. 18(3), 471–500 (2009)
Varaiya, P.: Design, simulation, and implementation of hybrid systems. In: Proceedings of the 20th International Conference on Application and Theory of Petri Nets (ICATPN), LNCS, vol. 1639, pp. 1–5. Springer, Berlin (1999)
Visser, W., Havelund, K., Brat, G.P., Park, S., Lerda, F.: Model checking programs. Autom. Softw. Eng. 10(2), 203–232 (2003)
Webster, M.P., Fisher, M., Cameron, N., Jump, M.: Formal methods for the certification of autonomous unmanned aircraft systems. In: Proceedings of the 30th International Conference on Computer Safety, Reliability and Security (SAFECOMP), LNCS, vol. 6894, pp. 228–242. Springer, Berlin (2011)
Wei, C., Hindriks, K.V.: An agent-based cognitive robot architecture. In: Programming Multi-Agent Systems, LNCS, vol. 7837, pp. 54–71. Springer, Berlin (2013)
Wooldridge, M.: An Introduction to Multiagent Systems. Wiley, Hoboken, NJ (2002)
Wooldridge, M., Rao, A. (eds.): Foundations of Rational Agency. Applied Logic Series. Kluwer Academic Publishers, Dordrecht (1999)
Acknowledgments
This research was partially funded by Engineering and Physical Sciences Research Council grants EP/F037201 and EP/F037570, and primarily occurred while the third and fifth authors were at University of Southampton. Our thanks go to a number of anonymous referees who have both improved the paper and made suggestions that will inform our thinking in future.
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix 1: Code for LEO satellite example
1.1 Appendix 1(a): A satellite agent
The code in this section is for an agent that is in direct control of a single satellite but which receives information on formations from a separate, coordinating, leader agent.
1.1.1 Appendix 1(i): The abstraction engine
It should be noted that, while we believe a BDI-style programming language to be an appropriate implementation language for \(R\), the Reasoning Engine, we are investigating the use of stream processing languages for \(A\), the Abstraction Engine. This is the subject of ongoing work. In the example here, however, the abstraction engine is programmed in our variant of the Gwendolen language.
Code for the Abstraction Engine, \(A\), is shown in Listing 6. We use standard BDI syntax, as described previously, extended with new constructs for manipulating the shared beliefs. \(+_{\Sigma }\) b and \(-_{\Sigma }\) b are used to indicate when an agent adds b to or removes b from the set of shared beliefs.
The code is split into roughly three sections for abstraction, reification and housekeeping (not shown). The key aim for this satellite is to take up a position in a formation of satellites. Lines 1–14 provide code for generating abstractions. As information about the satellite’s current location arrives from \(\varPi \) (via ‘stateinfo’) the agent (if it does not already believe itself to be in location ‘close_to(Pos)’) requests the calculation of the distance from its desired location (via comp_distance) which returns a judgment of whether the agent is “close enough” to the target position. This is then used to assert a shared belief about whether the agent is in position or not.
Similarly, information about the thruster status is used in lines 8–14. Thruster information arrives via perception as ‘thruster(X,L1,L2,P,C,V)’ which gives information about the pressure on the two incoming fuel lines (L1 and L2) and the output fuel line (P) as well as the current (C) and voltage (V) in thruster X. Based on this information, particularly the observation that the output fuel pressure has dropped below 1, the agent can assert or retract shared beliefs about whether a particular thruster is broken (lines 10 and 12).Footnote 11
The reification code in lines 18–42 tells the abstraction engine how to respond to requests for calculations or actions from the Reasoning Engine, \(R\), e.g., a request to ‘get_close_to’ is translated into a calculation request to \(\varOmega \) to call the function ‘plan_named_approach_to_location_multi’. The details of this code are of less interest in terms of verification of the Reasoning Engine, since they describe its effects upon the rest of the system rather than the external system’s effect on the Reasoning Engine. However, it is worth noting that some of these effects still involve the assertion of new shared beliefs (e.g., in lines 19–22, when the abstraction engine has a response to its calculation from the Continuous Engine it asserts the value of this response as a shared belief get_close_to(Pos, P)). Similarly it can be seen that a request to change fuel line (i.e., ‘change_line’ at line 36–43) involves setting several valves (‘run’ takes two arguments, the name of a MatLab function and a list of arguments to be supplied to that function. ‘pred’ allows a MatLab function call name to be composed from a number of strings), modifying the shared beliefs about which fuel line is being used (‘thruster_bank_line’), and then waiting for any change to take effect before asserting a shared belief that the thruster should no longer be broken. Note that, at this point, if the pressure is still low on the output fuel line then the shared belief that the thruster is broken will be reasserted the next time thruster data is perceived.
Finally, the housekeeping code handles some details of abstracting specific thruster information sent by \(\varPi \) into more generic information which passes the name of the thruster as a parameter, and the code for handling waiting. This is omitted from the code fragment shown.

Note that we can read off the changes in the shared beliefs of the system that may arise simply by looking for the occurrences of \(+_{\Sigma }\) and \(-_{\Sigma }\) that occur in the above code.
1.1.2 Appendix 1(ii): The reasoning engine
Code for the Reasoning Engine, \(R\), is shown in Code fragment 7. We use the same syntax as we did for the Abstraction Engine, \(A\), and for the rescue robots in Sect. 3. We additionally use the construction ‘*b’ to indicate that processing of a plan should suspend until some belief, b, becomes true. Here the actions, ‘perf’ and ‘query’, are interpreted by the environment as messages to \(A\) to adopt a goal. Calls to query pause execution of the plan in order to wait for a shared belief indicating a response from the calculation engine. The plans that are triggered in the abstraction engine by perf and query can be seen in the reification part of \(A\)’s code.
In the Reasoning Engine we use both achieve and perform goals (Riemsdijk et al. 2009). Achieve goals persist in the agent’s goal base until it believes them to be true, so plans for achieve goals may be enacted several times until they succeed. Perform goals, on the other hand, disappear once a plan associated with them has been executed and contain no implicit check that they have succeeded.
The code for \(R\) has several plans and one belief rule. A belief rule is a Prolog-style rule used for deducing beliefs. In this case it deduces that a thruster failure is repairable if the thruster is currently using the first fuel line.
assuming_formation (lines 6–10) is a perform goal that runs the agent through some general initialisation, i.e., finding the formation to be assumed (if not already known) and the agent’s position in that formation and then starting an attempt to achieve that position. The agent can either start out with the goal of assuming a formation, or can be sent the goal as a request from another agent.
Lines 12–20 of code handle instructions from a leader agent to drop the attempt to assume the current formation.
Lines 22–24 deal with converting any new beliefs (typically received from messages sent by a coordinating leader agent) about the position the agent is required to adopt (position) into a belief that the agent actually wants to adopt that position (my_position_is). Once a position has been adopted by the agent then no other suggestion is accepted.
none informs the agent that it is not needed for this formation and so it immediately asserts a belief that it is maintaining the desired position.
Lines 26–36 handle moving to a position, one case involves the agent requesting a plan to get there and the other case assumes the agent already has a plan.
Lines 39–56 handle the agent’s plans for getting into a state where it is maintaining a position, while handling possible aborts. Once it believes it is in the right place in the formation it will instruct the Abstraction Engine to initiate position maintenance procedures, perf(maintain_path). If it is not in the right place it sets up a goal to get there +!in_position(Pos) [achieve]. If a thruster is broken, but the system has not yet aborted, then the agent waits for the thruster to be fixed (because maintaining(Pos) is an achieve goal, once this plan is completed when the thruster is fixed, the agent will then select a different plan to achieve the move into position). Lastly if the system is aborted the agent will wait for new instructions. If the satellite successfully reaches a position then it will perform +! cleanup to remove any interim beliefs it has generated such as which plans it has and whether it is attempting to assume a formation.
Lines 57–60 involve informing a leader agent once the agent is maintaining its position. Lines 61–71 handle thruster failures either by attempting a repair or by aborting. Lines 73–85 handle aborts by dropping any goals to maintain a position, informing a leader agent of the abort and getting the satellite to cease any attempt to maintain a position. ‘perf(null)’ switches off the satellites thrusters, effectively stopping any maneuver it is attempting.

We have omitted from the code the initial beliefs and goals of the agent. The configuration of those beliefs and goals creates a number of different agents which we used during testing. For instance, if the agent already has beliefs about the formation that has been chosen and its position within that formation then it does not need to request information from the leader agent. Some initialisation and clean up code has also been omitted.
The architecture lets us represent the high-level decision making aspects of the system in terms of the beliefs and goals of the agent and the events it observes. So, for instance, when the Abstraction Engine, \(A\), observes that the thruster line pressure has dropped below 1, it asserts a shared belief that the thruster is broken. When the Reasoning Engine, \(R\), observes that the thruster is broken, it changes fuel line. This is communicated to \(A\), which then sets the appropriate valves and switches in the Physical Engine, \(\varPi \).
1.2 Appendix 1(b): A leader agent
Listing 8 shows a lead agent, aglead, which determines the position of other agents in a formation. This agent has several belief rules that are designed to establish that all agents have been informed of their positions in the formation (all_positions_assigned is true if there is no position in the formation which is not the position of an agent). The belief rule for desired_formation has two configurations: one in which the only formation to be attempted is a line; and the other in which the agent will start out attempting a square, and then change to a line. The belief one_formation determines which configuration is adapted and can be used to generate different agents from the same code.
Lines (15–24) handle the selection of a formation to be adopted and any clean-up of old formation choices, etc., that are required (sub-plans for achieving this clean-up are not shown).
The plan for in_formation (lines 26–31) is where most of the work happens. First, the leader chooses positions for all the agents in the system and informs them of their position. Then it informs all the agents of the formation to be adopted and waits for the other agents to tell it when they have reached their positions.
Lines 33–36 show the code for assigning positions. While there is an agent who has no position, and a position in the formation that has no agent assigned, the leader will assign that agent to that position and inform the agent of this fact. Since all_positions_assigned is an achieve goal, the plan continues to be selected until either there are no more available agents or no more available positions. The plan for inform_start (not shown) works in a similar way.
The description in Listing 8 is simplified from the actual code used. In particular we have omitted those parts that handle messages from follower agents, which report failures and aborts; we will not consider these aspects in the discussion of verification here.

Appendix 2: Adaptive cruise control: the abstraction engines
Listing 9 shows the abstraction engine for our simple example where a car attempts to drive a the speed limit in a single lane. As sensor input the abstraction engine receives the speed of the car and the acceleration dictated by pressure on the acceleration or brake pedals. It is also informed whether it is currently a safe distance from the car in front. These inputs are passed on to the Reasining Engine as shared beliefs in lines 1–14. Lines 16–20 handle instructions from the rational engine. Where the driver is using the acceleration or brake pedal the driver’s values are used for acceleration or braking, otherwise a simple accelerating or braking command is used and a random value invoked in the simulation.

Listing 10 shows the abstraction engine used in the lane changing example. The sensors now provide information about which lane car is in, the distance to the cars in front in both the current lane and the lane to the left, and whether the car is currently crossing lanes (i.e., maneuvering from one lane to another). The agent has an initial belief about close a car should be to justify initiating an overtaking maneouvre.

Appendix 3: Logics workbench input
The Logics Workbench is an interactive system aiming to facilitate the access to logic formalisms. It can be accessed online from an input shell currently located at http://www.lwb.unibe.ch/shell/.
We represented the agent concepts as propositions so \(\mathrm {\mathbf {B}}_{s} \, \mathsf {human}\) became bh, \(\mathrm {\mathbf {B}}_{a} \, at(0,0)\) became ba00, \(at(human,0,0)\) became ah00, \(at(robot, 0, 0)\) became ar00 and so on.
This allowed us to simply represent the hypotheses and theorems from Sect. 3. For instance \(\mathsf {found\_human}\) in (3) became

We defined each of the hypotheses in this way and then used provable to prove the theorem. The sequence of commands used were:

We proved (10) in a similar fashion with bsf representing \(\mathbf {B}_s \mathsf {found}\), bss representing \(\mathrm {\mathbf {B}}_{s} \, \mathsf {sent(lifter, human(X, Y))}\), blr representing \(\mathrm {\mathbf {B}}_{l} \, \mathsf {rec(searcher, human(X, Y))})\), and blf representing \(\mathbf {B}_l \mathsf {free(human)}\). The sequence of commands used were:

Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution License which permits any use, distribution, and reproduction in any medium, provided the original author(s) and the source are credited.
About this article
Cite this article
Dennis, L.A., Fisher, M., Lincoln, N.K. et al. Practical verification of decision-making in agent-based autonomous systems. Autom Softw Eng 23, 305–359 (2016). https://doi.org/10.1007/s10515-014-0168-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10515-014-0168-9