Position and velocity sensitivities at the triangular libration points in the restricted problem of three bodies when the bigger primary is an oblate body

Abstract

In this paper we have examined the stability of triangular libration points in the restricted problem of three bodies when the bigger primary is an oblate spheroid. Here we followed the time limit and computational process of Tuckness (Celest. Mech. Dyn. Mech. 61, 1–19, 1995) on the stability criteria given by McKenzie and Szebehely (Celest. Mech. 23, 223–229, 1981). In this study it was found that in comparison to other studies the value of the critical mass μ _c has been reduced due to oblateness of the bigger primary, i.e. the range of stability of the equilateral triangular libration points reduced with the increase of the oblateness parameter I and hence the order of commensurability was increased.

1 Introduction

It is well established that the libration points in the Restricted three-body problem are infinitesimally stable or linearly stable for the values of the mass ratio μ<μ _c =0.038521… , the critical mass. Leontovich (1962) established the non-linear stability of the triangular libration points and proved that the triangular libration points L ₄ and L ₅ are stable for all values of μ<μ _c except for a set of measure zero, where μ _c is the Rouths critical mass of the Restricted three-body problem.

Breakwell and Pringle (1965) discussed the motion of the third body around L ₄ in the Earth-Moon system using Von Zeipel’s method with an additional effect of the Sun’s gravitation. Also he did a detailed study of the stability of the triangular libration points.

Deprit and Palmore (1966), Deprit and Deprit-Bartholome (1967), Deprit et al. (1967), Markeev (1969) all discussed stability of triangular libration points with different methods and also established the order of commensurability of the long periodic and short periodic orbits. Alfriend (1970) and Nayfeh (1971) justified the work of Markeev (1969) that L ₄ is an unstable equilibrium point where the long periods and short periods of motion around L ₄ have commensurability 2 to 1.

Henrard (1970) established that the family of long periodic orbits at L ₄ does not evolve in a continuous manner with the mass ratio. Discontinuity appears not only at the mass ratios for which the long period of the equilibrium is a multiple of the short periods, but also at mass ratios when the global analysis of the family detects singular bifurcation orbits. Markeev (1973) and Sokol’skii (1975) studied the stability of the Lagrange solutions for the critical mass μ _c .

McKenzie and Szebehely (1981) introduced a new idea to test the stability of the equilateral triangular libration point L ₄. They defined the maximum velocity and maximum displacement envelopes within which the third body remains for a long time starting from the suitable initial conditions so that the third body may not cross the x-axis. The conditions of not crossing the x-axis were introduced as the stability criteria for the third body. By using all the stability criteria of McKenzie and Szebehely (1981), Tuckness (1995) excellently, investigated numerically the sensitivities of the third body around L ₄ when it is given positional and velocity deviations away from L ₄ with a suitable initial conditions. He used Poincare’s surface of sections to compare the periodic, quasi-periodic and stochastic regions to the trajectories with the definitions of stability given by McKenzie and Szebehely (1981). Moreover he also investigated the value of μ (the mass ratio) ranging from zero to linear critical mass 0.038521…. Using the stability criteria he determined some values of μ which are more stable than the others.

Here we extend the study of Tuckness (1995) for analyzing the effect of oblateness of the bigger primary on the stability of L ₄. All the other conditions and criteria will remain the same as those chosen by McKenzie and Szebehely (1981) and Tuckness (1995).

2 The equations of motion of the third body

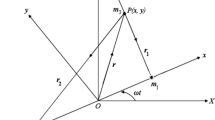
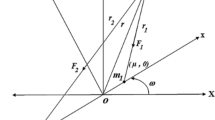
The equations of motion of the third body moving in the gravitational field of the two primaries, are

(1)

where

(2)

with

(3)

(4)

n is the mean angular velocity of the primaries about their centre of mass; I=A ₁−A ₃= oblateness parameter (0<I≪1); $A_{1} = \frac{a^{2}}{5R^{2}}=$ the moment of inertia of the oblate body about the equatorial radius; $A_{3} = \frac{c^{2}}{5R^{2}}=$ the moment of inertia of the oblate body about the polar radius; and

(5)

3 Location of libration points

For location of libration points the Jacobi’s integral (or Jacobi’s manifold) is

$$\dot{x}^{2} + \dot{y}^{2} - 2\varOmega (x,y) + C = 0, $$

where C is called Jacobi’s constant.

Libration points are the singularities of the manifold,

(6)

Following Szebehely (1967), Bhatnagar and Chawla (1977) the equilateral triangular libration points are given as

$$L_{4, 5} \equiv \biggl( \mu - \frac{1}{2} - \frac{3I}{2 ( 1 - \mu )}, \pm \frac{\sqrt{3}}{2} \biggl[ 1 + \frac{1 + 2\mu}{3 ( 1 - \mu )}I \biggr] \biggr). $$

4 Mathematical formulation for critical mass

Let (a, b) be the coordinates of the triangular libration point L ₄. Let ξ,η be the small variations in a & b respectively due to oblateness of the bigger primary, then (a+ξ,b+η) is a point in the vicinity of (a, b). Thus the variational equations of motion of the third body are given by

(7)

where

and

$$a = \mu - \frac{1}{2},\qquad b = \pm \frac{\sqrt{3}}{2}. $$

Let ξ=Pe ^λt&η=Qe ^λt be two particular solutions of the Eqs. (7), then the characteristic equation for the triangular libration points is

(8)

where λ ²=∧,

(9)

(10)

Let ∧₁ and ∧₂ be the roots of the Eq. (8), then

(11)

(12)

i.e.

(13)

Equation (13) is a quadratic equation in μ so the roots of this equation will give the critical value of the mass parameter μ. If μ _c is the critical value of μ then

(14)

If I=0, $\mu _{c} = \frac{1}{2} [ 1 - \sqrt{1 - \frac{16k^{2}}{27(k^{2} + 1)^{2}}} ]$ (McKenzie and Szebehely 1981 and Tuckness 1995).

4.1 Numerical integration

The numerical integration in this work were carried out using the classical fourth order Runge-Kutta method with automatic step-size control. The specified accuracy was at least eight or more significant decimal digits and double precision arithmetic was used in all computations. Tests were performed with different levels of accuracy and the specified accuracy was found to be sufficient for this study.

The Jacobian constant was calculated in order to observe the validity of the trajectory generations throughout the numerical integration. This constant of integration was checked to make sure that it remained constant to at least eight decimal places.

For numerical integration, we introduce $x = x_{1},y = x_{2},\dot{x} = x_{3},\dot{y} = x_{4}$ and reduce the two second order differential equations of motion given in (1) to the four first order differential equations as:

$$ \left . \begin{array}{l} \frac{dx_{1}}{dt} = x_{3}, \\[6pt] \frac{dx_{2}}{dt} = x_{4}, \\[6pt] \frac{dx_{3}}{dt} = 2nx_{4} + \frac{\partial \varOmega}{\partial x_{1}}, \\[6pt] \frac{dx_{4}}{dt} = - 2nx_{4} + \frac{\partial \varOmega}{\partial x_{2}}. \end{array} \right \} $$

(15)

with $r_{1}^{2} = (x_{1} - \mu )^{2} + x_{2}^{2}\& r_{2}^{2} = (x_{1} - \mu + 1)^{2} + x_{2}^{2}$.

4.2 Time limit for numerical integration

The study of the time limit was first undertaken by McKenzie and Szebehely (1981). The value of μ used in their study was μ=0.01214 (Earth-Moon system). The selection of the time interval t _f for the numerical integration was determined by examining the effect of t _f on the maximum distance that the third body was started from L ₄ along two given lines before its motion crossed the x-axis. As seen in Fig. 1, the first line points $120^{^{\circ}}$ away from L ₄ and the origin of the coordinate system. The second line is inclined at 300^∘ with respect to the x-axis, pointing toward the origin of the coordinate system. The dimensionless values of t _f they chose to study were:t _f =120, 240, 360, 480, 600, 720, 840, 960, corresponding to 564, 1128, 1692, 2256, 2820, 3384, 3948, and 4512 days for the Earth-Moon system. From Fig. 2, it can be seen that, as the time of integration increases, the maximum distance the third body may be displaced initially from L ₄ for librational motion to take place decreases. Also in Fig. 2 the maximum values of the initial velocity as a function of integration time is shown. After the first large change in the distance between 120 and 240 time units, the effect of the final time of integration appears to change the initial velocity by only small amounts. Since accuracy of the numerical integration becomes more questionable with an increase in the time of integration hence a reasonable value of t _f =600 is taken.

Fig. 1

Conditions for the time limit study

Fig. 2

Results of time limit study

By using Runge-Kutta method, further investigations were carried out by Tuckness (1995) with two other values of μ=0.0027 and μ=0.025, for θ=10^∘, 20^∘, 30^∘, 40^∘,…,360^∘. The values of μ=0.0027 and μ=0.025 were chosen because of the nature of maximum displacement and maximum velocity envelopes take place, whereas in our case, for the same values of θ and the same time limit (as in Tuckness), the two values of μ were reduced to μ=0.0026 and μ=0.024 due to the oblateness parameters I=0.01. For I=0.1 the corresponding value of μ is given by μ=0.024 for maximum velocity and displacement and two values of μ=0.012 and μ=0.021 were investigated for nearly non-librational motion around L ₄. In short, the area of the maximum velocity and maximum displacement envelope for μ=0.0026 is a maximum and a minimum for μ=0.024. As McKenzie and Szebehely (1981) and Tuckness (1995) four different values of t _f were investigated, t _f =100, 600, 1000, and 2000 dimensionless time units for both the maximum velocities and maximum displacements.

For both μ=0.0026 and μ=0.024 all values of t _f greater than 100 gave maximum displacement results within 0.001 dimensionless units of each other. For both μ=0.0026 and μ=0.024, all values of t _f greater than 100 resulted in the maximum velocities being within 0.01 dimensionless velocity units. Also, as the values of t _f increased, the differences in the magnitude of the maximum displacements and velocities decreased. At 1000 dimensionless time units only negligible differences existed on the order of 0.0001 for the maximum displacements and 0.001 for the maximum velocities. Therefore the same results are found for any value of t _f ≥1000. The value of t _f =100 did not allow enough time for the third body to librate around to the x-axis. This allowed much larger velocity and positional deviations. Therefore, from the studies undertaken by McKenzie and Szebehely (1981), Tuckness (1995) and from our investigations t _f =1000, dimensionless time units would be an acceptable integration time duration for μ=0.0026 and μ=0.024.

4.3 Comparison of maximum velocity and maximum displacement envelopes using Poincare’s surface of sections

In this section the maximum velocity and maximum displacement envelopes boundary values were investigated using time limits for numerical integration given by Tuckness (1995) and Poincare’s surface of sections. For this we need Hamilton’s equations of motion to be defined as follows:

Let at any time t, (x ₁,x ₂) be the position of the third body with momenta p ₁ and p ₂, then

(16)

Now the time rate of change of phase variables are:

(17)

Thus

(18)

The Hamiltonian is given by

(19)

A solution of the Hamiltonian equations of motion (18) can be represented as a trajectory in a four dimensional phase space. Because of the existence of the integral of motion Eq. (19), the trajectory lies in a three-dimensional subspace (H) which is equal to a constant of the phase space. The successive intersection of this three-dimensional trajectory with a two dimensional surface is called Poincare’s surface of section. The successive intersections of the 3-D trajectory with the surface $y = \frac{\sqrt{3}}{2} [ 1 + \frac{1 + 2\mu}{3 ( 1 - \mu )}I ]$ was taken for Poincare’s surface of section in $( x,\dot{x})$ or (x ₁,p ₁) plane, the results can be represented in a much more compact manner. There is no serious loss of information, because the most interesting trajectories of the projection are reflected in the corresponding properties of the set of points.

In case of Tuckness (1995) the phase space can be divided into three regions. One region contains primarily stochastic trajectories. It is connected to a second region containing large embedded islands. A third region consists of primarily regular trajectories and is isolated from the first two regions. From the Fig. 3 the phase space can be divided into three regions. One region contains stochastic trajectories not connected with the second region because of rare embedded islands due to oblateness parameter I. The third region contains primarily regular trajectories which are isolated from the first two regions. The maximum velocity and maximum displacement were investigated using the Poincare’s surface of sections method for various values of μ. Initial velocities and positions from the maximum velocity and maximum displacement envelopes were numerically integrated using Hamilton’s equations of motion from (16) to (19) and their intersection with the surface $y = \frac{\sqrt{3}}{2} [ 1 + \frac{1 + 2\mu}{3 ( 1 - \mu )}I ]$ were plotted. The equations of motion were integrated for 500 to 2000 orbits (or intersection) using the same Runge-Kutta integrator explained above and only the orbits for y>0 were plotted.

Fig. 3

Surface of Poincare section for μ=0.001, θ=108^∘

The velocity VL ₄=0.444 is the value of maximum velocity envelope in the 108^∘ direction which was found using the stability criteria under consideration. Figure 3 is the Poincare’s surface of section investigated for μ=0.001, θ=108^∘. Velocities greater than VL ₄=0.444 result in unstable motion according to the boundary envelopes established in the study. Velocities less than 0.444 are contained within the surfaces of boundary envelops depicted in Fig. 3. Also areas of apparent quasi-periodic solutions can be investigated from the Fig. 3 but it is too difficult to show.

Figure 4 depicts the Poincare surfaces of section investigated for μ=0.001, θ=0^∘ and maximum initial displacement allowed. In the enlarged view the chaotic regions had been reduced in comparison of Tuckness due to oblatness I.

Fig. 4

Surface of Poincare section for μ=0.001, θ=0^∘

4.4 Determination of stability of the third body using the maximum velocity and displacement envelopes

As seen earlier in this study, the sizes of the maximum velocity and maximum displacement envelopes vary according to the value of μ, I, the final time limit t _f and the boundary chosen. Since the final time limit t _f =1000 (as in Tuckness) is used in this study and the boundary is the x-axis (as in McKenzie et al.) so these two variables remain fixed. Therefore the size of the maximum velocity and maximum displacement envelopes varies according to μ & I. As seen from the previous section, when with the increase of I (oblateness) μ decreases, the maximum velocity and maximum displacement envelopes become more narrow.

The maximum velocity and displacement envelopes consisting of initial velocities and displacements respectively away from L _4, where according to previous definition, stable librational motions result. One could also say that arriving at L ₄ with the velocity and direction of the maximum velocity allowed would give the same results. Therefore, the maximum velocity envelope above would be thought of as maximum velocity arrival error envelopes, which could be thought of as the maximum displacement arrival error envelope. One could also think of the value of μ, which allowed the most arrival velocity error at L ₄, as being the most stable value of μ for arriving at velocity errors. Again, the same is true for the maximum displacement envelope.

The value of μ and I which allows the total amount of displacement error (all the displacement vectors of the maximum displacement envelope summed up) will have a maximum displacement envelope with the greatest enclosed area. Tuckness (1995) calculated the area of the displacement envelopes by considering the formula πab, where a and b are semi-major axis and semi-minor axis respectively. Also he considered the maximum displacement envelopes as the symmetric and uniform ellipse but the displacement envelopes are neither symmetric nor uniform. So we calculated the displacement envelope and velocity envelope by considering the formula $\frac{1}{2}\int r^{_{2}}d\theta$ with the limits of θ, the initial point of envelope to the final point of envelope.

Because the estimated area of the envelopes is a measure of stability, a comparison can be made on how stability varies according to the values of μ & I. According to Figs. 7 and 8, μ=0.0026 gives the maximum area for both the velocity and displacement envelopes for I=10⁻² and μ=0.024 gives the maximum velocity and displacement envelopes for I=10⁻¹. It was also found in Figs. 7 and 8 that μ=0.024 approximately has nearly zero area in both the maximum velocity and displacement envelopes for I=10⁻² while μ=0.012 and μ=0.023 both represent nearly zero displacement and velocity for I=10⁻¹. This helps to reinforce the ideas in the previous section that motion of the third body for values of μ=0.024 and 0.023 approximately are non-librational or unstable for I=10⁻², I=10⁻¹ respectively. In other words, for μ=0.024 and 0.023 approximately, very little velocity or displacement away from L ₄ will allow the third body to stay around L ₄ instead, it will cross the x-axis.

These appear to be distinct minimums which depict that librational motion is difficult to achieve. The minimums marked on Figs. 7 and 8 show a distinct relation to the values of μ and I which are related to the critical values; namely for three to one commensurability μ _c =0.0135160160, 0.0135156540, 0.0135065589, 0.0134260594 and for two to one commensurability the critical masses are μ _c =0.02429389714, 0.0242921132, 0.0242761497, 0.024125161 corresponding to I=0, 10⁻⁴, 10⁻³, 10⁻² respectively.

Following Pedersen (1933), Deprit and Deprit-Bartholome (1967) and Deprit et al. (1967) the ratio of the long period and short period orbits,

(20)

(21)

The expression for k ² as in (11) and value of μ _c as in (14) show that the frequency of occurrence of the critical values of the mass parameter increases as μ approaches zero.

From Eq. (11) we can calculate the values of μ for different values of I and that achieves an integer ratio between s ₁ and s ₂ (Table 1).

Table 1 Order of commensurability

The k values of one to seven are depicted in Figs. 7 and 8 which indicate an exponentially decreasing curve as a function of μ and I. From this observation it may be possible to arrive at an analytical expression that is the function of μ and I which governs the stability around the triangular libration point for the specific values of μ and I.

The curves that depict the areas of maximum velocity and displacement envelopes in Figs. 7 and 8 appear to have the same mathematical characteristic differing only in amplitude.

5 Conclusion

From Figs. 5 & 6 and graphs 7, 8, 9 & 10 we conclude that the range of stability reduces with the increase of oblateness parameter I. In other words we can say that with increase of I, the order of commensurability k increased. Ultimately the long period and short period will be changed due to I. The discussion can also be corroborated by the Table 1.

Fig. 5

Maximum displacement envelopes for μ=0.1214, I=0, 10⁻² (Earth-Moon system)

Fig. 6

Maximum velocity envelopes for μ=0.1214, I=0,10⁻² (Earth-Moon system)

Fig. 7

Area of maximum velocity envelopes versus μ

Fig. 8

Area of maximum displacement envelopes versus μ

Fig. 9

Graph of critical mass versus I

Fig. 10

Plotting of critical values versus commensurability