Effect of Flow Structures on Turbulence Statistics of Taylor-Couette Flow in the Torque Transition State

Abstract

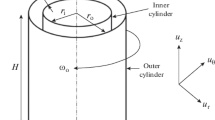
Direct numerical simulations of Taylor-Couette flow from R e= 8000 to 25000 have been conducted to investigate changes of turbulence statistics in the transition of the Reynolds number dependency of the mean torque near R e= 10000. The velocity fluctuations are decomposed into the contributions of the Taylor vortex and remaining turbulent fluctuations. Significant Reynolds number dependencies of these components are observed in the radial profiles of the Reynolds stress and the transmission of the mean torque. The contributions of Taylor vortex and turbulent components in the net amount of mean torque are evaluated. The Taylor vortex component is overtaken by the turbulent counterpart around R e= 15000 when they are defined as the azimuthally averaged component and the remnants. The results show that the torque transition can be explained by the competition between the contributions of azimuthally averaged Taylor vortex and the remaining turbulent components.

Appendix: A Relation between the Torque Transmission and the Net Mean Torque

A relation between the torque transmission in Eq. 3 and the net mean torque in Eq. 4 can be derived in the following steps. The local force in the azimuthal direction driving infinitesimal volume of fluid is written as Eqs. 9 and 10 when they are averaged in azimuthal and axial directions and in time.

$$\begin{array}{@{}rcl@{}} \frac{D\langle {\langle {u_{\theta}} \rangle_{\theta}} \rangle_{z}}{Dt} &=& \frac{1}{r^{2}}\frac{\partial}{\partial r} \left( r^{2}\langle {\langle {u_{r}u_{\theta}} \rangle_{\theta}} \rangle_{z}\right) \end{array} $$

(9)

$$\begin{array}{@{}rcl@{}} &=& \frac{1}{Re}\frac{1}{r^{2}}\frac{\partial}{\partial r} \left( r^{3}\frac{\partial}{\partial r}\frac{\langle {\langle {u_{\theta}} \rangle_{\theta}} \rangle_{z}}{r}\right) \end{array} $$

(10)

〈〈u _r u _θ 〉 _θ 〉 _z in the right hand side of Eq. 9 is equal to R _{r θ} $=\langle \langle {u_{r}^{\prime }u_{\theta }^{\prime }\rangle _{\theta }\rangle }z$ since 〈〈u _r 〉 _θ 〉z=0. Equations 9 and 10 give the expression of the Reynolds stress and the viscous terms for the driving force as follows,

$$\begin{array}{@{}rcl@{}} \langle {\langle {u_{r}^{\prime}u_{\theta}^{\prime}} \rangle_{\theta}} \rangle_{z} &=& {\int}_{r_{\mathrm{i}}}^{r} \frac{D\langle {\langle {u_{\theta}} \rangle_{\theta}} \rangle_{z}}{Dt} dr -2{\int}_{r_{\mathrm{i}}}^{r} \frac{\langle {\langle {u_{r}^{\prime}u_{\theta}^{\prime}} \rangle_{\theta}} \rangle_{z}}{r} dr \end{array} $$

(11)

$$\begin{array}{@{}rcl@{}} \frac{1}{Re}r\frac{\partial}{\partial r}\frac{\langle {\langle {u_{\theta}} \rangle_{\theta}} \rangle_{z}}{r} &=& {\int}_{r_{\mathrm{i}}}^{r} \frac{D\langle {\langle {u_{\theta}} \rangle_{\theta}} \rangle_{z}}{Dt} dr + \frac{1}{Re} r_{\mathrm{i}} \frac{\partial}{\partial r}\frac{\langle {\langle {u_{\theta}} \rangle_{\theta}} \rangle_{z}}{r}\bigg|_{r=r_{\mathrm{i}}} -2 \frac{1}{Re} {\int}_{r_{\mathrm{i}}}^{r} \frac{\partial}{\partial r}\frac{\langle {\langle {u_{\theta}} \rangle_{\theta}} \rangle_{z}}{r} dr . \end{array} $$

(12)

Then Eq. 13 can be derived by substituting Eqs. 11 and 12 into Eq. 3

$$ \left( 1-\frac{r^{2}}{r_{\mathrm{i}}^{2}} \right) G(r) = -2r^{2} {\int}_{r_{\mathrm{i}}}^{r} \frac{1}{r^{3}} \left( r^{2}\langle {\langle {u_{r}^{\prime}u_{\theta}^{\prime}} \rangle_{\theta}} \rangle_{z} - \frac{1}{Re}r^{3}\frac{\partial}{\partial r}\frac{\langle {\langle {u_{\theta}} \rangle_{\theta}} \rangle_{z}}{r} \right) dr . $$

(13)

Here the second term of the right hand side in Eq. 12 can be transformed to $r^{2}/{r^{2}_{i}}G(r)$ using Eq. 3 at r = r _i . By considering r = r _o in Eq. 13, a whole domain can be taken in account and Eq. 4 is derived.