Abstract
We introduce the notion of \(T\)-stability for torsion-free Higgs sheaves as a natural generalization of the notion of \(T\)-stability for torsion-free coherent sheaves over compact complex manifolds. We prove similar properties to the classical ones for Higgs sheaves. In particular, we show that only saturated flags of torsion-free Higgs sheaves are important in the definition of \(T\)-stability. Using this, we show that this notion is preserved under dualization and tensor product with an arbitrary Higgs line bundle. Then, we prove that for a torsion-free Higgs sheaf over a compact Kähler manifold, \(\omega \)-stability implies \(T\)-stability. As a consequence of this, we obtain the \(T\)-semistability of any reflexive Higgs sheaf with an admissible Hermitian–Yang–Mills metric. Finally, we prove that \(T\)-stability implies \(\omega \)-stability if, as in the classical case, some additional requirements on the base manifold are assumed. In that case, we obtain the existence of admissible Hermitian–Yang–Mills metrics on any \(T\)-stable reflexive sheaf.
Similar content being viewed by others
Notes
Indeed, even in the classical case of reflexive sheaves, there is no yet an equivalence of \(\omega \)-semistability (see [1] for more details).
If \({\mathfrak E}\) is \(T\)-stable (resp. \(T\)-semistable), the conditions on existence or not of holomorphic sections hold for any flag and any Hermitian flat Higgs line bundle; in particular, this is true if the flag is saturated
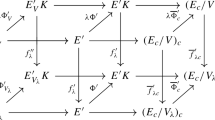
Since \({\mathfrak E}_{i}\subset {\mathfrak E}_{i+1}\), there exists a map \({\mathfrak E}/{\mathfrak E}_{i}\rightarrow {\mathfrak E}/{\mathfrak E}_{i+1}\) such that the obvious diagram commutes. Now, any element in \(\tilde{\mathfrak E}_{i}\) can be projected on \(\tilde{\mathfrak E}_{i}/{\mathfrak E}_{i}\cong {\mathfrak T}_{i}\subset {\mathfrak T}_{i+1}\), so it is zero in \({\mathfrak E}/\tilde{\mathfrak E}_{i+1}\) and hence \(\tilde{\mathfrak E}_{i}\subset \tilde{\mathfrak E}_{i+1}\) and \(\tilde{\mathcal{F}}\) is a flag, which is obviously saturated.
Notice that non \(T\)-semistability means that there exists a nonzero section of \(T_\mathcal{F}\otimes \mathcal{L}\) for some flag \(\mathcal{F}\) and some \({\mathfrak L}\) Hermitian flat Higgs line bundle, and such a section vanishes at least at some point.
References
Bando, S., Siu, Y.-T.: Stable Sheaves and Einstein–Hermitian Metrics, Geometry and Analysis on Complex Manifolds. World Scientific Publishing, River Edge (1994)
Biswas, I., Schumacher, G.: Yang–Mills equations for stable Higgs sheaves. Int. J. Math. 20(5), 541–556 (2009)
Bogomolov, F.A.: Holomorphic tensors and vector bundles on projective varieties. Math. USSR Izv. 13, 499–555 (1978)
Bruzzo, U., Graña Otero, B.: Metrics on semistable and numerically effective Higgs bundles. J. Reine. Ang. Math. 612, 59–79 (2007)
Cardona, S.A.H.: Approximate Hermitian–Yang–Mills structures and semistability for Higgs bundles I: generalities and the one-dimensional case. Ann. Glob. Anal. Geom. 42(3), 349–370 (2012). doi:10.1007/s10455-012-9316-2
Cardona, S.A.H.: Approximate Hermitian–Yang–Mills structures and semistability for Higgs bundles II: Higgs sheaves and admissible structures. Ann. Glob. Anal. Geom. 44(4), 455–469 (2013). doi:10.1007/s10455-013-9376-y
Cardona, S.A.H.: On vanishing theorems for Higgs bundles. Differ. Geom. Appl. 35, 95–102 (2014). doi:10.1016/j.difgeo.2014.06.005
Hitchin, N.J.: The self-duality equations on a Riemann surface. Proc. Lond. Math. 55, 59–126 (1987)
Kobayashi, S.: On two concepts of stability for vector bundles and sheaves. In: Proceedings of Aspects of Math. and its Applications, Elsevier Sci. Publ. B. V., pp. 477–484 (1986)
Kobayashi, S.: Differential Geometry of Complex Vector Bundles. Iwanami Shoten Publishers and Princeton University Press, Princeton (1987)
Li, J., Zhang, X.: Existence of approximate Hermitian–Einstein structures on semistable Higgs bundles. In: Proceedings of Calculus of Variations and Partial Differential Equations (2014). doi:10.1007/s00526-014-0733-x
Simpson, C.T.: Constructing variations of Hodge structure using Yang–Mills theory and applications to uniformization. J. Am. Math. Soc. 1, 867–918 (1988)
Simpson, C.T.: Higgs bundles and local systems. Publ. Math. IHES 75, 5–92 (1992)
Yano, K., Bochner, S.: Curvature and Betti numbers. Annals of Mathematics Studies 32, Princeton University Press, Princeton (1953)
Acknowledgments
This paper was mostly done during a stay of the author at the International School for Advanced Studies (SISSA) in Trieste, Italy. The author wants to thank SISSA for the hospitality and support. Finally, the author would like to thank U. Bruzzo for some useful comments and suggestions.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Cardona, S.A.H. \(T\)-stability for Higgs sheaves over compact complex manifolds. Ann Glob Anal Geom 48, 211–221 (2015). https://doi.org/10.1007/s10455-015-9466-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10455-015-9466-0