The influence of surface energetic heterogeneity on electrofluidic gating of a metal oxide surfaces

Abstract

We developed a theoretical model which describes the influence of the applied potential to the wall of an oxide nanochannel on the diffuse layer potential in the solution filling the nanopore. It was assumed that the surface of oxide is energetically heterogeneous and electrolyte ions from the solution can adsorb on channel walls. We performed calculations for two oxides: SiO₂ and Al₂O₃. It was found that energetically heterogeneous oxide surfaces strongly suppress gating potential. Moreover, taking into account ion adsorption considerably increased the electrokinetic potential and reduced the influence of applied potential on the electric double layer in the solution. The density of surface sites is the key parameter in the modeling of oxide nanochannels. Low density of surface hydroxyl groups significantly increases susceptibility on electrofluidic gating.

1 Introduction

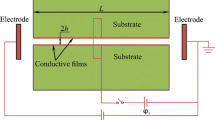
Nanofluidic devices have different properties than macro or microscopic structures (Eijkel and Berg 2010). In 2005 Karnik et al. (2005) described a nanofluidic transistor based on a metal/oxide/solution system. They observed that ionic conductance and the concentration of ions in a silicon dioxide nanochannel depended on the gate voltage applied to its walls (Fig. 1). The nanofluidic transistor is an analog of the metal–oxide–semiconductor field effect transistor (MOSFET). The electric field applied to nanochannel walls can control the ionic concentration and the composition of solution inside the nanochannel. Voltage gated nanochannels make possible “to integrate wet ionics with dry electronics seamlessly”, and since then they have been thoroughly studied (Guan et al. 2014). These devices can be used in field effect controlled electro-osmosis, as a molecular switch in DNA and protein transport or in field effect enhanced pressure driven energy conversion (Guan et al. 2014; Sparreboom et al. 2010).

Fig. 1

Schematic representation of nanofluidic transistor (electrically gated metal oxide nanochannel). The ionic conductance of electrolyte depends on the potential of gate electrode which is a layer of metal adjacent to the nanochannel

In nanofluidic systems where the surface/volume ratio is very high, the surface properties can considerably influence on the behavior of filling solution. The real surfaces are energetically heterogeneous and this fact should be considered in the theoretical description of any adsorption process. Models assuming energetic heterogeneity of surface have been successfully applied to described gas adsorption on solids (Rudzinski and Everett 1992), molecules adsorption from solution (Podkościelny and Nieszporek 2007) and ion adsorption from electrolyte solutions on metal oxides (Rudzinski et al. 1998).

The behavior of electrolyte solution confined in nanochannels whose walls are made of some metal oxide (e.g. SiO₂ or Al₂O₃) depends on the chemical reactivity of the surface. Metal oxide surfaces are covered with hydroxyl groups, SOH, which can dissociate or associate protons and bind electrolyte ions from solution creating electric charge on the surface. This charge induces opposite charge in solution and modifies solution flow caused by electric field (electroosmosis) (Sparreboom et al. 2010).

Jiang and Stein (Jiang and Stein 2010, 2011) investigated the influence of an applied external potential on the electric double layer at a metal oxide surface. They developed a general model based on the 2-pK and 1-pK mechanism of the protonation and deprotonation of surface hydroxyl groups. To describe electrofluidic gating they assumed that the system containing a metal gate electrode, an oxide insulator, the electric double layer, and bulk electrolyte was equivalent to the circuit of three capacitors connected in series (Fig. 2).

Fig. 2

The structure of electric double layer inside nanochannel and equivalent electric circuit of three capacitors connected in series. $\psi_{g}$—gate potential, $\psi_{0}$—surface potential, $\psi_{DL}$—diffuse layer (electrokinetic) potential, $\psi_{b}$—potential in bulk solution (it was assumed that $\psi_{b}$ = 0), $\sigma_{ox}$—induced charge in an oxide, $\sigma_{DL}$—diffuse layer charge, $c_{ox}$—oxide layer capacitance, $c_{S}$—Stern layer capacitance

When we apply positive potential to the metal electrode connected with oxide layer it induces more negative charge in part of oxide layer being in contact with solution (i.e. more SOH groups will dissociate protons). Application of negative potential reduces the negative charge of oxide surface being in contact with electrolyte [see Fig. 2 in ref. Jiang and Stein (2010)]. In other words the oxide layer behaves like a capacitor with dielectric, where electric charge on one plate (metal) induces the opposite charge on another plate (hydrated oxide surface in contact with solution).

In this paper we will extend the model proposed by Jiang and Stein (Jiang and Stein 2010) by including surface energetic heterogeneity and the adsorption of electrolyte ions on the oxide surface. This will improve the reliability of predictions of such models. We will analyze how the potential applied to nanochannel walls impact on diffuse layer potential inside the nanochannel. The last potential is a key parameter controlling the transport of ions in nanopore and it can be used to predict its conductance (Eijkel and Berg 2010).

2 Theory

The basic features of our model were depicted in Fig. 2. The main idea is that the whole system can be treated as three capacitors connected in a series (oxide layer capacitance, Stern layer capacitance and diffuse layer capacitance). The relations between electric potentials and charges can be described by well-known formulas:

$$ c_{ox} = \frac{{\sigma_{ox} }}{{\psi_{g} - \psi_{0} }} \, $$

(1)

$$ c_{S} = \frac{{\sigma_{DL} }}{{\psi_{0} - \psi_{DL} }} \, $$

(2)

$$ \sigma_{DL} = \, \sigma_{ox} + \sigma_{\text{chem}} \, $$

(3)

$$ \sigma_{DL} = \, \left( { 8N_{A} \cdot kT \cdot \varepsilon_{ 0} \varepsilon_{s} \cdot C \, \cdot 1 0^{ 3} } \right)^{{\frac{1}{2}}} \times \sinh \left( {\frac{{e\psi_{DL} }}{2kT}} \right) $$

(4)

where $\sigma_{ox}$ is a component of surface charge induced by applied external potential $\psi_{g}$ and $\sigma_{\text{chem}}$ is surface charge caused by ion adsorption on nanochannel walls and can be determined by application of the 2-pK surface complexation model combined with the Basic Stern Model of the interfacial region (2-pK BSM) (Piasecki et al. 2001). The relation (4) is the Gouy-Chapman equation describing the electric diffuse layer charge $\sigma_{DL}$ in symmetrical 1:1 electrolyte solution with a concentration of C (Stumm and Morgan 1996). In the last equation $\varepsilon_{0}$ is vacuum permittivity and $\varepsilon_{s}$ the relative dielectric constant of solution, $N_{A}$ is Avogadro’s number and the symbols k, T, e have their traditional physical meanings.

One can describe the formation of surface complexes shown in Fig. 2 by the following reactions and equilibrium constants:

$$ {\text{SO}}^{ - } + {\text{H}}^{ + } \overset {} \longleftrightarrow {\text{SOH}}^{0} , {\text{ K}}_{ 0} $$

$$ {\text{SO}}^{ - } + 2{\text{H}}^{ + } \overset {} \longleftrightarrow {\text{SOH}}_{2}^{ + } , {\text{ K}}_{ + } $$

(5)

$$ {\text{SO}}^{ - } + {\text{C}}^{ + } \overset {} \longleftrightarrow {\text{SO}}^{ - } {\text{C}}^{ + } , {\text{ K}}_{\text{C}} $$

$$ {\text{SO}}^{ - } + 2{\text{H}}^{ + } + {\text{A}}^{ - } \overset {} \longleftrightarrow {\text{SOH}}_{2}^{ + } {\text{A}}^{ - } , {\text{ K}}_{\text{A}} $$

where ${\text{SO}}^{ - }$ denotes deprotonated surface hydroxyl group at the oxide surface (empty adsorption site in our model). Taking into account the Eq. (5) the point of zero charge (PZC) can be defined as ${\text{PZC}} = \frac{1}{2}{\text{Log }}K_{ + }$ (Piasecki et al. 2001).

Additionally, compared to previous studies we included the energetic heterogeneity of oxide surface. We assumed that adsorption constants $K_{0} ,K_{ + } ,K_{C} ,K_{A}$ might have different values for different SOH groups.

Assuming Gaussian-like distribution of adsorption energy one arrives at the following expressions for the mean surface coverage by the i-th adsorption complex (Rudzinski et al. 1998),

$$ \theta_{it}^{{}} = \frac{{\left[ {K_{i}^{{}} f_{i} } \right]^{{{\raise0.5ex\hbox{$\scriptstyle {kT}$} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle {c_{i} }$}}}} }}{{1 + \sum\nolimits_{i} {\left[ {K_{i}^{{}} f_{i} } \right]^{{{\raise0.5ex\hbox{$\scriptstyle {kT}$} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle {c_{i} }$}}}} } }}\quad {\text{i}} = 0 , { } + , {\text{ A, C}} $$

(6)

where $\frac{kT}{{c_{i} }}$ are the dimensionless heterogeneity parameters (where $c_{i}$ denotes the variance of adsorption energy distribution), and $f_{i}$ are functions of pH and electrolyte ion activity. To simplify our analysis we assumed in calculations that heterogeneity parameters of different complexes have the same value $\frac{kT}{c}$. This means that we assumed that interactions between ${\text{SO}}^{ - }$ groups and different monovalent ions are highly correlated (Rudzinski et al. 1998).

The factors $f_{i}$ depend on pH and electrolyte ion activities $a_{C}$ and $a_{A}$, and can be expressed in the following way (Piasecki and Charmas 2013):

$$ f_{0} = \exp \left\{ { - \frac{{e\psi_{0} }}{kT} - 2.3{\text{pH}}} \right\} $$

$$ f_{ + } = \exp \left\{ { - \frac{{2e\psi_{0} }}{kT} - 4.6{\text{pH}}} \right\} $$

(7)

$$ f_{C} = a_{C} \cdot \exp \left\{ { - \frac{{e\psi_{0} }}{kT} + \frac{{e\sigma_{DL} }}{{kTc_{S} }}} \right\} $$

$$ f_{A} = a_{A} \cdot \exp \left\{ { - \frac{{e\psi_{0} }}{kT} - \frac{{e\sigma_{DL} }}{{kTc_{S} }} - 4.6{\text{pH}}} \right\} $$

The ion activities $a_{C}$ and $a_{A}$ can be calculated from electrolyte concentration C and ion activity coefficients $f_{C,A}$ calculated from the Davies equation applied for monovalent electrolyte solution at T = 25 °C (Stumm and Morgan 1996),

$$ Log \, f_{C,A} = - 0.5\left( {\frac{\sqrt I }{1 + \sqrt I } - 0.2I} \right) $$

(8)

where I is ionic strength of the solution.

The surface charge $\sigma_{\text{chem}}$ can be calculated by using the surface coverages defined in Eq. (6):

$$ \sigma_{\text{chem}} \, = {\text{e}} \cdot {\text{N}}_{\text{S}} \times \left( {\theta_{ + } + \theta_{A} - \theta_{C} - \theta_{ - } } \right) $$

(9)

where e is elementary charge and $N_{S}$ is surface site density $[{\text{sites}}/{\text{m}}^{2} ]$. The whole system of Eqs. (1–9) describing our model can be solved numerically using software like Mathematica.

3 Results and discussion

Applying the Eqs. (1–8) we can calculate how the diffuse layer potential $\psi_{DL}$ changes with the gate voltage $\psi_{g}$ assuming that pH and electrolyte concentration are constant. We cannot directly compare our results with an experiment. One can in principle measure the ionic current in a nanopore or the concentration of molecules using fluorescence technique but not the diffuse layer potential. Our primary goal is to understand which assumptions are crucial in theoretical modeling of voltage gated nanochannels.

We analyzed two different types of oxide nanochannels: the first made of SiO₂ and the second made of Al₂O₃. These two oxides are very often used to fabricate nanofluidic devices (Guan et al. 2014). In Table 1 we collected the parameters used in our calculations. They come from the article published by Sverjensky who had analyzed many experimental data sets and proposed a predictive model to determine the parameters such as protonation constants, equilibrium constants of ion adsorption, and inner layer capacitance (Sverjensky 2005).

Table 1 The parameter values used in the calculations were taken from Sverjensky paper (Sverjensky 2005) for $\alpha - {\text{SiO}}_{2}$ and $\gamma - {\text{Al}}_{ 2} {\text{O}}_{ 3}$ oxides and for NaCl as electrolyte

It was assumed that the oxide layer had a thickness $d_{ox} = 10$ nm. The same value was accepted in the paper by Jiang and Stein (Jiang and Stein 2010). It was also assumed that the external potential applied to the nanochannel, $\psi_{g}$, can be changed in the range from −10 V to +10 V. These two parameters have arbitrary but reasonable values. For example Karnik et al. applied a voltage range from −25 V to +25 V to investigate the conductance in nanofluidic tranistors (Karnik et al. 2005). To simplify data analysis and reduce the number of independent variables we defined an applied electrical field in the oxide layer $E_{g}$ (where $E_{g} = \frac{{\psi_{g} }}{{d_{ox} }}$). The electric capacitance of the oxide layer $c_{ox}$ can by calculated from the equation $c_{ox} = \frac{{\varepsilon_{0} \varepsilon_{ox} }}{{d_{ox} }}$, where $\varepsilon_{0}$ is vacuum permittivity and $\varepsilon_{ox}$ is the dielectric constant of an oxide. A reactive oxide surface acts as a buffer for external potential changes and its buffer capacity depends on the density of surface sites $N_{S}$, pH and electrolyte concentration (Eijkel and Berg 2010).

The electrofluidic gating is efficient when the diffuse layer potential $\psi_{DL}$ can be easily changed by gated voltage. The optimal situation is when one can change polarity and magnitude of $\psi_{DL}$. Flat graph of the function $\psi_{DL} (E_{g} )$ indicates that voltage gating is completely inefficient. To investigate how efficient electrofluidic gating is we calculated the potential at the onset of diffuse layer $\psi_{DL}$ (often assumed to equal the electrokinetic potential) as a function of $E_{g}$ keeping other parameters constant.

Figure 3 shows how for $SiO_{2}$ (PZC = 2) diffuse layer potential $\psi_{DL}$ changes with $E_{g}$ for two different pH values and salt concentrations (pH 5 and 7, C = 0.001 and 0.01 M). In each case the calculations were done for three different degrees of surface energetic heterogeneity ($kT/c$ = 1.0, 0.8, 0.6). Additionally, we checked how neglecting electrolyte ion adsorption influenced the $\psi_{DL} (E_{g} )$ curves. In our opinion it is a very important issue because localized ion adsorption has been neglected in almost every paper concerning voltage gated nanochannels.

Fig. 3

The potential at the onset of diffuse layer $\psi_{DL}$ as a function of an applied electrical field $E_{g}$ in SiO₂ layer ($E_{g}$ is equal to the applied potential $\psi_{g}$ divided by the oxide layer thickness $d_{ox}$). The calculations were made for two different pH and 1:1 electrolyte concentrations (pH 5 and 7, conc. = 0.001 and 0.01 M) and for three assumed degree of surface heterogeneity (red line for $kT/c$ = 1.0, which corresponds to homogenous surface, green line for $kT/c$ = 0.8, and blue line for $kT/c$ = 0.6). Two different scenarios was assumed: electrolyte ions were adsorbed on the oxide surface (solid lines) and there was no localized ion adsorption ($K_{C}$ = $K_{A}$ = 0, dashed lines). The 2-pK BSM parameters for SiO₂ were collected in Table 1 (Color figure online)

The most significant influence of $E_{g}$ on $\psi_{DL}$ was observed for pH 5 and C = 0.001 M and for a homogenous surface ($kT/c$ = 1.0). For pH 7 and C = 0.01 M we see almost flat lines, which indicates that the influence of external electric field on diffuse layer potential is very weak in this case. The increase of surface heterogeneity (from 1.0 to 0.6) decreases the effectiveness of voltage gating. We can also observe that the neglecting of electrolyte adsorption considerably decreases diffuse layer potential (especially for pH 7, C = 0.01 M).

Figure 4 presents the results for Al₂O₃ (PZC = 8.6). For pH 5 and when ion adsorption is “switched on” diffuse layer potential does not practically depend on $E_{g}$. The most effective gating is observed for the homogenous surface when pH 7 and C = 0.001 M. In all cases the increase of surface energetic heterogeneity worsens the results.

Fig. 4

The potential at the onset of diffuse layer $\psi_{DL}$ as a function of an applied electrical field $E_{g}$ in Al₂O₃ layer ($E_{g}$ is equal to the applied potential $\psi_{g}$ divided by the oxide layer thickness $d_{ox}$). The calculations were made for two different pH and 1:1 electrolyte concentrations (pH 5 and 7, conc. = 0.001 and 0.01 M) and for three assumed degree of surface heterogeneity (red line for $kT/c$ = 1.0, which corresponds to homogenous surface, green line for $kT/c$ = 0.8, and blue line for $kT/c$ = 0.6). Two different scenarios was assumed: electrolyte ions were adsorbed on the oxide surface (solid lines) and there was no localized ion adsorption ($K_{C}$ = $K_{A}$ = 0; dashed lines). The 2-pK BSM parameters for Al₂O₃ were collected Table 1 (Color figure online)

The absolute magnitude of the surface potential $\psi_{0}$ is bigger than the diffuse layer potential $\psi_{DL}$ but the difference is not large. Increase of the thickness of oxide layer $d_{ox}$ diminishes the absolute magnitude of $\psi_{0}$ and $\psi_{DL}$.

The influence of surface site density $N_{s}$ on $\psi_{DL} (E_{g} )$ is depicted in Fig. 5. It is evident from the results that tenfold reduction of the density of surface sites strongly affected the potential $\psi_{DL} (E_{g} )$ (especially for Al₂O₃, pH 5, C = 0.01 and “switched off” ion adsorption). It is interesting that Jiang and Stein in their calculations used very low $N_{s}$ values (e.g. $5\times 10^{17} {\text{ sites/m}}^{ 2}$ or even $1 \times 10^{17} {\text{ sites/m}}^{ 2}$) (Jiang and Stein 2010). These values are 10 or 100 times smaller than the values of surface site density normally used in surface complexation modeling (Sverjensky 2005).

Fig. 5

The potential at the onset of diffuse layer $\psi_{DL}$ as a function of an applied electrical field $E_{g}$ in SiO₂ or Al₂O₃ oxide layer. The other details are the same as in Figs. 3 and 4 with the exception of the values of surface site density which were assumed to be 10 times smaller the values given in Table 1 (i.e. N _s  = 0.45 for SiO₂ and N _s  = 0.8 for Al₂O₃)

Electrofluidic gating of nanochannels is the most effective when the solution pH is not far from PZC, electrolyte concentration is not to high (0.001 M or lower), the surface is energetically homogenous and the surface site density is low. These findings suggests that in nonofluidic transistors oxide surface should not be bare but rather coated with a chemically neutral substrate (to reduce $N_{s}$ and surface heterogeneity). The above modification can change solution flow in nanochannels.

In hydrophilic nanochannels we observe no-slip flow of solution (i.e. water molecules adjacent to the surface are immobile, slip length = 0). On hydrophobic surfaces slip flow is observed (slip length > 0) (Preocanin et al. 2012; Selmani et al. 2014; Sparreboom et al. 2010). It is interesting that gating voltage can modulate slip length in silica nanochannels and this phenomenon can be applied in pressure driven energy conversation by increasing the potential of streaming current (Vermesh et al. 2009).

Our modeling calculations are simplified and have some limitations. We dealt with isolated surfaces whereas in narrow channels overlapping of double layers of opposite walls should be taken into account (Huang et al. 2015).

Nevertheless for the first time we considered surface energetic heterogeneity to model the electrofluidic gating. Moreover, we took into account electrolyte ions adsorption on oxide surface—an important phenomenon so far neglected (Atalay et al. 2014). Finally, we used reliable and validated parameter set published by Sverjensky.

4 Conclusions

Besides pH of solution and electrolyte concentration another important parameter which influences electrofludic gating is surface energetic heterogeneity. More heterogeneous walls of nanochannel are more highly charged and more effectively suppress gating potential. To properly predict the behavior of electrofluidic transistor one should take into account localized adsorption of electrolyte ions (site binding). Inclusion of ion adsorption in the model increases the diffuse layer potential and counteracts electrofluidic gating. Surface site density is another important parameter. The lower the density of surface hydroxyl groups the less pronounced is the influence of surface heterogeneity and ion adsorption on voltage gated nanochannels.