Paralic Confinement: Models and Simulations

Abstract

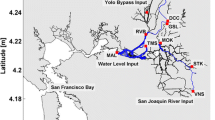
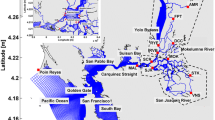
This paper deals with the mathematical modelling of confinement of paralic ecosystems. It is based on the recent paper (Frénod and Goubert in Ecol. Model. 200(1–2):139–148, 2007) that presents a modelling procedure in order to compute the confinement field of a lagoon.

Here, we improve the existing model in order to account for tide oscillations in any kind of geometry such as non-rectangular lagoons with a non-flat bottom. The new model, that relies on PDEs rather than ODEs, is then implemented thanks to the finite element method. Numerical results confirm the feasibility of confinement studies thanks to the introduced model.

Appendix: Equation for the Confinement

In this appendix we explain why, for any time t>0 and given a sufficiently large time T, the solution g _t =g _t (τ,x,y) of

$$ \left \{ \begin{array}{ll} \frac { {\partial {g_{t}}}}{ {\partial \tau }}(\tau,x,y)+\vec{v}(t-T+\tau,x,y)\cdot\nabla g_{t}(\tau ,x,y)=0,\\\quad\forall0<\tau<T,\forall(x,y)\in \Omega ,\\g_{t}(\tau,x,y)=T-\tau,\quad\forall0<\tau<T,\forall(x,y)\in\overline{\Gamma },\\g_{t}(0,x,y)=T,\quad\forall(x,y)\in \Omega ,\end{array} \right .$$

(65)

is such that g _t (T,x,y) is the value of the instantaneous confinement (see Definition 2) at instant t∈ℝ⁺ and position (x,y)∈Ω. It is indeed the case since the value g _t (τ,x,y) of g _t at time τ and in position (x,y)∈Ω is either the value of the initial data (i.e. T) or the value of g _t on $\overline{\Gamma }$ at a former time. For $(x_{0},y_{0})\in\overline{\Gamma}$, we consider the characteristic $(\tilde{X}(\tau,x_{0},y_{0},0),\tilde{Y}(\tau,x_{0},y_{0},0))$ which is such that its origin

$$ \bigl(\tilde{X}(0,x_{0},y_{0},0),\tilde{Y}(0,x_{0},y_{0},0) \bigr)=(x_{0},y_{0})\in\overline{\Gamma },$$

(66)

passing by (x,y). This means that, for a given τ ^∗=τ ^∗(t,x,y), we have

$$ \bigl(\tilde{X}\bigl(\tau^*,x_{0},y_{0},0\bigr),\tilde{Y}\bigl(\tau^*,x_{0},y_{0},0\bigr)\bigr)=(x,y)$$

(67)

and that it is solution to

$$ \left \{ \begin{array}{lr} \tfrac {\partial {\tilde{X}}}{\partial \tau }(\tau,x,y,s)=v_{1}(\tau-T+t,\tilde{X}(\tau;x,y,s),\tilde{Y}(\tau;x,y,s)),\\[0.2cm] \tfrac {\partial {\tilde{Y}}}{\partial \tau }(\tau,x,y,s)=v_{2}(\tau-T+t,\tilde{X}(\tau;x,y,s),\tilde{Y}(\tau;x,y,s)).\end{array} \right .$$

(68)

Notice that τ ^∗=τ ^∗(t,x,y) is the time for the characteristic to go from the border $\overline{\Gamma }$ to (x,y) when (x,y) is reached at time t. Hence it is, by definition, the value of the instantaneous confinement in (x,y) at time t.

Beside this, reasoning like in Sect. 2.3, we get that g remains constant along the characteristics $(\tilde{X}, \tilde{Y})$ meaning

(69)

i.e. the instantaneous confinement value in position (x,y) and time t. In order to get the ultimate equality in (69), we used (65).