Effect of quadratic pressure gradient term on a one-dimensional moving boundary problem based on modified Darcy’s law

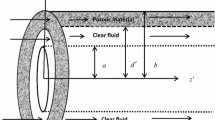
Abstract

A relatively high formation pressure gradient can exist in seepage flow in low-permeable porous media with a threshold pressure gradient, and a significant error may then be caused in the model computation by neglecting the quadratic pressure gradient term in the governing equations. Based on these concerns, in consideration of the quadratic pressure gradient term, a basic moving boundary model is constructed for a one-dimensional seepage flow problem with a threshold pressure gradient. Owing to a strong nonlinearity and the existing moving boundary in the mathematical model, a corresponding numerical solution method is presented. First, a spatial coordinate transformation method is adopted in order to transform the system of partial differential equations with moving boundary conditions into a closed system with fixed boundary conditions; then the solution can be stably numerically obtained by a fully implicit finite-difference method. The validity of the numerical method is verified by a published exact analytical solution. Furthermore, to compare with Darcy’s flow problem, the exact analytical solution for the case of Darcy’s flow considering the quadratic pressure gradient term is also derived by an inverse Laplace transform. A comparison of these model solutions leads to the conclusion that such moving boundary problems must incorporate the quadratic pressure gradient term in their governing equations; the sensitive effects of the quadratic pressure gradient term tend to diminish, with the dimensionless threshold pressure gradient increasing for the one-dimensional problem.

Appendix 1

Equation (1) can be rewritten as follows

$$\begin{aligned} p=\frac{1}{C_\mathrm{f} }\ln \rho -\frac{1}{C_\mathrm{f} }\ln \rho _0 +p_0. \end{aligned}$$

(56)

Differentiating the two sides of Eq. (56) with respect to x, we have

$$\begin{aligned} \frac{\partial p}{\partial x}=\frac{1}{C_\mathrm{f} \cdot \rho }\frac{\partial \rho }{\partial x}, \end{aligned}$$

(57)

Equation (57) can be rewritten as follows

$$\begin{aligned} \frac{\partial \rho }{\partial x}=C_\mathrm{f} \cdot \rho \frac{\partial p}{\partial x}, \end{aligned}$$

(58)

In the same manner as previously, from Eqs. (1) and (2) the following equations can also be deduced:

$$\begin{aligned} \frac{\partial \rho }{\partial t}= & {} C_\mathrm{f} \cdot \rho \frac{\partial p}{\partial t}, \end{aligned}$$

(59)

$$\begin{aligned} \frac{\partial \phi }{\partial t}= & {} C_\phi \cdot \phi \frac{\partial p}{\partial t}. \end{aligned}$$

(60)

The left-hand side of Eq. (4) can be expanded as follows

$$\begin{aligned} -\frac{\partial }{\partial x}\left( {\rho \cdot \upsilon } \right)= & {} \frac{k}{\mu }\cdot \rho \cdot \frac{\partial ^{2}p}{\partial x^{2}}+\frac{k}{\mu }\cdot \frac{\partial \rho }{\partial x}\cdot \frac{\partial p}{\partial x} \nonumber \\&-\frac{k\cdot \lambda \cdot C_\mathrm{f} }{\mu }\cdot \rho \cdot \frac{\partial p}{\partial x}, \end{aligned}$$

(61)

Substituting Eq. (58) into the right-hand side of Eq. (61) yields

$$\begin{aligned} -\frac{\partial }{\partial x}\left( {\rho \cdot \upsilon } \right)= & {} \underbrace{\frac{k}{\mu }\cdot \rho \cdot \frac{\partial ^{2}p}{\partial x^{2}}}_\mathrm{{Main\,Term}}+\underbrace{\frac{k\cdot C_\mathrm{f} }{\mu }\cdot \rho \cdot \left( {\frac{\partial p}{\partial x}} \right) ^{2}}_\mathrm{{Quadratic\,Gradient\,Term}} \nonumber \\&-\underbrace{\frac{k\cdot \lambda \cdot C_\mathrm{f} }{\mu }\cdot \rho \cdot \frac{\partial p}{\partial x}}_\mathrm{{Small\,Term}}, \end{aligned}$$

(62)

Because $\lambda <<1$, and $C_{\mathrm{f}} <<1$, the small term on the right-hand side of Eq. (62) can be neglected, and then Eq. (62) can be rewritten as follows

$$\begin{aligned} -\frac{\partial }{\partial x}\left( {\rho \cdot \upsilon } \right) =\underbrace{\frac{k}{\mu }\cdot \rho \cdot \frac{\partial ^{2}p}{\partial x^{2}}}_\mathrm{{Main\,Term}}+\underbrace{\frac{k\cdot C_\mathrm{f} }{\mu }\cdot \rho \cdot \left( {\frac{\partial p}{\partial x}} \right) ^{2}}_\mathrm{{Quadratic\,Gradient\,Term}}, \end{aligned}$$

(63)

In Eq. (63), the quadratic pressure gradient term is retained for the deduction of the governing equation.

Expanding the right-hand side of Eq. (4) yields

$$\begin{aligned} \frac{\partial \left( {\rho \phi } \right) }{\partial t}=\rho \frac{\partial \phi }{\partial t}+\phi \frac{\partial \rho }{\partial t}, \end{aligned}$$

(64)

Substituting Eqs. (59) and (60) into the right-hand side of Eq. (64) yields

$$\begin{aligned} \frac{\partial \left( {\rho \phi } \right) }{\partial t}= & {} \rho \cdot C_\phi \cdot \phi \cdot \frac{\partial p}{\partial t}+\phi \cdot C_\mathrm{f} \cdot \rho \cdot \frac{\partial p}{\partial t} \nonumber \\= & {} \rho \cdot \phi \cdot \frac{\partial p}{\partial t}\cdot \left( {C_\phi +C_\mathrm{f} } \right) =\rho \cdot \phi \cdot \frac{\partial p}{\partial t}\cdot C_\mathrm{t}. \end{aligned}$$

(65)

Substituting Eqs. (63) and (65) into Eq. (4), the governing equation in consideration of the quadratic pressure gradient term can be obtained as follows

$$\begin{aligned} \underbrace{\frac{k}{\mu }\cdot \rho \cdot \frac{\partial ^{2}p}{\partial x^{2}}}_\mathrm{{Main\,Term}}+\underbrace{\frac{k\cdot C_\mathrm{f} }{\mu }\cdot \rho \cdot \left( {\frac{\partial p}{\partial x}} \right) ^{2}}_\mathrm{{Quadratic\,Gradient\,Term}}=\rho \cdot \phi \cdot \frac{\partial p}{\partial t}\cdot C_\mathrm{t}.\nonumber \\ \end{aligned}$$

(66)

Equation (66) can be equivalently simplified, by canceling the variable $\rho$ on both sides, as follows

$$\begin{aligned} \frac{k}{\mu }\cdot \frac{\partial ^{2}p}{\partial x^{2}}+\frac{k\cdot C_\mathrm{f} }{\mu }\cdot \left( {\frac{\partial p}{\partial x}} \right) ^{2}=\phi \cdot \frac{\partial p}{\partial t}\cdot C_\mathrm{t}. \end{aligned}$$

(67)

1.1 Appendix 2

The dimensionless mathematical model, considering the quadratic threshold pressure gradient, for the one-dimensional Darcy’s flow in semi-infinite long porous media for the case of a constant flow rate at the inner boundary is as follows

$$\begin{aligned}&\frac{\partial ^{2}P_\mathrm{D} }{\partial x_\mathrm{D} ^{2}}-\alpha _\mathrm{D} \left( {\frac{\partial P_\mathrm{D} }{\partial x_\mathrm{D} }} \right) ^{2}=\frac{\partial P_\mathrm{D} }{\partial t_\mathrm{D} }, \end{aligned}$$

(68)

$$\begin{aligned}&\left. {P_\mathrm{D} } \right| _{t_\mathrm{D} =0} =0, \end{aligned}$$

(69)

$$\begin{aligned}&\left. {\frac{\partial P_\mathrm{D} }{\partial x_\mathrm{D} }} \right| _{x_\mathrm{D} =0} = -1, \end{aligned}$$

(70)

$$\begin{aligned}&\left. {P_\mathrm{D} } \right| _{x_\mathrm{D} \rightarrow \infty } = 0. \end{aligned}$$

(71)

First, introduce the following transform [52]:

$$\begin{aligned} P_\mathrm{D} =-\frac{1}{\alpha _\mathrm{D} }\cdot \ln U. \end{aligned}$$

(72)

Substituting Eq. (72) into Eqs. (68)–(71) yields

$$\begin{aligned}&\frac{\partial ^{2}U}{\partial x_\mathrm{D} ^{2}}=\frac{\partial U}{\partial t_\mathrm{D} } , \end{aligned}$$

(73)

$$\begin{aligned}&\left. U \right| _{t_\mathrm{D} =0} = 1, \end{aligned}$$

(74)

$$\begin{aligned}&\left. {\frac{\partial U}{\partial x_\mathrm{D} }} \right| _{x_\mathrm{D} =0} = \alpha _\mathrm{D} \cdot \left. U \right| _{x_\mathrm{D} =0} ,\end{aligned}$$

(75)

$$\begin{aligned}&\left. U \right| _{x_\mathrm{D} \rightarrow \infty } = 1. \end{aligned}$$

(76)

By the linear Laplace transform,

$$\begin{aligned} \ell [U]=\int \limits _0^\infty {U\cdot \exp \left( {-s\cdot t_\mathrm{D} } \right) \text {d}t_\mathrm{D}}. \end{aligned}$$

(77)

Equations (73)–(76) can be transformed as

$$\begin{aligned}&\frac{\partial ^{2}\ell [U]}{\partial x_\mathrm{D}^{2}}=s\ell [U]-1, \end{aligned}$$

(78)

$$\begin{aligned}&\left. {\frac{\partial \ell [U]}{\partial x_\mathrm{D} }} \right| _{x_\mathrm{D} =0} = \alpha _\mathrm{D} \cdot \ell [\left. {U]} \right| _{x_\mathrm{D} =0}, \end{aligned}$$

(79)

$$\begin{aligned}&\left. {\ell [U]} \right| _{x_\mathrm{D} \rightarrow \infty } =\frac{1}{s}. \end{aligned}$$

(80)

The analytical solution for Eqs. (78)–(80) can be solved as follows [52]

$$\begin{aligned} \ell [U]=-\frac{\alpha _\mathrm{D} \cdot \exp \left( {-x_\mathrm{D} \sqrt{s}} \right) }{\left( {\alpha _\mathrm{D} +\sqrt{s}} \right) s}+\frac{1}{s}. \end{aligned}$$

(81)

The following Laplace and inverse Laplace transforms are known [66–68] as

$$\begin{aligned}&\ell ^{-1}\left[ \frac{1}{s}\right] = 1 , \end{aligned}$$

(82)

$$\begin{aligned}&\ell ^{-1}\left[ \frac{\alpha _\mathrm{D} \cdot \exp \left( {-x_\mathrm{D} \sqrt{s}} \right) }{\left( {\alpha _\mathrm{D} +\sqrt{s}} \right) s}\right] \nonumber \\&\quad = -\exp \left( {\alpha _\mathrm{D} \cdot x_\mathrm{D} +\alpha _\mathrm{D} ^{2}\cdot t_\mathrm{D} } \right) \hbox {erfc}\left( {\alpha _\mathrm{D} \sqrt{t_\mathrm{D} }+\frac{x_\mathrm{D} }{2\sqrt{t_\mathrm{D} }}} \right) \nonumber \\&\qquad +\,\hbox {erfc}\left( {\frac{x_\mathrm{D} }{2\sqrt{t_\mathrm{D} }}} \right) . \end{aligned}$$

(83)

Therefore, from Eq. (81), we obtain

$$\begin{aligned} U= & {} \exp \left( {\alpha _\mathrm{D} \cdot x_\mathrm{D} +\alpha _\mathrm{D} ^{2}\cdot t_\mathrm{D} } \right) \hbox {erfc}\left( {\alpha _\mathrm{D} \sqrt{t_\mathrm{D} }+\frac{x_\mathrm{D} }{2\sqrt{t_\mathrm{D} }}} \right) \nonumber \\&+\,\hbox {erfc}\left( {\frac{x_\mathrm{D} }{2\sqrt{t_\mathrm{D} }}} \right) +1. \end{aligned}$$

(84)

Then, substituting Eq. (84) into Eq. (72), we obtain the exact analytical solution of $P_{\mathrm{D}}$ as follows

$$\begin{aligned} P_\mathrm{D}= & {} -\frac{1}{\alpha _\mathrm{D} }\cdot \ln \Bigg [ \exp \left( {\alpha _\mathrm{D} \cdot x_\mathrm{D} +\alpha _\mathrm{D} ^{2}\cdot t_\mathrm{D} } \right) \nonumber \\&\times \,\hbox {erfc}\left( {\alpha _\mathrm{D} \sqrt{t_\mathrm{D} }+\frac{x_\mathrm{D} }{2\sqrt{t_\mathrm{D} }}} \right) +\hbox {erfc}\left( {\frac{x_\mathrm{D} }{2\sqrt{t_\mathrm{D} }}} \right) +1 \Bigg ].\nonumber \\ \end{aligned}$$

(85)