Hemi-spectrum substitution after water signal fitting (HESWAF): an improvement of the modulus post-processing of MR spectra

Abstract

Objective

In a previous study, we have shown that modulus post-processing is a simple and efficient tool to both phase correct and frequency align magnetic resonance (MR) spectra automatically. Furthermore, this technique also eliminates sidebands and phase distortions. The advantages of the modulus technique have been illustrated in several applications to brain proton MR spectroscopy. Two possible drawbacks have also been pointed out. The first one is the theoretical decrease in signal-to-noise ratio (SNR) by a factor up to √2 when comparing the spectrum obtained after modulus versus conventional post-processing. The second pitfall results from the symmetrization of the spectrum induced by modulus post-processing, since any resonance or artifact located at the left of the water resonance is duplicated at the right of the water resonance, thus contaminating the region of the spectrum containing the resonances of interest. Herein, we propose a strategy in order to eliminate these two limitations.

Materials and methods

Concerning the SNR issue, two complementary approaches are presented here. The first is based on the application of modulus post-processing before spatial apodization, and the second consists in substituting the left half of the spectrum by the fit of the water resonance before applying modulus post-processing. The symmetrization induced by modulus post-processing then combines the right half of the original spectrum containing the resonances of interest with the left half of the water fit, free of noise and artifacts. Consequently, the SNR is improved when compared to modulus post-processing alone. As a bonus, any artifact or resonance present in the left half of the original spectrum is removed. This solves the second limitation.

Results

After validation of the technique on simulations, we demonstrated that this improvement of the modulus technique is significantly advantageous for both in vitro and in vivo applications.

Conclusion

By improving the SNR of the spectra and eliminating eventual contaminations, the new strategies proposed here confer an additional competitive advantage to the modulus post-processing technique.

Appendix

Let us follow step-by-step the flowchart depicted in Fig. 1b, starting with the raw CSI data block (see top left of the diagram). After applying FFT in the spatial dimension to these CSI data, we obtain a matrix (x, y, z, t) containing (Nx × Ny × Nz) voxels. The next step consists of extracting the FID of the first voxel, namely s(t), and fitting this FID using the HLSVD technique. The fitted water signal thus obtained, named h ₂ o(t), is reconstructed from the singular value deconvolution by selecting the resonances contained in the range [+0.5 ppm, −0.5 ppm] around the water resonance. Usually, when using the HLSVD technique, the signal h ₂ o(t) is subtracted to s(t) in order to remove the residual water signal. However, in this case, we use the resulting FFT of both s(t) and h ₂ o(t) signals, leading respectively to S(ω) and H ₂ O(ω), in order to calculate $\tilde{S}(\omega )$, the spectrum obtained after HESWAF post-processing. If the acquisition is performed with the water signal on-resonance, the spectrum S(ω) can be split in two parts: the upfield part (UFS), i.e., the half of the spectrum located at the right of the water signal, and the downfield part (DFS) i.e., the complementary half of the spectrum, located at the left of the water resonance. If we now assume that all the resonances of the metabolites of interest are located in the UFS, the DFS only contains noise and possibly artifacts and/or sidebands, and hence does not include any useful information. We then substitute this region [DFS of S(ω)] with the DFS extracted from the fitted water signal H ₂ O(ω). The UFS, containing the metabolites of interest, is not affected by this post-processing.

Substituting the DFS of S(ω) with the DFS of H ₂ O(ω) leads to a new spectrum signal $\tilde{S}(\omega )$ characterized by a DFS free of noise and artifacts. $\tilde{S}(\omega )$ can be described by:

$$\begin{aligned} \hat{S}(\omega ) &= S(\omega )\quad\;{\text{if}}\;\omega < 0 \\ &= H_{2} O(\omega )\quad\;{\text{if}}\;\omega > 0 \\ \end{aligned}$$

It is important to mention that the water fit H ₂ O(ω) is calculated for each spectrum individually. It is the only way to ensure that this post-processing step does not introduce any break in the new signal $\tilde{S}(\omega )$. $\tilde{S}(\omega )$ signal is still continuous, and its derivative is also continuous. This would not have been the case if we had simply removed or replaced the DFS with zero values.

The next step consists in applying a temporal inverse Fast Fourier transformation (iFFT) to the signal $\tilde{S}(\omega )$in order to return to the time domain before extracting the modulus. This step gives rise to a new FID signal, namely $\tilde{s}(t)$. We can now calculate the modulus of $\tilde{s}(t)$, and reintroduce the resulting signal, namely $\mathop {\tilde{s}}\limits_{\text{Mod}} (t)$, in the original CSI data file.

After processing all the voxels of the CSI experiment following the same procedure described above, an iFFT is applied in the spatial dimension, in order to come back to a new “raw” CSI data file (i.e., containing a collection of FIDs in the k-space). As a result, we have generated a new “raw” CSI data file corrected with the [HESWAF + modulus] technique that can then be processed using any standard post-processing software commonly used to analyze CSI data.

Let us call $\mathop {\tilde{S}}\limits_{\text{Mod}} (\omega )$ the spectrum obtained at the end of the spatial and temporal processing. The symmetrization induced by the modulus post-processing on $\mathop {\tilde{S}}\limits_{\text{Mod}} (\omega )$ will now combine the original UFS of S(ω) with the calculated free of noise/artifacts DFS of H ₂ O(ω). As described in our previous paper [1], the resonance intensity of the metabolites is divided by a factor of 2 (due to modulus post-processing), but now the noise is also expected to be reduced by the same factor (since half of the noise signal of the spectrum is removed by HESWAF post-processing), thus leading to the same SNR for both conventional and [HESWAF + modulus] post-processings.

HESWAF and the noise

After describing how to implement HESWAF, we now detail how this technique can further improve the SNR of spectra obtained with the modulus post-processing alone.

Let us first apply the HESWAF post-processing to the simulation of a noise-like NMR signal. It is well known that the FFT of a noise signal n(t), characterized by a zero mean Gaussian distribution and a standard deviation (SD) equal to σ, is a noise signal:

$$N(\omega ) = \sum\limits_{i = 1}^{\text{Npts}} {n(t)} {\text{ e}}^{i\omega t/N}$$

characterized by a zero mean Gaussian distribution and by a SD equal to σ√N, where N is the number of time points. Since the distribution of the noise signal N(ω) is centered on the zero value, the signal avoiding any discontinuity with HESWAF is naturally the null signal. HESWAF post-processing consists then in replacing the DFS of N(ω) by zero values, leading to a new signal $\tilde{N}(\omega )$. Without any post-processing, the iFFT of N(ω) will naturally lead back to the original noise signal:

$$n(t) = \frac{1}{N}\sum\limits_{i = 1}^{N} {N(\omega )} {\text{ e}}^{ - i\pi \omega t/N}$$

with a SD equal to σ. Since half of the points of N(ω) have been replaced by zero values, the iFFT $\tilde{N}(\omega )$ leads to a new noise signal expressed as:

$$\begin{aligned} \tilde{n}(t) = & \frac{1}{N}\sum\limits_{i = 1}^{N} {\tilde{N}(\omega )} {\text{ e}}^{ - i\pi \omega t/N} \\ = & \frac{1}{N}\sum\limits_{i = 1}^{N/2} {\tilde{N}(\omega )} {\text{ e}}^{ - i\pi \omega t/N} \\ \end{aligned}$$

Since half of the points have a zero value, the summation can be only performed on the remaining N/2 points different from zero. The SD of $\tilde{n}(t)$ will then be equal to $\frac{\sigma }{\sqrt 2 }$.

As a first consequence, the SD of the noise signal $\tilde{n}(t)$ obtained with HESWAF is reduced by a factor of √2 in comparison to the SD of the original noise signal n(t).

Let us now apply the modulus post-processing, as described in [1]. We then obtain a new signal:

$$\mathop {\tilde{N}}\limits_{\text{Mod}} (\omega ) = {\text{FFT}}\left( {\left\| {\tilde{n}(t)} \right\|} \right)$$

As explained in our previous publication, the modulus of a noise characterized by a zero mean Gaussian distribution is Rice distributed. This distribution can be approximated by a Gaussian distribution when the SNR is greater than three, and by a Rayleigh distribution when the SNR tends towards zero. The characteristics of the SNR obtained in both conditions have already been discussed in [1], and here we will just focus on the modification introduced by the application of the HESWAF technique. Concerning the Gaussian distribution, we have shown that if n(t) is characterized by a SD equal to σ, then the SD of $\mathop N\limits_{\text{Mod}} (\omega )$ defined by:

$$\mathop N\limits_{\text{Mod}} (\omega ) = {\text{FFT}}\left( {\left\| {n(t)} \right\|} \right)$$

is also equal to σ. Applying this reasoning to the present case implies that the SD of $\mathop {\tilde{N}}\limits_{\text{Mod}} (\omega )$ is equal to the SD of $\tilde{n}(t)$, which is equal to $\frac{\sigma }{\sqrt 2 }$. As far as the Gaussian approximation is valid, the noise SD of the signal obtained using HESWAF is reduced by a factor of √2 when compared to the SD obtained using modulus post-processing alone. This factor is equal to the decrease in SNR predicted by the theory when comparing modulus to conventional post-processing under the same condition of Gaussian approximation. Therefore, this mathematical development confirms that HESWAF allows to recover the SNR loss that was induced by modulus post-processing alone under the Gaussian condition.

Concerning the Rayleigh condition, since the noise is not centered on the zero value anymore, the situation is more complex and the noise characteristics obtained under this approximation will be discussed in the “Results” section.

Let us now introduce a mathematical representation of the HESWAF technique for these two noise distribution approximations. These mathematical representations will afterwards be used for the calculation of all the signals used for the simulations.

We will first model the Rayleigh approximation. If r(t) is a noise signal in the time domain, and R(ω) its FFT, replacing the DFS of R(ω) by zero values is mathematically equivalent to multiplying R(ω) function by the reverse of the unit step function defined by:

The HESWAF technique can then be expressed as:

And the iFFT of $\tilde{R}(\omega )$ gives rise to the following signal:

If we now extract the modulus of $\tilde{r}(t)$:

And apply FFT to this signal, we obtain:

Besides, the Gaussian approximation can be modelled by adding to the original noise signal r(t) a constant signal c(t), defined by:

$$c(t) = c,\quad \forall t$$

This gives rise to a new noise signal:

$$g(t) = r(t) + c$$

Using the same notation, we obtain a noise spectrum:

Despite the fact that $\mathop {\tilde{G}}\limits_{\text{Mod}} (\omega )$ and $\mathop {\tilde{R}}\limits_{\text{Mod}} (\omega )$ expressions look very similar, we will see in the “Simulations” section that the shape of the resulting noise signals is very different.

Simulations

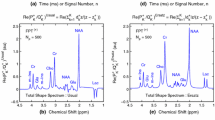
In order to estimate the noise behavior after modulus and [HESWAF + modulus] post-processings under both Rayleigh and Gaussian conditions, the following simulations were performed. Two complex noise signals were generated using IDL software (Interactive Data Language, Research Systems Inc., Boulder, CO, USA) in order to simulate the noise signal obtained with Rayleigh and Gaussian approximations, respectively. The signal simulating the Rayleigh condition, namely r(t), is composed by 2 × 4 K normally distributed pseudo random numbers with a mean of zero and a SD of 10. The signal simulating the Gaussian condition, namely g(t), is obtained by adding to r(t) a constant signal with an amplitude of 50. Figure 11 shows the resulting noise signals obtained under both conditions at each step of the post-processing, using either modulus post-processing alone, or combined [HESWAF + modulus] post-processing.

Fig. 11

Noise signal shape obtained at each step of the post-processing with modulus (R2, 3, G2, 3) and [HESWAF + modulus] (R4-8, G4-8) techniques. For the sake of clarity, the Rayleigh (Rx) and Gaussian (Gx) conditions are displayed in blue and orange colors, respectively

We will first describe the steps involved in modulus and [HESWAF + modulus] post-processings. Of course, the same steps are applied to both Rayleigh and Gaussian conditions.

In the case of modulus post-processing alone, the noise spectra obtained in both conditions, namely $\mathop R\limits_{\text{Mod}} (\omega )$ and $\mathop G\limits_{\text{Mod}} (\omega )$ (Fig. 11 R3, G3), are obtained after applying FFT to the module of r(t) and g(t) (Fig. 11 R2, G2).

In the case of [HESWAF + modulus] post-processing, r(t) and g(t) signals (Fig. 11 R1, G1) are first fast Fourier transformed, leading respectively to R(ω) and G(ω) (Fig. 11 R4, G4) signals. Second, the UFS of each signal is replaced by zero values, leading to $\tilde{R}(\omega )$ and $\tilde{G}(\omega )$ signals (Fig. 11 R5, G5). The following steps are: third, both signals are inverse fast Fourier transformed (Fig. 11 R6, G6), fourth the modulus is extracted (Fig. 11 R7, G7), and finally, the signals are fast Fourier transformed again, leading to the signals $\mathop {\tilde{R}}\limits_{\text{Mod}} (\omega )$ and $\mathop {\tilde{G}}\limits_{\text{Mod}} (\omega )$ (Fig. 11 R8 G8).

Interestingly, the noise signal obtained at the first step of [HESWAF + modulus] post-processing (Fig. 11 R4, G4) is identical to the noise signal obtained using conventional post-processing. These noise signals will hence be used as references when comparing the noise signals obtained with modulus versus [HESWAF + modulus] processings. Also, the noise signals obtained in modulus and [HESWAF + modulus] cases are both displayed after multiplication by a factor of 2 in order to compensate for the signal loss by a factor of 2 induced by modulus post-processing. This scale correction allows a direct visual comparison between the noise amplitudes obtained with the three post-processings, i.e., modulus alone (Fig. 11 R3, G3), [HESWAF + modulus] (Fig. 11 R8, G8), and conventional (Fig. 11 R4, G4).

We now discuss the differences regarding the noise characteristics resulting from the Rayleigh and Gaussian conditions.

If we first focus on the Rayleigh condition, Fig. 11 R8 clearly shows that the noise spectrum $\mathop {\tilde{R}}\limits_{\text{Mod}} (\omega )$ obtained after implementing HESWAF before the modulus technique leads to a non-uniform noise signal in the spectral dimension. In that case, the noise amplitude in the central area of the spectral window looks very similar to the noise obtained using modulus post-processing alone (Fig. 11 R3), whereas it decreases when moving to each extremity of the spectral window. On the contrary, as already mentioned in our previous work [1], we can observe here that applying modulus post-processing alone (Fig. 11 R3) does not introduce any SNR degradation when compared to conventional post-processing (Fig. 11 R4).

If we focus now on the Gaussian condition, we observe that the amplitude of the noise signal $\mathop {\tilde{G}}\limits_{\text{Mod}} (\omega )$ (Fig. 11 G8) obtained after [HESWAF + modulus] post-processing is decreased when compared to the signal $\mathop G\limits_{\text{Mod}} (\omega )$ obtained after modulus post-processing alone (Fig. 11 G3), whereas it is comparable to the noise signal G(ω) obtained after conventional post-processing (Fig. 11 G4).

Table 1a, b shows the noise SD obtained in time and frequency domains, respectively, when this simulation is repeated 1,000 times. Once again, the noise signals obtained after modulus post-processing, with or without integration of HESWAF correction, are multiplied by a factor of 2 in order to compensate for the loss in signal induced by modulus post-processing. Owing to this scale correction, the SD of the noise signal in the frequency domain is inversely proportional to the SNR obtained if a signal was added to the noise in the simulation. For more details regarding the mathematical expressions presented in these tables, one can refer to our previous publication [1], which describes the noise characteristics in the case of modulus post-processing.

Table 1 Noise characteristics of the noise signals obtained at several stages of the post-processing with modulus alone and [HESWAF + modulus] techniques

We will first discuss the data obtained in the temporal domain (Table 1). The two columns refer, respectively, to the original noise signal (see also Fig. 11 R1,G1) and to the noise signal obtained after application of HESWAF and iFFT (see also Fig. 11 R6,G6). We can notice that the noise SD is decreased by a factor of √2 after post-processing with the HESWAF technique. This very interesting point indicates that, after HESWAF post-processing, the SNR of the reconstructed FID is higher than the SNR of the original FID by a factor. If we transpose this result observed in simulations to acquired MR data, this means that after HESWAF post-processing, modulus extraction is performed on a signal whose SNR is higher than the SNR of the originally acquired FID. At this step, there are no differences in the noise characteristics between the Rayleigh and Gaussian conditions, since the modulus extraction has not yet been performed.

We discuss now the data obtained in the frequency domain, starting with the Gaussian condition (see columns PM_G3, PM_G4 and PM_G8, in Table 1 and Fig. 11). We observe that the SD of the noise signal obtained after [HESWAF + modulus] technique (Fig. 11 G8) is decreased by a factor when compared to the SD of the noise signal obtained using modulus post-processing alone (Fig. 11 G3). As expected, the SD of the noise (i.e., the SNR) obtained using the [HESWAF + modulus] technique (Fig. 11 G8) is equal to the SNR obtained using conventional post-processing (Fig. 11 G4).

If we focus now on the regions where the noise of the original FID follows a Rayleigh distribution (see columns PM_R3, PM_R4 and PM_R8, center and border in Table 1 and Fig. 11), we observe that, when we move from the center to the extremity of the frequency window, the SD of the noise signal obtained with the [HESWAF + modulus] technique (see column PM_R8 in Table 1 and Fig. 11) is between 1.1 and 4.6 times smaller than the one obtained using conventional post-processing (see column PM_R4 in Table 1 and Fig. 11). This results in an increased SNR from 1.1 to 4.6 times when comparing [HESWAF + modulus] versus conventional post-processings. The gain in SNR is reduced, but still present, when comparing [HESWAF + modulus] post-processing with modulus alone (see column PM_R3 in Table 1 and Fig. 11).

In practice, a FID acquired in vitro or in vivo usually includes a region where the Gaussian condition is predominant, as well as a region where the Rayleigh condition is predominant. The expected SNR of the resulting spectrum will then stand between the two limits (i.e., between 1 and 4.6 times the SNR obtained with conventional post-processing). Indeed, the final SNR value will be related to the percentage between the noise region that can be approximated by a Gaussian distribution versus the noise region that can be approximated by a Rayleigh distribution in the acquired FID. Of course, this SNR will also depend on the spectral region selected to calculate the SD of the noise. The good news is that the SNR of the spectrum obtained after [HESWAF + modulus] post-processing will be at least equal to the one obtained using conventional post-processing.

Let us come back to Fig. 11 R8 and make a little side comment that may be useful for users confused by the unusual shape of the noise spectrum displayed in this figure. Indeed, the shape of the noise obtained after [HESWAF + modulus] technique in the Rayleigh condition may be disturbing for comparative purposes. In such cases, there is a simple way to recover a “linear” shape (i.e., a noise of constant amplitude instead of a noise of decreasing amplitude at both extremities). To achieve this, a constant signal can simply be added to the acquired FID and then removed after [HESWAF + modulus] post-processing. If the value of the constant signal is selected to be higher than three times the SD of the noise in the original FID, the Gaussian condition will be fulfilled in the whole FID. As a result, the SNR of the spectrum obtained using [HESWAF + modulus] post-processing will be equal to the SNR of the spectrum obtained using conventional post-processing. Of course, in that case, the gain in SNR owing to the Rayleigh condition will be lost, but the original goal is reached: the SD of the noise now remains identical over the whole frequency range in the resulting spectrum. The red part of Fig. 1 shows how this extra post-processing step can be introduced in the HESWAF technique in order to recover a conventional noise shape in the Rayleigh case as well.

Finally, it is noteworthy that all the results described in this simulation section do not take into account the potential gain in SNR that can be achieved by performing modulus extraction before spatial filtering. Of course, this gain will be added to the gain in SNR resulting from the combination between HESWAF and modulus post-processings.