D-optimal experimental designs for a growth model applied to a Holstein-Friesian dairy farm

Abstract

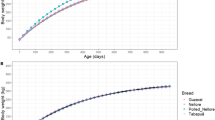
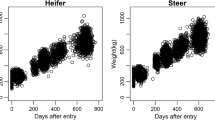
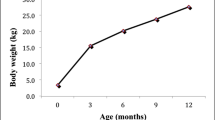
The body mass growth of organisms is usually represented in terms of what is known as ontogenetic growth models, which represent the relation of dependence between the mass of the body and time. This paper discusses design issues of West’s ontogenetic growth model applied to a Holstein-Friesian dairy farm in the northwest of Spain. D-optimal experimental designs were computed to obtain an optimal fitting of the model. A correlation structure has been included in the statistical model due to the fact that observations on a particular animal are not independent. The choice of a robust correlation structure is an important contribution of this paper; it provides a methodology that can be used for any correlation structure. The experimental designs undertaken provide a tool to control the proper weight of heifers, which will help improve their productivity and, by extension, the competitiveness of the dairy farm.

Appendix

Here the derivation of $M(\xi ,\theta )$ is made in detail to the more general case, that is, when the mean of the response and the covariance structure may share common parameters (Pázman 2004).

The information matrix for any design $\xi$ is equal to

$$\begin{aligned} M(\xi ,\theta )= \text {E}_\text {y}\left[ - \dfrac{\partial ^{2}\log f(y \! \mid \! t,\theta )}{\partial \theta ^{2}} \right] \!, \end{aligned}$$

and, assuming gausianity, the negative of the first order derivative of the log-likelihood function being

$$\begin{aligned} -\dfrac{\partial \log f(y \! \mid \! t,\theta )}{\partial \theta _i}&= \dfrac{1}{2}\left\{ \dfrac{\partial }{\partial \theta _i} \left[ (y-\eta (t,\theta ))^{'} \Sigma ^{-1} (\theta ) (y-\eta (t,\theta ))\right] \right. \\&\quad \left. +\, \dfrac{\partial }{\partial \theta _i} \left[ \log \det \Sigma (\theta )\right] \right\} \!. \end{aligned}$$

The first term is

$$\begin{aligned} -2(y\!-\!\eta (t,\theta ))^{'}\Sigma ^{-1}(\theta )\dfrac{\partial \eta (t,\theta )}{\partial \theta _i} \!-\!(y-\eta (t,\theta ))^{'} \Sigma ^{-1}(\theta )\dfrac{\partial \Sigma (\theta )}{\partial \theta _i}\Sigma ^{-1} (\theta )(y\!-\!\eta (t,\theta ))\!, \end{aligned}$$

and the second,

$$\begin{aligned} \dfrac{\dfrac{\partial \det \Sigma (\theta )}{\partial \theta _i}}{\det \Sigma (\theta )}&= \dfrac{tr\left[ \text {adj}(\Sigma (\theta ))\dfrac{\partial \Sigma (\theta ) }{\partial \theta _i} \right] }{det \Sigma (\theta )}= tr\left[ \dfrac{\text {adj}(\Sigma (\theta ))}{\det \Sigma (\theta )}\dfrac{\partial \Sigma (\theta )}{\partial \theta _i} \right] \\&= tr \left[ \Sigma ^{-1}(\theta ) \dfrac{\partial \Sigma (\theta )}{\partial \theta _i} \right] \!. \end{aligned}$$

The first term of the second order derivative is

$$\begin{aligned}&\dfrac{\partial }{\partial \theta _i \partial \theta _j}\left[ \dfrac{1}{2} (y-\eta (t,\theta ))^{'} \Sigma ^{-1}(\theta ) (y-\eta (t,\theta ))\right] =\dfrac{(\partial \eta (t,\theta ))^{'}}{\partial \theta _j}\Sigma ^{-1}(\theta )\dfrac{\partial \eta (t,\theta )}{\partial \theta _i}\,\\\\&\quad +\,(y-\eta (t,\theta ))^{'} \Sigma ^{-1}(\theta )\dfrac{\partial \Sigma (\theta )}{\partial \theta _j}\Sigma ^{-1} (\theta )\dfrac{\partial \eta (t,\theta )}{\partial \theta _i} -(y-\eta (t,\theta ))^{'}\Sigma ^{-1}(\theta )\dfrac{\partial \eta (t,\theta )}{\partial \theta _i\partial \theta _j}\\\\&\quad +\,(y-\eta (t,\theta ))^{'}\Sigma ^{-1}(\theta )\dfrac{\partial \Sigma (\theta )}{\partial \theta _i}\Sigma ^{-1}(\theta )\dfrac{\partial \eta (t,\theta )}{\partial \theta _j}\\\\&\quad +\,(y-\eta (t,\theta ))^{'} \Sigma ^{-1}(\theta )\dfrac{\partial \Sigma (\theta )}{\partial \theta _i}\Sigma ^{-1} (\theta )\dfrac{\partial \Sigma (\theta )}{\partial \theta _j}\Sigma ^{-1}(\theta )(y-\eta (t,\theta ))\\\\&\quad -\,\dfrac{1}{2}(y-\eta (t,\theta ))^{'} \Sigma ^{-1}(\theta )\dfrac{\partial \eta (t,\theta ))}{\partial \theta _i\partial \theta _j}\Sigma ^{-1} (\theta )(y-\eta (t,\theta )). \end{aligned}$$

and the second,

$$\begin{aligned} \dfrac{\partial }{\partial \theta _i \partial \theta _j}\left[ \dfrac{1}{2} \log \det \Sigma (\theta ) \right]&= -\dfrac{1}{2} tr\left[ \Sigma ^{-1}(\theta )\dfrac{\partial \Sigma (\theta )}{\partial \theta _j}\Sigma ^{-1}(\theta )\dfrac{\partial \Sigma (\theta )}{\partial \theta _i}\right] \\&\quad + \dfrac{1}{2} tr\left[ \Sigma ^{-1}(\theta ) \dfrac{\partial \Sigma }{\partial \theta _i\partial \theta _j}\right] \!. \end{aligned}$$

Considering that

$$\begin{aligned} \text {E}[(y-\eta (t,\theta ))]=0,\;\text {E}[(y-\eta (t,\theta ))^{'}(y-\eta (t,\theta ))]=\Sigma (\theta ) \end{aligned}$$

and for any vector $x$ and any symmetric matrix $A$,

$$\begin{aligned} \text {E}[x'Ax]=tr[A\text {E}(xx')]\!, \end{aligned}$$

the information matrix, obtained by calculating the expected value of the sum of the first and second term of the second order derivative, is expressed as follows,

$$\begin{aligned} \left( M(\xi ,\theta )\right) _{ij}&= \dfrac{\partial \eta ^{'}(t,\theta ) }{\partial \theta _j}\Sigma ^{-1}(\theta )\dfrac{\partial \eta (t,\theta ) }{\partial \theta _i} +tr\left[ \Sigma ^{-1}(\theta )\dfrac{\partial \Sigma (\theta ) }{\partial \theta _i}\Sigma ^{-1}(\theta )\dfrac{\partial \Sigma (\theta ) }{\partial \theta _j}\right] \\\\&\quad -\,\dfrac{1}{2}tr \!\left[ \Sigma ^{-1}(\theta )\dfrac{\partial \Sigma (\theta )}{\partial \theta _i \partial \theta _j} \right] \!- \dfrac{1}{2}tr \!\left[ \Sigma ^{-1}(\theta )\dfrac{\partial \Sigma (\theta ) }{\partial \theta _j} \Sigma ^{-1}(\theta ) \dfrac{\partial \Sigma (\theta ) }{\partial \theta _i} \right] \\&\quad +\,\dfrac{1}{2}tr\!\left[ \Sigma ^{-1}(\theta )\dfrac{\partial \Sigma (\theta )}{\partial \theta _i \partial \theta _j} \right] \\\\&= \dfrac{\partial \eta ^{'}(t,\theta ) }{\partial \theta _j}\Sigma ^{-1}(\theta )\dfrac{\partial \eta (t,\theta )}{\partial \theta _i} +\dfrac{1}{2}tr\left[ \Sigma ^{-1}(\theta )\dfrac{\partial \Sigma (\theta )}{\partial \theta _i}\Sigma ^{-1}(\theta )\dfrac{\partial \Sigma (\theta )}{\partial \theta _j} \right] \!. \end{aligned}$$