Emulator-assisted data assimilation in complex models

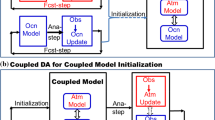
Abstract

Emulators are surrogates of complex models that run orders of magnitude faster than the original model. The utility of emulators for the data assimilation into ocean models is still not well understood. High complexity of ocean models translates into high uncertainty of the corresponding emulators which may undermine the quality of the assimilation schemes based on such emulators. Numerical experiments with a chaotic Lorenz-95 model are conducted to illustrate this point and suggest a strategy to alleviate this problem through the localization of the emulation and data assimilation procedures. Insights gained through these experiments are used to design and implement data assimilation scenario for a 3D fine-resolution sediment transport model of the Great Barrier Reef (GBR), Australia.

Appendices

Appendix 1

1.1 Gaussian process modeling

A detailed description of the Gaussian process modeling (GPM) can be found in Kitanidis (1986), Oakley and O’Hagan (2002), and Fuentes et al. (2003), and we outline only the general approach here. GPM is a Bayesian method for emulating complex deterministic models. The output from the model is considered a realization of a stochastic process, and the prior knowledge of this process is updated using an ensemble of model runs to form a posterior distribution. We formulate the prior knowledge by decomposing the model function into a mean component with an additive Gaussian error:

$$ f\left(\boldsymbol{\uptheta} \right)=m\left(\boldsymbol{\uptheta} \right)+e\left(\boldsymbol{\uptheta} \right), $$

(10)

where m(θ) = E[f(θ)] and e(θ) is a zero-mean Gaussian process. We further decompose the mean function into a linear sum of basis functions familiar from regression modeling:

$$ m\left(\boldsymbol{\uptheta} \right)=\mathrm{h}{\left(\boldsymbol{\uptheta} \right)}^{\mathrm{T}}\boldsymbol{\upbeta} . $$

Here, h(θ) is a vector of N _h known functions (regressors) and β is a vector of N _h unknown coefficients. We capture the dependence in this Gaussian process by modeling the covariance between two points as

$$ c\left({\boldsymbol{\uptheta}}_1,{\boldsymbol{\uptheta}}_2\right)={\sigma}^2r\left({\boldsymbol{\uptheta}}_1-{\boldsymbol{\uptheta}}_2\right), $$

where r(⋅) is a correlation function satisfying r(0) = 1 and σ ² is a variance parameter to be estimated. We adopt the following form for r(⋅),

$$ r\left({\boldsymbol{\uptheta}}_1-{\boldsymbol{\uptheta}}_2\right)= \exp \left\{-{\left({\boldsymbol{\uptheta}}_1-{\boldsymbol{\uptheta}}_2\right)}^T\tilde{\mathbf{R}}\left({\boldsymbol{\uptheta}}_1-{\boldsymbol{\uptheta}}_2\right)\right\}, $$

where $\tilde{\mathbf{R}}= diag\left\{{r}_i:i=1, \dots,\;{N}_{\theta}\right\}$ is a positive definite matrix of scale parameters.

Our prior knowledge can now be expressed in terms of the parameters β, σ ² and $\tilde{\mathbf{R}}$, but including $\tilde{\mathbf{R}}$ into the inference problem makes it intractable. Hence, the prior specification is completed by assigning a vague prior p(β, σ ²) ∝ σ ^− 2, and using empirical estimates of the {r _i }. The posterior distributions calculated may therefore be regarded as conditional on these estimates (Kennedy and O’Hagan 2001).

The prior distribution (10) is updated using a training sample

$$ \mathrm{y}=\left\{f\left({\boldsymbol{\uptheta}}_i\right):i= 1,\dots, {N}_y\right\}, $$

which is a set of model simulations for configurations {θ _i  : i = 1, …, N _y }.. The posterior distribution for x(⋅) given the training sample is a scaled Student t process (Kitanidis 1986; Fuentes et al. 2003),

$$ \frac{f\left(\boldsymbol{\uptheta} \right)-\widehat{m}\left(\boldsymbol{\uptheta} \right)}{\widehat{\sigma}\;\widehat{c}\left(\boldsymbol{\uptheta}, \boldsymbol{\uptheta} \right)}\sim {t}_{N_{\mathrm{y}}-{N}_h} $$

(11)

where

$$ \widehat{m}\left(\boldsymbol{\uptheta} \right)={\widehat{\boldsymbol{\upbeta}}}^T\mathbf{h}\left(\boldsymbol{\uptheta} \right)+{\left(\mathrm{y}-\mathbf{H}\widehat{\boldsymbol{\upbeta}}\right)}^{\mathrm{T}}{A}^{-1}t\left(\boldsymbol{\uptheta} \right), $$

(12)

$$ \begin{array}{l}\widehat{c}\left(\boldsymbol{\uptheta}, \boldsymbol{\uptheta} \right)=c\left(\boldsymbol{\uptheta}, \boldsymbol{\uptheta} \right)-t{\left(\boldsymbol{\uptheta} \right)}^T{\mathbf{A}}^{- 1}t\left(\boldsymbol{\uptheta} \right)+\\ {}{\left[\mathbf{h}\left(\boldsymbol{\uptheta} \right)-{\mathbf{H}}^T{\mathbf{A}}^{\mathit{\hbox{-}}1}t\left(\boldsymbol{\uptheta} \right)\right]}^T{\left({\mathbf{H}}^T{\mathbf{A}}^{- 1}\mathbf{H}\right)}^{- 1}\cdot \left[\mathbf{h}\left(\boldsymbol{\uptheta} \right)-{\mathbf{H}}^T{\mathbf{A}}^{- 1}t\left(\boldsymbol{\uptheta} \right)\right].\end{array} $$

(13)

Here, $\widehat{\boldsymbol{\upbeta}}={\left({\mathbf{H}}^{\mathrm{T}}{\mathbf{A}}^{- 1}\mathbf{H}\right)}^{- 1}{\mathbf{H}}^{\mathrm{T}}{\mathbf{A}}^{- 1}\mathrm{y}$ is a vector of regression coefficient estimates; (A) _ij  = c(θ _i , θ _j ) is the variance matrix for the design points; H = (h(θ ₁ ), …, h(θ _Ny ))^T; t(θ) = (c(θ, θ ₁ ), …, c(θ, θ _Ny))^T; and ${\widehat{\sigma}}^2=\frac{{\mathbf{y}}^T\left[{\mathbf{A}}^{- 1}-{\mathbf{A}}^{- 1}\mathbf{H}{\left({\mathbf{H}}^{\mathrm{T}}{\mathbf{A}}^{- 1}\mathbf{H}\right)}^{- 1}{\mathbf{H}}^{\mathrm{T}}{\mathbf{A}}^{- 1}\right]\mathbf{y}}{N_y-{N}_h- 2}.$

The mean value (Eq. (12)) is referred to as an emulator and gives a fast and cheap approximation of the unknown function. The first component of Eq. (12) is a generalized least squares prediction at point θ, and the second component improves the prediction by interpolating errors between the design points {θ _i  : i = 1, …, N _y } and the prediction point θ. The predictions at the design points are exactly the corresponding observations. As the prediction point θ moves away from the design points, the second component of Eq. (12) goes to zero, yielding the generalized least squares prediction. In our study, we assumed a constant covariance scale (r _i  ≡ r, ∀i). The regressor term was set to linear form h(θ)≡(1, θ).

Appendix 2

1.1 Sampling strategy

1.1.1 Importance sampling and residual resampling

According to the importance sampling technique, the posterior distribution (Eq. 7) can be expressed as a sum of weighted delta functions (Van Leeuwen 2009),

$$ p\left({\mathbf{x}}_i\left|{\mathbf{Y}}_i^o\right.\right)={\displaystyle \sum_{j=1}^N{w}_i^j\delta \left({\mathbf{x}}_i-{\mathbf{x}}_i^j\right)} $$

(14)

Here, i index refers to time, j index enumerates individual members of the ensemble, δ is a Kronecker delta function, and weights w read as follows

$$ {w}_i^j=\frac{p\left({\mathbf{y}}_i^o\left|{\mathbf{x}}_i^j\right.\right)}{{\displaystyle \sum_{j=1}^Np\left({\mathbf{y}}_i^o\left|{\mathbf{x}}_i^j\right.\right)}} $$

(15)

Using Eqs. (14) and (15), the mean of any function f(x) can be expressed as

$$ \overline{f{\left({\mathbf{x}}_i\right)}_{p\left({\mathbf{x}}_i\left|{\mathbf{Y}}_i^o\right.\right)}}={\displaystyle \int f\left({\mathbf{x}}_i\right)}\cdot p\left({\mathbf{x}}_i\left|{\mathbf{Y}}_i^o\right.\right)d{\mathbf{x}}_i={\displaystyle \sum_{j=1}^N{w}_i^j\cdot f\left({\mathbf{x}}_i^j\right)} $$

(16)

With Eq. (15), one can propagate forward in time weights of the ensemble members and, having known these weights, estimate statistical properties of that ensemble via Eq. (16). For a degenerate ensemble, however, the weight of most particles is close to zero, meaning that these particles represent implausible states of the simulated system. In some cases, the problem of the degeneracy can be addressed through the resampling of particles. The idea is to get rid of low-weight particles and increase the number of “healthy” particles (i.e., particles having high weights). An overview of the established resampling techniques is available in Van Leeuwen (2009). In our study, we employ the residual resampling technique. According to this method, all weights are multiplied by the ensemble size N. “Then n copies are taken of each particle i in which n is the integer part of Nw _i . After obtaining these copies of all members with Nw _i  > = 1, the integer parts of Nw _i are subtracted from Nw _i . The rest of the particles are drawn randomly from the resulting distribution. This method was introduced by Lui and Chen (1998), who report a substantial reduction in sampling noise and thus an improved performance of the filter …” (Van Leeuwen 2009).

1.1.2 Metropolis-Hastings sampling with differential-evolution proposal

Once the importance sampling residual resampling (IS-RR) step is complete, the assimilation scheme proceeds with Metropolis-Hastings Differential Evolution (MH-DE) sampling of Eq. (7) (Ter Braak 2006; Vrugt 2011). DE provides a random proposal particle in a way that acknowledges the distribution of the forecast particles. This new sample is either accepted or rejected according to MH criteria. The number of MH-DE iterations for every assimilation window in our study is set to 10 times the size of the ensemble of models. The key motivation behind MH-DE is to populate the ensemble with new healthy particles (note that IS-RR can produce identical copies of particles. MH-DE sampling is expected to diversify these samples).

A general MCMC sampling strategy is to draw a random sample from the proposal q() and accept it with probability.

$$ p\left({\mathbf{x}}_i^{j+1}\left|{\mathbf{x}}_i\right.\right)= \min \left[\frac{p\left({\mathbf{y}}_i^o\left|{\mathbf{x}}_i^{j+1}\right.\right)p\left({\mathbf{x}}_i^{j+1}\left|{\mathbf{Y}}_{i-1}^o\right.\right)q\left({\mathbf{x}}_i^j\left|{\mathbf{x}}_i^{j+1}\right.\right)}{p\left({\mathbf{y}}_i^o\left|{\mathbf{x}}_i^j\right.\right)p\left({\mathbf{x}}_i^j\left|{\mathbf{Y}}_{i-1}^o\right.\right)q\left({\mathbf{x}}_i^{j+1}\left|{\mathbf{x}}_i^j\right.\right)},\kern0.36em 1\right] $$

(17)

According to the DE proposal, samples from q() are given by

$$ {\mathbf{x}}_i^{j+1}={\mathbf{x}}_i^{h,j}+\gamma \left[{\mathbf{x}}_i^{n,j}-{\mathbf{x}}_i^{m,j}\right]+{\boldsymbol{\upvarepsilon}}_i $$

(18)

where x _i ^h,j, x _i ^n,j, and x _i ^m,j are random samples from p(x _i ^j|Y _i−1 ^o), γ is a scaling constant, and ε _i is an additive error term. Figure 11 illustrates DE sampling.

Fig. 11

Schematic representation of DE sampling

Since the DE proposal is symmetric, the acceptance probability (Eq.17) reduces to

$$ p\left({\mathbf{x}}_i^{j+1}\left|{\mathbf{x}}_i\right.\right)= \min \left[\frac{p\left({\mathbf{y}}_i^o\left|{\mathbf{x}}_i^{j+1}\right.\right)p\left({\mathbf{x}}_i^{j+1}\left|{\mathbf{Y}}_{i-1}^o\right.\right)}{p\left({\mathbf{y}}_i^o\left|{\mathbf{x}}_i^j\right.\right)p\left({\mathbf{x}}_i^j\left|{\mathbf{Y}}_{i-1}^o\right.\right)},\kern0.36em 1\right] $$

(19)

The likelihood function in Eq. (19) in our study is assumed to be Gaussian:

$$ p\left({\mathbf{y}}_i^o\left|{\mathbf{x}}_i^j\right.\right)\sim \exp \left\{-\frac{1}{2}{\left[{\mathbf{y}}_i^o-H\left({\mathbf{x}}_i^j\right)\right]}^T{\mathbf{R}}^{-1}\left[{\mathbf{y}}_i^o-H\left({\mathbf{x}}_i^j\right)\right]\right\} $$

(20)

Here, H(x _i ^j) is a measurement operator and R is the error covariance of the observation.

The forecast density in Eq. (19) is given by

$$ p\left(\mathbf{x}\left|{\mathbf{Y}}_{i-1}^o\right.\right)={{\displaystyle \int \left[p\left({\mathbf{x}}_i\left|{\mathbf{x}}_{i-1}\right.\right)p\left({\mathbf{x}}_{i-1}\left|{\mathbf{Y}}_{i-1}^o\right.\right)\right]d\mathbf{x}}}_{i-1} $$

(21)

Note that for a deterministic model, p(x _i |Y _i−1 ^o) = p(x _i−1|Y _i−1 ^o), where p(x _i−1|Y _i−1 ^o) can be interpreted as a “prior” distribution of the model. The probability of the acceptance (Eq. (19)) in this case is expressed as a ratio of likelihoods multiplied by the corresponding “priors.” In the degenerate case, the members of the ensemble tend to collapse into a relatively small subregion of the state space. The prior density p(x _i−1|Y _i−1 ^o) estimated from these samples will have its major support allocated within that subregion as well. For any new proposal located beyond that subregion, the prior probability and, hence, the probability of the acceptance are likely to be small—the ensemble will get stuck in the degenerate state. To facilitate the recovery of such ensembles from the degenerate state, in our study we assume the prior density to be constant, thus reducing the acceptance probability (Eq. (19)) to the ratio of likelihoods

$$ p\left({\mathbf{x}}_i^{j+1}\Big|{\mathbf{x}}_i\right)= \min \left[\frac{p\left({\mathbf{y}}_i^o\left|{\mathbf{x}}_i^{j+1}\right.\right)}{p\left({\mathbf{y}}_i^o\left|{\mathbf{x}}_i^j\right.\right)},\kern0.36em 1\right] $$

(22)

Probability (22) is consistent with the acceptance probability of a batch assimilation of data over the time window (t_i-1, t_i) under assumption of uninformative priors. Despite this assumption, the knowledge of observations prior to t_i-1, in our study, is still passed through to the new assimilation window via the allocation of prior samples delivered from the previous assimilation step. These prior samples are anticipated to reduce the number of the burn-off iterations typically required by the MCMC machinery. An impact of the assumption of the uninformative priors on the estimated posterior (7) has not been fully investigated in this study.