Abstract
This note shows that we can recover any complex vector \(\boldsymbol {x}_{0} \in \mathbb {C}^{n}\) exactly from on the order of n quadratic equations of the form |〈a i ,x 0〉|2=b i , i=1,…,m, by using a semidefinite program known as PhaseLift. This improves upon earlier bounds in Candès et al. (Commun. Pure Appl. Math. 66:1241–1274, 2013), which required the number of equations to be at least on the order of nlogn. Further, we show that exact recovery holds for all input vectors simultaneously, and also demonstrate optimal recovery results from noisy quadratic measurements; these results are much sharper than previously known results.
Similar content being viewed by others
Notes
Upon retrieving
 , a simple factorization recovers x
0 up to global phase, i.e. multiplication by a complex scalar of unit magnitude.
, a simple factorization recovers x
0 up to global phase, i.e. multiplication by a complex scalar of unit magnitude.For any unit-normed vector x, there is \(\boldsymbol {x}_{0} \in \mathcal {N}_{\epsilon}\) with ∥x 0∥2=1 and ∥x−x 0∥2≤ϵ, where ϵ>0.
The careful reader will note that we can get a far better constant by observing that the proof of Theorem 1.2 also yields ∥Y T ∥ F ≤1/4. Hence, we have
 .
.
References
R. Balan, P.G. Casazza, D. Edidin, On signal reconstruction without noisy phase, Appl. Comput. Harmon. Anal. 20, 345–356 (2006).
E.J. Candès, Y. Eldar, T. Strohmer, V. Voroninski, Phase retrieval via matrix completion, SIAM J. Imaging Sci. 6(1), 199–225 (2013).
E.J. Candès, T. Strohmer, V. Voroninski, Phaselift: exact and stable signal recovery from magnitude measurements via convex programming, Commun. Pure Appl. Math. 66, 1241–1274 (2013).
L. Demanet, P. Hand, Stable optimizationless recovery from phaseless linear measurements. ArXiv e-prints, August 2012.
R. Vershynin, Introduction to the non-asymptotic analysis of random matrices, in Compressed Sensing: Theory and Applications, ed. by Y.C. Eldar, G. Kutyniok (Cambridge University Press, Cambridge, 2012), pp. 210–268.
Acknowledgements
E.C. is partially supported by AFOSR under grant FA9550-09-1-0643 and by ONR under grant N00014-09-1-0258. X.L. thanks Vladislav Voroninski for useful discussions related to this project. We are grateful to an anonymous referee for helpful comments. This work was partially presented at the University of California at Berkeley in January 2012, and at the University of British Columbia in February 2012.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Michael Todd.
Rights and permissions
About this article
Cite this article
Candès, E.J., Li, X. Solving Quadratic Equations via PhaseLift When There Are About as Many Equations as Unknowns. Found Comput Math 14, 1017–1026 (2014). https://doi.org/10.1007/s10208-013-9162-z
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10208-013-9162-z
Keywords
- Phase retrieval
- PhaseLift
- Semidefinite relaxations of nonconvex quadratic programs
- Deviation inequalities for random matrices



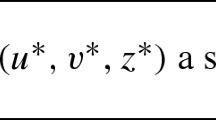

 , a simple factorization recovers x
0 up to global phase, i.e. multiplication by a complex scalar of unit magnitude.
, a simple factorization recovers x
0 up to global phase, i.e. multiplication by a complex scalar of unit magnitude. .
.