Convergence of Lowest Order Semi-Lagrangian Schemes

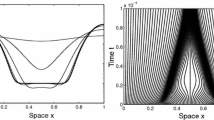
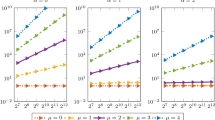
Abstract

We consider generalized linear transient advection-diffusion problems for differential forms on a bounded domain in ℝ^d. We provide comprehensive a priori convergence estimates for their spatiotemporal discretization by means of a first-order in time semi-Lagrangian approach combined with a discontinuous Galerkin method. Under rather weak assumptions on the velocity underlying the advection we establish an asymptotic L ²-estimate of order $O(\tau+h^{r}+h^{r+1}\tau^{-\frac{1}{2}}+\tau^{\frac{1}{2}})$, where h is the spatial meshwidth, τ denotes the time step, and r is the polynomial degree of the forms used as trial functions. This estimate can be improved considerably in a variety of special settings.

Appendix A: Auxiliary Estimates

We exploit the close relationship of the operator $\operatorname {\mathsf {L}}_{ \boldsymbol {\beta }}+ \operatorname {\mathcal {L}}_{ \boldsymbol {\beta }}$ and the bilinear form $({X^{\ast}_{-\tau}\omega},{X^{\ast}_{-\tau}\eta} )_{X_{\tau}(\varOmega)}$. In Sect. 3 we use the result of this section for $\operatorname {\mathsf {L}}_{ \boldsymbol {\beta }}+\operatorname {\mathcal {L}}_{ \boldsymbol {\beta }}$ to prove the well-posedness of (15). Also, the analysis of the auxiliary method of characteristics introduced in Sect. 6 is based on the following results for the bilinear form $({X^{\ast}_{-\tau}\omega},{X^{\ast}_{-\tau}\eta})_{X_{\tau}(\varOmega)}$.

Proposition A.1

Let β∈W ^1,∞(Ω) and ω,η∈L ² Λ ^k(Ω), then

• (a) we have the estimate

  $$ \bigl|{\bigl({X^\ast_{-\tau}\omega},{X^\ast_{-\tau}\eta}\bigr)_{X_\tau (\varOmega)}}\bigr|\leq C(DX_{-\tau}) \|{\omega}\|_{L^{2}\varLambda ^{k}({\varOmega })} \|{\eta}\|_{L^{2}\varLambda ^{k}({\varOmega })}, $$

  (50)

  with C(DX _−τ )=1+τC(D β) for τ sufficiently small;

• (b) the operator $\operatorname {\mathsf {L}}_{ \boldsymbol {\beta }}+ \operatorname {\mathcal {L}}_{ \boldsymbol {\beta }}$ is symmetric:

  $$ \bigl({\omega},{(\operatorname {\mathsf {L}}_{ \boldsymbol {\beta }}+\operatorname {\mathcal {L}}_{ \boldsymbol {\beta }}) \eta}\bigr)_\varOmega= \bigl({(\operatorname {\mathsf {L}}_{ \boldsymbol {\beta }}+\operatorname {\mathcal {L}}_{ \boldsymbol {\beta }}) \omega},{\eta}\bigr)_\varOmega,\quad\omega, \eta\in L^{2}\varLambda ^{k}({\varOmega }). $$

  (51)

  and we have the estimate

  $$ \bigl|{\bigl({\omega},{(\operatorname {\mathsf {L}}_{ \boldsymbol {\beta }}+\operatorname {\mathcal {L}}_{ \boldsymbol {\beta }}) \eta}\bigr)_\varOmega}\bigr| \leq C |{ \boldsymbol {\beta }}|_{ {\boldsymbol {W}}^{{1},{\infty}}({\varOmega })} \|{\omega}\|_{L^{2}\varLambda ^{k}({\varOmega })} \|{\eta}\|_{L^{2}\varLambda ^{k}({\varOmega })}. $$

  (52)

If β∈W ^2,∞(Ω) and ω,η∈L ² Λ ^k(Ω)

• (c) we have the expansion

  $$ \bigl({X^\ast_{-\tau}\omega},{X^\ast_{-\tau}\eta}\bigr)_{X_\tau(\varOmega)} = ({\omega},{\eta})_\varOmega- \tau\bigl({\omega },{(\operatorname {\mathsf {L}}_{ \boldsymbol {\beta }}+\operatorname {\mathcal {L}}_{ \boldsymbol {\beta }})\eta}\bigr)_\varOmega+ R( \boldsymbol {\beta },\tau) ({\omega},{\eta})_\varOmega, $$

  (53)

  with ∥R(β,τ)∥≤C(β)τ ² independent of ω and η.

Proof

(1) We first examine the special case of Ω being a domain in ℝ³.

The results follow directly from the corresponding vector proxy representations from Table 2. While the assertion (b) is obvious in ℝ³, we recall that

$$ \bigl({X^\ast_{-\tau}\omega},{X^\ast_{-\tau}\eta}\bigr)_{X_\tau(\varOmega)}= \int_{\varOmega} \omega\wedge X^{\ast}_{\tau} \star X^\ast_{-\tau }\eta $$

and hence, we find for differential forms ω in ℝ³ with vector correspondences u or u:

which yields the assertion (a). Taylor expansion of $\omega\wedge X^{\ast}_{\tau} \star X^{\ast}_{-\tau}\omega$ in τ finally proves assertion (c).

(2) General case (see also [32, Lemma 4.1]):

The proof for the general case is very similar, but involves certain technical notation from tensor calculus, if one aims at explicit formulas for the operator $\operatorname {\mathsf {L}}_{ \boldsymbol {\beta }}+\operatorname {\mathcal {L}}_{ \boldsymbol {\beta }}$ and the constants. By density of $\operatorname {\varLambda }^{k}({\varOmega })$ in L ² Λ ^k(Ω) it is enough to prove the assertions for smooth $\eta,\omega\in \operatorname {\varLambda }^{k}({\varOmega })$.

(a) By multilinearity we have for orthonormal vector fields e ₁,…,e _n and σ∈S(j,n), $\gamma\in \operatorname {\varLambda }^{j}({\varOmega })$ and x∈Ω [60, p. 610]:

(54)

where the quantities det((DX _τ (x)) _σ′,σ ) are known as the j-minors of the differential DX _τ (x) with respect to e ₁,…,e _n , i.e., the determinants of those submatrices of DX _τ (x) that contain the rows σ′ and columns σ. By the definition of the inner product of differential forms we have

$$ \bigl({X^\ast_{-\tau} \omega},{X^\ast_{-\tau} \eta} \bigr)_{X_\tau(\varOmega)} = \int_{X_\tau(\varOmega)} X^\ast_{-\tau}\omega\wedge \star X^\ast _{-\tau}\eta= \int_{X_\tau(\varOmega)} \bigl({X^\ast_{-\tau}\omega},{X^\ast _{-\tau}\eta}\bigr) \mu. $$

Hence, by the definition of the inner product of alternating forms and (54), we find

$$ \bigl({X^\ast_{-\tau}\omega},{X^\ast_{-\tau}\eta} \bigr)_{X_\tau(\varOmega)}= \bigl({\det(DX_\tau) {\mathbf {M}}_k(DX_{\tau})\omega},{{\mathbf {M}}_k(DX_{\tau })\eta}\bigr)_\varOmega, $$

(55)

with

This proves the assertion.

(b) We consider $\bar{\eta}$ and $\bar{\omega}$ to be extensions of η and ω to $\operatorname {\varLambda }^{k}({ \mathbb {R}^{n}})$ and assume β∈C ^∞(Ω). First, Cartan’s formula (7) and compatibility of exterior product and pullback yield:

$$ \begin{aligned} \bar{\eta}\wedge \star (\operatorname {\mathsf {L}}_{ \boldsymbol {\beta }}+ \operatorname {\mathcal {L}}_{ \boldsymbol {\beta }})\bar{\omega}&=\lim_{\tau\to0}\frac{1}{\tau} \bigl(\bar{\eta}\wedge\bigl(\star X^\ast_{\tau} \bar{\omega}- \star \bar{\omega}\bigr) - \bar{\eta}\wedge\bigl(X^\ast_{\tau} \star \bar{\omega}- \star \bar{\omega}\bigr)\bigr) \\ &= \lim_{\tau\to0}\frac{1}{\tau} \bar{\eta}\wedge\bigl(\star X^\ast_{\tau} \bar{\omega}- X^\ast_{\tau} \star \bar{\omega}\bigr) \\ &= \lim_{\tau\to0} \frac{1}{\tau} \bigl(\bar{\eta}\wedge \star X^\ast_{\tau} \bar{\omega}- X^\ast_\tau\bigl(X^\ast_{-\tau}\bar{\eta}\wedge \star \bar{\omega}\bigr)\bigr) \\ &= \lim_{\tau\to0} \frac{1}{\tau} \bigl(\bigl({\bar{\eta}},{X^\ast_\tau\bar{\omega}}\bigr)\mu- X^\ast_{\tau} \bigl({X^\ast_{-\tau} \bar{\eta}},{\bar{\omega}}\bigr) \mu\bigr). \end{aligned} $$

From the Taylor expansion DX _τ (x)=id+τD β(x)+O(τ ²) of DX _τ (x) around τ=0 and the Taylor expansion of det( ), $\det({\mathbf {A}}+\varepsilon {\mathbf {B}})= \det({\mathbf {A}})+\varepsilon \operatorname {tr}(\mathsf {Adj}({\mathbf {A}}){\mathbf {B}})+O(\varepsilon^{2})$ and (54) we infer

$$ \begin{aligned} &\bigl(X_\tau^\ast \gamma\bigr)_x({\mathbf {e}}_{\sigma(1)},\dots,{\mathbf {e}}_{\sigma(j)})\\ &\quad=\sum_{\sigma'\in S(j,n)} \det\bigl( (I_n)_{\sigma',\sigma}\bigr) \gamma_{X_\tau(x)}({\mathbf {e}}_{\sigma'(1)},\ldots, {\mathbf {e}}_{\sigma'(j)}),\\ & \qquad{}+\tau\sum_{\sigma' \in S(j,n)}\operatorname {tr}\bigl( \mathsf {Adj}\bigl( (I_n)_{\sigma',\sigma} \bigr) (D \boldsymbol {\beta }_{x})_{\sigma',\sigma}\bigr) \gamma_{X_\tau(x)}({\mathbf {e}}_{\sigma'(1)},\dots, {\mathbf {e}}_{\sigma'(j)})+O\bigl(\tau^2\bigr), \end{aligned} $$

(56)

with Adj and $\operatorname {tr}$ the adjugate and trace operator for matrices, and the unit matrix I _n ∈ℝ^n×n. Introducing the abbreviation

(57)

we find:

(58)

This result holds for any extension of ω and η and the assertion follows by density of $\operatorname {\varLambda }^{k}({\varOmega })$ in L ² Λ ^k(Ω), since ${\mathbf {M}}_{k}'(\cdot)$ depends only on the Jacobian of β. Thus we see that β∈W ^1,∞(Ω) is the minimal smoothness assumption for β.

(c) First, we see that:

$$ \begin{aligned} \frac{\partial}{\partial\tau} \bigl({X^\ast_{\tau} \omega},{X^\ast_{\tau}\eta}\bigr)_{X_{-\tau}(\varOmega)|_{\tau=0}} &=\lim_{\tau\to0}\frac{1}{\tau}\bigl(({\omega},{\eta})_\varOmega -\bigl({X^\ast_{-\tau} \omega},{X^\ast_{-\tau}\eta}\bigr)_{X_\tau(\varOmega)} \bigr) \\ &= \lim_{\tau\to 0} \frac{1}{\tau}\bigl(({\omega},{\eta})_\varOmega- \bigl({X^\ast_{-\tau} \omega},{\eta}\bigr)_{X_\tau(\varOmega)} \bigr) \\ &\quad+ \lim_{\tau\to 0}\frac{1}{\tau}\bigl(\bigl({X^\ast_{-\tau}\omega},{\eta} \bigr)_{X^\ast _\tau(\varOmega)} - \bigl({X^\ast_{-\tau} \omega},{X^\ast_{-\tau }\eta}\bigr)_{X_\tau(\varOmega)} \bigr) \\ &= \lim_{\tau\to 0} \frac{1}{\tau}\int_\varOmega\omega\wedge\bigl( \star \eta- X^\ast_\tau \star \eta\bigr)\\ &\quad + \lim_{\tau\to 0} \frac{1}{\tau}\int_\varOmega\omega\wedge X^\ast_\tau \star \bigl( \eta- X^\ast_{-\tau} \eta\bigr)\\ &= ({\omega},{\operatorname {\mathcal {L}}_{ \boldsymbol {\beta }}\eta})_\varOmega+ ({\omega },{\operatorname {\mathsf {L}}_{ \boldsymbol {\beta }}\eta})_\varOmega. \end{aligned} $$

Then the assertion follows by the Taylor expansion of (55). □

While the previous result is important in the treatment of the advection terms, the treatment of the diffusion requires certain multiplicative trace inequalities.

Recall that (12) implies an integration by parts formula for $\omega\in \operatorname {\varLambda }^{k}({\varOmega })$ and $\eta\in \operatorname {\varLambda }^{k+1}({\varOmega })$ on a bounded domain Ω:

$$ \int_{\partial\varOmega} \operatorname {tr}\omega\wedge \operatorname {tr}\star \eta= ({\operatorname {\mathsf {d}}\omega},{\eta})_\varOmega- ({\omega},{\operatorname {\mathsf {d}}\eta})_\varOmega. $$

Observe that the right-hand side is not a semidefinite bilinear form. Nevertheless we have a Cauchy–Schwarz type inequality:

Proposition A.2

Let Ω be a bounded domain with outward normal n _Ω . Then, we define a seminorm for $\omega\in \operatorname {\varLambda }^{k}({\varOmega })$ by

$$ |{\omega}|_{\partial\varOmega,\operatorname {tr}}^2:= \int_{\partial \varOmega} \operatorname {tr}\operatorname {\mathsf {i}}_{{\mathbf {n}}_\varOmega} (\omega \wedge \star \omega), $$

(59)

and have

$$ \biggl|\int_{\partial\varOmega} \operatorname {tr}\omega\wedge \operatorname {tr}\star \eta \biggr| \leq |{\omega}|_{\partial\varOmega,\operatorname {tr}} |{\eta }|_{\partial \varOmega,\operatorname {tr}},\quad\omega\in \operatorname {\varLambda }^{k}({\varOmega }),\ \eta\in \operatorname {\varLambda }^{k+1}({\varOmega }), $$

(60)

for $\omega\in \operatorname {\varLambda }^{k}({\varOmega })$ and $\eta\in \operatorname {\varLambda }^{k+1}({\varOmega })$.

Proof

According to [61, Prop. 1.2.6] we have:

$$ \operatorname {tr}\omega\wedge \operatorname {tr}\star \eta= (\omega, \operatorname {\mathsf {i}}_{{\mathbf {n}}_\varOmega}\eta) \operatorname {\mathsf {i}}_{{\mathbf {n}}_\varOmega}\mu, $$

where μ is the volume form of Ω. Hence, the assertion follows from the standard Cauchy–Schwarz inequality for the scalar product of alternating k-forms and

$$ (\omega,\omega)\operatorname {\mathsf {i}}_{{\mathbf {n}}_\varOmega} \mu= \operatorname {\mathsf {i}}_{{\mathbf {n}}_\varOmega} (\omega,\omega) \mu= \operatorname {\mathsf {i}}_{{\mathbf {n}}_\varOmega} (\omega \wedge \star \omega), $$

because, certainly, $(\operatorname {\mathsf {i}}_{{\mathbf {n}}_{\varOmega}} \eta,\operatorname {\mathsf {i}}_{{\mathbf {n}}_{\varOmega}} \eta) \leq(\omega, \omega)$. □

The next proposition states a multiplicative trace inequality (cf. [1, Theorem 3.10]) for the seminorm $|{\cdot}|_{\partial\varOmega,\operatorname {tr}}$ for a convex polygonal domain Ω.

Proposition A.3

Assume that Ω is a convex polygonal domain. Let h _Ω be the radius of the smallest n-dimensional ball that contains Ω and ρ _Ω the radius of the largest n-dimensional ball that is contained in Ω. Then we have:

$$ |{\omega}|_{\partial\varOmega,\operatorname {tr}}^2 \leq2 \frac{h_\varOmega}{\rho_\varOmega} \|{\omega}\|_{L^{2}\varLambda ^{k}({\varOmega })} {|{\omega}|}_{H^{1}\varLambda ^{k}({{\varOmega }})} + \frac{n}{\rho_\varOmega} \|{\omega}\|_{L^{2}\varLambda ^{k}({\varOmega })}^2. $$

(61)

Proof

Without loss of generality, we suppose that the center $\bar{x}$ of the largest inscribed ball is the origin of the coordinate system. We start from the following relation:

$$ \int_{\partial\varOmega} \operatorname {tr}\operatorname {\mathsf {i}}_{{\mathbf {x}}} (\omega\wedge \star \omega) = \int_\varOmega \operatorname {\mathsf {d}}\operatorname {\mathsf {i}}_{{\mathbf {x}}} (\omega\wedge \star \omega). $$

On the one hand we have the lower bound:

$$ \int_{\partial\varOmega} \operatorname {tr}\operatorname {\mathsf {i}}_{{\mathbf {x}}} (\omega\wedge \star \omega) \geq\min_{{\mathbf {x}}\in\partial\varOmega}\bigl({\mathbf {x}}\cdot {\mathbf {n}}_\varOmega({\mathbf {x}})\bigr) \int_{\partial\varOmega} \operatorname {tr}\operatorname {\mathsf {i}}_{{\mathbf {n}}_\varOmega} (\omega\wedge \star \omega) = \rho_\varOmega|{\omega}|_{\partial\varOmega, \operatorname {tr}}^2, $$

(62)

because $\int_{\partial\varOmega} \operatorname {tr}\operatorname {\mathsf {i}}_{{\mathbf {x}}} \mu= \int _{\partial \varOmega} {\mathbf {x}}\cdot {\mathbf {n}}_{\varOmega} \operatorname {\mathsf {i}}_{{\mathbf {n}}_{\varOmega}} \mu$. Moreover,

$$ \begin{aligned} \int_\varOmega \operatorname {\mathsf {d}}\operatorname {\mathsf {i}}_{{\mathbf {x}}} (\omega\wedge \star \omega)=\int_\varOmega \operatorname {\mathsf {L}}_{{\mathbf {x}}} (\omega\wedge \star \omega) = \int_\varOmega(\operatorname {\mathsf {L}}_{{\mathbf {x}}} + \operatorname {\mathcal {L}}_{{\mathbf {x}}}) (\omega\wedge \star \omega) - \int_\varOmega \operatorname {\mathsf {j}}_{{\mathbf {x}}} \operatorname {\delta }(\omega\wedge \star \omega). \end{aligned} $$

(63)

With the Cauchy inequality the second term on the right-hand side is estimated as

$$ \biggl|{\int_\varOmega \operatorname {\mathsf {j}}_{{\mathbf {x}}} \operatorname {\delta }(\omega\wedge \star \omega )}\biggr| \leq2 \sup_{{\mathbf {x}}\in\varOmega} |{{\mathbf {x}}}| \|{\omega}\|_{L^{2}\varLambda ^{k}({\varOmega })} {|{\omega}|}_{H^{1}\varLambda ^{k}({{\varOmega }})}. $$

(64)

Since, further, $(\operatorname {\mathsf {L}}_{{\mathbf {x}}}+\operatorname {\mathcal {L}}_{{\mathbf {x}}}) \mu=(\operatorname {div}{\mathbf {x}}) \mu$ (see (58) and (57)), the lower bound (62) together with (63) and (64) proves assertion (61). □