Abstract
We develop a framework for analyzing prepayment risk on defaultable callable bonds. We argue that prepayment risk emanates from the following informational asymmetry: Callable bond traders cannot determine the issuer’s firm value-maximizing call policy, and their best anticipation is the optimal refinancing policy given by a term structure model. We show that, from the callable bond holder perspective, the issuer’s departure from the optimal refinancing policy translates into an accrued exposure to market risk. The prepayment risk magnitude represents this risk transfer, and we show that callable bond traders can infer it from observable bond characteristics. Tests on callable bond transaction data provide strong evidence for prepayment risk and validate our conjecture that insurance companies trade callable bonds to reduce their exposure to prepayment risk magnitude.




Similar content being viewed by others
Notes
Homeowners’ motivations for prepayment on mortgage debt include non-financial determinants, which make the modelling of prepayment specific to these contracts.
An exception is Ahn and Wilmott (2003) who analyze the exercise policy of an OTC American option when the holder maximizes a CARA, a HARA, or a linear utility function. They find that the option writer gains from the difference between the price maximizing exercise time and the customer’s utility function maximizing exercise time. This analysis is not applied to corporate debt contracts, however.
The market risk factor is assumed to be common knowledge. In single-factor callable bond pricing models, it is represented by the instantaneous risk-free rate.
In Eq. (1), it is implicitly assumed that there exists a unique call threshold that establishes a clean division between the continuation region and the exercise region of the call option. Dixit and Pindyck (1994) prove that this assumption is verified when (i) the difference between the continuing payoff and the stopping payoff is monotonic in the state variable, and (ii) the state variable exhibits positive persistence of uncertainty. These two conditions are satisfied for most option pricing models.
As mentioned earlier, one reason for the issuer to call the bond early (i.e., \(h^{**}>h^{*}\)) is to get rid of restrictive covenants as an investment opportunity becomes available. Alternatively, one reason for the issuer to call the bond late (i.e., \(h^{**}<h^{*}\)) is to synchronize a change in leverage with a change in the capital budgeting policy.
Results are not reported for the sake of brevity, but are available upon request.
To this end, we need to compute the callable bond risk premium. This computation is performed in three steps. First, we calculate the yield to maturity of all straight bonds given their characteristics. Then, we subtract from the yield to maturity the value of the risk-free rate with corresponding time to maturity. We finally compute a \(120\times 109\) array of average risk premiums for every issuer and every month.
In their empirical study of corporate bond call policies, King and Mauer (2000) also observe more late calls than early calls.
Insurance companies will transact with counterparties that are less concerned with prepayment risk (e.g., counterparties that are not actively managing a bond portfolio).
The Move (Merrill Option Volatility Estimate) Index is the weighted average of implied volatilities on the 1-month options written on the 2-year, 5-year, 10-year, and 30-year Treasury bonds. The index is published by Merrill Lynch and can be downloaded from Bloomberg.
Elasticity is computed using the callable bond pricing formula in Proposition 2. Inputs such as the risk-free rate, coupon rate, call price, and risk premium are directly observable from the data. Other inputs related to the dynamics of the short rate (\(\theta , \kappa , \sigma \), and \( \lambda \)) are taken from the estimation of the term structure model (see “Appendix 4”).
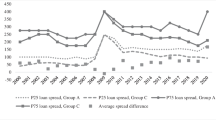
We also ran regressions with the variables of interest (\(c\), \(K\) and \(\eta \) ) taken separately. All variables of interest keep the right predicted sign but lose their significance. This can be attributed to the low level of variation of each of these variables (see Table 5). Consequently, the data only allow us to capture the combined effect of the variables of interest on the trade imbalance.
A duplicate is a transaction between two insurance companies reported one time as a buy transaction and another time as a sell transaction. We detected duplicates assuming their actual cost is the same by more or less 2.5 % and transaction dates differ by 5 days maximum. To avoid any bias, we removed both the buy and sell reportings of a duplicate.
Ideally, we would like to control for firm fixed effects using the identity of the trading insurance company. However, that information is not disclosed in the FISD/NAIC database, but the identity of the trading counterparty is. We therefore coded dummy variables for each of the top 30 counterparties of insurance companies (typically financial institutions or brokerage firms) as well as another dummy for all transactions for which the counterparty is not disclosed.
Fubini’s theorem gives general conditions under which the order of integration can be changed in iterated integrals. Specifically, it states that
$$\begin{aligned} \int _{X}\left( \int _{Y}f\left( x,y\right) \mathrm{d}y\right) \mathrm{d}x=\int _{Y}\left( \int _{X}f\left( x,y\right) \mathrm{d}x\right) \mathrm{d}y, \end{aligned}$$with \(f\left( x,y\right) \) being \(X\times Y\) integrable.
Note that Delbaen (1993) provides an integral representation for the consol \( E_{\mathbb {Q}}\left[ \exp \left( -\int _{0}^{\infty }r_{u}du\right) \right] \). Unfortunately, this result cannot be readily extended to the defaultable case, since a translated square-root process is not a square-root process. Nevertheless, we use Delbaen’s (1993) result to verify the accuracy of our numerical integration in the case where \(\eta =0\).
After February 22, 2002, the 30-year yield is adjusted from the 20-year yield with an extrapolation factor obtained from the St-Louis Federal Reserve Bank website.
The estimation window starts three years earlier to let the Kalman filter fit the data properly.
References
Acharya, V., Carpenter, J.: Corporate bond valuation and hedging with stochastic interest rates and endogenous bankruptcy. Rev. Financ. Stud. 15, 1355–1383 (2002)
Ahn, H., Wilmott, P.: On exercising American options: the risk of making more money than you expected. Wilmott Magazine, pp. 52–63 (2003)
Artzner, P., Delbaen, F.: Credit risk and prepayment option. Astin Bull. 22, 81–96 (1992)
Barnea, A., Haugen, R., Senbet, L.: A rationale for debt maturity structure and call provisions in the agency theoretic framework. J. Financ. 35, 1223–1234 (1980)
Barone, E., Barone-Adesi, G., Castagna, A.: Pricing bonds and bond options with default risk. Eur. Financ. Manag. 4, 231–282 (1998)
Bodie, Z., Taggart, R.: Future investment opportunities and the value of a call provision on a bond. J. Financ. 33, 1187–1200 (1978)
Boyce, W., Kalotay, A.: Tax differentials and callable bonds. J. Financ. 34, 825–838 (1979)
Campbell, J., Taksler, G.: Equity volatility and corporate bond yields. J. Financ. 58, 2321–2350 (2003)
Cox, J., Ingersoll, J., Ross, S.: A theory of the term structure of interest rates. Econometrica 53, 385–407 (1985)
Delbaen, F.: Consols in the CIR model. Math. Financ. 3, 125–134 (1993)
Deng, Y., Quigley, J., Van Order, R.: Mortgage terminations, heterogeneity and the exercise of mortgage options. Econometrica 68, 275–307 (2000)
Dixit, A., Pindyck, R.: Investment Under Uncertainty. Princeton University Press, Princeton (1994)
Duan, J.-C., Simonato, J.-G.: Estimating and testing exponential-affine term structure models by Kalman filter. Rev. Quant. Financ. Account. 13, 111–135 (1999)
Duffee, G.: Estimating the price of default risk. Rev. Financ. Stud. 12, 197–226 (1999)
Duffie, D., Singleton, K.: Modeling term structures of defaultable bonds. Rev. Financ. Stud. 12, 687–720 (1999)
Dunn, K., Spatt, C.: The effects of refinancing costs and market imperfections on the optimal call strategy and the pricing of debt contracts. In: Working Paper. Carneggie-Mellon University (1986)
Fisher, E., Heinkel, R., Zechner, J.: Dynamic recapitalization policies and the role of call and issue discounts. J. Financ. Quant. Anal. 24, 427–446 (1989)
Hotchkiss, E., Jostova, G.: Determinants of corporate bond trading: a comprehensive analysis. In: Working paper available at SSRN: http://ssrn.com/abstract=1001459 (2007)
Ingersoll, J.: An examination of corporate call policies on convertible securities. J. Financ. 32, 463–478 (1977a)
Ingersoll, J.: A contingent-claims valuation of convertible securities. J. Financ. Econ. 5, 289–322 (1977b)
Jarrow, R., Protter, P.: Structural versus reduced form models: a new information based perspective. J. Invest. Manag. 2, 1–10 (2004)
Jarrow, R., Turnbull, S.: Pricing derivatives on financial securities subject to credit risk. J. Financ. 50, 53–85 (1995)
Kim, I.J., Ramaswamy, K., Sundaresan, S.: Does default risk in coupons affect the valuation of corporate bonds? A contingent claims model. Financ. Manag. 22, 117–131 (1993)
King, T.-H., Mauer, D.: Corporate call policy for nonconvertible bonds. J. Bus. 73, 403–444 (2000)
Kraus, A.: An analysis of call provisions and the corporate refunding decision. Midl. Corp. Financ. J. 1, 46–60 (1983)
Longstaff, F., Tuckman, B.: Calling nonconvertible debt and the problem of related wealth transfer effects. Financ. Manag. 23, 21–30 (1994)
Mauer, D.: Optimal bond call policies under transaction costs. J. Financ. Res. 16, 23–37 (1993)
Nawalkha, N., Beliaeva, S.: Efficient trees for CIR and CEV short rate models. J. Altern. Invest. 10, 71–90 (2007)
Nelson, D., Ramaswamy, K.: Simple binomial process as diffusion approximations in financial models. Rev. Financ. Stud. 3, 393–430 (1990)
Shackleton, M., Sodal, S.: Smooth pasting as rate of return equalization. Econ. Lett. 89, 200–206 (2005)
Smith, C., Warner, J.: On financial contracting. J. Financ. Econ. 7, 117–161 (1979)
Stanton, R.: Rational prepayment and the valuation of mortgage-backed securities. Rev. Financ. Stud. 8, 677–708 (1995)
Vu, J.: An empirical investigation of calls of nonconvertible bonds. J. Financ. Econ. 16, 235–265 (1986)
Zheng, H., Thomas, L.C., Allen, D.E.: The duration derby: a comparison of duration based strategies in asset liability management. J. Bond Trading Manag. 1, 371–380 (2003)
Author information
Authors and Affiliations
Corresponding author
Additional information
The authors thank an anonymous referee as well as Lorenzo Garlappi (editor), Tony Berrada, Julien Hugonnier, Erwan Morellec, Nicolas Papageorgiou, Olivier Renault, Pascal St-Amour, and Mark Swanstrom for helpful comments. We also acknowledge excellent research assistance from Jean-Rémy Lassince and Si-Yang Wu. An earlier version of this work received the Southwest Finance Conference Best Paper Award. The usual disclaimer applies. Financial support from SSHRC, \(\hbox {IFM}^{2}\) and HEC Montreal is gratefully acknowledged.
Appendices
Appendix 1: Proof of Proposition 1
By definition, the optimal call threshold \(h^{*}\) satisfies
For a given call policy \(h\), the callable bond elasticity is given by
Hence,
This derivative at coordinate \(h=h^{*}\) can be written as
Therefore, the optimal threshold \(h^{*}\) that minimizes the callable bond value also minimizes the callable bond elasticity.
Appendix 2: Valuation of \(B_{\infty }\left( c,r\right) \)
Following Duffie and Singleton (1999) and Barone et al. (1998), the no-arbitrage value of the non-callable consol bond is given by
Using Fubini’s theorem,Footnote 18
The expectation in square brackets represents the value of the discount bond that is obtained from the Cox et al. (1985) formula, which yields
with
and \(\coth \left( x\right) :=\frac{e^{x}+e^{-x}}{e^{x}-e^{-x}}\). The integral in the valuation formula for \(B_{\infty }\left( c,r\right) \) is solved numerically with no difficulty.Footnote 19
Appendix 3: Proof of Proposition 2
Let \(g\left( r,h\right) \) denote the value of the perpetual American call written on the borrower’s financing instrument with call threshold \(h\) and strike \(K\). This call option entitles the borrower the right to put an end to her current defaultable callable consol with coupon \(c\) by paying the strike.
In the one-factor model, using Itô’s lemma and standard arbitrage arguments, \(g\) satisfies the following EDP (see Barone et al. 1998)
where \(g_{x}\) denotes the partial derivative of \(g\) with respect to \(x\). The general solution is
with \(C_{1}\) and \(C_{2}\) two constants and
and \(M\left( .;.;.\right) \) denotes the confluent hypergeometric function, and \(L\left( .;.;.\right) \) denotes the generalized Laguerre polynomials.
Boundary condition \(g\left( \infty ,h\right) =0\) implies that \(C_{2}=0\). The second boundary condition is the payoff upon exercise
Substituting into the general solution yields
Finally, the value of the defaultable callable coupon-bearing perpetuity is that of the equivalent non-callable perpetuity less the value of the call option
Appendix 4: Estimation of term structure model parameters
Consistent with our theoretical framework, we estimate a one-factor Cox–Ingersoll–Ross term structure model for the instantaneous risk-free rate. The risk-neutral dynamics of the instantaneous risk-free rate are
Following Duffee (1999) and Duan and Simonato (1999), our estimation method relies on the approximate linear Kalman filter applied to exponential-affine term structure models.
At time \(t\), the yield of the discount bond maturing in \(\tau \) units of time is given by
where the functions \(a\left( .\right) \) and \(b\left( .\right) \), defined in “Appendix 2,” contain all four parameters to estimate.
The filtering approach assumes that yields for different maturities are observed with errors of unknown magnitude. Specifically, observing \(N\) bonds with different maturities, we write the measurement equation as follows
where \(\varepsilon _{t,j}\) is a normally distributed error term with zero mean and standard deviation \(\sigma _{j}\).
Consider the discretized version of the stochastic process for \(r_{t}\) and denote by \(\Delta t\) the time step. The transition equation is given by
where \(\eta _{t+\Delta t}\) is an error term with zero mean and variance equal to
The measurement and transition equations characterize the state space on which we apply the standard Kalman filter recursion. Since the terms in the measurement equation are nonlinear and the error term in the transition equation is not normal, the Kalman filter methodology is only approximate in this case. However, Duan and Simonato (1999) provide Monte Carlo evidence that this procedure remains adequate for the Cox–Ingersoll–Ross model.
The risk-free yield curve is obtained from the St-Louis Federal Reserve Bank database. We use weekly observations of the 6-month, 1-, 2-, 3-, 5-, 10-, and 30-year US Treasury constant maturity ratesFootnote 20 from January 5, 1990, to December 26, 2003.Footnote 21 Estimation results are presented in the table below (standard errors are reported below in parentheses).
Kalman filter estimates of the Cox--Ingersoll--Ross model of US Treasury bond yields, January 1990--December 2003
\(\theta \) | \(\kappa \) | \(\sigma \) | \(\lambda \) |
|---|---|---|---|
\(\underset{\left( 0.005889\right) }{0.046581}\) | \(\underset{\left( 0.038419\right) }{0.287423}\) | \(\underset{\left( 0.000973\right) }{0.024373}\) | \(\underset{\left( 0.036529\right) }{-0.116064}\) |
Bond maturity | Measurement error |
|---|---|
6 months | \(\underset{\left( 0.000059\right) }{0.001918}\) |
1 year | \(\underset{\left( 0.014744\right) }{0.000001}\) |
2 years | \(\underset{\left( 0.000069\right) }{0.003166}\) |
3 years | \(\underset{\left( 0.000102\right) }{0.004368}\) |
5 years | \(\underset{\left( 0.000146\right) }{0.006188}\) |
10 years | \(\underset{\left( 0.000143\right) }{0.007571}\) |
30 years | \(\underset{\left( 0.000169\right) }{0.010519}\) |
Appendix 5: Dynamics of the CIR process in a binomial tree
We outline the procedure developed by Nawalkha and Beliaeva (2007). The CIR process for the short rate has non-constant volatility. As a consequence, its discretized version in a binomial tree entails that the tree is not recombining. Nelson and Ramaswamy (1990) use the following change of variable to fix this issue
where \(x_{t}\) denotes the variable that is used in the recombining binomial tree. By construction, the process \(x_{t}\) has unit volatility, and the up and down nodes can therefore be defined as \(x_{u}=x+\sqrt{\Delta t}\) and \(x_{d}=x-\sqrt{\Delta t}\) where \(\Delta t\) denotes the time step. However, the tree must be adjusted for the drift of the \(x_{t}\) process and for the constraint that the CIR process \(r_{t}\) must remain positive. Nawalkha and Beliaeva (2007) propose a truncation of the \(x-\)binomial tree at zero. They distinguish two cases.
-
If \(x>0\) then \(r>0\), the up and down nodes are
$$\begin{aligned} x_{u}&= x+\left( J+1\right) \sqrt{\Delta t} \\ x_{d}&= \max \left( 0,x+\left( J-1\right) \sqrt{\Delta t}\right) \!, \end{aligned}$$where \(J\) is an integer such that
$$\begin{aligned} J=\left\{ \begin{array}{l@{\quad }l} Z &{} \text {if}\,\,Z\,\,\text { is even} \\ Z+1 &{} \text {if }\,\,Z\,\,\text { is odd} \end{array} \right. \end{aligned}$$and
$$\begin{aligned} Z=Floor\left( \frac{\sqrt{x^{2}\sigma ^{2}\left( 1-\left( \kappa +\lambda \right) \Delta t\right) +4\kappa \theta \Delta t}-x\sigma }{\sigma \sqrt{ \Delta t}}\right) , \end{aligned}$$where \(Floor\left( u\right) \) is the integer value of \(u\), rounded down. The probabilities of up and down moves ensure that the drift of the short rate is correctly matched. They are given by
$$\begin{aligned} p_{u}&= \frac{\left( \kappa \theta -\left( \kappa +\lambda \right) r\right) \Delta t+r-r_{d}}{r_{u}-r_{d}} \\ p_{d}&= 1-p_{u}. \end{aligned}$$ -
If \(x=0\) then \(r=0\), the down node simply stays at zero \(x_{d}=0\). The up node is the node closest to the truncation line of zero which verifies
$$\begin{aligned} x_{u}\ge \frac{2}{\sigma }\sqrt{\kappa \theta \Delta t}. \end{aligned}$$The probabilities of up and down moves are given by
$$\begin{aligned} p_{u}&= \frac{\kappa \theta \Delta t}{r_{u}} \\ p_{d}&= 1-p_{u}. \end{aligned}$$
Rights and permissions
About this article
Cite this article
François, P., Pardo, S. Prepayment risk on callable bonds: theory and test. Decisions Econ Finan 38, 147–176 (2015). https://doi.org/10.1007/s10203-015-0162-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10203-015-0162-0