Analysis of discrete data by Conway–Maxwell Poisson distribution

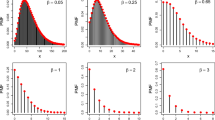
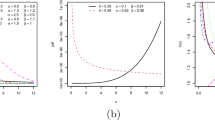
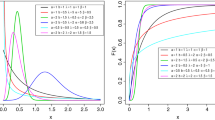
Abstract

In this paper, we further study the Conway–Maxwell Poisson distribution having one more parameter than the Poisson distribution and compare it with the Poisson distribution with respect to some stochastic orderings used in reliability theory. Likelihood ratio test and the score test are developed to test the importance of this additional parameter. Simulation studies are carried out to examine the performance of the two tests. Two examples are presented, one showing overdispersion and the other showing underdispersion, to illustrate the procedure. It is shown that the COM-Poisson model fits better than the generalized Poisson distribution.

Appendix

The Rao’s score test statistic is given by

$$\begin{aligned} T=VI^{-1} V^{T}, \end{aligned}$$

where $V$ is the score vector and $I$ is the information matrix. The score vector and the information matrix, obtained by evaluating the derivative of the log-likelihood function, $\ln L$ under the null hypothesis, are given by

$$\begin{aligned} V=\left( {\frac{\partial \ln L}{\partial \nu }} ,{\frac{\partial \ln L}{\partial \theta }} \right) , \end{aligned}$$

$$\begin{aligned} I=- \left[ \begin{array}{ll} E\left[ {\frac{\partial ^{2} \ln L}{\partial \nu ^{2}}} \right] &{} E\left[ {\frac{\partial ^{2} \ln L}{\partial \theta \partial \nu }} \right] \\ E\left[ {\frac{\partial ^{2} \ln L}{\partial \theta \partial \nu }} \right] &{} E\left[ {\frac{\partial ^{2} \ln L}{\partial \theta ^{2}}} \right] \end{array} \right] . \end{aligned}$$

The likelihood score functions, ${\frac{\partial \ln L}{\partial \theta }}$ and ${\frac{\partial \ln L}{\partial \nu }}$ are given by (11) and (12). The second-order partial derivatives of the probability mass function are

$$\begin{aligned} {\frac{\partial ^{2}\ln P(X=x)}{\partial \theta ^{2}}}&= -\frac{x}{\theta ^{2}}+ \frac{\displaystyle \left( \sum \nolimits _{j=1}^{\infty }{\frac{j\theta ^{j-1}}{(j!)^{\nu }}}\right) ^{2}}{\displaystyle \left( \sum \nolimits _{j=0}^{\infty }{\frac{\theta ^{j}}{(j!)^{\nu }}}\right) ^{2}} -\frac{\left( {\displaystyle {\sum \nolimits _{j=2}^{\infty }{\frac{(j-1)j\theta ^{j-2}}{(j!)^{\nu }}}}}\right) }{\displaystyle {\sum \nolimits _{j=0}^{\infty }\frac{\theta ^{j}}{(j!)^{\nu }}}},\\ {\frac{\partial ^{2}\ln P(X=x)}{\partial \nu ^{2}}} \!&= \! \frac{{\displaystyle \left( \sum \nolimits _{j=2}^{\infty }\frac{-\theta ^{j}}{(j!)^{\nu }}\ln (j!)\right) ^{2}\!-\!\left( \sum \nolimits _{j=0}^{\infty }\frac{\theta ^{j}}{(j!)^{\nu }}\right) \sum \nolimits _{j=2}^{\infty }\frac{\theta ^{j}}{(j!)^{\nu }}\ln (j!)^{2}}}{{\displaystyle \left( \sum \nolimits _{j=0}^{\infty }\frac{\theta ^{j}}{(j!)^{\nu }}^{2}\right) }},\\ {\frac{\partial ^{2}\ln P(X=x)}{\partial \nu \partial \theta }}&= \frac{1}{{\displaystyle \left( \sum \nolimits _{j=0}^{\infty }\frac{\theta ^{j}}{(j!)^{\nu } }\right) ^{2}}}\left\{ \sum _{j=0}^{\infty }\frac{\theta ^{j}}{(j!)^{\nu } }\left( \sum _{j=2}^{\infty }\frac{j\theta ^{j-1}}{(j!)^{\nu }}\ln (j!)\right) \right. \\&\left. \quad -\left( \sum \nolimits _{j=1}^{\infty }\frac{j\theta ^{j-1}}{(j!)^{\nu } }\right) \left( \sum \nolimits _{j=2}^{\infty }\frac{\theta ^{j}}{(j!)^{\nu }} \ln (j!)\right) \right\} . \end{aligned}$$

The LRT requires estimation of the models under the null and alternative hypotheses. By comparing the log-likelihood scores under the null and alternative hypotheses, the LRT gives evidence whether the deviation of one model from the other is statistically significant. The LR test statistic is

$$\begin{aligned} \mathrm {LR}=-2\ln \left( {\frac{L(\hat{\beta }^{*} ;x)}{L(\hat{\beta };x)}} \right) , \end{aligned}$$

where $\hat{\beta }^{*}$ is the restricted ML estimator (null) and $\hat{\beta }$ is the unrestricted ML estimator (alternative).