Self-scaled bounds for atomic cone ranks: applications to nonnegative rank and cp-rank

Abstract

The nonnegative rank of a matrix A is the smallest integer r such that A can be written as the sum of r rank-one nonnegative matrices. The nonnegative rank has received a lot of attention recently due to its application in optimization, probability and communication complexity. In this paper we study a class of atomic rank functions defined on a convex cone which generalize several notions of “positive” ranks such as nonnegative rank or cp-rank (for completely positive matrices). The main contribution of the paper is a new method to obtain lower bounds for such ranks. Additionally the bounds we propose can be computed by semidefinite programming using sum-of-squares relaxations. The idea of the lower bound relies on an atomic norm approach where the atoms are self-scaled according to the vector (or matrix, in the case of nonnegative rank) of interest. This results in a lower bound that is invariant under scaling and that enjoys other interesting structural properties. For the case of the nonnegative rank we show that our bound has an appealing connection with existing combinatorial bounds and other norm-based bounds. For example we show that our lower bound is a non-combinatorial version of the fractional rectangle cover number, while the sum-of-squares relaxation is closely related to the Lovász $\bar{\vartheta }$ number of the rectangle graph of the matrix. We also prove that the lower bound is always greater than or equal to the hyperplane separation bound (and other similar “norm-based” bounds). We also discuss the case of the tensor nonnegative rank as well as the cp-rank, and compare our bound with existing results.

Appendices

Appendix 1: Comments on the SDP relaxation $\tau _+^{\text {sos}}$

1.1 Parametrization of the rank-one variety

The semidefinite programming relaxation of $\tau _+$ corresponds to relaxing the constraint $L(X) \le 1 \; \forall X \in \mathcal A_+(A)$ by the following sum-of-squares constraint:

$$\begin{aligned} 1-L(X) = SOS(X) + \sum _{ij} D_{ij} X_{ij} (A_{ij} - X_{ij}) \quad \forall X \in {\mathbb {R}}^{m\times n} \text { rank-one} \end{aligned}$$

(49)

where SOS(X) is a sum-of-squares polynomial and $D_{ij}$ are nonnegative real numbers. One way to specify that the equality above has to hold for all X rank-one is to require that the two polynomials on each side of the equality are equal modulo the ideal I of rank-one matrices. This is the approach we adopted when presenting the sum-of-squares program for $\tau _+^{\text {sos}}(A)$ in (16).

Another approach to encode the constraint (49) is to parametrize the variety of rank-one matrices: indeed we know that rank-one matrices X have the form $X_{ij} = u_i v_j$ for all $i=1,\ldots ,m$ and $j=1,\ldots ,n$ where $u_i, v_j \in {\mathbb {R}}$. Thus one way to guarantee that (49) holds is to ask that the following polynomial identity (in the ring ${\mathbb {R}}[u_1,\ldots ,u_m,v_1,\ldots ,v_n]$) holds:

$$\begin{aligned} 1 - \sum _{ij} L_{ij} u_i v_j = SOS(u,v) + \sum _{ij} D_{ij} u_i v_j (A_{ij} - u_i v_j). \end{aligned}$$

(50)

It can be shown that these two approaches (working modulo the ideal vs. using the parametrization of rank-one matrices) are actually identical and lead to the same semidefinite programs.

1.2 Additional constraints

In this section we discuss how additional constraints on the semidefinite program (15) that defines $\tau _+^{\text {sos}}(A)$ can affect the value of the lower bound.

• First observe that the constraint (12) is a special case $k=i,l=j$ of the constraints

  $$\begin{aligned} (rr^T)_{ij,kl} \le r_{ij} A_{kl}, \end{aligned}$$

  for any i, j, k, l. This would correspond in the semidefinite program (15) to adding the inequalities

  $$\begin{aligned} X_{ij,kl} \le A_{ij} A_{kl}. \end{aligned}$$

  In Lemma 3 of Appendix 2 we show that these inequalities are automatically verified by any X feasible for the semidefinite program (15). Thus adding these inequalities does not affect the value of the bound.

• Another constraint that one can impose on X is elementwise nonnegativity, since $rr^T$ in (11) is nonnegative. We investigated the effect of this constraint numerically but on all the examples we tried the value of the bound did not change (up to numerical precision). We think however there might be specific examples where the value of the bound does change. Indeed as we show in Sect. 2.4 the quantity $\tau _+^{\text {sos}}$ is closely related to the Lovász $\vartheta$ number. It is known in the case of $\vartheta$ that adding a nonnegativity constraint can affect the value of the SDP. The version of the $\vartheta$ number with an additional nonnegativity constraint is sometimes denoted by $\vartheta ^+$ and was first introduced by Szegedy in [47] and extensive numerical experiments were done in [18] (see also [37]).

• Another family of constraints that one could impose in the SDP comes from the following observation: If $0 \le r \le a$ (with $r={{\mathrm{vec}}}(R)$ and $a={{\mathrm{vec}}}(A)$) then we have for any i, j, k, l:

  $$\begin{aligned} (a-r)_{ij} (a-r)_{kl} \ge 0, \end{aligned}$$

  i.e.,

  $$\begin{aligned} a_{ij} a_{kl} - r_{ij} a_{kl} - r_{kl} a_{ij} + (rr^T)_{ij,kl} \ge 0. \end{aligned}$$

  In the semidefinite program (15) these inequalities translate to:

  $$\begin{aligned} X_{ij,kl} \ge (2-t) A_{ij} A_{kl}. \end{aligned}$$

  (51)

  We observed that on most matrices the constraint does not affect the value of the bound. However for some specific matrices of small size the value can change: For example for the matrix

  $$\begin{aligned} A = \begin{bmatrix} 1&\quad 1\\ 1&\quad 1/2 \end{bmatrix} \end{aligned}$$

  we get the value 4 / 3 without the constraint (51) whereas with the constraint we obtain 3 / 2.

The constraints mentioned here would make the size of the semidefinite programs much larger, and on the examples we tested we did not actually observe a significant change in the values of the lower bound with these additional constraints. We have also noted that by including some of the additional constraints we lose some of the nice properties that the quantity $\tau _+^{\text {sos}}(A)$ satisfies. For example if we include the last set of inequalities (51) described above, the lower bound is no longer additive for block-diagonal matrices.

Appendix 2: Proof of properties of $\tau _+$ and $\tau _+^{\text {sos}}$

1.1 Invariance under diagonal scaling

• 1. We first prove invariance under diagonal scaling for $\tau _+$, then we consider $\tau _+^{\text {sos}}$. Let $A' = D_1 A D_2$ where $D_1$ and $D_2$ are two diagonal matrices with strictly positive entries on the diagonal. Observe that the set of atoms $\mathcal A_+(A')$ of $A'$ can be obtained from the atoms $\mathcal A_+(A)$ of A as follows:

  $$\begin{aligned} \mathcal A_+(A') = \{ D_1 R D_2 \; : \; R \in \mathcal A_+(A) \} =: D_1 \mathcal A_+(A) D_2. \end{aligned}$$

  (52)

  Indeed, if R is rank-one and $0 \le R \le A$ then clearly $D_1 R D_2$ is rank-one and satisfies $0 \le D_1 R D_2 \le D_1 A D_2 = A'$ thus $D_1 R D_2 \in \mathcal A_+(A')$. Conversely if $R' \in \mathcal A_+(A')$, then by letting $R = D_1^{-1} R D_2^{-1}$ we see that $R' = D_1 R D_2$ with R rank-one and $0\le R \le A$. Thus this shows equality (52). Thus we have:

  $$\begin{aligned} \begin{array}{ll} \tau _+(A') &{}= \min \left\{ t \; : \; A' \in t {{\mathrm{conv}}}(\mathcal A_+(A')) \right\} \\ &{}= \min \left\{ t \; : \; D_1 A D_2 \in t {{\mathrm{conv}}}(D_1 \mathcal A_+(A) D_2) \right\} \\ &{}= \min \left\{ t \; : \; D_1 A D_2 \in t D_1 {{\mathrm{conv}}}(\mathcal A_+(A)) D_2 \right\} \\ &{}= \min \left\{ t \; : \; A \in t {{\mathrm{conv}}}(\mathcal A_+(A)) \right\} \\ &{}= \tau _+(A). \end{array} \end{aligned}$$

  (53)

• 2. We now prove invariance under diagonal scaling for the SDP relaxation $\tau _+^{\text {sos}}$. For this we use the maximization formulation of $\tau _+^{\text {sos}}$ given in Eq. (16). Let L be the optimal linear form in (16) for the matrix A, i.e., $L(A) = \tau _+^{\text {sos}}(A)$ and L satisfies:

  $$\begin{aligned} 1 - L(X) = SOS(X) + \sum _{ij} D_{ij} X_{ij} (A_{ij} - X_{ij}) \ \mathrm{mod} \ I. \end{aligned}$$

  (54)

  Define the linear polynomial $L'(X) = L(D_1^{-1} X D_2^{-1})$. We can verify that:

  $$\begin{aligned} \begin{array}{ll} 1 - L'(X) &{}= 1 - L(D_1^{-1} X D_2^{-1}) \\ &{}= SOS(D_1^{-1} X D_2^{-1}) + \sum _{ij} D_{ij} \frac{X_{ij}}{(D_1)_{ii} (D_2)_{jj}} \left( A_{ij} - \frac{X_{ij}}{(D_1)_{ii} (D_2)_{jj}}\right) \ \mathrm{mod} \ I\\ &{}= SOS(D_1^{-1} X D_2^{-1}) + \sum _{ij} D_{ij} \frac{X_{ij}}{(D_1)_{ii}^2 (D_2)_{jj}^2} ( A'_{ij} - X_{ij} ) \ \mathrm{mod} \ I \end{array} \end{aligned}$$

  where in the last equality we used the fact that $A_{ij} = \frac{A'_{ij}}{(D_1)_{ii} (D_2)_{jj}}$. Thus this shows that $L'$ is feasible for the sum-of-squares program (16) for the matrix $A'$. Thus since $L'(A') = L(A) = \tau _+^{\text {sos}}(A)$, we get that $\tau _+^{\text {sos}}(A') \ge \tau _+^{\text {sos}}(A)$. With the same reasoning we can show that:

  $$\begin{aligned} \tau _+^{\text {sos}}(A) = \tau _+^{\text {sos}}(D_1^{-1}(D_1 A D_2) D_2^{-1}) \ge \tau _+^{\text {sos}}(D_1 A D_2) = \tau _+^{\text {sos}}(A'). \end{aligned}$$

  Thus we have $\tau _+^{\text {sos}}(A') = \tau _+^{\text {sos}}(A)$.

1.2 Invariance under permutation

The proof of invariance under permutation is very similar to the one for invariance under diagonal scaling. To prove the claim for $\tau _+$ one proceeds by showing that the set of atoms $\mathcal A_+(A')$ of $A'=P_1 A P_2$ can be obtained from the atoms of A by applying the permutations $P_1$ and $P_2$, namely:

$$\begin{aligned} \mathcal A_+(A') = \{ P_1 R P_2 \; : \; R \in \mathcal A_+(A) \} =: P_1 \mathcal A_+(A) P_2. \end{aligned}$$

For the SDP relaxation we also use the same idea as the previous proof by constructing a certificate $L'$ for $A'$ using the certificate L for A. We omit the details here since they are very similar to the previous proof.

1.3 Subadditivity

• 1. We first prove the subadditivity property for $\tau _+$, i.e., $\tau _+(A+B) \le \tau _+(A)+\tau _+(B)$. Observe that we have

  $$\begin{aligned} \mathcal A_+(A) \cup \mathcal A_+(B) \subseteq \mathcal A_+(A+B). \end{aligned}$$

  (55)

  Indeed if $R \in \mathcal A_+(A)$, i.e., R is rank-one and $0\le R \le A$, then we also have $0 \le R \le A+B$ (since B is nonnegative) and thus $R \in \mathcal A_+(A+B)$. Thus this shows $\mathcal A_+(A) \subseteq \mathcal A_+(A+B)$, and the same reason gives $\mathcal A_+(B) \subseteq \mathcal A_+(A+B)$, and thus we get (55). By definition of $\tau _+(A)$ and $\tau _+(B)$, we know there exist decompositions of A and B of the form $A = \sum _{i} \alpha _i R_i$ and $B = \sum _{j} \beta _j S_j$ where $\sum _{i} \alpha _i = \tau _+(A)$ and $\sum _{j} \beta _j = \tau _+(B)$ and where $R_i \in \mathcal A_+(A)$ for all i and $S_j \in \mathcal A_+(B)$ for all j. Adding these two decompositions, we get:

  $$\begin{aligned} A+B = \sum _{i} \alpha _i R_i + \sum _{j} \beta _j S_j \end{aligned}$$

  where $R_i \in \mathcal A_+(A+B)$ and $S_j \in \mathcal A_+(A+B)$ for all i and j. This decomposition shows that

  $$\begin{aligned} \tau _+(A+B) \le \tau _+(A) + \tau _+(B). \end{aligned}$$

• 2. We now prove the property for $\tau _+^{\text {sos}}$. Let (t, X) and $(t',X')$ be the optimal points of the semidefinite program (15) for A and B respectively (i.e., $t = \tau _+^{\text {sos}}(A)$ and $t' = \tau _+^{\text {sos}}(B)$). It is not hard to see that $(t+t',X+X')$ is feasible for the semidefinite program that defines $\tau _+^{\text {sos}}(A+B)$ (in particular we use the fact that since A and B are nonnegative we have $A_{ij}^2 + B_{ij}^2 \le (A_{ij}+B_{ij})^2$). Thus this shows that $\tau _+^{\text {sos}}(A+B) \le \tau _+^{\text {sos}}(A) + \tau _+^{\text {sos}}(B)$.

1.4 Product

• 1. We first show the property for $\tau _+$. We need to show that $\tau _+(AB) \le \min (\tau _+(A),\tau _+(B))$. To see why note that if $R \in \mathcal A_+(A)$, then $RB \in \mathcal A_+(AB)$. Thus if we have $A = \sum _{i} \alpha _i R_i$ with $R_i \in \mathcal A_+(A)$ and $\sum _i \alpha _i = \tau _+(A)$, then we get $AB = \sum _i \alpha _i R_i B$ where each $R_iB \in \mathcal A_+(AB)$ and thus $\tau _+(AB) \le \sum _i \alpha _i = \tau _+(A)$. The same reasoning shows that $\tau _+(AB) \le \tau _+(B)$, and thus we get $\tau _+(AB) \le \min (\tau _+(A),\tau _+(B))$.

• 2. We now prove the property for $\tau _+^{\text {sos}}$, i.e., we show $\tau _+^{\text {sos}}(AB) \le \min (\tau _+^{\text {sos}}(A),\tau _+^{\text {sos}}(B))$. We will show here that $\tau _+^{\text {sos}}(AB) \le \tau _+^{\text {sos}}(A)$, and a similar reasoning can then be used to show $\tau _+^{\text {sos}}(AB) \le \tau _+^{\text {sos}}(B)$. Let (t, X) be the optimal point of the semidefinite program (15) that defines $\tau _+^{\text {sos}}(A)$, i.e., $t = \tau _+^{\text {sos}}(A)$. We will show that the pair $(t,\tilde{X})$ with

  $$\begin{aligned} \tilde{X} = (B^T \otimes I_m) X (B \otimes I_m), \end{aligned}$$

  is feasible for the semidefinite program that defines $\tau _+^{\text {sos}}(AB)$ and thus this will show that $\tau _+^{\text {sos}}(AB) \le t = \tau _+^{\text {sos}}(A)$. Observe that we have ${{\mathrm{vec}}}(AB) = (B^T \otimes I_m) {{\mathrm{vec}}}(A)$ thus:

  $$\begin{aligned} \begin{bmatrix} t&\quad {{\mathrm{vec}}}(AB)^T\\ {{\mathrm{vec}}}(AB)&\quad \tilde{X} \end{bmatrix} = \begin{bmatrix} 1&\quad 0\\ 0&\quad B^T \otimes I \end{bmatrix} \begin{bmatrix} t&\quad {{\mathrm{vec}}}(A)^T\\ {{\mathrm{vec}}}(A)&\quad X \end{bmatrix} \begin{bmatrix} 1&\quad 0\\ 0&\quad B \otimes I \end{bmatrix} \end{aligned}$$

  and thus this shows that the matrix

  $$\begin{aligned} \begin{bmatrix} t&\quad {{\mathrm{vec}}}(AB)^T\\ {{\mathrm{vec}}}(AB)&\quad \tilde{X} \end{bmatrix} \end{aligned}$$

  is positive semidefinite.

  Using the definition of Kronecker product one can verify that the entries of $\tilde{X}$ are given by:

  $$\begin{aligned} \tilde{X}_{ij,kl} = \sum _{\alpha ,\beta =1}^{m'} B_{\alpha j} B_{\beta l} X_{i \alpha , k \beta }. \end{aligned}$$

  Using this formula we easily verify that $\tilde{X}$ satisfies the rank-one equality constraints:

  $$\begin{aligned} \tilde{X}_{ij,kl} = \tilde{X}_{il,kj} \end{aligned}$$

  since X itself satisfies the constraints.

Finally it remains to show that $\tilde{X}_{ij,ij} \le (AB)_{ij}^2$. For this we need the following simple lemma:

Lemma 3

Let (t, X) be a feasible point for the semidefinite program (15). Then $X_{ij,kl} \le A_{ij}A_{kl}$ for any i, j, k, l.

Proof

Consider the $2\times 2$ principal submatrix of X:

$$\begin{aligned} \begin{bmatrix} X_{ij,ij}&\quad X_{ij,kl}\\ X_{kl,ij}&\quad X_{kl,kl} \end{bmatrix}. \end{aligned}$$

We know that $X_{ij,ij} \le A_{ij}^2$ and $X_{kl,kl} \le A_{kl}^2$. Furthermore since X is positive semidefinite we have $X_{ij,ij} X_{kl,kl} - X_{ij,kl}^2 \ge 0$. Thus we get that:

$$\begin{aligned} X_{ij,kl}^2 \le X_{ij,ij} X_{kl,kl} \le (A_{ij} A_{kl})^2. \end{aligned}$$

Thus since $A_{ij} A_{kl} \ge 0$ we have $X_{ij,kl} \le A_{ij} A_{kl}$. $\square$

Using this lemma we get:

$$\begin{aligned} \tilde{X}_{ij,ij} = \sum _{\alpha ,\beta =1}^{m'} B_{\alpha j} B_{\beta j} X_{i \alpha , i \beta } \le \sum _{\alpha ,\beta =1}^{m'} B_{\alpha j} B_{\beta j} A_{i \alpha } A_{i \beta } = ((AB)_{ij})^2 \end{aligned}$$

which is what we want.

1.5 Monotonicity

Here we prove the monotonicity property of $\tau _+$ and $\tau _+^{\text {sos}}$. More precisely we show that if $A \in {\mathbb {R}}^{m\times n}_+$ is a nonnegative matrix, and B is a submatrix of A, then $\tau _+(B) \le \tau _+(A)$ and $\tau _+^{\text {sos}}(B) \le \tau _+^{\text {sos}}(A)$.

• 1. We prove the claim first for $\tau _+$. Let $I\subseteq [m]$ and $J\subseteq [n]$ such that $B=A[I,J]$ (i.e., B is obtained from A by keeping only the rows in I and the columns in J). Let $X \in {{\mathrm{conv}}}\mathcal A_+(A)$ such that $A = \tau _+(A) X$. Define $Y = X[I,J]$ and note that $Y \in {{\mathrm{conv}}}(\mathcal A_+(B))$. Furthermore observe that we have $B = A[I,J] = \tau _+(A) X[I,J] = \tau _+(A) Y$. Hence, since $Y \in {{\mathrm{conv}}}\mathcal A_+(B)$, this shows, by definition of $\tau _+(B)$ that $\tau _+(B) \le \tau _+(A)$.

• 2. We prove the claim now for the semidefinite programming relaxation $\tau _+^{\text {sos}}$. As above, let $I\subseteq [m]$ and $J\subseteq [n]$ such that $B=A[I,J]$. Let (t, X) be the optimal point in (15) for the matrix A. It is easy to see that (t, X[I, J]) is feasible for the semidefinite program (15) for the matrix $B=A[I,J]$. Thus this shows that $\tau _+^{\text {sos}}(B) \le \tau _+^{\text {sos}}(A)$.

1.6 Block-diagonal matrices

In this section we prove that if $A \in {\mathbb {R}}^{m\times n}_+$ and $B \in {\mathbb {R}}^{m'\times n'}_+$ are two nonnegative matrices and $A\oplus B$ is the block-diagonal matrix:

$$\begin{aligned} A \oplus B = \begin{bmatrix} A&\quad 0\\ 0&\quad B \end{bmatrix}, \end{aligned}$$

then

$$\begin{aligned} \tau _+(A\oplus B) = \tau _+(A) + \tau _+(B) \quad \text { and } \quad \tau _+^{\text {sos}}(A\oplus B) = \tau _+^{\text {sos}}(A) + \tau _+^{\text {sos}}(B) \end{aligned}$$

• 1. We first prove the claim for the quantity $\tau _+$. Observe that the set $\mathcal A_+(A\oplus B)$ is equal to:

  $$\begin{aligned} \mathcal A_+(A\oplus B) = \left\{ \begin{bmatrix} R&\quad 0\\ 0&\quad 0 \end{bmatrix} \; : \; R \in \mathcal A_+(A) \right\} \cup \left\{ \begin{bmatrix} 0&\quad 0\\ 0&\quad R' \end{bmatrix} \; : \; R' \in \mathcal A_+(B) \right\} . \end{aligned}$$

  (56)

  Indeed any element in $\mathcal A_+(A\oplus B)$ must have the off-diagonal blocks equal to zero (since the off-diagonal blocks of $A\oplus B$ are zero), and thus by the rank-one constraint at least one of the diagonal blocks is also equal to zero. Thus this shows that $\mathcal A_+(A\oplus B)$ decomposes as in (56).

  We start by showing $\tau _+(A \oplus B) \ge \tau _+(A) + \tau _+(B)$. Let $Y \in {{\mathrm{conv}}}\mathcal A_+(A \oplus B)$ such that

  $$\begin{aligned} A\oplus B = \tau _+(A\oplus B) Y. \end{aligned}$$

  Since $\mathcal A_+(A\oplus B)$ has the form (56), we know that Y can be decomposed as:

  $$\begin{aligned} Y = \sum _{i=1}^r \lambda _i \begin{bmatrix} R_i&\quad 0\\ 0&\quad 0 \end{bmatrix} + \sum _{j=1}^{r'} \mu _{j} \begin{bmatrix} 0&\quad 0\\ 0&\quad R'_{i'} \end{bmatrix}, \end{aligned}$$

  where $R_i \in \mathcal A_+(A), R'_{j} \in \mathcal A_+(B)$ and $\sum _i \lambda _i + \sum _{j} \mu _j = 1$ with $\lambda , \mu \ge 0$. Note that since $A\oplus B = \tau _+(A\oplus B) Y$ we have:

  $$\begin{aligned} A = \tau _+(A\oplus B) \sum _{i=1}^r \lambda _i R_i, \end{aligned}$$

  and

  $$\begin{aligned} B = \tau _+(A\oplus B) \sum _{j=1}^{r'} \mu _j R'_j. \end{aligned}$$

  Hence $\tau _+(A) \le \tau _+(A\oplus B) \sum _{i=1}^r \lambda _i$ and $\tau _+(B) \le \tau _+(A\oplus B) \sum _{j=1}^{r'} \mu _j$ and we thus get:

  $$\begin{aligned} \tau _+(A) + \tau _+(B) \le \tau _+(A\oplus B) \left( \sum _{i=1}^r \lambda _i + \sum _{j=1}^{r'} \mu _j\right) = \tau _+(A\oplus B). \end{aligned}$$

  We now prove the converse inequality, i.e., $\tau _+(A\oplus B) \le \tau _+(A) + \tau _+(B)$: Let $t=\tau _+(A)$, $t' = \tau _+(B)$ and $X \in {{\mathrm{conv}}}\mathcal A_+(A), X' \in {{\mathrm{conv}}}\mathcal A_+(B)$ such that $A = t X$ and $B = t' X'$. Define the matrix

  $$\begin{aligned} Y = \begin{bmatrix} \frac{t}{t+t'} X&\quad 0\\ 0&\quad \frac{t'}{t+t'} X' \end{bmatrix}, \end{aligned}$$

  and note that $A \oplus B = (t+t') Y$. If we show that $Y \in {{\mathrm{conv}}}\mathcal A_+(A\oplus B)$ then this will show that $\tau _+(A\oplus B) \le t + t'$. We can rewrite Y as:

  $$\begin{aligned} Y = \frac{t}{t+t'} \begin{bmatrix} X&\quad 0\\ 0&\quad 0 \end{bmatrix} + \frac{t'}{t+t'} \begin{bmatrix} 0&\quad 0\\ 0&\quad X'\end{bmatrix}, \end{aligned}$$

  and it is easy to see from this expression that $Y \in {{\mathrm{conv}}}\mathcal A_+(A\oplus B)$. We have thus proved that $\tau _+(A\oplus B) = \tau _+(A) + \tau _+(B)$.

• 2. We now prove the claim for the SDP relaxation $\tau _+^{\text {sos}}$. Let $a = {{\mathrm{vec}}}(A)$ and $b={{\mathrm{vec}}}(B)$. Since the matrix $A \oplus B$ has zeros on the off-diagonal, the SDP defining $\tau _+^{\text {sos}}(A\oplus B)$ can be simplified and we can eliminate the zero entries from the program. One can show that after the simplification we get that $\tau _+^{\text {sos}}(A\oplus B)$ is equal to the value of the SDP below:

  $$\begin{aligned} \begin{array}{ll} \text {minimize} &{} t\\ \text {subject to} &{} \begin{bmatrix} t &{}\quad a^T &{}\quad b^T\\ a &{}\quad X &{}\quad 0\\ b &{}\quad 0 &{}\quad X' \end{bmatrix} \succeq 0\\ &{} X_{ij,ij} \le A_{ij}^2 \quad \forall (i,j) \in [m]\times [n]\\ &{} X_{ij,kl} = X_{il,kj} \quad 1\le i < k \le m \text { and } 1\le j < l \le n\\ &{} X'_{i'j',i'j'} \le B_{i'j'}^2 \quad \forall (i',j') \in [m']\times [n']\\ &{} X'_{i'j',k'l'} = X_{i'l',k'j'} \quad 1\le i' < k' \le m' \text { and } 1\le j' < l' \le n' \end{array} \end{aligned}$$

  (57)

  It is well-known (see e.g., [26]) that the following equivalence always holds:

  $$\begin{aligned} \begin{bmatrix} t&\quad a^T&\quad b^T\\ a&\quad X&\quad 0\\ b&\quad 0&\quad X' \end{bmatrix} \succeq 0 \Longleftrightarrow \exists t_1,t_2 : t_1+t_2 = t, \quad \begin{bmatrix} t_1&\quad a^T\\ a&\quad X \end{bmatrix} \succeq 0,\quad \begin{bmatrix} t_2&\quad b^T\\ b&\quad X' \end{bmatrix} \succeq 0 \end{aligned}$$

  Using this equivalence, the semidefinite program (57) becomes:

  $$\begin{aligned} \begin{array}{ll} \text {minimize} &{} t_1 + t_2\\ \text {subject to} &{} \begin{bmatrix} t_1 &{}\quad a^T\\ a &{}\quad X \end{bmatrix} \succeq 0\\ &{} X_{ij,ij} \le A_{ij}^2 \quad \forall (i,j) \in [m]\times [n]\\ &{} X_{ij,kl} = X_{il,kj} \quad 1\le i < k \le m \text { and } 1\le j < l \le n\\ &{} \begin{bmatrix} t_2 &{}\quad b^T\\ b &{}\quad X' \end{bmatrix} \succeq 0\\ &{} X'_{i'j',i'j'} \le B_{i'j'}^2 \quad \forall (i',j') \in [m']\times [n']\\ &{} X'_{i'j',k'l'} = X_{i'l',k'j'} \quad 1\le i' < k' \le m' \text { and } 1\le j' < l' \le n' \end{array} \end{aligned}$$

  (58)

  The semidefinite program is decoupled and it is easy to see that its value is equal to $\tau _{+}^{\text {sos}}(A) + \tau _{+}^{\text {sos}}(B)$.

Appendix 3: Proof of Theorem 4 on the relation between combinatorial bounds and $\tau _+$ and $\tau _+^{\text {sos}}$

Proof of Theorem 4

• 1. We prove first that $\tau _+(A) \ge \chi _{\text {frac}}({{\mathrm{RG}}}(A))$. For convenience, we recall below the definitions of $\tau _+(A)$ and $\chi _{\text {frac}}({{\mathrm{RG}}}(A))$:

  $$\begin{aligned} \begin{array}{c|c} \tau _+(A) &{} \chi _{\text {frac}}({{\mathrm{RG}}}(A))\\ \hline \begin{array}{ll} \min &{} t\\ \text {s.t.} &{}\quad A \in t {{\mathrm{conv}}}(\mathcal A_+(A)) \end{array} &{} \begin{array}{ll} \text {min} &{} t\\ \text {s.t.} &{} \exists Y \in t {{\mathrm{conv}}}(\mathcal A_B(A))\\ &{} \quad \text { s.t. } \forall (i,j), \;\; A_{i,j} > 0 \; \Rightarrow \; Y_{i,j} \ge 1 \end{array} \end{array} \end{aligned}$$

  Let $t = \tau _+(A)$ and $X \in {{\mathrm{conv}}}(\mathcal A_+(A))$ such that $A = t X$. Consider the decomposition of X:

  $$\begin{aligned} X = \sum _{k=1}^r \lambda _k X_k, \end{aligned}$$

  where $X_k \in \mathcal A_+(A)$, $\lambda _k \ge 0$ and $\sum _{k=1}^r \lambda _k = 1$. Let $R_k = {{\mathrm{supp}}}(X_k)$ (i.e., $R_k$ is obtained by replacing the nonzero entries of $X_k$ with ones) and observe that $R_k \in \mathcal A_B(A)$. Define

  $$\begin{aligned} Y = t \sum _{k=1}^r \lambda _k R_k \in t {{\mathrm{conv}}}(\mathcal A_B(A)) \end{aligned}$$

  Observe that for any (i, j) such that $A_{i,j} > 0$ we have:

  $$\begin{aligned} Y_{i,j} = t \sum _{k:X_k[i,j]>0} \lambda _k \underbrace{R_k[i,j]}_{=1} \overset{(a)}{\ge } t \sum _{k:X_k[i,j]} \lambda _k \frac{X_k[i,j]}{A_{i,j}} \overset{(b)}{=} \frac{A_{i,j}}{A_{i,j}} = 1 \end{aligned}$$

  where in (a) we used the fact that $X_k \le A$ (by definition of $X_k \in \mathcal A_+(A)$) and in (b) we used the fact that $A = t\sum _{k} \lambda _k X_k$. Thus this shows that (t, Y) is feasible for the optimization program defining $\chi _{\text {frac}}({{\mathrm{RG}}}(A))$ and thus we have $\chi _{\text {frac}}({{\mathrm{RG}}}(A)) \le t = \tau _+(A)$.

• 2. We now show that $\tau _+^{\text {sos}}(A) \ge \bar{\vartheta }({{\mathrm{RG}}}(A))$. For convenience, we recall the two SDPs (17) and (22) that define $\tau _+^{\text {sos}}(A)$ and $\bar{\vartheta }({{\mathrm{RG}}}(A))$ below (note the constraint $X_{ij,ij} = A_{ij}^2$ in the SDP on the left appears as an inequality constraint in (17)—in fact it is not hard to see that with an equality constraint we get the same optimal value):

  $$\begin{aligned} \begin{array}{c|c} \tau _+^{\text {sos}}(A) &{} \bar{\vartheta }({{\mathrm{RG}}}(A))\\ \hline \begin{array}{rl} \text {min.} &{} t\\ \text {s.t.} &{} \begin{bmatrix} t &{} \pi (A)^T\\ \pi (A) &{} X \end{bmatrix} \succeq 0 \\ &{} \forall (i,j) \text { s.t. } A_{i,j} > 0: \;\; X_{ij,ij} = A_{ij}^2\\ &{} \forall (1,1)\le (i,j) < (k,l) \le (m,n):\\ &{} \qquad {\left\{ \begin{array}{ll} \text {if }\; A_{i,l} A_{k,j}=0\; : \; X_{ij,kl} = 0 \quad \text {(a)}\\ \text {if }\; A_{i,j} A_{k,l}=0 \; : \; X_{il,kj} = 0 \quad \text {(b)}\\ \text {else } \;\; X_{ij,kl} - X_{il,kj} = 0 \quad \text {(c)} \end{array}\right. } \end{array} &{} \begin{array}{rl} \text {min.} &{} t\\ \text {s.t.} &{} \begin{bmatrix} t &{}\quad 1^T\\ 1 &{}\quad X \end{bmatrix} \succeq 0 \\ &{} \forall (i,j) \text { s.t. } A_{i,j} > 0: \;\; X_{ij,ij} = 1\\ &{} \forall (1,1)\le (i,j) < (k,l) \le (m,n):\\ &{} \qquad {\left\{ \begin{array}{ll} \text {if } A_{i,l} A_{k,j}=0\; : \; X_{ij,kl} = 0 \quad \text {(a')}\\ \text {if } A_{i,j} A_{k,l}=0 \; : \; X_{il,kj} = 0 \quad \text {(b')}\\ \end{array}\right. } \end{array} \end{array} \end{aligned}$$

  Observe that the two semidefinite programs are very similar except that $\tau _+^{\text {sos}}(A)$ has more constraints than $\bar{\vartheta }({{\mathrm{RG}}}(A))$; cf. constraints (c) for $\tau _+^{\text {sos}}(A)$. To show that $\tau _+^{\text {sos}}(A) \ge \bar{\vartheta }({{\mathrm{RG}}}(A))$, let (t, X) be the solution of the SDP on the left for $\tau _+^{\text {sos}}(A)$. We will construct $X'$ such that $(t,X')$ is feasible for the SDP on the right and thus this will show that $\tau _+^{\text {sos}}(A) \ge \bar{\vartheta }({{\mathrm{RG}}}(A))$. Define $X'$ by:

  $$\begin{aligned} X' = {{\mathrm{diag}}}(\pi (A))^{-1} X {{\mathrm{diag}}}(\pi (A))^{-1}. \end{aligned}$$

  We show that $(t,X')$ is feasible for the SDP on the right: Note that:

  $$\begin{aligned} \begin{bmatrix} t&\quad 1^T\\ 1&\quad X' \end{bmatrix} = \begin{bmatrix} 1&\quad 0\\ 0&\quad {{\mathrm{diag}}}(\pi (A))^{-1} \end{bmatrix} \begin{bmatrix} t&\quad \pi (A)^T\\ \pi (A)&\quad X \end{bmatrix} \begin{bmatrix} 1&\quad 0\\ 0&\quad {{\mathrm{diag}}}(\pi (A))^{-1} \end{bmatrix} \succeq 0 \end{aligned}$$

  Second we clearly have $X'_{ij,ij} = A_{ij}^{-2} X_{ij,ij} = 1$. Finally constraints (a’) and (b’) are also clearly true. Thus this shows that $(t,X')$ is feasible for the SDP of $\bar{\vartheta }({{\mathrm{RG}}}(A))$ and thus $\bar{\vartheta }({{\mathrm{RG}}}(A)) \le t = \tau _+^{\text {sos}}(A)$.

$\square$

Appendix 4: $2\times 2$ Matrices

Proof of Lemma 2

First observe that it suffices to look at matrices A(e) for $0 \le e\le 1$. Indeed for $e \ge 1$, the matrix A(e) can be obtained from the matrix A(1 / e) by permuting the two columns then scaling the second row by e, namely we have:

$$\begin{aligned} \begin{bmatrix} 1&\quad 1\\ 1&\quad e \end{bmatrix} = \begin{bmatrix} 1&\quad 0\\ 0&\quad e \end{bmatrix} \begin{bmatrix} 1&\quad 1\\ 1&\quad 1/e \end{bmatrix} \begin{bmatrix} 0&\quad 1\\ 1&\quad 0 \end{bmatrix}. \end{aligned}$$

Thus by Theorem 3 on the properties of $\tau _+$ and $\tau _+^{\text {sos}}$ we have:

$$\begin{aligned} \tau _+(A(e)) = \tau _+(A(1/e)) \quad \text { and } \quad \tau _+^{\text {sos}}(A(e)) = \tau _+^{\text {sos}}(A(1/e)). \end{aligned}$$

In the following we thus fix $e \in [0,1]$ and $A=A(e)$ and we show that $\tau _+(A) = 2-e$ and $\tau _+^{\text {sos}}(A) = 2/(1-e)$.

• We first show that $\tau _+(A) = 2-e$. To prove that $\tau _+(A) \ge 2-e$ we exhibit a linear function L such that $L(R) \le 1$ for all $R \in \mathcal A_+(A)$. Define L by:

  $$\begin{aligned} L\left( \begin{bmatrix} a&\quad b\\ c&\quad d \end{bmatrix} \right) = b+c - e\cdot a. \end{aligned}$$

  We now show that $L(R) \le 1$ for all $R \in \mathcal A_+(A)$. Let $R = \left[ \begin{matrix} a &{} b\\ c &{} d \end{matrix}\right] \in \mathcal A_+(A)$, i.e., $ad=bc$ and $0 \le (a,b,c,d) \le (1,1,1,e)$. If $d=0$ then either $b=0$ or $c=0$ and we have $L(R) \le 1$ because $b,c \le 1$. If $d > 0$ we have:

  $$\begin{aligned} \begin{aligned} L(R)&= b+c - e\cdot a = b+c-e \frac{bc}{d} \\&\overset{(*)}{\le } b+c-bc = b\cdot 1 + (1-b) \cdot c \le \max (1,c) \le 1 \end{aligned} \end{aligned}$$

  where in (*) we used the fact that $e/d\ge 1$. Now for this choice of L we have $L(A) = 1 + 1 - e = 2-e$. Thus this shows that $\tau _+(A) \ge 2-e$. We now show that $\tau _+(A) \le 2-e$. For this we prove that $A \in (2-e) {{\mathrm{conv}}}(\mathcal A_+(A))$. We have the following decomposition of $\frac{1}{2-e} A$:

  $$\begin{aligned} \frac{1}{2-e} \begin{bmatrix} 1&\quad 1\\ 1&\quad e \end{bmatrix} \; = \; \lambda \begin{bmatrix} 1&\quad 1\\ e&\quad e \end{bmatrix} + \lambda \begin{bmatrix} 1&\quad e\\ 1&\quad e \end{bmatrix} + \mu \begin{bmatrix} 0&\quad 1\\ 0&\quad 0 \end{bmatrix} + \mu \begin{bmatrix} 0&\quad 0\\ 1&\quad 0\end{bmatrix} \end{aligned}$$

  where

  $$\begin{aligned} \lambda = \frac{1}{2(2-e)} \quad \text { and } \quad \mu = \frac{1-e}{2(2-e)}. \end{aligned}$$

  Note that $\lambda ,\mu \ge 0$, $2\lambda + 2\mu =1$ and that the four $2\times 2$ matrices in the decomposition belong to $\mathcal A_+(A)$. Thus this shows that $A \in (2-e) {{\mathrm{conv}}}(\mathcal A_+(A))$ and thus $\tau _+(A) \le 2-e$.

• We now look at the SDP relaxation $\tau _+^{\text {sos}}$ and we show that $\tau _+^{\text {sos}}(A(e)) = 2/(1+e)$. To do so, we exhibit primal and dual feasible points for the semidefinite programs (15) and (16) which attain the value $2/(1+e)$. These are shown in the table below:

  $$\begin{aligned} \begin{array}{c|c} Primal (SDP (15)) &{} Dual (SOS program (16))\\ \hline \begin{array}{l} t = \displaystyle \frac{2}{1+e}\\ X = \frac{1}{t} aa^T + \frac{1-e}{2} \underbrace{\begin{bmatrix} 1 &{}\quad 0 &{}\quad 0 &{}\quad e\\ 0 &{}\quad 1 &{}\quad -1 &{}\quad 0\\ 0 &{}\quad -1 &{}\quad 1 &{}\quad 0\\ e &{}\quad 0 &{}\quad 0 &{}\quad e^2\end{bmatrix}}_{\tilde{X}}\\ \;\;\text { where } a = {{\mathrm{vec}}}(A) \end{array} &{} \begin{array}{l} L(X) = \frac{1+2e}{(1+e)^2}(X_{12}+X_{21}) - \frac{e}{(1+e)^2} X_{11} - \frac{1}{(1+e)^2} X_{22}\\ SOS(X) = \left( 1-\frac{1}{1+e} X_{12}-\frac{1}{1+e}X_{21}\right) ^2 + \left( \frac{\sqrt{e}}{1+e} X_{11} - \frac{1}{\sqrt{e}(1+e)}X_{22}\right) ^2\\ D_{11} = \frac{e}{(1+e)^2} \qquad D_{12} = \frac{1}{(1+e)^2}\\ D_{21} = \frac{1}{(1+e)^2} \qquad D_{22} = \frac{1}{e(1+e)^2}\\ \nu = \frac{2}{(1+e)^2} \end{array} \end{array} \end{aligned}$$

  It is not hard to show that these are feasible points: For the primal SDP we have to verify that the matrix

  $$\begin{aligned} \begin{bmatrix} t&\quad a^T \\ a&\quad X \end{bmatrix} \end{aligned}$$

  is positive semidefinite. By Schur complement theorem this is equivalent to having $X \succeq aa^T / t$. This is true for the matrix X defined above since by definition $X = aa^T / t + (1-e)/2 \cdot \tilde{X}$ where $\tilde{X} \succeq 0$. Also one can easily verify that for any i, j we have $X_{ij,ij} = A_{ij}^2$. Finally the constraint $X_{(1,1),(2,2)} = X_{(1,2),(2,1)}$ is satisfied because we have:

  $$\begin{aligned} X_{(1,1),(2,2)} = X_{1,4} = \frac{1+e}{2} e + \frac{1-e}{2} e = e \end{aligned}$$

  and

  $$\begin{aligned} X_{(1,2),(2,1)} = X_{2,3} = \frac{1+e}{2} - \frac{1-e}{2} = e. \end{aligned}$$

  To verify that the SOS certificate is valid we need to verify that the following identity holds:

  $$\begin{aligned} 1-L(X) = SOS(X) + \sum _{i,j} D_{ij} X_{ij} (A_{ij} - X_{ij}) + \nu (X_{11}X_{22} - X_{12}X_{21}), \end{aligned}$$

  which can be easily verified. Also the objective value is:

  $$\begin{aligned} L(A) = \frac{1+2e}{(1+e)^2}\cdot 2 - \frac{e}{(1+e)^2} \cdot 1 - \frac{1}{(1+e)^2}\cdot e = \frac{2}{1+e}. \end{aligned}$$

$\square$

Appendix 5: Proof of Proposition 4

Sketch of proof of Proposition 4

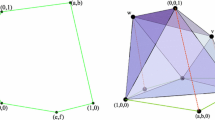
• We first prove the direction $\Rightarrow$: Let T be a triangle such that $S(a,b) \subset T \subset P$. We can clearly assume that the vertices of T are all on the boundary of P. Then since T has only 3 vertices, there is one edge of P that T does not touch.⁹ Assume without loss of generality that the edge that T misses is the edge joining $(1,-1)$ to (1, 1). In this case T has the form shown in Fig. 8a. It is easy to see that one can move the vertices of T so that it has the “canonical” form shown in Fig. 8b while still satisfying $S(a,b) \subset T \subset P$. The coordinates of the vertices of the canonical triangle are respectively $(a,-1), (a,1)$ and $(-1,0)$. Using a simple calculation one can show that this triangle contains S(a, b) if and only if $(1+a)(1+b) \le 2$.

• To show that the condition $(1+a)(1+b) \le 2$ is sufficient, it suffices to consider the triangle of the form depicted in Fig. 8(b) which can be shown to contain S(a, b) if $(1+a)(1+b) \le 2$.

$\square$

Fig. 8

a A triangle T such that $S(a,b) \subset T \subset P$. b Canonical form of triangle, where one side is parallel to the axis and touches the corresponding of S(a, b)

Appendix 6: Proof of Theorem 8 that $\tau _{\text {cp}}^{\text {sos}}(A) \ge {{\mathrm{rank}}}(A)$

Proof of Proposition 8

Let (t, X) be the optimal solution of the semidefinite program (45) where $t=\tau _{\text {cp}}^{\text {sos}}(A)$. Using Schur complement theorem we have that ${{\mathrm{vec}}}(A){{\mathrm{vec}}}(A)^T \preceq tX$. Furthermore we also have $X \preceq A \otimes A$, and thus if we combine these two inequalities we get:

$$\begin{aligned} {{\mathrm{vec}}}(A){{\mathrm{vec}}}(A)^T \preceq t (A\otimes A). \end{aligned}$$

Hence by Lemma 4 below we necessarily have $t \ge {{\mathrm{rank}}}(A)$.

Lemma 4

Let $A \in \mathbf{S}^n_+$ be a $n\times n$ positive semidefinite matrix. Then

$$\begin{aligned} {{\mathrm{rank}}}(A) = \min \left\{ t \; : \; {{\mathrm{vec}}}(A) {{\mathrm{vec}}}(A)^T \preceq t A\otimes A \right\} . \end{aligned}$$

Proof

Let $A = PDP^T$ be an eigenvalue decomposition of A where P is an orthogonal matrix and D is a diagonal matrix where the diagonal elements are sorted in decreasing order. Let $r={{\mathrm{rank}}}(A)=|\{i : D_{i,i} > 0\}|$ and denote by $I_r$ the identity matrix where only the first r entries are set to 1 (the other entries are zero). For $t\ge 0$, the following equivalences hold:

$$\begin{aligned}&{{\mathrm{vec}}}(A){{\mathrm{vec}}}(A)^T \preceq t A \otimes A \;\;\nonumber \\&\quad \Longleftrightarrow \;\; {{\mathrm{vec}}}(PDP^T){{\mathrm{vec}}}(PDP^T)^T \preceq t (P\otimes P) (D\otimes D) (P^T \otimes P^T)\nonumber \\&\quad \overset{\text {(a)}}{\Longleftrightarrow } \;\; (P\otimes P) {{\mathrm{vec}}}(D){{\mathrm{vec}}}(D)^T (P^T \otimes P^T) \preceq t (P\otimes P) (D\otimes D) (P^T \otimes P^T)\nonumber \\&\quad \overset{\text {(b)}}{\Longleftrightarrow } \;\; {{\mathrm{vec}}}(D){{\mathrm{vec}}}(D)^T \preceq t (D\otimes D)\nonumber \\&\quad \overset{\text {(c)}}{\Longleftrightarrow } \;\; {{\mathrm{vec}}}(I_r){{\mathrm{vec}}}(I_r)^T \preceq t (I_r\otimes I_r) \end{aligned}$$

(59)

where in (a) we used the well-known identity ${{\mathrm{vec}}}(PDP^T) = (P\otimes P){{\mathrm{vec}}}(D)$, in (b) we conjugated by $P\otimes P$ and in (c) we conjugated with $D^{-1/2} \otimes D^{-1/2}$ (where $(D^{-1/2})_{i,i} = (D_{ii})^{-1/2}$ if $D_{i,i} > 0$, else $(D^{-1/2})_{i,i} = 1$). The lemma thus reduces to show that

$$\begin{aligned} \min \left\{ t \; : \; {{\mathrm{vec}}}(I_r){{\mathrm{vec}}}(I_r)^T \preceq t (I_r \otimes I_r) \right\} = r. \end{aligned}$$

This is easy to see because ${{\mathrm{vec}}}(I_r)$ is an eigenvector of ${{\mathrm{vec}}}(I_r){{\mathrm{vec}}}(I_r)^T$ with eigenvalue r, and it is the only eigenvector of ${{\mathrm{vec}}}(I_r){{\mathrm{vec}}}(I_r)^T$ with a nonzero eigenvalue. Furthermore, ${{\mathrm{vec}}}(I_r)$ is also an eigenvector of $t(I_r \otimes I_r)$ with eigenvalue t. Thus the smallest t such that ${{\mathrm{vec}}}(I_r){{\mathrm{vec}}}(I_r)^T \preceq t (I_r \otimes I_r)$ is r. $\square$

Appendix 7: Proof of Theorem 9 that $\tau _{\text {cp}}(A) \ge c_{\text {frac}}(G(A))$

Proof of Theorem 9

Let $t = \tau _{\text {cp}}(A)$ and $X \in {{\mathrm{conv}}}(\mathcal A_{\text {cp}}(A))$ such that $A = t X$. Consider the decomposition of X:

$$\begin{aligned} X = \sum _{k=1}^r \lambda _k X_k, \end{aligned}$$

where $X_k \in \mathcal A_{\text {cp}}(A)$, $\lambda _k \ge 0$ and $\sum _{k=1}^r \lambda _k = 1$. Let $R_k = {{\mathrm{supp}}}(X_k)$ (i.e., $R_k$ is obtained by replacing the nonzero entries of $X_k$ with ones) and observe that $R_k \in \mathcal A_{\text {cl}}(A)$. Define

$$\begin{aligned} Y = t \sum _{k=1}^r \lambda _k R_k \in t {{\mathrm{conv}}}(\mathcal A_{\text {cl}}(A)) \end{aligned}$$

Observe that for any (i, j) such that $A_{i,j} > 0$ we have:

$$\begin{aligned} Y_{i,j} = t \sum _{k:X_k[i,j]>0} \lambda _k \underbrace{R_k[i,j]}_{=1} \overset{(a)}{\ge } t \sum _{k:X_k[i,j]} \lambda _k \frac{X_k[i,j]}{A_{i,j}} \overset{(b)}{=} \frac{A_{i,j}}{A_{i,j}} = 1 \end{aligned}$$

where in (a) we used the fact that $X_k \le A$ (by definition of $X_k \in \mathcal A_{\text {cp}}(A)$) and in (b) we used the fact that $A = t\sum _{k} \lambda _k X_k$. Thus this shows that (t, Y) is feasible for the optimization program defining $c_{\text {frac}}(G(A))$ and thus we have $c_{\text {frac}}(G(A)) \le t = \tau _{\text {cp}}(A)$. $\square$