1 Introduction

Traveling by train across the border between France and Spain used to involve the inconvenience of changing trains. French and Spanish trains operate on rails of different gauge. In order to resolve this issue, Spain adopted a variable gauge system that enables its trains to access the French railway network. Swedish and Polish railway companies employ variable gauge systems on cross-border services as well.

We consider a framework where an agent is associated with one of two platforms. Communication between two agents requires that they operate on a common platform. Adoption of a new platform is costly. The cost depends on the agent’s native platform. The benefit of communication depends on a subjective parameter reflecting the value the agent attaches to the interactions the new platform enables. The benefit of communication is increasing in the number of agents with whom one may interact.

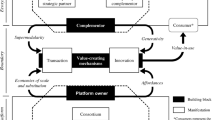
The term platform denotes a mode of operation, while the term communication denotes the possibility of interaction that having a platform in common affords. Refer to Fig. 1a. Agents are represented by nodes. The set of agents is partitioned in two groups. All members of each group share the same native platform. Agent j’s native platform is \(\alpha \). Platform adoption, that entails a platform-specific cost, is depicted by an arrow stemming from a node and pointing to a set of nodes. Individual j adopts platform \(\beta \). This enables her to communicate with each agent whose native platform is \(\beta \). The net benefit she derives depends on the number of agents she is able to communicate with [this is what Selten and Pool (1991) call ‘communicative benefit’] and the cost she had to face in order to adopt the new platform. Moreover, she becomes a source of value for all the agents whose native platform is \(\beta \), who are now able to communicate with her. This externality is a critical feature of the model.

Fig. 1
figure 1

a By adopting platform \(\beta \) agent j makes possible the interaction between her and each agent in \(N^{\beta }\). b An assignment that enables all agents to communicate with each other. c Two-sided adoption: at least one agent from each platform group adopts the platform foreign to her

Full size image

Two questions arise naturally. First, what is the efficient adoption pattern? Second, provided the previous question is resolved, how may a policy maker implement it? The central aim of this paper is to understand how the answer to these two questions is shaped by the inherent externality present in the situations we study.

The exercise of determining the efficient outcome constitutes a discrete optimization problem. We provide an algorithm that solves it and we address computational complexity issues. Figure 1b depicts a situation where all agents have a platform in common. Efficient outcomes do not necessarily entail that. Moreover, at the optimum, two-sided adoption, depicted in Fig. 1c, may occur.

Implementation is associated with the study of mechanisms. These objects associate a social outcome to the various values the primitives of the model may take. A mechanism can be evaluated on the basis of its properties. The following four properties feature prominently in this paper:

  1. 1.

    Assignment efficiency The mechanism always selects efficient outcomes.

  2. 2.

    Strategy-proofness The mechanism induces all agents to reveal whatever private information they may hold.

  3. 3.

    Individual rationality The mechanism does not force the participation of any agent.

  4. 4.

    Feasibility The mechanism relies exclusively on the resources generated within the economy.

It turns out that no mechanism satisfies all of the above requirements. There are, however, mechanisms that satisfy any three of them. We place particular emphasis on Assignment Efficiency and Strategy-Profness. Both these properties are shown to be inherently linked with incentives. A mechanism that violates either of them is prone to deficiencies that undermine the implementation exercise in a fundamental way. Appealing to a result due to Holmström (1979), embracing Assignment Efficiency and Strategy-Proofness entails confining our investigation to the family of Groves mechanisms (1973). The literature discussing such mechanisms does so primarily in three fairly distinct contexts. Pure public goods, excludable public goods and private goods.

In this paper we study Groves mechanisms in a context of private goods that accounts for the effect of an externality. It turns out that some of the conventional wisdom on Groves mechanisms does not carry through to our model. For example, the celebrated Pivotal mechanism here fails Feasibility. The nature of the externality we capture in our model causes the Pivotal mechanism to sometimes assign positive transfers, something that is disallowed in the framework of either public or private goods.

Our proposal involves two mechanisms. First, we look at individually rational Groves mechanisms. We show that such mechanisms are often in deficit and we provide sufficient conditions that determine when this is the case. We propose a mechanism that minimizes the deficit whenever it occurs. Second, we outline a methodology to design feasible Groves mechanisms. Following that, in economies comprising two agents, we single out the only feasible and symmetrical Groves mechanism that is not Pareto dominated by another strategy-proof, feasible and symmetrical mechanism.

Effectively the objective we pursue is to identify the best-in-class mechanism. When Feasibility is out of the picture the criterion that isolates the best mechanism is related to the incidence of the deficit. We do not focus on the worst case scenario (as in Bailey 1997; Cavallo 2006; Guo and Conitzer 2007; Moulin 2009) or on the asymptotic behavior of the deficit (as in Deb et al. 2006; Green and Laffont 1979; McAfee 1992). Rather we propose a mechanism that runs a lower deficit than any other mechanism in each economy where the deficit presents itself.

In order to isolate the best feasible Groves mechanism, we do not base our selection on sums of utilities but rather on their distribution (as in Guo and Conitzer 2008; Athanasiou 2013; Sprumont 2012). Loosely speaking, a mechanism Pareto dominates another one if the former generates, in each economy and for each agent, a higher amount of utility. This criterion turns out to be sharp enough to isolate a single feasible Groves mechanism when the discussion is confined to two-agent economies.

A natural application of our findings concerns the problem of language acquisition. The literature on this topics focuses on decentralized outcomes that may arise in situations similar to the ones we explore. In their seminal contribution Selten and Pool (1991) introduce a general model of language acquisition. They show that an equilibrium of the multi-country multilingual language acquisition model exists. The characterization of an equilibrium is then studied by Church and King (1993). More recently, Ginsburgh et al. (2006) and Gabszewicz et al. (2011) study qualitative properties of such equilibria in the context of bilingual societies. In our model one may rationalize different Nash Equilibria, exhibiting both one-sided as well as two-sided learning. However, the efficient outcome does not generically come about as a Nash Equilibrium.

This latter point provides the motivation for looking into the outcomes a Planner may bring about and how they compare with those that arise in the absence of intervention. Consider the following example. Peter and Mary speak English. Igor, Ivan and Natasha speak Russian. Both Peter and Mary attach significant value to communicating with Igor, Ivan and Natasha, but they face a cost of learning Russian that is prohibitive. Contrary to that, Igor, Ivan and Natasha attach no value to communicating with Peter and Mary, although for them the cost of learning English is smaller that the benefit it would create for Peter and Mary. Suppose that each individual’s strategy in this game consists of a decision on whether to learn the foreign language or not. At equilibrium no-one learns a foreign language, albeit for different reasons. However, the pattern of language acquisition that maximizes the sum of utilities involves Igor, Ivan and Natasha learning English. This example capture the nature of the externality that lies in the heart of the problem we study in this paper.

Section 2 introduces the model. Section 3 discusses efficiency. Section 4 introduces the axioms and presents the impossibility. Section 5 discusses individually rational Groves mechanisms. Section 6 discusses feasible Groves mechanisms. Section 7 concludes.

2 The model

The finite set of agents is denoted by \(N \subseteq \mathbb {N}\), with \(|N| \ge 2\). There are two platforms, \(\alpha \) and \(\beta \). For each \(\lambda \in \{\alpha ,\beta \}\), \(N^{\lambda }\) is the set of agents whose native platform is \(\lambda \). For each \(i \in N\), either \(i \in N^{\alpha }\) or \(i \in N^{\beta }\), but not both.

Each agent may adopt the platform that is foreign to her. Platform adoption is represented by the dichotomous variable \(l_{i}\in \{0,1\}\). We write \(l_i=1\) if adoption occurs, \(l_i=0\) otherwise. Let \(l_{N}=(l_{i})_{i\in N}\in \{0,1\}^{N}\) denote an assignment, the vector describing the action taken by each member of the population. Let \(\gamma : N\rightarrow \{\alpha ,\beta \}\) be such that for each \(i\in N\) and for each \(\lambda \in \{\alpha ,\beta \}\),

$$\begin{aligned} \gamma (i)= \lambda \Leftrightarrow i \in N^{\lambda }. \end{aligned}$$

The cost of platform adoption depends on the agent’s native platform. Let \(C=(c_{\alpha },c_{\beta })\in \mathbb {R}_{++}^{2}\). For each \(i \in N\), \(c_{\gamma (i)}\) is the cost of adoption agent i faces. We assume that both \(c_{\alpha }\) and \(c_{\beta }\) are finite.

The marginal benefit an agent derives from being able to communicate with agents that operate on a different native platform is denoted by the parameter \(\theta _i \in \mathbb {R}_+\). The total benefit of communication is proportional to the number of agents with whom one communicates. Consequently, the marginal benefit of communication is constant. Namely, for each \(i \in N\), at each \(l_N \in \{0,1\}^N\), the expression

$$\begin{aligned} \theta _{i}\sum _{j\in N\setminus N^{\gamma (i)}}\min \big \{1,l_{i}+l_{j}\big \}, \end{aligned}$$
(2.1)

specifies the gross benefit of agent i. For instance, going back the example in Fig. 1a, letting \(l_{j}=1\) and, for each \(i\in N\setminus \{j\}\), \(l_{i}=0\), agent j’s gross benefit becomes

$$\begin{aligned} \theta _{j}\big (\min \{1,2\}+\min \{1,2\}\big )=2\theta _{j}. \end{aligned}$$

Moreover, in the same figure, for each \(i \in N^{\alpha }\setminus \{j\}\), i’s net benefit equals 0, while each agent \(i \in N^{\beta }\) is now able to communicate with one more agent (j) so her benefit equals \(\theta _{i}\).

For each \(i \in N\), at each \(l_N \in \{0,1\}^N\), the expression

$$\begin{aligned} v_{i}(l_{N};\theta _{i})=\theta _{i}\sum _{j\in N\setminus N^{\gamma (i)}}\min \big \{1,l_{i}+l_{j}\big \}-l_{i}c_{\gamma (i)}, \end{aligned}$$

specifies the net benefit of agent i.

Accounting for the possibility of an individual transfer \(t_i \in \mathbb {R}\), the final utility of each \(i\in N\), at \(l_N \in \{0,1\}^N\), becomes

$$\begin{aligned} u_i(l_N,t_i;\theta _i)= v_i(l_N;\theta _i)+t_i. \end{aligned}$$

Preferences are quasi-linear.

Let \(\theta _{N^{\alpha }} \equiv (\theta _{i})_{i\in N^{\alpha }}\), \(\theta _{N^{\beta }} \equiv (\theta _{i})_{i\in N^{\beta }}\) and \(\theta _N \equiv (\theta _{i})_{i\in N}\). An economy is denoted by \(e=\big ((\theta _{N^{\alpha }},\theta _{N^{\beta }}),C\big )=\big (\theta _{N},C\big )\in \mathbb {R}_{+}^{N+2}\equiv \mathcal {E}\). Let \(t_{N}=(t_{i})_{i\in N}\in \mathbb {R}^{N}\). An allocation is a list \((l_N,t_N)\equiv (l_i,t_i)_{i\in N}\). Let \(Z=\{0,1\}^{N}\times \mathbb {R}^{N}\) be the set of all allocations. A mechanism is a function \(\varphi : \mathcal {E}\rightarrow Z\). It associates with each economy a single allocation, so that \(\varphi (e)=(l_{N},t_{N})\) and \(\varphi _{i}(e)=(l_{i},t_{i})\). Finally, for each \(e \in \mathcal {E}\) and each \(l_N \in \{0,1\}^{N} \), let \(\pi (l_N;e)=\sum _{i \in N}v_i\big (l_N;\theta _i\big )\) be the sum of net benefits generated by the assignment \(l_N\).

Many of the computational difficulties associated with the model stem from the min operator (Eq. 2.1). This operator ensures that even if two agents have two platforms in common, the benefit each derives from communicating with the other remains unchanged relative to the case of communication through a single platform.

The gross benefit does not account for people with whom one shares already the same native platform. This value is a constant. Therefore, it does not have any bearing on the maximization problem that underlies efficiency.

Finally, a platform carries no intrinsic value, it just serves as a means of communication. In addition, agents do not care with whom they communicate. They solely value the amount of communication. These assumptions serve to intensify the effect of the externality. Since our aim is precisely to study this effect, we have no interest in dampening its intensity.

3 Efficient assignments

In this section we discuss the problem of maximizing the sum of net benefits. Depending on the particular \(e\in \mathcal {E}\) at hand, we need to solve the following optimization problem:

$$\begin{aligned} P(e):\max _{l_{N}\in \{0,1\}^{N}} \sum _{i \in N} \left( \theta _i \left( \sum _{j \in N/N^{\gamma (i)}}min\{1,l_{i}+l_{j}\}\right) -l_ic_{\gamma (i)}\right) . \end{aligned}$$

For each \(e \in \mathcal {E}\), let \(\Sigma (e)\) be the set of assignments that solve P(e). We provide an algorithm that produces for each \(e \in \mathcal {E}\), one \(l_{N}\in \Sigma (e)\). For each \(e\in \mathcal {E}\), there are at most \(2^{|N|}\) candidate solutions. Since the set of candidate solutions is finite, for each \(e\in \mathcal {E}\), \(\Sigma (e)\ne \emptyset \).

A naive algorithm that solves P(e) enumerates all the candidate solutions. We propose an algorithm that runs in polynomial time, that is, it enables a computer to solve the problem quickly, far more so compared to the naive algorithm. We defer to the end of the section a more precise discussion of this matter.

The construction of the algorithm is founded on Lemmas 1, 2 and 3 presented below. These Lemmas provide properties of an optimal solution and allow pruning the search to a small subset of candidate solutions without missing at least one optimal solution. Lemma 1 states that if at the optimum an agent does not adopt the foreign platform, then so do all other agents who share her native platform and have a lower marginal benefit.

Lemma 1

For each \(e\in \mathcal {E}\), each \(\lambda \in \{\alpha ,\beta \}\) and each \(i_1, i_2 \in N^\lambda \), if \(\theta _{i_1} > \theta _{i_2}\) then for each \(l_{N}\in \Sigma (e)\), \(l_{i_{1}} \ge l_{i_{2}}\).

Proof

Without loss of generality let \(\lambda =\alpha \). Suppose, by way of contradiction, that there exists \(l_{N}\in \Sigma (e)\) such that \(l_ {i_1}=0\) and \(l_{i_2}=1\). Construct an alternative solution \(\tilde{l}_N\) such that

$$\begin{aligned} \tilde{l}_{j} = \left\{ \begin{array}{ll} l_j &{} \text { if } j \ne i_1, j\ne i_2, \\ 1 &{} \text { if } j = i_1, \\ 0 &{} \text { if } j = i_2. \\ \end{array} \right. \end{aligned}$$
(3.1)

Let \(S \subseteq N^\beta \) be such that for each \(i \in S\), \(l_i=\widetilde{l}_i=0\). By construction, \(\pi (\tilde{l}_N;e) - \pi (l_N;e)= (\theta _{i_1} - \theta _{i_2} )|S|\). By assumption, \(l_{N}\) is optimal and \(l_{i_{2}}=1\), with \(i_{2}\in N^{\alpha }\). If \(S=\emptyset \) then, for each \(i\in N^{\beta }\), \(l_{i}=1\). But if every agent in \(N^{\beta }\) adopted the foreign platform, it would be suboptimal for agent \(i_{2}\) to do the same. Therefore, \(S\ne \emptyset \). This implies that \((\theta _{i_1} - \theta _{i_2} )|S|>0\), the desired contradiction. \(\square \)

Consider some arbitrary assignment \(l_{N}\in \{0,1\}^{N}\) such that for some \(k\in N^{\alpha }\), \(l_{k}=0\). If agent k were to adopt the foreign platform, she would generate a social marginal contribution equal to

$$\begin{aligned} \theta _{k}\left( \vert N\setminus N^{\gamma (k)}\vert -\sum _{j\in N\setminus N^{\gamma (k)}}l_{j}\right) -c_{\gamma (k)}+\sum _{j\in N\setminus N^{\gamma (k)}}\theta _{j}(1-l_{j}). \end{aligned}$$

This value incorporates both her personal utility gain as well as the external effect (the last term in the expression). Lemma 2 states two familiar conditions necessary for optimality. Lemma 3 is a consequence of Lemmas 1 and 2.

Lemma 2

For each \(e\in \mathcal {E}\), each \(l_N\in \Sigma (e)\) and each \(i\in N,\)

  1. (1)

    if \(l_{i}=1\), then \(\theta _{i}\big (\vert N\setminus N^{\gamma (i)}\vert -\sum _{j\in N\setminus N^{\gamma (i)}}l_{j}\big )+\sum _{j\in N\setminus N^{\gamma (i)}}\theta _{j}(1-l_{j})-c_{\gamma (i)}\ge 0,\)

  2. (2)

    if \(l_{i}=0\), then \(\theta _{i}\big (\vert N\setminus N^{\gamma (i)}\vert -\sum _{j\in N\setminus N^{\gamma (i)}}l_{j}\big )+\sum _{j\in N\setminus N^{\gamma (i)}}\theta _{j}(1-l_{j})-c_{\gamma (i)}\le 0.\)

Proof

Conditions (1) and (2) are necessary for \(l_{N}\in \Sigma (e)\). Indeed, if \(l_{N}\in \Sigma (e)\), then for each \(i\in N\) unilaterally reducing the amount of communication (first condition), or unilaterally increasing the amount of communication (second condition) must decrease the sum of utilities. \(\square \)

Lemma 3

For each \(e\in \mathcal {E}\), \(\lambda \in \{\alpha ,\beta \}\) and \(l_N \in \Sigma (e)\), if there exists \(i^{*}\in N^{\lambda }\), such that \(\theta _{i^{*}} \ge \theta _i\) for each \(i \in N^\lambda \) and \(l_{i^{*}}=0\) then

$$\begin{aligned} l_i = 0\qquad \text {for all} \ i \in N^\lambda \end{aligned}$$
(3.2)
$$\begin{aligned}&l_i = \left\{ \begin{array}{ll} 1 &{} \quad \text {if } |N^\lambda |\theta _i + \sum _{j \in N^\lambda }\theta _j - c_{\gamma (i)} > 0 \\ 0 &{} \quad \text {otherwise} \\ \end{array} \right.&\text {for all} \ i \in N\setminus N^\lambda \end{aligned}$$
(3.3)

Proof

Implication (3.2) follows from Lemma 1. Implication (3.3) follows from Lemma 2. \(\square \)

Proposition 1

For each \(e\in \mathcal {E}\), if the assignment \(l_N \in \{0,1\}^{N}\) is selected by the algorithm defined in Table 1, then \(l_N \in \Sigma (e).\)

Table 1 The algorithm
Full size table

The proof is omitted. It relies on Lemmas 1, 2 and 3. The design of the algorithm relies on the results presented in this section. It is defined in Table 1. The algorithm performs approximately \(|N^\alpha ||N^\beta |\) arithmetic operations. Using this fact it can be shown that for |N| large enough, the algorithm takes less than \(\eta |N|^2\) operations, where \(\eta \) is some constant independent of e. Thus, the proposed algorithm is a polynomial-time algorithm. This picture changes radically if we consider instances of the problem involving a partition of the population in more than two native platform groups. It can be shown (a proof is available on request) that such a problem is NP-complete, that is, one does not expect to find an efficient algorithm as is the case when each agent is associated with one of two native platforms.

In what follows we provide an example that explains how the algorithm functions. Consider the economy \(e=(((0.8,0.1),(2,0.1,0)),(1.6,1.1))\) (namely \(\theta _{N_\alpha }=(0.8,0.1)\), \(\theta _{N_\beta }=(2,0.1,0)\) and \(C=(1.6,1.1)\)) and consider the problem \(P((0.8,0.1),\,(2,0.1,0)),(1.6,1.1))\). By Lemma 1 either agent 1 adopts \(\beta \) or no one in \(N^\alpha \) adopts \(\beta \). Therefore, create two subproblems.

Assume first that \(l_1=0\). By Lemma 1 we obtain \(l_2=0\). Lemma 3 determines how many agents in \(N^\beta \) will adopt the foreign platform, given \(l_1=l_2=0\). Assume \(l_3=1\). The overall surplus generated by this action is \(|N ^\alpha |\theta _3 + \sum _{j \in N^\alpha }\theta _j - c_{\gamma (3)}=2\,\times \,2\,+\,0.8\,+\,0.1\,-\,1.1=3.8\). Similarly, if \(l_4=1\), we obtain \(0.1\,\times \,2\,+\,0.8\,+\,0.1\,-\,1.1=0\). Finally, if \(l_5=1\), we obtain \(0\,\times \,2\,+\,0.8\,+\,0.1\,-\,1.1=-0.2\). Hence, \(V_1=3.8\). This step generates the first candidate solution, \(\big ((0,0),(1,0,0)\big )\) with corresponding value \(V_1=3.8\).

Assume now that \(l_1=1\). Consider \(M_1: = |N^{\beta }|\theta _1 + \sum _{j \in N^{\beta }}\theta _j - c_{\alpha }=0.8*3+2+0.1+0-1.6=2.9\), remove agent 1 from the problem and proceed to the next step. Let \(l_2=0\). Again apply Lemma 3. If \(l_3=1\) then the overall surplus generated by this action (given there is only agent 2 in \(N^\alpha \) and she is not adopting the foreign platform) is \(2+0.1-1.1=1\). It is easy to check that \(l_4=1\) and \(l_5=1\) would generate a negative overall surplus. In this subproblem only agent 3 adopts the foreign platform and \(V_2=1\). The second candidate solution is \(\big ((1,0),(1,0,0)\big )\) with corresponding value is \(M_1+V_2=3.9\).

Finally, let \(l_2=1\) and compute \(M_2: = |N^{\beta }|\theta _1 + \sum _{j \in N^{\beta }}\theta _j - c_{\alpha }=0.1*3+2+0.1+0-1.6=0.8\). This step provides the last candidate solution: \(\big ((1,1),(0,0,0)\big )\). The corresponding value is \(M_1+M_2=3.7\). The algorithm generates three candidate solutions (out of \(2^5\) a priori candidates). The optimal assignment is \(\big ((1,0),(1,0,0)\big )\). This example, apart from illustrating how the algorithm works, demonstrates two important points regarding efficiency. First, at the optimum, full communication does not necessarily ensue. Second, and perhaps more surprisingly, optimal assignments may entail that agents from both sides adopting the foreign platform.

4 Axioms

In this section we formally define Strategy-Proofness, Assignment Efficiency and Individual Rationality and discuss their implications. Although these axioms may be motivated by appealing to normative considerations, we emphasize their significance in alleviating the incentive problem. In our framework a mechanism can be manipulated in three ways:

  1. (1)

    The agent may misreport private information.

  2. (2)

    The agent may choose not to conform to the prescriptions of the mechanism.

  3. (3)

    The agent may refuse to participate.

The axioms we present in this section tackle the issues listed above. Although the policy maker observes each agent’s native platform and she is aware of the costs that adoption entails, she does not know the marginal benefit of any agent. As a consequence, some agents might find it profitable to behave strategically and misreport it. We require of mechanisms to always induce, for each agent, a weakly dominant strategy to report truthfully her marginal benefit. Let \(\theta _{N\setminus \{i\}}=(\theta _{1},\ldots ,\theta _{i-1},\theta _{i+1},\ldots ,\theta _{|N|}) \in \mathbb {R}_{+}^{N-1}\).

Strategy-proofness For each \(e \in \mathcal {E}\), \(i \in N\) and \(\theta _i' \in \mathbb {R}_+ \),

$$\begin{aligned} u_i\left( \varphi _i(\theta _N,C);\theta _i\right) \ge u_i\left( \varphi _i(\theta '_i,\theta _{{N \setminus \{i\}}},C);\theta _i\right) . \end{aligned}$$

A mechanism is Assignment Efficient if, for each economy in the admissible domain, it selects an allocation that involves an assignment that maximizes the sum of net benefits. Assignment Efficiency differs from Pareto Efficiency in that it does not require transfers to sum up to zero.

Assignment efficiency For each \(e \in \mathcal {E}\), if \((l_{N},t_{N})=\varphi (e)\) then \(l_N \in \Sigma (e)\).

The way Assignment Efficiency prevents manipulation is not immediately apparent. In order to make it explicit we need to introduce the following axiom.

Non-compliance proofness For each \(e\in \mathcal {E}\), with \((l_N,t_N)=\varphi (e)\), if for some \(i\in N\), \(l_{i}=0\), then

$$\begin{aligned} \theta _{i}\left( \vert N\setminus N^{\gamma (i)}\vert -\sum _{j\in N\setminus N^{\gamma (i)}}l_{j}\right) -c_{\gamma (i)}\le 0. \end{aligned}$$

An allocation may be such that an agent is instructed not to adopt a foreign platform, although she finds it profitable to unilaterally deviate and adopt it. Non-Compliance Proofness requires that this is never the case. Assignment Efficiency implies Non-Compliance Proofness. Indeed, if for some \(e\in \mathcal {E}\), \((l_{N},t_{N})=\varphi (e)\) is such that for some \(i\in N\), \(l_{i}=1\) and \(\theta _{i}\big (\vert N\setminus N^{\gamma (i)}\vert -\sum _{j\in N\setminus N^{\gamma (i)}}l_{j}\big )-c_{\gamma (i)} > 0 \), then the necessary condition (2) in Lemma 2 does not hold. Hence, \(l_{N}\notin \Sigma (e)\). It needs to be noted that the axiom does not prevent all possible deviations by a single agent. However, it prevents precisely those forms of defiance that Assignment Efficiency rules out. Hence, it exposes the role Assignment Efficiency plays in improving conformity to the prescriptions of the mechanism.

A mechanism satisfies Individual Rationality if no agent is coerced into participation. All agents must enjoy a positive utility as a result of their participation.

Individual rationality For each \(e \in \mathcal {E}\) and \(i \in N\), \(u_i(\varphi _{i}(e);\theta _i) \ge 0\).

Holmström (1979) shows that a mechanism defined over a convex domain of preferences, as is the case here, satisfies Assignment Efficiency and Strategy Proofness if and only if it belongs to the family of Groves mechanisms (1973). A mechanism belonging to this family is associated with a transfer composed of two parts. First, each agent receives the total net benefit obtained by all other agents at the assignment chosen by the mechanism. Second, each agent receives a sum of money that does not depend on her own marginal benefit.

A mechanism \(\varphi ^{g}\) belongs to the family of \(\mathbf {Groves \ Mechanisms}\) if and only if for each \(e \in \mathcal {E}\), if \((l_N,t_N)=\varphi ^{g}(e)\) then \(l_N \in \Sigma (e)\) and for each \(i \in N\) and some arbitrary function \(h_i: \mathbb {R}^{N-1}_{+}\rightarrow \mathbb {R}\)

$$\begin{aligned} t_i=\sum _{j \ne i} v_j(l_N;\theta _i)-h_i(\theta _{N \setminus \{i\}}). \end{aligned}$$

A mechanism is by definition single-valued. Moreover, for some \(e\in \mathcal {E}\), \(\Sigma (e)\) may not be a singleton. Therefore, there may exist welfare equivalent Groves mechanisms that only disagree on the tie-breaking rule. The sum of the transfers associated with a Groves mechanism may be either positive or negative. The former case corresponds to a budget deficit, while the latter to a budget surplus. Either constitutes a welfare loss. However, there is a particular difficulty pertaining to the deficit. It necessitates tapping into resources that are not generated within the economy. Feasible mechanisms are self-sufficient.

Feasibility For each \(e \in \mathcal {E}\), if \((l_N,t_N)=\varphi (e)\) then \(\sum _{i \in N}t_i \le 0.\)

The agenda we pursue in this paper is set by the following result. One needs to make a choice between an individually rational Groves mechanism, at the expense of Feasibility and a feasible Groves mechanism, at the expense of Individual Rationality.

Proposition 2

There exists no mechanism \(\varphi \) that satisfies Strategy Proofness, Individual Rationality, Feasibility and Non-Compliance Proofness.

Proof

We construct a counter-example. Suppose that some mechanism \(\varphi \) satisfies the axioms. Let \(e\in \mathcal {E}\) be such that \(N=\{1,2\}\), with \(1\in N^{\alpha }\) and \(2\in N^{\beta }\). Moreover, let \(\theta _{1}=\theta _{2}>c_{\alpha }=c_{\beta }>0\) and \(c_{\alpha }+c_{\beta }>\theta _{1}\). Finally, let \((l_{N},t_{N})=\varphi (e)\). Given our assumptions, if \(l_{N}=(0,0)\), Non-Complinace Proofness is violated. Hence,

$$\begin{aligned} l_{N}\in \big \{0,1\big \}^{2}\setminus \big \{(0,0)\big \} =\big \{(1,0),(0,1),(1,1)\big \}\equiv \Lambda . \end{aligned}$$

Assume, first, that \(l_{N}=(1,0)\) and suppose that \(u_1\big ((l_1,t_1);\theta _{1}\big )\ge \theta _{1}\) and \(u_2\big ((l_2,t_2);\theta _{2}\big )\ge \theta _{2}\). Therefore, \(u_1(l_N,t_1;\theta _{1})+u_2(l_N,t_2;\theta _{2})\ge \theta _{2}+\theta _{1}\), or put equivalently \(\theta _{1}-c_{\alpha }+\theta _{2}+t_{1}+t_{2}\ge \theta _{1}+\theta _{2}\), which implies

$$\begin{aligned} t_{1}+t_{2}\ge c_{\alpha }&\qquad \big [\theta _{1}, \theta _{2}\text { cancel out} \big ]\nonumber \\ t_{1}+t_{2}>0&\qquad \big [\text {by assumption } c_{\alpha }>0\big ] \end{aligned}$$
(4.1)

By Feasibility, inequality (4.1) constitutes a contradiction. This reasoning applies for each \(l_{N}\in \Lambda \). Therefore, for each \(l_{N}\in \Lambda \), either \(u_1(l_N,t_1;\theta _{1})<\theta _{1}\) or \(u_2(l_N,t_2;\theta _{2})<\theta _{2}\). Without loss of generality, suppose that \(u_1(l_N,t_1;\theta _{1})<\theta _{1}\).

Let \(e^{\prime }=\big (\theta ^{\prime }_{N},(c_{\alpha },c_{\beta })\big )\) be identical to e except for the fact that \(\theta _{1}^{\prime }=0\). Let \((l_{N}^{\prime },t_{N}^{\prime })=\varphi (e^{\prime })\). Suppose that \(l_{N}^{\prime }=(1,1)\). By Individual Rationality, \(t^{\prime }_{1}\ge c_{\alpha }\text { and }\theta ^{\prime }_{2}-c_{\beta }+t^{\prime }_{2}\ge 0.\) Therefore, \(\theta _{2}^{\prime }+t_{1}^{\prime }+t_{2}^{\prime }\ge c_{\alpha }+c_{\beta }\). Moreover, by construction \(c_{\alpha }+c_{\beta }>\theta _{2}=\theta _{2}^{\prime }\ge 0\). Combining the last two observations we obtain \(t_{1}^{\prime }+t_{2}^{\prime }>0\), which contradicts Feasibility. Hence, \(l_{N}^{\prime }\ne (1,1)\). By Non-Complinace Proofness, applying the same reasoning as before, we obtain \(l_{N}^{\prime }\ne (0,0)\). Hence,

$$\begin{aligned} l_{N}^{\prime }\in \big \{0,1\big \}^{2}\setminus \big \{(0,0),(1,1)\big \}=\big \{(1,0),(0,1)\big \}\equiv \Lambda ^{\prime }. \end{aligned}$$

Therefore, by Individual Rationality, either \(t_{1}^{\prime }\ge c_{\alpha }\) (if \(l_{N}^{\prime }=(1,0)\)) or \(t_{1}^{\prime }\ge 0\) (if \(l_{N}^{\prime }=(0,1)\)). Thus, for each \(l_{N}^{\prime }\in \Lambda ^{\prime }\), \(u_{1}\big (\varphi _{1}(e^{\prime });\theta _{1}\big )\ge \theta _{1}\). Moreover, by assumption, \(u_{1}\big (\varphi _{1}(e);\theta _{1}\big )< \theta _{1}\). Hence, \(\varphi \) violates Strategy-Proofness, a contradiction. \(\square \)

Proposition 2 marks a difference between our framework and other economic environments. Examples of feasible and individually rational Groves mechanisms are provided by Guo and Conitzer (2007) and Moulin (2009) (among others) as solutions to the problem of assigning a finite number of identical objects to a greater finite number of agents. For the public good provision problem, under natural assumptions on the domain of preferences, a similar impossibility arises (Moulin 1988). Parkes (2001) provides two sufficient conditions, on the domain of economies, for a feasible Groves mechanism to satisfy Individual Rationality.Footnote 1 It should be noted that Parkes’ conditions are not satisfied in our framework.

5 Individually rational Groves mechanisms

In this section we focus on Groves mechanisms that satisfy Individual Rationality. As shown before, such mechanisms violate Feasibility. As we will see it is relatively simple to isolate, among them, a mechanism that minimizes the deficit (i.e., maximizes the revenues). The natural question to raise next concerns the incidence of the deficit. We provide conditions on the economy that, when met, imply that any individually rational Groves mechanism will be in deficit in that economy. Inspection of these sufficient conditions suggest that the deficit is, indeed, a prevalent phenomenon.Footnote 2

For each \(e \in \mathcal {E}\) and each \(i \in N\) let \(e^i\) denote an economy that is otherwise identical to e, except for the fact that agent i’s marginal benefit has been set equal to zero. Formally, if \(e=(\theta _{N},C)\), then \(e^i=\big ((0,\theta _{N \setminus \{i\}}),C\big )\). In addition, let \(l^i_N \in \Sigma (e^i)\).

The Minimal Deficit Mechanism (MDM) For each \(e \in \mathcal {E}\), \((l_N,t_N)=\varphi ^{md}(e)\) if and only if \(l_N \in \Sigma (e)\) and, for each \(i \in N\),

$$\begin{aligned} t_i=\sum _{j \ne i} v_j\left( l_N;\theta _j\right) -\sum _{j \ne i} v_j\left( l_N^i;\theta _j\right) - v_i\left( l_N^i;0\right) . \end{aligned}$$

Roughly speaking, the transfer of the MDM constitutes an assessment of the impact each agent’s marginal benefit has on the optimal sum of net benefits. In order to obtain the MDM from within the family of Groves mechanisms one needs to set, for each \(e \in \mathcal {E}\) and each \(i \in N\),

$$\begin{aligned} h_i\left( \theta _{N \setminus \{i\}}\right) =\pi \left( l^i_N;e^i\right) =\sum _{j \ne i} v_j\left( l_N^i;\theta _j\right) + v_i\left( l_N^i;0\right) . \end{aligned}$$

The following example illustrates the MDM. Consider the economy

$$\begin{aligned} e=(((2,1,0.1),(0.8,0.1)),(1.1,1.6)). \end{aligned}$$

Refer to Fig. 2. Dots represent agents. Agents whose native platform is \(\alpha \) are grouped on the left column, while agents whose native platform is \(\beta \) are grouped on the right column. The number in parenthesis is the name of the agent. The figure depicts the original economy along with the five economies we obtain by setting, each time, the marginal benefit of one agent equal to zero. An arrow stemming from a node representing agent \(i \in N\) and pointing to a set of nodes stands for \(l_i=1\). The absence of an arrow stands for \(l_i=0\). The figure depicts \(l_N \in \Sigma (e)\), as well as \(l^i_N\in \Sigma (e^{i})\), for each \(i=1,\ldots , 5\). For instance, \(l_N=(0,0,0,1,1)\). The value of \(\pi (l^i_N;e^i)\), for each \(i \in N\), lies at the bottom of each diagram. This piece of information allows one to compute the MDM transfers at e: \(t_N=(-0.2,-0.2,0,0.9,1.6)\). The MDM produces a deficit equal to 2.1.

Fig. 2
figure 2

An example illustrating the calculations that underlie the MDM

Full size image

The properties of the MDM have already been studied by Krishna and Perry (1998) as part of what they call the generalized Vickrey, Clarke, Groves mechanisms. They show, in a more general framework, that some instances of such mechanisms minimize the sum of transfers associated with any assignment efficient, individually rational and Bayesian incentive compatible mechanism. As a consequence, in our framework the MDM minimizes the deficit whenever it occurs and the result that follows (Lemma 4) is logically implied by Krishna and Perry’s result. However, its proof helps to better understand how the externality present in our framework works. In our setting, by removing an agent from the economy, one deprives the remaining agents from any benefit they may derive from being able to communicate with her. This simple observation explains why the MDM needs to be distinguished from the Pivotal mechanism (see Clarke 1971; Moulin 1986). Let \(l_{N\setminus \{i\}}=(l_{1},\ldots ,l_{i-1},l_{i+1},\ldots ,l_{|N|})\). In order to obtain the Pivotal mechanism from the family of Groves mechanisms one needs to set, for each \(e \in \mathcal {E}\) and each \(i \in N\),

$$\begin{aligned} h_i\left( \theta _{N \setminus \{i\}}\right) =\sum _{j \ne i}v_j\left( l'_{N \setminus \{i\}};\theta _j\right) , \end{aligned}$$

where \(l'_{N\setminus \{i\}} \in \Sigma (\theta _ {N \setminus \{i\}},C)\). The \(h_i(.)\) component of the Pivotal transfer is obtained by removing agent i from the economy altogether and then calculating the optimal sum of net benefits in her absence. In the canonical public good provision model whether an agent is removed from the economy or her valuation of the project is set to zero, amounts to the same effect. In our framework, an agent is still a source of value for the rest even if her marginal benefit is equal to zero. Removing her from the economy amounts to more than deducting her net benefit from the total sum. Moreover, in the pure public good provision problem the transfers associated with the Pivotal mechanism are non-positive. This is no longer the case in our framework. The following lemma asserts that any individually rational Groves mechanism generates at least as much deficit as the MDM.

Lemma 4

If for some \(e \in \mathcal {E}\) the MDM generates a deficit then, in the same economy, any mechanism satisfying Assignment Efficiency, Strategy-Proofness and Individual Rationality generates a greater or equal deficit.

Proof

By Assignment Efficiency and Strategy-Proofness we need to compare our mechanism with other mechanisms belonging to the Groves family of mechanisms. Moreover, by Individual Rationality we need to have, for each \(e \in \mathcal {E}\) and each \(i \in N\),

$$\begin{aligned} u_i(\varphi ^g(e);\theta _i)=v_i(l_N;\theta _i)+t_i=\sum _{i \in N}v_i(l_N;\theta _i)-h_i(\theta _{N \setminus \! \{i\}})\ge 0, \end{aligned}$$
(5.1)

with

$$\begin{aligned} \sum _{i \in N} v_{i}(l_{N};\theta _{i})=\sum _{i \in N}\left( \theta _{i}\sum _{j\in N\!\setminus \! N^{\gamma (i)}}\min \big \{1,l_{i}+l_{j}\big \}-l_{i}c_{\gamma (i)}\right) , \end{aligned}$$

where \(l_N \in \Sigma (e)\). Since the component \(h_i(\theta _{N\!\setminus \!\{i\}})\) is independent of \(\theta _i\), Eq. 5.1 entails

$$\begin{aligned} h_i(\theta _{N \!\setminus \! \{i\}}) \le \min _{\theta _i} \left\{ \sum _{j \in N} v_j(l_N^i;\theta _j)\right\} =\sum _{j \ne i} v_j(l_N^i;\theta _j)+v_i(l^i_N;0), \end{aligned}$$
(5.2)

where \(l_{N}^{i} \in \Sigma (e^{i})\). Moreover,

$$\begin{aligned} \sum _{i \in N}t_i=\sum _{i \in N} \sum _{j \ne i} v_j(l_N;\theta _j)-\sum _{i \in N} h_i(\theta _{N \!\setminus \! \{i\}}). \end{aligned}$$

By Eq. 5.2,

$$\begin{aligned} \sum _{i \in N}t_i \ge \sum _{i \in N} \sum _{j \ne i} v_j(l;\theta _j)- \sum _{i \in N} \sum _{j \ne N} v_j(l^i;\theta _j)-\sum _{i \in N}v_i(l_N^i;0). \end{aligned}$$
(5.3)

This means that, as soon as an individually rational mechanism generates a deficit, it generates at least as much deficit as in the right-end side of Eq. 5.3. Hence in order to minimize the deficit produced by the mechanism we need to set

$$\begin{aligned} h_i(\theta _{N \!\setminus \! \{i\}}) = \sum _{j \ne i} v_j(l_N^i;\theta _j) + v_i(l_N^i;0). \end{aligned}$$

\(\square \)

Pápai (2003) uses a similar argument to identify a sufficient condition for a Groves mechanism to be individually rational. In her framework an individually rational Groves mechanism cannot charge the agents more than the Pivotal does. This is not the case here as Lemma 4 demonstrates.

We can now introduce the main result of this section. The next proposition demonstrates that in a significant sub-domain of the set of admissible economies any Groves mechanism satisfying Individual Rationality runs a deficit. In light of the previous discussion, in all these instances, the MDM is the most desirable solution among all the individually rational Groves mechanisms. Proposition 3 involves a condition. It depends on all the parameters of the economy, namely its size, the profile of preferences and costs. For each economy at which the condition is met any individually rational Groves mechanism runs a deficit. The proposition assumes, without loss of generality, that \(c_{\alpha } \le c_{\beta }\). The proof can be found in “Appendix 1”.

For each \(e \in \mathcal {E}\) and each \(T>0\) let \(\zeta (T,e)=|\{i\in N\; |\; \theta _{i}<T\}|\).

Proposition 3

For each \(e \in \mathcal {E}\) such that \(c_{\alpha } \le c_{\beta }\), if

  1. (a)

    \(|N^{\alpha }|\le |N^{\beta }|\) and there exists \(T>0\) such that \(|N^{\beta }| \ge \frac{c_{\alpha }}{T}+\frac{c_{\beta }}{T}+\zeta (T,e)+1,\) then any Individually Rational Groves mechanism runs a deficit.

  2. (b)

    \(|N^{\alpha }| \ge \frac{c_\beta }{c_\alpha } |N^{\beta }|\) and there exists \(T > 0\) such that \(|N^{\alpha }| \ge \frac{c_{\beta }}{c_{\alpha }}\big (\zeta (T,e) +1\big ) + \frac{2c_{\beta }}{T}\), then any Individually Rational Groves mechanism runs a deficit.

The following examples elaborate on Propositions 3. Consider the economy

$$\begin{aligned} e=\Big (\big ((3,2,1,0),(3,3,2,2,1.5,1.5,0.5)\big ),(1,2)\Big ). \end{aligned}$$

The number of agents with \(\theta _i\) less than 1, i.e., \(\zeta (1, e)\), is 2. Hence, \(\zeta (1,e) + 1+ \frac{c_{\alpha } + c_{\beta }}{1} = 6<|N^{\beta }|=7\). By Proposition 3 (a), in this economy any individually rational Groves mechanism runs a deficit. Consider, next, the economy

$$\begin{aligned} e=\Big (\big ((\epsilon ,\ldots ,\epsilon ),(\epsilon ,\ldots ,\epsilon )\big ),(q\epsilon ,q\epsilon )\Big ), \end{aligned}$$

where \(\epsilon >0\) and \(q\in \mathbb {N}\). The number of agents with \(\theta _i\) less than \(\epsilon \), i.e., \(\zeta (\epsilon , e)\), is equal to zero. Moreover, \(|N^{\alpha }| = \frac{c_\beta }{c_\alpha } |N^{\beta }|=|N^{\beta }|\). We obtain

$$\begin{aligned} \frac{q\epsilon }{q\epsilon }(\zeta (\epsilon ,e) +1) + \frac{2q\epsilon }{\epsilon }=1+2q. \end{aligned}$$

Hence, as soon as \(|N^{\alpha }|\ge 1 +2q\), by Proposition 3 (b), in this economy any individually rational Groves mechanism runs a deficit.

We need to emphasize three points. First, the domain restrictions ‘almost’ do not rely on preferences. In effect, they only involve agents who attach a low value to the possibility of communication. Second, the domain restrictions do not require the economy to involve a large number of agents, unless both costs are enormous. Even in such a case though, one needs only one of the two groups to be adequately large for the result to come through. Finally, in economies that involve a large enough number of agents any individually rational Groves mechanism runs a deficit.

6 Feasible Groves mechanisms

In this section we drop Individual Rationality in favor of Feasibility. The restriction to feasible Groves mechanisms reflects a physical constraint often imposed on the implementation effort. The policy maker is not mandated to resort to outside funding. She may only rely on her power to tax agents which may be, for the purposes of this section, complemented by her ability to coerce participation.

Given the analysis performed so far, there is a simple class of mechanisms that accomplishes the task. It will serve in this section as a benchmark. In order to construct it we need to rely on a particular feature of the MDM. For each economy, let the set of assignments that ensure that each pair of agents have a platform in common be denoted by \(L^{f}(e).\) Footnote 3

Consider within this set the subset of assignments that are the least costly. That is, for each \(e\in \mathcal {E}\), let

$$\begin{aligned} L^{f*}(e)\equiv \underset{l_N\in L^{f}(e)}{{\text {argmin}}} \;\sum _{i\in N}l_ic_{\gamma (i)} \end{aligned}$$

Moreover, for each \(l_N^{*} \in L^{f*}(e)\), let

$$\begin{aligned} \underline{c}=\sum _{i\in N}l_i^{*}c_{\gamma (i)}. \end{aligned}$$

Notice that in order to compute the value \(\underline{c}\) one does not need to know the vector of marginal benefits. Moreover, for each economy the total cost pertaining to the efficient assignment is less or equal to the value \(\underline{c}\) for that economy. The mechanism we present below charges all individuals an amount \(\frac{\underline{c}}{|N|}\) on the top of what they were charged by the MDM. Recall that \(l_N^i \in \Sigma (e^i)\).

The Translated Minimal Deficit Mechanism (TMDM) For each \(e \in \mathcal {E}\), \((l_N,t_N)=\varphi ^{tmd}(e)\) if and only if \(l_N \in \Sigma (e)\) and, for each \(i \in N\)

$$\begin{aligned} t_i=\sum _{j \ne i} v_j\left( l_N;\theta _i\right) -\sum _{j \ne i} v_j\left( l_N^i;\theta _j\right) - v_i\left( l_N^i;0\right) -\frac{\underline{c}}{|N|}. \end{aligned}$$

Relative to the MDM, the TMDM levies an extra amount \(\underline{c}\) that aims at ensuring Feasibility. Moreover, the TMDM collects an equal share of this extra amount from each agent. One may imagine alternative ways of distributing this extra burden. However, as long as a Groves mechanism levies an amount \(\underline{c}\) over the amount the MDM levies, it will satisfy Feasibility. This is a direct consequence of the following Lemma.

Lemma 5

For each \(e \in \mathcal {E}\), if \((l_N,t_N)=\varphi ^{md}(e)\), then

$$\begin{aligned} \sum _{i \in N}t_i \le \sum _{i \in N}l_{i}c_{\gamma (i)}. \end{aligned}$$

Proof

For each \(e \in \mathcal {E}\) and each \(i \in N\), if \(l_N \in \Sigma (e)\) and \(l_N^i \in \Sigma (e^i)\), then

$$\begin{aligned} \theta _{i}\sum _{j\in N \!\setminus \! N^{\gamma (i)}}\min \{1, l_{i}+l_{j}\}\ge \sum _{i \in N} v_i(l_N;\theta _i) -\sum _{j \ne i} v_j(l_N^i;\theta _j)-v_i(l_N^i;0). \end{aligned}$$

If that were not true, by rearranging the terms of the inequality one would obtain

$$\begin{aligned}&\pi (l_{N}^{i}; e^{i})=\sum _{j \ne i} v_j(l_N^i;\theta _j) +v_i(l_N^i;0)\\&\quad <\sum _{i \in N} v_i(l_N;\theta _i) -\theta _{i}\sum _{j\in N \!\setminus \! N^{\gamma (i)}} \min \{1, l_{i}+l_{j}\}=\pi (l_{N}; e^{i}), \end{aligned}$$

which constitutes a contradiction, as, by assumption, \(l_N^i \in \Sigma (e^i)\). Summing over \(i\in N\) we obtain

$$\begin{aligned} \sum _{i\in N} \theta _{i}\sum _{j\in N\!\setminus \! N^{\gamma (i)}}\min \{1,l_{i}+l_{j}\}\ge |N| \pi (l_N;e)-\sum _{i\in N}\pi (l^i_N;e^i). \end{aligned}$$

The left-hand side of the previous equation represents the total gross benefit deriving from communication at \(l_N\). A simple algebraic manipulation yields

$$\begin{aligned} \sum _{i\in N}l_ic_{\gamma (i)}\ge (N-1)\pi (l_N;e)-\sum _{i\in N}\pi (l^i_N;e^i)=\sum _{i \in N}t_i. \end{aligned}$$

\(\square \)

Lemma 5 provides a rough idea of the challenge one needs to overcome when designing feasible Groves mechanisms. If the policy maker knows for each \(e \in \mathcal {E}\), with \((l_N,t_N)=\varphi ^{md}(e)\), the value \(\sum _{i\in N}l_{i}c_{\gamma (i)}\), then she has at her disposal a rough rule of thumb that she may apply in order to comply with Feasibility. However, Lemma 5 does not do much more than point in the right direction. The value \(\sum _{i\in N}l_{i}c_{\gamma (i)}\) varies with the economy and there is no a priori reason to be hopeful that collecting the information required to calculate it complies with Strategy-Proofness. The TMDM circumvents this issue by utilizing the fact that for each \(e \in \mathcal {E}\), each \(l_{N}\in \Sigma (e)\) and each \(l^{\prime }_{N}\in L^{f*}(e)\), we have \(\sum _{i\in N}l_{i}c_{\gamma (i)}\le \sum _{i\in N}l_{i}^{\prime }c_{\gamma (i)}=\underline{c}.\) Footnote 4

Using the TMDM as a benchmark we now turn to the question of what constitutes a ‘good’ feasible Groves mechanism. In what follows we confine our discussion to a two-agent environment. A brief remark at the end of this section explains why this concession is necessary.

Let \(N^{\alpha }=\{1\}\) and \(N^{\beta }=\{2\}\) and \(c=c_{\alpha }<c_{\beta }\), so that if ever adoption is efficient, it is individual 1 that adopts \(\beta \). An economy is denoted by \(e=(\theta _{N},c)\in \mathbb {R}_{+}^{3}\)=\( \mathcal {E}_2\). Figure 3 below depicts the TMDM defined over \( \mathcal {E}_2\). Although restrictive, this environment is still worth investigating as an instance of bilateral cooperation.

Fig. 3
figure 3

The vector of transfers \(\left( {\begin{array}{c}t^{tmd}_{1}\\ t^{tmd}_{2}\end{array}}\right) \) for each profile \((\theta _{1},\theta _{2})\in \mathbb {R}_{+}\) according to the TMDM in the two-agent case. Agent 1 adopts if \(\theta _{1}+\theta _{2}\ge c\). She does not otherwise

Full size image

In order to build a notion of what constitutes a ‘good’ feasible Groves mechanism we rely on the following axiom, Symmetry with respect to Adoption Costs, or simply Symmetry. Let \(\tau : \{1,2\}\rightarrow \{1,2\}\) be such that \(\tau (i)=j\) for each \(i,j\in N\) and \(\theta _{\tau (N)}\) denote the vector \(\theta _{N}\) permuted according to \(\tau \). In the two-agent setting Symmetry effectively requires that the distribution of utilities that an allocation induces does not depend on the agent-specific cost that adoption entails. The axiom constitutes a minimal legitimacy requirement that all mechanisms should naturally fulfill as agents cannot be considered responsible for the cost deriving from adopting a foreign platform. The axiom states that the consequences of a mechanism in utility terms should be invariant to the swapping of preference parameters. It should be noted that swapping preferences is still shy of fully swapping identities, as adoption costs are platform specific and exogenous.

Symmetry For each \(e \in \mathcal {E}_2\), \(i\in N\),

$$\begin{aligned} u_{i}\big (\varphi _{i}(\theta _{N},c);\theta _{i}\big )=u_{\tau (i)}\big (\varphi _{\tau (i)}(\theta _{\tau (N)},c);\theta _{\tau (i)}\big ).\ \end{aligned}$$

Let \(\Phi _2\) be the set of Strategy-Proof, Symmetrical and Feasible mechanisms defined over \( \mathcal {E}_2\). For each pair of mechanisms \(\varphi ,\varphi ^{\prime }\in \Phi _2\), \(\varphi \) Pareto dominates \(\varphi ^{\prime }\) if and only if for each \(c \in \mathbb {R}_+\), each \(\theta _N \in \mathbb {R}^2_+\) and each \(i \in N\)

$$\begin{aligned} u_{i}\big (\varphi _{i}(\theta _N,c);\theta _i\big )\ge u_{i}\big (\varphi '_{i}(\theta _N,c);\theta _i\big ), \end{aligned}$$

moreover, for some \(\tilde{\theta }_N \in \mathbb {R}^+_2\) and some \(j\in N\),

$$\begin{aligned} u_{j}\big (\varphi _{j}(\tilde{\theta }_N,c); \tilde{\theta _j}\big )> u_{j}\big (\varphi '_{j}(\tilde{\theta }_N,c); \tilde{\theta _j}\big ). \end{aligned}$$

A mechanism \(\varphi \in \Phi _2\) is Second Best Efficient if and only if there does not exist another mechanism \(\varphi ^{\prime }\in \Phi _2\) such that \(\varphi ^{\prime }\) Pareto dominates \(\varphi \). In a different economic environment, Moulin (1986) and Guo et al. (2013) demonstrate that, for two-agent economies, the Pivotal Mechanism is the only Groves mechanism that is not Pareto dominated by another Groves mechanism. We will show that there exists a unique Second Best Efficient Groves mechanism in \(\Phi _2\). The following condition (adapted from Athanasiou 2013) is necessary for a mechanism to be Second Best Efficient.

A mechanism \(\varphi \in \Phi _2\) satisfies Condition A if and only if for each \(e \in \mathcal {E}_2\) and each \(i\in N\), there does not exist \(\epsilon >0\) such that for each \(x\ge 0\)

$$\begin{aligned} \big (l_{N}(x),t_{N}(x)\big )=\varphi \big ((x,\theta _{N\!\setminus \!\{i\}}),c\big )\text { and } \sum _{j\in N}t_{j}(x)+\epsilon \le 0. \end{aligned}$$

A mechanism violating Condition A enables us to perturb it slightly in order to produce a new mechanism that Pareto dominates the original. The perturbation involves giving one agent a little bit more at a single valuation and for all profiles comprising this valuation. By construction, the mechanism thus created retains Strategy-Proofness and, courtesy of the violation of Condition A, remains feasible.

Proposition 4

A mechanism \(\varphi \in \Phi _2\) is Second Best Efficient only if it satisfies Condition A.

Proof

Suppose that \(\varphi \in \Phi _2\) is Second Best Efficient. By way of contradiction let there exist \(e^{\prime }=(\theta _{N}^{\prime }, c^{\prime })\in \mathcal {E}_2\) and \(\epsilon >0\) such that for some \(j\in \{1,2\}\)

$$\begin{aligned}&\big (l_{N}^{\prime }(x),t_{N}^{\prime }(x)\big )=\varphi \big ((x,\theta ^{\prime }_{N\!\setminus \!\{j\}}), c^{\prime }\big ),\text { and}\\&\quad \text {for each } x\ge 0,\;\; \sum _{i\in N}t_{i}^{\prime }(x)+\epsilon \le 0. \end{aligned}$$

Without loss of generality, let \(j=1\). Consider the mechanism \(\hat{\varphi }\) constructed in the following way: For each \(e=\big ((\theta _{1},\theta _{2}),c\big )\in \mathcal {E}_2\) if either \(\theta _{1}\ne \theta _{2}^{\prime }\) or \(\theta _{2}\ne \theta _{2}^{\prime }\) or \(c\ne c^{\prime }\), then \(\hat{\varphi }(e)=\varphi (e)\). Otherwise, \(\hat{\varphi }\big ((x,\theta ^{\prime }_{2}),c^{\prime }\big )=\big (\hat{l}_{N}(x),\hat{t}_{N}(x)\big )\), where, for each \(x\ge 0\),

  1. (i)

    \(\hat{l}_{N}(x)=l_{N}^{\prime }(x)\),

  2. (ii)

    \(\hat{t}_{1}(x)=t_{1}^{\prime }(x)+\epsilon \) and \(\hat{t}_{2}(x)=t_{2}^{\prime }(x)\),

Moreover for each \(x\ge 0\), \(\hat{\varphi }\big ((\theta ^{\prime }_{2},x),c^{\prime }\big )=\big (\big (\hat{l}_{2}(x),\hat{l}_{1}(x)),\big (\hat{t}_{2}(x),\hat{t}_{1}(x)\big )\big )\). By assumption, \(\varphi \) satisfies Strategy-Proofness and Symmetry. Hence, by construction, so does \(\hat{\varphi }\). By assumption, \(\varphi \) satisfies Feasibilty. Hence, since the negation of Condition A is true, by construction, so does \(\hat{\varphi }\). Therefore, \(\hat{\varphi }\in \Phi _2\). By construction, for each \(e\in \mathcal {E}_2\) and each \(i\in \{1,2\}\),

$$\begin{aligned} u_{i}\big (\hat{\varphi }(e);\theta _{i}\big )\ge u_{i}\big (\varphi (e);\theta _{i}\big ). \end{aligned}$$

Moreover, by construction, for each \(x\ge 0\),

$$\begin{aligned} u_{1}\Big (\hat{\varphi }\big ((x,\theta ^{\prime }_{2}),c^{\prime }\big );\theta _{1}\Big )>u_{1}\Big (\varphi \big ((x,\theta ^{\prime }_{2}), c^{\prime }\big );\theta _{1}\Big ). \end{aligned}$$

Therefore, \(\varphi \) cannot be Second Best Efficient, a contradiction. \(\square \)

Refer to Fig. 3. The TMDM does not satisfy Condition A. Let \(\theta _1= \theta '_1 < c\), so that the value of the sum of the transfers prescribed by the TMDM only depends on \(\theta _2\). For each \(\theta _2 \ge 0\), \(\sum _{j\in N}t^{tmd}_{j}(\theta _2) < 0\). Therefore it is possible to build a mechanism \(\hat{\varphi }\big ((\theta ^{\prime }_{1},x),c\big )=\big (\hat{l}_{N}(x),\hat{t}_{N}(x)\big )\), in such a way that, for each \(x \ge 0\), \(\hat{l}_{N}(x)=l_{N}^{tmd}(x)\), \(\hat{t}_{1}(x)=t_{1}^{tmd}(x)\) and \(\hat{t}_{2}(x)=t_{2}^{tmd}(x)+\epsilon \). This mechanism is feasible (for some \(\epsilon > 0\)) and, by construction, Pareto dominates \(\varphi ^{tmd}\).

The Second Best Mechanism (SBM) For each \(e \in \mathcal {E}_2\), \((l_N,t_N)=\varphi ^{sbm}(e)\) if and only if \(l_N \in \Sigma (e)\) and, for each \(i \in N\),

$$\begin{aligned} t_{1} = \left\{ \begin{array}{ll} v_{2}(l_{N};\theta _{2})+f(\theta _{2}) &{}\quad \text {if } \theta _{2}\le c,\\ f(\theta _{2}) &{}\quad \text {if } \theta _{2}> c. \end{array} \right. \end{aligned}$$

and

$$\begin{aligned} t_{2} = \left\{ \begin{array}{ll} v_{1}(l_{N};\theta _{1})+f(\theta _{1}) &{}\quad \text {if } \theta _{1}\le c,\\ f(\theta _{1})-c &{}\quad \text {if } \theta _{1}> c, \end{array} \right. \end{aligned}$$

where,

$$\begin{aligned} f(\theta _i) = \left\{ \begin{array}{ll} 0 &{}\quad \text {if } \theta _i \le \frac{c}{2}\\ \frac{c}{2}-\theta _i &{}\quad \text {if } \frac{c}{2}<\theta _i \le c\\ \frac{c}{2} &{}\quad \text {if } \theta _i> c. \end{array}, \right. \end{aligned}$$

Figure 4 depicts the SBM for some arbitrary \(c\in \mathbb {R}_{+}\). The mechanism violates Individual Rationality at each \((\theta _{N},c)\in \mathcal {E}\) such that either \(\theta _{1}<c\) or \(\theta _{2}<c\).

Fig. 4
figure 4

The vector of transfers \(\left( {\begin{array}{c}t^{sbm}_{1}\\ t^{sbm}_{2}\end{array}}\right) \) for each profile \((\theta _{1},\theta _{2})\in \mathbb {R}_{+}\) according to the SBM in the two-agent case. Agent 1 adopts if \(\theta _{1}+\theta _{2}\ge c\). She does not otherwise

Full size image

Proposition 5

A mechanism \(\varphi \in \Phi _2\) satisfying Assignment Efficiency is Second Best Efficient if and only if it is the SBM.

The proof can be found in “Appendix 2”. The subtlety of Proposition 5 becomes apparent by comparing the SBM with the TMDM. The Pareto criterion does not rank the two. The TMDM is preferred to the SBM by agent 1 in economy \(e=(\theta _{N},c)\in \mathcal {E}^{2}\) such that \(\theta _{1}\in (0,\frac{c}{2})\), \(\theta _{2}\in (\frac{c}{2},c)\) and \(\theta _{1}+\theta _{2}>c\). The mechanism that Pareto dominates the TMDM, hence rendering it not Second Best Efficient, must be itself not Second Best Efficient.

Naturally the reader may wonder whether the methodology we apply in the two-agent case extends to the general case. The combinatorial nature of the problem makes this very difficult to ascertain. Our proof hinges on the fact that for each \(e \in \mathcal {E}_2\), \(\Sigma (e) \subseteq \big \{(0,0),(1,0)\big \}\). In the general framework the set \(\Sigma (e)\) varies widely as the economy changes. As a consequence, the number of cases one needs to check in order to arrive at a result becomes too big. For this reason we believe that a more general result is out of reach.

7 Concluding remarks

This paper focuses on Groves mechanisms in a model of private goods with externalities. We provide an algorithm that identifies the set of efficient assignments. Following that, we tackle the issue of implementing one of such assignments by means of a Groves mechanism. The externality present in the problem changes the characteristics of well-known solutions like the Pivotal Mechanism that, in our framework, is no longer feasible. Indeed we show that there is no Groves mechanism that is both individually rational and feasible. This fact forces us to explore two distinct avenues.

We first look at Groves mechanisms that are individually rational and among them we single out the mechanism that minimizes the amount of outside funding. We also provide quite general conditions under which an individually rational Groves mechanism runs a deficit. We then look at feasible Groves mechanisms. It is relatively simple to find examples of such mechanisms. However, the task of determining mechanisms that are Pareto undominated by some strategy-proof, symmetrical and feasible mechanism is more involved. Within the simpler, but still meaningful, domain of economies comprising only two agents we show that there is a single Groves mechanism that satisfies this property.

Although the paper focuses on Groves mechanisms, it is worth making the point that there are interesting mechanisms not belonging to this class that merit further investigation (see for example Moulin and Shenker 1992; Moulin 1994). To keep things simple let us maintain the simplifying assumptions we made in the previous section. For instance, consider the mechanism (adapted from Moulin 1988) defined over two-agent economies depicted in Fig. 5. Effectively, the mechanism asks agents to announce their marginal benefit. If the announcements are such that either \(\theta _{1}<\frac{c}{2}\) or \(\theta _{2}<\frac{c}{2}\) there is no platform adoption and each agent receives a transfer equal to zero. Otherwise, agent 1 adopts and \(t_{1}=\frac{c}{2}=-t_{2}\). This simple mechanism satisfies Strategy-Proofness, Individual Rationality and Feasibility (in fact, the sum of transfers always equals zero). Alas, it violates Non-Compliance Proofness and, thus, Assignment Efficiency. To see that, suppose that \(\theta _{2}=0<c<\theta _{1}\). The mechanism prescribes to agent 1 to refrain from adoption. Nonetheless, agent 1 can ensure a higher utility if she deviates from the proposed allocation and adopts the foreign platform. Aside from this deficiency, one should not be hasty in dismissing the mechanism depicted in Fig. 5. Applying the reasoning employed in the proof of Proposition 4, it can be demonstrated that it is Second Best Efficient. This fact alludes to the existence of interesting mechanisms outside the Groves family. Its implications are left for future research.

Fig. 5
figure 5

The vector of transfers \(\left( {\begin{array}{c}t_{1}\\ t_{2}\end{array}}\right) \) for each profile \((\theta _{1},\theta _{2})\in \mathbb {R}_{+}\). Agent 1 adopts if both \(\theta _{1}\ge \frac{c}{2}\) and \(\theta _{2}\ge \frac{c}{2}\). She does not otherwise

Full size image