1 Introduction

The main goal of writer-recognition is to determine whether two handwritten samples were produced by the same person. However, signatures, even those belonging to the same individual, will be different in size, pen pressure, velocity, direction and in many other aspects. It is for this reason that signature recognition has historically been difficult. The number of features analyzed fundamentally depends on the type of sensors the writing surface, or tablet, utilizes. The features captured comprise a feature set; any signature can be represented by a description of its unique feature set members. The analysis of handwritten documents is important in many domains including in business, forensic casework and banking. Handwriting does need to be considered on an individual basis as each person has unique style of writing.

Depending on type of devices utilized, the source can be processed either as a digital image or, when a signature is collected using a specialized device (tablet) as a dynamic feature set. However, not every technology captures signature information in the same way. Some systems have a static approach, only capturing an image of the completed signature and thus do not record the unique behavioral elements associated with the production of a signature. The capturing of dynamic features during signature production allows for a more precise analysis of a nature of a signature because additional features, such as velocity, pressure points, strokes and accelerations, can be recorded, in addition to the signature static characteristics [1]. This technique is to be preferred because dynamic features are very difficult to imitate. Unfortunately, these systems require both user-cooperation and complex hardware.

Signature features are very often grouped into global and local. Global features describe an entire signature and can determined by a discrete Wavelet or Hough transform, horizontal and vertical projections, as well as through many other approaches [2–8]. On the other hand, local features refer to dynamic properties including the pen’s motion, its slant, pressure, tremor and so on. It should be noted, also, that in practice it is impossible to take all possible factors into consideration.

Signature verification methods are also classified into on-line or off-line, depending on whether it is the signature dynamic or its static features that are extracted and analyzed. These classifications are well known in the research community [1, 2, 4, 9]. Off-line signature verification is based solely on a signature scanned or photographic image. Research in this area predominantly focuses on image processing techniques. On-line signature verification is based on signatures time-domain characteristics and is an accepted biometric technology. It should be noted that some dynamic characteristic can be also be utilized in the role of static, off-line characteristics: the x, y discrete coordinates of a signature form the shape of the signature for example.

The data acquisition phase has some inherent limitations, including potential issues with a signature length. In the case of signatures that are excessively long, the recognition system to may find it difficult to identify the unique data points of a signature during the data analysis phase, and both pre-processing and the recognition stage may come to consume excessive time. On the other hand, for signatures that are too short, the data set may not be representative enough leading to an excessively high false accept rate (FAR) coefficient (that is, an impostor could become authorized by the system).

A second limitation is the environment itself and the conditions under which a person produces their signature. For example, two signatures taken from an individual may differ substantially due to differences in the writer’s position. The complexity of signatures is one of the greatest problems faced in the design of credible classifiers that can function reliably in an identification or verification mode. The repeatability of signatures, even those of the same person, displays large discrepancies. For example, a signatory may utilize similar but different velocities, pen pressures and accelerations for each signature. Additional difficulties arise in relation to those either assuming another person’s identity or concealing their own identity through an attempt to imitate the other’s signature. One way to identify people is through each individual biometric characteristic. The production of signatures is part of behavioral biometrics and is a widely accepted and often readily collectable biometric characteristic.

Given these observations, it follows that signature recognition processes are difficult tasks but that recognition is possible if features can be appropriately extracted. Recognition methods of handwritten signatures have been studied extensively and developed over many years [1–4, 7, 9–12]. Unfortunately, a reliable comparison of the different approaches is difficult due to inconsistencies in the standards applied in this field [13, 14]. In practice, different databases are used, each holding a different number of original and forged signatures. Datasets of biometric features of signatures are most often composed of private (thus unavailable) signatures as well as signatures sourced from publicly available databases. It is a well-known fact that recognition performance decreases when the number of samples in a database of biometric features is increased [14]. This can be seen upon the addition of even a small number of additional database records. Unfortunately, such an important remark has been ignored in many publications [14]. We therefore postulate that any results presented should be normalized. In the approach presented here, all obtained results were based on the SVC 2004 (Signature Verification Competition) database (http://www.cse.ust.hk/svc2004). This allows us to compare our results with the achievements of other researchers. It should be noted that other signature databases are also available. For example, the popular Spanish MCYT can be used [15]. All such databases incorporate the same content objects: a range of different genuine and forged signatures from a number of unknown persons. Thus, it is sufficient that experiments are conducted on any one of the biometric signature databases.

Another issue is that in many papers the results reported use different evaluative coefficients (FAR, FRR, EER), they focus on different factors (accuracy, sensitivity, specificity) and the results are presented on different charts (ROC, CMC). Unfortunately, any one of these parameters is usually treated as one single factor completely representing the quality of the biometric system being described. Additional difficulties arise from the fact that in many papers there is no information about the origin of the forged signatures. Forgery is a criminal act for the purpose of fraud or deceit: for example, signing another person name to a check without the payee’s permission or authorization. Forged signatures can be of a random, simple or professional character. Thus, the nature of the fraud is of great importance. More extensive descriptions of forged signatures are reported in [16]. These issues described are all obstacles precluding a perfect comparison of the results achieved. All biometric systems try to minimize the inconveniences mentioned above, so they use only the most essential elements with the greatest biometric influence.

Currently, there are many measures that can be used to specify the extent of similarity between different objects [13, 17–20], all of which are based on an analysis of the objects features. Unfortunately, the repeatability of a signature features is often low and, in extreme cases, even very low [5, 13, 16]. For this reason, classical similarity measures applied directly to signature analysis often returns a low signature recognition level. The selection and reduction methods are well known and frequently used in practice for the solution of various verification problems [12, 13, 18, 19, 21–23]. Dimensionality reduction has been studied widely by researchers within many different scientific areas including biology, medicine, computer vision and machine learning [24–30]. A survey of various dimensionality reduction methods is listed in the references [17, 31]. Traditional dimensionality reduction methods endeavor to project the original data onto a latent, lower dimensional space, while preserving the important properties of the original data. Unfortunately, there can be no guarantee that the distribution of a dataset one domain is similar in its distribution(s) in a dimensionally reduced space: this is especially so for complex biometric data [11, 21, 31]. The multiple-parameter capture of handwritten signatures produces high-dimensional data and, currently, around 40 features can be either captured or computed [17]. Unfortunately, some features have low discriminant value. Thus we do need to utilize some sort of dimensionality reduction algorithm as part of our biometric data reduction.

The algorithm presented in this work not only selects which features of a signature to incorporate, but it also identifies from the set of available measures the best similarity measures that should be utilized. Thus it directly minimizes signature verification error. However, the most important feature of the approach proposed is its ability to choose and utilize different signature features and different similarity measures for each individual. For each individual, this selection forms a “new composed feature”. On the basis of this new composed feature, similarities between signatures are automatically calculated. The algorithm presented here is based on a statistical analysis of each individual’s signature features—undertaken for each signature in the database—and the two stages of a proposed signature verification method are clearly distinguished: training and verification. During the training stage, training sets are generated. Utilizing these sets it is then possible to evaluate, for each individual, which features and which methods of analysis would be best able to distinguish an original signature from a forgery. The best measures—those that identify genuine signatures—are then associated with that individual. This information is then utilized during signature verification. Nowadays, biometric methods of signature analysis are well recognized, widely quoted and broadly represented in the literature [1, 2, 5, 6, 8–10, 13, 32]. Unfortunately the signature verification levels reported are still inadequate. This remains a challenge for future investigations. In the present study, a new composed feature selection method is proposed for signature classification. This proposed method can then be incorporated into both off-line and on-line signature verification methods. In the future, when new similarity measures have been developed, the concepts presented here can be developed further.

2 Determination of a composed signature feature values

The main goal of this paper is to analyze and identify two kinds of objects, original and forged signatures; in other words, the verification of signature genuineness. It should be noted that other types of objects can be analyzed: for example, the identification of genuine and counterfeited banknotes. It is for this reason that a two-class recognition problem is presented here.

In the first step, two sets of signatures are gathered for each person. Let the set containing the original signatures be denoted as follows:

$$\pi_{1} = \{ S_{1} ,S_{2} , \ldots ,S_{c} \}.$$
(1)

Let the set containing the same person forged signatures be denoted as:

$$\pi_{2} = \{ S_{1}^{\varDelta } ,S_{2}^{\varDelta } , \ldots ,S_{d}^{\varDelta } \} .$$
(2)

Professionally forged versions of a person signature are difficult to obtain. In practice, the set π 2 will consist of either professionally forged signatures (if they are available) or of other people’s randomly selected signatures (random forgeries). In the recording process, discrete signature features are sampled by a device (tablet), so signature S can be represented as a set of z points:

$$S = \left\{ {{\mathbf{s}}(1),{\mathbf{s}}(2), \ldots ,{\mathbf{s}}(z)} \right\} .$$
(3)

During signing, the tablet is able to continuously collect a large number of different values of dynamic variables, including the pressure of the pen on the surface of the tablet, the position of the pen, its velocity, and acceleration and so on (Fig. 1).

Fig. 1
figure 1

The discrete set of the points comprising signature S

Full size image

In this way, each discrete point s(t), t = 1, …, z is associated with features recorded by the device. In the field of biometrics, values of these variables are referred to as the signature biometric features, because they form part of the characteristics of each given individual [30, 33]. For simplification, throughout this paper these characteristics will be referred to as features. Let the set of attainable features be denoted as follows:

$$F = \{ f_{1} ,f_{2} , \ldots ,f_{u} \} .$$
(4)

Then, each discrete point s(t) = [f t1 , f t2 , …, f t u ] is a vector of recorded features.

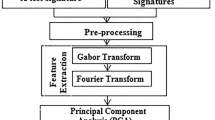
The most widely used signature features are presented in Table 1.

Table 1 List of analyzed features
Full size table

Objects (here, signatures) can be compared by means of a range of different similarity coefficients. Let a set of these methods be labeled as:

$$M = \{ \omega_{1} ,\omega_{2} , \ldots ,\omega_{k} \}.$$
(5)

Thus, the set M is comprised of all the methods and mathematical rules which could be included in the classification process. In this paper, various different similarity coefficients are taken into consideration. The most popular coefficients and similarity measures are reported in [17]. Table 2 presents various similarity computation methods. These similarity computation methods were utilized in the practical tests reported in this paper.

Table 2 List of similarity measures or coefficients [17]
Full size table

Let P i be the ith discrete point of a signature P, and Q i be the ith discrete point of signature Q, and i = 1, …, z. These points represent the same features as measured and recorded from both the P and the Q signatures. Hence, the similarity of these features present in these two signatures can be expressed as:

  • for the Euclidean distance:

    $$d_{\text{Euc}} = \left( {\sum\limits_{i = }^{z} {\left| {P_{i} - Q_{i} } \right|^{2} } } \right)^{1/2}$$
    (6)

  • for the Czekanowski coefficient :

    $$s_{\text{Czek}} = \frac{{2\sum\nolimits_{i = 1}^{z} {\hbox{min} (P_{i} ,Q_{i} )} }}{{\sum\nolimits_{i = 1}^{z} {\left( {P_{i} + Q_{i} } \right)} }},$$
    (7)

and so on for the other elements of Table 2, in accordance with the details reported in Ref. [17].

For example, the recorded pen pressure at point i can be analyzed, and the likewise for the others features. Each pair of signatures analyzed by means of the similarity measures listed in Table 2 should first be normalized: their lengths made equal. Differences in the size of signatures lead to a range of problems in signature comparison. To accomplish this normalization, the well-known dynamic time warping (DTW) technique [34] was applied to the normalization of the data stream coming from the tablet. If these data streams have different time lengths, then these data streams must be unified at corresponding points and be matched to each other. The DTW algorithm is used to identify the corresponding points of the two data streams. This normalization technique is widely known and has been described in detail elsewhere in the literature [45, 15].

Through the use of the same feature f m  ∊ F occurring in two objects, the similarity of these two objects can be computed by the method ω j  ∊ M. We assume that we can construct a set FM of all possible combinations of feature–method (FM) pairs:

$$FM = \{ \varepsilon_{i} \prec (f_{m} ,\omega_{j} )_{i} :f_{m} \in F, \omega_{j} \in M\} , \,\, i = 1, \ldots ,u \cdot k,$$
(8)

where

(f m , ω j ) i :

the i-th pair: “object feature (f m )—analysis method (ω j )”, m = 1, …, u, j = 1, …, k, i = 1, …, u · k

u :

the number of features possessed by this object,

k :

the number of methods used for a comparison of the features

Data prepared in this way can be appropriately ordered in a matrix form. The matrix X is based on the object set π 1. The matrix contains values of the similarity coefficients Sim calculated between the pairs of objects from the set π 1. Let [S i  ↔ S j ] denotes pair of the signatures S 1 and S 2. The matrix X is comprised of the one-columnar vectors [S i  ↔ S j ]. Generally, this matrix has the following structure:

$$X = \left[ {\left[ {S_{1} \leftrightarrow S_{2} } \right], \ldots ,\left[ {S_{1} \leftrightarrow S_{c} } \right], \ldots ,\left[ {S_{c - 1} \leftrightarrow S_{c} } \right]} \right]_{{(u \cdot k) \times \left( {\begin{array}{*{20}c} c \\ 2 \\ \end{array} } \right)}} = \left[{\mathbf{x}}_{1} , \ldots ,{\mathbf{x}}_{{\left( {\begin{array}{*{20}c} c \\ 2 \\ \end{array} } \right)}} \right],$$
(9)

where S i , S j the ith and jth original signatures of a given person, c the number of all genuine signatures of a given person

Each columnar vector holds the similarity values calculated between a single pair of signatures from the set π 1. These similarities are computed using each possible “feature-method” pair. An example of the first columnar vector from the matrix X is shown below:

$${\mathbf{X}} \mathrel\backepsilon {\mathbf{x}}_{1}^{{}} = [S_{1} \leftrightarrow S_{2} ] = \left[ {\begin{array}{*{20}c} {{\text{Sim}}(S_{1} ,S_{2} )^{{(f_{1} ,\omega_{1} )_{1 \cdot 1} }} } \\ \vdots \\ {{\text{Sim}}(S_{1} ,S_{2} )^{{(f_{1} ,\omega_{k} )_{1 \cdot k} }} } \\ \vdots \\ {{\text{Sim}}(S_{1} ,S_{2} )^{{(f_{u} ,\omega_{1} )_{u \cdot 1} }} } \\ \vdots \\ {{\text{Sim}}(S_{1} ,S_{2} )^{{(f_{u} ,\omega_{k} )_{u \cdot k} }} } \\ \end{array} } \right]_{(u \cdot k) \times 1},$$
(10)

where \({\text{Sim}}(S_{a} ,S_{b} )^{{(f_{m} ,\omega_{j} )_{i} }}\)—the ith similarity coefficient of the feature f m of the objects S a , S b  ∊ π 1. The similarity is determined by means of the method ω j .

Finally, the fully populated matrix X holds \((u \cdot k) \times \left( {\begin{array}{*{20}c} c \\ 2 \\ \end{array} } \right)\) elements.

The second matrix Y is based on the π 1 and π 2 sets. It can be observed that matrix X is constructed from the original signatures of a given person (say person Q) while the matrix Y holds the original and the forged signatures of the same person Q. The matrix Y is built as follows:

$${\mathbf{Y}} = \left[ {\left[ {S_{1} \leftrightarrow S_{1}^{\varDelta } } \right], \ldots ,\left[ {S_{1} \leftrightarrow S_{d}^{\varDelta } } \right], \ldots ,\left[ {S_{c} \leftrightarrow S_{d}^{\varDelta } } \right]} \right]_{(u \cdot k) \times (c \cdot d)} = [{\mathbf{y}}_{1} , \ldots ,{\mathbf{y}}_{c \cdot d} ],$$
(11)

where S i , S Δ j the ith genuine and the jth forged signature of a given person, d the number of all unauthorized (forged) signatures of a given person.

The columns of the matrix Y are constructed similarly to the columns of the matrix X. The first columnar vector has the following structure:

$${\mathbf{Y}} \mathrel\backepsilon {\mathbf{y}}_{1}^{{}} = [S_{1} \leftrightarrow S^{\varDelta }_{1} ] = \left[ {\begin{array}{*{20}c} {{\text{Sim}}(S_{1} ,S_{1}^{\varDelta } )^{{(f_{1} ,\omega_{1} )_{1 \cdot 1} }} } \\ \vdots \\ {{\text{Sim}}(S_{1} ,S_{1}^{\varDelta } )^{{(f_{1} ,\omega_{k} )_{1 \cdot k} }} } \\ \vdots \\ {{\text{Sim}}(S_{1} ,S_{1}^{\varDelta } )^{{(f_{u} ,\omega_{1} )_{1 \cdot u} }} } \\ \vdots \\ {{\text{Sim}}(S_{1} ,S_{1}^{\varDelta } )^{{(f_{u} ,\omega_{k} )_{u \cdot k} }} } \\ \end{array} } \right]_{(u \cdot k) \times 1},$$
(12)

where: \({\text{Sim}}(S_{a} ,S_{b}^{\varDelta } )^{{(f_{m} ,\omega_{j} )_{i} }}\)— the ith similarity coefficient of the feature f m of the objects S a  ∊ π 1 and S b  ∊ π 2.

Similarity was determined via use of the method ω j .

The matrix Y includes only the similarities between the original and forged signatures of one given person. Similarities between the different original signatures are not calculated. Hence, the fully populated matrix Y contains (u · k) × (c · d) elements.

Matrices X and Y always have the same u · k rows.

In both the matrices X and Y, each Sim value represents the value of one signature composed feature.

3 The features reduction

Very often, objects are described by means of a large number of features. Some of these features are similar, even for different objects, while others are unique. The main goal of this investigation is to select those features that allow for different objects to be distinguished. When there are a large number of features, the best features may be difficult to identify. Thus, features with a low impact on the verification process should be removed, if at all possible. Additionally, features (see Table 1) can be compared by means of different methods (listed in Table 2). For this reason, feature selection and the choice of the best similarity measures are significant challenges. However, if these tasks are performed satisfactorily, then objects will be able to be correctly verified.

As was previously mentioned, the process of signature verification is conducted on the basis of the available features. The feature selection process should result in the ability to significantly distinguish a given signature features from the same features in the other signatures in the database. Feature extraction is the most vital but most difficult step of any recognition system. The accuracy of the system depends mainly on the number and quality of the object features. Modern devices can record many different signature features including velocity, pen pressure, azimuth and pen acceleration. For signatures, nowadays, about fifty features are either directly captured (shape), measured (discrete points and time) or computed (velocity and acceleration between signature discrete points). In many cases, to improve recognition levels and accuracy measures, several copies of the same person signature are collected which leads to a large number of features being contained in a system. However, in practice, this volume of data leads to an excessively long verification period, especially when the database itself holds many records. One of the problems with high-dimensional datasets is that, in many cases, not all the variable data are required for a proper understanding of the underlying phenomena of interest. Additionally, the high dimensionality of the features space makes it difficult to utilize many recognition algorithms. In other words, dimensionality reduction is an effective, even necessary, method of downsizing data. The majority of verification algorithms have data some dimensionality limitation, so that, practically, only restricted forms of data can be processed. In this paper, it is also proposed that data dimensionality reduction be undertaken.

A reduction in the large number of features can be achieved during the reduction and feature selection process. These methods are well known and have been widely discussed in the literature [12, 21, 25, 30, 31, 35–37]. One of these methods is Hotelling’s discriminant analysis [36, 38–40, 49]. This technique can also be successfully adapted to the solving of biometric system tasks. This statistical approach will be described in some detail here because it has not yet been applied in the domain of biometrics and, when applied to the signature verification process, it gives better results in comparison to the well-known principal components analysis (PCA) and singular value decomposition (SVD) methods. For any given signature, the Hotelling approach removes those features which possess the smallest discriminant power.

3.1 Hotelling statistic

The reduction of a dimensionality of a dataset can be achieved through the use of Hotelling’s T 2 statistic. While, in practice, many other methods of data reduction are widely known, as will be shown later the approach proposed in this paper results in a superior level of object recognition in comparison to other statistical measures. For many of the available statistical methods, the ability to use the method depends on the data having, or complying with, a specific probability distribution. For this reason, the investigation of data distributions is one of the major issues in biometrics. Unfortunately, these restrictions are often simply ignored, producing research results open to incorrect interpretation.

Hotelling’s T 2 method requires that data display a normal distribution. Several phenomena observed in nature, medicine and industry have such a Gaussian distribution. The values of measurements from nature can be shown to be the sum or average of a large number of independent small random factors, so that, regardless of the distribution of each of these individual factors, the total distribution will approach normal. This requires that the total, global process is comprised of many random processes of which none is dominant. The Hotelling statistic is a multivariate generalization of the one-sample t Student’s distribution [12, 26, 36, 38]. A univariate distribution is a probability distribution of one single random variable, in contrast to a multivariate distribution, where we are observing the probability distribution of many independent vectors.

Given this assumption, we have:

$$t = \frac{{\bar{y} -\upmu}}{s}\sqrt n,$$
(13)

where s is a sample standard deviation:

$$s = \sqrt {\frac{1}{n - 1}\sum\limits_{i = 1}^{n} {(y_{i} - \bar{y})^{2} } }.$$
(14)

Then

$$t^{2} = \frac{{(\bar{y} -\upmu)^{2} }}{{s^{2} }}n = n(\bar{y} -\upmu)(s^{2} )^{ - 1} (\bar{y} -\upmu),$$
(15)

and statistical evaluations t 2 can be considered in the context of the Snedecor’s F distribution due to t 2 ∼ F 1,n−1.

Equation (13) can be simply generalized to a p-dimensional vector. Given the basic definition of the one-sample Hotelling statistic, we have n independent vectors of dimension p, observed over time, where p is the cardinal number of the set of objects characteristics being measured [36, 37]. These data can be presented as observation vectors. If this is done the observation vectors produce the following matrix:

$${\mathbf{Y}} = \left[ {\begin{array}{*{20}c} {y_{11} } & {y_{12} } & \cdots & {y_{1n} } \\ {y_{21} } & {y_{22} } & \cdots & {y_{2n} } \\ \vdots & \vdots & \vdots & \vdots \\ {y_{p1} } & {y_{p2} } & \cdots & {y_{pn} } \\ \end{array} } \right] = \left[ {{\mathbf{y}}_{1} ,{\mathbf{y}}_{2} , \ldots ,{\mathbf{y}}_{n} } \right].$$
(16)

In other words, the ith row of the matrix Y represents the ith feature from all p features over all observations; the jth column represents the jth observation from all of the n observations.

The vectors \(\varvec{y}_{i}\), i = 1, …, n form a p-dimensional normally distributed population N p (μ, Σ), with a mean vector μ and a covariance matrix Σ. The parameters μ and Σ are obviously unknown, hence they need to be estimated.

The value μ can be expressed by a mean vector:

$${\bar{\mathbf{y}}} = \frac{1}{n}{\mathbf{Y}} \cdot {\mathbf{j}} = \frac{1}{n}\sum\limits_{i = 1}^{n} {{\mathbf{y}}_{i} = } \left[ {\begin{array}{*{20}c} {\bar{y}_{1} } \\ {\bar{y}_{2} } \\ \vdots \\ {\bar{y}_{p} } \\ \end{array} } \right],$$
(17)

where j is an n × 1 dimensional vector; j = [1, 1, …, 1]T consists only of ones.

The covariance matrix Σ, of dimension p × p, can be estimated by utilizing the unbiased estimator:

$$\varvec{S} = \frac{1}{n - 1}\sum\limits_{i = 1}^{n} {({\mathbf{y}}_{i} - {\bar{\mathbf{y}}})} ({\mathbf{y}}_{i} - {\bar{\mathbf{y}}})^{T} .$$
(18)

Hence \(E(\varvec{S})\varvec{ = }\varSigma\) and \(E(\bar{\varvec{y}})\varvec{ = }{\varvec{\upmu}}\).

In this case we obtain a one-sample, T 2-Hotelling’s distribution with the covariance matrix \(\varvec{S}\):

$$T^{2} = n({\bar{\mathbf{y}}} - {\varvec{\upmu}})^{T} \varvec{S}^{ - 1} ({\bar{\mathbf{y}}} - {\varvec{\upmu}}) .$$
(19)

The main goal of this paper is to analyze and recognize two kinds of signatures (objects): original and forged signatures. These sets of signatures form two classes of objects. For this reason, the basic Hotelling statistic needs to be extended to a two-sample T-squared statistic.

In the two-sample problem we have two sets of independent vectors of features, which form two observation matrices:

$$\begin{gathered} {\mathbf{X}} = \left[ {\begin{array}{*{20}c} {x_{11} } & {x_{12} } & \cdots & {x_{1n} } \\ {x_{21} } & {x_{22} } & \cdots & {x_{2n} } \\ \vdots & \vdots & \vdots & \vdots \\ {x_{p1} } & {x_{p2} } & \cdots & {x_{pn} } \\ \end{array} } \right] = \left[ {{\mathbf{x}}_{1} ,{\mathbf{x}}_{2} , \ldots ,{\mathbf{x}}_{n} } \right], \hfill \\ {\mathbf{Y}} = \left[ {\begin{array}{*{20}c} {y_{11} } & {y_{12} } & \cdots & {y_{1m} } \\ {y_{21} } & {y_{22} } & \cdots & {y_{2m} } \\ \vdots & \vdots & \vdots & \vdots \\ {y_{p1} } & {y_{p2} } & \cdots & {y_{pm} } \\ \end{array} } \right] = \left[ {{\mathbf{y}}_{1} ,{\mathbf{y}}_{2} , \ldots ,{\mathbf{y}}_{m} } \right]. \hfill \\ \end{gathered}$$
(20)

The object features create vectors x i , i = 1, …, n and y j , j = 1, …, m, and together they form a p-dimensional normally distributed population x i  ∼ N p (μ, ∑), y i  ∼ N p (μ, ∑) with the same mean vector μ and the covariance matrix Σ. As previously, we can define the mean vectors:

$${\bar{\mathbf{x}}} = \frac{1}{n}{\mathbf{X}} \cdot {\mathbf{j}} = \frac{1}{n}\sum\limits_{i = 1}^{n} {{\mathbf{x}}_{i} } = \left[ {\begin{array}{*{20}c} {\bar{x}_{1} } \\ {\bar{x}_{2} } \\ \vdots \\ {\bar{x}_{p} } \\ \end{array} } \right]{\hfill \text{ and } \hfill }{\bar{\mathbf{y}}} = \frac{1}{m}{\mathbf{Y}} \cdot {\mathbf{g}} = \frac{1}{m}\sum\limits_{i = 1}^{m} {{\mathbf{y}}_{i} } = \left[ {\begin{array}{*{20}c} {\bar{y}_{1} } \\ {\bar{y}_{2} } \\ \vdots \\ {\bar{y}_{p} } \\ \end{array} } \right],$$
(21)

where j is an n × 1 dimensional vector and \(\varvec{g}\) is a similar m × 1 dimensional vector.

The variance–covariance matrix Σ, of dimension p × p, can be estimated by the unbiased estimators:

$$\begin{gathered} \varvec{S}_{1} = \frac{1}{n - 1}\sum\limits_{i = 1}^{n} {({\mathbf{x}}_{i} - {\bar{\mathbf{x}}})} ({\mathbf{x}}_{i} - {\bar{\mathbf{x}}})^{T} , \hfill \\ \varvec{S}_{2} = \frac{1}{m - 1}\sum\limits_{i = 1}^{m} {({\mathbf{y}}_{i} - {\bar{\mathbf{y}}})} ({\mathbf{y}}_{i} - {\bar{\mathbf{y}}})^{T} . \hfill \\ \end{gathered}$$
(22)

In Hotelling’s primary, fundamental definition, it was assumed that the mean vectors and covariance matrices are the same for both populations [37]. Both of the homogeneous covariance matrices, \(\varvec{S}_{1}\) and \(\varvec{S}_{2}\), are estimators of the common covariance matrix Σ. A better estimate can be obtained by pooling the two estimates. Hence, for the two-class case, the pooled common variance–covariance matrix is formed as a maximum likelihood estimator with weighted average of group variances:

$$\varvec{S} = \frac{{\varvec{S}_{1} (n - 1) + \varvec{S}_{2} (m - 1)}}{n + m - 2}.$$
(23)
$$\varvec{S} = \frac{1}{n + m - 2}\left( {\sum\limits_{i = 1}^{n} {({\mathbf{x}}_{i} - {\bar{\mathbf{x}}})} ({\mathbf{x}}_{i} - {\bar{\mathbf{x}}})^{T} + \sum\limits_{i = 1}^{m} {({\mathbf{y}}_{i} - {\bar{\mathbf{y}}})} ({\mathbf{y}}_{i} - {\bar{\mathbf{y}}})^{T} } \right).$$
(24)

These pooled approaches work if the samples are large and even, if the variances are equal, with non-normally distributed data [36]. Given this, as previously, the two-sample Hotelling’s T 2 statistic for a pooled covariance matrix \(\varvec{S}\) is defined as follows:

$$T^{2} = ({\bar{\mathbf{x}}} - {\bar{\mathbf{y}}})^{T} \left[ {\varvec{S}\left( {\frac{1}{n}\varvec{ + }\frac{1}{m}} \right)} \right]^{ - 1} ({\bar{\mathbf{x}}} - {\bar{\mathbf{y}}})\varvec{ = }\frac{n \cdot m}{n + m}({\bar{\mathbf{x}}} - {\bar{\mathbf{y}}})^{T} \varvec{S}^{ - 1} ({\bar{\mathbf{x}}} - {\bar{\mathbf{y}}}).$$
(25)

The homogeneity of the variances \(\varvec{S}_{1}\) and\(\varvec{S}_{2}\) can be evaluated and confirmed by use of Bartlett’s test [35, 36] as will be explained in the following paragraphs. Assuming equal variances is a major assumption, and using pooled procedures if the variances are, in fact, unequal gives poor results. If, from the analyzed data, it becomes apparent that the variances are unpooled then, in place of (24), a new estimator needs to be introduced in which the covariance matrices are utilized separately:

$$\varvec{V} = \frac{{\varvec{S}_{1} }}{n}\varvec{ + }\frac{{\varvec{S}_{2} }}{m}.$$
(26)

In this situation, a two-sample Hotelling’s T 2 statistic for matrix \(\varvec{V}\), is now defined as follows:

$$T^{2} = ({\bar{\mathbf{x}}} - {\bar{\mathbf{y}}})^{T} \varvec{V}^{ - 1} ({\bar{\mathbf{x}}} - {\bar{\mathbf{y}}}).$$
(27)

If the samples are small, we can look at the Hotelling’s T 2 statistic as an F-statistic. Let:

$$\tilde{F} = \frac{n + m - p - 1}{p(n + m - 2)}T^{2},$$
(28)

so that (28 is asymptotically F-distributed with p degrees of freedom for the numerator and n + m − p − 1 for the denominator [12]. Thus, the Hotelling’s T 2 statistic is well approximated by Snedecor’s distribution F:

$$\tilde{F} \sim F_{p,n + m - p - 1,\alpha },$$
(29)

where α denotes the chosen significance level.It can be demonstrated that, for large samples, \(\tilde{F} = T^{2}\) and T 2 ∼ χ 2 p,α [36]. Hence:

$$T^{2} \sim \chi_{p,\alpha }^{2}.$$
(30)

This means that, in this case, the Hotelling’s T 2 statistic can be approximated well by means of the Chi square distribution. In the approach presented in this paper, only formula (29) was used.

3.2 The Hotelling reduction of composed signature features

Now we return to the collected and prepared data. For a given signature, Hotelling’s approach enables the removal of those features which have the smallest discriminant power. In practice, discriminant analysis is useful when deciding whether a particular “feature-method” pair (f, ω) is an effective contributor to the classification process. If the feature-method pair is not such a contributor, then this given pair can be removed. Utilizing this procedure, only pairs with the greatest discriminant power will be left from all possible pairs.

Some recognition methods have better discriminant properties than others: a particular method can better recognize some signature features while some features are insignificant and should be rejected. The better recognition methods and significant features are unknown a priori, and must be discovered by the analysis to be undertaken. However, for any given signature, only its best discriminant features and the methods that recognize these features will, ultimately, be selected.

The reduction of features can be carried out gradually. In each successive step, the feature responsible for the smallest change in the multidimensional discrimination measure is eliminated [12, 35].

The dimensionality reduction algorithm can be executed in several steps, leading to a data reduction of matrices X and Y. In practice, according to (10) and (12), the similarity values Sim of the composed features between signatures is used in the data reduction process.

Reduction of the dimensionality of matrices was performed, step by step, for every available “feature-method” pair. The algorithm implemented can be shown in the form of the following pseudocode:

In this way, the dimensionality of the matrices is successively reduced. After the full reduction process has completed, the reduced matrices are now denoted as \({\tilde{\mathbf{X}}}\) and \({\tilde{\mathbf{Y}}}\).

The procedure, as described, is executed for every person Ω. The results are stored in the set FM Ω ⊂ FM, in which only the best discriminating (f, ω)Ω pairs are stored. It is these pairs that best distinguish a genuine signatures of a person Ω from its forged signatures.

It should also be noted that the previously described process of data reduction needs to be repeated every time, when a new signature is added to the database, as the main set FM will be changed. Thus, the process is conducted on a closed set of data.

4 Statistical parameters of the new data

The classical Hotelling’s T 2 method requires that the data have a normal (Gaussian) distribution [38]. After data preparation, the matrices X and Y include different values with respect to the original Hotelling statistic. This process of data modification has been explained in Sect. 2. However, these new values should now be evaluated statistically again.

The database we utilized in this research contains signatures acquired from 40 people, with 20 genuine signatures and 20 forged signatures for each person, so that in total there are 1,600 signatures. In the experiments, every element of Tables 1 and 2 were utilized, so u = 10 and k = 22. During each experiment, c = 10 genuine and d = 5 forged signatures were randomly selected. This was done many times, until every instance of each signature had been utilized. During the experiments, appropriate X and Y matrices were created always of the sizes: matrix \([{\mathbf{X}}]_{{_{{(u \cdot k) \times \left( {\begin{array}{*{20}c} c \\ 2 \\ \end{array} } \right)}} }}\) as 220 × 45; matrix [Y](u·k)×(c·d) of 220 × 50.

4.1 Independence

The subjects in both populations were uncorrelated so they are could be independently sampled. In our case, the genuine signatures were collected independently of the attempted forgeries.

4.2 Mean vectors

Hotelling’s assumption implies that the data from populations i = 1, 2 are to be sampled with their mean being μ i . Essentially, this assumption means that there are no sub-populations comprising the main population. In our experiment, this condition could be violated as the forged signatures could have been produced by more than one individual.

4.3 Multivariate normality (MVN)

Because Hotelling’s technique assumes multivariate normality of the data, it is important to ensure that the new data complies with this pattern. Visualizing MVN is impossible for more than two dimensions so, for this reason, it is demonstrated by scatter plots for each pair of variables. Under bivariate normality, concentrated elliptical cloud of points should be observed on each plot. Matrix X, created as part of the research, is high-dimension matrix. Because of the large number of possible scatter plots, only a proportion of them have been depicted in Fig. 2. The portions of the scatter plots not shown have a similar point distribution to that shown in the clouds here.

Fig. 2
figure 2

Bivariate normality of the data of matrix X: the concentration of selected data points inside the elliptical area, with a 95 % confidence interval

Full size image

Similar results were obtained for matrix Y.

Additionally, the Central Limit Theorem dictates that the mean vectors of samples will be approximately multivariate normally distributed regardless of the distribution of the original variables [35]. Hence, Hotelling’s T 2method is not sensitive to violations of this assumption. Thus, the multivariate normality of the data has been confirmed.

4.4 Homogeneity of covariance

This assumption has been assessed by means of Bartlett’s test [35, 36]. This test should be used for normally distributed data. It has been proven above that a normal multivariate distribution is guaranteed. The variances are judged to be unequal if B t  > χ df−1,α , where B t is the Bartlett statistic and χ df−1,α is the critical value of the Chi square distribution with degrees of freedom df and a significance level of α. In our experiments, the Bartlett’s statistic was computed for the matrices X and Y data (the same for covariance matrices \(\varvec{S}_{1}\) and\(\varvec{S}_{2}\)). For this reason, the T 2 statistic (25) or the values produced by Eq. (27) would be appropriate to be used during the feature reduction process.

5 Signature verification

In the approach proposed, the k-Nearest Neighbor (k-NN) method was applied [11, 35]. Genuine signatures were sourced from the database, so these signatures formed the first class of objects, class π 1. The forged signatures formed the second class of the signatures, class π 2. Determination of the sets FM Q was required to be able to verify the signatures written by person Q.

Let S Ω be the signature of some person Ω, in need of verification. This person presents himself or herself as being person Q, for example. The truth value of the assertion made by Ω should be able to be automatically verified. Let the reduced matrixes X and Y be denoted as \({\tilde{\mathbf{X}}}\) and\({\tilde{\mathbf{Y}}}\). After reduction, these matrices maintain the same number of rows (say r ≤ u · k). Together, the matrices \({\tilde{\mathbf{X}}}\) and \({\tilde{\mathbf{Y}}}\) form a new global matrix \({\mathbf{H}} = \left[ {{{\tilde{\mathbf X} \tilde{Y} }}} \right]_{{r \times \left[ {\left( {\begin{array}{*{20}c} c \\ 2 \\ \end{array} } \right) + (c \cdot d)} \right]}}\). The matrix H includes the similarities between all the signatures of person Q stored in the database; these similarities have been computed on the basis of selected features and selected recognition methods. Columns of the matrix H can be treated separately as vectors h. Let the dimension of the matrix H be defined as r × l, where \(l = \left( \begin{gathered} c \\ 2 \\ \end{gathered} \right) + (c \cdot d)\); then:

$${\mathbf{H = }}\left[ {{\mathbf{h}}^{1} ,{\mathbf{h}}^{2} , \ldots ,{\mathbf{h}}^{l} } \right]\quad {\mathbf{h}}^{i} = \left[ {h_{1}^{i} ,h_{2}^{i} , \ldots ,h_{r}^{i} } \right]^{T},$$
(31)

hence

$${\mathbf{H = }}\left[ {\begin{array}{*{20}c} {h_{1}^{1} ,h_{1}^{2} , \ldots ,h_{1}^{l} } \\ {h_{2}^{1} ,h_{2}^{2} , \ldots ,h_{2}^{l} } \\ \vdots \\ {h_{r}^{1} ,h_{r}^{2} , \ldots ,h_{r}^{l} } \\ \end{array} } \right]_{r \times l},$$
(32)

if \({\mathbf{h}}^{j} \in {\tilde{\mathbf{X}}} \to {\mathbf{h}}^{j} \in \pi_{1}\) and if \({\mathbf{h}}^{j} \in {\tilde{\mathbf{Y}}} \to {\mathbf{h}}^{j} \in \pi_{2}\), j = 1, …, l.

Because the classifier works in verification mode, the person to be classified Ω, appears as a person Q, for example. Given this, a signature S Q of person Q is randomly selected from the database. In this stage of verification, the most distinctive common features and signature similarity measures of the person Q have been established. This means that the matrix H for this signature is known. For this reason only a new vector h Ω = [h Ω1 , h Ω2 , …, h Ω r ]T needs to be created. The elements of the vector h Ω are determined as follows:

$$h_{i}^{\varOmega } = Sim(S^{\varOmega } ,S^{Q} )^{{(f,\omega )_{i}^{{}} }} ,\,i = 1, \ldots ,r,$$
(33)

where

S Ω :

the signature to be verified,

S Q :

randomly selected original signatures of person Q,

\(h_{i}^{\varOmega } = Sim(S^{\varOmega } ,S^{Q} )^{{(f,\omega )_{i}^{{}} }}\) :

similarity between signature S Ωand signature S Q. This similarity has been determined using the ith pair (f, ω) i from the set FM Q

In the next stage, the set D of Euclidean distances between vector h Ω and all successive vectors h i ∊ H is calculated:

$$D = \left\{ {d({\mathbf{h}}^{\varOmega } \varvec{,}{\mathbf{h}}^{j} } \right\}d({\mathbf{h}}^{\varOmega } \varvec{,}{\mathbf{h}}^{j} = \left[ {\sum\limits_{i = 1}^{r} {\left( {h_{i} - h_{i}^{j} } \right)^{2} } } \right]^{1/2} ,\quad j = 1, \cdots ,l.$$
(34)

From the distances in the set D the smallest k distances are selected. The verified signature S Ω is classified into class π 1 or π 2 by means of the k-NN classifier. The final classification results are established on the basis of a voting score, which depends on the number nb of neighbors belonging to class π 1 or π 2. In works [10] and [17], the authors report that the most suitable value for nb can be estimated by simulation, but in practice can be approximated by the square root of the number of complete cases:

$$nb =\left[ {\left( {\left( \begin{gathered} c \\ 2 \end{gathered} \right) + (c \cdot d)} \right)^{1/2} }\right].$$
(35)

Let D1 and D2 be the sets of numbers which show how many times signature S Q has been classified into class π 1 or π 2, respectively:

$$\begin{gathered} d({\mathbf{h}}^{\varOmega } ,{\mathbf{h}}^{j} ) \in D1 \,{\text{ if }}:{\mathbf{h}}^{j} \to \pi_{1}, \hfill \\ d({\mathbf{h}}^{\varOmega } ,{\mathbf{h}}^{j} ) \in D2 \,{\text{ if }}:{\mathbf{h}}^{j} \to \pi_{2}. \hfill \\ \end{gathered}$$
(36)

Let the cardinality of the sets be denoted by symbol #; the classification voting principle can then be formulated as follows:

$$S^{\varOmega } :\left\{ {\begin{array}{*{20}l} {{\text{genuine signature of the person }}Q} \hfill & {\text{for}} \hfill & {\# D1 > \# D2} \hfill \\ {{\text{forged signature of the person }}Q} \hfill & {\text{for}} \hfill & {\# D1 \le \# D2} \hfill \\ \end{array} }. \right.$$
(37)

6 Interpretation and comparison of the methods

In this paper, the features of the object have become more widely understood because the features themselves and the best methods for recognizing these features have been formed into a new form of statistical data. In our opinion, this constitutes a new technique of data mining.

The feature reduction methods based on Hotelling statistic were also compared to two well-known analytical methods: principal component analysis (PCA) and singular value decomposition (SVD). As presentation of multidimensional data is difficult, graphical presentation will be limited to those cases where, after reduction, only two-dimensional data remained.

In the experiments conducted, the captured signatures’ features and similarity coefficients, obtained as seen in Tables 1 and 2, were considered. In this section, the attempt to verify person Ω will be performed. This individual claims to be a person Q.

For this demonstration the principles of a method only one of signatures stored in the database has been selected. Signatures of person Q were divided into two groups. Let the first group consist of ten original signatures (c = 10) of person Q, while the second group consists of five forged signatures (d = 5) of the same person. The classification process is undertaken on the basis of the h i ∊ H vectors, where \(i = 1, \ldots ,(c \cdot d) + \left( {\begin{array}{*{20}c} c \\ 2 \\ \end{array} } \right) = 95\). This means that the k-NN classifier always has a constant pool of available vectors to compare, and each of them has the dimension r. The k-NN classifier works with the nine neighbors, which follows from the estimation detailed in Eq. (35). The way that the identity of person Q is to be verified will be shown below. In our experiments as described here, until verified, the individual Ω should be recognized as an unauthorized person, Q.

6.1 Hotelling reduction method

As discussed previously, in the experiment ten original signatures and five forged signatures associated with each person have been analyzed. From this signatures dataset we obtain 95 vectors h i ∊ H, i = 1, …, 95. During the real reduction process, let the two best discriminant pairs (f 6, ω 2) and (f 3, ω 1) be selected. In other words, feature f 6 of person Q’s signature best distinguishes this signature from all the other signatures in the database when f 6 is evaluated using similarity measure ω 2. The same explanation can be given for the second pair (f 3, ω 1). It means that h i vectors have dimensionality of r = 2. Figure 3 plots the similarity distribution between the different signatures of person Q. It also represents the similarities between the different genuine signatures of the person Q and the similarities between their original and forged signatures. In practice, each point (triangle or circle) in this plot has its own individual label. For example, label (1–5) represents the similarity between the original signatures Number 1 and Number 5 of person Q, while label (8-5F) represents the similarity between original signature Number 8 and the forged signature Number 5. For simplicity, only selected labels are shown. Figure 2 presents the decision-making areas for the trained classifier and shows the class to which a point with the specific coordinates would be assigned. The same figure plots the decision area of the k-NN classifier during classification of the individual Ω. The signature of person Ω will be recognized as the signature of an individual who wants to obtain unauthorized access to the resources.

Fig. 3
figure 3

Mutual similarities between signatures of the person Q and k-NN classification area of the person Ω

Full size image

Figure 3 clearly shows by means of visible separation border that the genuine and the forged signatures of individual Q are well distinguished. This was done by using only two signature features and two similarity measures. In practice, beyond two-dimensional cases, multidimensional cases need to be processed.

6.2 The PCA and SVD reduction methods

The proposed method was compared with two other methods well known in the literature: PCA [10, 41, 42] and SVD [42, 43]. PCA and SVD are two eigenvalue-based methods used to reduce high-dimensional datasets to fewer dimensions while still retaining important information. PCA is known as a system of unsupervised learning. Both methods give the same or similar results but, due to various numerical factors, the results obtained differ slightly. As before, feature reduction refers to the mapping of original high-dimensional data onto a lower dimensional space.

Let a dataset of the n-dimensional data points X = {x 1, x 2, …, x a } be an observation space.

Then, for the PCA or SVD methods:

x i  ∊ R n → z i  ∊ R d: z i  = Gx i , where G is a transformation matrix consisting of the d principal components, d ≪ n and i = 1, …, a. The vector \({\mathbf{x}}_{\varvec{i}}\) is original recorded data, while z i represents data transformed according to the properties of the transformation matrix G.

For the Hotelling method:

\({\mathbf{x}}_{i} = [x_{1} ,x_{2} , \ldots ,x_{n} ] \in {\mathbf{R}}^{n} \to {\mathbf{z}}_{i} = [x_{{i_{1} }} , \ldots ,x_{{i_{d} }} ] \in {\mathbf{R}}^{d}\), and elements of vector z i create a subset of the set of elements of the vector x i , d ≪ n, and i = 1, …, a.

Similarly, the signatures of one person, Q, will be analyzed. In the PCA method, the covariance matrix and those principal components (PCs) which account for the greatest variance in the data set are calculated for the matrix H. Table 3 shows the selected factor loadings obtained for the first seven PCs. After this calculation, the cumulative percentage of the variance was computed. The first principal component (PC 1) is the most important—it describes most of the total variability of the data (above 87 %). The first two PCs describe more than 93 % of the total variance. The remaining components explain successively less of the variance of a data. The components are interpreted by observing the contributions of the primary variables to the construction of the main components. For a given principal component (PC), the maximum absolute value of the coefficient of any original variable represents the maximum contribution that this variable can make to the construction of this PC. Note that, in this example, the PC 1 is associated with all of the shown pairs (f, ω), while PC 2 is mainly associated with the pairs (f 5, ω 2) and (f 5, ω 1). Table 3 shows the largest contributions to the construction of each PC.

Table 3 The most important factor loadings (absolute values below 0.1 were omitted)
Full size table

The interaction between the main components, PC 1 and PC 2, is plotted below (Fig. 4a). Two data points on the plot are closer together when they are more similar to each other [41]. The PCA score plot is useful to understand the similarity between signatures. Analysis of SVD components is similar.

Fig. 4
figure 4

Dispersion of the original loadings (a); Enlarged fragment of the cloud loadings with the important loadings I and C (b)

Full size image

Figure 4 shows that the most important loadings are I, which corresponds to the pair (f 4, ω 1) and C, which correspond to the pair (f 7, ω 1). Points lying near to the beginning of the coordinate system can not be taken into consideration because their vectors are too close to the projection of this plane. The PC-based categorization is shown in Fig. 5. This figure presents the decision-making areas for the trained classifier and shows the class to which a point with specific coordinates would be assigned. The same figure plots the k-NN classifier decision area during classification of the individual seeking verification, Ω.

Fig. 5
figure 5

Mutual similarities between signatures of the person Q in the PCA category (a); and k-NN classification area of the person Ω (b)

Full size image

This experiment has shown that person Ω, on the basis of the reduced set of data, will be recognized and authorized as individual Q. However, recognition based on Hotelling’s data reduction indicates a different decision.

In practice, the above-presented graphic interpretation is unnecessary. The main goal of this representation was to demonstrate the basic ideas behind the methods. All computations boil down to determination of the matrix H. Different methods form different structures for matrix H, so the k-NN classifier gives a different classification of the object Ω.

In the proposed Hotelling-based reduction approach, it is very convenient that appropriate signature features and similarity coefficients (Tables 1, 2) are always automatically selected.

7 Results obtained

The results of proposed classification, based on an adaptive feature selection, have been compared with the results of a classification that utilizes the complete feature set. Comparison of the results achieved allows us to estimate how the proposed method influences the reduction of classification error. As was previously stated, in the experiments signatures of forty people were tested. All available signatures from database were divided into sets containing data for one person. For each person, c = 10 genuine and d = 5 forged signatures were randomly selected. Hence, (10 + 5) × 40 = 600 signatures were analyzed. The database used was a subset of the SVC 2004 database. Matrices X and Y were constructed on the basis of these selected signatures. The training set was used to fit a statistical model. The remaining signatures were treated as validation signatures. The proposed classifier was finally used in its verification mode. The classification of a test signature was undertaken by comparing it against a set of genuine and forged signatures for the person being verified. During the research, classification was performed using, either, all the available features and comparison methods, or by using only those features and methods pre-selected for the currently to-be-verified individual. In the investigations themselves, all the elements of both Tables 1 and 2 were utilized. In regards to using the PCA/SVD methods, boundary feature-method reduction should be defined a priori. The best results were obtained for the 2nd, 6th and 12th PCA/SVD components. The false acceptance rate (FAR) and false rejection rate (FRR) errors levels for the different methods of composed feature reduction are shown in Tables 4 and 5.

Table 4 False accepted rate (FAR). For varying numbers of reference signatures, varying feature vector dimensions
Full size table
Table 5 False rejection rate (FRR) for varying numbers of reference signatures, varying feature vector dimensions
Full size table

Under the classical approach, for a given recognition threshold t, the FAR(t) is defined as the experimentally determined ratio of the number of imposter scores exceeding the value of t to the total number of imposter scores [33]. Analogously, FRR(t) is the experimentally determined ratio of the number of genuine scores not exceeding threshold t to the total number of genuine scores. Since, in our experiments, no acceptance threshold level needed to be determined, the FAR/FRR coefficients have been established in an alternative manner [33]:

$${\text{FAR}} = \frac{\text{NFA}}{\text{NIVA}},$$
(38)

where:

NFA:

number of false acceptances,

NIVA:

number of impostor verification attempts,

$${\text{FRR}} = \frac{\text{NFR}}{\text{NEVA}},$$
(39)

where:

NFR:

number of false rejections,

NEVA:

number of enrollee verification attempts

$${\text{Accuracy}} = \frac{\text{NCV}}{\text{NAVA}},$$
(40)

where:

NCV:

number of correct verifications,

NAVA:

number of all verification attempts

These results were obtained for varying numbers of signatures from the set π 1 (genuine signatures) and the set π 2 (forged signatures), and for varying numbers of reduced features. The FRR ratio represents genuine signatures classified as forged signatures, while FAR represents forged signatures classified as genuine. It accepted that a perfect biometric would neither reject any authorized individual (FRR = 0), nor would it accept any unauthorized individual (FAR = 0). Instead, in practice, highly secure biometric systems operate with small FAR/FRR values. It is impossible to have low error rates (close to zero) for both FAR and FRR at the same time. The relation between false acceptance and false rejection rates can be established by choosing a threshold point where FAR and FRR values are balanced, the so-called equal error rate (EER) point. Given the nature of these investigations, the EER point was not determined—the threshold t has not been established.

Tables 4 and 5 show that it was when using the method proposed in this work that the smallest FAR/FRR coefficients were obtained: FAR = 1.08 % and FRR = 2.53 %. These results are significantly better than the results obtained using the PCA/SVD method. The smallest FAR/FRR ratio was obtained when the number of original signatures in the set π 1 was five and the number of forged signatures in the set π 2 was three. All of the forged signatures used were professionally counterfeited.

Additionally, the new data-type classification proposed in this paper was compared to other classifiers, all proven in literature and implemented in the WEKA system [44]:

  • k-Nearest Neighbors Classifier (k-NN) [11],

  • Random Forest: forest of random trees (RanF) [45],

  • Random Tree: tree that considers K randomly chosen attributes at each node (RanT) [45],

  • J48 - C4.5 decision tree (J48) [46],

  • PART - PART decision list (PART) [47]

The Nearest Neighbors Classifier assumes that a new object has membership of a class on the basis of comparing it against a set of sample (prototype) objects. During classification, a voting process of k-neighbors is used. This classifier is particularly useful for classifying data with a multi-dimensional input space. The next two classifiers listed are the Random Forest and the Random Tree. The Random Forests is built up from an ensemble of Random Trees which, in contrary to classic decision trees, are built using randomly selected subsets of features for each node. Also tested were the C4.5 algorithm-based J48 decision tree classifier and the PART classifier, both of which use a divide-and-conquer approach to constructing a partial C4.5 decision tree during each iteration, turning the “best” leaf into a rule.

In our experiments, the measurement time was determined on an Intel Core2Duo E7400 processor, 2.8 GHz computer with 8 GB of RAM and running the Windows 7 × 64 operation systems.

The classifier producing the greatest Accuracy level was selected as the best method–having the best recognition. The experiment was conducted on both unreduced and reduced datasets. The highlights in Table 6 show that the best recognition level was achieved using the k-NN classifier working on reduced set of composed feature values of a signatures. For this data, the k-NN classifier gives a significant better Accuracy level when compared to a RanF classifier working on a set of composed feature values of unreduced signatures.

Table 6 FAR, FRR and accuracy measures for various classification methods applied to both unreduced and reduced datasets
Full size table

The results obtained were also compared with other solutions for which a range of various signature recognition techniques have been applied. A brief overview of these results is presented here in Table 7.

Table 7 A comparison of the performance of various signature recognition systems
Full size table

Unfortunately, making any reliable comparison of these various approaches is rather difficult, due to inconsistencies in the accepted evaluative standards. In practice, various databases are used containing different numbers of original and forged signatures. These datasets of biometric features are generally comprised of private (and hence unavailable) signatures in addition to signatures obtained from commercially published databases. For this reason, the results presented here are unable to be presented in a properly unified manner. However, Table 7 does show that the results achieved by the approach proposed in this paper are the best when compared to all of the other published methodologies.

In addition, the results achieved here have been compared with results of classifications based on the raw signature features acquired directly from the tablet. In these cases, the matrices X, Y and H have not been used and the classification has been achieved using only these dynamic signature features. Prior to classification, the feature vectors were all scaled to a common length and normalized. In order to equalize the signature lengths, instead of DTW the FNP method was used to scale the data vectors to a specific, experimentally selected, length of B = 30 points. This way classification error was minimized [1]. This was required to set an arbitrary length for each signature vector, an outcome that cannot be guaranteed from the DTW method which automatically adjusts the length of each pair of vectors.

Algorithm 2. The pseudocode for equalizing sequences for use with the FNP method:

The length of the signature for any given person has been experimentally established so as to minimize classification error. In our case, discrete points of signatures from the database have been all normalized to the same length of 30 discrete points. Utilizing all of the captured features, the results of the dynamic data classification are presents Table 8.

Table 8 FAR, FRR and accuracy for various classification methods applied to the raw data
Full size table

The results presented in Table 8 show that classification based on the raw signature data has a high classification error for every type of classifier, always returning a worse recognition level than the data from Table 6 in which the classification was performed on a complete and then on a reduced dataset. Additionally, processing time for single signature verification was significantly longer for a raw signature features.

The correctness of the results shown in Tables 4 and 5 was also statistically verified using appropriate comparative studies. The results obtained were compared using a k-fold cross-validation and the paired t-method [12, 48]. In the k-fold cross-validation, the data set is partitioned into k disjoint subsets of the same size. A single subset is used as the validation data while the remaining k - 1 subsets are used as training data. The cross-validation process is then repeated k times. The advantage of this method is that all observations are utilized for both the training and the validation part and each observation is used in the validation process exactly once.

This process can be described in more detail. Let there be two classification algorithms: A and B. The algorithms are to be tested on the basis of the same data set X. Let there be two sets: the training set {T i :i = 1, …k} and the validation set {V i :i = 1, …k}. Under the proposed k-fold cross-validation, the set X is divided into disjoint subsets X i  ∊ X, i = 1, …k as follows:

$$\begin{array}{*{20}l} {V_{1} = X_{1} } \hfill & {T_{1} = X_{2} \cup X_{3} \cup \ldots \cup X_{k} } \hfill \\ {V_{2} = X_{2} } \hfill & {T_{2} = X_{1} \cup X_{3} \cup \ldots \cup X_{k} } \hfill \\ \vdots \hfill & \vdots \hfill \\ {V_{k} = X_{k} } \hfill & {T_{k} = X_{1} \cup X_{2} \cup \ldots \cup X_{k - 1} } \hfill \\ \end{array}$$
(41)

The misclassification rate in fold i is defined as follows:

$$p_{i}^{A} = \frac{1}{N}\sum\limits_{j = 1}^{N} {{\text{err}}_{j}^{A} } , \, p_{i}^{B} = \frac{1}{N}\sum\limits_{j = 1}^{N} {{\text{err}}_{j}^{B} }, \,$$
(42)

where

$${\text{err}}_{j}^{A(B)} = \left\{ {\begin{array}{*{20}l} 1 \hfill & {{\text{if classifier }}A (B ) {\text{ gives a classification error}}} \hfill \\ 0 \hfill & {\text{otherwise}} \hfill \\ \end{array} }, \right.$$
(43)

and N is the number of examples classified by both algorithms.

In addition, let the error differences of a pair-wise algorithm be described in the form:

$$p_{i} = p_{i}^{A} - p_{i}^{B}.$$
(44)

Bearing in mind that p A i and p B i have an approximately normal distribution, their mutual difference should also be normally distributed. Thus, we could assume that p i  ∼ N(0, δ 2). Because both parameters μ and δ are unknown, they have to be estimated from the mean and the standard deviation. For this assumption simply defined the appropriate estimators:

$$m = \frac{1}{k}\sum\limits_{i = 1}^k {p_i} \,\,{\rm and}\,\,{s^2} = \frac{1}{k - 1}\sum\limits_{i = 1}^k {({p_i} - m} {)^2} .$$
(45)

Thus, under the null hypothesis H 0:μ = 0 (vs H 1:μ ≠ 0) we obtained a statistic t-distributed with k - 1 degrees of freedom [25]:

$$\frac{{\sqrt k (m - 0)}}{s} = \frac{{m\sqrt k }}{s}\, \sim \,t_{{k - 1}} .$$
(46)

When the value t k-1 is outside of the range ( − t α/2,k−1, t α/2,k−1) we can reject the hypothesis H 0 and we can claim that the algorithms A and B produce statistically different results. This is evaluated at the level of significance α. We could also check, for example, whether the algorithm A generated smaller errors than the algorithm B. In this case, we applied a one-sided t test ( − ∞, t α/2,k−1). The results obtained have been collated in Tables 9, 10. All computations were performed with respect to a significance level of α = 0.05 with k = 10. From the values listed in the well-known t-distribution tables, we obtained the range \(\left({- {t_{\alpha/2,k - 1}},{t_{\alpha/2,k - 1}}} \right) = \left({- {t_{0.025,9}}, + {t_{0.025,9}}} \right) = \left({- 2.685, + 2.685} \right).\)

From Table 9, then, it followed that the Hotelling and the PCA approaches return different recognition results and that the Hotelling method generated a smaller number of FAR errors, with t k−1 ∼ 35.10, so the Hotelling’s technique should be preferred.

Table 9 PCA and Hotelling comparison by means of the cross-validation paired t test—for the FAR mode
Full size table

Similar results were produced for the comparison of the Hotelling and PCA methods when the FRR coefficient was utilized as the evaluative criteria. All computations are presented in Table 10. In this case, t k−1 ∼ 4.74, so the Hotelling features analysis again gives better results than the PCA technique. Exactly the same comparison was conducted between the Hotelling and the SVD methods. These results have all been presented in Tables 11 and 12, which include results for which the FAR/FRR coefficient was estimated. In these cases, the appropriate t-distributed values returned for the values from Table 11 were t k−1 ∼ 34.79 and, for the values listed in Table 12, t k−1 ∼ 52.00. It can thus be observed that the Hotelling method gives significantly better object recognition in comparison to the SVD technique.

Table 10 PCA and Hotelling comparison by means of cross-validation paired t test—for the FRR mode
Full size table
Table 11 SVD and Hotelling comparison by means of the cross-validation paired t test—for the FAR mode
Full size table
Table 12 SVD and Hotelling comparison by means of cross-validation paired t test—for the FRR mode
Full size table

8 Conclusions

In this paper, the features of the object of interest have become are more extensively understood because the classical features and the best methods of recognizing them have together been formed into a new form of statistical data. In our opinion, this can be treated as a new data mining technique. The originality of the proposed approach follows from the fact that the classifier utilizes not only the features extracted, but also the best similarity measures appropriate to any given problem. From the investigation conducted, it then was seen that the FSM method gives the best object recognition level when compared to two other widely used methods in which only the features of an object are analyzed. Under the proposed approach, the feature space is intimately connected with the set of similarity measures to be used in the recognition process. Such an association is a new proposition: a composition signatures feature values. However, such an approach has not yet been applied.