1 Introduction

Energy-efficient LED lamps and luminaires have become popular in general lighting. It is estimated that in 2020 the global market share of LED lamps will be almost 70 % in general lighting and that luminous efficacies will grow beyond 200 lm / W [1, 2]. To exploit the full energy saving potential of the solid state lighting (SSL) technology, lamp types with best luminous efficacies should be selected for the future use. Unfortunately, various optical and electrical properties of LED lamps make them more challenging to measure for luminous efficacy than traditional incandescent lamps. The lowest measurement uncertainties of luminous efficacy currently achieved at National Metrology Institutes (NMIs) are around 1 % (k = 2) [3]. The uncertainties for testing and calibration laboratories that actually characterize the new products coming to market are significantly higher; over hundred laboratories took part in a recent comparison measurement of SSL products which indicated a spread as high as ±5 % in luminous efficacy results [4].

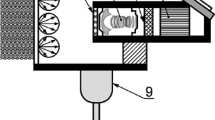
Total luminous flux measurement is needed in the determination of the luminous efficacy of a light source. It can be performed with either a goniometric [5, 6] or an absolute integrating sphere method [3, 7, 8]. Both methods require absolute illuminance measurement as a calibration procedure. If the spectrum of the light source is limited to the visible wavelength range, as is the case with white LED lamps, a recently introduced method [9, 10] can be used for accurately realizing the absolute illuminance. The method makes use of the predictable quantum efficient detector (PQED) [11–13], an induced-junction photodiode based primary standard of optical power operated at room temperature [14]. The responsivity of the PQED is very near to that of an ideal quantum detector, and moreover, it can be predicted with an uncertainty less than 0.01 % in the visible wavelength range [11, 15]. The most notable difference between traditional photometer-based illuminance measurement and the PQED method is that the latter does not utilize filters of any kind; only the precision aperture is placed in front of the PQED, as shown in Fig. 1. The PQED method has many benefits, such as simplified traceability chain and lower uncertainty due to the well-known responsivity [10]. However, determination of the aperture area still remains as one of the most critical factors affecting the measurement uncertainty of illuminance [10] and, consequently, luminous efficacy.

Fig. 1
figure 1

Schematic structure of the PQED (predictable quantum efficient detector) and the precision aperture. The angle between the photodiodes arranged in a wedged trap configuration is 15°

Full size image

Several methods for determining the area of an aperture have been developed, which utilize either mechanical contact [16, 17] or optical techniques [18–25]. In addition, a spatially uniform irradiance source can be used to compare the area of two apertures [16, 26, 27]. While most methods measure the diameter of a round aperture, some measure the area directly and can be used to measure irregular apertures. Lassila et al. developed such an optical method for direct determination of aperture area [18–20], in which a two-dimensional superposition of equally spaced Gaussian laser beams is used to form a uniform irradiance distribution. In practice, this is accomplished by having an intensity-stabilized laser beam and scanning the aperture in front of the laser beam. The light passing through the aperture at each position is collected using an integrating sphere and then detected with a photodetector. The method has been validated by comparing the measured area of apertures of different sizes to the area determined using mechanical contact methods [18–20].

This paper describes an upgrade to the laser scanning method. In the improved method, the aperture is attached to the PQED detector and the whole package is transversely scanned relative to the laser beam, as show in Fig. 2. This method has the benefit of having identical geometry in the laser scanning of the aperture area and in the actual photometric measurement. Furthermore, the aperture and detector assembly does not have to be dismantled for aperture calibration. The measurement setup required for the laser scanning method is relatively simple and, therefore, existing laser facilities [14, 28] can be exploited directly or with minor modifications.

Fig. 2
figure 2

Measurement setup for the laser scanning method using the PQED

Full size image

The acceptance angle of the PQED is small compared to that of an integrating sphere, as seen in Fig. 1. Therefore, differences between the diffraction effects of an overfilling plane wave and of a combination of Gaussian laser beams at the circular aperture have to be taken into account. A numerical calculation method for studying these effects is discussed in this paper. The calculation utilizes the Rayleigh–Sommerfeld (RS) diffraction integral [29], which is applied to the geometry of the PQED and the aperture. Simulation results for different aperture sizes and two different distances between the aperture and the detector are presented. Based on these results and uncertainties demonstrated for the original laser scanning method, an anticipated uncertainty is given for determination of the aperture area using the upgraded method. In addition, the propagation of the reduced uncertainty of aperture area to the uncertainty of PQED-based illuminance measurement and, consequently, to the luminous flux measurement is discussed. Finally, the impact of many recent advances in electrical and optical measurements of LED lamps—including those presented here—on the luminous efficacy measurements of white LED lamps is assessed.

2 Theory

2.1 LED photometry

Photometric quantities are obtained from corresponding radiometric quantities by taking into account the relative spectral responsivity of the human vision. This is calculated by spectrally weighting the radiometric quantity with the luminous efficiency function V(λ), which describes the relative spectral responsivity of the human eye under daylight conditions [30]. Luminous efficacy η v, given in lumens per watt, is typically used to assess the energy efficiency of a light source. It is defined as the ratio

$$ \eta_{\text{v}} = {{\varPhi_{\text{v}} } \mathord{\left/ {\vphantom {{\varPhi_{\text{v}} } P}} \right. \kern-0pt} P} , $$
(1)

where Φ v is the total luminous flux and P is the electrical power consumption of the lamp. Determining the luminous flux over 4π solid angle around the lamp requires the illuminance measurement over a small solid angle as a calibration procedure. In the absolute integrating sphere method, the luminous flux of the lamp to be measured is compared with an external luminous flux which is produced using a precision aperture and known illuminance [7, 8]. If an LED lamp is used as the external source, the PQED method can be used to measure its illuminance. Goniophotometers, on the other hand, determine the total luminous flux by measuring the illuminance of the light source at various solid angles [5, 6]. The illuminance responsivity of the detector used in the goniophotometer can be calibrated against the PQED.

For the PQED and aperture assembly, the illuminance can be calculated using the equation [9]

$$ E_{\text{v}} = \frac{{K_{\text{m}} Fi}}{{As\left( {\lambda_{ 0} } \right)}}, $$
(2)

where constant K m = 683.002 lm/W is the maximum luminous efficacy for photopic vision, i is the measured photocurrent, and s(λ 0) is the absolute responsivity of the detector at the V(λ) peak wavelength of λ 0 = 555 nm in standard air [30]. The effect of the drastic deviation between the spectral shapes of the V(λ) and the relative spectral responsivity of the PQED, s rel(λ) = s(λ)/s(λ 0) ≈ λ/λ 0, is corrected with the spectral mismatch correction factor

$$ F = \frac{{\int {\varPhi_{{{\text{e,}}\lambda }} \left( \lambda \right)V\left( \lambda \right)d\lambda } }}{{\int {\varPhi_{{{\text{e,}}\lambda }} \left( \lambda \right)s_{\text{rel}} \left( \lambda \right)d\lambda } }} , $$
(3)

were Φ e,λ (λ) is the spectral radiant flux of the lamp.

As seen in Eq. (2), the uncertainty in the measurement of the area A directly affects the uncertainty of the illuminance. In addition, the geometric area and the effective area of the aperture may differ, because the edge of any aperture is not infinitely thin. The angle of incidence of light hitting the aperture edge wall depends on the distance between the LED lamp and the aperture. However, if the distance between the lamp and the aperture is significantly larger than the diameter of both the aperture and the source—which is typically the case—the maximum glancing angle of the incident light is small. For example, in [9] the maximum glancing angle of the incident light is 0.06°. In such cases the deviation of geometric and effective area can be negligible.

2.2 Laser scanning method for the aperture area determination

The laser scanning method is described in detail in [18–20]. Therefore, only a brief introduction is given here. If an aperture is illuminated with spatially uniform known irradiance E e, and the radiant flux Φ e that passes through is measured, the aperture area can be calculated as

$$ A = {{\varPhi_{\text{e}} } \mathord{\left/ {\vphantom {{\varPhi_{\text{e}} } {E_{e} }}} \right. \kern-0pt} {E_{e} }}, $$
(4)

given that the aperture is placed perpendicular to the propagation direction of the light. The key point of the laser scanning method is that the known irradiance is produced by a superposition of equally spaced identical Gaussian laser beams. In practice this is accomplished by having an intensity-stabilized laser beam and moving the aperture—or in this case the aperture and PQED assembly—in front of the laser beam in horizontal (x) and vertical (y) directions. The radiant flux is obtained by summing the transmitted fluxes Φ j,k measured for each laser beam position (j,k)

$$ \varPhi_{\text{e}} = \sum\limits_{j = 1}^{{n_{x} }} {\sum\limits_{k = 1}^{{n_{y} }} {\varPhi_{j,k} } } , $$
(5)

where n x and n y are the number of steps in x and y direction, respectively. When assuming stable radiant flux Φ L for the laser beam, the total effective power of the laser beam grid is n x n y Φ L, and with step lengths of ∆x and ∆y for x and y direction, respectively, the total area of the laser grid is n x ∆xn y ∆y. When the side lengths of the grid, n x ∆x and n y ∆y, are much larger than the width of the laser beam and ∆x and ∆y are much smaller than the width of the laser beam, the irradiance near the center of the laser beam grid is obtained as

$$ E_{e} = \frac{{n_{x} n_{y} \varPhi_{\text{L}} }}{{n_{x} \varDelta xn_{y} \varDelta y}} = \frac{{\varPhi_{\text{L}} }}{\varDelta x\varDelta y} . $$
(6)

The exact derivation of Eq. (6) is presented in [19] for a relaxed requirement of the beam grid dimensions and general beam shape, not limited to a perfect Gaussian. For an aperture considerably smaller than the laser beam lattice, the aperture area can now be obtained by combining Eqs. (4, 5, 6):

$$ A = \varDelta x\varDelta y\sum\limits_{j = 1}^{{n_{x} }} {\sum\limits_{k = 1}^{{n_{y} }} {{{\varPhi_{j,k} } \mathord{\left/ {\vphantom {{\varPhi_{j,k} } {\varPhi_{\text{L}} }}} \right. \kern-0pt} {\varPhi_{\text{L}} }}} } . $$
(7)

The power of the laser beam can be measured with a separate detector, but it is far more convenient to use small enough beam to pass through the aperture entirely when positioned at the center of the aperture, and measure the ratios Φ j,k /Φ L with the PQED. It was estimated in [18] that relative throughput of 0.9999 requires the ratio of the aperture diameter D a and the e −2 diameter of the beam D b to satisfy the condition

$$ {{D_{\text{a}} } \mathord{\left/ {\vphantom {{D_{\text{a}} } {D_{\text{b}} }}} \right. \kern-0pt} {D_{\text{b}} }} \ge 2. 2. $$
(8)

It was also approximated that the beam diameter to beam grid step length ratio

$$ {{D_{\text{b}} } \mathord{\left/ {\vphantom {{D_{\text{b}} } {\varDelta x}}} \right. \kern-0pt} {\varDelta x}} \ge 2.8 $$
(9)

results in reasonably uniform illumination when the individual contributions are summed. Finally, when the above relations hold, the side length of the laser beam grid should be at least twice the aperture diameter. This guarantees that the detector receives no light from the outermost beams.

2.3 Rayleigh–Sommerfeld diffraction integral

The calculations in Sect. 2.2 do not take into account diffraction effects at the aperture edge. The diffraction theory discussed here considers only monochromatic scalar wave fields. A monochromatic scalar wave has the form

$$ V\left( {{\mathbf{r}},t} \right) = U\left( {\mathbf{r}} \right)e^{ - i\omega t} , $$
(10)

where r is the location vector, ω is the angular frequency of the wave, t is time and U(r) is the space-dependent part, which satisfies the Helmholz equation:

$$ \left( {\nabla^{2} + k^{2} } \right)U\left( {\mathbf{r}} \right) = 0 , $$
(11)

where k = 2πλ −1 is the wavenumber and λ is the wavelength. There are many methods to approximate the diffraction field. Given the dimensions of the problem in hand, where the size of the aperture and the detector are comparable with the distance between the two, the Rayleigh–Sommerfeld (RS) diffraction integral was considered to be the most suitable. For example, the conditions required for the suitability of the more simple Fresnel approximation do not hold [31]. If the aperture is located on the xy plane and centered on the z axis, the RS diffraction integral becomes [29]:

$$ U_{RS} \left( {x,y,z} \right) = \iint_{{\mathcal{A}}} {U\left( {x^{\prime},y^{\prime},0} \right)}\left( {\frac{1}{s} - ik} \right)\frac{{ze^{iks} }}{{2\pi s^{2} }}dx^{\prime}dy^{\prime} , $$
(12)

where \( s = \sqrt {\left( {x - x^{\prime}} \right)^{2} + \left( {y - y^{\prime}} \right)^{2} + z^{2} } \) and surface \({\mathcal{A}}\) corresponds to the aperture. By defining

$$ U_{0} \left( {x^{\prime},y^{\prime}} \right) \equiv \left\{ {\begin{array}{*{20}l} {U\left( {x^{\prime},y^{\prime},0} \right)} & {\text{if}} & {\left( {x^{\prime},y^{\prime}} \right) \in {\mathcal{A}}} \\ 0 & {\text{if}} & {\left( {x^{\prime},y^{\prime}} \right) \notin {\mathcal{A}}} \\ \end{array} } \right. , $$
(13)

and

$$ h\left( {x - x^{\prime},y - y^{\prime}} \right) \equiv \left( {\frac{1}{s} - ik} \right)\frac{{ze^{iks} }}{{2\pi s^{2} }} , $$
(14)

the convolution theorem can be used to rewrite Eq. (12) as

$$ \begin{aligned} U_{RS} \left( {x,y,z} \right) = & \int_{ - \infty }^{\infty } {\int_{ - \infty }^{\infty } {U_{0} \left( {x^{\prime},y^{\prime}} \right)} } h\left( {x - x^{\prime},y - y^{\prime}} \right)dx^{\prime}dy^{\prime} \\ & = {\mathsf{F}}^{ - 1} \left\{ {{\mathsf{F}}\left\{ {U_{0} \left( {x^{\prime},y^{\prime}} \right)} \right\}{\mathsf{F}}\left\{ {h\left( {x^{\prime},y^{\prime}} \right)} \right\}} \right\} \\ \end{aligned} $$
(15)

where \( {\mathsf{F}} \) denotes the two-dimensional spatial Fourier transform and \( {\mathsf{F}^{-1}} \) is the inverse Fourier transform. For RS diffraction integral, the latter Fourier transform can be calculated as [29]

$$ {\mathsf{F}}\left\{ {h\left( {x^{\prime},y^{\prime}} \right)} \right\} = \exp \left( {ikz\sqrt {1 - \lambda^{2} \left( {f_{{x^{\prime}}}^{2} + f_{{y^{\prime}}}^{2} } \right)} } \right) $$
(16)

where \( f_{{x^{\prime}}} \) and \( f_{{y^{\prime}}} \) are coordinates in the spatial-frequency domain. Finally, as evanescent waves are not taken into account, Eq. (16) is replaced in the calculations with transfer function

$$ H\left( {f_{{x^{\prime}}} ,f_{{y^{\prime}}} } \right) = \left\{ {\begin{array}{*{20}c} {\exp \left( {ikz\sqrt {1 - \lambda^{2} \left( {f_{{x^{\prime}}}^{2} + f_{{y^{\prime}}}^{2} } \right)} } \right)} & {{\text{if}}\begin{array}{*{20}c} {} \\ \end{array} \left( {f_{{x^{\prime}}}^{2} + f_{{y^{\prime}}}^{2} } \right) \le \lambda^{ - 2} } & {} \\ 0 & {\text{otherwise}} & {} \\ \end{array} } \right. . $$
(17)

Replacing the latter Fourier transformation of Eq. (15) with the transfer function is often referred as the angular spectrum method. However, in computer calculations it is not mandatory, as the Fourier transform can also be performed numerically. The pros and cons of both approaches are discussed in Sect. 3.2.

2.4 Gaussian laser beam

The field of a laser beam with an ideal beam quality can be expressed as a Gaussian beam which is a solution to the small-angle approximation of Eq. (11) [32]

$$ \left( {\frac{{\partial^{2} }}{{\partial x^{2} }} + \frac{{\partial^{2} }}{{\partial y^{2} }} + 2ik\frac{\partial }{\partial z}} \right)U\left( {\mathbf{r}} \right) = 0 . $$
(18)

The equation for the Gaussian field with amplitude U 0 is

$$ \begin{aligned} U_{G} \left( {x,y,z} \right) = \hfill \\ U_{0} \frac{{w_{0} }}{w\left( z \right)}\exp \left[ { - \frac{{x^{2} + y^{2} }}{{w^{2} \left( z \right)}}} \right]\exp \left[ {i\left( {kz + k\frac{{x^{2} + y^{2} }}{2R\left( z \right)} - \tan^{ - 1} \left( {\frac{z}{{z_{0} }}} \right)} \right)} \right] \hfill \\ \end{aligned} , $$
(19)

where the beam spot size w(z), the beam radius of curvature R(z) and Rayleigh range z 0 are given as

$$ w\left( z \right) = w_{0} \sqrt {1 + \left( {\frac{z}{{z_{0} }}} \right)^{2} } , $$
(20)
$$ R\left( z \right) = z + \frac{{z_{0}^{2} }}{z} , $$
(21)
$$ z_{0} = \frac{{\pi w_{0}^{2} }}{\lambda } . $$
(22)

The spot size w(z) corresponds to the distance from the z axis at z where the intensity has dropped by a factor of e −2, and w 0 is the spot size at the beam waist located at the z = 0 plane.

The beam profile of some lasers may deviate significantly from the ideal profile shape. In such a case, spatial filtering can be used to improve the quality of the beam [18, 20, 28, 32]. In addition, the spot size of the beam can be simultaneously adjusted to meet criteria given in Eqs. (8) and (9) [28, 32]. For analysis of the scanning method and numerical simulations, perfectly Gaussian beam was assumed. However, it should be noted that to produce the uniform irradiance distribution, the beam profile does not have to be Gaussian or even symmetric [19].

3 Computer simulations of diffraction losses

3.1 Calculation procedure

Equation (16) is well suited for numerical evaluation, as instead of direct numerical integration of the diffraction integral for each observation point, Fast Fourier transform (FFT) [31, 32] can be used to compute the whole field at once. In the numerical calculation, the electric field is then represented by a matrix U where each element (U) ij has the value of the field at a corresponding coordinate (x i ,y j ). The electric field of a laser beam at the aperture plane is given by Eq. (19) and the center of the beam is cycled through the points in the beam scan grid. In the case of a plane wave illuminating the aperture, the electric field value is just a constant for the entire aperture plane. The aperture matrix A and detector matrix D are represented in such a way that the elements have value 1 within the aperture or the detector, respectively, 0.5 at the edges and 0 otherwise. The field going through the aperture is then obtained by element-by-element multiplication of U and A (denoted here with the symbol \(\circ\)) and the diffracted field Q is calculated according to Eqs. (15) and (17) with two-dimensional FFT and inverse FFT, denoted by IFFT,

$$ {\mathbf{Q}} = {\text{IFFT}}\left( {{\text{FFT}}\left( {{\mathbf{U}} \circ {\mathbf{A}}} \right) \circ {\mathbf{H}}} \right) $$
(23)

where H is defined by Eq. (17). Finally, the field at the detector is obtained as \( {\mathbf{Q}} \circ {\mathbf{D}} \), from which the relative irradiance matrix can be calculated as the square of the absolute value of the elements. For the assessment of total diffraction loss, the total detected radiant flux is calculated by performing a two-dimensional trapezoidal numerical integration over the detector area.

3.2 Sampling

Since numerical calculations use a finite number of grid points to represent the aperture and observation plane fields, one must pay attention to proper sampling to avoid numerical errors in the calculation. When FFT is used, the number of points N is selected as a power of 2 to optimize the algorithm. The Nyquist sampling criterion states that if f max is the maximum (spatial) frequency with which the field changes in the sampling space, the aliasing is avoided when the sampling step δ in the sampling window satisfies the condition \( 2\delta \le f_{\hbox{max} }^{ - 1} \). However, since the aperture is finite in its extent, the Fourier transform of the field at the aperture has infinite extent in the spatial-frequency domain [33]. Therefore, the Nyquist criterion for sampling the \( U_{0} \left( {x^{\prime},y^{\prime}} \right) \), given in Eq. (13), can never be truly met.

When the size of the sampling window is N × N, the width of the window is L = Nδ. The size of the sampling window is the same for both \( U_{0} \left( {x^{\prime},y^{\prime}} \right) \) and \( H\left( {f_{{x^{\prime}}} ,f_{{y^{\prime}}} } \right) \), but the latter is sampled in the spatial-frequency domain, where sampling step is \( \delta_{f} = L^{ - 1} \) and the width of the window \( L_{f} = N\delta_{f} = \delta^{ - 1} \). The Nyquist criterion in sampling \( H\left( {f_{{x^{\prime}}} ,f_{{y^{\prime}}} } \right) \) gives an approximate lower limit for δ [34]

$$ \delta \ge \sqrt {\frac{\lambda z}{N}} . $$
(24)

Then again, increasing the sampling step δ increases aliasing in computing the FFT of \( U_{0} \left( {x^{\prime},y^{\prime}} \right) \) and decreases the extent of the sampling window in the spatial-frequency domain L f. Thus, selecting the sampling step is a compromise between the two.

The limit given in Eq. (24) could be avoided by calculating \( {\mathsf{F}}\left\{ {h\left( {x^{\prime},y^{\prime}} \right)} \right\} \) numerically instead of using the analytical solution given in Eq. (16). However, an accurate calculation in the geometry of the PQED and the aperture would require larger number of sampling points [34] and one additional FFT, resulting in significantly longer computation times. Therefore, the calculation procedure described in Sect. 3.1 was used. The width of the sampling window L and number of sampling points N were selected to be 12 mm and 4096, respectively. This selection results in a step size around δ ≈ 3 µm, which should be small enough to properly sample the beam fields which—apart from the aperture edge—vary rather slowly. Moreover, the selection also satisfies the transfer function sampling condition given in Eq. (24).

3.3 Simulation geometry and parameters

The geometry of the aperture diffraction problem is shown in Fig. 3. Default values, given in Table 1, are used in the simulations unless otherwise noted. The diameter of the circular aperture D a is selected to be 3 mm to match the diameter used in the illuminance measurements with the PQED [9, 10]. The shortest mechanically practical distance between the detector and the aperture is d = 20 mm. The detector edge length h = 10 mm corresponds to the cross section of the transverse dimensions of the PQED photodiodes in the wedged trap configuration (see Fig. 1). The cross section is approximately square in shape. The reliability of the calculation procedure and sampling conditions applied to the geometry of Fig. 3 is assessed in “Appendix”.

Fig. 3
figure 3

Geometry of the aperture diffraction simulation

Full size image
Table 1 Default values used in the simulations
Full size table

The laser used in the setup is assumed to be a HeNe laser with wavelength in air of 632.8 nm. The selected beam size and step size in the scanning are selected based on Eqs. (8, 9). However, the laser spot size at beam waist w 0 and the waist-to-aperture distance d w are not exactly known in practice. Therefore, the spot size at the beam waist was defined to be 0.999765 times the spot size at the aperture. This in turn results in waist-to-aperture distance d w = 50 mm. These values are assumed to be reasonable for a rather well collimated laser beam.

The resulting laser scan grid based on values of Table 1 is illustrated in Fig. 4. Together the 289 beams form a spatially uniform illumination at the aperture, as shown in Fig. 5. To reduce the computational time, the largest beam grid step size to meet the condition in Eq. (9) was used. For the actual measurement of aperture area, a smaller beam grid step size can be used if better uniformity is required.

Fig. 4
figure 4

Laser beam scan grid. The red dots show the grid, the red circle shows the beam size and the black circle marks the aperture

Full size image
Fig. 5
figure 5

Sum of the laser beam intensities at the aperture. The amplitude of each individual beam is 1

Full size image

3.4 Simulation results

The intensity at the aperture and calculated diffraction pattern at the detector for a single laser beam hitting the edge of the aperture, as in Fig. 4, is shown in Fig. 6a, b, respectively, whereas the combined diffraction pattern of all the laser beams and the plane wave diffraction pattern are shown in Fig. 7. The patterns for the laser beams and the plane wave have been made comparable by normalizing them with the total energy integrated at the aperture. It is remarkable how the two different situations produce considerably different diffraction patterns, as shown in Fig. 7a, but the intensities in the shadow area of the detector, as shown in Fig. 7b, are almost identical, and virtually all intensity seems to fall on the detector.

Fig. 6
figure 6

Relative irradiance at the aperture (a) and diffraction pattern at the detector (b) for a single laser beam hitting the edge of the aperture

Full size image
Fig. 7
figure 7

Sum of laser beam diffraction patterns (red) and plane wave diffraction pattern at the detector (blue) over full detector area (a) and zoomed to the shadow area (b)

Full size image

The diffraction losses were calculated for different aperture sizes up to 6 mm at aperture-to-detector distances of 20 and 33 mm. The latter distance corresponds to the detector assembly used in the previous illuminance measurements. The laser beam radius, waist distance, and beam grid step were changed accordingly while other parameters were kept the same. The results of these calculations are shown in Fig. 8. For the aperture-to-detector distance of 20 mm, the relative diffraction losses are less than 10−5 for all modeled aperture diameters. For the distance of 33 mm, apertures 3 mm or less in diameter have similarly small losses, but larger apertures have higher diffraction losses up to 10−4. However, the difference between diffraction losses of the combined laser beam grid and plane wave diffraction is less than 10−6.

Fig. 8
figure 8

Calculated diffraction losses for different aperture diameters at the aperture-to-detector distances of a 20 mm and b 33 mm

Full size image

The aperture area is determined using monochromatic laser beam, but in the photometric measurements the light source is broadband. Therefore, also the wavelength dependence of the diffraction loss was calculated for an overfilling plane wave. The results are shown Fig. 9. For the aperture-to-detector distance of 20 mm, the wavelength dependence is insignificant, less than 10−7 for most of the visible wavelength range. At the distance of 33 mm, the diffraction losses increase rapidly for wavelengths longer than 600 nm; at wavelengths around 800 nm the diffraction losses are around 10−4.

Fig. 9
figure 9

Calculated diffraction losses for a plane wave as a function of wavelength

Full size image

4 Anticipated uncertainty

Using the original laser scanning method, a standard uncertainty of 0.013 % has been demonstrated for the area determination of an aperture 3 mm in diameter [19]. This uncertainty was dominated by the uncertainty of the length scale in the linear translator movement, which was checked with an interferometer measuring the displacement of a corner-cube reflector fixed to the moving carriage. The largest deviations between the nominal and true distances were about 300 nm, measured over 6 mm movement of the linear translator. Since then improved linear translator resolutions and smaller uncertainties for length scale have been demonstrated. For example, in [22] systematic uncertainty in the readings of the stage position was estimated to be 2.6 × 10−6 times the travel, and the random uncertainty in stage position was around 20 nm. In addition to the length scale accuracy, one has to take into account the non-orthogonality of the axes [20, 25] and the cross-coupling between the linear stages through roll, pitch and yaw straightness [25]. It is also important that the plane of the position measurement is the same as the plane where the aperture is located. This can be achieved by right selection of the corner-cube reflector position in the interferometer measurement. With improved length scale measurement and precise alignment, a standard uncertainty below 0.01 % can be anticipated for the area determination of an aperture 3 mm in diameter using the upgraded laser scan method.

For illuminance measurements of white LED lamps, a standard uncertainty of 0.13 % has been demonstrated [10]. Here the uncertainty was mainly due to uncertainty of aperture area and uncertainties arising from the determination of the spectral mismatch correction factor of Eq. (3). Using the upgraded method, the aperture area would be scanned in identical geometry as the illuminance measurement. If the distance between the detector and the aperture is around 20 mm, the diffraction losses are insignificant in both cases, and for longer distances they can be corrected. Therefore, one can safely assume that a standard uncertainty around 0.1 % could be achieved for illuminance measurement using the PQED. For this value, other uncertainty components are estimated as given in [10].

The increased accuracy of the illuminance measurement using the PQED translates directly into a reduced uncertainty in luminous efficacy. Further, when an LED lamp is used as the external source in the calibration procedure of the integrating sphere, the uncertainties due to spectral mismatch are also reduced [10]. These improvements in the measurement of luminous flux and recent improvements in the measurement of the electrical power [35, 36] are discussed in [37]. After implementing these improvements and the reduced uncertainty of illuminance measurement due to improved aperture area measurement discussed in this paper, an uncertainty around 0.5 % (k = 2) in the luminous efficacy measurement of LED lamps could be achieved.

5 Conclusions

The uncertainty in photometric measurements of LED lamps can be improved with the PQED-based realization of photometric unit. However, determining the area of the aperture used with PQED still remains as one of the most critical factors affecting the measurement uncertainty. To address this issue, an upgrade to an existing optical method for direct determination of aperture area was developed. In the upgraded method, the aperture and PQED assembly is transversely scanned relative to an intensity-stabilized Gaussian laser beam. This effectively forms a two-dimensional superposition of laser beams with uniform irradiance distribution. The aperture area can be calculated by measuring the light passing through the aperture at each position with the PQED. The method is very beneficial in cases where the PQED is used with the aperture, such as photometric measurements, as measurement of the aperture area does not require removing the aperture from the PQED. Such dismantling and separate measurement would produce a significant risk of either dust contamination of the PQED or damaging of the sharp aperture edge. Furthermore, the uncertainty due to aperture alignment is decreased as the geometry is identical in both the laser scanning of the aperture area and in the actual measurement.

To estimate the differences between the diffraction effects of the overfilling plane wave and of the combination of Gaussian laser beams at the aperture, a numerical calculation method based on the Rayleigh–Sommerfeld diffraction integral was applied to the geometry of the PQED and aperture assembly. Simulation results for different aperture sizes and two different distances between the aperture and the detector are presented. The results indicate that diffraction effects are insignificant when the distance between the aperture and the photodiodes of the PQED is around 20 mm. At the distance of 33 mm, the diffraction losses for both the plane wave and laser beams increase at larger aperture diameters, but due to identical geometry in the aperture area determination and actual measurement, the difference between the two decreases, as seen in Fig. 8b.

In practice, the cross section of the aperture edge consists of two rounded corners and a rough wall area between the corners. The rounded corner facing the incoming light may produce deviation between the geometrical and effective area of the aperture. Mechanical contact methods, for example, measure the geometrically shortest distance between opposite points on the aperture wall, but due to the rounded corner and high glancing reflectance, the detector behind the aperture may collect light from a larger effective area than the area determined by the geometrical aperture diameter measurement. Surface roughness of the aperture edge can cause a similar deviation between the geometrical and effective aperture area, especially for light propagation directions deviating slightly from the optical axis. When the aperture is permanently fixed to the detector and the upgraded method of this paper is used for the aperture area measurement, the light collection geometry will automatically take into account the effective aperture area in the illuminance measurement.

The simulations assume the aperture to be perfectly circular within the step size of the grid of δ ≈ 3 µm. The deviations from an ideal circle have the same order of magnitude as the edge roughness of high quality apertures, which is in the scale of few micrometers [23, 24]. As described by Eq. (A1) of “Appendix”, diffraction features on the optical axis can be described as interference of elementary spherical waves originating at the center of the aperture and close to the edge of the aperture. The phase difference between the center and the edge remains below π within a rim of width 4 μm close to the edge in the conditions of Figs. 7a and 10. It is thus suggested that any deviation from an ideal circular aperture of that magnitude would reduce such sharp features close to the optical axis as shown in Fig. 7a. The effect of scattered light from imperfect edges on the diffraction losses is thus assumed to be insignificant, as the total diffraction losses are mostly less than 10−4 and the diffraction patterns have very little sharp features in the shadow area.

Fig. 10
figure 10

Normalized irradiance on z axis for a plane wave diffracted by a 3 mm circular aperture calculated using the numerical method (blue line) and analytical solution of Eq. (A1) (red line)

Full size image

The incident light was assumed to be a plane wave or perfectly Gaussian laser beam in the diffraction calculations. The former assumption is sufficient for a distant source. The latter can be adequately achieved using beam shaping optics and characterizing the conditions with a beam profiler [28]. Future work could include diffraction calculations for irregularly shaped or jagged-edge apertures and for sources that are not adequately approximated with the plane wave. Matching of the angular divergence of the detected LED light and the Gaussian laser beam would yield identical conditions for scattering at the edge walls. These effects can be studied by modifying the aperture matrix A and by calculating the electric field matrix U for a more suitable source at a given distance, respectively.

It was estimated that a standard uncertainty below 0.01 % could be achieved for the area determination of an aperture 3 mm in diameter using the upgraded laser scan method. This estimate is based on the uncertainty demonstrated for the original laser scanning method, improvements in linear translator resolution and in the determination of the length scale demonstrated since, and the diffraction calculations conducted in this paper. The improved uncertainty of the aperture area determination would result in standard uncertainty around 0.1 % for illuminance measurement of LED lamps using the PQED method. Finally, it was estimated that an uncertainty around 0.5 % (k = 2) could be achieved for the luminous efficacy measurement of LED lamps by utilizing the PQED illuminance measurement as a calibration procedure in the determination of luminous flux together with the recent improvements in the measurement of the electrical power of the LED lamps.