1 Introduction

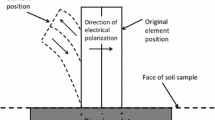
The bender element test is the most commonly used dynamic test in experimental soil mechanics. This test is used to measure small-strain, or “elastic” stiffness of soil. A bender element is a small plate made of piezoceramic material that deflects when a voltage is sent through it. Similarly when a bender element is moved, a voltage is generated. Pairs of these bender elements can be inserted into soil samples in standard soil mechanics tests (e.g. in a triaxial apparatus or an oedometer), as illustrated schematically in Fig. 1. During a bender element test a voltage is sent through the transmitter bender element; this produces movement, which in turn generates a seismic (stress) wave that propagates through the sample. The receiver bender element moves when the seismic wave reaches it. The induced movement causes a voltage to be produced and creates an electrical signal that can be read on an oscilloscope. During this process it is the seismic wave that propagates through the sample and generates the motion of the soil particles. There are two modes of propagation which are distinguished by the relative directions of oscillation and propagation. Compressional (P-) waves have particle motion parallel to the direction of propagation. Shear (S-) waves have particle motion perpendicular to the direction of propagation. The speed of propagation of the shear wave component, \(V_{S}\), is used to calculate \(G_{max}\), the small strain shear modulus as follows:

$$\begin{aligned} G_{\max } =\rho V_s^2 \end{aligned}$$
(1)

where \(\rho \) is the overall sample density. Application of Eq. 1 assumes the soil response is elastic. The use of bender elements to measure small strain stiffness was originally proposed by Shirley and Hampton [1], and use of bender elements in both commercial and research-orientated testing is now pervasive (e.g. Alvorado [2], Sadek [3], Kuwano and Jardine [4]).

Fig. 1
figure 1

Schematic diagram of a typical bender element test set-up in a triaxial cell apparatus

Full size image

To calculate \(V_{S}\) the travel distance and travel time of the shear component of the seismic wave must be known. The travel distance of the shear wave component is taken as the tip to tip distance between the transmitting and receiving bender elements. There is uncertainty surrounding the travel time determination, as outlined in references including Blewett et al. [5] and in the international comparative study organized by TC-29 of the International Society for Soil Mechanics and Foundation Engineering [6]. This uncertainty leads to challenges in the interpretation of the test data and the use of bender elements. The system is clearly complex; there is a point source of energy that then propagates through the sample and is measured at a single, point receiver. In a physical test uncertainty about the magnitude of the bender deflection and the nature of the contact between the bender element and the soil, amongst other issues, add to this complexity. There is therefore merit in creating simpler, numerical models of the system to isolate the various sources of complexity, motivating the continuum based numerical analyses of Arroyo et al. [7] and Rio [8]. While these studies have advanced understanding of the mechanics of bender element tests, they are restricted as they assume the material to be a solid continuum, and do not explicitly consider the particulate nature of soil.

This paper exploits the particle scale details that can be monitored in discrete element method (DEM) simulations to analyse the micromechanics of the response of an idealized granular material during a bender element test. Thornton [9] and Cui et al. [10] amongst many others have illustrated the use of DEM simulations to explore how the particle-scale interactions in a granular material directly affect the macromechanical response. To date, most DEM analyses in geomechanics and granular materials in general have considered quasi-static material response, however dynamic analyses are possible and a small number of researchers including Hazzard et al. [11], Li and Holt [12], Mouraille et al. [13] and Marketos [14] have used DEM to simulate wave propagation in both bonded (cemented) and unbonded (cement-free) granular materials. These prior research studies did not focus in detail however on the relationship between the wave propagation properties, such as wave speed, and the micromechanical properties, such as inter-particle contact stiffness and none of these studies focussed specifically on bender element testing.

The work presented here is a development of the earlier preliminary simulations by Carter [15] and Clement [16]. An ideal, relatively simple, system of hexagonally packed uniform disks was selected. Despite the ideal nature of the model used here the system response is complex, highlighting the pedagogical benefit of developing a fundamental understanding starting from consideration of a relatively simple system. The propagation of the wave was tracked by considering both the particle velocities and the representative particle stresses. Then four alternative methods to determine the wave travel time were compared, before exploring the relationship between the particle-scale DEM model parameters and the shear wave speed recorded. Given the widespread use of bender elements in research and industry and the challenges associated with their use, this study is timely.

2 Simulation approach

The numerical code used in this project was the commercial DEM code \(\text{ PFC}^\mathrm{2D}\) Version 3.1 (Itasca Consulting Group [17]). The sample consisted of 759 hexagonally packed uniformly-sized disks of radius 2.9 mm as illustrated in Fig. 2. A hexagonal packing is the densest packing that can be achieved for two-dimensional uniform circular disks and each disk had 6 contacts. This grain packing was previously considered, from a soil mechanics perspective, by Rowe [18], O’Sullivan et al. [19], and Velicky and Caroli [20]. The system is highly ideal, comprising uniform disks on a lattice packing and exhibits a mechanical response that differs from soil. Nevertheless, in an early study Thornton [21] showed convincingly that insight into the mechanical response of granular materials can be obtained by considering uniform spheres on lattice packings. Fundamental laboratory studies considering wave propagation through an idealised sand comprised of glass beads have been obtained by Jia et al. [22], Liu and Nagel [23], Liu [24] and Makse et al. [25]. In contrast to [22] our work considers only the initial, low frequency response. Furthermore, as the system has a homogeneous, lattice packing and so (within the limits of numerical precision) the contact force network is also effectively homogeneous and we cannot develop on the hypotheses of Liu et al. who examined preferential propagation along strong force chains. (Note that the effect of small geometrical perturbations of the lattice is considered by O’Sullivan et al. [19] and Velicky and Caroli [20].)

Fig. 2
figure 2

Illustration of DEM test sample configuration

Full size image

Also relevant is the analytical work of Santamarina and Cascante [26], who considered the stiffness of regular packings of monodisperse and polydisperse spheres. Their work included a review of the analytical relations between fabric, grain properties and the effective overall system for three-dimensional regular assemblies of uniform spheres. They observed similarities between the response trends predicted analytically for ideal systems and empirical relationships derived for real physical soils. Just as in the case of the work by [26], the system chosen for consideration here is very stable and, under small perturbations, there is no change in contact configuration, i.e. the material can be considered elastic as plasticity is associated with contact breakage and sliding (in the absence of grain breakage). Real granular materials are three-dimensional, however as argued by O’Sullivan [27], in fundamental research studies there is merit in restricting consideration to a two-dimensional system. The two-dimensional analogue is particularly useful here as particle motion is restricted to one plane, enabling clear visualisation and understanding of the wave propagation through the sample. In addition many researchers have demonstrated that invaluable insight can be gained from considering two-dimensional analogue models of real soil; the most notable contributions include Oda et al. [28], Kuhn [29] and Rothenburg and Bathurst [30].

The contact force model used here can be described by a linear spring acting in parallel with a viscous dashpot, both in the normal and shear directions (see [17]). The normal force due to the spring \(F_{n,sp}\) is given by \(F_{n,sp} =k_n\, \alpha \), and the increment in the shear spring force \(\delta F_{s,sp}\) is given by \(\delta F_{s,sp} =k_s \delta s\), where \(k_{n}, k_{s}\) are the normal and shear spring stiffnesses, \(\alpha \) is the grain overlap, and \(\delta \)s is the increment in contact shear displacement. The force due to the dashpot \(D\) is added to the spring force. The magnitude of this force, whose direction is always opposite to the velocity vector, can be calculated through \(D=2\beta \sqrt{mk}|V|\), where \(\beta \) is the critical damping ratio, \(m\) is the effective mass of the 2 grains in contact, and \(k\) is the contact spring stiffness and \(V\) is the (normal or shear) contact velocity. Table 1 gives the parameters used. While Hertzian contact mechanics shows that there is a non-linear relationship between force and displacement at elastic particle contacts, for small perturbations around the equilibrium position a Hertzian spring can be approximated by a spring with a stiffness equal to the tangent to the Hertzian curve at that point justifying the use of linear contact springs. The two-dimensional disks are assumed to have a unit thickness for the purpose of relating our two-dimensional system to three-dimensional elasticity equations. The sample was initially isotropically compressed to a stress of 1MPa using rigid wall boundaries on all four sides. Once this stress state had been achieved the side walls were removed and a numerical membrane was applied to simulate triaxial cell boundary conditions, as bender elements are most frequently deployed in triaxial test samples. The membrane algorithm used was detailed by Cheung and O’Sullivan [31]. Referring to Fig. 2 forces are applied to the particles located along the lateral sides of the sample to achieve the specified confining pressure, while allowing free deformation as in a physical triaxial test sample. These applied forces were maintained constant during the wave propagation simulation.

Table 1 The sample and bender element properties used for a representative bender element test on the DEM sample
Full size table

The issue of impedance mismatch between the boundaries and the sample has been previously examined by Lee and Santamarina [32] in an experimental setting. In their work the large impedance mismatch between the rigid top and bottom boundaries and the sample was used to reflect the waves several times inside the sample. In the work presented here there is large impedance mismatch at the top and bottom boundaries as the elastic spheres are encountering rigid walls. This results in almost full reflection of the wave from the walls. The impedance mismatch between the balls and the simulated flexible boundaries is much lower as the boundary is simply applied forces to the boundary particles. This leads to lower reflection from the lateral boundaries and more absorption of the energy as work against the boundary forces.

As in the preliminary simulations of [15] and [16] the bender elements were modelled as single disks. A disk near the base of the sample was chosen to be the transmitting bender element and a disk near the top of the sample was chosen to be the receiving bender element, as shown in Fig. 2. The input wave was simulated by applying a single-period sine pulse displacement to the transmitter disk. The amplitude of the motion was 12.5 \(\mu \)m, which is relatively small; the average overlap at the end of isotropic compression was of 6.65 \(\mu \)m. While different types of pulses can be used, (e.g. Jovicic et al. [33] used a square pulse); a single sine pulse is most commonly used and is recommended by TC-29 [6]. Figure 3 illustrates the transmitted and received signals for a representative bender element test simulation. In principle a bender element test is applied to an elastic system. Here particle displacements large enough to cause (plastic) irreversible sliding were only experienced in the immediate vicinity of the bender element.

Fig. 3
figure 3

Transmitted and received signal from a representative numerical bender element test carried out on the DEM sample, key points on the received signal used to calculate \(V_{S}\) are illustrated as is the arrival time predicted based on measurement of G in a static probe

Full size image

3 Overview of system response

The motion of the wave was tracked through the sample by measuring the particle-scale responses. Snapshots of the system response at selected points were created for the simulated bender element test shown in Fig. 3 and these are illustrated in Figs. 4, 5, 6, 7, 8 and 9. In Figs. 4 and 5 the particle velocities at 24 selected time points, labelled (a) to (x) are plotted as arrows, whose length is proportional to the magnitude of the particle velocity. Similarly Figs. 6 and 7 illustrate the normalised representative mean stresses acting on the particles at the same time points and Figs. 8 and 9 illustrate the relative representative particle shear stresses.

Fig. 4
figure 4

Particle velocities vectors for time points (a) to (l) where (a) represents the start of the bender element test and (l) represents a point that is 2.2 input wave periods (0.027 s) after start of test. The length of each arrow is proportional to the magnitude of the particle velocity

Full size image
Fig. 5
figure 5

Particle velocities vectors for time points (m) to (x) which are 2.4 and 4.6 input wave periods (0.030 and 0.057 s) respectively after start of test. The length of each arrow is proportional to the magnitude of the particle velocity

Full size image
Fig. 6
figure 6

Particles coloured according to normalised representative particle mean stresses, \(\langle {p^{p}} \rangle \) for time points a–l

Full size image
Fig. 7
figure 7

Particles coloured according to normalised representative particle mean stresses, \(\langle {p^{p}} \rangle \) for time points m–x

Full size image
Fig. 8
figure 8

Particles coloured according to relative representative particle shear stresses, \(\langle {s^{p}} \rangle \) for time points (a) to (l)

Full size image
Fig. 9
figure 9

Particles coloured according to relative representative particle shear stresses, \(\langle {s^{p}} \rangle \) for time points (m) to (x)

Full size image

It should be noted that as the stress distribution within the particles is obviously heterogeneous the representative particle stress tensors \(( {{\overline{\sigma }}_{ij}^p })\) were calculated in \(\text{ PFC}^\mathrm{2D}\) by considering the contact forces that act on each particle following Potyondy and Cundall [34], as follows:

$$\begin{aligned} \overline{\sigma }_{ij}^p =\frac{1}{V^{p}}\sum _{c=1}^{N^{c,p}} {f_j^c x_i^c } \end{aligned}$$
(2)

where, \(f^{c}\) represents the contact force at location \(x^{c}, V^{p}\) is the volume of the particle and \(N^{c, p}\) is the number of inter-particle contacts that act on particle \(p\). The representative mean stress for each particle \((p^{p})\) in a two-dimensional system is then given by \(p^{p}=\frac{\bar{{\sigma }}_{ii}^p }{2}=\frac{\bar{{\sigma }}_{xx}^p +\bar{{\sigma }}_{yy}^p }{2}\). The individual representative particle mean stresses were normalised by the initial representative mean stresses for the same particle, \(p^{p}_{0}\), just before the bender element test was carried out when the system was in equilibrium under the applied isotropic confining pressure [point (a)—the origin of the time axis in Figs. 4, 5, 6, 7, 8 and 9). These normalised stresses, \(\langle {p^{p}} \rangle =\frac{p^{p}}{p^{p}_0 }\), were used to isolate the effect of the stress wave on the particle stresses from the stresses induced by the applied confining pressure, which was kept constant for the duration of the test.

A representative particle shear stress was calculated as \(s^{p}=\frac{\overline{\sigma }_{ij}^p }{2}=\frac{\overline{\sigma }_{xy}^p +\overline{\sigma }_{yx}^p }{2}\). Note that when the system is in equilibrium and the particles are at rest, rotational equilibrium will require a symmetric stress tensor with \(\overline{\sigma }_{xy}^p =\overline{\sigma }_{yx}^p \) in the absence of boundary moments. However as the wave propagates through the sample the particles will move and no longer be in static equilibrium and so \(\overline{\sigma }_{xy}^p \ne \overline{\sigma }_{yx}^p \), and \(s^{p}\) will merely give an indication of the representative shear stress. The data presented in Figs. 8 and 9 are the relative representative particle shear stresses, \(\langle {s^{p}} \rangle \), i.e. \(\langle {s^{p}}\rangle =s^{p}-s_0^p \), where \(s_0^p \) is the representative particle shear stress before the bender element test is carried out. Using relative shear stress produced clearer images than normalised shear stress. The simulation can be considered to be quasi-static at the isotropic stress stage before the bender element test is begun. The shear stresses are subtracted from the shear stresses at the isotropic stress state before the bender element test is begun. Therefore any changes seen in the shear stresses on the plots are due to the wave propagation through the sample.

Lee and Santamarina [32] proposed that the transmitter bender element motion results in the cogeneration of a shear (S-) wave central lobe and compressional (P-) wave side lobes in the sample. Analysis of the particle velocities, the normalised representative particle mean stresses and the relative particle shear stresses allow exploration of this hypothesis.

During the duration captured in Fig. 4 the displacement of the transmitted particle causes a small amplitude seismic wave to develop in the sample. Figure 4b–d illustrates an S-wave circular lobe forming around the transmitter disk. This is indicated by the dominant horizontal orientation of particle velocities, i.e. orthogonal to the direction of wave propagation. In Fig. 4e, f it is clear that as this shear wave moves up through the sample a corresponding P-wave is developing at the sides of the sample. This compressional wave is illustrated as particle velocities which have a direction parallel to the direction of wave propagation. The net result is a complex, vortex-like motion within the sample, with the central particles moving from left to right and the outer particles moving vertically; to the right of the bender particle they move upwards, to the left downwards. The particles close to the right boundary of the sample have a horizontal velocity component directed away from the sample centre and a vertical component that is directed upwards. In the prior DEM simulations described by [12] a planar S-wave was input using a large body of particles as a transmitter. Particle velocity measurements also clearly showed a vortex-like pattern in the motion of the particles which were positioned further along the sample.

In Fig. 4g–l the propagation of the P-waves and S-wave through the sample is clearly illustrated as particles further up the sample start to move and multiple subsystems of interacting disks whose velocities form vortex-like patterns are observed. As the first shear wave moves further from the transmitter disk (Fig. 4g) a second shear wave is seen to develop behind it. As both the shear and compressional waves become more established it is observed that the compressional wave travels at a higher speed than the shear wave and leads the shear wave by Fig. 4k. The smaller amplitude of the P-wave makes it harder to observe than the S-wave. In Fig. 4j in the top half of the sample the particles towards the right side move upwards, while the particles towards the left side move downwards indicating the P-wave has propagated through the sample.

Figure 5 shows the time period from the point at which the previous Fig. 4l was generated to the arrival of both P- and S-wave at the receiver disk. The striking difference between Fig. 5m and x is the reduction in magnitude of the particle velocity. This loss in magnitude is a result of a loss of energy from the system. Some of the energy loss is due to the viscous damping model (a dashpot) used at the contacts in the simulation. The flexible boundaries on the lateral sides of the sample absorb some energy too as body work done by the applied forces in opposition to the boundary particle motion. These sources of energy dissipation are coupled with the geometric effects of energy radiating from a point source. The ability to observe this attenuation of the seismic wave by consideration of particle velocities in the sample during propagation is a feature unique to DEM. Throughout this latter stage of the simulation, the complexity of the response remains evident with multiple subsystems with vortex-like displacement patterns developing through the sample. The complexity of the response inhibits interpretation on the basis of affine and non-affine components of motion [25]; when this sample is deformed the significance of the non-affine motion will be greatly reduced due to the regular lattice packing used.

The plots of the normalised representative particle mean stresses \(\langle {p^{p}} \rangle \) in Figs. 6 and 7 complement the observations of particle velocities. Referring to Fig. 6b, the particles immediately to the right of the bender (moving to the right, with a positive x-displacement) experience an increased compressive stress as the bender moves to the right, while particles immediately to the left experience a decreased compressive stress. The anti-symmetrical nature of the response is more clearly visible than it was when considering the velocity vectors. When the motion of the bender particle reverses, Fig. 6d, the distribution of stresses reversed. Thus, immediately to the right of the now left moving bender particle, there is a zone of reduced compressive stress. Further to the left there is a transition to a zone of increased compressive stress as a consequence of the earlier bender movement to the right. At point (f) there is once again a reversal of the stresses as the bender is moving to the right from a time of 0.09 ms until the end of the period. From points (f) to (x) the stress response is more complex as the particle stresses respond to the particle motion.

The magnitude of the compressive stress is directly related to the strain energy and there is clearly an ongoing conversion of kinetic energy into strain energy and vice-versa as the wave propagates through the system. Energy loss can be observed in Fig. 7m–x as the light and dark patches become steadily less pronounced. Figure 7r clearly shows quite a number of alternating light and dark patches in the sample indicating continuing propagation of the disturbance inside the sample. By comparing Fig. 7r to the directions of the arrows in Fig. 5r a clearer picture of the seismic wave behaviour can be presented. The velocity data (Fig. 5r) indicate the presence of both S-waves and P-waves. P-waves are shown to be located primarily on the sides of the sample and S-waves are located in the centre of the sample. The velocities and stresses can be correlated to some extent; considering the counter-clockwise vortex just above the sample mid-height (Fig. 5r) the particles at the left of the sample move downwards and inwards, corresponding to an increase in mean stress (in comparison to the initial value), while the particles at the right move upwards and outwards, corresponding to a decrease in mean stress. A similar observation is made by comparing Figs. 5v and 7v, i.e. where the particles are moving inwards towards the sample centre there is an increase in mean stress and vice-versa.

Upon movement of the transmitter disk the magnitudes of the relative representative particle shear stresses \(\langle {s^{p}} \rangle \) are shown to change. Initially the observed magnitude of the shear stress increase spreads symmetrically from the transmitter disk (Fig. 8a, b). However, upon reversal of the disk motion direction (Fig. 8c, d) the response looses symmetry and becomes more complex. In response to the reversal of motion a second shear wave grows around the transmitter disk. By Fig. 8f a third shear wave is seen to develop and the transmitter disk now stops moving. Throughout the rest of Fig. 8 up to point (l) the propagation of the wave through the sample is observed. There is a concentration of shear stress in the centre of the sample and this can be explained by the central motion of the shear wave travelling through the centre of the sample as already discussed.

Figure 9 offers interesting insight into the arrival of the shear stress disturbance at the receiver disk. Regions of increased relative shear stress magnitude propagate through the sample. An initial region of non-zero relative shear stress magnitude is seen to arrive at the receiver disk at Fig. 9 somewhere between snapshots (o) and (n). This corresponds with the point at which a signal registers. However, a second zone of with larger relative shear stress magnitude is seen to arrive at appoint point (r). This corresponds to the first local minimum shown on the received signal which is taken as the arrival point when using the start–start method of travel time determination as outlined below. The seismic wave is seen to be heavily attenuated in Fig. 9 and the wave amplitude represented by the change in relative representative particle shear stresses is shown to decrease from Fig. 9m to x. The reduction in energy in the system has been explained above and the shear stress plot in Fig. 9 offers further proof of this loss of energy. Observation of Fig. 9m–x again highlights the complexity of the response, there now are a number of areas of increased shear stress propagating through the centre of the sample and along the sides.

4 Analysis of received signal

A representative received signal from a DEM simulation of a bender element test is given in Fig. 3. It bears similar characteristics to acoustical signals in a DEM sample measured by Garcia and Medina [35] and to the signal received during experimental tests; data from a representative experimental bender element test carried out by Viggiani and Atkinson [36] is shown in Fig. 10. Referring to Fig. 3 it is clear that a more complex signal was received than was transmitted, just as is observed in the physical test data in Fig. 10. The added complexity arose because there were a number of different waves and wave reflections influencing the receiver disk’s motion as has been shown in Figs. 4, 5, 6, 7, 8 and 9. The received signal that resulted from these different waveforms had a smaller amplitude when compared with the transmitted signal, see Fig. 3. This smaller amplitude was a consequence of energy dispersion or dissipation, both mechanical and geometrical as discussed above. When carrying out a physical bender element test a number of checks are recommended to ensure the quality of the test as outlined in [2] and [32]. These checks should also be applied to the test simulated in DEM. For example, the number of full shear wavelengths that occur in the sample, \(\text{ R}_\mathrm{d}\), should be above 4 and the \(\text{ R}_\mathrm{d}\) value in this simulation was 4.11. The value of wavelength, \(\lambda \), divided by \(\text{ d}_{50}\) should also be as high as possible. The value of \(\lambda /\text{ d}_{50}\) for this simulation was 8.44 which is reasonably high.

Fig. 10
figure 10

Representative experimental bender element signal from Viggiani and Atkinson [36]. The clean sinusoid A–B–C is the transmitted signal. A–A \(^{\prime }\) represents the travel time for the start–start method. B–B \(^{\prime }\) and C–C \(^{\prime }\) represent the travel time for alternative implementations of the peak–peak method

Full size image

When the bender element test was simulated using DEM, the sample was explicitly modelled as a multi-degree of freedom system. Trying to clearly identify and understand the different wave-forms present in the signal represents a significant challenge for this work and for experimental work carried out using bender elements. Care was taken in this fundamental study to ensure the system remained elastic and relatively low values of viscous damping were used. All the contacts in the system were continuously monitored to confirm that there was little or no slippage of particles in the system, except for the transmitter particle, and no change in coordination number (i.e. average number of contacts per particle). Slippage of particles leads to a permanent change in the arrangement of particles in the system resulting in a plastic deformation that will not be recovered. However, the small amounts of slipping particles (around the transmitter) are regained proving that any strain induced by the transmitter disk is reversible and that the system behaviour can be considered to be elastic.

5 Calculating \(\text{ G}_{\max }\) from bender element results

The data presented in Figs. 3, 4, 5, 6, 7, 8 and 9 indicate that the model can capture key elements of bender element response as observed in the laboratory and predicted from continuum analyses. The idealised nature of the system considered here (i.e. elastic system, perfect contact between bender element and tested material) makes it well-suited to use in a fundamental study on how best to interpret bender element data. To calculate \({G}_{max}\) using Eq. 1 it is necessary to know the overall sample density \((\rho )\) and the S-wave velocity \((V_{S})\). The sample dimensions were used to calculate the sample area and using this area and the summation of the individual masses of the particles the overall sample density was calculated as:

$$\begin{aligned} \rho =\frac{A_{solids} \times \rho _{solids} }{A_{total} } \end{aligned}$$
(3)

To calculate \(V_{S}\) the travel distance and travel time must be measured. The travel distance was given by the distance between the receiver and transmitter disk centroids, which are marked on Fig. 2. Determining the travel time was less straightforward, as has been discussed by [36] amongst others. Different methods can be used to identify the arrival of the shear wave and these include start–start (or point of first inflection), peak–peak and cross-correlation. Researchers who have explored measuring seismic wave velocity and have demonstrated prior use of the methods considered here include Jovicic and Coop [37]; Arulnathan et al. [38] and Alvarado [2].

The travel time determination methods that were considered in the current study are:

  1. a.

    Start–start,

  2. b.

    Peak–peak,

  3. c.

    Signal decomposition.

  4. d.

    Cross-correlation of signals,

The \(\text{ G}_{\max }\) obtained for each method was compared with the \(\text{ G}_\mathrm{max }\) measured in a biaxial compression test on the same sample configuration.

5.1 Start–start

This method has also been referred to as the point of first inflection method and was used by [37] amongst others. The start of the S-wave at the receiver, and thus the arrival time, is taken to be the point of first local minimum. Figure 3 illustrates the point of first local minimum on the received signal. The travel time is then taken as the time difference between the start of the transmitter signal and this arrival time. On Fig. 10 it is the time difference between points A to A\(^{\prime }\). The theory behind this method is that the initial deflection is the arrival of the faster P-wave and the change in direction of the received signal marks the arrival of the S-wave. However, as experimentalists have not been able to track the waves propagating through the sample this differentiation between P- and S-wave arrivals is hypothetical. To date, use of this method can only be justified by the fact that it has been used many times and on many different samples and has often given reasonably accurate results. As outlined above in the discussion related to Fig. 9 there seems to be some correlation between the magnitude of the relative shear stresses and the received signal. This is preliminary evidence that there is a rationale for using this method, however further analyses considering more complex configurations (random assemblies of 3D particles) is needed.

5.2 Peak–peak

This method involves analysis of both the transmitted and received signals. The peak–peak travel time is taken to be the time difference between a peak on the transmitted signal and its equivalent peak on the received signal. As illustrated in Fig. 3 the location of the equivalent peak on the received signal is often not clear. For example, referring to Fig. 10, there are two possible peak–peak measurements i.e. B to B\(^{\prime }\) and C to C\(^{\prime }\). In previous studies, such as Leong et al. [39], the equivalent peak has been taken to be either the first peak on the received signal or the maximum peak on the received signal. Often these different peaks represent a large difference in the computed travel time. This method offers the advantage that identification of a peak is not affected by noise in the received signal but its use is difficult to justify due to this ambiguity.

5.3 Signal decomposition

A complete decomposition of the received signal is a simple method for determining the travel time of the shear wave in the sample that is not widely used. A fast fourier transform (FFT) was performed on the signal of Fig. 3 in Matlab. The FFT essentially calculates the amplitudes (\(A\)) and phase angles \((\phi )\) of the constituents of the signal if this was to be expressed as a sum of a number of sinewaves of different frequencies \((\omega )\).

When using this method care needs to be taken so that the sampling rate used for the output signal is not too low. The signal was sampled with a period \(\text{ T}_\mathrm{sampling }\) which here is directly related to the mechanical timestep of the DEM simulation (constant in this case). The mechanical timestep needed to be small enough to ensure that the received signal could be plotted as a relatively smooth waveform. If it was too large the waveform would appear too jagged and it would not be possible to accurately decompose it to its constituent parts, as the largest frequency that can be calculated with the FFT is equal to half the sampling frequency. The mechanical timestep chosen here was therefore significantly smaller than the critical time step required for stable DEM analysis.

The resultant waveforms were then plotted together on Fig. 11 in order to compare the frequencies and amplitudes of each of the constituent cosine waves. The constituent parts can be summed together to inspect the validity of the decomposition. If the waves summed to a good approximation of the original signal then the signal decomposition was considered accurate enough. The decomposition was successfully validated by selecting the lowest 15 frequencies to represent the majority of the signal’s amplitude. Figure11 includes the received signal, the 5 cosine waves with the lowest frequencies as well as summation of the 15 cosine waves with the lowest frequencies. The wave with the largest amplitude was taken to represent the waveform from the transmitted signal. In this case it was the waveform with the third lowest frequency, \(\omega _{3}\). The point where this waveform first crosses the x-axis represents the arrival of this waveform at the receiver end of the sample.

Fig. 11
figure 11

A plot of the received signal and the five constituent waveforms with the five lowest frequencies for the numerical bender element test simulation considered in Figs. 3, 4, 5, 6, 7, 8 and 9

Full size image

In using the signal decomposition approach care must be taken to ensure an accurate result. Specifically an appropriate length of signal should be considered in the decomposition. Here the signal length selected was the maximum time period for which the first 15 components, when summed together accurately captured the signal upon inversion. The amplitudes and phases of the summation and of the original received signal were compared and the decomposition was considered valid as the percentage errors were smaller than 10 % in either of these checks. This check ensured that the received signal was decomposed to a high degree of accuracy and gave confidence in the arrival time which was subsequently determined from this method. It should be noted that this technique seems to work well, but as it seems not fully justified theoretically more research is required on this topic.

5.4 Cross-correlation method

The cross-correlation method is a more conventional use of the fast Fourier transform in signal analysis and has been proposed in a number of papers. Implementation of the method in the current study followed the procedure outlined in [36] and [38]. As in method (c) the sampling rate, \(\text{ T}_\mathrm{sampling}\), can affect the accuracy of the cross-correlation method. \(\text{ T}_\mathrm{sampling}\) should be as low as possible so that all the relevant constituent waves are included in the decomposition. A discrete fast fourier transform (FFT) of both transmitted and received signals was computed. These two FFT’s were divided and then an inverse FFT of the result was taken. This represents the cross-correlation function which was then plotted in Fig. 12. The absolute maximum of this function was taken to represent the point of arrival of the predominant wave-form and that represents the travel time of the shear wave in the sample. The shear wave is generally considered by those using bender elements to be the predominant wave-form at the receiving end as this is the wave-form that is input to the sample by the transmitter element. The implementation of the cross-correlation function used here was validated against code developed and used by [2] on experimental bender element signals.

Fig. 12
figure 12

The cross-correlation function plotted as a function against time for the numerical bender element test simulation considered in Figs. 3, 4, 5, 6, 7, 8 and 9

Full size image

6 Calculating \(\text{ G}_{\max }\) from biaxial compression test

A static biaxial compression test to find a reference \({G}_{max},\) and using Eq. 1 a reference \(V_{S}\), was performed on the sample of disks. The boundary conditions were identical to those used in the bender element test, and the transverse stress was kept at a constant value. The top rigid wall platen was moved vertically down at a constant velocity until a set axial strain value was reached. From a biaxial compression test it was possible to plot deviator stress, \(q\), versus axial strain, see Fig. 13. It is a straight line as a linear elastic contact model is used and there was no slippage at the particle contacts. The slope of this graph gave a value for Young’s Modulus, \(E\).

$$\begin{aligned} E=\frac{dq}{d\varepsilon _{axial} } \end{aligned}$$
(4)

where \(q\) is the deviatoric stress \((\sigma _\mathrm{y}-\sigma _\mathrm{x})\) and \(\varepsilon _\mathrm{axial}\) is the axial strain during the compression test. Comparison of this type of static probe with bender element data was also carried out by Sadek [3].

Fig. 13
figure 13

A plot of q versus axial strain where \(\text{ q} = \sigma _{y}-\sigma _{x}\) and a plot of transverse strain versus axial strain

Full size image

By monitoring the transverse strain during the simulation it was possible to plot transverse strain versus axial strain on Fig. 13. The Poisson’s ratio, \(\upsilon \), was calculated using Eq. 5:

$$\begin{aligned} \upsilon =-\frac{d\varepsilon _{trans} }{d\varepsilon _{axial} } \end{aligned}$$
(5)

where \(\varepsilon _{trans}\) is the transverse strain during the compression test. In order to calculate a Poisson ratio value the axial versus transverse strain curve was approximated by a straight line. The calculated Poisson ratio was very small (0.0035), but this is expected due to the regular packing of the sample, and the fact that the normal and shear spring stiffnesses are identical. The extremely low values of Poisson’s ratio mean that any changes in Poisson’s ratio due to non-linearity will lead to negligible differences in the calculation of \({G}_{max}\). The values of Young’s modulus and Poisson’s ratio were used to calculate \({G}_{max}\) for the sample using Eq. 6:

$$\begin{aligned} G_{\max } =\frac{E}{2(1+\nu )} \end{aligned}$$
(6)

7 Results

A parametric study in which the DEM model parameters (contact stiffness, particle density and viscous damping coefficient) were systematically varied was carried out to assess the influence of these parameters on the wave propagation velocity and to compare the various options available for travel time determination. The frequency of the input signal was also adjusted as different frequencies are often used in physical bender element tests.

The “base case” of simulation parameters, are listed Table 1. Then the chosen parameter was adjusted separately, maintaining the other parameters at the base value. Both the normal and tangential stiffness’s were kept equal to one another when varied from the “base case” value. The results for varying contact stiffness are shown in Table 2 and Fig. 14a. Considering Table 2, there are some large percentage errors in the results obtained from the different methods. Such large errors have been previously observed in studies such as TC29 [6], Hardy [40] and Greening et al. [41]. In [6] a large dataset of tests on one sand type was prepared, different travel time determination approaches were used and for a given void ratio differences in the calculated \(G\) value were as large as 50 %. In [40] a reference \({G}_{max}\) is calculated from the input parameters of the finite difference model, \(E\) and \(\nu \). When travel times for a parametric study on bender element input frequency were calculated errors exceeding 20 % were noted when using the start–start method of travel time determination for a signal of a given frequency. When the frequency domain method was used, namely the phase sensitive detection method, these errors could rise to be as much as 140 %. Greening et al. [41] reported differences of as much as 30 % between shear wave velocity measurements obtained using first arrival time and frequency domain methods. As \(G_{max}\) is proportional to \(V_{S}^{2}\) any difference in travel time determination provides a much larger difference in \({G}_{max}\) values. The variation in the measured shear wave velocity \((V_{S})\) as a function of the interpretation approach used show the values for the signal decomposition method to be the most consistent and are within 10 % error of the value for \(\mathrm{G}_{\max }\) measured using biaxial compression on identical samples.

Table 2 Comparison of values of \(\text{ G}_{\mathrm{max}}\) calculated from the bender element test using different travel time determination techniques for three different inter-particle contact spring stiffness’s with the \(\text{ G}_{\mathrm{max}}\) value obtained in a static probe
Full size table
Fig. 14
figure 14

Results for a parametric study carried out on the DEM sample. a \(\text{ V}_\mathrm{S}\) versus \(\surd \)K, (K is the inter-particle contact spring stiffness); b \(\text{ V}_\mathrm{S}\) versus \(1/\surd \rho \), (\(\rho \) is the particle density); c \(\text{ V}_\mathrm{S}\) versus viscous damping ratio; d \(\text{ V}_\mathrm{S}\) versus bender element frequency

Full size image

The \({V}_{S}\) values were used as the metric to assess the sensitivity of the system response to the input parameters. The travel time values used were those obtained using the signal decomposition method which had been proven to be the most accurate method. As would be expected for this elastic system, referring to Fig. 14a, b \(\mathrm{V}_\mathrm{S}\) was proportional to the stiffness, \(\surd K\) (where \(K = k_{n} = k_{s})\) and inversely proportional to \(\surd \rho \). Considering the sample to be a system of particles connected by springs of stiffness \(K\), it is reasonable to expect that the overall shear stiffness, \(G\), would be linearly proportional to the root of the contact stiffness, \(\surd K\). The linear relationship between \(V_{S}\) and \(1/\surd \rho \) was also expected as a consequence of Eq. 1. For low values of viscous damping, \(<\)0.01, the system response appeared relatively insensitive to damping and this can be seen in Fig. 14c. However at larger damping values, the measured \(V_{S}\) values were indeed sensitive to viscous damping. Finally the effect of bender element frequency on shear wave speed was explored. The results for this study can be found in Fig. 14d. The sensitivity to frequency might be due to the use of the viscous damping model at the contacts. Viscosity at the inter-particle contacts leads to dispersion of the signal as it travels through the sample as outlined in Sadd et al. [42]. This dispersion can be observed in Fig. 3 as the received signal is “broader” than the transmitted signal.

8 Conclusions

Bender element tests are important in soil mechanics research and geotechnical engineering practice as a means to measure the small strain stiffness of soil. Uncertainties exist regarding bender element test interpretation and there is merit in looking at the fundamental mechanics of this test in detail. Here, a simple, idealised, elastic system of disks was considered. The DEM simulation data captured the main features of response that are observed in laboratory bender element tests. A key advantage of the two-dimensional DEM simulation was the ability to visually examine particle scale response to the bender element input wave. Examining this micromechanical data illustrated the wave propagation motion in a way that was previously not possible. The assumptions of [32] were seen to hold true for this two-dimensional case, however the response is highly complex. The reversal of the direction of the transmitter disk particle added to the complexity of the response. Circular shear wave lobes were seen to travel through the centre of the sample and P-wave lobes were seen to travel through along the sides of the sample. A relation was observed between the changes in shear stress and the received signal. Sub-systems of particles formed within the sample that interacted to generate vortex-like particle velocity patterns as has been observed in [12]. The particle velocities and representative particle mean stresses were linked; in general when the particle velocities were directed towards the centre of the sample the stress increased, and vice-versa.

Four different methods of travel time determination were critically assessed using DEM and many of the existing methods were shown to be unreliable even when applied to this very simple system. A new method, proposed here, involves the Fourier decomposition of a received signal as a means to determine the arrival time of the shear wave at the receiver disk. This method has shown promise and there is good agreement between results of this method and the results of a biaxial compression test on the sample. Further development is planned to test the rigour of this travel time determination method.